Nanoscopic interactions of colloidal particles can suppress millimetre drop splashing

Abstract

The splashing of liquid drops onto a solid surface is important for a wide range of applications, including combustion and spray coating. As the drop hits the solid surface, the liquid is ejected into a thin horizontal sheet expanding radially over the substrate. Above a critical impact velocity, the liquid sheet is forced to separate from the solid surface by the ambient air, and breaks up into smaller droplets. Despite many applications involving complex fluids, their effects on splashing remain mostly unexplored. Here we show that the splashing of a nanoparticle dispersion can be suppressed at higher impact velocities by the interactions of the nanoparticles with the solid surface. Although the dispersion drop first shows the classical transition from deposition to splashing when increasing the impact velocity, no splashing is observed above a second higher critical impact velocity. This result goes against the commonly accepted understanding of splashing, that a higher impact velocity should lead to even more pronounced splashing. Our findings open new possibilities to deposit large amount of complex liquids at high speeds.

---

The impact of a liquid drop is at the core of many natural or industrial processes.^1,2 With the recent developments of 3D-printing applications, more complex liquids are increasingly used, including nanoparticles dispersions³ or bio-materials.⁴ On top of the already challenging problem of splashing of Newtonian liquids, it is therefore important to consider the possible effects of the complex fluids on the deposition process. Some researchers have investigated drop impacts of complex fluids.⁵ Many of these studies focus on the maximum spreading diameter.^6,7 Some studies looking at the splashing of complex liquid drops have focused on preventing the drop from rebounding on a hydrophobic surface, after the retraction process.^8–14 Only few studies have demonstrated an effect of the complex liquid composition on splashing, namely during the expansion of the lamella.^15,16

Splashing is an important aspect of the impact dynamics, to determine whether the initial drop will break into smaller droplets or not. The splashing of the impacting drop can be beneficial for combustion application, to maximise the surface area, while it is detrimental for the accuracy of inkjet printing, or the spreading of chemicals on crops.^14,17,18 Splashing is expected to occur for all liquids above a critical impact velocity, called the splashing threshold. The work of Xu et al. (2005)¹⁹ showed that splashing could be suppressed by reducing the ambient pressure, for the first time demonstrating the key role of the ambient air. This led to a renewed interest in the problem of drop impact splashing, trying to propose new models taking into account the effect of air.

When the drop splashes onto the solid surface, it first ejects a thin liquid film radially.^20,21 The separation of this liquid sheet from the solid surface and its subsequent breakup lead to the formation of smaller droplets, and therefore splashing.¹ These observations have been combined into the model of Riboux and Gordillo (2014)²² for the impact of a low viscosity Newtonian liquid onto a smooth, partially wetting solid surface.^22–26 They explain the liftoff of the expanding lamella by the combination of a viscous lubrication force from the air in front of the contact line and an inertial aerodynamic Bernoulli suction force from the air above the edge of the lamella. Splashing can be predicted when this combined lift force is sufficient to input a vertical velocity to the edge of the lamella larger than its capillary-inertial retraction velocity. More recent studies suggest that the viscous lubrication force is dominant in the lift force responsible for splashing.^26–28 A very recent study has demonstrated that micron-sized droplets stop splashing at higher impact velocities.²⁹

Previous experimental observations have shown that the splashing threshold is mostly not affected by the wetting conditions,^30–32 except for superhydrophobic surfaces obtained by hierarchical texture and random roughness on the substrate.^33,34 In contrast, the numerical work of Yokoi (2011)³⁵ has shown that a larger dynamic contact angle can promote splashing. More recently Quetzeri-Santiago et al.³⁶ demonstrated that splashing is affected by the maximum dynamic advancing contact angle. The splashing threshold is also affected by the surface roughness.^37,38 Finally, splashing can also be controlled by impacting the drop onto a soft substrate.³⁹

The problem of splashing on a solid surface is closely related to the complex problem of moving contact lines and dynamic contact angles.^40–44 Recently, it has been proposed that the dynamics of the contact line is affected by kinetic effects in the gas, using the Boltzmann model rather than a classical slip length model.^45,46

The geometry of splashing can be classified in prompt splash or corona splash, depending on the fluid properties, surface roughness and air properties.^37,47–53 For prompt splash, the droplets immediately separate from the advancing lamella on the substrate, while for corona splash the liquid sheet separates from the surface and rises above the surface before breaking into smaller droplets. The dynamics of the ejected lamella in the corona splash regime is strongly affected by the liquid viscosity, with larger deflection angles of the lamella for low viscosity liquids, leading to crown-shaped corona splashes, in contrast to a nearly horizontal splashing observed for more viscous liquids.^21,54–56 Different splashing patterns can be distinguished as the liquid viscosity increases.^57,58 For the more viscous liquids, a separate regime appears between deposition and corona splashing, for which the liquid sheet separates from the surface, but does not break into separate droplets.⁵¹ Interestingly, splashing has not been observed experimentally above a viscosity of about 20 mPa s. It is not clear whether this is due to experimental limitations to reach the splashing threshold, or if it is a fundamental limit for splashing.

In the present study, focusing on the impact of a silver nanoparticle dispersion, we observe for the first time a liquid for which an impacting drop stops splashing above a critical impact velocity. The type of splashing we observe is the viscous type of corona splashing, with a thin liquid sheet emitted horizontally around the impacting drop. We investigate the origin of this phenomenon by changing the dispersion concentration, the coating of the solid particles and the solid surface properties. The experimental results suggest that splashing is suppressed due to the larger molecular interactions induced by the coating of the nanoparticles.

We consider a silver nanoparticle dispersion in tetradecane from Sigma-Aldrich (736 511), identified as SA dispersion hereafter. The silver content is about 52% in weight, with particle size smaller than 10 nm (see Appendix). This represents only 7.3% in volume due to the large density of silver. The SA dispersion has dynamic viscosity μ = 12 mPa s (over a large range of shear rates, see below), density ρ = 1473 kg m⁻³ and surface tension σ = 29 mN m⁻¹. We produce a drop from a flat tip stainless steel needle connected to a syringe by a tubing. The dispersion in the syringe is released in a quasisteady way to produce a drop of diameter D. The drop falls under gravity to impact onto the solid surface. The effect of the impact velocity V is systematically investigated by changing the impact height up to 2 meters. The Weber number and Reynolds number are defined respectively as We = ρDV²/σ and Re = ρDV/μ. We first consider solid surfaces consisting of microscope glass slides of area 26 × 76 mm² and roughness 2 nm. A new glass slide is used for each experiment to prevent contamination from previous experiments. The glass slide is first cleaned by rinsing with Milli-Q water, and then with ethanol, and finally dry-blowing from the centre to the perimeter with pressurised nitrogen. The dynamics of the drop impacting on the solid surface is recorded from the side with backlight imaging, using a high-speed camera (Photron SA-X2) connected to a Navitar telecentric zoom lens.

The morphology of the SA dispersion drop after impact at different velocities is shown in the left panel of Fig. 1. At low impact velocities, the drop of SA dispersion simply spreads onto the solid substrate without any splashing. As the impact velocity increases, a transition to splashing is observed. Unexpectedly, a second threshold in impact velocity is observed for the SA dispersion, above which the drop does not splash anymore during the impact. The first transition to splashing is similar to what is expected for Newtonian liquids like water or silicone oils. We verified this classical behaviour by comparing in the right panel with a Newtonian fluid of similar viscosity (9.35 mPa s silicone oil, in the right panel of Fig. 1). However, the second transition from splashing to deposition when increasing the impact velocity was not observed for the silicone oil. Previous experimental or numerical studies have shown that the liquid drop always splashes above the splashing threshold impact velocity, for liquid of viscosity up to 20 mPa s.^1,21,51

Fig. 1 Comparison of the splashing dynamics of the SA silver dispersion (left, We = 216, 511, 604, 1263, D = 1.82 mm) with a silicone oil of similar material properties μ = 9.35 mPa s and σ = 20.1 mN m⁻¹ (right, We = 164, 463, 555, 1169, D = 2.03 mm). The scale bar is 2 mm, same for all panels.

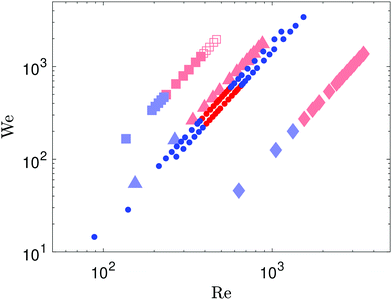
The splashing behaviour of these two liquids is systematically reported in the parameter space of Fig. 2, including two drop sizes for the SA dispersion. We also compared the impact dynamics with the pure solvent of the SA dispersion, tetradecane, as well as a more viscous Newtonian liquid, 19 mPa s silicone oil. All liquids showed a transition from deposition to splashing above a critical impact velocity. The 19 mPa s silicone oil drops showed a second transition at higher impact velocities, where the ligaments formed from the rupture of the ejecta sheet did not completely separate from the main deposited liquid. However the splashing of an ejecta sheet and its destabilisation in ligaments was still retained. The complete suppression of splashing above a second impact velocity threshold, without any ejecta sheet formed, was only observed for the SA dispersion drops. Only smooth deposition without splashing was observed above this second threshold within our experimental range. This suggests that below that second splashing transition, the dispersion behaves similarly as the pure liquid, while as the impact velocity increases, the nanoparticles inhibit the formation of the liquid sheet and thus prevent splashing.

Fig. 2 Parameter space in the Re vs. We parameters plane. Splashing regime for the SA dispersion (●, two drop diameters D = 1.82 & 2.32 mm, with the larger drop size corresponding to the lower line), compared to three Newtonian liquids: pure solvent (♦, μ = 2.33 mPa s, σ = 26.6 mN m⁻¹, D = 2.37 mm) and two silicone oils: μ = 9.35 mPa s (▲, σ = 20.1 mN m⁻¹, D = 2.03 mm) & μ = 19 mPa s (■, σ = 20.6 mN m⁻¹, D = 2.06 mm). Blue symbols correspond to smooth deposition, and red full symbols correspond to splashing. Faint symbols are used for the Newtonian liquids, presented for reference. The open red square symbols (used for the 19 mPa s silicone oil) represent cases for which the instability is still present at the edge of the liquid sheet, but droplets did not completely detach from the main drop, and were pulled back by the connecting liquid string.

We then systematically varied the concentration of the silver dispersion. Diluting the dispersion from 52 wt% to 41.5 wt% already recovers the classical splashing behaviour similar to the 9.35 mPa s silicone oil, with splashing always observed above the splashing threshold (Fig. 3). This suggests that the suppression of splashing is due to the interactions between the particles at higher impact velocities. Highly concentrated dispersions can develop non-Newtonian flow behaviour as observed in colloidal suspensions,^59,60 including shear-thinning, shear-thickening and dynamic shear jamming.^61,62 During drop impact splashing, the liquid forced into the lamella experiences high shear rates. The hypothesis of shear-thickening effects in the dispersion would increase the fluid viscosity locally. A higher viscosity of the liquid at the relevant shear rates during impact would increase the splashing threshold,¹ which would be consistent with the suppression of splashing observed in our experiments. However, the typical viscosity and concentration for dispersions exhibiting such non-Newtonian effects are usually higher.⁶³

Fig. 3 Parameter space of the performed experiments. Effect of nanoparticles concentration in the SA dispersion on the splashing regimes. In the blue cases we observed spreading, in the red ones splashing. For cases (1) & (2) (52 wt%), we observe the return to the spreading case for large impact height. (1) 52 wt%, D = 2.32 mm, (2) 52 wt%, D = 1.82 mm, (3) 41.5 wt%, D = 1.88 mm, (4) 21.1 wt%, D = 2.12 mm, (5) 0 wt%, pure tetradecane, D = 2.37 mm, (6) 9.35 mPa s silicone oil, D = 2.03 mm.

We measured the rheology of the dispersion with an Anton Paar rheometer MCR702 (Fig. 4). The rotational measurements did not show any non-Newtonian behaviour, with a constant viscosity independent of the shear rate, up to 10⁴ s. We can estimate the typical shear rates experienced during the impact of the drop on the solid surface. For a drop of diameter D = 2.3 mm, impacting at V ≥ 2.3 m s⁻¹, and estimating the thickness of the lamella to be of the order of δ ∼ D/10, the shear rate would be of the order of V/δ ≥ 10⁴ s⁻¹. It is therefore possible that the rheometer is not able to reach the shear rates experienced during the fast formation of the lamella during spreading. However, we would expect some deviation of the viscosity from the Newtonian behaviour as the shear rate approaches 10⁴ s⁻¹. Therefore, we could not find any evidence of non-Newtonian behaviour of the dispersion that would be responsible for suppressing splashing. Another possibility is that the non-Newtonian behaviour of the silver dispersion cannot be captured with this type of rheological measurement method, for example due to impulsive effects.

Fig. 4 Flow curve of the SA Silver dispersion, measured with an Anton Paar rheometer MCR702.

To understand the origin of the suppression of splashing beyond the SA commercial dispersion, we produced separate controlled nanoparticle dispersions. Such nanoparticles are not stable in the solvent and need to be stabilised by molecules on their surface. We first produced a stable nanoparticle dispersion with a coating of dodecanoic acid (2 nm silver nanoparticles in tetradecane with 55 wt%). We repeated the drop impact experiments with this dispersion. It also showed the transition to splashing, as for the previous SA dispersion. Around the height where the transition to non-splashing was observed for the SA dispersion, a reduction of splashing was indeed observed (Fig. 5). This suggests that there is a generic mechanism behind the reduction of splashing of nanosuspensions at high concentrations. However, contrarily to the SA dispersion, the splashing did not disappear completely, as can be seen from the small droplets ejected in Fig. 5(b), and more pronounced splashing was recovered at higher impact velocities (Fig. 5c).

Fig. 5 Comparison of the splashing behaviour of silver nanoparticles dispersions stabilised either by (a–c) dodecanoic acid, with 55 wt%, 2 nm, σ = 29 mN m⁻¹, D = 1.86 mm, or (d–f) oleic acid, with 49.5 wt%, 2.3 nm, σ = 29 mN m⁻¹, D = 1.92 mm. N is the total number of splashed droplets. (a) We = 466, N = 30, (b) We = 554, N = 9, (c) We = 1042, N = 24, (d) We = 448, N = 10, (e) We = 533, N = 11, (f) We = 1003, N = 0. The scale bar is 2 mm, same for all panels.

A second dispersion was then produced by coating the nanoparticles with oleic acid (2.3 nm silver nanoparticles in tetradecane with 49.5 wt%). This molecule has a longer chain than the dodecanoic acid, but also a different molecular structure due to the c=c double bond. That dispersion showed the same behaviour as the SA dispersion with a first transition to splashing, and then a second transition to non-splashing at higher impact velocities (Fig. 5d-f). The threshold velocities were similar as with the SA dispersion. The comparison of the dodecanoic acid and oleic acid coated dispersions demonstrates the critical effect of the particles coating. Changes at the nanoscale on the particles capping agent can affect the macroscopic splashing behaviour of the dispersion drop.

The main discovery of this study is that molecular changes at the surface of nanoparticles can control the macroscopic dynamics of the drop deposition process on a solid surface. However, much work remains to be done to understand the exact mechanisms leading to the suppression of splashing at higher impact velocities. This observation completely changes our perspective on the classical dynamic wetting problems such as drop impact or dip-coating, which rely on a critical velocity above which there is splashing or air entrainment. This system thus offers a macroscopic way to investigate nanoscopic interactions at high velocities. While this is crucial for the fundamental understanding of the dynamics of contact lines, our findings also have important applications such as for fast printing of complex materials.

Conflicts of interest

There are no conflicts to declare.

Appendix

Preparation of the controlled dispersions

All solvents were purchased from Acros, silver nitrate from Sigma Aldrich (99.9999% trace metals basis), ascorbic acid from Grüssing and the capping agents from abcr. The AgNO₃ NP dispersions were synthesised following the procedure published by Lee et al. (2006).⁶⁴ First, three stock solutions were prepared: (1) 21.640 g AgNO₃ was dissolved in 48 mL Butylamin, (2) 1.091 g ascorbic acid was dissolved in 3 mL Butylamin and (3) 11.795 g dodecanoic acid or 18.5 mL of oleic acid was dissolved in 15 mL toluene. In a 500 mL three-neck flask with reflux condenser, 200 mL of toluene was added, followed by the addition of the stock solution 3, containing the capping agent and the stock solution 1, containing AgNO₃. The mixture was heated until reflux. Then the stock solution 2, containing the ascorbic acid was added in one shot and the flask was closed quickly. Caution!The reaction can over boil. The reaction was then refluxed for 1 h. The reaction mixture turns from transparent to dark brown, indicating the formation of Ag NPs. After the reaction mixture was cooled down to room temperature, the mixture was added dropwise into 2 L of methanol to precipitate and purify the silver NPs. After discarding the supernatant (methanol mixture) the precipitate containing the Ag NPs was resdispersed in 125 mL of toluene. This step was repeated in total three times. In the last step, the NPs were dispersed in 5 mL tetradecane to achieve high NP concentration. The concentration of the NP solution was determined with a Mettler Toledo TGA/SDTA 851e under N₂ atmosphere.

We did not measure the viscosity and surface tension of the controlled dispersion, but we expect them to be similar to the SA dispersion.

Characterisation of the SA dispersion

We have performed different characterisations of the dispersion, including TEM (Fig. 6) and DLS (Fig. 7), showing consistent properties as provided by the manufacturer.

Fig. 6 TEM (Transmission Electron Microscopy) measurement of the SA dispersion, with magnification 380 000×. The scale bar is 5 nm long.

Fig. 7 DLS (Dynamic Light Scattering) measurement of the SA dispersion.

Acknowledgements

This work was funded by the Dutch Polymer Institute under the “Inkjet-Printing of Suspensions” project, and from the National Natural Science Foundation of China (grant # 11542016, 11702210 and 11850410439) and the Project B18040. M.-J. T. is also supported by the Cyrus Tang Foundation through the Tang Scholar program.

References

1. C. Josserand and S. T. Thoroddsen, Annu. Rev. Fluid Mech., 2016, 48, 365–391.
2. A. L. Yarin, I. V. Roisman and C. Tropea, Collision Phenomena in Liquids and Solids, Cambridge University Press, Cambridge, 2017.
3. K. Fu, Y. Yao, J. Dai and L. Hu, Adv. Mater., 2017, 29, 1603486.
4. W. Zhu, X. Ma, M. Gou, D. Mei, K. Zhang and S. Chen, Curr. Opin. Biotechnol., 2016, 40, 103–112.
5. V. Bertola and M. Marengo, in Drops and Bubbles in Contact with Solid Surfaces, ed. M. Ferrari, L. Liggieri and R. Miller, CRC Press, 2013, ch. 11, pp. 267–298.
6. V. Bertola and M. D. Haw, Powder Technol., 2015, 270, 412–417.
7. F. Boyer, E. Sandoval-Nava, J. H. Snoeijer, J. F. Dijksman and D. Lohse, Phys. Rev. Fluids, 2016, 1, 013901.
8. V. Bergeron, D. Bonn, J. Y. Martin and L. Vovelle, Nature, 2000, 405, 772–775.
9. V. Bergeron, C. R. Phys., 2003, 4, 211–219.
10. J. J. Cooper-White, R. C. Crooks and D. V. Boger, Colloids Surf., A, 2002, 210, 105–123.
11. D. Bartolo, A. Boudaoud, G. Narcy and D. Bonn, Phys. Rev. Lett., 2007, 99, 174502.
12. V. Bertola, Colloids Surf., A, 2010, 363, 135–140.
13. M. I. Smith and V. Bertola, Phys. Rev. Lett., 2010, 104, 154502.
14. M. Song, J. Ju, S. Luo, Y. Han, Z. Dong, Y. Wang, Z. Gu, L. Zhang, R. Hao and L. Jiang, Sci. Adv., 2017, 3, e1602188.
15. R. Crooks and D. V. Boger, J. Rheol., 2000, 44, 973–996.
16. E. J. Vega and A. A. Castrejón-Pita, Exp. Fluids, 2017, 58, 57.
17. C. W. Visser, Y. Tagawa, C. Sun and D. Lohse, Soft Matter, 2012, 8, 10732–10737.
18. C. W. Visser, P. E. Frommhold, S. Wildeman, R. Mettin, D. Lohse and C. Sun, Soft Matter, 2015, 11, 1708–1722.
19. L. Xu, W. W. Zhang and S. R. Nagel, Phys. Rev. Lett., 2005, 94, 184505.
20. S. Mandre, M. Mani and M. P. Brenner, Phys. Rev. Lett., 2009, 102, 134502.
21. M. M. Driscoll, C. S. Stevens and S. R. Nagel, Phys. Rev. E, 2010, 82, 036302.
22. G. Riboux and J. M. Gordillo, Phys. Rev. Lett., 2014, 113, 024507.
23. G. Riboux and J. M. Gordillo, J. Fluid Mech., 2015, 772, 630–648.
24. G. Riboux and J. M. Gordillo, Phys. Rev. E, 2017, 96, 013105.
25. J. M. Gordillo, G. Riboux and E. S. Quintero, J. Fluid Mech., 2019, 866, 298–315.
26. J. Hao, J. Lu, L. Lee, Z. Wu, G. Hu and J. M. Floryan, Phys. Rev. Lett., 2019, 122, 054501.
27. Z. Jian, C. Josserand, S. Popinet, P. Ray and S. Zaleski, J. Fluid Mech., 2018, 835, 1065–1086.
28. J. M. Gordillo and G. Riboux, J. Fluid Mech., 2019, 871, R3.
29. M. Usawa, Y. Fujita, Y. Tagawa, G. Riboux and J. M. Gordillo, Phys. Rev. Fluids, 2021, 6, 023605.
30. I. V. Roisman, A. Lembach and C. Tropea, Adv. Colloid Interface Sci., 2015, 222, 615–621.
31. A. Latka, A. M. P. Boelens, S. R. Nagel and J. J. de Pablo, Phys. Fluids, 2018, 30, 022105.
32. T. C. de Goede, N. Laan, K. G. de Bruin and D. Bonn, Langmuir, 2018, 34, 5163–5168.
33. C. Lv, P. Hao, X. Zhang and F. He, Appl. Phys. Lett., 2016, 108, 141602.
34. E. S. Quintero, G. Riboux and J. M. Gordillo, J. Fluid Mech., 2019, 870, 175–188.
35. K. Yokoi, Soft Matter, 2011, 7, 5120–5123.
36. M. A. Quetzeri-Santiago, K. Yokoi, A. A. Castrejón-Pita and J. R. Castrejón-Pita, Phys. Rev. Lett., 2019, 122, 228001.
37. A. Latka, A. Strandburg-Peshkin, M. M. Driscoll, C. S. Stevens and S. R. Nagel, Phys. Rev. Lett., 2012, 109, 054501.
38. M. A. Quetzeri-Santiago, A. A. Castrejón-Pita and J. R. Castrejón-Pita, Sci. Rep., 2019, 9, 15030.
39. C. J. Howland, A. Antkowiak, J. R. Castrejón-Pita, S. D. Howison, J. M. Oliver, R. W. Style and A. A. Castrejón-Pita, Phys. Rev. Lett., 2016, 117, 184502.
40. D. Bonn, J. Eggers, J. Indekeu, J. Meunier and E. Rolley, Rev. Mod. Phys., 2009, 81, 739–805.
41. J. H. Snoeijer and B. Andreotti, Annu. Rev. Fluid Mech., 2013, 45, 269–292.
42. Y. Sui, H. Ding and P. D. M. Spelt, Annu. Rev. Fluid Mech., 2014, 46, 97–119.
43. S. Afkhami, J. Buongiorno, A. Guion, S. Popinet, Y. Saade, R. Scardovelli and S. Zaleski, J. Comput. Phys., 2018, 374, 1061–1093.
44. L. Chen, E. Bonaccurso, T. Gambaryan-Roisman, V. Starov, N. Koursari and Y. Zhao, Curr. Opin. Colloid Interface Sci., 2018, 36, 46–57.
45. J. E. Sprittles, J. Fluid Mech., 2015, 769, 444–481.
46. J. E. Sprittles, Phys. Rev. Lett., 2017, 118, 114502.
47. R. Rioboo, C. Tropea and M. Marengo, Atomization Sprays, 2001, 11, 155–165.
48. L. Xu, Phys. Rev. E, 2007, 75, 056316.
49. L. Xu, L. Barcos and S. R. Nagel, Phys. Rev. E, 2007, 76, 066311.
50. S. T. Thoroddsen, K. Takehara and T. G. Etoh, J. Fluid Mech., 2012, 706, 560–570.
51. J. Palacios, J. Hernández, P. Gómez, C. Zanzi and J. López, Exp. Therm. Fluid Sci., 2013, 44, 571–582.
52. J. Hao, Phys. Fluids, 2017, 29, 122105.
53. D. A. Burzynski, I. V. Roisman and S. E. Bansmer, J. Fluid Mech., 2020, 892, A2.
54. C. S. Stevens, A. Latka and S. R. Nagel, Phys. Rev. E, 2014, 89, 063006.
55. A. Latka, Soft Matter, 2017, 13, 740–747.
56. M. R. Moore, J. P. Whiteley and J. M. Oliver, J. Fluid Mech., 2018, 846, 711–751.
57. M. Qin, C. Tang, S. Tong, P. Zhang and Z. Huang, Int. J. Multiphase Flow, 2019, 117, 53–63.
58. M. Qin, C. Tang, Y. Guo, P. Zhang and Z. Huang, Langmuir, 2020, 36, 4917–4922.
59. É. Guazzelli and J. F. Morris, A Physical Introduction to Suspension Dynamics, Cambridge University Press, Cambridge, 2012.
60. J. Mewis and N. J. Wagner, Colloidal Suspension Rheology, Cambridge University Press, New York, New York, USA, 2012.
61. I. R. Peters, S. Majumdar and H. M. Jaeger, Nature, 2016, 532, 214–217.
62. S. Majumdar, I. R. Peters, E. Han and H. M. Jaeger, Phys. Rev. E, 2017, 95, 012603.
63. J. F. Morris, Annu. Rev. Fluid Mech., 2020, 52, 121–144.
64. K. J. Lee, B. H. Jun, T. H. Kim and J. Joung, Nanotechnology, 2006, 17, 2424–2428.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm01367f

---