Surface tensiometry of phase separated protein and polymer droplets by the sessile drop method

Abstract

Phase separated macromolecules play essential roles in many biological and synthetic systems. Physical characterization of these systems can be challenging because of limited sample volumes, particularly for phase-separated proteins. Here, we demonstrate that a classic method for measuring the surface tension of liquid droplets, based on the analysis of the shape of a sessile droplet, can be effectively scaled down to measure the interfacial tension between a macromolecule-rich droplet phase and its co-existing macromolecule-poor continuous phase. The connection between droplet shape and surface tension relies on the density difference between the droplet and its surroundings. This can be determined with small sample volumes in the same setup by measuring the droplet sedimentation velocity. An interactive MATLAB script for extracting the capillary length from a droplet image is included in the ESI.

---

1 Introduction

Solutions of macromolecules have long been known to phase separate into liquid domains that share the same solvent but differ in their composition.^1–3 An essential feature of these droplets is their extremely low surface tension, γ. Classically, this can be determined by the spinning drop method⁴ where a relatively low density droplet is placed in a horizontal capillary tube that is spun very rapidly along its axis of symmetry. By quantifying the shape of the droplet as a function of the rotation rate, the surface tension can be determined with stunning accuracy, with reports of surface tensions as low as 1 μN m⁻¹.

Liquid–liquid phase separation of macromolecular solutions has enjoyed intense interest in recent years thanks to the discovery that many membrane-less compartments within eukaryotic cells appear to be liquid droplets of phase-separated macromolecules.^5,6 Examples include P granules,⁷ P bodies,⁸ Cajal bodies⁹ and nucleoli.¹⁰ Membraneless organelles have complex compositions, including a large number of distinct RNAs and proteins. The bulk of the proteins found in these droplets are intrinsically-disordered and lack globular structure.^11–14 These proteins readily phase separate in vitro to form a dilute ‘supernatant’ phase and a protein-rich phase, which can take the form of liquid droplets, hydrogels, fibrils or aggregates.¹⁵ The tendency of intrinsically disordered proteins to phase separate is thought to underlie the formation of membraneless compartments in the cell.^16–18 Precise physical characterisation of droplets in vitro can provide insights into the molecular scale interactions of their components, and potentially shed light on their physiology in vivo.

The essential challenge in characterizing the properties of these droplets is their size. Typically no more than a few microns across in vivo, larger droplets can be formed in vitro. However, the production and purification of protein is labor intensive and expensive, and total volumes of the protein-rich phase are typically limited to the μL scale. Such samples are too small for conventional mechanical measurements. For example, quantification of bulk mechancial properties through conventional rheometry requires at least 100 μL of material. In the last twenty years, a number of new approaches have been developed to scale-down rheological measurements.¹⁹ Among these, particle tracking microrheology is well-suited to measure the linear rheology of phase separated droplets.^20,21

Similarly efficient and effective approaches have not yet been established to characterize the surface mechanical properties of droplets. Classic spinning drop measurements can work for droplets on the μL scale, but only if they are less dense than their surroundings. In principle, the spinning droplet method could be applied to a small droplet of the protein-depleted phase within a larger volume of the protein-rich phase, but that would require volumes of the protein-rich phase around 1000 μL. A number of methods have been introduced in recent years to estimate the surface tension of micron-scale phase separated droplets. The most popular method is based on measuring the time it takes for two droplets to fuse.²² In principle, this method can be very accurate if the rheology of the droplets is known. While fusion times are easy to calculate from first principles in bulk, they can be strongly modified when droplets are in contact with a surface, as contact lines can dramatically slow down the movement of any droplet.²³ Imaging of fusion events in the absence of contact lines is very challenging. At droplet volume fractions low enough to clearly resolve the dynamics, fusion events are rare. Optical tweezers can be used to initiate fusion, but care has to be taken to avoid contributions of optical forces to the fusion time as well as photo- and thermal damage to the droplets.²⁴ Measurements of the force required to statically deform a droplet can also be used to accurately determine the surface tension using optical tweezers²⁵ or atomic force microsopy.^26,27

Alternatively, the shape of droplets of an appropriate size contains sufficient information to accurately determine their surface tension. For conventional simple liquids, made of small molecules, this is done through the analysis of photographs of millimeter scale pendant or sessile droplets.^28,29 Surface tension is most easily inferred from the shape of a droplet when its radius is larger than the capillary length, . Here, Δρ is the density difference between a droplet and its surroundings and g is the acceleration due to gravity. The tiny values of surface tension for phase-separated droplets of macromolecules are somewhat mitigated by a simultaneous reduction of the density difference (e.g.ref. 30). All together, this leads to reported values of the capillary length varying from [scr O, script letter O] (10 mm) to [scr O, script letter O] (100 mm).⁴ This corresponds to droplets with volumes of the order [scr O, script letter O] (nL). By analyzing the shape of fused fluorescently tagged nucleoli from giant Xenopus oocytes, Feric et al. determined their capillary length to be of order [scr O, script letter O] (10 mm).³¹ One challenge of this approach is that the density difference between the droplet and surrounding fluid needs to be known accurately. This can be inferred from sedimentation speeds of microscopic droplets when the viscosities of the droplet and surroundings are known.³²

Here, we apply established methods of sessile droplet shape analysis to determine the surface tension of phase-separated macromolecular droplets with unknown density. Using a standard camera equipped with a telecentric lens, we quantify phase separated liquid droplets, made of polymers or proteins, with surface tensions ranging from 7 to 90 μN m⁻¹. We determine the density difference between the droplet and continuous phases in the same setup by measuring the droplets' sedimentation velocity. Typical values of the density difference range from 30 to 150 kg m⁻³. This approach is attractive for the in vitro measurement of phase-separated proteins because it uses small sample volumes and the proteins do not need to be fluorescently tagged.

2 Droplet preparation and imaging

We determine the surface tension of phase-separated macromolecular liquids from the shape of sessile droplets (Section 3) and the speed of sedimenting droplets (Section 4). For a meaningful surface tension measurement, these droplets must be immersed in their co-existing liquid phase. Typically, the denser macromolecule-rich phase forms the droplet, and the macromolecule-poor phase forms the continuous phase. These coexisting phases are pre-equilibrated, and readily separated by centrifugation.

To image droplets, we use a typical optical setup for sessile droplet analysis,^33,34 described in the Materials and methods. Droplets are illuminated by an extended light source and imaged with a telecentric lens. To limit artifacts due to refraction, the droplet and its co-existing continuous phase are held in a rectangular cuvette. A typical image of dextran-rich droplet in its co-existing dextran-poor continuous phase is shown in Fig. 1. A series of droplets of different sizes of the same material are shown as insets to Fig. 2. The droplet shape, r_exp(z), is manually extracted from the acquired images in MATLAB, using the script included in the ESI.†

Fig. 1 Image of a sessile dextran-rich droplet in a continuous dextran-poor phase on a PEG-ylated glass surface. d is maximum width of the droplet and H is the height of the droplet from the contact surface.

Fig. 2 Sessile droplet shape analysis. Images of sessile dextran-rich droplets in a dextran-poor continuous phase. The scale bars are 200 μm. Dashed-green lines on the droplets shown best fit curves to the droplet shape. These images are superimposed over a scatter plot of the Neumann number and aspect ratio, H/d. The dashed-grey curve is Neumann number in the perfect case where the sessile droplet has a contact angle of 180°, calculated numerically using eqn (1)–(3).

Large droplets, appropriate for surface tension measurements, described in Section 3, can be formed by direct pipetting of the droplet phase into its coexisting continuous phase. Alternatively, a droplet dispersion can be pipetted into the same continuous phase. The latter approach allows for a wider range of droplet sizes, including smaller droplets appropriate for sedimentation velocity measurements of Section 4.

To accurately determine the 3D shape of the droplet from such 2D images, droplets must be axisymmetric. As we will see in Section 3, the accuracy of the surface tension measurement is best for droplets with a large contact angle. Phase separated droplets of proteins often interact strongly with standard glass and plastic surfaces, spreading to very low contact angles and adopting non-axisymmetric shapes due to pinning. Therefore, the bottom of the cuvette needs to be very clean and functionalized to minimize spreading. A PEG-silane treated coverslip placed at the bottom of the cuvette is sufficient for the droplets studied here. The protocol for creating this is described in the Materials and methods.

3 Droplet shape analysis

The equilibrium shape of a liquid droplet is determined by a balance of surface tension and hydrostatic pressure. For a droplet with cylindrical symmetry, this is captured by the axisymmetric Laplace equation:³⁵

The coordinate system, including s, r, z, θ, is defined in Fig. 1. The left-hand side of the equation gives the contribution from gravity, which increases linearly from the top of the droplet. The right-hand side of the equation gives the contribution of surface tension to the droplet pressure, which is determined by the local curvature. The constant P* = 2γ/R₀ is the pressure at the top of the droplet, where R₀ is the local radius of curvature.

To simplify the equation, we scale r, s and z by the capillary length (indicated by over-bars) and rearrange to obtain

where β = L_c/R₀, the inverse square root of the standard Bond number. This is now a one-parameter shape equation that we solve numerically with the geometric requirements:

The last equation holds at the top of the drop, and represents the fact that the two principle surface curvatures are equal at this point.³⁵

To extract the material properties of the droplet, we find the values of β and L_c that minimise the difference between the numerical solution, and the non-dimensionalised shape of the droplet, r_exp/L_c. Examples of the fits to droplet shape superimposed on raw droplet images are found in the insets to Fig. 2. An interactive MATLAB script for fitting droplet shape is found in the ESI.†

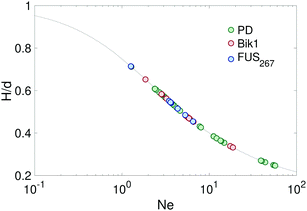
Previous work has shown that sessile droplet measurements of the surface tension are only accurate when the Neumann number, Ne = R₀H/L_c² = H/(L_cβ) > 0.3, where H is the height of the droplet from the substrate.³⁶ For smaller Ne, droplets are effectively spherical, and it is not possible to extract a meaningful value of γ. Practically speaking, Ne can be increased by increasing droplet size, or by increasing the contact angle of the droplet. A scatter plot of the Neumann number and droplet aspect ratio for a series of dextran-rich droplets in a dextran-poor continous phase are shown in Fig. 2.

4 Sedimentation velocity

The sessile droplet measurement gives us the capillary length,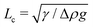 . To extract the surface tension, we need to know the density difference between the droplet and continuous phases. For relatively inexpensive molecules like PEG and dextran, milliliter scale samples of each phase can easily be produced, enabling standard density measurements of each phase.²⁹ For proteins, we require a technique that can be performed with sub-microlitre scale droplets.

The density difference between the two phases can easily be determined by measuring the sedimentation speed of small droplets in the same setup used for the sessile droplet shape experiments. Example data for the PEG-dextran system is shown in Fig. 3. Images of a sedimenting dextran-rich droplet, acquired at equally spaced time intervals are shown in the inset. As shown by the straight line through their centers, these droplets move at a steady sedimentation velocity. The sedimentation speed depends on the droplet size, and is plotted over a factor of eight in droplet radius in Fig. 3.

Fig. 3 Sedimenting droplets. Inset shows a timeseries of a dextran-rich droplet sedimenting in a dextran-poor continuous phase. Each image is separated by 2.1 s. The dashed line through the droplet centers shows that the sedimentation speed is linear. The main plot shows sedimentation speeds of 24 such droplets plotted against droplet radius.

The sedimentation velocity, v, is determined by a balance of the buoyant force and viscous drag. For a spherical droplet of radius R, the buoyant force is 4πΔρgR³/3. When the droplet viscosity, η_d, is much larger than the viscosity of the continuous phase, η_c, the viscous drag is given by the familiar Stokes form, 6πη_cRv. Balancing the forces and solving for the density difference, we find

If the continuous phase viscosity is comparable or larger than the droplet viscosity, the previous equation is corrected by a factor that depends on the viscosity ratio:³⁷

Note, however, that this correction is never more than a 33% change in density.

Since macromolecule-rich fluids tend to be much more viscous than simple liquids, eqn (4) is usually quite accuruate for protein and coacervate droplets in their typical buffers. However, for systems with signficant macromolecule concentrations in both phases eqn (5) may be necessary. In such cases, independent measurements of the viscosities of both phases are suggested. For the PEG-dextran example of Fig. 3, η_c/η_d = 0.05, so that eqn (4) is accurate to <2%.

For fixed compositions of the droplet and continuous phases, the sedimentation velocity should scale like the square of the droplet radius. This can be verified by rearranging eqn (4) or (5). The dashed-line in Fig. 3 shows a good fit of the sedimentation speed to the R² form over this range of droplet radii. Systematic deviations from this size-dependence can indicate that the droplets are not an appropriate size.

On the one hand, droplets need to be significantly bigger than the resolution of the imaging system. On the other hand, the droplets have to be small enough that they maintain a spherical shape while falling. To remain spherical, droplets require the capillary number, Ca = vη_c/γ ≪ 1.^38,39 Inserting this into eqn (4), this requirement becomes that R ≪ L_c. This criterion contradicts the requirement for accurate sessile droplet measurements, R ≳ L_c. Therefore, one should not use the same droplets for sedimentation velocity and surface tension measurements. For that reason, we prefer to pipette a premixed emulsion into the continuous phase. However, when multiple droplets fall near each other, hydrodynamic interactions can dramatically effect their sedimentation velocity.^40,41 Therefore, sedimentation measurements should be limited to extremely dilute, well-separated droplets.

The sedimentation of large droplets can also be impacted by inertial effects, quantified by the Reynolds number, Re = ρ_cvR/η_c. Eqn (4) and (5) are only valid when Re ≪ 1. For the largest expected density differences (around 500 kg m⁻³) in the least viscous continuous phase (an aqueous continuous phase with no macromolecules, η_c ≈ 10⁻³ Pa s), inertial effects will be negligible for droplets less than 100 mm in radius.

5 Results and discussion

We demonstrate sessile droplet tensiometry for three different phase separated macromolecular droplets. The physical properties of mixtures of PEG and dextran have been thoroughly studied by other means, and therefore allow us to easily compare our approach with previous results. We chose a far-from critical mixture of 8 kDa PEG and 500 kDa dextran,⁴ with the dextran-rich phase making up the droplets. We further consider two phase-separated proteins, FUS₂₆₇ and Bik1. FUS is a widely studied protein related to neurodegnerative diseases.⁴² It features a disordered N-terminal domain and a folded C-terminal domain. Here, we work with just the first 267 amino acids of the disordered domain. Finally, Bik1 is a protein found in yeast that is associated with microtubules during cell division.^43,44

Measured values of the surface tension and relative density of each of these droplets is shown in Fig. 4. The surface tensions of these systems, shown in Fig. 4a, range from about 7 to 90 μN m⁻¹. For each measurement of the capillary length, the Neumann number was greater than 0.3, as shown in Fig. 7. The density differences between the two phases, shown in Fig. 4b, range from 30 to 150 kg m⁻³. The surface tension and density values for PEG/dextran agree well with literature data.⁴ To connect sedimentation speeds of the FUS and Bik1 droplets to density differences, we assumed that the continuous phase viscosity is the same as water, and that the inner phase is much more viscous, the latter is justified by the microrheology measurements in Fig. 5. For dextran droplets, we measured the viscosities of both phases with a rheometer, which were 150 ± 50 and 3.9 ± 0.1 mPa s, for the dextran-rich and dextran-poor phases respectively.

Fig. 4 Surface tension, density, and the capillary length. (a) Surface tensions with example images of droplets enriched in dextran, Bik1, and FUS₂₆₇. The scale bar is 200 μm. (b) Density differences of the same droplets. Box plots showing median values (red lines), 25th and 75th percentiles (blue boxes), and total span of results (black bars). The number above each box plot indicates the number of droplets measured. (c) Ashby plot of surface tension and density difference showing simple liquids (gray blob) and macromolecular liquids (green blob). Dashed lines are contours of the capillary length.

Fig. 5 Viscosity and the capillary velocity. (a) Box plot of the viscosities for Bik1 and FUS₂₆₇ with the inset mean-squared displacements of 0.1 μm radii tracers in Bik1 and FUS₂₆₇ droplets. The number above each box indicates the numbers of the tracers. (b) Ashby plot of surface tension and viscosity showing simple liquids (gray blob) and macromolecular liquids (green blob). The viscosity of the underlined simple liquids are used in this graph. Dashed lines are contours of constant capillary velocity γ/η.

While the two protein systems have similar capillary lengths, around 160 μm, they have very different surface tensions and densities. The surface tension of Bik1 is 7 μN m⁻¹, much smaller than the surface tension of FUS₂₆₇, about 90 μN m⁻¹. There are no measurements of the surface tension of these specific protein droplets. The surface tension of other phase-separated protein droplets measured through other means have been reported to range from 0.4–100 μN m⁻¹.^{7,22,25,31,45} Bik1 droplets had a significantly smaller density mismatch than FUS₂₆₇ droplets, about 29 kg m⁻³ and 135 kg m⁻³, respectively. Using a nominal protein density of 1300 kg m⁻³, these density differences imply respective protein volume fractions within the droplets of 10% and 45%. There are few measurements of the densities of phase-separated protein droplets. Feric et al.³² measured the density of the nucleolus (composed of a complex mixture of proteins and nucleic acids) using a similar sedimentation method, and found a value of 1140 kg m⁻³. This is similar to our measured value of FUS₂₆₇ droplets, about 1135 kg m⁻³.

These values are placed in a broader context using an Ashby plot of surface tension and density in Fig. 4c. In addition to these three droplets, we include a selection of droplets of far-from-critical simple liquid combinations. This plot higlights an essential feature that contrasts macromolecular droplets (shaded light green), from simple liquids (shaded gray): macromolecular droplets tend to have very low surface tensions, even when they are far from critical. Contours of the capillary length, L_c, are indicated by the dashed lines in Fig. 4c. While simple liquids have capillary lengths from the millimeter to centimeter scales, our macromolecular droplets have capillary lengths between 100 μm and 1 mm.

To complete our mechanical characterization, we measured the rheological properties of the protein droplets using standard particle tracking microrheology,¹⁹ as described in the Materials and methods. Mean-squared displacements of ≈0.1 μm radius tracer particles embedded in each of the three droplet phases all show a linear dependence on time, as shown in the inset of Fig. 5. This confirms that each droplet behaves as a simple Newtonian liquid, with no signs of viscoelasticity. Since the mean-squared displacements are linear, the rheology of each of the droplets is simply characterized by their viscosity. The viscosities of the Bik1 and FUS₂₆₇ droplets are 18.2 and 1.2 Pa s, respectively.

An Ashby diagram showing the surface tension and viscosity of droplets is shown in Fig. 5b. It helps to illustrate potential advantages of the sessile droplet method over the popular ‘fusion method’ for determing the surface tension. In the latter case, the time it takes for the droplets to coalesce at low Reynolds number is set by the ratio of the droplet size and the capillary velocity V_c = γ/η_d. Thus, with a knowledge of η_d, γ can be extracted. If the capillary velocity is too high, fusion events cannot be resolved. The dashed lines on Fig. 5b indicate contours of constant capillary velocity. While the fusion of Bik1 droplets in the lower right corner of this diagram can be easily resolved, microscopic fusion experiments become much more challenging as droplets move to the top left of the diagram. The capillary velocities of dextran and FUS₂₆₇ droplets are a hundred-fold higher, around 100 mm s⁻¹. For typical 10 mm droplets, resolution of fusion events would require frame rates around 100 frames per second.

6 Conclusion

Sessile droplet shape analysis is a robust method to assess the surface tension of phase separated liquid droplets, capable of measuring surface tensions over at least four orders of magnitude. With the integration of a simple density measurement based on sedimentation velocity, this method is an efficient and effective choice for measuring the surface tensions of droplets where only microliters of material are readily available, such as condensed phases of proteins. This simple method has the added benefit of providing easy access to the overall droplet concentration, a quantity which has been largely overlooked in the literature on phase-separated proteins.

Compared to the popular droplet fusion technique, the sessile droplet method offers several advantages. First, it can measure a broader range of droplets, because only the most viscous droplets will have slow enough fusion events to be resolved with standard imaging systems. Second, it is not subject to systematic errors associated with contact line sliding.^23,46 Third, viscoelasticity is expected to change the dynamics of droplet fusion. Sessile droplet shape analysis can work with viscoelastic droplets, as long as they have no elastic memory at long times.

One challenge of the current approach is that the droplets should have as large a contact angle as possible. To achieve Ne > 0.3, one typically requires contact angles greater than 90°. Larger contact angles will also typically reduce pinning, which is important so that the droplets remain axisymmetric. While a simple PEG-ylated surface was sufficient for the cases studied here, different surface treatments may be needed for other droplets. In cases where appropriate surface treatments are not readily available, a similar shape analysis of pendant droplets could be more convenient.

7 Materials and methods

7.1 Macromolecular droplets

PEG/Dextran. Polyethylene glycol (PEG) 8 kDa and dextran 500 kDa were purchased from Sigma Aldrich and Alfa Aeser, respectively. We quantified the properties of dextran-rich droplets phase separated from an aqueous mixture of 5.6 wt/wt% PEG and 7 wt/wt% Dextran.⁴ These were prepared from stock solutions of PEG (30 wt/wt% in DI water) and dextran (10 wt/wt% in DI water) that were premixed and stored at 4 °C.

FUS low complexity domain (LCD). Histidine- and Gb1-tagged FUS (residues 1–267) was overexpressed in E. coli strain BL21 (DE3) at 20 °C overnight. The protein's molecular weight is ≈26 kDa. The protein was purified under denaturing conditions on a nickel affinity chromatography column, followed by enzymatic cleavage of the tags with TEV protease. Additional affinity chromatography removed the cleaved products. Finally, the protein was concentrated up to 2 mM in the presence of 6 M urea and stored at −80 °C. To initiate phase separation, the stock protein solution is diluted 30× in a buffer (50 mM HEPES, 150 mM NaCl, pH 7.5).

Bik1. N-Terminally tagged hexa-histidine – thrombin cleavage site – S. cerevisiae full length Bik1 (H6-TCS-Bik1) was overexpressed in E. coli strain BL21-CodonPlus (DE3)-RIPL (Agilent) at 20 °C overnight. Protein samples were purified by nickel affinity and size exclusion chromatography in 20 mM Tris pH 7.5, 500 mM NaCl, 10% glycerol supplemented with 10 mM Imidazole and 10 mM 2-mercaptoethanol (nickel affinity) or 1 mM DTT (size exclusion). H6-TCS-Bik1 protein samples were concentrated up to 265 μM and stored at −80 °C in size exclusion buffer. The molecular weight of this protein is ≈52 kDa. To induce phase separation, the stored protein stock is diluted 6× in a buffer (20 mM Tris, 150 mM NaCl, pH 7.5).

7.2 Surface passivation

In order to characterize droplet properties it is important to create surfaces that the droplets do not spread on. This both allows the creation of stable droplets with a finite contact angle, and avoids losing protein from the system as it adheres to any free surfaces in the sample chamber. We create such surfaces by passivating the surface of glass coverslips with a PEG silane, (3-[methoxy(polyethyleneoxy)propyl]trimethoxysilane, 6–9 PEG-units) bought from ABCR GmbH.

To coat the coverslips, we immerse them using a glass staining rack in a constantly-stirred solution containing 2300 mg of PEG silane, 500 mL of toluene, and 800 μL of aqueous hydrochloric acid (hydrochloric acid fuming 37% from VWR, MilliporeSigma). After 18 hours at room temperature, the coverslips are rinsed once in toluene (toluene 99.7+% from Alfa Aesar), and then twice more with ethanol (ethanol, denatured with IPA from Alcosuisse), before being dried with clean, dry air. Finally coverslips are stored in a dry chamber with a dessicant until required for use.

7.3 Sedimenting and sessile droplets

The optical setup for these experiments is shown in Fig. 6. In this figure, light source is a 3.5′′ × 6′′ White, LED Backlight (Edmundoptics), the lens is a 0.5 × −1.0 × VariMagTL™ Telecentric Lens (Edmundoptics) and the camera is a CMOS Camera from Thorlabs (DCC3240M – High-Sensitivity USB 3.0, 1280 × 1024, Global Shutter, Monochrome Sensor). Note the use of a telecentric lens, which ensures accurate size measurements. Samples are held in a 2.5 mL 12.5 × 12.5 × 45 mm³ cuvette, with a PEG-ylated coverslip placed inside.

Fig. 6 A schematic of the experimental setup for falling and sessile droplets experiments.

The cuvette is fill with about 200 μL of the continuous phase, which is separated from the co-existing droplet phase by centrifugation (10 min at 14 rcf). We consistently use the denser phase for sedimentation experiments (enriched in dextran or protein). Droplet phase or a coexisting dilute mixture of droplets in the continuous phase are added from the top with a micropipette. For sedimentation experiments, a series of images is recorded as the droplets fall, typically around 3 fps. For sessile droplet experiments, one must wait for the droplet to reach its equilibrium shape after coming in contact with the surface, which can take several minutes and depends on the size of the droplet and its capillary velocity.

Fig. 7 The Neumann number calculated for all the sessile droplets of the 3 systems. Note that they are all greater than 0.3.

7.4 Particle tracking microrheology

We used 0.2 μm diameter fluorescent carboxyl microspheres (λ/480, 520 nm) available at ∼1% solids (w/v) aqueous suspensions from Bangs Laboratories, Inc. To add the particles in FUS₂₆₇ and Bik1 droplets, beads were added to the buffer used to dilute the stocks protein solutions for droplet formation. Beads spontaneously partitioned in the condensed (protein-rich) phase of both FUS₂₆₇ and Bik1. Sample chambers are constructed from PEG-ylated coverslips (Section 7.2) and double sided tape, which acts both as a spacer and sealant to limit evaporation.

Samples are imaged with fluorescence on a Nikon eclipse Ti-U inverted microscope with an Oil Nikon Apo TIRF 100× objective and recorded with a ORCA Flash 4.0 v2 (digital CMOS C11440-22CU) Hamamatsu camera, controlled by μManager. For each protein droplet, 200 frames we acquired with 10 ms exposures at 300 ms intervals.

Images were analyzed in MATLAB. Particle centers were found by fitting to a Gaussian distribution. Particle locations were linked into trajectories using.⁴⁷ Diffusion coefficents were determined by fitting the mean-squared displacement versus time. The viscosity was determined from the diffusion coefficient using the Stokes–Einstein equation.

D = k_BT/6πRη, (6)

where k_B is Boltzmann constant, T is the absolute temperature and R is the radius of the particle.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge Thomas Schweizer, Solenn Riedel, and Andrea Testa for help with rheology, Tianqi Sai for help with particle sizing, Cristina Manatscha for help with cloning. We acknowledge financial support from the Swiss National Science Foundation grants 172824 (MI, A. L. T. and ERD) and 170976 (LE and FHTA) as well as the EMBO fellowship LTF-388-2018 (LE).

Notes and references

1. W. Ostwald and R. Köhler, Kolloid-Z., 1927, 43, 131–150.
2. H. B. De Jong, Protoplasma, 1932, 15, 110–173.
3. J. T. G. Overbeek and M. Voorn, J. Cell. Comp. Physiol., 1957, 49, 7–26.
4. Y. Liu, R. Lipowsky and R. Dimova, Langmuir, 2012, 28, 3831–3839.
5. A. A. Hyman and C. P. Brangwynne, Cell, 2011, 21, 14–16.
6. S. C. Weber and C. P. Brangwynne, Cell, 2012, 146, 1188–1191.
7. C. P. Brangwynne, C. R. Eckmann, D. S. Courson, A. Rybarska, C. Hoege, J. Gharakhani, F. Jülicher and A. A. Hyman, Science, 2009, 324(5935), 1729–1732.
8. N. Kedersha, G. Stoecklin, M. Ayodele, P. Yacono, J. Lykke-Andersen, M. J. Fritzler, D. Scheuner, R. J. Kaufman, D. E. Golan and P. Anderson, J. Cell Biol., 2005, 169(6), 871–884.
9. M. Strzelecka, S. Trowitzch, G. Weber, R. Lurmann, A. C. Oates and K. M. Neugebauer, Nat. Struct. Mol. Biol., 2010, 17, 403–409.
10. C. P. Brangwynne, T. J. Mitchison and A. A. Hyman, Proc. Natl. Acad. Sci. U. S. A., 2010, 108(11), 4334–4339.
11. P. E. Wright and H. J. Dyson, Nat. Rev. Mol. Cell Biol., 2015, 16(1), 18–29.
12. A. K. Dunker, M. S. Cortese, P. Romero, L. M. Iakoucheva and V. N. Uversky, FEBS J., 2005, 272(20), 5129–5148.
13. J. H. Dyson and P. E. Wright, Curr. Opin. Struct. Biol., 2002, 12(1), 54–60.
14. P. Tompa and A. Fersht, Chapman and Hall/CRC, 2009.
15. P. G. Vekilov, Soft Matter, 2010, 6, 5254–5257.
16. J. K. Weber, R. L. Jack, C. R. Schwantes and V. S. Pande, Biophys. J., 2014, 107(4), 974–984.
17. N. Kedersha, P. Ivanov and P. Anderson, Trends Biochem. Sci., 2013, 36(10), 494–506.
18. P. Tompa and P. Csermely, FASEB J., 2004, 18(11), 1169–1175.
19. E. M. Furst and T. M. Squires, Microrheology, Oxford University Press, 2017.
20. N. Taylor, S. Elbaum-Garfinkle, N. Vaidya, H. Zhang, H. A. Stoneb and C. P. Brangwynne, Soft Matter, 2016, 12, 9142.
21. T. Murakami, S. Qamar and J. Q. Lin, et al. , Neuron, 2015, 88(4), 678–690.
22. S. Elbaum-Garfinkle and K. S. Younghoon Kim, et al. , Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7189–7194.
23. J. Hernández-Sánchez, L. Lubbers, A. Eddi and J. Snoeijer, Phys. Rev. Lett., 2012, 109, 184502.
24. A. Blázquez-Castro, Micromachine, 2019, 10, 507.
25. L. M. Jawerth, M. Ijavi, M. Ruer, S. Saha, M. Jahnel, A. A. Hyman, F. Jülicher and E. Fischer-Friedrich, Phys. Rev. Lett., 2018, 121, 258101.
26. L. Zitzler, S. Herminghaus and F. Mugele, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 155436.
27. S. E. Anachkov, I. Lesov, M. Zanini, P. A. Kralchevsky, N. D. Denkov and L. Isa, Soft Matter, 2016, 12, 7632–7643.
28. S. M. Saad and A. W. Neumann, Adv. Colloid Interface Sci., 2016, 238, 62–87.
29. E. Atefi, J. A. M. Jr and H. Tavana, Langmuir, 2014, 30, 9691–9699.
30. D. Aarts, J. Phys. Chem. B, 2005, 109, 7407–7411.
31. M. Feric, N. Vaidya and T. S. Harmon, et al. , Cell, 2016, 165, 1686.
32. M. Feric and C. P. Brangwynne, Nat. Cell Biol., 2013, 15, 1253.
33. K. Sefiane, L. Tadrist and M. Douglas, Int. J. Heat Mass Transfer, 2003, 46, 4527–4534.
34. J. Drelich, Surf. Innovations, 2013, 1, 248–254.
35. O. Del Ro and A. Neumann, J. Colloid Interface Sci., 1997, 196, 136–147.
36. J. Yang, K. Yu and Y. Y. Zuo, Langmuir, 2017, 33, 8914–8923.
37. J. Hadamard, C. R. Acad. Sci., 1911, 152, 1735–1738.
38. J. Rallison, Annu. Rev. Fluid Mech., 1984, 16, 45–66.
39. H. A. Stone, Annu. Rev. Fluid Mech., 1994, 26, 65–102.
40. R. H. Davis and A. Acrivos, Annu. Rev. Fluid Mech., 1985, 17, 91–118.
41. P. Segre, E. Herbolzheimer and P. Chaikin, Phys. Rev. Lett., 1997, 79, 2574.
42. A. Patel, H. O. Lee and L. Jawerth, et al. , Cell, 2015, 162, 1066–1077.
43. K. A. Blake-Hodek, L. Cassimeris and T. C. Huffaker, Mol. Biol. Cell, 2010, 21, 2013–2023.
44. V. Berlin, C. A. Styles and G. R. Fink, Cell Biol., 1990, 111, 2573–2586.
45. S. Alberti, A. Gladfelter and T. Mittag, Cell, 2019, 176, 419.
46. J. H. Snoeijer and B. Andreotti, Annu. Rev. Fluid Mech., 2013, 45, 269–292.
47. J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sm01319f

---