The squeeze strengthening effect on the rheological and microstructured behaviors of magnetorheological fluids: a molecular dynamics study
Pei
Pei
 ab and
Yongbo
Peng
ab and
Yongbo
Peng
 *ac
*ac
aState Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, P. R. China. E-mail: pengyongbo@tongji.edu.cn
bCollege of Civil Engineering, Tongji University, Shanghai 200092, P. R. China
cShanghai Institute of Disaster Prevention and Relief, Tongji University, Shanghai 200092, P. R. China
First published on 13th October 2020
Abstract
Systematic molecular dynamics simulations are conducted on magnetorheological (MR) fluids under steady state, squeeze flows and shear flows. The present study concerns the squeeze-assisted MR fluid strengthening and correlates the suspensions’ macroscopic rheological properties to their microstructure evolution in terms of the aggregation kinetics. Simulation results demonstrate that the squeeze strengthening effect on the rheological properties of MR fluids is enhanced with the increasing magnetic field and becomes more prominent for dilute suspensions, but weakened with the increasing squeeze rate after the critical squeeze rate is surpassed. By microscopic inspection, it is found that the rheological properties of MR fluids under squeeze flows are consistent with the microstructured behaviors of MR suspensions in terms of the particle distribution, cluster kinetics, particle connectivity and magnetic energy. This study provides a microstructural insight into the squeeze-assisted MR fluid strengthening, which helps to attain an elegant design of MR devices with high shear performance requirements.
1. Introduction
Magnetorheological (MR) fluids are known as a kind of intelligent materials, which show a rapid and reversible transition from a free-flowing state to a solid state upon the application of an external magnetic field. Due to the unique rheological properties and high controllability, MR fluids have been widely exploited with broad applications in diverse fields, such as civil engineering,1,2 bioengineering,3,4 automotive industry,5,6 and aerospace engineering.7,8Shear yield stress is a key parameter for the evaluation of MR fluids and the design of associated MR devices.9,10 Usually, a high shear yield stress can be enabled by conventional MR fluids, which are dispersions of micron-sized magnetic particles in a non-magnetic medium. However, a higher performance level is always required by MR fluids due to the constantly evolving industries and technologies. To meet the ongoing industrial requirements, much effort has been contributed to improving the shear yield stress of this smart material, either from the perspective of MR formulations11–13 or from the operation by introducing external measures.14–17
Over the past few decades, the squeeze-assisted MR fluid strengthening has gradually aroused significant interest, ever since Tang et al.18,19 pioneeringly put forward that the shear yield stress of MR fluids could be significantly enhanced by compression. The effect of compression on the performance of MR fluids in the case of an experimental approach has been largely reported in the literature. For example, Zhang et al.20 designed an apparatus to investigate the squeeze strengthening effect on MR fluids and proposed a semi-empirical model to explain the mechanism behind this effect. Kordonski and Gorodkin21 experimentally explored the impact of squeeze flows on the rheological properties of MR fluids, and found that compression normal to the magnetic field created more shear stress increment than imposed along the magnetic field direction. Based on a series of experimental investigations, Bigue et al.22–24 correlated the squeeze strengthening effect on MR fluids with the Péclet number, which could be used to predict the squeeze strengthening behavior as well as guide the initial design of super-strong MR devices. In general, the squeezing enables a higher MR effect under an external magnetic field. There are also many experimental and theoretical research studies concerning MR fluids in the squeeze mode, in which the normal stress or force is intensively investigated.25–27 It is worth noting that the normal stress is of significant interest in studying the rheological properties of MR suspensions with compression. The main reason is that the normal stress is the basic motivation for the applications of MR fluids in the squeeze mode. Meanwhile, for those in the shear mode, especially associated with the squeeze strengthening effect, the normal stress of MR fluids should also be paid sufficient attention. Because the normal stress is closely related to the bulk behaviors of MR suspensions, a full investigation on shear and normal stresses from the perspective of the microscopic scale contributes to a thorough understanding of the squeeze strengthening effect of MR fluids as well as to important implications for practical applications.
However, the microscopic investigations on the squeeze-assisted MR fluid strengthening are not involved in the aforementioned experimental research studies, although the rheological properties of the MR fluids are inherently related to the microstructured behaviors of MR suspensions. In fact, the understanding of the microstructure evolution is important for the optimization of MR suspension systems, and it enables the development of MR devices with high performance. However, the existing techniques of experimental observation may have limitations in exploiting the microstructured behaviors of concentrated MR fluids due to their inherent opacity. In this regard, De Vicente et al.28 employed the particle-level simulation method to examine the microstructured behaviors of MR fluids under squeeze flows. They correlated the normal force increase of MR fluids to squeeze-assisted percolating clusters. But their simulation study is limited to dilute suspensions at a very slow strain rate, which is not applicable for highly concentrated MR fluids undergoing fast loading rates that are often encountered in practical applications. As a further extension of this simulation work, Ruiz-López et al.29 inspected the effect of the particle concentration and initial configuration on the squeeze flow behavior of MR fluids based on particle-level simulations. However, the influence of the squeeze rate is ignored as well in this research. Besides, the simulation exploration regarding the MR fluids undergoing squeeze flows is rare to see, let alone the one concerning the shear yield stress under the squeeze strengthening effect, although there are some simulations concerning MR fluid analogues with compression, such as electrorheological fluids.30
In summary, the physical mechanisms behind the microstructure evolution of MR fluids under squeeze flows are still open. Since the mechanical and rheological properties of the suspensions are a macroscopic reflection of their microscopic behavior, some researchers have concentrated on exploiting the microscopic behavior of MR fluids in terms of aggregation kinetics.31–35 The particles’ aggregation kinetics can not only reflect the system resistance to external excitation but also determine the system response time, and is thus worthy of investigation from the scientific and industrial points of view. Actually, there are very few papers concerning the aggregation kinetics of MR fluids with compression. Therefore, a thorough study on the mechanism of the squeeze strengthening rheological properties of MR fluids in terms of the aggregation kinetics needs to be conducted. To this end, the numerical simulation method based on the particle level can be employed to explore the microstructure evolution of MR suspensions with compression. Representative methods include the Monte Carlo simulation,36,37 Brownian dynamics simulation,38,39 molecular dynamics simulation,34,40 dissipative particle dynamics simulation,41,42 Lattice-Boltzmann simulation,43,44etc., which are often used to model the MR fluids from a microscopic level. Among the above simulation methods, the molecular dynamics simulation is the most commonly used one; it also has broad application prospects in many other composite materials and engineering fields, such as electrorheological fluids,45 magnetorheological gels,46 magnetorheological elastomers,47 carbon nanotubes,48,49 and concrete.50 Therefore, in the current work, we explore the aggregation kinetics of MR fluids under squeeze flows by performing molecular dynamics simulations, with emphasis on the particle distribution, cluster kinetics, particle connectivity and magnetic energy.
The rest of the paper is organized as follows: in Section 2, the molecular dynamics simulation is conducted on MR fluids under steady state, squeeze flows and shear flows; based on the simulation results, the rheological properties of the suspensions at different magnetic fields, particle concentrations and squeeze rates are analyzed in Sections 3; Section 4 correlates the rheological behavior of MR fluids to the microscopic structures of particles in terms of their aggregation kinetics. In the final section, the conclusions and prospects are presented.
2. Molecular dynamics simulations
Molecular dynamics simulations are carried out to explore the microstructured behaviors of the MR fluids under steady state, squeeze flows and shear flows. Fig. 1 shows the schematic diagram of the simulation system, in which the magnetic particles are simplified as N monodisperse spherical particles suspended in a continuous phase. The simulation domain is contained in a cuboid box with periodic boundary conditions in all directions for approximating a large suspension system. At the initial time, the magnetic particles are randomly distributed in the simulation box. They are then structured and maintained at a steady morphology under a uniform magnetic field applied in the z direction. The subsequent squeeze flows are imposed opposite to the magnetic field direction. To eliminate the increase of particle concentration caused by the squeeze-induced gap narrowing, a constant volume operation is adopted by expanding the length along the y-axis in the squeezing process. The shear flows are imposed along the x direction at last.2.1. Simulation details
 between the suspended particles and the surrounding continuous phases, Brownian forces FB, and particle gravity forces Fg. The detailed definitions for all the forces involved in the simulation system are given below.
between the suspended particles and the surrounding continuous phases, Brownian forces FB, and particle gravity forces Fg. The detailed definitions for all the forces involved in the simulation system are given below.
The magnetic interaction force is computed based on the dipole–dipole approximation, as expressed by
Fijd = Fm[(1 − 3cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θij)er − sin2θijeθ] θij)er − sin2θijeθ] | (1) |
The hydrodynamic force is simplified as the Stokes drag, defined as
 | (2) |
 | (3) |
v∞(ri) = ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ziex ziex | (4) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is shear rate; and ex is the unit vector denoting the X-direction.
is shear rate; and ex is the unit vector denoting the X-direction.
To prevent particles from overlapping, the Lennard-Jones potential is employed to calculate the short-range repulsive force which is expressed as follows:
 | (5) |
The resultant force Fg of gravity and buoyancy imposed on particle i is given by
 | (6) |
The Brownian force FB is a stochastic force in R3 space, with the statistics of its component53
| E[FB(t)] = 0, E[FB(t + τ)FB(t)] = 2Dδ(τ) | (7) |
Finally, the Langevin equation is employed to describe the motion of each particle, as expressed in eqn (6), in which subscripts i and j are employed for denoting two arbitrary magnetic particles i and j, respectively:
 | (8) |
| length: ls = d = 2r force: Fs = Fm time: ts = 6πηcr2/Fm | (9) |
| Simulation parameters | Value |
|---|---|
| Particle diameter, d | 1.0 × 10−5 m |
| Particle density, ρp | 7800 kg m−3 |
| Relative permeability of particles, μp | 1000 |
| Viscosity of carrier fluid, ηc | 0.3 Pa s |
| Density of carrier fluid, ρc | 3600 kg m−3 |
| Relative permeability of carrier fluid, μc | 1 |
| Temperature, T | 298 K |
| Time step, Δt | 1.99 × 10−7 s |
| Simulation box, (Lx, Ly, Ly) | (30 × 10−5 m, 15 × 10−5 m, 15 × 10−5 m) |
The atom type of hybrid/sphere/dipole in LAMMPS is used to describe the magnetic particles. At first, all the particles are created with the initial velocities following a Maxwell–Boltzmann distribution. The interparticle interactions are obtained based on the neighbor list method within a cutoff radius rc* = 2.5. Then the equation of motion is numerically solved using the velocity-Verlet algorithm. The whole simulation process includes three steps. First, a uniform magnetic field is applied in the suspension system to achieve a steady state, which is recognized by a static suspension system full of particle chains and aggregates with negligible changes happening as time passes. In this respect, each simulation case is run 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps to reach a steady state. It is worth noting that the uniform magnetic field continues on during all the rest of the simulation. Next, the squeeze flows are imposed on the stationary structures at a constant squeeze rate until a scheduled strain (γc = 0.6) is reached. Third, a steady shear flow is exerted on the squeeze-assisted structures for further exploring the shear properties of MR fluids after their exposure to squeeze flows.
000 steps to reach a steady state. It is worth noting that the uniform magnetic field continues on during all the rest of the simulation. Next, the squeeze flows are imposed on the stationary structures at a constant squeeze rate until a scheduled strain (γc = 0.6) is reached. Third, a steady shear flow is exerted on the squeeze-assisted structures for further exploring the shear properties of MR fluids after their exposure to squeeze flows.
In this work, the magnetic field strength, particle volume fraction and squeeze rate are the main focuses, and the corresponding simulation cases are listed in Table 2. It should be noted that a low squeeze rate will increase the simulation time to a large extent, since the final compression strain is fixed at 0.6 for all the simulation cases. For example, at a fixed particle volume fraction of 5.0% and a fixed magnetic field of 100 kA m−1, the simulation time for a squeeze rate of 1.0 s−1 is about 1242 seconds (3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps), which is nearly 8 times larger than the simulation time for the squeeze rate at 9.0 s−1 (144 seconds, 335
000 steps), which is nearly 8 times larger than the simulation time for the squeeze rate at 9.0 s−1 (144 seconds, 335![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps). Thus, to keep computational efficiency, the squeeze rate is fixed at 7.5 s−1 in the simulation cases when the magnetic field or particle concentration is the critical variable of concern.
000 steps). Thus, to keep computational efficiency, the squeeze rate is fixed at 7.5 s−1 in the simulation cases when the magnetic field or particle concentration is the critical variable of concern.
| Simulation case | Particle volume fraction (%) | Particle number | Magnetic field (kA m−1) | Squeeze rate (s−1) |
|---|---|---|---|---|
| 1 | 5 | 645 | 50 | 7.5 |
| 2 | 5 | 645 | 100 | 7.5 |
| 3 | 5 | 645 | 150 | 7.5 |
| 4 | 5 | 645 | 200 | 7.5 |
| 5 | 10 | 1289 | 100 | 7.5 |
| 6 | 15 | 1934 | 100 | 7.5 |
| 7 | 20 | 2578 | 100 | 7.5 |
| 8 | 10 | 1289 | 100 | 3.0 |
| 9 | 10 | 1289 | 100 | 4.5 |
| 10 | 10 | 1289 | 100 | 6.0 |
| 11 | 10 | 1289 | 100 | 9.0 |
The macroscopic shear stress τxz is thus calculated as follows:56
 | (10) |
Similarly, the macroscopic normal stress in the suspension can be obtained by29
 | (11) |
2.2. Simulation validation
We take two steps to validate the simulation model. First, to validate the steady-state simulation, the molecular dynamics simulation is conducted on the MR fluids (φ = 5.0%) under a uniform magnetic field (100 kA m−1) as an example. The corresponding simulation data are collected to obtain the statistical information on the particle aggregation kinetics, which are verified by comparison with previous experimental findings. Second, to validate the squeeze flow simulation, we perform a series of simulations, from which the normal stress upon compression is calculated and then compared with previous simulation data and theoretical predictions. | (12) |
 | (13) |
Fig. 2 shows the variations of the described statistical variables along with the dimensionless simulation time. It can be observed that at the initial time, the value of Nc approaches the value of N1, revealing a uniform and separated distribution of particles, though Na ≠ 0 demonstrates that a fraction of particles are aggregated. Two vertical dashed lines divide the aggregation process into three stages. In the first stage, S(t), l(t) and Na(t) all exhibit a slightly increasing trend while N1(t) and Nc(t) gradually decrease. This is because the particles are initially separated and their interactions are weak. In the second stage, these statistical variables all exhibit a power-law dependency on time, showing a fast aggregation speed due to active particle interactions at this stage. In the third stage, all the statistical variables attain a plateau region, indicating a steady state of the suspension system. Among all the statistical variables concerning aggregation kinetics of MR suspensions, the weight average cluster size S(t) is the most interesting, which has been frequently studied.31,33–35,57,58 Here, we select S(t) for further discussion. According to the literature,34,35,59 the variation trend of S(t) along with time t at the first and second stages can be described by
| S(t) = S(0)[1 + (t/tsc)z] | (14) |
| S(t*) = 1 + (t*/0.005)0.66 | (15) |
 | ||
| Fig. 2 Statistical variables as a function of dimensionless simulation time for MR fluids (φ = 5.0%) under a uniform magnetic field (H = 100 kA m−1). | ||
A comparison is then made between the simulation data and fitting equation, as shown in Fig. 3, in which a reasonably good consistency is observed. To sum up, the aggregation kinetics of MR fluids described above is in qualitative agreement with previous experimental observations31,34,35,60 as well as quantitative agreement with the theoretical predictions,59 which has demonstrated the credibility and accuracy of simulation results presented in this study.
 | ||
| Fig. 4 Dimensionless and normalized normal stresses as a function of (1 − ε) for MR fluids with compression at a fixed squeeze rate of 7.5 s−1. | ||
With reference to ref. 29, we further normalized the normal stress by dividing the normal yield stress derived by Ruiz-López et al.,26 as expressed in eqn (14). The normalized dimensionless normal stress τzz*/τYC* is thus obtained and depicted as a function of (1 − ε) in Fig. 4. It is clear to see that the scaled data from different magnetic fields and particle volume fractions all reasonably collapse onto a master curve, indicating a good consistency between the simulation results with the predictions from the theoretical model proposed by Ruiz-López et al.26
 | (16) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
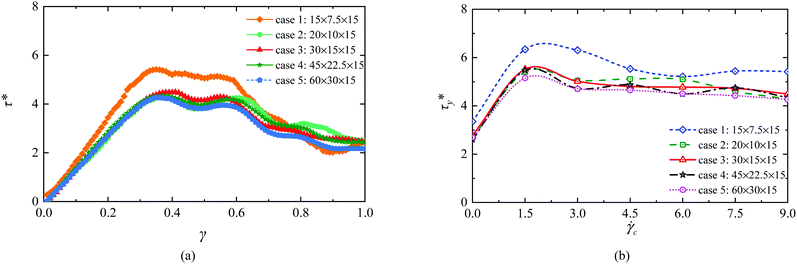
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, which is often used in the simulation studies of MR fluids. For example, the box size is 22 × 11 × 11 in ref. 61, 20 × 10 × 10 in ref. 55, and 10 × 5 × 5 in ref. 62 and 63. To further validate the suitability of this simulation box size in modeling MR fluids, a series of simulations have been conducted by taking the box size as a control variable. The original simulation box size (30 × 15 × 15) is regarded as a benchmark, and the box sizes of the supplemental simulation cases are derived by proportionally changing the original simulation box lengths in X- and Y-directions. The corresponding box sizes for different simulation cases are given as follows: Case 1, 15 × 7.5 × 15; Case 2, 20 × 10 × 15; Case 3, 30 × 15 × 15; Case 4, 45 × 22.55 × 15; and Case 5, 60 × 30 × 15. Other critical simulation parameters, such as magnetic field (H = 100 kA m−1), particle volume fraction (φ = 10.0%) and squeeze rate (
1, which is often used in the simulation studies of MR fluids. For example, the box size is 22 × 11 × 11 in ref. 61, 20 × 10 × 10 in ref. 55, and 10 × 5 × 5 in ref. 62 and 63. To further validate the suitability of this simulation box size in modeling MR fluids, a series of simulations have been conducted by taking the box size as a control variable. The original simulation box size (30 × 15 × 15) is regarded as a benchmark, and the box sizes of the supplemental simulation cases are derived by proportionally changing the original simulation box lengths in X- and Y-directions. The corresponding box sizes for different simulation cases are given as follows: Case 1, 15 × 7.5 × 15; Case 2, 20 × 10 × 15; Case 3, 30 × 15 × 15; Case 4, 45 × 22.55 × 15; and Case 5, 60 × 30 × 15. Other critical simulation parameters, such as magnetic field (H = 100 kA m−1), particle volume fraction (φ = 10.0%) and squeeze rate (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c = 9.0 s−1), remain the same for the above five simulation cases. The shear stress versus shear strain curves obtained from different simulation cases are then compared in Fig. 5(a). It is observed that the stress curves in Cases 2 to 5 are similar to each other except for the stress curve in Case 1. We further varied the squeeze rates in the above five simulation cases to obtain the corresponding shear stress information. The shear yield stresses as a function of box size and squeeze rate are depicted in Fig. 5(b). It is clear that all the curves show a similar variation trend and the shear yield stresses from different box sizes at the same squeeze rates are close except for the stresses from a box size of 15 × 7.5 × 15. The significant stress differences between Case 5 and other cases may be attributed to the small box size and small width-height ratio of the simulation box used in Case 1, evidencing the influence of simulation box size on the stress components. However, the stress differences between Case 3 and Cases 4 and 5, which are caused by expanding the box lengths in X- and Y-directions by a factor of 1.5 or 2, are small enough to be neglected, indicating that the selected simulation box size is suitable for rheology investigation.
c = 9.0 s−1), remain the same for the above five simulation cases. The shear stress versus shear strain curves obtained from different simulation cases are then compared in Fig. 5(a). It is observed that the stress curves in Cases 2 to 5 are similar to each other except for the stress curve in Case 1. We further varied the squeeze rates in the above five simulation cases to obtain the corresponding shear stress information. The shear yield stresses as a function of box size and squeeze rate are depicted in Fig. 5(b). It is clear that all the curves show a similar variation trend and the shear yield stresses from different box sizes at the same squeeze rates are close except for the stresses from a box size of 15 × 7.5 × 15. The significant stress differences between Case 5 and other cases may be attributed to the small box size and small width-height ratio of the simulation box used in Case 1, evidencing the influence of simulation box size on the stress components. However, the stress differences between Case 3 and Cases 4 and 5, which are caused by expanding the box lengths in X- and Y-directions by a factor of 1.5 or 2, are small enough to be neglected, indicating that the selected simulation box size is suitable for rheology investigation.
On the other hand, in Section 2.2, the simulation results using the original box concerning aggregation kinetics and normal stress of MR fluids have been verified in comparison with previous experimental and theoretical investigations and a good consistency is achieved. To conclude, the simulation box size (30 × 15 × 15) is suitable to accurately model MR fluids from the aspects of microstructured behaviors and rheological properties.
3. Rheological properties
In this section, the rheological properties of MR fluids are first examined, with emphasis on the shear stress and normal stress.3.1. Shear stress
In order to explore the effect of the squeeze rate on the shear stress of MR fluids, the suspension with a particle volume fraction of 10.0% under an external magnetic field of 100 kA m−1 is investigated as an example. More details for simulation parameters are provided in Tables 1 and 2. The suspensions are first subjected to a uniform magnetic field for 20 ms to reach a steady state. Squeeze flows at different rates are then imposed on the stationary structures and ceased as soon as the compressive strain arrives at 0.6. Finally, shear flows are applied in the squeeze-assisted structure. Fig. 6 shows the dimensionless relationship curves between the shear stress and shear strain of the suspensions at different squeeze rates. When the squeeze rate is zero, i.e. no squeeze flows are applied, the shear stress versus shear strain curve shows a typical variation trend.64 It can be summarized as follows: at a relatively low shear strain level, the shear stress grows linearly before the elastic-limit yield stress is reached; as the shear strain increases, the shear stress shows a nonlinear increasing trend before the static yield stress is reached; at a high shear strain level, the shear stress first decreases, then increases to the dynamic yield stress, and finally fluctuates to a plateau value as the shear strain progresses. Concerning the effect of the squeeze rate, it is clear from Fig. 6 that the static and dynamic yield stresses are both enhanced with compression. Interestingly, the shear stress versus shear strain curves of the compressed suspensions show a similar variation trend to that of the suspensions without compression before the dynamic yield stress is reached. After the dynamic yield stress is exceeded, shear stresses in the compressed suspensions show an obvious decreasing trend with the increase of shear strain and finally decrease to a same stress level as the suspensions without compression. In the meantime, it is worth noting that the shear stress shows an increasing trend with the decreasing squeeze rate, though the relationship curves between shear stress and shear strain for the suspensions at different squeeze rates are close. | ||
| Fig. 6 Shear stress vs. shear strain curves of MR fluids at different squeeze rates: the particle volume fraction and magnetic field strength are fixed at 10.0% and 100 kA m−1, respectively. | ||
To obtain a higher shear stress level, more simulation cases regarding the squeeze rate (γc = 0.5, 1.0 1.5, 2.0, 2.5 s−1) are added. Fig. 7 shows the dimensionless shear yield stress τy* as a function of the squeeze rate. It is seen that the highest yield stress is obtained when the squeeze rate reaches 1.0 s−1. The critical squeeze rate is thus denoted as ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c = 1.0 s−1, see the critical point in Fig. 7. At an increasing squeeze rate, the yield stress increases sharply before the critical point is reached and decreases slowly after the critical point is surpassed. This finding is important for the definition of a reasonable squeeze rate, i.e.,
c = 1.0 s−1, see the critical point in Fig. 7. At an increasing squeeze rate, the yield stress increases sharply before the critical point is reached and decreases slowly after the critical point is surpassed. This finding is important for the definition of a reasonable squeeze rate, i.e., ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c = 7.5 s−1, to be used in the analysis of critical variables of concern such as the magnetic field and particle concentration in the following sections.
c = 7.5 s−1, to be used in the analysis of critical variables of concern such as the magnetic field and particle concentration in the following sections.
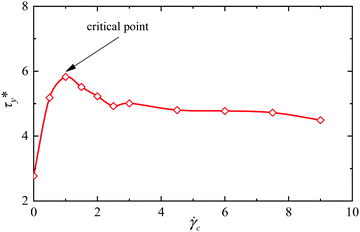 | ||
| Fig. 7 Shear yield stress of MR fluids as a function of squeeze rate: the particle volume fraction and magnetic field strength are fixed at 10.0% and 100 kA m−1, respectively. | ||
To examine the effect of the magnetic field and particle concentration, the dimensionless shear yield stresses τy* of MR fluids in the absence and presence of squeeze flows as a function of magnetic field strength and particle volume fraction are shown in Fig. 8(a) and (b), respectively. As observed in Fig. 8(a), the shear yield stress increases with increasing magnetic field strength; the compression can effectively enhance the yield stress to a larger extent at a higher magnetic field strength. Concerning the effect of particle concentration, it is obvious in Fig. 8(b) that the shear yield stress is positively correlated with the particle volume fraction. And the shear yield stress in the suspensions without compression is increased almost linearly with the particle concentration while the shear yield stress in the compressed suspensions exhibits a logarithmic growth with the particle concentration. This implies that the squeeze strengthening effect is more prominent for the dilute suspensions.
 | ||
Fig. 8 Shear yield stress of MR fluids in the absence and presence of squeeze flows (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c = 7.5 s−1): (a) varying magnetic field (φ = 5.0%) and (b) varying particle volume fraction (H = 100 kA m−1). c = 7.5 s−1): (a) varying magnetic field (φ = 5.0%) and (b) varying particle volume fraction (H = 100 kA m−1). | ||
3.2. Normal stress
The normal stresses of MR fluids with a fixed particle volume fraction of 10.0% and a fixed magnetic field strength of 100 kA m−1 at different squeeze rates as a function of shear strain are depicted in Fig. 9. It is seen that the normal stresses in the compressed suspensions are much larger than those in the suspensions without compression (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c = 0.0 s−1), but the variation trends of normal stress in all the suspensions are similar. There are mainly three regions in the tendency of normal stress along with shear strain, which is similar to the experimental observations on the magnetorheological gels recorded in ref. 46. In the first region (Region I), the normal stress remains essentially constant as shear strain increases. This is mainly because the suspensions are filled with the field-induced columnar structures aligned in the field direction at a low shear strain level. However, it should be noted that there is a little difference from the tendency between the normal stresses in the suspensions with and without compression, i.e. the normal stress in the compressed suspensions shows a slightly increasing tendency; while the normal stress in the suspensions without compression shows a slightly decreasing tendency. In the second region (Region II), the normal stress shows a rapid downtrend with the increasing shear strain for both suspensions with and without compressions, due to columnar structures undergoing inclination and deformation to resist shear flows. As the shear strain further progresses, the normal stress fluctuates more seriously in the third region (Region III), which is mainly attributed to the field-induced structures experiencing continuous breakup and rearrangement under a large shear strain. Furthermore, it can be seen from Fig. 9 that after the critical squeeze rate (
c = 0.0 s−1), but the variation trends of normal stress in all the suspensions are similar. There are mainly three regions in the tendency of normal stress along with shear strain, which is similar to the experimental observations on the magnetorheological gels recorded in ref. 46. In the first region (Region I), the normal stress remains essentially constant as shear strain increases. This is mainly because the suspensions are filled with the field-induced columnar structures aligned in the field direction at a low shear strain level. However, it should be noted that there is a little difference from the tendency between the normal stresses in the suspensions with and without compression, i.e. the normal stress in the compressed suspensions shows a slightly increasing tendency; while the normal stress in the suspensions without compression shows a slightly decreasing tendency. In the second region (Region II), the normal stress shows a rapid downtrend with the increasing shear strain for both suspensions with and without compressions, due to columnar structures undergoing inclination and deformation to resist shear flows. As the shear strain further progresses, the normal stress fluctuates more seriously in the third region (Region III), which is mainly attributed to the field-induced structures experiencing continuous breakup and rearrangement under a large shear strain. Furthermore, it can be seen from Fig. 9 that after the critical squeeze rate (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c = 1.0 s−1) is surpassed, the increasing squeeze rate exerts an adverse impact on the normal stress of MR fluids in the first region. A similar phenomenon can be found in the experimental investigations concerning electro-rheological fluids reported by Chio and McIntyre et al.,65,66 respectively, i.e., the normal stress of electrorheological fluids is increased with the decrease of the squeeze rate. However, in the second and third regions, the normal stress of MR fluids becomes less sensitive to the squeeze rate.
c = 1.0 s−1) is surpassed, the increasing squeeze rate exerts an adverse impact on the normal stress of MR fluids in the first region. A similar phenomenon can be found in the experimental investigations concerning electro-rheological fluids reported by Chio and McIntyre et al.,65,66 respectively, i.e., the normal stress of electrorheological fluids is increased with the decrease of the squeeze rate. However, in the second and third regions, the normal stress of MR fluids becomes less sensitive to the squeeze rate.
 | ||
| Fig. 9 Normal stress of MR fluids at different squeeze rates as a function of shear strain: the particle volume fraction and magnetic field strength are fixed at 10.0% and 100 kA m−1, respectively. | ||
Fig. 10(a) shows the normal stress versus shear strain of MR fluids in the absence (dashed lines and hollow symbols) and presence (solid lines and solid symbols) of squeeze flows under different magnetic fields and particle volume fractions. The squeeze rate for all the squeezed suspensions is fixed at 7.5 s−1. It can be observed that the normal stress is increased under squeeze flows. And the higher the magnetic field, the larger extent of the normal stress can be improved by the squeeze flows. Besides, it is noted that the curves of normal stress versus shear strain in all cases show a similar variation trend, characterized by the three typical regions described above. As observed in Fig. 10(b), similar trends are also seen in the suspensions with different particle volume fractions that the normal stress is increased under squeeze flows, and it has a positive relationship with the particle concentration. However, as the particle concentration increases, the normal stress in the compressed suspensions gets closer to the suspensions without compression, which implies that the squeeze strengthening effect on the normal stress is less remarkable with the increase of particle volume fraction.
4. Microstructure evolution
The bulk behaviors of MR fluids are closely related to their microscopic structures. To gain insight into the effect of squeeze flows on the MR fluids, we seek to characterize their microstructured behaviors in terms of aggregation kinetics under steady magnetic fields and squeeze flows. The critical factors that influence the aggregation kinetics of suspensions such as the magnetic field, particle concentration and squeeze rate are investigated. Meanwhile, the statistical quantities for representing the aggregation kinetics, i.e., the particle distribution, cluster kinetics, particle connectivity and magnetic energy, are particularly addressed to probe the mechanism of the squeeze strengthening effect.4.1. Particle distribution
To have a particle-level insight, the time evolution of particles’ positions in the absence and presence of squeeze flows is monitored by calculating the particle distribution ratio, which is defined as the ratio of the particle number between different coordinates along the x or y-axis to the total particle number in the simulation system. Fig. 11 shows the particle distribution ratio of MR fluids (φ = 10.0%) without compression under a uniform magnetic field (H = 100 kA m−1) at typical instants of simulation times of 0, 4, 8, 12, 16 and 20 ms. It is seen that the values of the particle distribution ratios along different coordinates are basically the same at the initial state (t = 0 ms), see the x-axis in Fig. 11(a) and the y-axis in Fig. 11(b), demonstrating that the particles are uniformly distributed in the suspensions when no magnetic field is applied. Once the magnetic field is applied, the particle distribution ratios along the x-axis and y-axis both fluctuate to show a non-uniform distribution, demonstrating that the suspensions have gradually arrived at a steady morphology as the simulation time passes. It is because, under the action of a magnetic field, the suspended particles get magnetized and form into chain-like and column structures aligned with the field direction (z-axis). As a result, the particle distribution ratio becomes larger at the coordinates where the chain-like and columnar structures are located and become smaller at the coordinates where obvious gaps between the field-induced structures appear. The stationary structures of MR suspensions obtained from the steady-state simulation are then used as the initial configuration for the squeeze simulation. Fig. 12 shows the particle distribution ratios of MR fluids under squeeze flows (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c = 7.5 s−1) at different compressive strains. It is seen that the particle distribution ratio along the x-axis gradually levels off under an increasing compressive strain. It should be noted that the gap distance of the simulation box narrows down under squeeze flows, while the length of the simulation box along the x-axis remains unchanged. The narrowing gap contributes to the collapse of the field-induced chain-like structures, resulting in the formation of many shorter and stronger columnar structures. As a consequence, the x-component separation between particles shortens, resulting in a more uniform distribution of the particle distribution ratio along the x-axis. The variation trend of the particle distribution ratio along the y-axis under increasing compressive strain is similar to that along the x-axis. It should be noted that the length of the simulation box along the y-axis is continuously elongated to retain a constant volume of the simulation box during the compression process. However, the particle distribution ratios for different compressive strains nearly decrease to zero around y* = −12 and y* = 12. It is revealed, meanwhile, that the particles mainly remain in the center zone of the y-axis, which may be related to the dominant role of magnetic interaction forces in the particle motion. To illustrate this point, the data collected from the compression simulation in this section are used to estimate the magnitudes of all the force terms included in the governing equation, i.e., eqn (4).
c = 7.5 s−1) at different compressive strains. It is seen that the particle distribution ratio along the x-axis gradually levels off under an increasing compressive strain. It should be noted that the gap distance of the simulation box narrows down under squeeze flows, while the length of the simulation box along the x-axis remains unchanged. The narrowing gap contributes to the collapse of the field-induced chain-like structures, resulting in the formation of many shorter and stronger columnar structures. As a consequence, the x-component separation between particles shortens, resulting in a more uniform distribution of the particle distribution ratio along the x-axis. The variation trend of the particle distribution ratio along the y-axis under increasing compressive strain is similar to that along the x-axis. It should be noted that the length of the simulation box along the y-axis is continuously elongated to retain a constant volume of the simulation box during the compression process. However, the particle distribution ratios for different compressive strains nearly decrease to zero around y* = −12 and y* = 12. It is revealed, meanwhile, that the particles mainly remain in the center zone of the y-axis, which may be related to the dominant role of magnetic interaction forces in the particle motion. To illustrate this point, the data collected from the compression simulation in this section are used to estimate the magnitudes of all the force terms included in the governing equation, i.e., eqn (4).
 | ||
| Fig. 11 Particle distribution ratio of MR fluids (φ = 10.0%, H = 100 kA−m−1) without compression at typical instants of simulation time: (a) x-axis and (b) y-axis. | ||
 | ||
Fig. 12 Particle distribution ratios of MR fluids (φ = 10.0%, H = 100 kA m−1, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c = 7.5 s−1) under different compressive strains: (a) x-axis and (b) y-axis. c = 7.5 s−1) under different compressive strains: (a) x-axis and (b) y-axis. | ||
 into two parts, i.e., particle–velocity relevant component Fvi and ambient–fluid–velocity relevant component Fv∞. To derive the range of the magnitudes of the two force components, the particle motion data from a typical simulation (H = 100 kA m−1, φ = 10.0%,
into two parts, i.e., particle–velocity relevant component Fvi and ambient–fluid–velocity relevant component Fv∞. To derive the range of the magnitudes of the two force components, the particle motion data from a typical simulation (H = 100 kA m−1, φ = 10.0%, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c = 7.5 s−1,
c = 7.5 s−1, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) = 1 s−1) are used as an example to address the problem. Fig. 13(a) and (b) show the time evolution of the two viscous force components of five randomly-selected particles (p1, p2, p3, p4 and p5) during the squeezing and shearing processes, respectively. It is seen that, under squeeze flows, the magnitudes of ambient–fluid–velocity relevant forces (Fv∞) gradually increase, whereas the magnitudes of particle–velocity relevant forces (Fvi) fluctuate greatly. As for the shearing process, the magnitudes of ambient–fluid–velocity relevant forces mainly remain at a very small value due to the small applied shear rate while the magnitudes of particle–velocity relevant forces fluctuate to higher values. Subsequently, to make the analysis results more general and representative, time evolution of the average magnitudes of viscous force components, Fvave (particle–velocity relevant) and
= 1 s−1) are used as an example to address the problem. Fig. 13(a) and (b) show the time evolution of the two viscous force components of five randomly-selected particles (p1, p2, p3, p4 and p5) during the squeezing and shearing processes, respectively. It is seen that, under squeeze flows, the magnitudes of ambient–fluid–velocity relevant forces (Fv∞) gradually increase, whereas the magnitudes of particle–velocity relevant forces (Fvi) fluctuate greatly. As for the shearing process, the magnitudes of ambient–fluid–velocity relevant forces mainly remain at a very small value due to the small applied shear rate while the magnitudes of particle–velocity relevant forces fluctuate to higher values. Subsequently, to make the analysis results more general and representative, time evolution of the average magnitudes of viscous force components, Fvave (particle–velocity relevant) and  (ambient–fluid–velocity relevant), are calculated by averaging the corresponding force components of all the particles, as shown in Fig. 13(c) and (d). It is seen that, in the squeezing process, Fvave shows a slight increasing trend with significant fluctuations, and
(ambient–fluid–velocity relevant), are calculated by averaging the corresponding force components of all the particles, as shown in Fig. 13(c) and (d). It is seen that, in the squeezing process, Fvave shows a slight increasing trend with significant fluctuations, and  increases slowly and finally surpasses Fvave. During the shearing process, Fvave fluctuates as well but
increases slowly and finally surpasses Fvave. During the shearing process, Fvave fluctuates as well but  basically remains at a small constant value (Fig. 14).
basically remains at a small constant value (Fig. 14).
 | (17) |
Based on the above analysis, it is noted that the magnetic force of two vertically contacting particles in a chain is several orders of magnitudes higher than the gravitational and Brownian forces. Though the viscous force under squeeze or shear flows is increased as the simulation proceeds, it still much lower than the magnetic force. Therefore, the magnetic force is dominant in the simulation, especially upon the application of a high magnetic field. Therefore, compared to other force terms, the magnetic attractions are strong enough to keep magnetic particles in the center zone without scattering too far in all directions when the squeeze flows are applied in the suspensions. Consequently, one might recognize that the implicit carrier fluids are squeezed to the rim of the simulation box under squeeze flows, resulting in an increase of local particle concentration that contributes to the squeeze-assisted MR fluid strengthening. It is worth noting that this fluid–particle separation phenomenon has been described in the literature66,68 and demonstrated to depend on fluid viscosity, squeeze rate, and magnetic field.
4.2. Cluster kinetics
The evolution of particle distribution of MR fluids under steady state and squeeze flows has been analyzed and compared. To further have a direct observation on the particle aggregation undergoing squeeze flows, we characterize the average cluster size and cluster number as a function of compressive strain. Fig. 15(a) shows the relationship curves between cluster size l(t), cluster number N(t) and compressive strain ε under different magnetic fields and particle volume fractions. The squeeze rate for all the suspensions is fixed at 7.5 s−1. It is seen that the average cluster size increases and the cluster number decreases with the increasing compressive strain under a low magnetic field. Improving the magnetic field strength can increase the cluster size, but the increment is not obvious when the magnetic field strength exceeds 100 kA m−1. This is because the total number of particles is constant at a fixed particle volume fraction and the increasing magnetic field has a more significant impact on the direction and anisotropy of particle aggregates instead of their sizes. Since the cluster kinetics is not strong evidence for supporting the fact that increasing magnetic field strength improves the rheological properties of the compressed MR fluids, the direction and anisotropy of particle aggregation under different magnetic fields will be further discussed in the next subsection.In Fig. 15(b), it is seen that the average cluster size increases and the cluster number decreases with the increasing particle concentration, due to the formation of larger clusters and thicker columnar structures. However, it is also observed that as the particle concentration increases, both the cluster size and cluster number tend to become more insensitive to the compressive strain and gradually level off with the increasing compressive strain. This implies that the squeeze strengthening effect on the rheological properties of MR fluids becomes less prominent with the increasing particle volume fraction, which is consistent with the macroscopic phenomenon illustrated in Fig. 8(b).
4.3. Particle connectivity
To further correlate the microstructure to macroscopic rheological properties of MR fluids, we now characterize the direction and anisotropy of particle aggregates by using the particle connectivity C(θ),69 which is defined as the ratio of the particle number N(θ) to the total number of particles N minus one, as expressed by | (18) |
The particle connectivity of MR fluids (φ = 5.0%) under different magnetic fields in the absence (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c = 0.0 s−1) and presence (
c = 0.0 s−1) and presence (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c = 7.5 s−1) of squeeze flows is depicted as a function of angle θ, as presented in Fig. 16. It is seen that for the uncompressed suspensions under a low magnetic field (e.g., 50 kA m−1), only a smaller peak appears at θ = 0°, indicating that there are mainly single chains aligned with the magnetic field direction in the suspensions. When the squeeze flows are applied in the same suspensions, the peak at θ = 0° remains unchanged and a new higher peak appears at θ = 60°, suggesting the formation of thicker chains and columnar structures. It can also be observed that, under an increasing magnetic field strength, the peaks at θ = 0° and θ = 60° for the compressed suspensions both increase faster compared to that of the uncompressed suspensions, demonstrating that increasing the magnetic field strength can strengthen the impact of compression on the particle connectivity. Due to the increasing particle connectivity, the structure verticalness, anisotropy and lateral complexity are increased, which enhances the structures’ resistance to the imposed shear flows. As a consequence, the macroscopic rheological properties of MR fluids are greatly strengthened.
c = 7.5 s−1) of squeeze flows is depicted as a function of angle θ, as presented in Fig. 16. It is seen that for the uncompressed suspensions under a low magnetic field (e.g., 50 kA m−1), only a smaller peak appears at θ = 0°, indicating that there are mainly single chains aligned with the magnetic field direction in the suspensions. When the squeeze flows are applied in the same suspensions, the peak at θ = 0° remains unchanged and a new higher peak appears at θ = 60°, suggesting the formation of thicker chains and columnar structures. It can also be observed that, under an increasing magnetic field strength, the peaks at θ = 0° and θ = 60° for the compressed suspensions both increase faster compared to that of the uncompressed suspensions, demonstrating that increasing the magnetic field strength can strengthen the impact of compression on the particle connectivity. Due to the increasing particle connectivity, the structure verticalness, anisotropy and lateral complexity are increased, which enhances the structures’ resistance to the imposed shear flows. As a consequence, the macroscopic rheological properties of MR fluids are greatly strengthened.
 | ||
Fig. 16 Particle connectivity of MR fluids (φ = 5.0%) under different magnetic fields in the absence and presence of squeeze flows: (a) without compression and (b) with compression (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c = 7.5 s−1). c = 7.5 s−1). | ||
In Fig. 17, the particle connectivity of MR fluids with different particle volume fractions under a fixed magnetic field (H = 100 kA m−1) in the absence and presence of squeeze flows (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c = 7.5 s−1) is illustrated as a function of angle θ. It shows that under a low particle volume fraction (φ = 5.0%), the peak value at θ = 60° of is increased when the suspensions are squeezed. However, when the particle volume fraction exceeds 10.0%, the peak values at θ = 0° and θ = 60° of the compressed suspensions is instead smaller than the suspensions without compression. It can be drawn that the squeeze strengthening effect on the particle connectivity is more prominent for the dilute suspensions, which is accountable for the conclusions obtained in Section 3 that the squeeze strengthening effect is more effective for improving the rheological properties of dilute suspensions.
c = 7.5 s−1) is illustrated as a function of angle θ. It shows that under a low particle volume fraction (φ = 5.0%), the peak value at θ = 60° of is increased when the suspensions are squeezed. However, when the particle volume fraction exceeds 10.0%, the peak values at θ = 0° and θ = 60° of the compressed suspensions is instead smaller than the suspensions without compression. It can be drawn that the squeeze strengthening effect on the particle connectivity is more prominent for the dilute suspensions, which is accountable for the conclusions obtained in Section 3 that the squeeze strengthening effect is more effective for improving the rheological properties of dilute suspensions.
 | ||
Fig. 17 Particle connectivity of MR fluids with different particle volume fractions under a uniform magnetic field (H = 100 kA m−1): (a) without compression and (b) with compression (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c = 7.5 s−1). c = 7.5 s−1). | ||
The effect of the squeeze rate on the particle connectivity of MR fluids at a fixed particle volume fraction of 10.0% and a fixed magnetic field of 100 kA m−1 is examined, as presented in Fig. 18. It can be observed that after the critical squeeze rate is surpassed, the peaks at θ = 0° and θ = 60° both increase with the decrease of the squeeze rate, because a lower squeeze rate allows more reconstruction time for particle aggregates which contributes to the formation of more compact and stronger structures. The structure verticalness, anisotropy and lateral complexity are thus improved at a decreasing squeeze rate. The macroscopic reflection is the enhanced rheological properties, as shown in Fig. 6, 7 and 9.
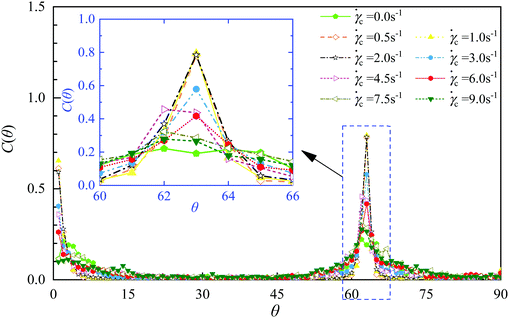 | ||
| Fig. 18 Particle connectivity of MR fluids under squeeze flows at different squeeze rates: the particle volume fraction and magnetic field strength are fixed at 10.0% and 100 kA m−1, respectively. | ||
4.4. Magnetic energy
To characterize the whole structuration process of MR suspensions including the steady state and compression state, the time evolution of the magnetic energy of MR fluids is inspected herein. The magnetic energy between particles i and j can be estimated as follows:Uij = U0(1 − 3cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θij) θij) | (19) |
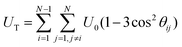 | (20) |
As can be seen from eqn (16), the magnetic energy is correlated with the magnetic field, particle concentration and θij. It is difficult to separate these three contributions because θij is dependent on both the magnetic field and particle concentration. Nevertheless, to facilitate the study of the impacts of the magnetic field and particle concentration on the magnetic energy, we still analyzed the effect of θij by depicting the normalized magnetic energy Uij/U0 against θij, as presented in Fig. 19. It can be drawn that the absolute value of Uij/U0 decreases with θij before a critical angle of 54.7° is reached. Besides, it is worth noting that the interparticle interaction is attractive when 0° ≤ θij < 54.7° and repulsive when 54.7° < θij ≤ 90°.70 When the suspensions are filled with single chain-like structures aligned in the field direction, the probability of θij = 0 is high, suggesting a high attractive magnetic energy between the particles in the fluids. With the formation of lateral connected structures, the probability of two adjacent particles positioned at an angle of around 60° is increased and thus the repulsive magnetic energy is increased.
Fig. 20(a) shows the time evolution of dimensionless magnetic energy per particle, UT*/N, in MR fluids (φ = 5.0%) under different magnetic fields. As can be seen, when the suspension system is under a fixed magnetic field without compression, the absolute value of the dimensionless magnetic energy per particle, denoted by Ua = |UT*/N|, increases sharply at a short time, which is attributed to an active particle motion at the initial aggregation process. After the peak value is surpassed, the particle magnetic energy remains essentially constant as time evolves, suggesting that the suspensions have reached a steady morphology due to the formation of chain-like structures. When the squeeze flows (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c = 7.5 s−1) are imposed on the stationary structures, the particle magnetic energy almost stays constant before a critical compressive strain is reached. After the critical point is exceeded, Ua shows a decreasing trend with the increasing compressive strain. It is known that the squeeze flows facilitate the formation of lateral elongated structures and thus results in the increase of particle connectivity at θ = 60°, which can be reflected in Fig. 16. As a consequence, the probability of θij = 60° is increased, which is the direct reason for the decrease of Ua upon compression. From Fig. 20, we can also conclude that the greater the applied magnetic field strength, the faster the increasing speed and the higher the value of Ua will be. It is mainly attributed to a higher magnetic dipole moment and a higher probability of θij = 60° under an increasing magnetic field.
c = 7.5 s−1) are imposed on the stationary structures, the particle magnetic energy almost stays constant before a critical compressive strain is reached. After the critical point is exceeded, Ua shows a decreasing trend with the increasing compressive strain. It is known that the squeeze flows facilitate the formation of lateral elongated structures and thus results in the increase of particle connectivity at θ = 60°, which can be reflected in Fig. 16. As a consequence, the probability of θij = 60° is increased, which is the direct reason for the decrease of Ua upon compression. From Fig. 20, we can also conclude that the greater the applied magnetic field strength, the faster the increasing speed and the higher the value of Ua will be. It is mainly attributed to a higher magnetic dipole moment and a higher probability of θij = 60° under an increasing magnetic field.
 | ||
Fig. 20 Time evolution of magnetic energy per particle in MR fluids (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c = 7.5 s−1): (a) varying magnetic field (φ = 5.0%) and (b) varying particle volume fraction (H = 100 kA m−1). c = 7.5 s−1): (a) varying magnetic field (φ = 5.0%) and (b) varying particle volume fraction (H = 100 kA m−1). | ||
Fig. 20(b) shows the time evolution of average magnetic energy per particle in MR fluids with different particle volume fractions. Before compression, the absolute value of particle magnetic energy shows a rapid increase at the initial stage and then gradually reaches a plateau. When the squeeze flows (![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c = 7.5 s−1) are applied in the suspensions, the particle magnetic energy shows a slight increasing trend at first and then fluctuates periodically with a decreasing trend. It is because the increasing particle concentration contributes to the formation of multiple-chains and columnar structures, more and more particles are positioned at an angle around 60°. However, at the highest particle volume fraction (φ = 20.0%), the magnetic energy per particle becomes positive when the compressive strain attains 0.6, indicating that the repulsive interaction becomes more prominent among particles. As a consequence, the squeeze strengthening effect on the rheological properties of MR fluids becomes less remarkable at an increasing particle concentration.
c = 7.5 s−1) are applied in the suspensions, the particle magnetic energy shows a slight increasing trend at first and then fluctuates periodically with a decreasing trend. It is because the increasing particle concentration contributes to the formation of multiple-chains and columnar structures, more and more particles are positioned at an angle around 60°. However, at the highest particle volume fraction (φ = 20.0%), the magnetic energy per particle becomes positive when the compressive strain attains 0.6, indicating that the repulsive interaction becomes more prominent among particles. As a consequence, the squeeze strengthening effect on the rheological properties of MR fluids becomes less remarkable at an increasing particle concentration.
5. Conclusions
In this study, a systematic investigation is conducted on MR fluids under steady state, squeeze flows and shear flows based on the molecular dynamics simulation, with main attention focused on the squeeze-assisted MR fluid strengthening. The squeeze strengthening effect on the rheological properties of MR fluids is first examined and then correlated to the microstructured behaviors of MR suspensions in terms of their aggregation kinetics. The main conclusions are summarized as follows:(1) Under steady-state simulation, the particle distribution ratios along the x-axis and y-axis fluctuate from the initially uniform distribution, presenting a non-uniform particle distribution as time evolves. Under squeeze flow simulation, the particle distribution ratio along the x-axis gradually levels off with the increasing compressive strain, and the particle distribution ratio along the y-axis nearly decreases to zero at y* = ±12. This implies that the particles mainly remain in the center zone, while the implicit carrier fluids are squeezed to the rim of the simulation box under squeeze flows. The local particle concentrations of MR fluids are thus increased, which contributes to the squeeze-assisted MR fluid strengthening.
(2) A critical squeeze rate, i.e., ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) c = 1.0 s−1, is characterized. Before reducing to the critical squeeze rate, the particle connectivity of MR fluids is increased with decreasing squeeze rate, due to the formation of more compact and stronger structures, leading to the improvement of the structure verticalness, anisotropy and lateral complexity. The corresponding macroscopic reflection is as follows: as the squeeze rate increases, the shear yield stress of MR fluids is sharply increased before the critical squeeze rate is reached and decreased slowly after the critical squeeze rate is surpassed; the normal stress of MR fluids at a low shear strain level is decreased after the critical squeeze rate is surpassed, but becomes insensitive to the squeeze rate at a high shear strain level.
c = 1.0 s−1, is characterized. Before reducing to the critical squeeze rate, the particle connectivity of MR fluids is increased with decreasing squeeze rate, due to the formation of more compact and stronger structures, leading to the improvement of the structure verticalness, anisotropy and lateral complexity. The corresponding macroscopic reflection is as follows: as the squeeze rate increases, the shear yield stress of MR fluids is sharply increased before the critical squeeze rate is reached and decreased slowly after the critical squeeze rate is surpassed; the normal stress of MR fluids at a low shear strain level is decreased after the critical squeeze rate is surpassed, but becomes insensitive to the squeeze rate at a high shear strain level.
(3) With increasing magnetic field strength, the increment of cluster size upon compression becomes nonobvious when the magnetic field strength exceeds 100 kA m−1; while the particle connectivity keeps growing sharply. The absolute value of the magnetic energy per particle in MR fluids increases along with the magnetic field strength, which is attributed to a high magnetic dipole moment and a high probability of θij = 60°. It is demonstrated that increasing the magnetic field strength can strengthen the impact of compression on the microscopic structures. Consequently, the macroscopic shear stress and normal stress are both improved.
(4) With increasing particle concentration, the average cluster size increases and the cluster number in MR fluids decreases, but both of them tend to become more insensitive to the squeeze flows, gradually leveling off as the compressive strain increases. Compared to the suspensions without compression, the particle connectivity in the compressed suspensions is increased when the particle volume fraction is low but decreased as the particle volume fraction exceeds 10.0%. The magnetic energy per particle in MR suspensions with high concentrations becomes positive as the compressive strain attains 0.6, indicating prominent repulsive interactions among particles. To sum up, the squeeze strengthening effect on the microstructured behaviors of MR fluids is more prominent for the dilute MR suspensions.
This study provides a microstructural insight into the squeeze-assisted MR fluid strengthening, which is believed to have implications in the design and optimization of MR dampers. It is noted that high performance-level dampers are always in great demand in engineering fields, especially for civil engineering, where MR dampers are mainly in shear, valve and shear-valve combined modes. The future research work can be focused on designing high-performance-level MR dampers for structural vibration control by combining squeeze and shear modes. In this respect, the optimum particle concentration and squeeze rate need to be further characterized for practical applications.
Conflicts of interest
The authors declare that they have no conflicts of interest to this work.Acknowledgements
The supports from the National Natural Science Foundation of China (Grant No. 51878505, 51678450, and 51725804) and the Ministry of Science and Technology of PR China (Grant No. SLDRCE19-B-26) are highly appreciated.References
- S. Cesmeci, F. Gordaninejad, K. L. Ryan and W. Eltahawy, Mechatronics, 2019, 64, 19 CrossRef.
- Y. B. Peng and Z. K. Zhang, J. Eng. Mech., 2020, 146, 16 Search PubMed.
- S. X. Guo, Y. Song, X. C. Yin, L. S. Zhang, T. Tamiya, H. Hirata and H. Ishihara, IEEE Trans. Robot., 2019, 35, 685–696 Search PubMed.
- Y. H. Hwang, S. R. Kang, S. W. Cha and S. B. Choi, Smart Mater. Struct., 2019, 28, 14 CrossRef.
- M. Wei, X. T. Rui, W. Zhu, F. F. Yang, L. L. Gu and H. T. Zhu, Smart Mater. Struct., 2020, 29, 13 Search PubMed.
- X. J. Zhang, Y. Yang, K. H. Guo, S. L. Sun, G. J. He and Z. H. Li, Smart Mater. Struct., 2020, 29, 10 Search PubMed.
- C. Han, B. G. Kim, B. H. Kang and S. B. Choi, J. Intell. Mater. Syst. Struct., 2020, 31, 198–208 CrossRef.
- R. Pilon, A. Landry-Blais, B. Gillet, A. Pin, J. P. L. Bigue and J. S. Plante, J. Intell. Mater. Syst. Struct., 2020, 31, 945–955 CrossRef.
- G. Bossis, O. Volkova, S. Lacis and A. Meunier, in Ferrofluids, Springer, 2002, pp. 202–230 Search PubMed.
- Y. B. Peng, Z. K. Zhang, J. G. Yang and L. H. Wang, J. Mech., 2019, 35, 549–562 CrossRef.
- D. Kittipoomwong, D. J. Klingenberg and J. C. Ulicny, J. Rheol., 2005, 49, 1521–1538 CrossRef CAS.
- M. Chand, A. Shankar, K. Jain and R. Pant, RSC Adv., 2014, 4, 53960–53966 CAS.
- S. Lee, K.-Y. Shin and J. Jang, Nanoscale, 2015, 7, 9646–9654 RSC.
- I. Jonkkari, E. Kostamo, J. Kostamo, S. Syrjala and M. Pietola, Smart Mater. Struct., 2012, 21, 075030 CrossRef.
- A. Becnel, S. Sherman, W. Hu and N. Wereley, J. Appl. Phys., 2015, 117, 17C708 CrossRef.
- Y. Rabbani, M. Ashtiani and S. H. Hashemabadi, Soft Matter, 2015, 11, 4453–4460 RSC.
- C. Hegger and J. Maas, J. Intell. Mater. Syst. Struct., 2016, 27, 1895–1907 CrossRef CAS.
- X. Tang, X. Zhang, R. Tao and Y. Rong, J. Appl. Phys., 2000, 87, 2634–2638 CrossRef CAS.
- R. Tao, J. Phys.: Condens. Matter, 2001, 13, R979 CrossRef CAS.
- X. Zhang, X. Gong, P. Zhang and Q. Wang, J. Appl. Phys., 2004, 96, 2359–2364 CrossRef CAS.
- W. Kordonski and S. Gorodkin, J. Rheol., 2016, 60, 129–139 CrossRef CAS.
- J.-P. Lucking Bigué, F. Charron and J.-S. Plante, J. Intell. Mater. Syst. Struct., 2015, 26, 1844–1855 CrossRef.
- J.-P. Lucking Bigué, F. Charron and J.-S. Plante, J. Intell. Mater. Syst. Struct., 2018, 29, 72–81 CrossRef.
- J.-P. Lucking Bigué, F. Charron and J.-S. Plante, J. Intell. Mater. Syst. Struct., 2018, 29, 62–71 CrossRef.
- C. Guo, X. Gong, S. Xuan, L. Qin and Q. Yan, Rheol. Acta, 2013, 52, 165–176 CrossRef CAS.
- J. A. Ruiz-López, R. Hidalgo-Alvarez and J. de Vicente, Rheol. Acta, 2016, 55, 215–221 CrossRef.
- W. Horak, Smart Mater. Struct., 2018, 27, 065022 CrossRef.
- J. de Vicente, J. A. Ruiz-López, E. Andablo-Reyes, J. P. Segovia-Gutiérrez and R. Hidalgo-Alvarez, J. Rheol., 2011, 55, 753–779 CrossRef CAS.
- J. Ruiz-López, Z. Wang, R. Hidalgo-Alvarez and J. de Vicente, J. Rheol., 2017, 61, 871–881 CrossRef.
- Z. Wang, S. Xuan, W. Jiang and X. Gong, RSC Adv., 2017, 7, 25855–25860 RSC.
- P. Domínguez-García, S. Melle, J. Pastor and M. Rubio, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 76, 051403 CrossRef.
- C. P. Reynolds, K. E. Klop, F. A. Lavergne, S. M. Morrow, D. Aarts and R. P. A. Dullens, J. Chem. Phys., 2015, 143, 6 CrossRef.
- K. Shahrivar, E. Carreon-Gonzalez and J. de Vicente, Microfluid. Nanofluid., 2017, 21, 9 CrossRef.
- K. Shahrivar, E. Carreón-González and J. de Vicente, Smart Mater. Struct., 2017, 26, 105031 CrossRef.
- K. Shahrivar, E. Carreón-González, J. R. Morillas and J. de Vicente, Soft Matter, 2017, 13, 2677–2685 RSC.
- A. Satoh, Colloids Surf., A, 2016, 504, 393–399 CrossRef CAS.
- K. Okada and A. Satoh, J. Magn. Magn. Mater., 2017, 437, 29–41 CrossRef CAS.
- A. Rosa, G. Abade and F. Cunha, Phys. Fluids, 2017, 29, 092006 CrossRef.
- J. P. Segovia-Gutierrez, J. de Vicente, R. Hidalgo-Alvarez and A. M. Puertas, Soft Matter, 2013, 9, 6970–6977 RSC.
- B. Tanygin, V. Kovalenko, M. Petrychuk and S. Dzyan, J. Magn. Magn. Mater., 2012, 324, 4006–4010 CrossRef CAS.
- A. Satoh and R. W. Chantrell, Mol. Phys., 2006, 104, 3287–3302 CrossRef CAS.
- W. Li and Q. Li, Nonlinear Dyn., 2018, 91, 2141–2155 CrossRef.
- Y. Fu, J. Yao, H. Zhao, G. Zhao and Y. Qiu, Soft Matter, 2019, 15, 6867–6877 RSC.
- Y. Ido, H. Sumiyoshi and H. Tsutsumi, Comput. Fluids, 2017, 142, 86–95 CrossRef.
- J. Cao, J. Huang and L. Zhou, J. Phys. Chem. B, 2006, 110, 11635–11639 CrossRef CAS.
- H. Pang, L. Pei, C. Sun and X. Gong, J. Rheol., 2018, 62, 1409–1418 CrossRef CAS.
- P. A. Sánchez, O. V. Stolbov, S. S. Kantorovich and Y. L. Raikher, Soft Matter, 2019, 15, 7145–7158 RSC.
- D. De Domenico and H. Askes, Composites, Part B, 2018, 153, 285–294 CrossRef CAS.
- L. Wang and H. Hu, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 195412 CrossRef.
- T. Titscher and J. F. Unger, Comput. Struct., 2015, 158, 274–284 CrossRef.
- D. H. Kim, S.-H. Chu, K. H. Ahn and S. J. Lee, Korea-Australia Rheology Journal, 1999, 11, 233–240 Search PubMed.
- J. A. Ruiz-López, Z. W. Wang, J. C. Fernández-Toledano, R. Hidalgo-Alvarez and J. de Vicente, Rheol. Acta, 2016, 55, 245–256 CrossRef.
- J. F. Brady and G. Bossis, Annu. Rev. Fluid Mech., 1988, 20, 111–157 CrossRef.
- S. Plimpton, Fast parallel algorithms for short-range molecular dynamics, Sandia National Labs., Albuquerque, NM (United States), 1993.
- Y.-B. Peng, R. Ghanem and J. Li, J. Intell. Mater. Syst. Struct., 2012, 23, 1351–1370 CrossRef.
- M. Doi and S. F. Edwards, The theory of polymer dynamics, Oxford University Press, 1988 Search PubMed.
- J. Cernak, G. Helgesen and A. T. Skjeltorp, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 70, 8 CrossRef.
- T. Ukai, H. Morimoto and T. Maekawa, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 6 CrossRef.
- D. Sohn, J. Magn. Magn. Mater., 1997, 173, 305–313 CrossRef CAS.
- P. Dominguez-Garcia, J. M. Pastor and M. A. Rubio, Eur. Phys. J. E: Soft Matter Biol. Phys., 2011, 34, 7 CrossRef.
- C. Ekwebelam and H. See, Rheol. Acta, 2009, 48, 19–32 CrossRef CAS.
- B. T. Wilson and D. J. Klingenberg, J. Rheol., 2017, 61, 601–611 CrossRef CAS.
- J. C. Ulicny, K. S. Snavely, M. A. Golden and D. J. Klingenberg, Appl. Phys. Lett., 2010, 96, 231903 CrossRef.
- J. De Vicente, D. J. Klingenberg and R. Hidalgo-Alvarez, Soft Matter, 2011, 7, 3701–3710 RSC.
- S. Choi, H. Choi, Y. Choi and N. Wereley, J. Appl. Polym. Sci., 2005, 96, 1924–1929 CrossRef CAS.
- E. C. McIntyre and F. E. Filisko, J. Rheol., 2010, 54, 591–603 CrossRef CAS.
- D. Liu, M. Maxey and G. Karniadakis, J. Micromech. Microeng., 2005, 15, 2298 CrossRef.
- I. Ismail, S. A. Mazlan, H. Zamzuri and A. G. Olabi, Jpn. J. Appl. Phys., 2012, 51, 067301 CrossRef.
- J. Fernández-Toledano, J. Ruiz-López, R. Hidalgo-Álvarez and J. de Vicente, J. Rheol., 2015, 59, 475–498 CrossRef.
- A. Anupama, V. Kumaran and B. Sahoo, J. Ind. Eng. Chem., 2018, 67, 347–357 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |