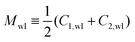Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Active shape oscillations of giant vesicles with cyclic closure and opening of membrane necks†
Simon
Christ
 a,
Thomas
Litschel
a,
Thomas
Litschel
 b,
Petra
Schwille
b,
Petra
Schwille
 b and
Reinhard
Lipowsky
b and
Reinhard
Lipowsky
 *a
*a
aTheory and Bio-Systems, Max Planck Institute of Colloids and Interfaces, 14424 Potsdam, Germany. E-mail: lipowsky@mpikg.mpg.de; Fax: +49 331 5679602; Tel: +49 331 5679600
bCellular and Molecular Biophysics Max Planck Institute of Biochemistry, 82152 Martinsried, Germany
First published on 7th September 2020
Abstract
Reaction-diffusion systems encapsulated within giant unilamellar vesicles (GUVs) can lead to shape oscillations of these vesicles as recently observed for the bacterial Min protein system. This system contains two Min proteins, MinD and MinE, which periodically attach to and detach from the GUV membranes, with the detachment being driven by ATP hydrolysis. Here, we address these shape oscillations within the theoretical framework of curvature elasticity and show that they can be understood in terms of a spontaneous curvature that changes periodically with time. We focus on the simplest case provided by a attachment–detachment kinetics that is laterally uniform along the membrane. During each oscillation cycle, the vesicle shape is transformed from a symmetric dumbbell with two subcompartments of equal size to an asymmetric dumbbell with two subcompartments of different size, followed by the reverse, symmetry-restoring transformation. This sequence of shapes is first analyzed within the spontaneous curvature model which is then extended to the area-difference-elasticity model by decomposing the spontaneous curvature into a local and nonlocal component. For both symmetric and asymmetric dumbbells, the two subcompartments are connected by a narrow membrane neck with a circular waistline. The radius of this waistline undergoes periodic oscillations, the time dependence of which can be reasonably well fitted by a single Fourier mode with an average time period of 56 s.
1 Introduction
Both biological and biomimetic membranes such as lipid bilayers in their fluid state are highly flexible and can attain a striking variety of different morphologies. Particularly useful model systems for this polymorphism are giant unilamellar vesicles (GUVs) which are formed by single lipid bilayers.1–3 So far, most studies of GUVs have focussed on their equilibrium shapes or on their morphological response to external perturbations such as hydrodynamic flows and external electric fields. The shape transformations of cellular membranes, on the other hand, are often driven by molecular processes coupled to nucleotide hydrolysis. One example is provided by the endocytosis of nanoparticles by the outer plasma membrane which requires membrane fission, often achieved by GTP-hydrolyzing proteins such as dynamin.4 Another example is the Min protein system which hydrolyzes ATP to position the bacterial cell division machinery in Escherichia coli.5In a recent experimental study, the Min protein system was encapsulated within GUVs which were then observed to undergo cyclic shape oscillations.6 The protein system contained two Min proteins, MinD and MinE, which periodically attach to and detach from the inner leaflet of the GUV membranes. MinD attaches to lipid membranes when bound to ATP.7,8 MinE binds to membrane-bound MinD-ATP and the resulting MinD-ATP-MinE complex stimulates ATP hydrolysis by MinD, causing both proteins to unbind again from the membrane.
Here, we address these shape oscillations within the theoretical framework of curvature elasticity as recently reviewed in ref. 9. We first focus on the spontaneous curvature model10–12 and show that the vesicle shape oscillations can be understood in terms of a preferred or spontaneous membrane curvature that changes periodically in time. The spontaneous curvature provides a quantitative measure for the molecular asymmetry between the two leaflets of the lipid bilayers. For the GUV membranes considered here, only the inner leaflets are exposed to the Min proteins and the resulting bilayer asymmetry will depend on the coverage of the inner leaflet by these proteins. Because this coverage changes with time, so does the resulting bilayer asymmetry and the associated spontaneous curvature. In addition, we generalize the spontaneous curvature model and consider the area-difference-elasticity (ADE) model13–15 to take into account that the lipid bilayers studied in ref. 6 were composed of two phospholipids that are not expected to undergo frequent flip-flops between the two bilayer leaflets.
In the absence of flip-flops, the number of lipids is conserved separately in each leaflet of the bilayer membrane, which implies that the area difference between the two leaflets has a preferred value. In the ADE model, this constraint is taken into account by a nonlocal term that is added to the membrane's local bending energy, which has the same form as in the spontaneous curvature model. Therefore, in the present paper, we will view the area-difference-elasticity model as a generalization of the spontaneous curvature model.9,15 Alternatively, one may start from the bilayer coupling model,16 which considers the area difference between the two bilayers as another geometric control parameter in addition to membrane area and vesicle volume, and regard the ADE model as a generalized bilayer coupling model.17
As far as the recent experiments6 are concerned, we focus on the simplest case in which the cyclic changes of the membrane fluorescence were observed to be laterally uniform, corresponding to a laterally uniform attachment–detachment kinetics of the Min proteins. Furthermore, our detailed analysis of the observed shape oscillations as described here reveals that the GUVs conserve both vesicle volume and membrane area during these oscillations. As a consequence, the vesicle shapes are calculated for constant volume-to-area ratio and a laterally uniform spontaneous curvature that changes periodically in time. Furthermore, for each time point, we determine the (meta)stable GUV shape(s) corresponding to the instantaneous value of the spontaneous curvature.
These GUV shapes exhibit two subcompartments which are connected by narrow membrane necks as displayed in Fig. 1 and 2. These membrane necks are a direct consequence of curvature elasticity9,12,18,19 and have been experimentally observed for a variety of lipid compositions.20,21 More recently, it was shown that these necks are essential for the formation of multispherical vesicle shapes22 and for the controlled division of GUVs into two daughter vesicles.23In vivo, membrane necks are also formed by cellular membranes, e.g., during endo- and exocytosis.24
 | ||
| Fig. 1 Symmetry-breaking transformation during one shape oscillation: comparison of experimentally observed vesicle shapes in (a–c) with theoretically calculated shapes in (d–f). The neck radius Rne attains its largest value of 1.17 μm in (a and d) and its smallest value of 0.12 μm in (c and f). The up-down symmetry of the symmetric dumbbells (blue shape contours) in (a and d) and (b and e) is broken for the asymmetric dumbbell (red shape contour) in (c and f). The three images in panels a–c were obtained by differential interference contrast microscopy6 and represent three subsequent frames of the time-lapse Movie 1 (ESI†). The dashed vertical lines in panels d–f represent axes of rotational symmetry. | ||
 | ||
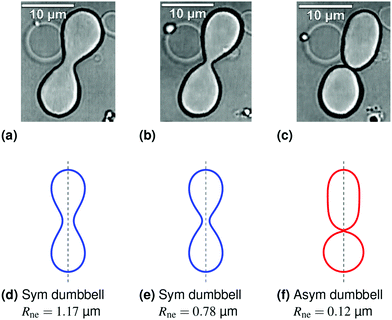
| Fig. 2 Symmetry-restoring transformation during one shape oscillation: comparison of experimentally observed vesicle shapes in (a–c) with theoretically calculated shapes in (d–f). The neck radius Rne attains its smallest value of 0.12 μm in (a and d) and its largest value of 0.95 μm in (c and f). The up-down symmetry is broken for the red shapes in (a and d) and (b and e) but restored for the blue shape in (c and f). The asymmetric shape in (a and d) is the same shape as in Fig. 1c and f but flipped upside-down. The three images in panels a–c represent three subsequent frames of the time-lapse Movie 1 (ESI†). | ||
 | ||
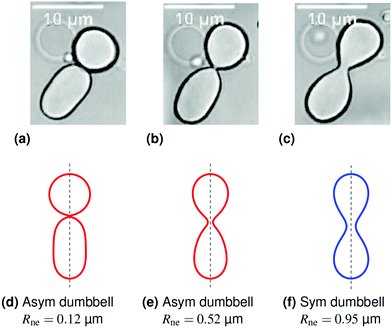
Fig. 3 Morphology diagram of prolates and dumbbells for positive spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) with 0.7 ≤ with 0.7 ≤ ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ≤ 2.8 and volume-to-area ratio v ≥ 0.6. The horizontal line with v = 1 corresponds to a single sphere. Along the solid line L1+1, the vesicles form limit shapes consisting of two different spheres connected by a closed membrane neck. The location of this line is given by the algebraic expression in eqn (8). Along the solid line L2* with ≤ 2.8 and volume-to-area ratio v ≥ 0.6. The horizontal line with v = 1 corresponds to a single sphere. Along the solid line L1+1, the vesicles form limit shapes consisting of two different spheres connected by a closed membrane neck. The location of this line is given by the algebraic expression in eqn (8). Along the solid line L2* with 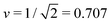 and and 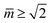 , the vesicles consist of two equally sized spheres connected by a closed neck. The parameter region between the two lines L1+1 and L2* defines the yellow stability regime for (1 + 1)-spheres, in which the vesicle shape depends only on v but is independent of , the vesicles consist of two equally sized spheres connected by a closed neck. The parameter region between the two lines L1+1 and L2* defines the yellow stability regime for (1 + 1)-spheres, in which the vesicle shape depends only on v but is independent of ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) . The black dotted line Dpear separates up-down symmetric from asymmetric dumbbells with open necks. The latter line is obtained using cubic splines to connect numerical and analytical solutions. The solid blue and red circles correspond to shapes with v = 0.768 as displayed in Fig. 4a, the solid red and blue squares to shapes with . The black dotted line Dpear separates up-down symmetric from asymmetric dumbbells with open necks. The latter line is obtained using cubic splines to connect numerical and analytical solutions. The solid blue and red circles correspond to shapes with v = 0.768 as displayed in Fig. 4a, the solid red and blue squares to shapes with 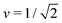 as in Fig. 4b. The solid blue and red diamonds with v = 0.670 represent the selected shapes in Fig. 1 and 2 with the parameter values as in Table 2. The symmetric (blue) and asymmetric (red) diamonds belong to two different energy branches, see Fig. 6 and 7 further below. as in Fig. 4b. The solid blue and red diamonds with v = 0.670 represent the selected shapes in Fig. 1 and 2 with the parameter values as in Table 2. The symmetric (blue) and asymmetric (red) diamonds belong to two different energy branches, see Fig. 6 and 7 further below. | ||
A priori, our theoretical approach can be justified by the observed separation of time scales between the time period of the Min oscillations, which is about one minute,25,26 and the time it takes a giant vesicle to relax to a new stable state, which takes only a few seconds.27,28 Because of this time scale separation, one should be able to describe the observed non-equilibrium shape transformations by a sequence of stable shapes corresponding to the instantaneous value of the spontaneous curvature. Such a description is indeed possible as shown here.
During each complete oscillation cycle, the vesicle shape is transformed from an up-down symmetric dumbbell with two subcompartments of equal size to an asymmetric dumbbell with two subcompartments of different size, see Fig. 1, followed by the reverse, symmetry-restoring transformation, see Fig. 2. In these two figures, the symmetric and asymmetric dumbbells are displayed in blue and red color, respectively. This color code will be used throughout the paper. These two types of dumbbells belong to two different branches of the GUV's bending energy. In the spontaneous curvature model, the symmetric branch is stable whereas the asymmetric one is metastable. In the area-difference-elasticity model, both branches represent stable shapes.
The narrow membrane necks in Fig. 1 and 2 have a waistline that defines the neck radius Rne. This neck radius changes during each shape oscillation as shown in the two figures. In the spontaneous curvature model, the neck radius exhibits a different dependence on the spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) for the symmetric and asymmetric branches of dumbbells: along the symmetric branch, the neck radius decreases with increasing
for the symmetric and asymmetric branches of dumbbells: along the symmetric branch, the neck radius decreases with increasing ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) whereas it increases along the asymmetric dumbbell. In the area-difference-elasticity model, the neck radius decreases with increasing local spontaneous curvature, both along the symmetric and along the asymmetric branch.
whereas it increases along the asymmetric dumbbell. In the area-difference-elasticity model, the neck radius decreases with increasing local spontaneous curvature, both along the symmetric and along the asymmetric branch.
Our article is organized as follows. In the next section, we briefly describe our experimental system, consisting of Min proteins encapsulated in GUVs, as experimentally studied in ref. 6. The following section contains a reminder about the theory of curvature elasticity. We will first use the spontaneous curvature model, for which the GUV shapes are solely determined by two dimensionless shape parameters, the volume-to-area ratio v and the rescaled spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) . We then analyze the experimentally observed shapes as shown in Fig. 1a–c and 2a–c and conclude that these shapes have constant volume-to-area ratio which we will take to be v = 0.670. For this v-value, we study the possible vesicle shapes as we vary the spontaneous curvature
. We then analyze the experimentally observed shapes as shown in Fig. 1a–c and 2a–c and conclude that these shapes have constant volume-to-area ratio which we will take to be v = 0.670. For this v-value, we study the possible vesicle shapes as we vary the spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) and find both symmetric and asymmetric dumbbells for a certain range of
and find both symmetric and asymmetric dumbbells for a certain range of ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) -values. In Section 4.6, we extend the spontaneous curvature model to the area-difference-elasticity model by decomposing the spontaneous curvature
-values. In Section 4.6, we extend the spontaneous curvature model to the area-difference-elasticity model by decomposing the spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) into a local and a nonlocal component.
into a local and a nonlocal component.
2 Min proteins enclosed by GUVs
The aqueous buffer enclosed by the GUVs contained two Min proteins, MinD and MinE, as well as ATP. The corresponding solution concentrations were 1.5 μM MinD, 1.4 μM eGFP-MinD, 3 μM MinE, and 5 mM ATP.6 Thus, about half of the MinD proteins were fluorescently labeled and the overall MinD concentration was roughly equal to the MinE concentration. The lipid bilayer of the GUVs was composed of zwitterionic DOPC (1,2-dioleoyl-sn-glycero-3-phosphocholine) and anionic DOPG (1,2-dioleoyl-sn-glycero-3-phosphoglycerol) in a ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
MinD can bind ATP and then attaches onto lipid membranes.7 MinE binds to membrane-bound MinD-ATP and the resulting MinD-ATP-MinE complex stimulates ATP hydrolysis by MinD, causing both proteins to desorb again from the membrane. In the presence of a sufficient amount of ATP, this MinDE system undergoes many cycles of membrane attachment and detachment. For osmotically deflated vesicles, this periodic molecular process leads to shape oscillations of the vesicles which can be directly observed in the optical microscope.6 Different types of shape oscillations have been detected; the two most frequent types of oscillations were denoted by ‘periodic dumbbell splitting’ and ‘periodic budding’ in ref. 6.
Here, we will focus on the dumbbell case as displayed in Fig. 1 and 2. In this case, the fluorescence of the GFP-labeled MinD adjacent to the inner leaflet of the GUV membrane was observed to be laterally uniform. Therefore, membrane segments with a lateral extension of about 300 nm can be considered to have a laterally uniform molecular composition which implies that they have uniform elastic properties as well. Furthermore, it is well understood that the shape of uniform GUV membranes strongly depends on the preferred or spontaneous curvature of these membranes.9
3 Spontaneous curvature model
The GUV membranes have a lateral dimension of many μm and a molecular thickness of only 4 to 5 nm. Based on this separation of length scales, we ignore the molecular structure of these membranes and describe them as smoothly curved surfaces. Any such surface can be characterized locally by its two principal curvatures, C1 and C2, which define the mean curvature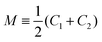 and the Gaussian curvature G ≡ C1C2.
and the Gaussian curvature G ≡ C1C2.
The spontaneous curvature model9,10–12 is then defined by the membrane's bending energy as given by‡
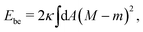 | (1) |
In order to actually compute the shape of a GUV, we need to take two additional constraints into account as provided by the membrane area A and the vesicle volume V.9,11,12 These constraints are included via two Lagrange multipliers, the mechanical membrane tension Σ and the difference ΔP ≡ Pin − Pex between the pressures Pin and Pex within the interior and exterior aqueous solutions. The stable membrane shapes, corresponding to minimal bending energy, are then obtained by minimizing the shape energy
| F = −ΔPV + ΣA + Ebe | (2) |
3.1 Two independent shape parameters
The shape energy in eqn (2) depends on two curvature-elastic parameters, the bending rigidity κ and the spontaneous curvature m, as well as on two geometric parameters, the membrane area A and the vesicle volume V. It is convenient to take the bending rigidity κ as the basic energy scale and to consider the area-derived vesicle size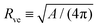 | (3) |
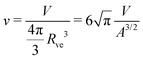 | (4) |
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = mRve. = mRve. | (5) |
In the following, we will discuss the stable vesicle shapes in the context of two-dimensional morphology diagrams that depend on the two independent shape parameters v and ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) . By definition, the volume parameter v satisfies
. By definition, the volume parameter v satisfies
| 0 ≤ v ≤ 1 with v = 1 for a single sphere. | (6) |
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ≥ 0.
≥ 0.
It is important to note that the stable GUV shapes depend on the two shape parameters v and ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) but are not uniquely determined by these two parameters alone. Indeed, for given values of v and
but are not uniquely determined by these two parameters alone. Indeed, for given values of v and ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) , the vesicle can usually attain several (meta)stable shapes that form distinct branches of the bending energy.12 The number of distinct branches becomes particularly large when one considers multispherical shapes consisting of a variable number of small and large spheres.9,22
, the vesicle can usually attain several (meta)stable shapes that form distinct branches of the bending energy.12 The number of distinct branches becomes particularly large when one considers multispherical shapes consisting of a variable number of small and large spheres.9,22
3.2 Computational methods for stable vesicle shapes
The stable shapes of the GUVs are provided by the local minima of the bending energy for given membrane area and vesicle volume. In order to actually calculate these stable shapes, i.e., to actually minimize the shape energy in eqn (2), two computational methods have been particularly useful. First, axisymmetric membrane shapes, which are completely determined by their 1-dimensional shape contours, can be obtained by solving a set of ordinary differential equations.12,19 Second, one may consider multispherical shapes consisting of a variable number of large and small spheres connected by closed membrane necks.9,22 Within the morphology diagrams, the axisymmetric shapes with smooth shape contours and the multispherical shapes are separated by boundary lines of limit shapes. As we approach such a line from one side, we obtain smoothly curved shapes with narrow membrane necks that become eventually closed at the boundary line. As we approach the latter line from the multispherical side, we observe multispherical shapes that depend only on v but not on![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) . Thus, for constant v, the latter approach is characterized by a certain fixed multispherical shape.
. Thus, for constant v, the latter approach is characterized by a certain fixed multispherical shape.
The closure of a narrow membrane neck as obtained from a smoothly curved shape is somewhat counterintuitive. When viewed on molecular scales, the membrane neck has the shape of an hourglass. The corresponding waistline consists of saddle points, characterized by two principal curvatures, the negative contour curvature C1,wl < 0 perpendicular to the waistline and the positive principal curvature C2,wl = 1/Rne > 0 parallel to the waistline. When the neck closes, the neck radius goes to zero and the principal curvature C2,wl diverges. However, the mean curvature
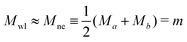 | (7) |
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ne ≡ MneRve =
ne ≡ MneRve = ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) then implies a unique relationship between
then implies a unique relationship between ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) and the volume-to-area ratio v, see eqn (8) further below.
and the volume-to-area ratio v, see eqn (8) further below.
The simplest multispherical shape is provided by (1 + 1)-spheres consisting of two spheres connected by a closed membrane neck. The corresponding stability regime for this morphology is displayed in Fig. 3 as the yellow subregion. This regime is bounded by two lines of limit shapes denoted by L1+1 and L2*. Approaching the line L1+1 from outside the stability regime, the closure of the membrane neck leads to asymmetric dumbbells consisting of a large and a small sphere with two different radii. Approaching the line L2* from outside the stability regime, the closure of the membrane neck leads to symmetric dumbbells consisting of two equally sized spheres. The process of neck closure is illustrated in Fig. 4 for asymmetric dumbbells with v = 0.768 and for symmetric dumbbells with 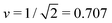 .
.
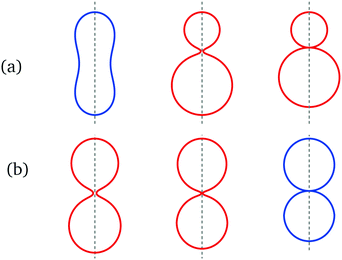 | ||
Fig. 4 Examples for dumbbell shapes with open and closed necks: (a) Dumbbells with v = 0.768, corresponding to the three solid circles in Fig. 3. From left to right, these shapes have the rescaled spontaneous curvatures ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = 1.2, 1.3 and ≥1.56, where the rightmost shape corresponds to the limit shape L1+1 with v = 0.768; (b) Dumbbells with = 1.2, 1.3 and ≥1.56, where the rightmost shape corresponds to the limit shape L1+1 with v = 0.768; (b) Dumbbells with 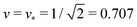 corresponding to the three solid squares in Fig. 3. From left to right, these shapes have the spontaneous curvature corresponding to the three solid squares in Fig. 3. From left to right, these shapes have the spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = 1.167, 1.352, and = 1.167, 1.352, and 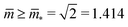 . . | ||
The line L1+1 is described by the functional relationship12
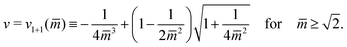 | (8) |
The line L2* is located at9
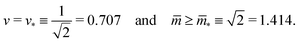 | (9) |
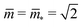 and
and 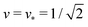 . At this corner point of the morphology diagram, the dumbbell shape consists of two equally sized spheres with radius
. At this corner point of the morphology diagram, the dumbbell shape consists of two equally sized spheres with radius 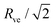 and vanishing bending energy. In the following, the limit shapes along the two boundary lines will provide useful reference shapes.
and vanishing bending energy. In the following, the limit shapes along the two boundary lines will provide useful reference shapes.
In Fig. 3, we also included the dotted line Dpear at which the vesicle undergoes a discontinuous transition from up-down symmetric to up-down asymmetric dumbbells with open necks.12 Along the transition line Dpear, the two types of dumbbells have the same bending energy.
The partial morphology diagram displayed in Fig. 3 contains additional stability regimes for multispheres consisting of Nl large spheres and Ns small spheres with Nl + Ns ≥ 3. Such (Nl + Ns)-spheres have been observed for cholesterol-containing membranes which were exposed to asymmetric sugar solutions.22 The general theoretical method to determine these multispheres has been developed in ref. 9 and has been used to determine their stability regimes within the spontaneous curvature model.22
Lines of multispherical limit shapes with up to Nl + Ns = 3 shapes were also obtained in the bilayer coupling model12,16,17 and within the area-difference-elasticity model.29 A graphical method to determine the shapes in the area-difference-elasticity model from those in the bilayer coupling model has also been described.17
However, in what follows, we will not consider (Nl + Ns)-spheres with Nl + Ns ≥ 3 because the experimentally observed vesicle shapes with v = 0.670 as displayed in Fig. 1 and 2 involve only two subcompartments connected by a narrow membrane neck, in close analogy to the (1 + 1)-spheres, which are formed for somewhat larger v-values with 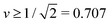 , i.e., at and above the line L2* displayed in Fig. 3 and described by eqn (9).
, i.e., at and above the line L2* displayed in Fig. 3 and described by eqn (9).
4 Analysis of experimental observations
4.1 Theoretical analysis of GUV shapes
Our theoretical analysis is based on the time-lapse Movie 1 (ESI†) which consists of 200 snapshots or frames, each of which displays a different image of the same GUV as obtained by differential interference contrast microscopy. This GUV represents one out of four individual GUVs for which the same mode of shape oscillations has been reported.6 The time-lapse Movie 1 (ESI†) was taken with the predefined time interval Δt = 7.61 s between successive frames and displays the whole series of 200 frames within 20 s, corresponding to about 1500 s or 25 min real time. Apart from a few frames at the beginning and at the end, the movie consists of 26 complete shape oscillations with an average time period of 55.9 s as described in more detail further below.All individual snapshots of Movie 1 (ESI†) are consistent with the view that the observed shapes represent essentially axisymmetric shapes that are tilted with respect to the focal plane and are deformed by relative displacements of the two subcompartments with respect to the closed membrane neck, which acts as a flexible hinge. The two shape sequences in Fig. 1a–c and 2a–c have been selected because they can be well approximated by axisymmetric shapes without additional deformations arising from relative displacements around the hinge-like membrane neck.
During the observed shape changes, both the membrane area and the volume of the GUVs were essentially conserved. These properties were explicitly demonstrated for the six snapshots in Fig. 1a–c and 2a–c by fitting splines to the shape contours of these images, assuming rotational symmetry of the shapes, and then measuring the membrane area A and the vesicle volume V as well as the neck radius Rne.30,31 The numerical estimates for these geometric quantities are given in Table 1 which also displays the resulting volume-to-area ratio v = 0.670 ± 0.01. The latter value implies that the vesicle has been significantly deflated, compared to a spherical shape with v = 1, by the osmotic pressure arising from the hypertonic conditions in the exterior aqueous solution.6
| A [μm2] | V [μm3] | v | R ne [μm] | |
|---|---|---|---|---|
| Fig. 1a | 390 ± 30 | 490 ± 60 | 0.68 ± 0.01 | 1.1 ± 0.2 |
| Fig. 1b | 380 ± 30 | 470 ± 60 | 0.68 ± 0.01 | 0.8 ± 0.2 |
| Fig. 1c | 380 ± 30 | 460 ± 50 | 0.66 ± 0.02 | <0.3 |
| Fig. 2a | 380 ± 30 | 470 ± 53 | 0.67 ± 0.01 | <0.3 |
| Fig. 2b | 380 ± 30 | 463 ± 52 | 0.68 ± 0.01 | 0.6 ± 0.2 |
| Fig. 2c | 380 ± 30 | 483 ± 55 | 0.68 ± 0.01 | 0.9 ± 0.2 |
The theoretical shapes in Fig. 1d–f and 2d–f were then calculated using the volume-to-area ratio v = 0.670 and several values of the rescaled spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) as given in Table 2 and displayed in the morphology diagram of Fig. 3. Furthermore, to obtain the dimensionful quantities from the dimensionless ones, we used the vesicle size
as given in Table 2 and displayed in the morphology diagram of Fig. 3. Furthermore, to obtain the dimensionful quantities from the dimensionless ones, we used the vesicle size 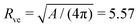 μm as obtained from the area A = 390 μm2 of the image in Fig. 1a, see first row in Table 1.
μm as obtained from the area A = 390 μm2 of the image in Fig. 1a, see first row in Table 1.
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) that were used to compute the dumbbell shapes in Fig. 1d–f and 2d–f, see also Fig. 6. The third column contains the rescaled neck radius
that were used to compute the dumbbell shapes in Fig. 1d–f and 2d–f, see also Fig. 6. The third column contains the rescaled neck radius ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) ne = Rne/Rve of the computed shapes. The spontaneous curvature m =
ne = Rne/Rve of the computed shapes. The spontaneous curvature m = ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) /Rve and the neck radius Rne =
/Rve and the neck radius Rne = ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) neRve in the fourth and fifth column were computed using the vesicle size
neRve in the fourth and fifth column were computed using the vesicle size 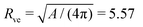 μm as obtained from the membrane area A = 390 μm2 for the image in Fig. 1a
μm as obtained from the membrane area A = 390 μm2 for the image in Fig. 1a
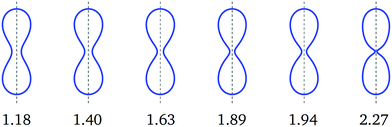 | ||
Fig. 5 Symmetric dumbbell shapes (blue) for constant volume-to-area ratio v = 0.670 and rescaled spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) as given by the numerals below the shapes. The first three shapes correspond to the blue diamonds in Fig. 3. This sequence of shapes illustrates the closure of the membrane neck along the symmetric branch as we increase the value of the spontaneous curvature as given by the numerals below the shapes. The first three shapes correspond to the blue diamonds in Fig. 3. This sequence of shapes illustrates the closure of the membrane neck along the symmetric branch as we increase the value of the spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) from 1.18 to 2.27. from 1.18 to 2.27. | ||
4.2 Two branches of stable dumbbells
All dumbbells computed for the symmetry-breaking transformation in Fig. 1d–f and for the symmetry-restoring transformation in Fig. 2d–f have the same volume-to-area ratio v = 0.670 but differ in their![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) -values, see Table 2. Both types of shape transformations involve up-down symmetric as well as asymmetric dumbbells. The symmetric dumbbells are formed for a wide range of
-values, see Table 2. Both types of shape transformations involve up-down symmetric as well as asymmetric dumbbells. The symmetric dumbbells are formed for a wide range of ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) -values as illustrated in Fig. 5. For these dumbbells, the neck radius monotonically decreases as we increase the spontaneous curvature
-values as illustrated in Fig. 5. For these dumbbells, the neck radius monotonically decreases as we increase the spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) .
.
In contrast, the asymmetric dumbbells with an open neck as in Fig. 1f and 2d, e are only found for a relatively small range of ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) -values. Indeed, when we start from a certain asymmetric dumbbell and increase the spontaneous curvature, the resulting dumbbells become more and more symmetric until we reach the bifurcation point Bop, which is provided by a symmetric dumbbell with an open neck and has spontaneous curvature
-values. Indeed, when we start from a certain asymmetric dumbbell and increase the spontaneous curvature, the resulting dumbbells become more and more symmetric until we reach the bifurcation point Bop, which is provided by a symmetric dumbbell with an open neck and has spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) (Bop). At the latter
(Bop). At the latter ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) -value, the asymmetric branch merges with the symmetric one and the asymmetric branch ceases to exist for
-value, the asymmetric branch merges with the symmetric one and the asymmetric branch ceases to exist for ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) >
> ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) (Bop).
(Bop).
On the other hand, when we decrease the spontaneous curvature, the neck radius of the asymmetric dumbbell becomes smaller and smaller until we reach the limit shape Lps with a closed neck for spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) (Lps). The closed neck of this limit shape connects a spherical with a prolate subcompartment. Therefore, the branch of stable asymmetric dumbbells with an open neck is limited to those values of the spontaneous curvature that satisfy
(Lps). The closed neck of this limit shape connects a spherical with a prolate subcompartment. Therefore, the branch of stable asymmetric dumbbells with an open neck is limited to those values of the spontaneous curvature that satisfy
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) (Lps) < (Lps) < ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) < < ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) (Bop). (Bop). | (10) |
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) (Lps) is estimated to be 1.84 ± 0.04 and the value of
(Lps) is estimated to be 1.84 ± 0.04 and the value of ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) (Bop) is somewhat larger than 1.933. For all
(Bop) is somewhat larger than 1.933. For all ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) -values within the interval as given by eqn (10), the vesicle can also form a symmetric dumbbell. Therefore, asymmetric dumbbells always coexist with symmetric ones. Examples for this coexistence of symmetric and asymmetric dumbbells are provided in Fig. 6. Inspection of this figure reveals that, in contrast to the symmetric dumbbells, the neck radius of the asymmetric dumbbells increases with increasing spontaneous curvature. At the bifurcation point Bop with
-values within the interval as given by eqn (10), the vesicle can also form a symmetric dumbbell. Therefore, asymmetric dumbbells always coexist with symmetric ones. Examples for this coexistence of symmetric and asymmetric dumbbells are provided in Fig. 6. Inspection of this figure reveals that, in contrast to the symmetric dumbbells, the neck radius of the asymmetric dumbbells increases with increasing spontaneous curvature. At the bifurcation point Bop with ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) (Bop) ≃ 1.933, the neck radius has the value
(Bop) ≃ 1.933, the neck radius has the value ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) ne = 0.11.
ne = 0.11.
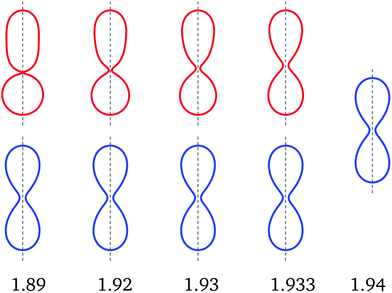 | ||
Fig. 6 Up-down symmetric (blue) and asymmetric (red) dumbbells for v = 0.670 and five values of the rescaled spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) as indicated by the numerals below the shapes. The asymmetric dumbbells with as indicated by the numerals below the shapes. The asymmetric dumbbells with ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = 1.89 and 1.93 correspond to the red diamonds in Fig. 3. The two types of shapes coexist between = 1.89 and 1.93 correspond to the red diamonds in Fig. 3. The two types of shapes coexist between ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = 1.89 and = 1.89 and ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = 1.933. For = 1.933. For ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = 1.94, only the symmetric shape is found which implies that the asymmetric branch merges with the symmetric one at a critical value of the spontaneous curvature slightly above = 1.94, only the symmetric shape is found which implies that the asymmetric branch merges with the symmetric one at a critical value of the spontaneous curvature slightly above ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = 1.933. Comparison of the asymmetric and symmetric shapes reveals that the asymmetric shapes approach the symmetric ones in a continuous manner as we increase the spontaneous curvature towards its critical value. This conclusion is further corroborated by the corresponding energy branches in Fig. 7. Note that the neck radius of the asymmetric (red) dumbbells increases with increasing = 1.933. Comparison of the asymmetric and symmetric shapes reveals that the asymmetric shapes approach the symmetric ones in a continuous manner as we increase the spontaneous curvature towards its critical value. This conclusion is further corroborated by the corresponding energy branches in Fig. 7. Note that the neck radius of the asymmetric (red) dumbbells increases with increasing ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) , in contrast to the behavior of the symmetric (blue) dumbbells. For more details on the dependence of the dumbbell shapes on the spontaneous curvature, see Movie 2 (ESI†). , in contrast to the behavior of the symmetric (blue) dumbbells. For more details on the dependence of the dumbbell shapes on the spontaneous curvature, see Movie 2 (ESI†). | ||
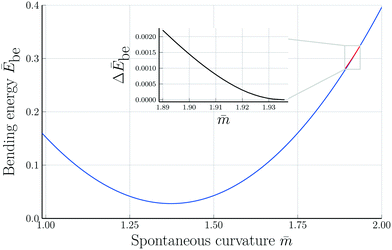 | ||
Fig. 7 Rescaled bending energy Ēbe = Ebe/(8πκ) as a function of rescaled spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) for volume-to-area ratio v = 0.670. The Ēbe-values are displayed in blue for the symmetric dumbbells and in red for the asymmetric ones. The inset shows the energy difference ΔEbe between the metastable asymmetric and the stable symmetric branch, as defined in eqn (12). The asymmetric branch (red) has a slightly larger bending energy than the symmetric branch (blue). Therefore, the asymmetric branch represents a branch of metastable shapes. The two branches merge with a common tangent at a critical for volume-to-area ratio v = 0.670. The Ēbe-values are displayed in blue for the symmetric dumbbells and in red for the asymmetric ones. The inset shows the energy difference ΔEbe between the metastable asymmetric and the stable symmetric branch, as defined in eqn (12). The asymmetric branch (red) has a slightly larger bending energy than the symmetric branch (blue). Therefore, the asymmetric branch represents a branch of metastable shapes. The two branches merge with a common tangent at a critical ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) -value slightly above -value slightly above ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = 1.933, see Fig. 6. The symmetric branch exhibits a pronounced minimum at = 1.933, see Fig. 6. The symmetric branch exhibits a pronounced minimum at ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = 1.373 which reflects the vicinity of the corner point with = 1.373 which reflects the vicinity of the corner point with  and and 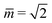 , at which the bending energy vanishes, see the morphology diagram in Fig. 3. , at which the bending energy vanishes, see the morphology diagram in Fig. 3. | ||
It follows from the dumbbell shapes in Fig. 6 that the spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) (Bop), at which the asymmetric branch merges with the symmetric one, is somewhat larger than
(Bop), at which the asymmetric branch merges with the symmetric one, is somewhat larger than ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = 1.933. Furthermore, the asymmetric dumbbell with
= 1.933. Furthermore, the asymmetric dumbbell with ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = 1.89 must be quite close to the limit shape Lps because the membrane neck of the latter dumbbell is almost closed and the smaller subcompartment has already an essentially spherical shape. To estimate the spontaneous curvature
= 1.89 must be quite close to the limit shape Lps because the membrane neck of the latter dumbbell is almost closed and the smaller subcompartment has already an essentially spherical shape. To estimate the spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) (Lps) for the prolate-sphere limit shape, we compute the mean curvature Mnpol at the north pole of the asymmetric dumbbells and the mean curvature Mspol at the south pole of these dumbbells. As we approach the limit shape Lps, the rescaled mean curvatures
(Lps) for the prolate-sphere limit shape, we compute the mean curvature Mnpol at the north pole of the asymmetric dumbbells and the mean curvature Mspol at the south pole of these dumbbells. As we approach the limit shape Lps, the rescaled mean curvatures ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) npol ≡ MnpolRve and
npol ≡ MnpolRve and ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) spol ≡ MspolRve should satisfy the asymptotic equality
spol ≡ MspolRve should satisfy the asymptotic equality
![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) npol + npol + ![[M with combining macron]](https://www.rsc.org/images/entities/i_char_004d_0304.gif) spol ≈ 2 spol ≈ 2![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) (Lps), (Lps), | (11) |
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) (Lps) of the prolate-sphere limit shape. A second estimate is provided by extrapolating the asymmetric branch in Fig. 8 to
(Lps) of the prolate-sphere limit shape. A second estimate is provided by extrapolating the asymmetric branch in Fig. 8 to ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) ne = 0, see red star in Fig. 8a.
ne = 0, see red star in Fig. 8a.
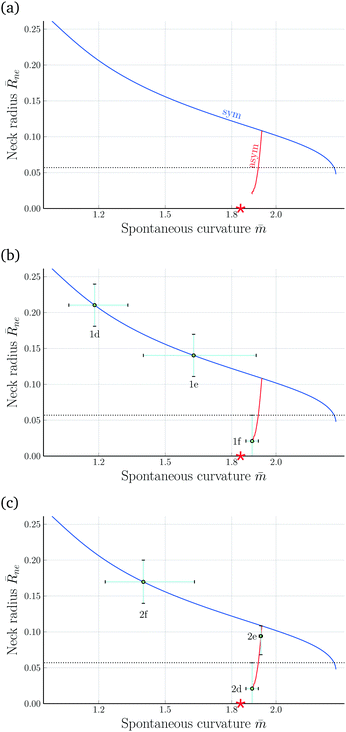 | ||
Fig. 8 Rescaled radius ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) ne = Rne/Rve of membrane neck as a function of spontaneous curvature ne = Rne/Rve of membrane neck as a function of spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) for v = 0.670: (a) computed variation of the neck radius along the symmetric (blue) and asymmetric (red) dumbbell branches. The corresponding shapes are displayed in Fig. 6 and Movie 2 (ESI†). As we increase the spontaneous curvature for v = 0.670: (a) computed variation of the neck radius along the symmetric (blue) and asymmetric (red) dumbbell branches. The corresponding shapes are displayed in Fig. 6 and Movie 2 (ESI†). As we increase the spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) , the neck radius decreases along the symmetric but increases along the asymmetric branch. The red star indicates the estimate , the neck radius decreases along the symmetric but increases along the asymmetric branch. The red star indicates the estimate ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ≃ 1.84 for the spontaneous curvature of the prolate-sphere limit shape Lps with ≃ 1.84 for the spontaneous curvature of the prolate-sphere limit shape Lps with ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) ne = 0; (b) evolution of neck radius and spontaneous curvature for the three shapes in Fig. 1 that describe the symmetry-breaking transformation; and (c) evolution of neck radius and spontaneous curvature for the three shapes in Fig. 2 that describe the symmetry-restoring transformation. The error bars of the neck radius correspond to the uncertainty of the neck radius as obtained by approximating the experimental shape contours in Fig. 1a–c and 2a–c with splines, truncated at the bifurcation point and the threshold of the optical resolution. The error bars of the spontaneous curvature correspond to the resulting uncertainty of the spontaneous curvature given the non-linear shape of the curve. The horizontal dotted lines represent the optical resolution limit of 300 nm. ne = 0; (b) evolution of neck radius and spontaneous curvature for the three shapes in Fig. 1 that describe the symmetry-breaking transformation; and (c) evolution of neck radius and spontaneous curvature for the three shapes in Fig. 2 that describe the symmetry-restoring transformation. The error bars of the neck radius correspond to the uncertainty of the neck radius as obtained by approximating the experimental shape contours in Fig. 1a–c and 2a–c with splines, truncated at the bifurcation point and the threshold of the optical resolution. The error bars of the spontaneous curvature correspond to the resulting uncertainty of the spontaneous curvature given the non-linear shape of the curve. The horizontal dotted lines represent the optical resolution limit of 300 nm. | ||
4.3 Two branches of the bending energy
The symmetric and asymmetric dumbbells as displayed in Fig. 6 belong to two different branches of the bending energy Ebe as shown in Fig. 7. As described in the previous subsection, these two branches coexist for the![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) -interval with
-interval with ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) (Lps) <
(Lps) < ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) <
< ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) (Bop) with
(Bop) with ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) (Lps) ≃ 1.84 and merge continuously into a single symmetric branch when the spontaneous curvature reaches the bifurcation value
(Lps) ≃ 1.84 and merge continuously into a single symmetric branch when the spontaneous curvature reaches the bifurcation value ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) =
= ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) (Bop) with 1.933 <
(Bop) with 1.933 < ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) (Bop) < 1.94, where the numerical values apply to v = 0.670. The continuous bifurcation at spontaneous curvature
(Bop) < 1.94, where the numerical values apply to v = 0.670. The continuous bifurcation at spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) (Bop) is confirmed by the functional form of the bending energy, see inset in Fig. 7. The latter inset displays the rescaled bending energy difference
(Bop) is confirmed by the functional form of the bending energy, see inset in Fig. 7. The latter inset displays the rescaled bending energy difference| ΔĒbe ≡ (Ēasybe − Ēsybe)/(8πκ) | (12) |
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) -value close to 1.94. The latter behavior agrees with the shape evolution in Fig. 6, which directly demonstrates that the up-down asymmetric shapes become more and more symmetric as we approach the bifurcation value
-value close to 1.94. The latter behavior agrees with the shape evolution in Fig. 6, which directly demonstrates that the up-down asymmetric shapes become more and more symmetric as we approach the bifurcation value ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) (Bop) of the spontaneous curvature.
(Bop) of the spontaneous curvature.
In the spontaneous curvature model, the bending energy difference ΔĒbe displayed in the inset of Fig. 7 is always positive, i.e., the asymmetric branch has an increased bending energy compared to the symmetric one. Further below, we will consider the area-difference-elasticity model and study the bending energies as a function of the local spontaneous curvature mloc. In the latter case, the branch of asymmetric shapes has a lower bending energy and, thus, becomes the stable state of minimal bending energy.
4.4 Closing and opening of membrane necks
For each dumbbell shape, the two subcompartments are connected by a membrane neck with a circular waistline. The radius of this waistline defines the neck radius Rne, see Fig. 1 and 2, which changes during the shape oscillations. Thus, in addition to the global up-down symmetry of the dumbbells, these shapes can also be distinguished by their neck radius Rne which represents a local property.In Fig. 8a, we display the rescaled neck radius
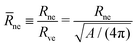 | (13) |
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = mRve, along the symmetric (blue) and asymmetric (red) branch of dumbbells. In addition to the two branches of the neck radius as a function of spontaneous curvature, the two panels b and c of Fig. 8 contain the numerical values of
= mRve, along the symmetric (blue) and asymmetric (red) branch of dumbbells. In addition to the two branches of the neck radius as a function of spontaneous curvature, the two panels b and c of Fig. 8 contain the numerical values of ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) ne and
ne and ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) for the three dumbbell shapes in Fig. 1 and 2. The latter plots show once more that, in the spontaneous curvature model, the neck radius decreases and increases monotonically along the symmetric and asymmetric branches, respectively, as we increase the spontaneous curvature of the GUV membrane. These plots also show how the uncertainties in the neck radius lead to different uncertainties in the spontaneous curvature, depending on the value of the radius as well as the branch to which the shape belongs. The steeper the curve of the neck radius is, the more accurate can the spontaneous curvature be estimated. Additionally the branch bifurcation point and the optical limit are natural boundaries at which the error bars can be truncated.
for the three dumbbell shapes in Fig. 1 and 2. The latter plots show once more that, in the spontaneous curvature model, the neck radius decreases and increases monotonically along the symmetric and asymmetric branches, respectively, as we increase the spontaneous curvature of the GUV membrane. These plots also show how the uncertainties in the neck radius lead to different uncertainties in the spontaneous curvature, depending on the value of the radius as well as the branch to which the shape belongs. The steeper the curve of the neck radius is, the more accurate can the spontaneous curvature be estimated. Additionally the branch bifurcation point and the optical limit are natural boundaries at which the error bars can be truncated.
4.5 Time dependence of active shape oscillations
The time-lapse Movie 1 (ESI†) consists of 200 individual snapshots or frames which were taken with the predefined time interval Δt = 7.61 s between successive frames. We number the frames by the index i from i = 1 to i = 200 and label each frame as ‘open’ if it displays an open neck and as ‘closed’ if the neck appears to be closed on the optical image. In this way, we map the sequence of 200 vesicle images onto a sequence of open and closed states. Both types of states are persistent and form short subseries of successive open states that alternate with short subseries of successive closed states.We identify neck closure events to be provided by those frames that display a closed neck and are directly preceded by a frame with an open neck. Furthermore, a complete shape oscillation is defined by the sequence of Δi frames between two successive closure events. Such a sequence consists of a subseries of three to four successive images with closed necks, followed by a subseries of three to four successive images with open necks. Movie 1 (ESI†) displays 191 frames between the first and the last closure event, which form 26 complete shape oscillations. Thus, the average number of frames, 〈Δi〉, per complete shape oscillation is equal to 191/26 = 7.35 frames and the average time period for one complete oscillation is given by 〈Δi〉Δt = 7.35 × 7.61 s = 55.9 s, which is similar to the cycle time observed for Min oscillations in other compartments.25,26
Most of the 26 complete shape oscillations consist of 7 or 8 successive images or frames. The 7-frame oscillations are observed 15 times, the 8-frame oscillations 10 times. In addition, we observe one complete oscillation with only 6 successive frames. Thus, including these statistical fluctuations, we obtain the estimate
| Δi = 〈Δi〉 ± 1 = 7.35 ± 1 |
The theoretical shapes in Fig. 1 and 2 were obtained for the parameter values in Table 2. The resulting time-dependence of the spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) is shown in Fig. 9 where we plot
is shown in Fig. 9 where we plot ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) versus the frame index i which corresponds to the time
versus the frame index i which corresponds to the time
| t = (i − 1)Δt = (i − 1) × 7.61 s | (14) |
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) =
= ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) (i) in Fig. 9, the GUV shape has a certain neck radius Rne = Rne(
(i) in Fig. 9, the GUV shape has a certain neck radius Rne = Rne(![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) ) as plotted in Fig. 8b and c. When we combine these two relationships, we obtain the time dependence of the neck radius Rne = Rne(i) as shown in Fig. 10.
) as plotted in Fig. 8b and c. When we combine these two relationships, we obtain the time dependence of the neck radius Rne = Rne(i) as shown in Fig. 10.
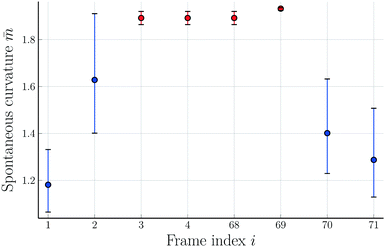 | ||
Fig. 9 Rescaled spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) versus frame index i. The frame i was taken at time t = (i − 1) × 7.61 s after the initial frame with index i = 1. The blue data points correspond to up-down symmetric dumbbell shapes, the red data points to asymmetric ones. The symmetry-breaking transformation in Fig. 1 corresponds to i = 1, 2, and 3, the symmetry-restoring transformation in Fig. 2 to i = 68, 69, and 70. The image i = 4 displays a slightly distorted version of i = 3 and is thus taken to have the same versus frame index i. The frame i was taken at time t = (i − 1) × 7.61 s after the initial frame with index i = 1. The blue data points correspond to up-down symmetric dumbbell shapes, the red data points to asymmetric ones. The symmetry-breaking transformation in Fig. 1 corresponds to i = 1, 2, and 3, the symmetry-restoring transformation in Fig. 2 to i = 68, 69, and 70. The image i = 4 displays a slightly distorted version of i = 3 and is thus taken to have the same ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) -value as i = 3. The image i = 71 displays a symmetric dumbbell with an increased neck radius compared to i = 70. This increased radius implies the spontaneous curvature -value as i = 3. The image i = 71 displays a symmetric dumbbell with an increased neck radius compared to i = 70. This increased radius implies the spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = 1.32. The combined sequence of all eight images represents one complete shape oscillation with an average time period of 55.9 s. The error bars are obtained as in Fig. 8. = 1.32. The combined sequence of all eight images represents one complete shape oscillation with an average time period of 55.9 s. The error bars are obtained as in Fig. 8. | ||
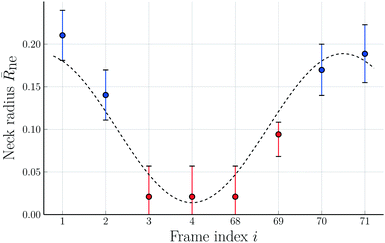 | ||
Fig. 10 Rescaled neck radius ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) neversus frame index i corresponding to time t = (i − 1) × 7.61 s. Direct inspection of the frame with index i = 71 leads to the neck radius neversus frame index i corresponding to time t = (i − 1) × 7.61 s. Direct inspection of the frame with index i = 71 leads to the neck radius ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) ne = 0.189 for this image. The combined sequence of all eight images represents one complete shape oscillation which takes, on average, 55.9 s. The color code of the data points is the same as in Fig. 9. The trigonometric curve (dashed black line) through the data provides the best fit to a single Fourier mode as parametrized by eqn (15). The error bars are obtained as in Fig. 8. ne = 0.189 for this image. The combined sequence of all eight images represents one complete shape oscillation which takes, on average, 55.9 s. The color code of the data points is the same as in Fig. 9. The trigonometric curve (dashed black line) through the data provides the best fit to a single Fourier mode as parametrized by eqn (15). The error bars are obtained as in Fig. 8. | ||
Because of the relatively large error bars for the data in Fig. 10, depicting the time-dependence of the neck radius ![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) ne, it is difficult to fit these data in a quantitative manner. The presumably simplest fit is provided by a single Fourier mode of the form
ne, it is difficult to fit these data in a quantitative manner. The presumably simplest fit is provided by a single Fourier mode of the form
![[R with combining macron]](https://www.rsc.org/images/entities/i_char_0052_0304.gif) ne = a + b ne = a + b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos[2π(i − 1)/7], cos[2π(i − 1)/7], | (15) |
4.6 Modifications arising from area-difference-elasticity
In the previous sections, we described the curvature elasticity of the vesicle membrane by the spontaneous curvature model as given by eqn (1). From the theoretical point of view, this model directly applies to lipid bilayers with at least one lipid component that undergoes frequent flip-flops between the two bilayer leaflets, as recently confirmed experimentally for lipid bilayers with cholesterol.22,23 The vesicle membranes studied in ref. 6, on the other hand, contained the two phospholipids DOPC and DOPG as well as a very small mole fraction of labeled DOPE, all of which are not expected to undergo frequent flip-flops on the experimentally relevant time scales. In the latter situation, we need to generalize the spontaneous curvature model to the area-difference-elasticity model,13–15 which can, however, be mapped back onto the spontaneous curvature model by decomposing the spontaneous curvature into a local and a nonlocal contribution.9,15In the absence of flip-flops, each leaflet has a fixed number of lipids which generates an additional constraint on the area difference between the two leaflets. This area difference is proportional to the integrated (or total) mean curvature
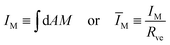 | (16) |
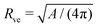 in eqn (3) has been used to define the dimensionless curvature ĪM.§
in eqn (3) has been used to define the dimensionless curvature ĪM.§
When we include the constraint on the area difference and, thus, the integrated mean curvature, we arrive at the area-difference-elasticity (ADE) model with the energy13–15
| EADE = Ebe′ + DADE | (17) |
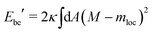 | (18) |
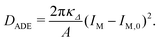 | (19) |
The second bending rigidity κΔ is, in general, difficult to determine but is typically comparable to κ.14 In order to eliminate one parameter, we will focus on the case with κΔ equal to κ. The reference value IM,0, on the other hand, can be estimated from the integrated mean curvatures of the six shapes displayed in Fig. 1 and 2. The resulting numerical values of the dimensionless quantity ĪM = IM/Rve are displayed in Table 3. The best estimate for the reference value IM,0 ≡ x is now obtained by minimizing the root-mean-square deviation
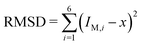 | (20) |
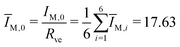 | (21) |
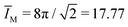 .
.
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) nlo as obtained from eqn (23) with κΔ/κ = 1, the spontaneous curvature
nlo as obtained from eqn (23) with κΔ/κ = 1, the spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) as in Table 2, and the local spontaneous curvature
as in Table 2, and the local spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) loc =
loc = ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) −
− ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) nlo. The nonlocal spontaneous curvature
nlo. The nonlocal spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) nlo is positive and negative for symmetric and asymmetric shapes, respectively. Apart from Fig. 1d, the local spontaneous curvature
nlo is positive and negative for symmetric and asymmetric shapes, respectively. Apart from Fig. 1d, the local spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) loc differs from
loc differs from ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) only by a few percent
only by a few percent
The stationary shapes of the area-difference-elasticity model are also stationary shapes of the spontaneous curvature model13–15 provided we use the identification9,15
m = mloc + mnlo or ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = = ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) loc + loc + ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) nlo nlo | (22) |
with the nonlocal spontaneous curvature
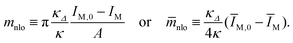 | (23) |
![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) loc can then be computed via
loc can then be computed via ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) loc =
loc = ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) −
− ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) nlo.|| The numerical values for the local and nonlocal spontaneous curvature obtained in this manner for the shapes in Fig. 1 and 2 are provided in Table 3.
nlo.|| The numerical values for the local and nonlocal spontaneous curvature obtained in this manner for the shapes in Fig. 1 and 2 are provided in Table 3.
The rescaled ADE energy is now given by
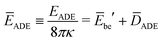 | (24) |
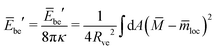 | (25) |
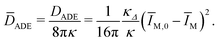 | (26) |
The ADE model depends on four dimensionless parameters: the volume-to-area ratio v, the local spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) loc, the reference value ĪM,0 of the integrated mean curvature, and the rigidity ratio κΔ/κ. For the fixed parameter values v = 0.670, ĪM,0 = 17.63, and κΔ/κ = 1, we are left with only one dimensionless parameter, the local spontaneous curvature
loc, the reference value ĪM,0 of the integrated mean curvature, and the rigidity ratio κΔ/κ. For the fixed parameter values v = 0.670, ĪM,0 = 17.63, and κΔ/κ = 1, we are left with only one dimensionless parameter, the local spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) loc. Within the ADE model, this latter parameter depends on the amount of Min proteins bound to the inner leaflet of GUV membrane. The time-dependent oscillation of the local spontaneous curvature
loc. Within the ADE model, this latter parameter depends on the amount of Min proteins bound to the inner leaflet of GUV membrane. The time-dependent oscillation of the local spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) loc is displayed in Fig. S2 (ESI†). Comparison with the time dependence of
loc is displayed in Fig. S2 (ESI†). Comparison with the time dependence of ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) in Fig. 9 shows that, in contrast to
in Fig. 9 shows that, in contrast to ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) , the local curvature
, the local curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) loc decreases monotonically during the symmetry restoring transformation between frame 68 and 70.
loc decreases monotonically during the symmetry restoring transformation between frame 68 and 70.
The dependence of the ADE energies on ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) loc is displayed in Fig. 11. Note that the ADE energy of the asymmetric branch is now below the energy of the symmetric one and that the energy difference
loc is displayed in Fig. 11. Note that the ADE energy of the asymmetric branch is now below the energy of the symmetric one and that the energy difference
| ΔĒADE = ĒasyADE − ĒsyADE | (27) |
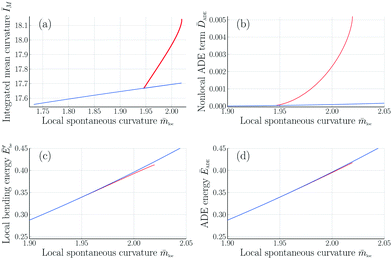 | ||
Fig. 11 Integrated mean curvature and different energy contributions in the ADE model as functions of the local spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) loc for rigidity ratio κΔ/κ = 1. The symmetric and asymmetric branches are displayed as blue and red lines, respectively: (a) Integrated mean curvature ĪM as in eqn (16); (b) Nonlocal area-difference-elasticity term loc for rigidity ratio κΔ/κ = 1. The symmetric and asymmetric branches are displayed as blue and red lines, respectively: (a) Integrated mean curvature ĪM as in eqn (16); (b) Nonlocal area-difference-elasticity term ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) ADE as in eqn (26); (c) local bending energy Ēbe′ as in eqn (25); and (d) ADE energy ĒADE which is equal to the sum of the local and nonlocal terms in panels b and c. In contrast to the spontaneous curvature model, see Fig. 7, the energy of the asymmetric branch is now below the energy of the symmetric one. All quantities were computed for volume-to-area ratio v = 0.670 and reference value ĪM,0 = 17.63 of the integrated mean curvature. ADE as in eqn (26); (c) local bending energy Ēbe′ as in eqn (25); and (d) ADE energy ĒADE which is equal to the sum of the local and nonlocal terms in panels b and c. In contrast to the spontaneous curvature model, see Fig. 7, the energy of the asymmetric branch is now below the energy of the symmetric one. All quantities were computed for volume-to-area ratio v = 0.670 and reference value ĪM,0 = 17.63 of the integrated mean curvature. | ||
5 Discussion
In this study, we analyzed the recently observed shape oscillations of giant vesicles in a quantitative manner, using the framework of curvature elasticity. In the latter framework, the simplest model is provided by the spontaneous curvature model in which the shape of a uniform vesicle membrane depends on two dimensionless parameters, the volume-to-area ratio v, see eqn (4), and the rescaled spontaneous curvature![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) = mRve. A detailed theoretical analysis of Movie 1 (ESI†) showed that the shape oscillations conserve both the vesicle volume and the membrane area which implies a constant value of v (Table 2). Our analysis also revealed that the observed shape oscillations can be understood in terms of a time-dependent spontaneous curvature, which varies in a cyclic, almost periodic manner.
= mRve. A detailed theoretical analysis of Movie 1 (ESI†) showed that the shape oscillations conserve both the vesicle volume and the membrane area which implies a constant value of v (Table 2). Our analysis also revealed that the observed shape oscillations can be understood in terms of a time-dependent spontaneous curvature, which varies in a cyclic, almost periodic manner.
Surprisingly, these shape oscillations were found to involve two energy branches of the vesicle membrane, corresponding to up-down symmetric and up-down asymmetric dumbbells, see Fig. 6 and 7. The latter two figures imply that the two branches merge in a continuous manner. During each complete shape oscillation, the vesicle morphology undergoes a symmetry-breaking transformation (Fig. 1) at which an up-down symmetric dumbbell with two subcompartments of equal size transforms into an up-down asymmetric dumbbell with two subcompartments of different sizes, followed by the reverse, symmetry-restoring transformation (Fig. 2). In the spontaneous curvature model, the bending energy of the asymmetric branch exceeds the bending energy of the symmetric one (Fig. 7).
The phospholipids studied in ref. 6 are unlikely to undergo frequent flip-flops between the two leaflets of the bilayer membranes. To take this absence of flip-flops into account, we extended the spontaneous curvature model to the area-difference-elasticity (ADE) model by decomposing the spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) into a local and a nonlocal component, see eqn (22) and (23). In the ADE model, the attachment–detachment kinetics of the Min proteins leads to variations of the local spontaneous curvature
into a local and a nonlocal component, see eqn (22) and (23). In the ADE model, the attachment–detachment kinetics of the Min proteins leads to variations of the local spontaneous curvature ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) loc as given in Table 3 for the observed shapes in Fig. 1 and 2. Furthermore, the branch of asymmetric dumbbells is now located below the branch of symmetric ones, both for κΔ/κ = 1 (Fig. 11) and for κΔ/κ = 2 (Fig. S3, ESI†). Therefore, both the symmetric and the asymmetric dumbbells that have been observed experimentally (Fig. 1 and 2) are likely to represent stable shapes of minimal bending energy.
loc as given in Table 3 for the observed shapes in Fig. 1 and 2. Furthermore, the branch of asymmetric dumbbells is now located below the branch of symmetric ones, both for κΔ/κ = 1 (Fig. 11) and for κΔ/κ = 2 (Fig. S3, ESI†). Therefore, both the symmetric and the asymmetric dumbbells that have been observed experimentally (Fig. 1 and 2) are likely to represent stable shapes of minimal bending energy.
The branch of asymmetric dumbbell shapes observed here involves a prolate-sphere limit shape Lps, consisting of a prolate and a spherical subcompartment which are connected by a closed membrane neck. In the present study, we studied the volume-to-area ratio v = 0.670 for which we obtained the estimate ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) (Lps) ≃ 1.84 for the spontaneous curvature at which this limit shape Lps is formed. Such prolate-sphere limit shapes are expected to be stable within a whole region of the morphology diagram as defined by the two shape parameters v and
(Lps) ≃ 1.84 for the spontaneous curvature at which this limit shape Lps is formed. Such prolate-sphere limit shapes are expected to be stable within a whole region of the morphology diagram as defined by the two shape parameters v and ![[m with combining macron]](https://www.rsc.org/images/entities/i_char_006d_0304.gif) , in close analogy to the stability regime for the two-sphere vesicles in Fig. 3. For the prolate-sphere limit shapes, the corresponding stability regime remains to be determined and will add another layer to the morphological complexity of vesicle shapes.
, in close analogy to the stability regime for the two-sphere vesicles in Fig. 3. For the prolate-sphere limit shapes, the corresponding stability regime remains to be determined and will add another layer to the morphological complexity of vesicle shapes.
One unexpected outcome of our analysis is that the coupling of membrane curvature to active processes can reveal new branches of vesicle shapes that have not been observed before. In the present study, such shapes are provided by asymmetric dumbbells with volume-to-area ratio 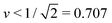 . Thus, it should be rather interesting to extend our study, both experimentally and theoretically, to different values of v and to see whether or not the Min-induced shape oscillations typically involve distinct branches of (meta)stable shapes.
. Thus, it should be rather interesting to extend our study, both experimentally and theoretically, to different values of v and to see whether or not the Min-induced shape oscillations typically involve distinct branches of (meta)stable shapes.
Finally, in the present study, the two subcompartments of the GUVs were always connected by a narrow membrane neck. From the theoretical point of view, a sufficiently large spontaneous curvature can cleave such a neck by curvature-induced constriction forces,9 as recently demonstrated for GUVs that were exposed to His-tagged proteins.23 Therefore, an interesting and challenging objective for future studies is to cleave these necks by combining the Min proteins studied here with other curvature-generating molecules.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Jaime Agudo-Canalejo for advice on the numerical solution of the shape equations and acknowledge support by the Max Planck Society and the Federal Ministry of Education and Research (BMBF) via the MaxSynBio consortium. Open Access funding provided by the Max Planck Society.Notes and references
-
Structure and Dynamics of Membranes, ed. R. Lipowsky and E. Sackmann, Elsevier, Amsterdam, 1995 Search PubMed
.
-
Physics of Biological Membranes, ed. P. Bassereau and P. Sens, Springer Nature, 2018 Search PubMed
.
-
The Giant Vesicle Book, ed. R. Dimova and C. Marques, Taylor & Francis, 2020 Search PubMed
.
- B. Antonny, C. Burd, P. de Camilli, E. Chen, O. Daumke, K. Faelber, M. Ford, V. A. Frolov, A. Frost, J. E. Hinshaw, T. Kirchhausen, M. M. Kozlov, M. Lenz, H. H. Low, H. McMahon, C. Merrifield, T. D. Pollard, P. J. Robinson, A. Roux and S. Schmid, EMBO J., 2016, 35, 2270–2284 CrossRef CAS
.
- P. A. de Boer, R. E. Crossley, A. R. Hand and L. I. Rothfield, EMBO J., 1991, 10, 4371–4380 CrossRef CAS
.
- T. Litschel, B. Ramm, R. Maas, M. Heymann and P. Schwille, Angew. Chem., Int. Ed., 2018, 57, 16286–16290 CrossRef CAS
.
- Z. Hu, E. P. Gogol and J. Lutkenhaus, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 6761–6766 CrossRef CAS
.
- M. Loose, E. Fischer-Friedrich, C. Herold, K. Kruse and P. Schwille, Nat. Struct. Mol. Biol., 2011, 18, 577–583 CrossRef CAS
.
-
R. Lipowsky, The Giant Vesicle Book, Taylor & Francis, 2020, pp. 73–168 Search PubMed
.
- W. Helfrich, Z. Naturforsch., 1973, 28c, 693–703 Search PubMed
.
- H. Deuling and W. Helfrich, J. Phys., 1976, 37, 1335–1345 CrossRef CAS
.
- U. Seifert, K. Berndl and R. Lipowsky, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, 1182–1202 CrossRef
.
-
U. Seifert, L. Miao, H.-G. Döbereiner and M. Wortis, The Structure and Conformation of Amphiphilic Membranes, Springer-Verlag, 1992, pp. 93–96 Search PubMed
.
- L. Miao, U. Seifert, M. Wortis and H.-G. Döbereiner, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 5389–5407 CrossRef
.
- H.-G. Döbereiner, E. Evans, M. Kraus, U. Seifert and M. Wortis, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 4458–4474 CrossRef
.
- S. Svetina and B. Žekš, Eur. Biophys. J., 1989, 17, 101–111 CrossRef
.
- S. Svetina and B. Žekš, The Anatomical Record, 2002, 268, 215–225 CrossRef
.
- B. Fourcade, L. Miao, M. Rao, M. Wortis and R. Zia, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 49, 5276–5286 CrossRef CAS
.
- J. Agudo-Canalejo and R. Lipowsky, Soft Matter, 2016, 12, 8155–8166 RSC
.
- H.-G. Döbereiner, J. Käs, D. Noppl, I. Sprenger and E. Sackmann, Biophys. J., 1993, 65, 1396–1403 CrossRef
.
- T. Tanaka, R. Sano, Y. Yamashita and M. Yamazaki, Langmuir, 2004, 20, 9526–9534 CrossRef CAS
.
- T. Bhatia, S. Christ, J. Steinkühler, R. Dimova and R. Lipowsky, Soft Matter, 2020, 1246–1258 RSC
.
- J. Steinkühler, R. L. Knorr, T. Bhatia, S. Bartelt, S. Wegner, R. Dimova and R. Lipowsky, Nat. Commun., 2020, 11, 905 CrossRef
.
- P. Bassereau, R. Jin, T. Baumgart, M. Deserno, R. Dimova, V. A. Frolov, P. V. Baskirov, H. Grubmüller, R. Jahn, H. J. Risselada, L. Johannes, M. M. Kozlov, R. Lipowsky, T. J. Pucadyil, W. F. Zeno, J. C. Stachowiak, D. Stamou, A. Breuer, L. Lauritsen, C. Simon, C. Sykes, G. A. Voth and T. R. Weikl, J. Phys. D: Appl. Phys., 2018, 51, 343001 CrossRef
.
- A. Dajkovic and J. Lutkenhaus, J. Mol. Microbiol. Biotechnol., 2006, 11, 140–151 CrossRef CAS
.
- K. Zieske and P. Schwille, eLife, 2014, 3, e03949 CrossRef
.
- F. Brochard and J. Lennon, J. Phys., 1975, 36, 1035–1047 CrossRef
.
- H. Duwe, J. Käs and E. Sackmann, J. Phys., 1990, 51, 945–962 CrossRef CAS
.
- B. Božič, G. Gomišček, V. Kralj-Iglič, S. Svetina and B. Žekš, Eur. Biophys. J., 2002, 31, 487–496 CrossRef
.
- J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld, B. Schmid, J.-Y. Tinevez, D. J. White, V. Hartenstein, K. Eliceiri, P. Tomancak and A. Cardona, Nat. Methods, 2012, 9, 676–682 CrossRef CAS
.
- H. H. Ku, J. Res. N.B.S. C Eng. Inst., 1966, 70, 263–273 Search PubMed
.
- P. K. Mogensen and A. N. Riseth, J. Open Source Software, 2018, 3, 615 CrossRef
.
Footnotes |
| † Electronic supplementary information (ESI) available: Supplementary text on shape equations for and numerical computation of axisymmetric vesicle shapes; Fig. S1 with parametrization of shape contours; Fig. S2 with time dependence of local spontaneous curvature; Fig. S3 for ADE model with κΔ/κ = 2; captions of Movie 1 and Movie 2; Movie 1 with observed vesicle shapes; Movie 2 with computed vesicle shapes. See DOI: 10.1039/d0sm00790k |
| ‡ Strictly speaking, the expression in eqn (1) is the bending energy functional that is defined for an arbitrary vesicle shape and should be distinguished from the bending energy as obtained for a certain stable shape. For notational simplicity, we will ignore this distinction here. |
| § The dimensionless integrated mean curvature ĪM is related to the dimensionless area difference Δa as discussed in ref. 12, 16 and 17 by ĪM = 4πΔa. |
| ¶ In ref. 17, the prefactor π in eqn (19) is combined with the second bending rigidity κΔ to define the nonlocal bending energy κr ≡ πκΔ. |
| || All barred curvatures are dimensionless and obtained from the unbarred ones by multiplication with the basic length scale Rve. |
| This journal is © The Royal Society of Chemistry 2021 |