 Open Access Article
Open Access ArticleThe role of entropy in wetting of polymer brushes†
Liz I. S.
Mensink
a,
Sissi
de Beer
 *b and
Jacco H.
Snoeijer
*b and
Jacco H.
Snoeijer
 a
a
aPhysics of Fluids and the MESA+ Institute, University of Twente, PO box 217, 7500 AE Enschede, The Netherlands
bSustainable Polymer Chemistry and the MESA+ Institute, University of Twente, PO box 217, 7500 AE Enschede, The Netherlands. E-mail: s.j.a.debeer@utwente.nl; Tel: +31 53 4893170
First published on 8th December 2020
Abstract
The wetting of polymer brushes exhibits a much richer phenomenology than wetting of normal solid substrates. These brushes allow for three wetting states, which are partial wetting, complete wetting and mixing. Here, we study the transitions between these wetting states for brushes in contact with polymer melts and compare them to predictions using enthalpic arguments based on brush and melt interactions. We show that the transitions are shifted compared to the enthalpic predictions and that the shifts can be positive or negative depending on the length of the melt polymer and the brush grafting density. The reason for this is that these brush and melt parameters can have a positive or negative effect on the entropic contribution to the free energy of the system. Our results highlight the relevance of entropy in predicting the exact wetting transitions, which is important for the design of brush-based coating applications.
1 Introduction
Polymer brushes consist of long macromolecules densely end-attached to a surface.1 They are popular building blocks in the design of functional surface coatings due to their versatility and simplicity to manipulate.2,3 For example, these brushes have been employed as smart sensors4–6 or to manage surface lubricity7–9 and adherence.10,11 Surface wettability is also tuned straightforwardly with polymer brushes, which has resulted in the development of moisture management systems12 and self-cleaning surfaces.13 For these applications, it is important to understand the wetting of polymer brushes.Wetting of polymer brushes deviates from wetting behavior on solid surfaces.14,15,60 Solids can be either partially or completely wetted. In contrast, polymer brush coatings can also absorb liquids, which gives rise to three wetting states, partial and complete wetting and the mixed state.16,17 The wetting state of the system depends on the brush–liquid interactions and the self-affinity of the brush (see Fig. 1). The three different states are separated by two transition-lines: the mixing to demixing transition (dashed) and the complete to partial wetting transition (dash-dot). To a large extent, these transitions can be understood using enthalpic arguments. When the affinity of the brush with the liquid, εBL, is less strong than the average self-affinities for the brush, εBB, and the liquid, εLL, the transition from mixing to demixing will occur. This happens when one goes from left to right crossing the vertical gray dashed line, W = εBB + εLL − 2εBL = 0, in Fig. 1. If the self-affinity of the liquid, εLL, is stronger than the affinity of the brush with the liquid, εBL, a transition from complete wetting to partial wetting can be observed. This happens when one goes from left to right, crossing the inclined gray dash-dotted line in Fig. 1. Though these enthalpic arguments capture the global behavior, there are clear deviations between the predicted transitions (gray) and the transitions extracted from recent molecular dynamics (MD) simulations17 (black). These deviations have been attributed to entropic effects.17 Yet, to what extend and in what direction entropy can affect these deviations is not yet studied in detail.
 | ||
| Fig. 1 (a–c) Snapshots of simulation cells showing a polymer droplet (blue), interacting with a polymer brush (orange) for the three wetting states. (d) Interaction-based phase diagram depicting the relation between the states of wetting and brush self-interaction εBB and the interaction parameter W. Observed are mixing (red triangles), complete wetting (orange squares) and partial wetting states (yellow circles). The gray lines indicate the enthalpic predictions for the mixing to demixing transition (W = εBB + εLL − 2εBL = 0, dashed) and the transition from complete to partial wetting (εBL = εLL, dash-dot). The black lines give the transitions observed in the MD simulations of ref. 17. | ||
In this paper, we will elucidate the role of entropy in the prediction of the wetting phase diagram of brushes wetted by polymeric nanodroplets. From early work on the wetting of brushes by chemically identical polymer melts, it is known that entropic effects can cause counter-intuitive phenomena such as demixing14,16,18–23 between the brush and the melt. This effect has been observed to strongly depend on the grafting density and the molecular weight of the melt and can result in autophobic dewetting,14,16,22,24,25 where melt droplets are formed on the chemically identical brush.
To understand the phenomena of demixing of chemically identical brushes and melts, reported previously,14,16,18–23 one needs to consider the different entropic contributions to the free energy.18 Without end-grafting of brush-polymers, melt and brush-polymers would mix to gain translational entropy. However, since brush-polymers are constrained, they cannot gain translational entropy upon mixing. Instead, their entropy is reduced by mixing due to the elastic penalty for stretching upon absorption of the melt. Because brush stretching depends on the grafting density of the brush, the mixing to demixing transition depends on the grafting density as well.18,19,26 Moreover, the translational entropy depends on the length of the melt-chains and, therefore, the mixing to demixing transition depends on the polymer length too.18,19,26
To understand autophobic dewetting, as reported previously,14,22,24,25 we have to consider the effect of entropy on the spreading parameter S. The spreading parameter is defined as S = γBV − (γBL + γLV), where γBV, γBL and γLV are the interfacial tensions between the solid brush and vapor phase (BV), the brush and liquid melt phase (BL) and the melt and vapor phase (LV), respectively. When the spreading parameter is positive (S > 0), complete wetting occurs and the droplet will partially wet the surface when S < 0. The interfacial tension between chemically identical brushes and melts γBL is negatively proportional to the difference in entropy before and after bringing the brush and melt in contact. For short melt polymers and low grafting densities, the change in entropy is positive. Contrarily, the change in entropy is negative for long melt polymers and high grafting densities. Thus, complete wetting is observed for short chains and low grafting densities, while partial wetting is observed for large chains and high grafting densities.14,22,24,25
The above described demixing and autophobicity effects are well characterized for brush–melt systems that are chemically identical.18–23 Yet, for many applications, the brushes will be in contact with chemically distinct media.27–29 The role of entropy in wetting and, in particular, the wetting transitions for brush–melt systems of chemically distinct media is still largely unexplored and we address this in the present paper, where we study the role of entropy on the wetting transitions of polymer brushes wetted by polymer droplets, using MD simulations.
2 Model and methods
We use a coarse-grained polymer model, based on the bead-spring model initially developed by Kremer and Grest.30 This model is well-known to qualitatively reproduce the static and dynamic response of polymer brushes.31–33 Non-bonded interactions within this model are described using the Lennard-Jones (LJ) potential: | (1) |
Throughout this paper, we will employ Lennard-Jones units in which σ and ε define the units of length and the unit of energy, respectively. Considering for example poly(ethylene), these units can be converted to real values for the polymers using ε = 30 meV and σ = 0.5 nm.34 We use a finite extensible nonlinear elastic (FENE) potential combined with the repulsive part of the Lennard-Jones potential to describe the bonded interactions between consecutive beads within the polymer chains:
 | (2) |
Fig. 2(a) shows a typical snapshot of our simulation cell. The snapshots are rendered using VMD.35 Our simulation cells consist of a wall composed of single layer of Lennard-Jones particles (red) in a triangular lattice with polymers (orange) anchored by one end to the wall particles. Each individual brush-polymer consists of NB = 100 repeat units for all simulations presented. The density at which these polymers are attached to the surface is varied as σGD = 0.067, 0.15, 0.2, 0.27 chains per σ2, which equals approximately 1.3, 3, 4 and 5.3 times the critical grafting density for brush formation under poor solvent conditions. For grafting densities above this critical grafting density, the system is in the brush regime. For grafting densities below the critical grafting density, the system is in the so-called mushroom regime. This means our simulations are performed in the brush regime, which is also apparent from the snapshots and density profiles given in Fig. 2(b). They show a step-wise change in the brush density, which is clearly different from the strong variation in density observed for the mushrooms that are formed at densities below the critical grafting density.36
The polymer brush is in contact with a uniform polymer melt with a constant chain length that is varied between N = 2 and N = 64 for individual simulations. The total number of beads present in the polymer melt is kept constant, so the amount of molecules wetting the brush is varied (for N = 2 there are 8000 melt molecules, for N = 64 we simulated 250 melt molecules).
Our simulations are performed at a constant box-size and volume V, in a quasi-2D setup, as shown in Fig. 2(a). Our simulation box is periodic in x and y, with a boxlength in x of at least 108σ, depending on the spreading of the droplet. For small contact angles, we increased the boxsize in x to 218σ. The boxlength in y is limited to 15σ to suppress Rayleigh instabilities in the infinitely long cylindrical droplet. Yet, it is large enough to ensure that there are no self-interactions between polymer chains (gyration radius for the largest polymers of N = 64 is smaller than 6σ). Moreover, in this setup line-tension effects are negligible for droplets with radii that are larger than Rd = 7σ.37 Our droplets are all larger than Rd = 21.5σ. For such large radii, the difference between 3D and 2D contact angles are less 2 degrees.
The equations of motion are solved using the velocity Verlet algorithm as implemented in LAMMPS,38 using a timestep of Δt = 0.005τ. The simulations are performed in the NVT ensemble. The temperature T is kept constant at kBT = 1ε (kB being the Boltzmann constant) using a Langevin thermostat with a damping coefficient of ξ = 1τ−1. The simulation cells are equilibrated for 107 timesteps before the production runs of 107 timesteps during which the observables are extracted.
From the production runs we extract the density of the brush and the melt as a function of the distance from the wall in slabs of 0.2σ. From these density profiles overlap integrals are calculated, which equal the product of the brush and the melt density integrated over the distance:39 , with ρM and ρB representing the densities of melt and brush, respectively. These overlap integrals are employed to determine whether the brush and the melt have mixed or not. For the mixed state, the overlap integral will reach a maximum value. From this maximum overlap value, we determine the mixing to demixing transition to occur at 50% of this maximum. We note that the transition between the mixed state is not sharp, but instead evolves gradually via partial penetration starting at the top of the brush,17,21,40,41 as visualized in the ESI,† Fig. S1. We also compute the contact angle of the melt droplet from the production runs, by fitting spherical caps to the isodensity contours of the droplet, following a procedure previously reported.37
, with ρM and ρB representing the densities of melt and brush, respectively. These overlap integrals are employed to determine whether the brush and the melt have mixed or not. For the mixed state, the overlap integral will reach a maximum value. From this maximum overlap value, we determine the mixing to demixing transition to occur at 50% of this maximum. We note that the transition between the mixed state is not sharp, but instead evolves gradually via partial penetration starting at the top of the brush,17,21,40,41 as visualized in the ESI,† Fig. S1. We also compute the contact angle of the melt droplet from the production runs, by fitting spherical caps to the isodensity contours of the droplet, following a procedure previously reported.37
To tune the affinity between the brush and the melt, relative to the self-interaction of the brush, we alter the strength of the Lennard-Jones potential via ε. We study two different strengths for the self-interaction of the brush εBB, namely εBB = 1 and εBB = 1.5. When εBB is high enough, polymer brushes are attracted to one another, resulting in a collapsed polymer brush structure. We checked that for these εBB's, the bare brushes are indeed in the collapsed state (see ESI,† Fig. S2). This is in contrast to simulations by others et al.,42 where brush-wetting was studied for low εBB and, thus, (implicit) good solvent conditions. Similarly to soft elastomers,43–47 brushes can deform due to surface tension and form wetting ridges.48 Due to our choice of εBB, the brushes are relatively hard and wetting ridges are small and do not affect the macroscopic contact angle.17
We vary the interaction between the polymer brush and polymer melt εBL between 0.375 and 1.5, while εLL = 1 is kept constant, so that we move through the interaction-based phase diagram from Fig. 1(d) along horizontal lines. From the simulations, we aim to extract generic relations and we do not intend to model particular types of polymers. We allow all sorts of interactions, including interactions of entropic origin, and do not limit this to van der Waals potentials. Therefore, mixing rules do not apply49 and we can vary εBB and εBL independently from each other. The interactions between the wall and the polymer- and liquid-beads is kept purely repulsive (ε = 1, σ = 1 and rc = 21/6σ) to prevent preferential adsorption near the wall50 and higher order wetting transitions.51
3 Results and discussion
3.1 Mixing–demixing
First, we discuss the results of the MD simulations, addressing the mixing to demixing transition. In our simulations, we varied the grafting density and melt polymerization, for varying values of W = εBB + εLL − 2εBL and for two values of εBB. Generally, the calculation of relative excluded volumes instead of ε's is preferred to determine mixing–demixing transitions.52,53 However, conclusions will only be qualitatively different when liquid and polymer particles are not the same size.54 In our systems all particles have the same size such that qualitative differences due to this simplification are expected to be minor.From the simulations, we first determine whether the system is in a mixed or demixed state. This was done using the overlap integral of density profiles for the brush and the polymer melt. A high overlap integral means that mixing occurs, whereas a low overlap integral indicates demixing. By taking the overlap integral for several values of W, data-sets were gathered for constant values of N and σGD. These data-sets were then interpolated to determine whether each data point was above or below the transition-point. The resulting six phase diagrams are given in Fig. 3, where the red squares denote a mixed state and the orange triangles or yellow circles represent the demixed (complete or partial) wetting state. We call these phase diagrams, geometry based phase diagrams, in contrast to the interaction based phase diagram of Fig. 1.
The different phase diagrams in Fig. 3 from left to right display the results for varying values for the interaction parameter W, and from top to bottom the brush–brush interaction strength εBB. These geometry-based phase diagrams illustrate that there is a shift in the mixing to demixing transition for chemically distinct melts wetting a brush, compared to the chemically identical wetting case at W = 0. The top row shows the mixing transition for εBB = 1.0 and the bottom row shows εBB = 1.5. In the left and right columns, we show the effect of a shift in the interaction parameter to an increased and a decreased net attraction (ΔW = ±0.0625). From the top row (εBB = 1.0), we see that for W = −0.0625 (top left), only mixing occurs for our settings. These results are in qualitative agreement with previous observations for brush-coated particles in a polymer matrix.55 Only for very high grafting densities and melt chain lengths, which are not studied in the present work, one would expect to see a transition for such a negative interaction parameter.
For W = 0 (top middle in Fig. 3), we see a mixing to demixing transition. For high grafting densities and long melt-polymers, the system is in the demixed state. For these geometric conditions, there is an entropic penalty for mixing, because long melt polymers cannot gain much translational entropy by mixing and the entropic penalty for stretching is high for the already stretched polymers in high density brushes. In contrast, short polymers can gain much more translational entropy by mixing and the polymers in low density brushes stretch only little upon mixing, such that there is an effective entropy gain when short polymers are absorbed by low density brushes. Thus, mixing will occur for these geometric conditions.
For W = 0.0625 (top right in Fig. 3), the mixing to demixing transition has shifted to lower N and σGD. Under these conditions, the gain in translational entropy upon mixing needs to overcome the entropic costs of stretching brush polymers and the attractive interactions within the brush and the melt. Therefore, there is mixing for very short polymers (N = 2) only.
In the bottom row (εBB = 1.5), we observe no phase transitions for W = −0.0625 (bottom left), where we observe only mixing, and for W = 0.0625 (bottom right), where we instead observe only demixing. For W = 0, (bottom middle) we observe a phase-transition similar to the one for W = 0 and εBB = 1.0, but shifted downward, implying that demixing occurs for shorter chains compared to εBB = 1.0. From this we can conclude that the free energy cost to stretch the brush polymers has increased, which is consistent with the stronger interaction between the brush polymers.
To predict the transition between mixing and demixing, we will briefly discuss the theoretical work of ref. 19, which has been based on ref. 56. For chemically identical melts and droplets, the free energy in a mean field approximation is given by:
 | (3) |
| L ∝ aNBN−1/3σGD1/3. | (4) |
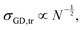 | (5) |
Eqn (3) can be modified to also take into account cases where the brush and melt are chemically distinct.19,56 In such cases, enthalpic interactions are incorporated using the Flory–Huggins interaction parameter  , with z being the coordination number, which is related to average number of neighbors of a polymer unit. The Flory Huggins parameter is proportional to our interaction parameter W. Due to enthalpic interactions, the free energy of the brush is now described by:
, with z being the coordination number, which is related to average number of neighbors of a polymer unit. The Flory Huggins parameter is proportional to our interaction parameter W. Due to enthalpic interactions, the free energy of the brush is now described by:
 | (6) |
Only positive excluded volumes are allowed such that (1 − 2Nχ)/N should remain positive. From this equation, the transition between mixing and demixing can be obtained:
 | (7) |
Through the phase diagrams for εBB = 1 with a phase transition present (Fig. 3, top row middle and right), we fitted these theoretical prediction (eqn (5) and (7)) of the mixing to demixing transition. For chemically identical brush and melt (eqn (5)), we introduced a prefactor α, which was utilized as a fitting parameter. This fitting parameter can be related to the effective monomer size and we found it to equal α = 0.82. For the chemically distinct system (W = 0.0625), we introduced a second fitting parameter β to correct for the difference between our interaction parameter  and the definition of the Flory Huggins parameter
and the definition of the Flory Huggins parameter 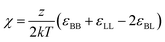 , resulting in a fit of the form:
, resulting in a fit of the form:  . From the data obtained for W = 0.0625, we obtained α = 0.82 (kept fixed) and β = 1.75. The fits are shown as black lines in Fig. 3. It is clear that the numerical data are well described by the dependency of eqn (7).
. From the data obtained for W = 0.0625, we obtained α = 0.82 (kept fixed) and β = 1.75. The fits are shown as black lines in Fig. 3. It is clear that the numerical data are well described by the dependency of eqn (7).
From the geometry-based phase diagrams we see that a shift in W strongly changes the mixing to demixing transition point, as was predicted by eqn (7). This prediction, however, is strictly speaking only valid in the case of positive excluded volume interactions, meaning that (1 − 2Nχ) > 0. For our setting of W = 0.0625, this is only the case for N = 8, 4 and 2. Still, for the theoretical prediction at εBB = 1.0 in Fig. 3, this prediction remains consistent with our numerical results. The data for εBB = 1.5 cannot be fitted with the same equations, because εBB, εBL and εLL are not equal at W = 0 and, therefore it does not represent chemically identical melts and brushes.
So far, we have discussed the effect of different brush-melt affinities on the transitions in the geometry based phase diagram, as represented in Fig. 3. Now, we would like to discuss how variations in σGD and N influence the transitions in the interaction-based phase diagram of Fig. 1. In Fig. 1, the black dashed line indicates Wtr for mixing to demixing at N = 32 and σGD = 0.15 chains per σ2. But, they can be anticipated to change when σGD and N are varied. Therefore, we determined the transition point in the interaction parameter Wtr, for varying values of the polymer melt and the grafting density, and the results are presented in Fig. 4. The datapoints illustrate the shift in the transitions due to entropy for εBB = 1.0 (blue triangles) and εBB = 1.5 (green circles) compared to transitions based on enthalpic arguments alone (grey dashed lines).
In Fig. 4(a), Wtr is shown as a function of N for σGD = 0.15 chains per σ2. For small chains, the transition occurs at W > 0, meaning that entropy is gained by mixing. In contrast, the longer melt chains show a shift to negative Wtr, because long chains gain less translational entropy than shorter chains. This smaller amount of entropy gain is not enough to compensate for the entropic penalty to stretch the polymer brush in order to mix. Fig. 4(b) depicts Wtr for varying σGD with N = 32, indicating a shift to positive Wtr for lower grafting density brushes, and a lower, negative Wtr for higher grafting densities. This effect of the grafting density is caused by densely grafted brushes having to pay a higher entropic penalty for stretching upon mixing, compared to less densely grafted brushes.
In summary, when regarding only enthalpic interactions, the mixing to demixing transition occurs at W = 0. Entropic interactions can increase or decrease Wtr, depending on N and σGD, where shorter chains and lower grafting densities tend to increase Wtr, meaning that entropy is gained from mixing. Our simulations for both chemically identical and chemically distinct brushes and melts, show good agreement to theoretical predictions from eqn (7) on the occurrence of the mixing to demixing transition. We have compared this theoretical transition both to a direct geometry-based phase diagram of our system, and to exact predictions of this transition, based on our data.
3.2 Partial wetting–complete wetting
We now focus on the transition from partial wetting to complete wetting. For the demixed states in Fig. 3, we made the distinction between complete wetting (orange triangles) and partial wetting (yellow circles). In the case of εBB = 1.0 we see a transition directly from mixing to partial wetting for all grafting densities except the highest, where a complete wetting state is observed. For εBB = 1.5 we observe a transition from mixing to complete wetting. One can expect a complete to partial wetting transition for εBB = 1.5 too, but for higher values of W only, as is also illustrated in Fig. 1.Next, we will consider the effect of the grafting density and melt polymer length on the interaction-based phase diagram of Fig. 1. To do so, we plot in Fig. 5 the contact angles (determined by spherical fits to isodensity profiles of the melt droplet37) as a function of the interaction parameter W for the different melt-polymer lengths (left graph εBB = 1.5 and middle graph εBB = 1.0) and grafting densities (right graph). The data shows an increasing θ for increasing W, caused by the lower brush–melt interactions for higher interaction parameters, that directly influence the wettability between the brush and melt. The data also reveals an increased wettability for shorter melt chains. For example for W = 0.375, we observe a contact angle of 78° for larger chains (N ≤ 16), while it reduces to θ < 50° for N = 2.
The increased wettability upon reducing the chain length is caused partly by the lower surface tensions of shorter polymer melt chains57 (see also ESI,† Fig. S3). Moreover, analysis of the density profiles indicate that the overlap integral increases for melts of decreasing chain length, which shows that there is more mixing between the melt and the brush for shorter melt chains. Interestingly, the penetration depths, which we define as the full width half maximum of the peak in ρBρM(z), is not affected by the chain length of the melt (e.g. at W = 0.375 and εBB = 1.5, the penetration depth is 1.9 ± 0.3σ) for all N. This means that the system of short chains increases its mixing entropy by decreasing the contact angle and, thus, increasing the contact area.
Our results on the increased wettability for shorter melt chains are in qualitative agreement with experimental contact angle measurements of alkane droplets on poly(dimethylsiloxane),58 which indeed showed that the contact angle decreases upon decreasing the length of the alkane-chain. The right graph depicts θ plotted against W for varying σGD. This data illustrates the rather weak dependency of the contact angle on the grafting density, also in agreement with experimental observations.58
To examine how the complete to partial wetting transition in the interaction-based phase diagram (Fig. 1) changes upon varying the brush grafting density or melt chain length, we extract Wtr from Fig. 5 by interpolating an exponential function fitted to the contact angles in Fig. 5. The Wtr between partial and complete wetting is the W for which θ has reached 0. The resulting Wtr is shown in Fig. 6, as a function of N (left), and of σGD (right). The wetting transitions based on the enthalpic estimate εLL = εBL are given as the blue and green dash-dotted lines, for εBB = 1.0 and εBB = 1.5, respectively.
In the left graph of Fig. 6, we see a rise in Wtr to positive values for very short chains N. We can explain this through the increased wettability for small N, that was observed from Fig. 5. As mentioned, short chains have lower surface tensions γBL and γLV (see also ESI,† Fig. S3), owing to a higher entropic contribution to the free energy for shorter chains as compared to longer chains. For longer chains, we reach a constant value for Wtr, as their surface tensions become similar (see Fig. 5). We assume this is caused by a limit to the intermolecular forces that can significantly contribute to the surface tension of a liquid melt.
The right graph of Fig. 6 shows the dependency of Wtr on the grafting density. We observe that Wtr slightly decreases upon increasing the grafting density. As mentioned above, the reason for this is the rather weak dependency of the spreading parameter on the grafting density, which is also in agreement with predictions from de Gennes.59
The data from Fig. 6(a) can be compared directly to the interaction-based phase diagram of Fig. 1. By doing so, we can compare how wetting transitions shift by changing the polymer melt length. From our data, we find that shorter N values would cause the complete to partial wetting transition to shift to the right, compared to the interaction-based phase diagram of Fig. 1 (here, transitions are marked using black lines), which determined for N = 32. In fact, for the shortest melt chains, our Ntr also shifts past the theoretical predictions as given in Fig. 1 (gray lines).
To conclude this section, we demonstrate that a transition from complete to partial wetting strongly depends on the length of the melt polymers N and depends only slightly on the grafting density σGD. Furthermore, we report greater wettability for shorter melt chains, due to their having a lower surface tension than their longer counterparts.
4 Conclusions
In summary, our results illustrate that wetting transitions are shifted due to entropic effects compared to predictions based on enthalpic effects alone. This shift depends on the length of the melt polymer N and the brush grafting density σGD. When regarding only enthalpic interactions, the mixing to demixing transition occurs at Wtr = 0. Entropic interactions can increase or decrease Wtr, depending on N and σGD, where shorter chains and lower grafting densities tend to increase Wtr, meaning that entropy is gained from mixing. The opposite is true for long chains and high grafting densities, where mixing decreases the entropy such that Wtr decreases to values below 0. Our results for both chemically identical and chemically distinct brushes and melts show good agreement to mean field theory describing the effect of N and σGD on the mixing to demixing transition. When considering the transition from complete to partial wetting, we find that short melt chains show higher wettability, meaning that they gain more translational entropy upon wetting a surface completely, as compared to long melt chains. As a result, the interfacial free energies for short chains, γBL and γLV, are smaller. Therefore, there is a strong effect of N on Wtr and complete wetting is observed for small N even for very high melt–melt interactions. In contrast, we observe that the complete to partial wetting transition depends only weakly on the grafting density. This indicates that, for the partial to complete wetting transitions, the brush can in many situations be regarded as a simple polymer film. Nevertheless, our results show that entropic effects have to be incorporated when considering wetting transitions, which is important in the design of potential applications such as brush-based sensors or self-cleaning surfaces.Conflicts of interest
There are no conflicts to declare.Acknowledgements
L. M. and J. H. S. acknowledge financial support from ERC (the European Research Council) Consolidator Grant No. 616918. NWO and SurfSara are acknowledged for HPC resources: this work was carried out on the Dutch national e-infrastructure with the support of SURF Cooperative. (L. M. NWO project number 16265 and S. d. B. reference code #45666).References
- S. T. Milner, Science, 1991, 251, 905 CrossRef CAS PubMed.
- O. Azzaroni, J. Polym. Sci., Part A: Polym. Chem., 2012, 50, 3225 CrossRef CAS.
- W.-L. Chen, R. Cordero, H. Tran and C. K. Ober, Macromolecules, 2017, 50, 4089–4113 CrossRef CAS.
- I. Tokareva, S. Minko, J. H. Fendler and E. Hutter, J. Am. Chem. Soc., 2004, 126, 15950–15951 CrossRef CAS PubMed.
- H. Merlitz, G.-L. He, C.-X. Wu and J.-U. Sommer, Phys. Rev. Lett., 2009, 102, 115702 CrossRef PubMed.
- L. I. Klushin, A. M. Skvortsov, A. A. Polotsky, S. Qi and F. Schmid, Phys. Rev. Lett., 2014, 113, 068303 CrossRef CAS PubMed.
- M. Chen, W. H. Briscoe, S. P. Armes and J. Klein, Science, 2009, 323, 1698–1701 CrossRef CAS PubMed.
- J. Yu, N. E. Jackson, X. Xu, Y. Morgenstern, Y. Kaufman, M. Ruths, J. J. de Pablo and M. Tirrell, Science, 2018, 360, 1434–1438 CrossRef CAS PubMed.
- Y. Yu, Y. Yao, S. van Lin and S. de Beer, Eur. Polym. J., 2019, 112, 222–227 CrossRef CAS.
- J. D. Willott, T. J. Murdoch, G. B. Webber and E. J. Wanless, Macromolecules, 2016, 49, 2327–2338 CrossRef CAS.
- Y. Yu, R. A. Lopez de la Cruz, B. D. Kieviet, H. Gojzewski, A. Pons, G. J. Vancso and S. de Beer, Nanoscale, 2017, 9, 1670–1675 RSC.
- H. Yang, H. Zhu, M. M. R. M. Hendrix, N. J. H. G. M. Lousberg, G. de With, A. C. C. Esteves and J. H. Xin, Adv. Mater., 2013, 25, 1150–1154 CrossRef CAS PubMed.
- J. A. Howarter and J. P. Youngblood, Adv. Mater., 2007, 19, 3838–3843 CrossRef CAS.
- A. Halperin and P. G. de Gennes, J. Phys., 1986, 47, 1243–1247 CrossRef CAS.
- D. Long, A. Ajdari and L. Leibler, Langmuir, 1996, 12, 1675–1680 CrossRef CAS.
- C. M. Wijmans, E. B. Zhulina and G. J. Fleer, Macromolecules, 1994, 27, 3238–3248 CrossRef CAS.
- L. I. S. Mensink, J. H. Snoeijer and S. de Beer, Macromolecules, 2019, 52, 2015–2020 CrossRef CAS PubMed.
- P. G. de Gennes, Macromolecules, 1980, 13, 1069 CrossRef CAS.
- M. Aubouy and E. Raphael, J. Phys. II, 1993, 3, 443–448 CrossRef CAS.
- G. S. Grest, Phys. Rev. Lett., 1996, 76, 4979 CrossRef CAS PubMed.
- P. G. Ferreira, A. Ajdari and L. Leibler, Macromolecules, 1998, 31, 3994–4003 CrossRef CAS.
- J. H. Maas, G. J. Fleer, F. A. M. Leermakers and M. A. Cohen Stuart, Langmuir, 2002, 18, 8871–8880 CrossRef CAS.
- C. Pastorino, K. Binder, T. Kreer and M. Müller, J. Chem. Phys., 2006, 124, 064902 CrossRef CAS PubMed.
- G. Reiter and R. Khanna, Phys. Rev. Lett., 2000, 85, 5599–5602 CrossRef CAS PubMed.
- X. Zhang, F. K. Lee and O. K. C. Tsui, Macromolecules, 2008, 41, 8148–8151 CrossRef CAS.
- M. Aubouy, G. H. Fredrickson, P. Pincus and E. Raphael, Macromolecules, 1995, 28, 2979–2981 CrossRef CAS.
- F. Zhou and W. T. S. Huck, Phys. Chem. Chem. Phys., 2006, 8, 3815 RSC.
- K. Park, S. H. Park, E. Kim, J.-D. Kim, S.-Y. An, H. S. Lim, H. H. Lee, D. H. Kim, D. Y. Ryu, D. R. Lee and J. H. Cho, Chem. Mater., 2010, 22, 5377–5382 CrossRef CAS.
- S. Liu, R. Eijkelenkamp, J. Duvigneau and G. J. Vancso, ACS Appl. Mater. Interfaces, 2017, 9, 37929–37940 CrossRef CAS PubMed.
- G. S. Grest and K. Kremer, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 33, 3628 CrossRef CAS PubMed.
- S. de Beer and M. H. Müser, Soft Matter, 2013, 9, 7234 RSC.
- S. de Beer, L. I. S. Mensink and B. D. Kieviet, Macromolecules, 2016, 49, 1070–1078 CrossRef CAS.
- T. Kreer, Soft Matter, 2016, 12, 3479–3501 RSC.
- K. Kremer and G. S. Grest, J. Chem. Phys., 1990, 92, 5057–5086 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33 CrossRef CAS.
- G. S. Grest and M. Murat, Macromolecules, 1993, 26, 3108–3117 CrossRef CAS.
- J. H. Weijs, A. Marchand, B. Andreotti, D. Lohse and J. H. Snoeijer, Phys. Fluids, 2011, 23, 022001 CrossRef.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1 CrossRef CAS.
- T. Kreer, M. H. Müser, K. Binder and J. Klein, Langmuir, 2001, 17, 7804 CrossRef CAS.
- C. Gay, Macromolecules, 1997, 30, 5939–5943 CrossRef CAS.
- A. D. Kazakov, A. A. Polotsky, E. B. Zhulina, T. M. Birshtein, F. A. M. Leermakers and O. V. Borisov, Macromolecules, 2020, 53, 387–397 CrossRef CAS.
- A. Milchev, D. I. Dimitrov and K. Binder, Biomicrofluidics, 2010, 4, 032202 CrossRef CAS PubMed.
- M. E. R. Shanahan, J. Phys. D: Appl. Phys., 1987, 20, 945 CrossRef CAS.
- E. R. Jerison, Y. Xu, L. A. Wilen and E. R. Dufresne, Phys. Rev. Lett., 2011, 106, 186103 CrossRef PubMed.
- J. H. Weijs, B. Andreotti and J. H. Snoeijer, Soft Matter, 2013, 9, 8494–8503 RSC.
- Z. Cao and A. V. Dobrynin, Macromolecules, 2015, 48, 443–451 CrossRef CAS.
- R. Dey, M. van Gorcum, F. Mugele and J. H. Snoeijer, Soft Matter, 2019, 15, 6469–6475 RSC.
- F. Léonforte and M. Müller, J. Chem. Phys., 2011, 135, 214703 CrossRef PubMed.
- J. N. Israelachvili, Intermolecular and Surface Forces, Academic Press, Elsevier, USA, 2011 Search PubMed.
- R. Descas, J.-U. Sommer and A. Blumen, Macromol. Theory Simul., 2008, 17, 429 CrossRef CAS.
- L. G. MacDowell and M. Müller, J. Chem. Phys., 2006, 124, 084907 CrossRef PubMed.
- P. de Gennes, Scaling Concepts in Polymer Physics, Cornell University Press, 1979 Search PubMed.
- M. Rubinstein and R. Colby, Polymer Physics, Oxford University Press, Oxford, 2003 Search PubMed.
- D. Mukherji, C. M. Marques, T. Stuehn and K. Kremer, Nat. Commun., 2017, 8, 1374 CrossRef PubMed.
- I. Borukhov and L. Leibler, Macromolecules, 2002, 35, 5171–5182 CrossRef CAS.
- E. Zhulina and O. Borisov, J. Colloid Interface Sci., 1991, 144, 507–520 CrossRef CAS.
- D. N. Theodorou, Macromolecules, 1989, 22, 4578–4589 CrossRef CAS.
- D. F. Cheng, C. Urata, B. Masheder and A. Hozumi, J. Am. Chem. Soc., 2012, 134, 10191–10199 CrossRef CAS PubMed.
- P. G. de Gennes, Rev. Mod. Phys., 1985, 57, 827 CrossRef CAS.
- S. Hartmann and U. Thiele, Eur. Phys. J. Spec. Top., 2020, 229, 1819–1832 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: (1) Snapshots and density profiles for increasing N displaying the transition from mixing to complete to partial wetting, (2) brush swelling as a function of the self-interaction between the polymers and (3) surface tension calculations for the melt. See DOI: 10.1039/d0sm00156b |
| This journal is © The Royal Society of Chemistry 2021 |





