Open Access Article
Open Access ArticleEffect of thermal formation/dissociation cycles on the kinetics of formation and pore-scale distribution of methane hydrates in porous media: a magnetic resonance imaging study†
Mehrdad
Vasheghani Farahani
 a,
Xianwei
Guo
b,
Lunxiang
Zhang
*b,
Mingzhao
Yang
b,
Aliakbar
Hassanpouryouzband
a,
Xianwei
Guo
b,
Lunxiang
Zhang
*b,
Mingzhao
Yang
b,
Aliakbar
Hassanpouryouzband
 c,
Jiafei
Zhao
c,
Jiafei
Zhao
 b,
Jinhai
Yang
b,
Jinhai
Yang
 *a,
Yongchen
Song
b and
Bahman
Tohidi
a
*a,
Yongchen
Song
b and
Bahman
Tohidi
a
aHydrates, Flow Assurance & Phase Equilibria Research Group, Institute of GeoEnergy Engineering, Heriot-Watt University, Edinburgh, EH14 4AS, UK. E-mail: petjy@hw.ac.uk
bKey Laboratory of Ocean Energy Utilization and Energy Conservation of Ministry of Education, Dalian University of Technology, Dalian 116024, China. E-mail: lunxiangzhang@dlut.edu.cn
cSchool of Geosciences, University of Edinburgh, Grant Institute, West Main Road, Edinburgh, EH9 3JW, UK
First published on 8th February 2021
Abstract
A magnetic resonance imaging study was conducted to explore the kinetics and spatial characteristics of the thermally induced methane hydrate formation in both synthetic and natural sediment samples. Low-resolution images were taken from the sediment samples during the hydrate formation and dissociation stages of three consecutive thermal cycles and the induction time, hydrate formation rate and duration, spatial distribution of water, and saturation of all co-existing phases were determined in order to understand the effect of the first cycle of the formation/dissociation on the subsequent cycles. The results demonstrate that the induction and hydrate formation times of the second and third thermal cycles decrease due to the memory effect, enhanced dissolution of methane in the aqueous phase and the redistribution of water associated with the first cycle of the hydrate formation and dissociation. Moreover, the hydrate formation proceeds with a fairly smooth and fast trend in the subsequent cycles primarily due to the multiple nucleation events, in contrast with the traditionally believed “fits and starts” manner which was observed for the first cycle. The thermal cycles for the natural sediment sample were compared with those for the synthetic sediment sample in terms of the induction time, hydrate formation behaviour and duration, and spatial distribution to understand how the sediment particle type and size distribution could influence the cyclic hydrate formation/dissociation. High-resolution images were also taken from the samples and used to infer the spatial distribution of methane hydrates, gas and water in pore space after completion of the hydrate formation stage of each thermal cycle, by applying an innovative image analysis approach.
1. Introduction
Gas hydrates are nonstoichiometric inclusion compounds in which molecules of a guest species such as CH4, CO2, and H2 occupy and stabilize cages formed by water molecules under favourable thermodynamic conditions of high pressure and low temperature.1,2 Massive reserves of natural gas hydrates exist in permafrost and marine sediments, potentially providing huge low carbon energy resources3 and CO2 storage sink.4,5 The other side of the coin, however, is that methane emission to the atmosphere associated with the dissociation of natural gas hydrates may aggravate global warming because methane is considerably more potent than CO2 as a greenhouse gas.6 Apart from that, gas hydrates could be a serious geohazard due to the adverse influence of global warming on the geomechanical stability of gas hydrate deposits in both marine and permafrost environments, given the fact that the geomechanical, geophysical and hydrologic properties of gas hydrate-bearing sediments are essentially controlled by the presence of hydrates.7,8Gas hydrates are sensitive to changes in temperature.9 Such sensitivity substantially affects the response of gas hydrate-bearing sediments in different hydrate-based applications. For instance, methane release from natural gas hydrate-bearing sediments is believed to be still a slow and chronic process.10 However, it could be exacerbated by the human-caused global warming and local environmental temperature rise. In particular, thawing of permafrost and retreat of the ice sheets at Arctic and Antarctic regions may lead to the enhanced emission of trapped methane into the atmosphere, amplifying global warming,11 and endangering ecosystems and infrastructures in the polar regions. In the same line, cyclic temperature changes in the surface can alter the subsurface temperature up to 1 km;12 as such, the thickness, top and bottom of hydrate deposits located in the regions up to 1 km depth will be affected by these natural cycles. The top boundary of hydrate occurrence zone is usually shallower than 200 m in gas hydrate-bearing subglacial and permafrost settings, expanding upward and downward simultaneously in response to temperature cycles in the surrounding environment.13 In contrast with deep submarine gas hydrate reservoirs where liberated methane is usually oxidized aerobically once it reaches ocean waters,14 for permafrost and subglacial hydrates there is a higher risk for reaching the released methane into the atmosphere as it will encounter less barrier in its pathways to the surface.15 Indeed, some of the liberated natural gas from these reservoirs may have already reached the atmosphere.16 Returning to the effect of the cyclic temperature changes on shallow hydrate reserves, these could also alter hydrate composition, saturation, and distribution which in turn could cause geomechanical instabilities.17 A similar issue could occur during drilling gas hydrate reservoirs, production of natural gas from gas hydrate reserves13 or storing CO2 in these reservoirs.18 Furthermore, recovery of deep warm fluid either in the context of geothermal energy or conventional fossil fuels could trigger dissociation of hydrate where the warm fluid well crosses hydrate stability zone.19 Taking the above reasons into account, it is of importance to characterise the response of the gas hydrate-bearing sediments to the cyclic temperature change, which can then be informed to the advancement in understanding of how global warming and climate change would affect the geomechanical strength and stability of gas hydrate-bearing marine and permafrost sediments and in developing large-scale long-term monitoring and predicting programs for the shallow gas hydrate reserves in the future.
Accurate prediction of the response of gas hydrate-bearing sediments to the thermal stimuli is almost impossible unless the occurrence, quantity and pore-scale distribution of hydrates are well known.2 It is also essential to understand the kinetics of hydrate formation in porous media and recognize the pore-scale phenomena associated with the hydrate nucleation, growth, dissociation and reformation processes as well as the interactions of hydrates with the other coexisting phases (free gas and water/ice) and host sediment.20 The main challenges are to understand how (i) the saturation and pore-scale distribution of hydrates are influenced by the variations in chemistry, lithology, local tectonic activity and the nature of the gas supply, (ii) the presence of hydrates evolves the physical properties of a gas hydrate-bearing porous medium, and (iii) these physical properties alter with the redistribution of hydrates due to the dissociation at one site and reforming at another location. The latter could also be further complicated to evaluate when being associated with the memory effect.1
To date, numerous studies have been conducted on simulated hydrate-bearing sediment samples in laboratory, attempting to address the aforementioned challenges, a comprehensive review in this regard can be found elsewhere.2 However, there is still one big question: Do the synthesized hydrate-bearing sediment samples necessarily represent the naturally occurring gas hydrate deposits? In fact, the majority of experimental studies are concerned with the synthetic hydrate-bearing sediment samples, primarily due to the economic and technical challenges associated with the recovery of intact core samples preserved at in situ PT conditions using pressure core-sampling methods.21 In laboratory, however, it has been revealed that the procedure followed for the hydrate formation markedly influences its pore-scale distribution in porous media.17 In addition, suitability of use of other hydrate formers such as THF (miscible with water) or CO2 (considerably more soluble in water than hydrocarbons) as proxies for methane and/or synthetic sediments such as glass beads as a proxy for natural sediments has been always an issue of contention.2,22 It is clear that the presence of different minerals, particularly clay, influences not only the physical properties of the host sediment, but also the formation, dissociation, and pore-scale distribution of hydrates in pore space.23 These challenges all necessitate the investigation of the effect of different hydrate formation procedures, hydrate analogues and synthetic porous media on the physical properties of simulated gas hydrate-bearing sediment samples measured in laboratory.
The evolution mechanism of the gas hydrate formation/dissociation in porous media is associated with complex multiphase transition processes and fluid movement/redistribution.24–26 The conventional methods for investigating the kinetics of the hydrate formation/dissociation processes in laboratory usually deal with monitoring the measurable bulk properties such as the rate of changes in pressure, temperature and gas composition and reporting the apparent rate constants which may not fully represent the intrinsic kinetics.20 Recently, the visualization techniques such as X-ray micro-CT and Magnetic Resonance Imaging (MRI) have been extensively employed to study the kinetics the hydrate formation/dissociation in conjunction with the pore-scale associated phenomena, owing to their capability of both space and time resolution of the hydrate processes.20 X-ray micro-CT imaging has shown to be a promising technique for understanding the pore structure, fluid saturation and fluid movement in porous media.27–31 However, it is quite difficult to distinguish methane hydrates from water/ice, particularly at fine-grained sediments, hence a contrast agent or the other hydrate formers (Xe, Kr,…) is often used as a proxy for methane to form hydrates.32,33
Similar to the X-ray micro-CT imaging, MRI was previously used to study the behaviour of THF hydrates,34–36 which then extended to other hydrate formers such as CO2 (ref. 37) and CH4.38 Several works have been performed so far using MRI to investigate formation and dissociation of methane hydrates in different size sand particles,20 followed by attempts to characterise CO2/CH4 exchange for integrated methane recovery and CO2 storage purposes.39 Recently, different dissociation approaches were applied to methane hydrates and the behaviour of the hydrates were monitored to develop optimum methodologies for gas extraction from gas hydrate reservoirs.40–42 Fast depressurization was also applied and ice formation was observed due to endothermic nature of hydrate dissociation.40,43 The influence of water flow erosion on hydrate dissociation was investigated by monitoring gas and water migration processes.44,45 More recently, CH4 formation behaviour was monitored by MRI to investigate water, gas and hydrate saturation and spatial distribution within mesoporous media.26,33,46,47 Despite the substantial effect of the multiple thermal cycles on the properties of gas hydrate-bearing sediments, to the best of our knowledge, there is lack of in situ observation studies in this regard.
In this work, we explored the kinetics of the thermally stimulated methane hydrate formation and dissociation using high-field MRI in both synthetic and natural sediment samples to understand how the cyclic changes in temperature influence the process of the hydrate formation in porous media. The effect of the thermal cycles on the induction time and hydrate formation rates together with the evolution of the pore-scale distribution was investigated by taking low-resolution (128 px × 128 px) images during the hydrate formation and dissociation stages from both sediment samples. The spatial distribution of methane hydrates, gas and water in pore space was also closely observed by taking high-resolution (512 px × 512 px) images prior and after the completion of the hydrate formation stage of each cycle.
2. Experimental section
2.1. Materials
Research-grade methane with certified purity of 99.99 vol% was supplied by Dalian Special Gases Company. Deionized water (resistivity: 18.2 MΩ cm at 25 °C) was produced using an Integral Water Purification System (Aquapro2S, Aquapro International Company, USA). A well-characterised silica sand from Fife, Scotland was used as the natural sediment. The natural silica sand has a density (ρs) of 2.64 g cm−3, particle sizes ranging from 1.2 to 600 μm, and a mean diameter of 256.5 μm. A detailed characterisation of Fife silica sand can be found in our recently published study.48 Quartz glass beads (ASONE Co. Ltd., Japan) with a density of 2.50 g cm−3, mean diameter of 200 μm (BZ-02) and particle size of 177–250 μm were also used as the synthetic sediments. The particle size distribution curves of both synthetic and natural sediments are also provided in ESI.† According to our X-ray diffraction (XRD) analysis, Fife sand consists of four minerals: quartz (around 97%), microcline (around 3%), calcite (trace), and kaolinite (trace). Such a mineral composition is quite close to that of glass beads (i.e. pure quartz). The mean diameter of Fife sand is close to that of quartz glass beads as well. These similarities will enable us to compare the role of the particle size distribution on the kinetics and spatial characteristics of the thermally induced methane hydrates formation in natural sediments with those in synthetic sediments, in a mineralogy-independent manner. This is essential because the other minerals, particularly clay, if present in natural sediments at higher contents, would impose their own influence on the hydrate formation and dissociation processes as well as the pore-scale distribution of the co-existing phases (hydrates, free gas, and water) in pore space. In fact, their presence could be associated with further complicated pore-scale phenomena which would not be expected to occur when using only quartz glass beads as the porous media.2.2. Experimental apparatus
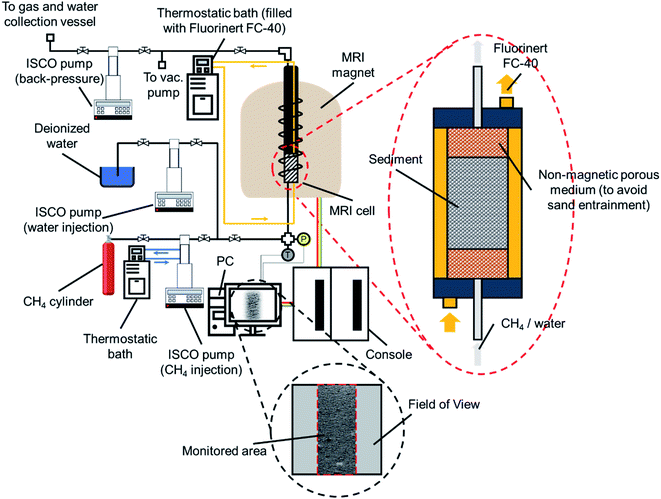
Fig. 1 presents the experimental apparatus, consisting of a 9.4 T MRI system (400 MHz, Varian, USA), a high-pressure MRI cell made of a nonmagnetic material (polyamide) with an inner diameter of 15 mm and a length of 200 mm, two thermostatic baths (F25-ME, Julabo, Germany, accuracy: ±0.01 °C), three high-pressure pumps (ISCO 260D, Teledyne Technologies, Lincoln, USA), a vacuum pump and a data acquisition system. The MRI cell was surrounded by a jacket connected to one of the thermostatic baths filled with Fluorinert FC-40 (3M, St. Paul, MN, USA) as a coolant to control the experimental temperature while minimizing the interference of radiofrequency field artifacts on the imaging system. The data acquisition system includes a digital pressure transducer (Nagano, Japan, accuracy: ±0.1 MPa) and a thermal probe (Yamari Industries, Japan, accuracy: ±0.1 K).2.3. Experimental procedure
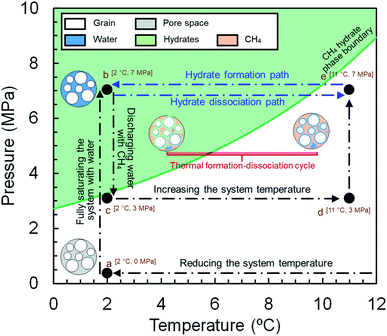
The experiments for both synthetic and natural sediment samples were conducted with a similar procedure schematically illustrated in Fig. 2, simulating the process occurring in nature for a typical hydrate-bearing sediment exposed to thermally induced formation/dissociation cycles at a constant pore pressure. The high-pressure MRI cell was firstly washed with deionized water, cleaned and filled with dry sediments. When loading the cell, it was tapped regularly and gently on a hard surface to visually ensure the homogeneity of the sediment sample. The cell was then placed inside the MRI magnet, connected to the rest of the experimental apparatus and vacuumed to ensure removal of the residual air. Thereafter, the temperature of the thermostatic baths was set to 2.0 °C and deionized water was injected using a ISCO pump to fully saturate the sediment sample at a rate of 0.5 ml min−1 until the pore pressure of the cell becomes stable at 7 MPa for at least 1 hour (a → b in Fig. 2). A low-resolution and a high-resolution image were taken from the sample at this stage (see Section 2.4). Next, the pressure was reduced to 3 MPa and the fully saturated sediment sample was discharged by injection of a high-pressure methane stream into the cell in several seconds using another ISCO pump, in which around 70–75% of water in the pore space was replaced by methane and accordingly, the initial water content was adjusted (b → c in Fig. 2) to the saturation of 25–30%. It can be seen in Fig. 2 that the injection pressure is outside the methane hydrate phase boundary hence no hydrate formation would be expected at this stage. The system temperature was then set to 11.0 °C (c → d in Fig. 2) and methane was injected into the cell at a rate of 5.0 ml min−1 until the pore pressure reached the desired value of 7 MPa (d → e in Fig. 2). The low- and high-resolution images were taken from the sample at this stage as well to obtain the initial water saturation and examine the homogeneity of the water distribution in the field of view (FOV) prior to the hydrate formation stage. Finally, the temperature reduced to 2.0 °C to start hydrate formation (e → b in Fig. 2) while keeping the cell connected to the ISCO pump in order to compensate for the gas consumption and maintain the pore pressure at 7 MPa during the hydrate formation stage. The low-resolution images were continuously acquired from the sediment sample until the MRI signals became stable and the methane injection rate into the cell became almost zero, indicating the completion of the hydrate formation process. After taking a high-resolution image from the sample upon completion of the hydrate formation, the system underwent a temperature increase to 11.0 °C to dissociate hydrates and complete the first thermal cycle of the hydrate formation/dissociation (b → e in Fig. 2). During the hydrate dissociation stage, the cell was kept connected to the ISCO pump with a maximum withdrawal rate of 10.0 ml min−1 to maintain the pore pressure at 7 MPa while minimizing the viscous pressure-driven redistribution and/or expulsion of water. The low-resolution images were continuously acquired during the hydrate dissociation stage as well. The first cycle was then followed by two consecutive cycles with an identical temperature adjustment and image acquisition procedure.2.4. Image acquisition and processing
Non-destructive MRI scanning with a spin-echo multi-slice (SEMS) pulse sequence was selected to monitor the micro-images of 1H densities in liquid water during the experiment. It should be noted that 1H in liquid water could only be detected at the operating conditions due to its much shorter transverse relaxation time compared with that of 1H in CH4 or hydrates.49 The intensity or brightness of each pixel in a micro-image is proportional to the number of 1H in the liquid phase, which is correlated with the amount of liquid water. As a consequence, the hydrate formation, which is associated with the disappearance of 1H from the liquid water, must be equivalent to the darkening of the micro-images. Such a correlation enables us to obtain the water, hydrates, and gas saturations via analysing the micro-images and calculating their mean intensity (MI) over a predefined region of interest (ROI).20As mentioned, the low-resolution images with a data matrix size of 128 px × 128 px were acquired during the hydrate formation and dissociation stages, providing the required data for the investigation of the kinetics of hydrate formation. The high-resolution images with data matrix sizes of 512 px × 512 px were taken from the sample prior and after completion of each hydrate formation stage in order to capture the spatial distribution of methane hydrates, gas and water in the pore space. The parameters of the SEMS sequence are provided in Table 1:
| No. | Parameter | Value | |
|---|---|---|---|
| Low-resolution (128 px × 128 px) | High-resolution (512 px × 512 px) | ||
| 1 | Repetition time | 1000 ms | 1000 ms |
| 2 | Echo time | 4.39 ms | 8.39 ms |
| 3 | Averages | 1 | 1 |
| 4 | FOV | 30 mm × 30 mm | 30 mm × 30 mm |
| 5 | Monitored area | 15 mm × 30 mm | 15 mm × 30 mm |
| 6 | Thickness | 2.0 mm | 2.0 mm |
| 7 | Pixel resolution | 0.234 × 0.234 mm2 per px2 | 0.059 × 0.059 mm2 per px2 |
| 8 | Acquisition time | 128 s | 512 s |
The procedure followed in this study to find the saturation of each phase is detailed in our previous published works.36,47,49 This procedure has shown to be a reliable approach for obtaining the saturation of each phase and has been used in the other MRI studies as well.20,50 Briefly, it involves obtaining the mean intensity (MI) values of the MRI signals at the fully and partially saturated states prior to the hydrate formation (Ifull and I0, respectively) and the instantaneous MI values during the hydrate formation and dissociation stages (Ii). The initial and instantaneous water saturations (Sw0 and Sw, respectively) could be calculated using eqn (1) and (2):
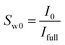 | (1) |
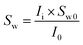 | (2) |
The hydrate and gas saturations (Sh and Sg, respectively) could be obtained using eqn (3) and (4):
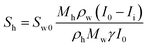 | (3) |
| Sg = 1 − Sw − Sh | (4) |
| Mh = Mg + γMw | (5) |
| No. | Parameter | Value | Unit |
|---|---|---|---|
| a At 2.0 °C. | |||
| 1 | M g | 16.04 | g mol−1 |
| 2 | M w | 18.02 | g mol−1 |
| 3 | γ | 5.78 | — |
| 4 | ρ h | 0.91 | g cm−3 |
| 5 | ρ w | 1.00 | g cm−3 |
It should be noted that the values of ρh and γ were determined using our in-house PVT modelling software.51
The water conversion rate in each hydrate formation stage could be also calculated by forward differentiation:
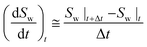 | (6) |
3. Results and discussion
3.1. Kinetics
In this section, we explore how the thermally induced formation/dissociation cycles influence the kinetics of the methane hydrate formation in both synthetic and natural sediment samples. Table 3 provides detailed information of the thermal cycles obtained from the MI variations of the low-resolution magnetic resonance images against time for both sediment samples undergoing three consecutive thermal cycles. It should be noted that the image analysis was carried out on a ROI with a data matrix size of 50 px × 100 px cropped out of the 128 px × 128 px images, away from the cell walls in order to minimize the effect of the walls and artifacts on the MI values.49| Sediment type | Initial water saturation (−) | Induction time (min) | Hydrate formation time (min) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| C#1 | C#2 | C#3 | C#1 | C#2 | C#3 | C#1 | C#2 | C#3 | |
| Synthetic | 0.292 | 0.256 | 0.238 | 23.5 | 12.8 | 10.7 | 980.5 | 681.5 | 731.5 |
| Natural | 0.246 | 0.213 | 0.209 | 81.4 | 76.1 | 69.7 | 1118.5 | 753.5 | 625.5 |
In Table 3, the initial water saturation refers to its value just before adjusting the system temperature to 2.0 °C. By definition, the induction time is the time elapsed until the appearance of a certain detectable volume of hydrate nuclei,52 which is equivalent to the darkening of the images and accordingly, decrease in the MI values. Therefore, the induction time is the duration between adjusting the system temperature to 2.0 °C until the first noticeable decrease in the MI values, corresponding to the hydrate nucleation. The hydrate formation time is the duration between adjusting the system temperature to 2.0 °C until the completion of the hydrate formation, which was confirmed when there is not any noticeable change in the MI values and the gas injection into the cell becomes negligible. Given the acquisition of the images from both synthetic and natural sediment samples started immediately after adjusting the system temperature to 2.0 °C and all acquired images have a timestamp with them, the induction and hydrate formation times could be simply calculated by monitoring the variations in the MI values against time. According to Table 3, the initial water saturations of the second and third thermal cycles at the ROI are slightly lower than that of the first cycle for both sediment samples. Such decreases could be caused by:
(i) Downward movement of water due to the gravity during each experiment (see Section 3.2.1 for a further discussion).
(ii) Dissolution of water in the gas phase and its expulsion during the hydrate dissociation stage: As mentioned in Section 2.3, pure methane was injected into the cell to increase the pore pressure of the system to 7 MPa. The pore pressure was also maintained at 7 MPa during the hydrate formation and dissociation stages. Therefore, it is expected that depending on the PT conditions, a small amount of the initially injected water migrates from the aqueous phase to the gas phase in order to reach the thermodynamic equilibrium during the formation and dissociation stages of each cycle. Water may stay in the gas phase as the moisture content and/or get removed from the system during the dissociation stage, leading to further migration of water molecules to the gas phase and accordingly, further decrease in the MI values. In Table 3, it can be seen that the initial water saturation decrease from the second cycle to the third cycle is much lower than that from the first cycle to the second cycle for both synthetic and natural sediment samples. This implies that a small amount of water migrated from the aqueous phase to the gas phase during the formation and dissociation stages of the first cycle and kept the gas phase relatively saturated with water in the next thermal cycles. Hence, we believe this factor could be the main reason for the slight decrease of the initial water saturations of the second and third thermal cycles than that of the first cycle for both synthetic and natural sediment samples.
(iii) Viscous pressure-driven expulsion of liquid water during the hydrate dissociation stage: As mentioned in Section 2.3, the maximum gas withdrawal rate was set to 10.0 ml min−1 during the hydrate dissociation stage of each cycle to minimize the viscous pressure-driven redistribution and/or expulsion of liquid water. Despite this consideration, it would be still possible for gas to displace water during the dissociation stage, particularly at the larger pores where the capillary pressure is lower. Therefore, liquid water could become redistributed in the system or even removed from the cell during the dissociation stage.
(iv) Capillarity induced redistribution of water associated with the hydrate formation/dissociation (which will be discussed in details).
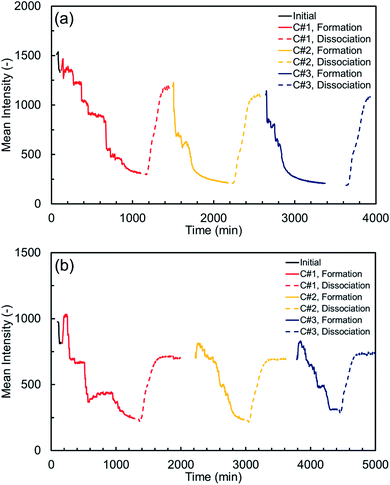
The MI variations were also plotted against time for both synthetic and natural sediment samples in Fig. 3. As observed, each thermal cycle consists of a hydrate formation stage (including the induction time), at which the MI values decrease due to the successive nucleation and growth of the methane hydrate crystals, and a dissociation stage, at which the MI values increase as the hydrate crystals dissociate due to the temperature rise in the system. The dissociation stage is assumed complete when there is not any noticeable change in the MI values. As can also be seen, there are two abrupt changes in the MI values for each thermal cycle: one immediately after adjusting the system temperature to 2.0 °C and the other immediately after adjusting the temperature to 11.0 °C. Such abrupt changes – which are more obvious for the natural sediment sample – happened due to the sensitivity of the intensity values to the temperature. Thus, they could appropriately confirm that the temperature at the ROI has been changed to the desired values in a few minutes after the temperature adjustment. However, care was taken to exclude these changes when analysing the variations in the water and hydrate saturations.
According to Table 3 and Fig. 3, the induction and hydrate formation times together with the behaviour of the MI variations in the hydrate formation stage at the first thermal cycle are different from those at the second and third cycles for both sediment samples. Such differences clearly confirm the influence of the first cycle of the hydrate formation/dissociation on the subsequent cycles and the sediment type and characteristics appear to play an important role as well. To further investigate this, it is essential to know which key factors control the hydrate formation in porous media and understand how they contribute to promoting the hydrate nucleation and growth. It is believed that the process of the hydrate formation in a porous medium occurs in “fits and starts” manner because the hydrate nucleation is a stochastic phenomenon and its degree of randomness depends on several factors such as the thermodynamic conditions, PT driving forces, sediment type and characteristics, the solubility of the hydrate former in water, and salinity, thermal history and interestingly, pore-scale distribution of pore water in the system.1 In our experiments, since both sediment particles were almost pure quartz with the average grain sizes of larger than 10 μm, and deionized water was used to form hydrates, the equilibrium thermodynamic conditions for the methane hydrate formation would be expected not to be shifted due to the pore size inhibition or salinity.53 Therefore, there would be around 8 °C temperature difference between the target temperature (2.0 °C) and equilibrium temperature at 7.0 MPa (9.7 °C, according to our in-house PVT modelling software) for methane hydrates, providing a high enough driving force to trigger the nucleation. This is why the induction times of all thermal cycles are not too long for both sediment samples; however, it is clear that the first thermal cycle has reduced the induction times of the subsequent cycles, particularly for the synthetic sediment sample. Here, we investigate the effect of the other key contributing factors on the kinetics of methane hydrate formation in each sediment sample.
As can also be seen in Table 3, the hydrate formation times of the second and third cycles are both around 25% lower than that of the first cycle. Fig. 3(a) also shows that the MI values decrease in several sudden and gradual manners during the hydrate formation stage of the first cycle whereas the variations in the subsequent cycles are fairly smoother. The hydrate formation in porous media is not a uniform process and nucleation of the hydrate crystals occurs at different locations and times, greatly depending on the availability of the gas–water interface. In particular, it is believed that the probability of the hydrate nucleation and growth rate is higher at locations with small particle size (higher specific surface area) and low water content.20 Therefore, the redistribution of water throughout the system due to the first hydrate formation/dissociation cycle provides further gas–water interfaces which substantially enhances the nucleation probability and results in a lower induction time (as discussed earlier). Apart from that, instead of a highly stochastic and slow decrease in the MI values due to the limited number of nucleation (sudden decreases) and growth of already formed nuclei (gradual decreases) in the first cycle, there would be remaining nuclei (methane-water clusters) throughout the medium in the subsequent cycles, which facilitate the hydrate formation process by eliminating the critical size barrier, leading to a fairly smoother and faster decrease in the MI values.
It is interestingly observed in Fig. 3(a) that sudden decreases in the MI values are sometimes followed by an increase, reflecting the self-limiting behaviour of the hydrate nucleation and/or capillarity induced water redistribution in porous media. As a result of the local heat release and temperature rise due to the hydrate nucleation, the regions in the vicinity of the nucleation sites could be temporarily taken out of the stability zone, making the PT conditions unfavourable for the hydrate formation, or even causing the dissociation of the neighbouring hydrate crystals.20 Hydrate formation is also associated with a capillarity induced water redistribution. In fact, water-wetting hydrate crystals could reduce the effective pore size of the medium, change surface energy, and consequently enhance the local capillary suction, causing water to be drawn toward the hydrate formation front.60 These factors might temporarily result in the presence of a higher amount of water in the ROI hence more MI values. It can be seen in Fig. 3(a) that such behaviour occurs for the second and third cycles differently than for the first one. While the variations of the MI values during the hydrate formation stage of the first cycle is relatively stepped with no obvious increase, it looks fairly curved in the subsequent cycles with a number of increases. This behaviour is due to the multiple and fast hydrate nucleation events throughout the ROI in the second and third cycles, compared to the first cycle where the nucleation events do not occur at different locations simultaneously and growth of the hydrate nuclei results in the gradual decrease of the MI values. In addition, hydrate forms initially in dendritic crystals with high surface areas (less energy-efficient) during early rapid hydrate nucleation and growth in the second and third cycles, hence it would be able to hold and draw a higher amount of water towards itself until it recrystallizes into compact energy-efficient configurations.61,62
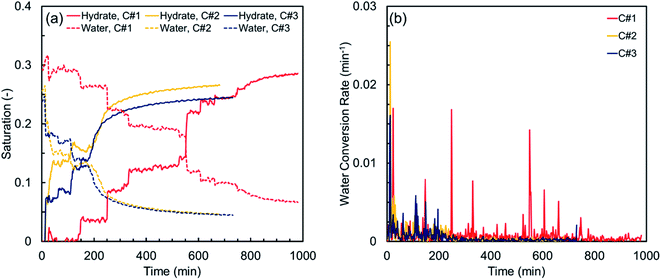
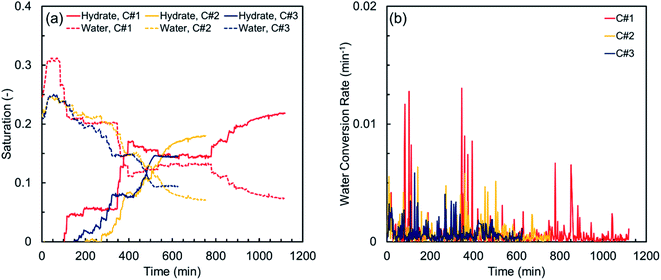
Fig. 4 illustrates the hydrate and water saturations (eqn (2) and (3)) together with the water conversion rate (eqn (6)) for the synthetic sediment sample versus time. As observed, there is still some residual water after completion of each thermal cycle, which is unavailable for the hydrate formation owing to its low chemical potential and/or being occluded from the gas phase by the already formed hydrate crusts.63 The residual water saturations for the synthetic sediment sample at the end of the hydrate formation stage are 0.067, 0.046, and 0.044 for the first, second and third cycles, respectively, corresponding to 77.1, 82.1, and 81.5% total water conversion to hydrates. Increase of the total water conversion to hydrates for the synthetic sediment sample with the thermal cycle indicates that the pore-scale phenomena associated with the first cycle of the formation/dissociation had a substantial influence not only on the induction and hydrate formation times, but also on the total water conversion to hydrates.
Although the first thermal cycle did not have a strong influence on the induction times of the second and third cycles, it had a remarkable effect on the hydrate formation time. According to Table 3, the hydrate formation times of the second and third cycles are 32.6 and 44.1% lower than that of the first cycle. Such remarkable decrease in the hydrate formation time could be attributed to the effect of the pore water redistribution on the grain surfaces in the first cycle because the memory effect and the dissolved methane gas are unlikely to promote the hydrate nucleation here, as discussed earlier. In fact, in contrast with the relatively well-rounded synthetic sediment sample with high sphericity, the redistribution of water in the natural sediment sample with different sphericity and roundness could increase the gas–water interface and promote the likelihood of multiple nucleation events. This effect could be confirmed by comparing the smoother and faster behaviour of the MI values in the second and third cycles with that of the first cycle in Fig. 3(b).
The hydrate and water saturations in conjunction with the water conversion rate for the natural sediment sample are plotted versus time in Fig. 5. Similar to what observed for the synthetic sediment sample, there is still some remaining water unavailable for the hydrate formation during each thermal cycle. The residual water saturations for the natural sediment sample at the end of the hydrate formation stage are 0.073, 0.071, and 0.094 for the first, second and third cycles, respectively, corresponding to 70.3, 66.6, and 55.1% total water conversion to hydrates, showing a decreasing trend with the thermal cycle, in contrast with that of the synthetic sediment sample. Therefore, it could be speculated that the influence of the thermal cycles on the residual water saturation after completion of an individual hydrate formation highly depends on the sediment characteristics, particularly type and particle size distribution since they control the capillarity in porous media and accordingly, determine the water and gas distributions and the availability of the gas–water interface. For the natural sediment sample with a much wider particle size distribution and more capillarity at the small pores in comparison with the synthetic sediment sample, it is possible to have a higher amount of water, obscured by the already formed hydrates with no direct contact with the gas phase. Decrease of the total water conversion to hydrates for the natural sediment sample with the thermal cycle could be also attributed to the amount of dissolved methane remaining in the aqueous phase after the dissociation in each cycle. For instance, while the redistribution of pore water during the hydrate formation and dissociation stages of the first cycle increases the gas–water interface and hydrate formation rate, the probability of hydrate nucleation in the aqueous phase could substantially decrease because there would be less dissolved methane in water, limiting the diffusion of the hydrate crystal into the aqueous phase.
3.2. Spatial characteristics
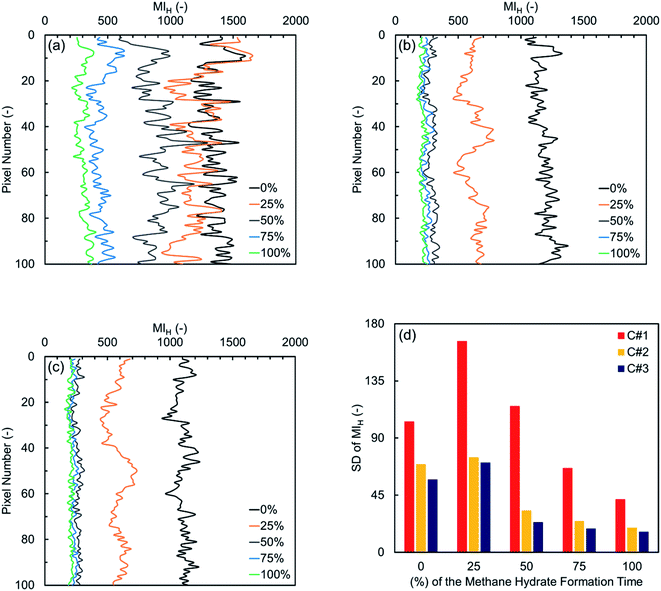
Fig. 6(a) depicts the MIH values versus pixel number in the first thermal cycle for the synthetic sediment sample. As observed in a pore-scale, water is heterogeneously distributed along the sample initially, suggesting that water was not homogeneously distributed in pore space after the initial gas injection. The consumption and/or redistribution of water due to the nucleation events during the first and second quarters maintain or even increase the heterogeneity along the sample. At the end of the third and final quarters, however, the residual water distribution becomes more homogeneous along the ROI. In Fig. 6(b) and (c) illustrating the variations in the subsequent cycles, the initial water distribution along the sample is relatively homogenous, influenced by the hydrate formation/dissociation in the first cycle. For both subsequent cycles, the heterogeneity at the end of the first quarter becomes slightly higher, mainly due to the multiple nucleation events throughout the sample, and it can also be seen that the water content and distribution are almost the same along the sample at the end of the other quarters. Therefore, it could be concluded that the cyclic hydrate formation/dissociation may promote homogeneous distribution of water and gas in porous media. It should be also noted that, according to Fig. 6(a)–(c), the gravity appears not to have a measurable influence on the water distribution along the sample because higher MIH values were not observed at the bottom of the sample over time.
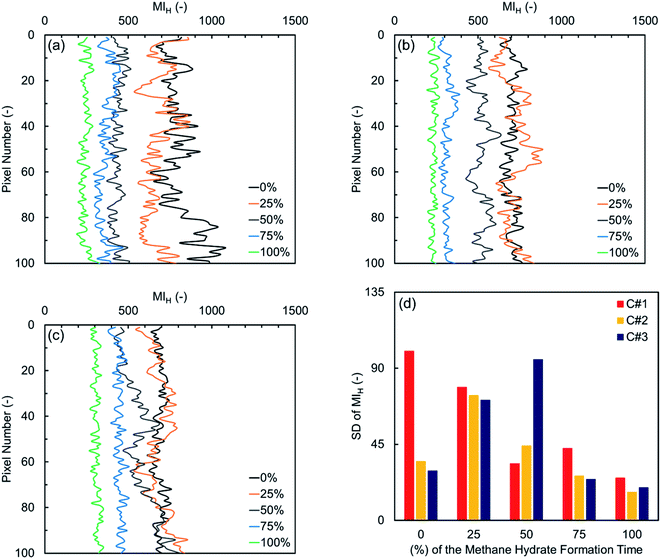
Fig. 7(a) illustrates the MIH values versus pixel number in the first thermal cycle for the natural sediment sample. Similar to what observed for the synthetic sediment sample, the initial water distribution along the natural sediment sample is markedly heterogeneous, due to the inhomogeneous displacement of water by methane during the gas injection step. Over time, however, the formation of the hydrate crystals and redistribution of water lead to a more homogeneous water distribution along the sample. In Fig. 7(b) and (c) providing the variations in the second and third cycles, it can be seen that water is homogeneously distributed along the sample initially, affected by the hydrate formation and dissociation in the first cycle. As discussed in Section 3.1.2, the induction time of these two cycles was not influenced by the first cycle as noticeably as their hydrate formation time. Thus, it can be seen that the heterogeneity of the water distribution along the sample increases during the first and second quarters. Compared with the distribution of water for the synthetic sediment sample at the end of the third and final quarters, the water distribution here is relatively heterogeneous, primarily due to the differences in the capillarity imposed by the particle size distribution. Therefore, in contrast to what observed for the synthetic sediment sample, the water distribution in the natural sediment sample did become evener but the change in the homogeneity was not as significant as in the synthetic sediment sample at the end of the third and final quarters. This may suggest that the effect of the cyclic hydrate formation/dissociation on the fluid distribution in the pore space does exist but becomes weaker in natural sediments.
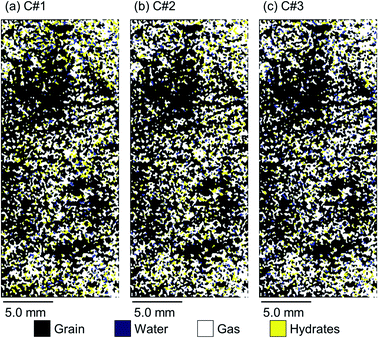
The high-resolution images were analysed using MATLAB Image Processing Toolbox, attempting to find the 2D spatial distribution of the co-existing phases (hydrates, water, and methane) at the ROI upon completion of the hydrate formation stage of each thermal cycle for both synthetic and natural sediment samples. To the best of our knowledge, there is not any similar work in the literature applying this method on the high-resolution magnetic resonance images to obtain the spatial distribution of gas hydrates in porous media. It should also be noted that our method is similar to the Differential Imaging Technique, which has been used by the other scholars in the X-ray micro-CT imaging studies.64,65
The procedure followed in this study for determination of the spatial distribution of the co-existing phases in the sediment samples relies on the evolution of the intensity values of each pixel during the hydrate formation process as well as the values of the porosity and saturations. This procedure holds three assumptions:
(1) The grain particles keep being still during the whole process. The re-arrangement of the grain particles during each experiment could be caused by either the injection of gas or hydrate-forced heave. As discussed in Section 2.3, methane was injected into the cell with a rate of 5.0 ml min−1 in order to minimize the possibility of the viscous driven re-arrangement of the grain particles. Moreover, according to Table 3, the initial water saturation for both sediment samples are less than 30%. Therefore, the hydrate saturation at the end of the thermal cycles is not higher than 30% (see Fig. 4(a) and 5(a)), hence it is not expected that the hydrate-forced heave would be able to displace the grain particles.
(2) The volume occupied by the hydrate crystals is provided by water. Our experimental studies on the partially saturated hydrate-bearing sediment samples have shown that the volume occupied by hydrates is provided by pore water even though the gas saturation slightly decreases due to the volume expansion associated with the conversion of water to hydrate crystals with a lower density.
(3) The values of the porosity and saturations obtained for the sample by using the other methods are valid for the ROI. In this study, the saturation of each individual phase has been obtained by analysing the images acquired from the same region with only a different resolution. It should also be noted that the porosity values of the sediment samples were assumed to be around 40–43%, according to our previous studies.66,67
The procedure includes three steps. The first step is to analyse the high-resolution image at the fully water-saturated state to obtain the spatial distribution of the grains as well as the pore space throughout the image in compliance with the porosity of the sample. Next, the image at the partially saturated state is analysed and compared with that at the fully saturated state in compliance with the water and gas saturations to obtain the regions whose water content is removed during the gas injection step. The analysis at this step yields the initial water distribution prior to the hydrate formation. The final step is to conduct the analysis on the image taken after the completion of the hydrate formation stage with respect to the saturation values to recognize the pixels occupied by the hydrate crystals. In this study, the first step was conducted once for each sediment sample, and the second and third steps were carried out for each individual cycle independently.
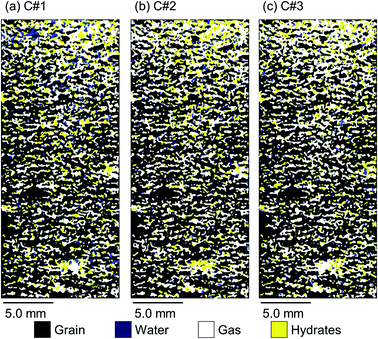
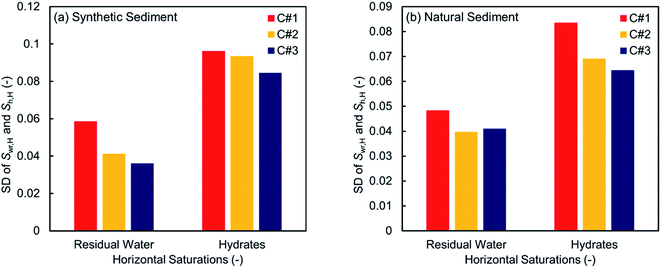
Fig. 8 and 9 illustrate 2D spatial distribution of the co-existing phases at the ROI after completion of the hydrate formation stage of the first, second, and third thermal cycles for both synthetic and natural sediment samples, respectively. In Table 4, we compared the hydrates and residual water saturations obtained via analysing the low-resolution images at the end of the hydrate formation stage of all three cycles with those obtained via analysing the high-resolution images for both synthetic and natural sediment samples. As observed, the relative difference of the hydrates and water saturations are less than 8 and 16% for the synthetic sediment sample, and less than 3 and 12% for the natural sediment sample, respectively, confirming the reliability of the proposed method. In Fig. 8 and 9, an interesting observation according to the distribution of hydrates is the co-existence of different pore-scale habits including pore-filling, load-bearing and even cementation throughout both samples. This implies that different pore-scale habits may co-exist in gas hydrate-bearing porous media with a given gas hydrate saturation and it might not be logical to assign marginal hydrate saturation values for each habit. However, we believe further investigation is necessary to be conducted at different initial water saturations by employing MRI or the other available pore-scale visualisation techniques. The hydrate and residual water saturations in the horizontal direction (Sh,H, Swr,H) were also obtained, their SD values were calculated, and provided in Fig. 10. As can be seen, the spatial distribution of hydrates and residual water in the second and third cycles is more homogeneous throughout the sediment for both sediment samples, influenced by the first thermal cycle of the hydrate formation/dissociation.
| Sediment type | Cycle | Residual water saturation (−) | Hydrates saturation (−) | ||||
|---|---|---|---|---|---|---|---|
| L | H | Rel. difference (%) | L | H | Rel. difference (%) | ||
| Synthetic | C#1 | 0.067 | 0.073 | 8.213 | 0.286 | 0.276 | 3.440 |
| C#2 | 0.046 | 0.054 | 16.522 | 0.266 | 0.245 | 8.011 | |
| C#3 | 0.044 | 0.048 | 8.780 | 0.245 | 0.239 | 2.482 | |
| Natural | C#1 | 0.073 | 0.082 | 12.701 | 0.218 | 0.220 | 0.772 |
| C#2 | 0.071 | 0.070 | 0.744 | 0.180 | 0.182 | 1.314 | |
| C#3 | 0.094 | 0.097 | 3.131 | 0.146 | 0.150 | 3.063 | |
The proposed method is able to distinguish methane hydrates from pure water in fine-grained porous media; however, there are some sources of uncertainty associated with the method. For instance, this method was applied on 2D magnetic resonance images hence would not be able to capture 3D nature of the hydrate formation in porous media. Moreover, the thickness of each pixel is 2.0 mm hence its intensity is averaged through a relatively large volume. This is possibly why we still observe some regions where residual water neighbours the gas phase at the end of the hydrate formation stage. In fact, it would be ideally expected that no gas–water interface is found throughout the sample upon completion of the hydrate formation. Apart from that, since the images were taken after the completion of the hydrate formation stage, it was not possible to monitor the redistribution and/or expulsion of water during the process. Nevertheless, the method could be improved by using state-of-the-art fast MRI technologies and modifying the image acquisition parameters and/or experimental method (imaging sequences, coil design, …) in future studies, attempting to minimize the uncertainties.
This work efficiently assisted with shedding light on the gas hydrate nucleation and growth phenomena in porous media and provided further insights into the kinetics of the hydrate formation. One potentially interesting study aligned with this work is to further investigate the effect of the other driving forces triggering the nucleation events since the thermally induced hydrate formation process studied here would not be necessarily associated with the mass transfer from/to the system, despite the pressure-induced process. The effects of the other key factors such as the salinity, initial saturation, and history of pore water together with the sediment mineralogy, clay content and degree of consolidation are also necessary to be investigated. These experimental studies could effectively help with gaining more insights into the process of the hydrate formation in porous media and improve the accuracy of the models aiming at the prediction of the physical properties and response of gas hydrate-bearing sediments to different stimuli.
4. Conclusions
In this work, the kinetics and spatial characteristics of the thermally induced methane hydrates formation in both synthetic and natural sediment samples were studied by using magnetic resonance imaging. Low-resolution images were taken from each sediment sample during the hydrate formation and dissociation stages of three consecutive thermal cycles in order to investigate how the first cycle of the formation/dissociation could influence the induction time, hydrate formation rate, and saturations of each phase in the subsequent cycles. High-resolution images taken from the samples were also used to infer the spatial distribution of methane hydrates, gas and water in pore space upon completion of each thermal cycle.The experimental results demonstrate that the kinetics of the hydrate formation in porous media is substantially influenced by the thermally induced cyclic formation/dissociation processes. It was indicated that the induction and hydrate formation times of the second and third thermal cycles decrease due to the memory effect, enhanced dissolution of methane in the aqueous phase and the redistribution of water associated with the first cycle of the hydrate formation and dissociation. Moreover, the hydrate formation proceeds in traditionally believed “fits and starts” manner in the first cycle, characterised by the stepped trend due to the limited nucleation followed by growth, in contrast with the fairly smooth and curved trend in the subsequent cycles, due to the multiple and fast hydrate nucleation events. The induction times of the thermal cycles for the natural sediment sample were compared with those for the synthetic sediment sample to understand the effect of the sediment grain type and size distribution. The results indicated that the induction times of all three cycles for the natural sediment sample are much longer and the effect of the first cycle on the induction times of the subsequent cycles is not strong. The low-resolution images were also used to analyse the spatial characteristics of the hydrate formation stage of all thermal cycles for both sediment samples. Lastly, an innovative method was proposed for the first time in which the high-resolution images were used to obtain the 2D spatial distribution of the co-existing phases (methane hydrates, gas, and water) after completion of the hydrate formation stage of each thermal cycle for both synthetic and natural sediment samples.
Conflicts of interest
The authors declare no financial conflicts of interests.Acknowledgements
The authors would gratefully acknowledge Heriot-Watt University for providing the PhD funding for Mehrdad Vasheghani Farahani through James Watt Scholarship.References
- E. D. Sloan Jr and C. A. Koh, Clathrate Hydrates of Natural Gases, CRC press, 2007, vol. 20074156, DOI:10.1201/9781420008494.
- A. Hassanpouryouzband, E. Joonaki, M. Vasheghani Farahani, S. Takeya, C. Ruppel, J. Yang, N. J. English, J. M. Schicks, K. Edlmann, H. Mehrabian, Z. M. Aman and B. Tohidi, Gas Hydrates in Sustainable Chemistry, Chem. Soc. Rev., 2020, 49(15), 5225–5309, 10.1039/c8cs00989a.
- M. D. Max, Natural Gas Hydrate in Oceanic and Permafrost Environments, Springer Science & Business Media, 2003, vol. 5 Search PubMed.
- A. Hassanpouryouzband, J. Yang, A. Okwananke, R. Burgass, B. Tohidi, E. Chuvilin, V. Istomin and B. Bukhanov, An Experimental Investigation on the Kinetics of Integrated Methane Recovery and CO2 Sequestration by Injection of Flue Gas into Permafrost Methane Hydrate Reservoirs, Sci. Rep., 2019, 9(1), 1–9, DOI:10.1038/s41598-019-52745-x.
- P. Jadhawar, J. Yang, A. Chapoy and B. Tohidi, Subsurface Carbon Dioxide Sequestration and Storage in Methane Hydrate Reservoirs Combined with Clean Methane Energy Recovery, Energy Fuels, 2020, 35(2), 1567–1579, DOI:10.1021/acs.energyfuels.0c02839.
- M. Allen, M. Babiker, Y. Chen, H. d. Coninck, S. Connors, R. v. Diemen and O. P. Dube, IPCC Report Global Warming of 1.5 C, Summary for Policymakers, 2018 Search PubMed.
- M. Maslin, M. Owen, R. Betts, S. Day, T. D. Jones and A. Ridgwell, Gas Hydrates: Past and Future Geohazard?, Philos. Trans. R. Soc., A, 2010, 368(1919), 2369–2393, DOI:10.1098/rsta.2010.0065.
- A. Okwananke, A. Hassanpouryouzband, M. Vasheghani Farahani, J. Yang, B. Tohidi, E. Chuvilin, V. Istomin and B. Bukhanov, Methane Recovery from Gas Hydrate-Bearing Sediments: An Experimental Study on the Gas Permeation Characteristics under Varying Pressure, J. Pet. Sci. Eng., 2019, 180, 435–444, DOI:10.1016/j.petrol.2019.05.060.
- D. Li, D. Wang and D. Liang, P-Wave of Hydrate-Bearing Sand under Temperature Cycling, Geophysics, 2011, 76(1), E1–E7, DOI:10.1190/1.3515263.
- C. D. Ruppel and J. D. Kessler, The Interaction of Climate Change and Methane Hydrates, Rev. Geophys., 2017, 55(1), 126–168, DOI:10.1002/2016RG000534.
- F. M. O'Connor, O. Boucher, N. Gedney, C. D. Jones, G. A. Folberth, R. Coppell, P. Friedlingstein, W. J. Collins, J. Chappellaz, J. Ridley and C. E. Johnson, Possible Role of Wetlands, Permafrost, and Methane Hydrates in the Methane Cycle under Future Climate Change: A Review, Rev. Geophys., 2010, 48(4) DOI:10.1029/2010RG000326.
- C. D. Ruppel, Methane Hydrates and Contemporary Climate Change, Nat. Eduction Knowl., 2011, 2(12), 12 Search PubMed.
- C. D. Ruppel and W. F. Waite, Timescales and Processes of Methane Hydrate Formation and Breakdown, With Application to Geologic Systems, J. Geophys. Res.: Solid Earth, 2020, 125(8), e2018JB016459, DOI:10.1029/2018JB016459.
- W. S. Reeburgh, Oceanic Methane Biogeochemistry, Chem. Rev., 2007, 107(2), 486–513, DOI:10.1021/cr050362v.
- K. Andreassen, A. Hubbard, M. Winsborrow, H. Patton, S. Vadakkepuliyambatta, A. Plaza-Faverola, E. Gudlaugsson, P. Serov, A. Deryabin, R. Mattingsdal, J. Mienert and S. Bünz, Massive Blow-out Craters Formed by Hydrate-Controlled Methane Expulsion from the Arctic Seafloor, Science, 2017, 356(6341), 948–953, DOI:10.1126/science.aal4500.
- P. Serov, S. Vadakkepuliyambatta, J. Mienert, H. Patton, A. Portnov, A. Silyakova, G. Panieri, M. L. Carroll, J. L. Carroll, K. Andreassen and A. Hubbard, Postglacial Response of Arctic Ocean Gas Hydrates to Climatic Amelioration, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(24), 6215–6220, DOI:10.1073/pnas.1619288114.
- W. F. Waite, J. C. Santamarina, D. D. Cortes, B. Dugan, D. N. Espinoza, J. Germaine, J. Jang, J. W. Jung, T. J. Kneafsey, H. Shin, K. Soga, W. J. Winters and T. S. Yun, Physical Properties of Hydrate-Bearing Sediments, Rev. Geophys., 2009, 47(4) DOI:10.1029/2008RG000279.
- A. Hassanpouryouzband, J. Yang, B. Tohidi, E. Chuvilin, V. Istomin, B. Bukhanov and A. Cheremisin, CO2 Capture by Injection of Flue Gas or CO2-N2 Mixtures into Hydrate Reservoirs: Dependence of CO2 Capture Efficiency on Gas Hydrate Reservoir Conditions, Environ. Sci. Technol., 2018, 52(7), 4324–4330, DOI:10.1021/acs.est.7b05784.
- R. Freij-Ayoub, C. Tan, B. Clennell, B. Tohidi and J. Yang, A Wellbore Stability Model for Hydrate Bearing Sediments, J. Pet. Sci. Eng., 2007, 57(1–2), 209–220, DOI:10.1016/j.petrol.2005.10.011.
- S. A. Bagherzadeh, I. L. Moudrakovski, J. A. Ripmeester and P. Englezos, Magnetic Resonance Imaging of Gas Hydrate Formation in a Bed of Silica Sand Particles, Energy Fuels, 2011, 25(7), 3083–3092, DOI:10.1021/ef200399a.
- S. Dai, R. Boswell, W. F. Waite, J. Jang, J. Y. Lee and Y. Seol, What Has Been Learned from Pressure Cores, in The 9th International Conference on Gas Hydrates, 2017, pp. 25–30 Search PubMed.
- T. M. Vlasic, P. D. Servio and A. D. Rey, THF Hydrates as Model Systems for Natural Gas Hydrates: Comparing Their Mechanical and Vibrational Properties, Ind. Eng. Chem. Res., 2019, 58(36), 16588–16596, DOI:10.1021/acs.iecr.9b02698.
- W. J. Winters, R. W. Wilcox-Cline, P. Long, S. K. Dewri, P. Kumar, L. Stern and L. Kerr, Comparison of the Physical and Geotechnical Properties of Gas-Hydrate-Bearing Sediments from Offshore India and Other Gas-Hydrate-Reservoir Systems, Mar. Pet. Geol., 2014, 58(PA), 139–167, DOI:10.1016/j.marpetgeo.2014.07.024.
- P. Mohammadmoradi and A. Kantzas, Direct Geometrical Simulation of Pore Space Evolution through Hydrate Dissociation in Methane Hydrate Reservoirs, Mar. Pet. Geol., 2018, 89, 786–798, DOI:10.1016/j.marpetgeo.2017.11.016.
- L. Lei, Y. Seol, J. H. Choi and T. J. Kneafsey, Pore Habit of Methane Hydrate and Its Evolution in Sediment Matrix – Laboratory Visualization with Phase-Contrast Micro-CT, Mar. Pet. Geol., 2019, 104, 451–467, DOI:10.1016/j.marpetgeo.2019.04.004.
- T. X. Le, S. Rodts, D. Hautemayou, P. Aimedieu, M. Bornert, B. Chabot and A. M. Tang, Kinetics of Methane Hydrate Formation and Dissociation in Sand Sediment, Geomech. Energy Environ., 2020, 23, 100103, DOI:10.1016/j.gete.2018.09.007.
- S. Jin, S. Takeya, J. Hayashi, J. Nagao, Y. Kamata, T. Ebinuma and H. Narita, Structure Analyses of Artificial Methane Hydrate Sediments by Microfocus X-Ray Computed Tomography, Jpn. J. Appl. Phys., 2004, 43(8 A), 5673–5675, DOI:10.1143/JJAP.43.5673.
- P. B. Kerkar, K. Horvat, K. W. Jones and D. Mahajan, Imaging Methane Hydrates Growth Dynamics in Porous Media Using Synchrotron X-Ray Computed Microtomography, Geochem., Geophys., Geosyst., 2014, 15(12), 4759–4768, DOI:10.1002/2014GC005373.
- L. Lei, Y. Seol and K. Jarvis, Pore-Scale Visualization of Methane Hydrate-Bearing Sediments With Micro-CT, Geophys. Res. Lett., 2018, 45(11), 5417–5426, DOI:10.1029/2018GL078507.
- S. Takeya, S. Muromachi, A. Hachikubo, R. Ohmura, K. Hyodo and A. Yoneyama, X-Ray Attenuation and Image Contrast in the X-Ray Computed Tomography of Clathrate Hydrates Depending on Guest Species, Phys. Chem. Chem. Phys., 2020, 22(47), 27658–27665, 10.1039/d0cp05466f.
- J. Lv, J. Zhao, L. Jiang, Y. Liu and H. Mu, A Review of Micro Computed Tomography Studies on the Gas Hydrate Pore Habits and Seepage Properties in Hydrate Bearing Sediments, J. Nat. Gas Sci. Eng., 2020, 83, 103555, DOI:10.1016/j.jngse.2020.103555.
- G. He, X. Luo, H. Zhang and J. Bi, Pore-Scale Identification of Multi-Phase Spatial Distribution of Hydrate Bearing Sediment, J. Geophys. Eng., 2018, 15(5), 2310–2317, DOI:10.1088/1742-2140/aaba10.
- Y. Zhang, Y. Zhao, X. Lei, M. Yang, Y. Zhang and Y. Song, Quantitatively Study on Methane Hydrate Formation/Decomposition Process in Hydrate-Bearing Sediments Using Low-Field MRI, Fuel, 2020, 262, 116555, DOI:10.1016/j.fuel.2019.116555.
- S. Gao, W. House and W. G. Chapman, NMR/MRI Study of Clathrate Hydrate Mechanisms, J. Phys. Chem. B, 2005, 109(41), 19090–19093, DOI:10.1021/jp052071w.
- J. Zhao, L. Yao, Y. Song, K. Xue, C. Cheng, Y. Liu and Y. Zhang, In Situ Observations by Magnetic Resonance Imaging for Formation and Dissociation of Tetrahydrofuran Hydrate in Porous Media, Magn. Reson. Imaging, 2011, 29(2), 281–288, DOI:10.1016/j.mri.2010.08.012.
- L. Zhang, Y. Kuang, S. Dai, J. Wang, J. Zhao and Y. Song, Kinetic Enhancement of Capturing and Storing Greenhouse Gas and Volatile Organic Compound: Micro-Mechanism and Micro-Structure of Hydrate Growth, Chem. Eng. J., 2020, 379, 122357, DOI:10.1016/j.cej.2019.122357.
- J. n. Zheng, L. Jiang, P. Wang, H. Zhou and M. Yang, MRI Observation of CO2-C3H8 Hydrate-Induced Water Migration in Glass Sand, Chem. Eng. Sci., 2019, 207, 1096–1106, DOI:10.1016/j.ces.2019.07.038.
- Z. Cheng, Y. Zhao, W. Liu, Y. Liu, L. Jiang and Y. Song, Kinetic Analysis of Nano-SiO2 Promoting Methane Hydrate Formation in Porous Medium, J. Nat. Gas Sci. Eng., 2020, 79, 103375, DOI:10.1016/j.jngse.2020.103375.
- G. Ersland, J. Husebø, A. Graue, B. A. Baldwin, J. Howard and J. Stevens, Measuring Gas Hydrate Formation and Exchange with CO2 in Bentheim Sandstone Using MRI Tomography, Chem. Eng. J., 2010, 158(1), 25–31, DOI:10.1016/j.cej.2008.12.028.
- L. Zhang, J. Zhao, H. Dong, Y. Zhao, Y. Liu, Y. Zhang and Y. Song, Magnetic Resonance Imaging for In-Situ Observation of the Effect of Depressurizing Range and Rate on Methane Hydrate Dissociation, Chem. Eng. Sci., 2016, 144, 135–143, DOI:10.1016/j.ces.2016.01.027.
- Y. Song, L. Zhang, Q. Lv, M. Yang, Z. Ling and J. Zhao, Assessment of Gas Production from Natural Gas Hydrate Using Depressurization, Thermal Stimulation and Combined Methods, RSC Adv., 2016, 6(53), 47357–47367, 10.1039/c6ra05526e.
- L. Zhang, Y. Kuang, X. Zhang, Y. Song, Y. Liu and J. Zhao, Analyzing the Process of Gas Production from Methane Hydrate via Nitrogen Injection, Ind. Eng. Chem. Res., 2017, 56(26), 7585–7592, DOI:10.1021/acs.iecr.7b01011.
- Z. Fan, C. Sun, Y. Kuang, B. Wang, J. Zhao and Y. Song, MRI Analysis for Methane Hydrate Dissociation by Depressurization and the Concomitant Ice Generation, Energy Procedia, 2017, 105, 4763–4768, DOI:10.1016/j.egypro.2017.03.1038.
- B. Chen, M. Yang, H. Sun, D. Wang, L. Jiang and Y. Song, Visualization Study on the Promotion of Depressurization and Water Flow Erosion for Gas Hydrate Production, Energy Procedia, 2019, 158, 5563–5568, DOI:10.1016/j.egypro.2019.01.586.
- B. Chen, H. Sun, J. Zheng and M. Yang, New Insights on Water-Gas Flow and Hydrate Decomposition Behaviors in Natural Gas Hydrates Deposits with Various Saturations, Appl. Energy, 2019, 259, 114185, DOI:10.1016/j.apenergy.2019.114185.
- B. Wang, J. Zhao, Y. Song, X. Lv, Y. Li, W. Pang and Q. Li, Dynamical Mechanism of Hydrate Formation Resulting from Free Gas Migration into Seeping Seafloor Sediments, Energy Procedia, 2019, 158, 5329–5335, DOI:10.1016/j.egypro.2019.01.634.
- L. Zhang, M. Sun, L. Sun, T. Yu, Y. Song, J. Zhao, L. Yang and H. Dong, In-Situ Observation for Natural Gas Hydrate in Porous Medium: Water Performance and Formation Characteristic, Magn. Reson. Imaging, 2020, 65, 166–174, DOI:10.1016/j.mri.2019.09.002.
- A. Hassanpouryouzband, J. Yang, B. Tohidi, E. Chuvilin, V. Istomin and B. Bukhanov, Geological CO2 Capture and Storage with Flue Gas Hydrate Formation in Frozen and Unfrozen Sediments: Method Development, Real Time-Scale Kinetic Characteristics, Efficiency, and Clathrate Structural Transition, ACS Sustainable Chem. Eng., 2019, 7(5), 5338–5345, DOI:10.1021/acssuschemeng.8b06374.
- L. Zhang, L. Sun, M. Sun, X. Lv, H. Dong, Y. Miao, L. Yang, Y. Song and J. Zhao, Analyzing Spatially and Temporally Visualized Formation Behavior of Methane Hydrate in Unconsolidated Porous Media, Magn. Reson. Imaging, 2019, 61, 224–230, DOI:10.1016/j.mri.2019.06.005.
- A. Rojas Zuniga, M. Li, Z. M. Aman, P. L. Stanwix, E. F. May and M. L. Johns, NMR-Compatible Sample Cell for Gas Hydrate Studies in Porous Media, Energy Fuels, 2020, 34(10), 12388–12398, DOI:10.1021/acs.energyfuels.0c02383.
- A. Hassanpouryouzband, M. V. Farahani, J. Yang, B. Tohidi, E. Chuvilin, V. Istomin and B. Bukhanov, Solubility of Flue Gas or Carbon Dioxide-Nitrogen Gas Mixtures in Water and Aqueous Solutions of Salts: Experimental Measurement and Thermodynamic Modeling, Ind. Eng. Chem. Res., 2019, 58(8), 3377–3394, DOI:10.1021/acs.iecr.8b04352.
- J. W. Mullin, Crystallization, Elsevier, 2001, DOI:10.1016/B978-0-7506-4833-2.X5000-1.
- E. V. L. Rees, T. J. Kneafsey and Y. Seol, Methane Hydrate Distribution from Prolonged and Repeated Formation in Natural and Compacted Sand Samples: X-Ray CT Observations, J. Geophys. Res., 2011, 2011, 1–15, DOI:10.1155/2011/791815.
- P. Buchanan, A. K. Soper, H. Thompson, R. E. Westacott, J. L. Creek, G. Hobson and C. A. Koh, Search for Memory Effects in Methane Hydrate: Structure of Water before Hydrate Formation and after Hydrate Decomposition, J. Chem. Phys., 2005, 123(16), 164507, DOI:10.1063/1.2074927.
- M. Yang, Y. Song, L. Jiang, N. Zhu, Y. Liu, Y. Zhao, B. Dou and Q. Li, CO2 Hydrate Formation and Dissociation in Cooled Porous Media: A Potential Technology for CO2 Capture and Storage, Environ. Sci. Technol., 2013, 47(17), 9739–9746, DOI:10.1021/es401536w.
- W. Liu, S. Wang, M. Yang, Y. Song, S. Wang and J. Zhao, Investigation of the Induction Time for THF Hydrate Formation in Porous Media, J. Nat. Gas Sci. Eng., 2015, 24, 357–364, DOI:10.1016/j.jngse.2015.03.030.
- J. Zhao, C. Wang, M. Yang, W. Liu, K. Xu, Y. Liu and Y. Song, Existence of a Memory Effect between Hydrates with Different Structures (I, II, and H), J. Nat. Gas Sci. Eng., 2015, 26, 330–335, DOI:10.1016/j.jngse.2015.06.031.
- Y. S. Kim, B. D. Lim, J. E. Lee and C. S. Lee, Solubilities of Carbon Dioxide, Methane, and Ethane in Sodium Chloride Solution Containing Gas Hydrate, J. Chem. Eng. Data, 2008, 53(6), 1351–1354, DOI:10.1021/je800074z.
- D. Grasso, K. Subramaniam, M. Butkus, K. Strevett and J. Bergendahl, A Review of Non-DLVO Interactions in Environmental Colloidal Systems, Rev. Environ. Sci. Bio/Technol., 2002, 1(1), 17–38, DOI:10.1023/A:1015146710500.
- T. J. Kneafsey, L. Tomutsa, G. J. Moridis, Y. Seol, B. M. Freifeld, C. E. Taylor and A. Gupta, Methane Hydrate Formation and Dissociation in a Partially Saturated Core-Scale Sand Sample, J. Pet. Sci. Eng., 2007, 56(1–3), 108–126, DOI:10.1016/j.petrol.2006.02.002.
- B. Tohidi, R. Anderson, M. B. Clennell, R. W. Burgass and A. B. Biderkab, Visual Observation of Gas-Hydrate Formation and Dissociation in Synthetic Porous Media by Means of Glass Micromodels, Geology, 2001, 29(9), 867–870, DOI:10.1130/0091-7613(2001)029<0867:VOOGHF>2.0.CO;2.
- P. Servio and P. Englezos, Morphology of Methane and Carbon Dioxide Hydrates Formed from Water Droplets, AIChE J., 2003, 49(1), 269–276, DOI:10.1002/aic.690490125.
- M. B. Clennell, M. Hovland, J. S. Booth, P. Henry and W. J. Winters, Formation of Natural Gas Hydrates in Marine Sediments 1. Conceptual Model of Gas Hydrate Growth Conditioned by Host Sediment Properties, J. Geophys. Res.: Solid Earth, 1999, 104(B10), 22985–23003, DOI:10.1029/1999jb900175.
- Q. Lin, Y. Al-Khulaifi, M. J. Blunt and B. Bijeljic, Quantification of Sub-Resolution Porosity in Carbonate Rocks by Applying High-Salinity Contrast Brine Using X-Ray Microtomography Differential Imaging, Adv. Water Resour., 2016, 96, 306–322, DOI:10.1016/j.advwatres.2016.08.002.
- Y. Gao, Q. Lin, B. Bijeljic and M. J. Blunt, X-Ray Microtomography of Intermittency in Multiphase Flow at Steady State Using a Differential Imaging Method, Water Resour. Res., 2017, 53(12), 10274–10292, DOI:10.1002/2017WR021736.
- M. Vasheghani Farahani, A. Hassanpouryouzband, J. Yang and B. Tohidi, Heat Transfer in Unfrozen and Frozen Porous Media: Experimental Measurement and Pore-Scale Modeling, Water Resour. Res., 2020, 56(9) DOI:10.1029/2020WR027885.
- Y. Kuang, L. Zhang, Y. Song, L. Yang and J. Zhao, Quantitative Determination of Pore-Structure Change and Permeability Estimation under Hydrate Phase Transition by NMR, AIChE J., 2020, 66(4), e16859, DOI:10.1002/aic.16859.
Footnote |
| † Electronic supplementary information (ESI) available: Two movies illustrating the thermally induced hydrate formation/dissociation for both synthetic and natural sediment samples. MI values for both synthetic and natural sediment samples versus time. The particle size distribution curves of both synthetic and natural sediments. See DOI: 10.1039/d0se01705a |
| This journal is © The Royal Society of Chemistry 2021 |