Using high-throughput virtual screening to explore the optoelectronic property space of organic dyes; finding diketopyrrolopyrrole dyes for dye-sensitized water splitting and solar cells

Abstract

Organic dyes based on conjugated chromophores such as diketopyrrolopyrrole (DPP) have a large range of uses beyond providing colour to other materials, such as in dye-sensitized solar cells, dye-sensitized photoelectrochemical cells, dye-sensitized colloidal photocatalysts and organic photovoltaics. We perform a high-throughput virtual screening using the xTB family of density functional tight-binding methods to map the optoelectronic property space of ∼45 000 DPP dyes. The large volume of data at our disposal allows us to probe the difference between symmetric and asymmetric dyes and to identify the apparent boundaries of the optoelectronic property space for these dyes, as well as which substituents give access to particular combinations of properties. Finally, we use our dataset to screen for DPP dyes that can drive the reduction of protons to molecular hydrogen when illuminated as part of dye-sensitized photoelectrochemical cells or dye-sensitized colloidal photocatalysts, or as dyes for TiO₂-based dye-sensitized solar cells.

---

Introduction

The use of dyes and pigments is inherently linked to their ability to absorb light. For example, the di(p-chlorophenyl) derivative of diketopyrrolopyrrole (DPP) absorbs most of the visible spectrum, reflecting back only red light. As a result this DPP^1,2 is a red pigment, world famous as Ferrari red or pigment red 254. Similarly, the chemically related indigo molecule absorbs green to red light, reflecting back only blue light, and is the dye that colours jeans blue.³

However, the use of organic dyes and pigments is not limited to simply providing colour, they also find application in dye-sensitized solar-cells (DSSCs)^4–20 dye-sensitized photocatalysts^21–26 and in organic electronics, for example in organic field-effect transistors (OFETs),^2,27,28 organic photovoltaics (OPV)²⁹ and materials for singlet fission.^30–33 In DSSCs, the ability of a dye to absorb light of a particular range of wavelengths and inject photoexcited electrons or holes into a semiconductor that would otherwise be transparent to that light, ultimately leads to the generation of an electrical current.³⁴ Similarly, the dye sensitizer in a dye-sensitized photocatalyst or photoelectrochemical cell (DS-PEC) absorbs light and initiates an electron transfer process, ultimately resulting in the splitting of water into molecular hydrogen and oxygen.^24,26

Organic dyes and pigments, which we will refer to simply as “dyes” hereafter, generally consist of a conjugated core, the chromophore after which dyes are typically named, which is augmented with substituents. The function of these substituents can be to improve the adsorption of the dye on a substrate (e.g. carboxylic or phosphonic acid groups), to improve the solubility (e.g. long alkyl chains to improve the solubility in organic solvents), or to modify the optoelectronic properties of the chromophore, e.g. electron withdrawing/donating groups or aromatic substituents, which extend the conjugation.

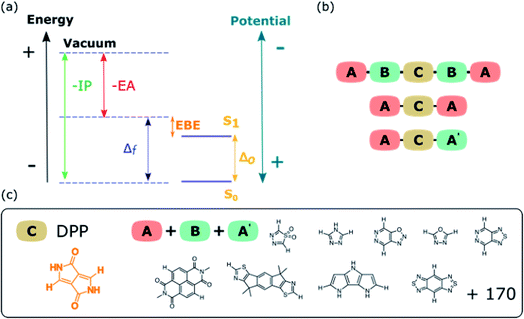
Understanding the suitability of dyes for particular applications such as DS-PECs, DSSCs or organic photovoltaics, requires knowledge of the dyes optical gap (Δ_O), fundamental gap (Δ_f), exciton binding energy (EBE), and ionization potential (IP) and electron affinity (EA) values (see Fig. 1a), among other things. The optical gap is the maximum wavelength (or minimum energy) of light able to excite a molecule and generate an exciton, an excited electron–hole pair. The IP and EA are the energy required to extract an electron from a molecule and the energy released when an electron is added, respectively. Finally, the difference between IP and EA is the fundamental gap, the energy required to generate a non-interacting pair of an excited electron and hole, which is larger than the optical gap by an amount that equals the exciton binding energy.

Fig. 1 (a) Definition of −IP, −EA, Δ_O, Δ_f; and EBE, (b) composition of the different dyes studied in terms of their building block with an example ABCBA dye and (c) dye building blocks (explicitly shown hydrogen atoms, other than those connected to nitrogen atoms, indicate carbon atoms where building blocks can be connected to other building blocks in the dyes).

The number of possible dyes to consider increases rapidly with the number of substituents and/or substituent sites to consider. Recently, for example, Fallon and co-workers studied nearly 10 000 indigo dyes with (time-dependent) density functional theory (TD-)DFT for their application in singlet-fission.³³ However, even with a relatively small library of substituents and either allowing oligomeric side-chains, e.g.ABCBA, where C is the core of the dye and A and B substituents, or allowing for asymmetric substitution, e.g.ACA′, with two different As, as in D–π–A dyes, it is possible to come up with even larger families of dyes. Screening 10 000+ dyes experimentally would be practically impossible. Studying such families of dyes computationally using (TD-)DFT would be, at least currently, equally a laborious task, even if this is now routinely done for smaller libraries of dyes.^15,17 Recently, however, we showed that workflows based on the computationally efficient density functional tight-binding method – GFN-xTB – developed by Grimme and co-workers,³⁵ and its IPEA-xTB³⁶ and sTDA-xTB³⁷ extensions, allowed one to screen the optoelectronic properties of co-polymers³⁸ and small aromatic molecules of much larger libraries than currently feasible with (TD-)DFT and with a comparable accuracy.

Here we use the same approach and apply it to different families of DPP-based dyes with the sequences ABCBA, ACA and ACA′. DPP and its derivatives are a well-known class of semiconducting molecules with a wide range of applications besides that of a pigment. DPP derivatives have been used as dyes for DSSCs,^8,11,18 DS-PEC²⁵ and OPV,³⁹ as well as in OFETs.^2,29 The attractive features of DPP include good thermal stability and photostability, as well as the fact that it can be easily functionalised to improve solubility or to provide an anchoring group to allow for adsorption of the dye on a substrate, such as a TiO₂ photoanode in a DSSC. We use our screening to understand the general features of the optoelectronic property space of DPP-based dyes, as well as predict the common molecular elements for DPP-based dyes that have the right combination of properties for dye-sensitized photocatalytic proton reduction to molecular hydrogen.

Methodology

Screening workflow

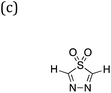
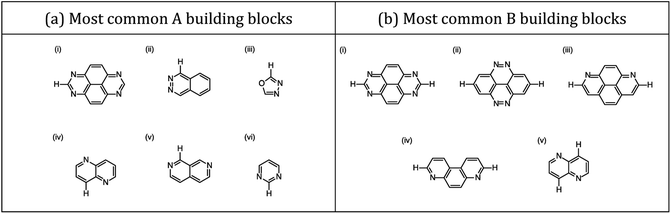
Three families of dyes with a diketopyrrolopyrrole core (C) and compositions ABCBA (32 041 dyes), ACA′ (15 931 dyes) and ACA (179 dyes), in which the A and B units taken from the same library of 179 common (heterocyclic) aromatic building blocks (see Fig. 1b and c and S1†), were explored computationally. Using a Python pipeline, all possible combinations within these specific sequences were constructed using stk,^40,41 a Python library that takes functionality from RDKit,⁴² an opensource cheminformatics toolkit. In the case of asymmetric building blocks, we only considered one unique orientation when constructing dyes. For each dye structure, 30 conformers were generated using the Experimental-Torsion Distance Geometry with additional basic knowledge (ETKDG) algorithm.⁴³ The lowest energy conformer for each structure was then determined using the Merck Molecular Force Field (MMFF)⁴⁴ as implemented in RDKit.

Subsequently, the optoelectronic properties of each lowest energy conformer were calculated. The ionisation potential (IP) and electron affinity (EA) of each molecule were predicted using the (GFN/IPEA)-xTB^36,37,45 family of semi-empirical tight-binding methods using the xtb code.⁴⁶ The optical gap was approximated as the lowest energy singlet excitation and calculated both using the sTDA-xTB method as implemented in the sTDA code⁴⁷ and long-range corrected tight-binding DFT (LRC-TD-TB-DFT) as implemented in the DFTBaby code.⁴⁸ In the latter case, we limited ourselves to molecules containing only carbon, hydrogen, oxygen and nitrogen (CHON) atoms. A generalised Born solvation model is available within GFN-xTB and was therefore used for the optimisation and IP/EA calculations. As there is no solvation model implemented for sTDA or LRC-TD-TB-DFT, the optical gap calculations were performed in the absence of a solvation model.

Validation and calibration of (GFN/IPEA/sTDA)-xTB/LRC-TD-TB-DFT results to (TD-)DFT

For the validation of the xTB/LRC-TD-TB-DFT calculated properties of the different dyes, the properties of sub-sets of each were also calculated using ΔDFT (to calculate IP and EA) and TD-DFT (to calculate the optical gap) respectively. Our functional/basis set choices were B3LYP/6-311G** (ref. 49–52) for the ground state geometry and ΔDFT calculations and ωB97X/6-311+G** (ref. 53) for the TD-DFT calculations. We use a range-separated functional for the TD-DFT calculations because the donor acceptor character of some of the dyes means that those dyes are likely to have low lying charge-transfer excited states. Such excited-states are spuriously stabilised⁵⁴ by non-range-separated functionals, which in that case would mean that the optical gap of dyes with low-lying charge transfer states would be underestimated. Moreover, sTDA-xTB/LRC-TD-TB-DFT both include range-separated exchange. The balanced treatment of local and charge-transfer states by a range-separated functional, such as ωB97X, does come at the expense of a slight blue-shift⁵⁵ of all predicted optical gaps and means that we cannot reliably calculate exciton binding energy values. As part of the ΔDFT calculations we optimise the anionic and cationic versions of the dyes and as such the ΔDFT IP and EA values correspond to adiabatic potentials. This is in contrast to their xTB counterparts, which are technically vertical potentials, though they have previously been argued to be good predictors of adiabatic values.³⁶ All (TD-)DFT calculations were run using Gaussian 16.⁵⁶ Finally, we used a subset of the results of these (TD-)DFT calculations to fit linear calibration models that translate the xTB/LRC-TD-TB-DFT values to the DFT scale^38,57,58 and the remainder to validate the fitted models.

Results and discussion

Validation and calibration of the high-throughput approach

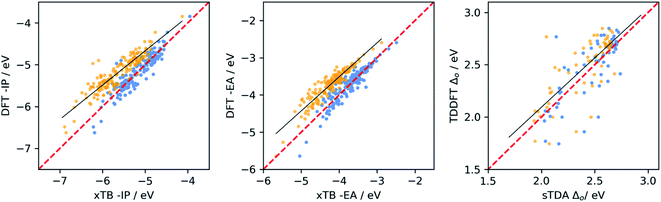
We calibrated the performance of (sTDA/IPEA-)xTB and LRC-TD-TB-DFT relative to (TD-)DFT for dyes in water by performing ΔDFT and TD-DFT calculations on a sub-set of 105 dyes, chosen so as to sample the whole range each of the properties can take. We then fitted a linear model that maps the semi-empirical results to an approximate DFT scale. The sub-set of dyes included ABCBA, ACA′ and ACA dyes. We also used (TD-)DFT to calculate the −IP, −EA and optical gap of building blocks and performed a similar calibration for the combination of the sub-set of dyes and the library of all the building blocks.

Fig. 2 shows the resulting calibration curves when using the dyes only. Calibration curves obtained using the dyes and building blocks can be found in the ESI (Fig. S2 and S3),† as well as calibration curves for optical gap values calculated with LRC-TD-TB-DFT rather than sTDA-xTB (Fig. S3†). Table 1 gives the coefficient of determination (r²) and mean absolute error (MAE) values for the different fits and Table S1 in the ESI† the fit coefficients.

Fig. 2 Calibration curves for −IP (left), −EA (centre) and optical gap (right) for the dyes, as calculated with (IPEA/sTDA)-xTB and B3LYP(IP/EA)/ωB97X (optical gap). Uncalibrated data points (yellow), calibrated data points (blue) and calibration line (black), as well as the x = y (red dashed line) to guide the eye.

Table 1 Mean absolute error (MAE) values and r² values for the calibration performed on the dyes, where the first column indicates for which dataset the fitting parameters are obtained

Fitting data	Property	r ^2	MAE/eV (calibration set)	MAE/eV (validation set)
Dyes + building blocks	IP	0.90	0.16	0.22
	EA	0.96	0.13	0.17
	ΔO (sTDA)	0.91	0.20	—
	ΔO (DFTbaby)	—	—	—
Dyes	IP	0.83	0.13	0.12
	EA	0.86	0.12	0.16
	ΔO (sTDA)	0.47	0.12	—
	ΔO (DFTbaby)	—	—	—
Dyes + building blocks (no sulfur)	IP	0.76	0.19	—
	EA	0.93	0.15	—
	ΔO (sTDA)	0.92	0.20	0.18
	ΔO (DFTbaby)	0.89	0.27	0.21
Dyes (no sulfur)	IP	0.86	0.13	—
	EA	0.92	0.12	—
	ΔO (sTDA)	0.59	0.12	0.13
	ΔO (DFTbaby)	0.69	0.12	0.14

---

From the data in Table 1, it is clear that for −IP and −EA there is generally a good correlation between the values predicted by IPEA-xTB and DFT. For the optical gap the correlation is poor, but improves significantly when excluding dyes containing sulfur (see Fig. S4 and S6 in the ESI†). Use of sTDA-xTB for some sulfur-containing dyes appears problematic and results in outliers, something we have not previously observed in the case of polymers^38,57 and small molecules.⁵⁸ Hence in the remainder of the manuscript, in the case of optical gap value prediction, we only consider dyes that lack sulfur and only contain carbon, hydrogen oxygen and/or nitrogen (CHON).

The data in Table 1 also shows that in most cases the correlation is better, r² closer to 1, when considering dyes and building blocks in combination rather than the dyes alone. However, the latter also results in generally larger MAE values. Both effects are probably the result of the much larger range of values sampled for each of the properties when including building blocks. This raises the question of which calibration is most useful for the purpose of this study. As we are most interested in making good quality prediction for the dyes, we considered a sub-set of 15 dyes not included in the calibration. This sub-set included ABCBA, ACA′ and ACA dyes, as in the calibration stage. The results of this validation can be found in Fig. 3 and Table S2.† It is clear that the best results for the dyes are obtained when using the calibration fitted to the dyes only, and we will use that calibration in the remainder of the paper. Finally, we also performed a similar calibration for the dyes in benzene, the results of which can be found in Tables S3 and S4 of the ESI.†

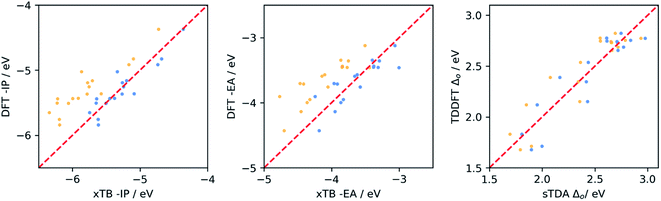Fig. 3 Comparison between DFT and (sTDA-/IPEA-)xTB calibrated using the fitting parameters obtained from Fig. 2 (above, dyes-only data-set). Uncalibrated data points (yellow) and calibrated data points (blue), as well as the x = y (dashed red line to guide the eyes).

The property spaces spanned by the different DPP dyes and property–property relationships

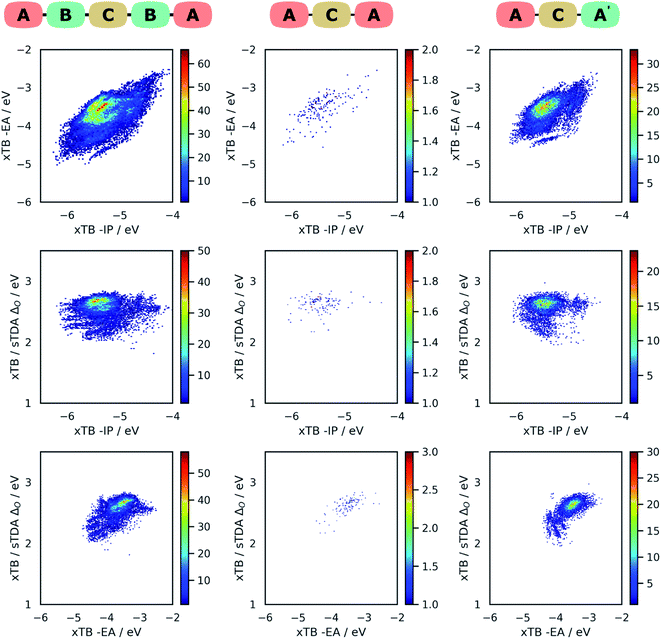
Fig. 4 shows projections of the predicted optoelectronic property space of the different families of DPP dyes and the DPP core dissolved in water, the 3D vector space spanned by the molecules' −IP, −EA and Δ_O values, projected on 2D surfaces spanned by (i) −IP and −EA, (ii) −IP and Δ_O and (iii) −EA and Δ_O. Fig. 5 shows the corresponding convex hulls that enclose all data-points for the different families. Fig. S7–S10 in the ESI† show the same information for DPP dyes dissolved in water and benzene before calibration, and Fig. S11 and S12† those for benzene after calibration. For reasons discussed above, plots involving optical gap data only show points for the subset of dyes containing only CHON (14 641 ABCBA, 7260 ACA′ and 121 ACA dyes). The optoelectronic property spaces of the different families of DPP dyes dissolved either in water and benzene look qualitatively similar, though there are quantitative differences.

Fig. 4 2D histograms of the slices of property space spanned by −IP and −EA (top row), −IP and optical gap (centre row), and −EA and optical gap (bottom row), for the ABCBA, ACA′ and ACA dyes (left to right).

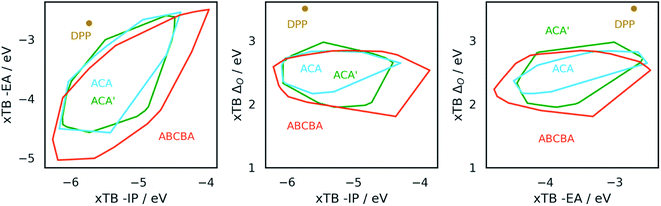Fig. 5 Convex hulls enclosing the property space of −IP and −EA (left), −IP and optical gap (centre), and −EA and optical gap (right), for the ABCBA, ACA′ and ACA dyes.

From Fig. 4 and 5 it is evident that the different dye families occupy the same region of property space, but that the ABCBA dyes allow for deeper −EA values, shallower −IP values and lower Δ_O values than the ACA′ and ACA dyes. The ACA′ and ACA dyes are very similar in terms of the −IP and −EA values they allow for, but the minimum optical gap of ACA′ dyes is ∼0.5 eV smaller than for their symmetric ACA counterparts. It is also pertinent to point out the DPP core lies in a different part of property space than that spanned by the different dye families. In terms of −IP and −EA, the −IP and −EA value of the DPP core lie separately, each within the distribution of −IP and −EA values of the dyes but the combination of the −IP and −EA value of DPP lies considerably outside the −IP and −EA convex hulls of the dyes. The optical gap of DPP even lies outside the distribution of optical gap values of the dyes. This is to be expected though, as extending the π-system by adding conjugated side-chains should always result in a lowering of the optical gap compared to the non-substituted core.

In terms of the correlation of the different dye properties, the 2D histograms shown in Fig. 4 reveal in general a weak correlation between the investigated properties. The −IP and −EA values of the dyes are most strongly correlated, where in general, deeper −IP dyes also have a deeper −EA values, and vice versa. No particular trend is observed between −IP and Δ_O however, the plot of Δ_Ovs. −EA suggests that dyes with shallower −EA values are more likely to have larger optical gaps than dye with deep −EA values.

Relationships between the properties of the dyes and those of their building blocks

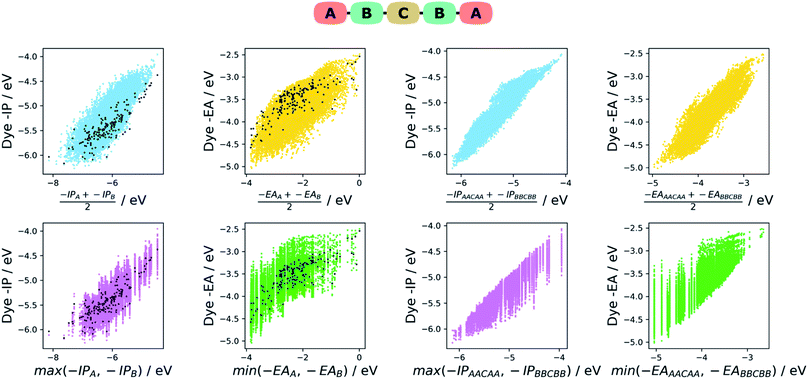
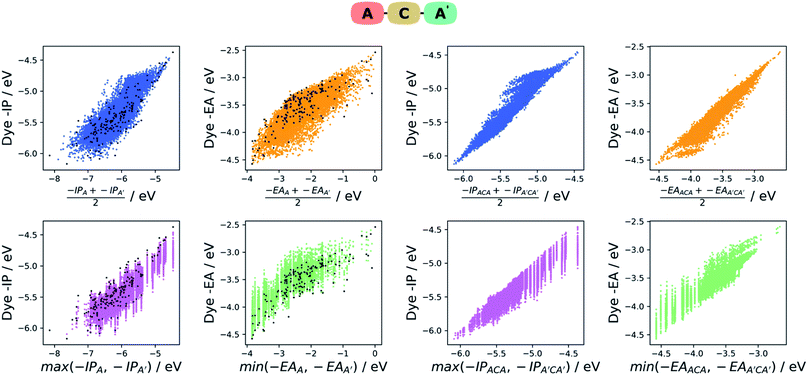
Intuitively one would assume that the properties of a given dye would be correlated with those of its constituent A and B units. In the absence of first principle insight into the form that such a relationship would take, we explore two empirical models based on our earlier work on co-polymers,⁵⁷ the averaging model and the max–min model. In the averaging model, we assume the −IP value of a dye to be correlated with the average −IP value of the A and B units and similar for −EA. In the max–min model, we assume in contrast that the −IP value of a dye correlates with the shallower (the less negative) of the −IP values of the A and B units and in the case of the dye −EA value the deeper (the most negative) of the −EA values of the two units. For each model, we plot the results, as well as analyse the strength of the correlation between the properties predicted by the model and those of the dye. For the latter, we perform a simple linear fit of the dye properties to those predicted by the model and evaluate the coefficient of determination (r²). The fitting step removes the effects of systematic shifts between the dye properties and those of the models and is in our opinion a fairer test of how good a predictor of the dye properties the different models are.

In the case of the averaging model, we average the −IP/−EA for the A and B units (e.g. −IP_average = (−IP_A + −IP_B)/2) and plotted them against the dye −IP/−EA. As can be seen on the left of Fig. 6 for the ABCBA dyes, the −IP_average and −EA_average values appear reasonably correlated with the −IP and −EA values of the dye, although there are significant differences in the absolute values. These latter differences are the results of rigid-shifts and after fitting of −IP_average and −EA_average to their corresponding dye values we find r² values of 0.65 and 0.46 respectively. In the case of the ACA′ dyes, see left of Fig. 7, again the average model seems to be a reasonable predictor of the dyes −IP and −EA values with r² values of 0.70 and 0.63.

Fig. 6 Property–property relationships between the ABCBA dyes and their constituent building blocks as described by the averaging model (top row) and the max/min model (bottom row) using the building block properties (left four panels) and AACAA dyes (right four panels) as input. Points for the ACA dyes shown in black.

Fig. 7 Property–property relationships between the ACA′ dyes and their constituent building blocks as described by the averaging model (top row) and the max/min model (bottom row) using the building block properties (left four panels) and ACA dyes (right four panels) as input. Points for the ACA dyes shown in black.

In the case of the max/min model, we predict the −IP and −EA values of the dye to be the shallowest −IP and deepest −EA of the A or B unit. For both the ABCBA (left of Fig. 6) and ACA′ (left of Fig. 7) dyes, the max/min model performs similarly to the averaging model with r² values after linear fit of 0.71 (−IP) and 0.50 (−EA) for the ABCBA dyes and 0.77 (−IP) and 0.69 (−EA) for the ACA′ dyes. In the case of the ACA dyes, there is no need to average or select the shallowest −IP or deepest −EA value. However, the points for the ACA dyes shown on the left of Fig. 6 and 7 show that again the −IP and −EA values are correlated reasonably well with those of the A unit (r² of 0.72 for −IP and 0.67 for −EA).

The dyes thus clearly inherit their electronic character from their constituent components and it appears that the electronic properties of the A and B units dominate that of the DPP core. This dominance probably arises from the fact that the −IP and −EA values of the DPP core lie near the average of the distributions of −IP and −EA values from the library from which A and B are taken (see Fig. S13†). The correlation between the −IP and −EA values of A and B and those of the dye, also means that one can make informed guesses about the electronic properties of DPP dyes without doing calculations on the dyes themselves, something which might be interesting in the case of A or B units that are not in our library. Finally, while we only consider DPP dyes here, we believe based on these results that similar correlations should exist for dyes with other cores.

Relationships between the properties of ABCBA and ACA′ dyes and those of their corresponding AACAA and ACA dyes

The two models discussed above can similarly be used to describe the relationship between the −IP and −EA of the ABCBA and ACA′ dyes and their corresponding dyes with the same building blocks in the A, B and A′ positions, i.e. the corresponding AACAA/BBCBB and ACA/ACA′ dyes. Indeed that is exactly what we did in our previous work³⁸ on co-polymers, where we related the properties of binary co-polymers to those of their respective homopolymers. On the right of Fig. 6, the results for averaging and max/min model for the ABCBA dyes are shown, and below them on the right of Fig. 7 are the results for the same models in the case of the ACA′ set of dyes.

We find that the averaging model performs very well for the ABCBA dyes with r² values of 0.90 and 0.79 for −IP and −EA, respectively, a strong improvement in comparison to the model using the building blocks. The averaging model for the ACA′vs.ACA/A′CA′ comparison Fig. 7 also yielded improved r² values of 0.93 and 0.92 for −IP and −EA, respectively. The max/min model performed slightly worse than the averaging model, yielding r² of 0.86 and 0.68 for the ABCBA dye's −IP and −EA, respectively and 0.90 and 0.86 for ACA′ dye's IP and EA, respectively, but again better than the same model using the building block values as input. The improved correlations observed here using the properties of the AACAA and ACA dyes as input rather than those of the building block is most likely just because the AACAA and ACA dyes are more similar electronically to the ABCBA and ACA′ dyes than the building blocks. Again, even though we only study DPP dyes here, we believe that similar correlations exist for dyes with other cores.

Effect of the asymmetric nature of ACA′ dyes

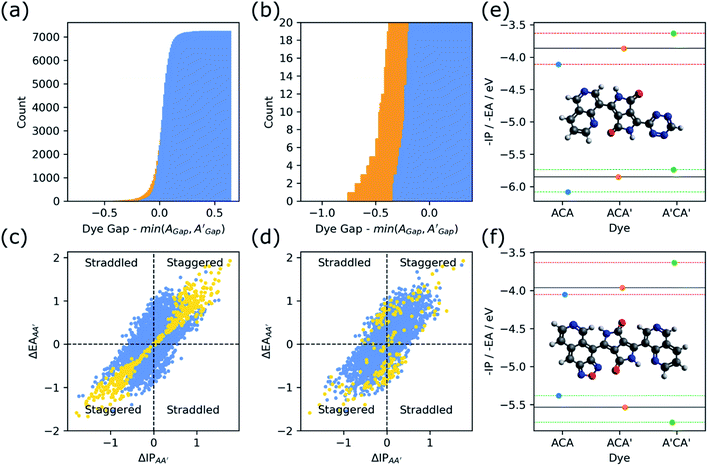
We also explored in the case of ACA′ dyes to what extent their asymmetric nature results in a reduction of the optical and/or fundamental gap with respect to their symmetric ACA and A′CA′ counterparts. Fig. 8 shows a cumulative histogram of the optical and fundamental gap of the ACA′ dyes as a function of the difference between the optical/fundamental gap of the ACA′ dye and that of their ACA or A′CA′ counterpart with the smallest optical/fundamental gap. As can be seen from Fig. 8 a small but significant amount of ACA′ dyes have a fundamental and/or optical gap that is smaller than their ACA and A′CA′ counterparts. Inspection of such dyes shows that they generally combine electron-poor and electron-rich building blocks and hence are clear examples of D–π–A dyes (see Fig. S14†).

Fig. 8 (a) Cumulative histogram of ACA′ dyes for which the optical gap (blue) or fundamental gap (orange) is less than that of both related ACA and A′CA′ dyes, negative values, or larger than at least one of the related dyes, positive values), (b) zoomed in version of the cumulative histogram, (c) ACA dyes with an fundamental gap lower than both (yellow) or larger than at least one (blue) of that of their ACA and A′CA′ counterparts (yellow) as a function of the offset between the −IPs and −EAs of the ACA and A′CA′ dyes, (d) plot of ACA dyes with an optical gap lower than both (yellow) or larger than at least one (blue) of that of their ACA and A′CA′ counterparts as a function of the offset between the −IPs and −EAs of the ACA and A′CA′ dyes, (e) example of ACA′ dyes where the ACA/A′CA′ −IP and −EA values are staggered, and (f) example of ACA′ dyes where the ACA/A′CA′ −IP and −EA values are straddled.

One possible way to analyse if ACA′ dyes are likely to have D–π–A character is to consider the relative positions of the −IP and −EA values of their ACA and A′CA′ counterparts, akin to what we previously considered in the case of binary co-polymers.³⁸ The hypothesis would be that when the −IP and −EA values of the ACA dye straddle the −IP and −EA values of the A′CA′ dye, or other way around, the corresponding ACA′ dye would have D–π–D or A–π–A character, and that only when the −IP and −EA values of the ACA dye are staggered with respect the −IP and −EA values of the A′CA′ dye, the equivalent ACA′ has D–π–A character. In line with this hypothesis, in the first scenario the max/min model using the ACA/A′CA′ −IP and −EA values as input would predict that the ACA′ dye would inherit its −IP and −EA values of the same ACA/A′CA′ counterpart, the dye being straddled. While in the second scenario, the max/min model would predict that the ACA′ dye inherits the −IP value of one of its ACA/A′CA′ counterparts and its −EA value of the other.

Fig. 8 also includes plots where ACA′ dyes are plotted as a function of the difference in the −IP values and −EA values of their ACA/A′CA′ counterparts and coloured depending on if their optical/fundamental gap is lower or higher than at least one of those ACA/A′CA′ counterparts. If the differences for −IP and −EA are either both negative or both positive the ACA and A′CA′ dyes are staggered, while if one difference is positive and the other is negative one straddles the other. Indeed, in the case of the fundamental gap a staggered alignment of the −IP and −EA values of the ACA and A′CA′ dyes is an excellent predictor if the fundamental gap of an ACA′ dye is smaller than its ACA/A′CA′ counterparts. It is a less good predictor in the case of the optical gap probably because there are other effects at play. One such effect could be that dyes differ in their exciton binding energy, the difference between optical and fundamental gap and a measure of how strong the excited electron and hole interact electrostatically in the lowest excited-state. Sadly, the fact that during calibration we have had to use, for the reasons outlined in the method section, a different DFT functional while calculating the optical gap than for −IP and −EA, we cannot reliably estimate exciton binding energy values using our approach for these dyes.

Dye candidates for dye-sensitized proton reduction and DSSCs

For the application of DPP dyes in combination with TiO₂ nanoparticles in dye-sensitized photocatalysis, certain optical and electronic criteria must be fulfilled on top of the obvious requirement of the dye to be stable in water under illumination:

(a) The IP* of the dye, the potential associated with the ability of the excited dye to donate an electron, should be more negative than the conduction band maximum of TiO₂ in order to inject electrons into the TiO₂ nanoparticle.

(b) The IP of the dye should be more positive than that of the water or sacrificial electron donor (e.g. ascorbic acid or triethanolamine) oxidation potential.

(c) The optical gap of the dye should be small enough to absorb as much visible light as possible and preferably absorb in the near-infrared (NIR) region,

assuming that the injection of an electron in to the TiO₂ by the exciton is faster than the extraction of a hole from the dye by a sacrificial electron donor (SED) or water. If that is not true, IP* in condition (a) would be replaced by EA and IP in condition (c) by EA* (the potential associated with the ability of the excited dye to donate a hole). The difference between IP* and EA and that between EA* and IP is the exciton binding energy, which is likely to be small, 0.1–0.3 (e)V, in the presence of a high dielectric permittivity solvent like water based on our previous work.^59–61 Therefore, we consider in the following EA in condition (a) and IP in condition (b), both approximating IP* by EA and EA* by IP, as well as allowing us to be ambivalent about the relative kinetics of electron donation and electron acceptance.

At pH 2.5, the likely pH of an ascorbic acid solution,^62,63 the conduction band edge of TiO₂ lies at ∼−0.30 V (∼0.20 V (ref. 64) at pH 1 and a −0.09 V Nernstian shift to correct the value to pH 2.5) with respect to SHE (and thus ∼−4.1 V with respect to vacuum) and the reduction potential for the one-hole oxidation of ascorbic acid at ∼0.7 V (∼−5.1 V with respect to vacuum). It is also necessary for the dye to absorb visible light and therefore the optical gap must be small enough to absorb light with energy below 2.95 eV. As the optical gap is relevant, the dyes discussed here are limited to those within the CHON sub-set. Within this proton reduction region there are 10 941 ABCBA CHON dyes. Out of the 121 unique CHON building blocks in our library, 118 are present on the A site and 113 on the B site of these ABCBA dyes. All the building blocks present on the B site are present on the A site. In the case of the ACA′ dyes the watersplitting region contains 6527 CHON dyes. Of the 121 building blocks considered, only 4 of these are not found on the ACA′ dyes in this region. For more details see below in the structure–property section.

Supposing an additional offset of 0.4 V, to take into account the kinetically required driving force and/or to correct for that we screen for IP and EA rather than EA* and IP*, making the IP and EA thresholds 1.1 V and −0.7 V vs. SHE (−IP and −EA −5.5 and −3.7 V with respect to vacuum, respectively), respectively, our dye class is narrowed down to 849 CHON ABCBA dyes in total. Of these, the maximum optical gap is 2.77 eV and the minimum 2.51 eV – higher than what would be preferable for adequate visible light absorption. Within this set of dyes there are 82 A building blocks and 44 B building blocks. For the ACA′ dyes, the number of dyes under these constraints is 1518, with the maximum and minimum optical gaps being 2.81 and 2.44 eV, respectively. Oxidising water, rather than a sacrificial electron donor such as ascorbic acid or triethanolamine, is thermodynamically much harder, requiring an IP at pH 7 larger than 1.12 V, when including the additional driving force (0.82 V without), meaning that even fewer dyes can drive this half-reaction.

As the dielectric permittivity of solvents used in DSSCs, such as acetonitrile, is not that dissimilar to water when taking into account the inverse dependence of −IP and −EA on the dielectric permittivity of the solvent,⁵⁹ we can also consider which of our ABCBA and ACA′ dyes would make good candidates for use in TiO₂-based DSSCs. In acetonitrile solutions containing Li⁺ cations Redmond and Fitzmaurice⁶⁵ report that the conduction band edge of TiO₂ lies at ∼−0.7 V vs. SHE (−3.2 V with respect to vacuum), while Boschloo and Hagfeldt⁶⁶ report that the standard reduction potential of the I₃⁻/3I⁻ redox couple lies at ∼+0.3 V vs. SHE (−4.7 V with respect to vacuum). Using these values, 8952 ABCBA dyes are in principle suitable for TiO₂-based DSSCs. Out of the 121 unique CHON building blocks in our library, 119 are present on the A site and 107 on the B site of these ABCBA dyes. Of these, the maximum optical gap is 2.84 eV and the minimum 2.2 eV – higher than what would be preferable for adequate visible light absorption. Similarly, in the case of ACA′ dyes, 519 dyes lie in this region, containing 119 unique building blocks, with maximum and minimum optical gap values of 2.98 and 2.00 eV, respectively. Again, adding an offset of 0.4 V, reduces the number of dyes in the TiO₂-based DSSC region to 2303 ABCBA (105 unique building blocks on the A site and 50 on the B site) and 803 ACA′ (97 unique building blocks) dyes. Not surprisingly, adding the offset also increases the minimum optical gap of the dyes to 2.50 (ABCBA) and 2.52 (ACA′) eV.

It is worth mentioning, that in addition to the properties we discuss, it is necessary for a dye to have an anchoring group through which to adsorb the dye onto the semiconductor surface.⁶⁷ While appropriate anchoring groups such as phosphonic acid or carboxylic acid have not been included in our screening, they are typically electronically benign with respect to the electronic and optical properties of the dyes themselves, and would not pose a problem in terms of our analysis. This assumption is supported by explicit calculations of the −IP, −EA and optical gap of a small number of dyes with anchoring groups (see Table S5†), which gave mean changes/mean absolute changes of −0.03/+0.19 in −IP, −0.18/+0.37 in −EA, and −0.10/+0.18 in the optical gap, upon inclusion of an anchoring group. A more advanced screening, which would also consider the kinetics of electron injection into the semiconductor by the dye, however, would probably require to include the building blocks with explicit anchoring groups in the screening.

Structure–property relationships

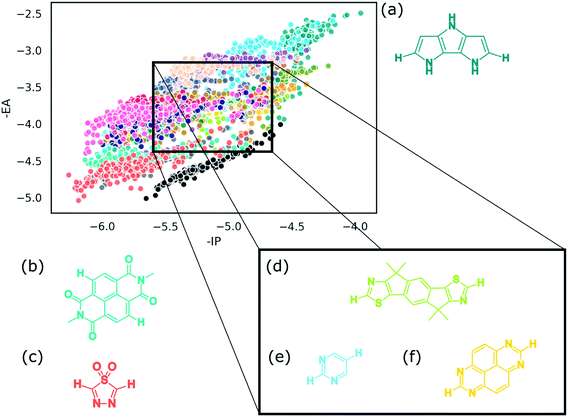
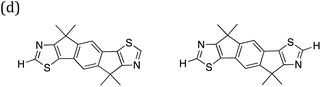
Identification of the dominant building blocks in particular regions of chemical space can give an idea of what combinations of chemical moieties lead to certain dye properties. Having gridded up a the plot of the −IP/−EA slice of property space of the ABCBA dyes (see Fig. 9) and determined which building blocks occur most often on the A and B sites we focus below on a few areas of interest: the extremities of the plot – the top right and bottom left corners, the middle sections and also the region that is relevant to the application of dyes in water-splitting.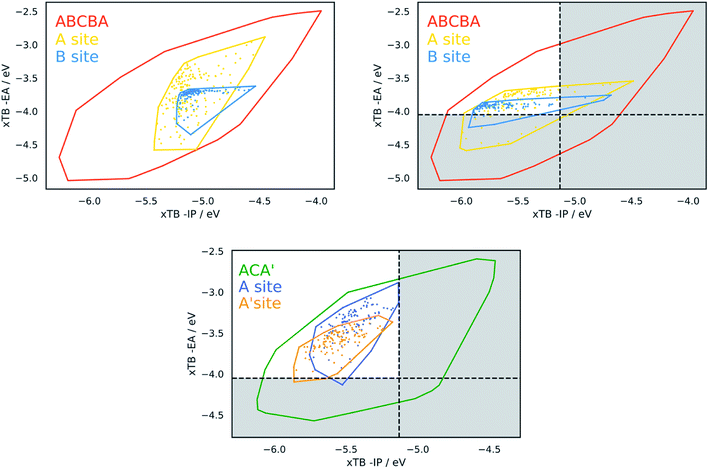

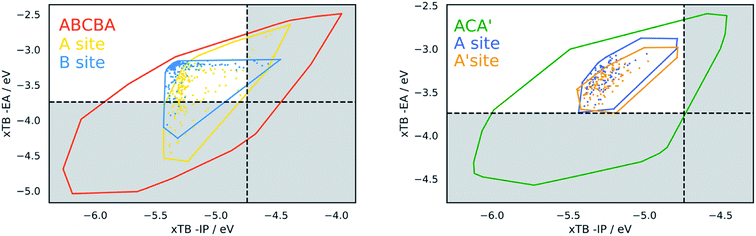
Fig. 9 Scatter plot showing the −IP/−EA slice of property space for the most common A and B units of the ABCBA dyes, when residing on the B-site. The building blocks shown are the most common A and B building blocks in (a) the top corner (−IP: ≥−4.8, −EA: ≥−3.3) (b) and (c) the bottom corner (−IP: <−6, −EA: <−4.3) and (d)–(f) the middle section of the grid (−IP: −6 to −4.8, −EA: −4.3 to −3.3). The colours of the building blocks matches of the corresponding points in the scatter plot (explicitly shown hydrogen atoms, other than those connected to nitrogen atoms, indicate carbon atoms where building blocks can be connected to other building blocks).

Top right corner. The top right section of the grid was taken to lie within the boundaries of −IP more positive or equal to −4.8 eV and −EA more positive than or equal to −3.3 eV. The fused-pyrrole building block shown in Fig. 9a (see also Table 2) is the most common building block on both the A and B site in this region containing 1529 dyes, occurring 73 times on the A site and 162 times on the B site. As there are 179 building blocks in the library this means 41% and 91% respectively of dyes with this building block on the A or B site, lie in this region. The implication of this is that the building block on the B site has greater control of the dye's overall properties. This observation is even more apparent upon inspection of the convex hulls in Fig. 10 and S15–S20† for building blocks on the A site (yellow) and on the B site (blue), in which the B convex hull is smaller, with the points more localised in the top right corner. This feature is even more pronounced in other regions of the −IP/−EA slice of property space. The nature of the building block itself, very electron rich, is in line with the shallow −IP and −EA of the resulting dyes.

Table 2 Most common building blocks on the A and B site within the regions of the −IP/−EA slice of property space of the ABCBA dyes discussed in the text. The labels (a)–(f) correspond to those used in Fig. 9 (explicitly shown hydrogen atoms, other than those connected to nitrogen atoms, indicate carbon atoms where building blocks can be connected to other building blocks in the dyes)

−IP/−EA limits (eV)	Dominant A building block	Dominant B building block
Top corner, −IP ≥ −4.8; −EA ≥ −3.3
Bottom corner, −IP < −6.0; −EA < −4.3
Middle region, −IP (−5.3, −4.8); −EA (−4.3, −3.3)
Middle region, −IP (−6, −5.3); −EA (−4.3, −3.3)

---

Fig. 10 Convex hulls for selected building blocks on the different sites in dyes. Top left, the building block shown in section (c) of Table 2 on the A site (yellow) and B site (blue) of ABCBA dyes. Top right. Building block (i) in Fig. 11(b) on the A site (yellow) and B site (blue) of ABCBA dyes. Bottom, the two most common building blocks in the proton reduction region for ACA′ dyes (blue = benzene, yellow = 1,6-naphthyridine). The unshaded regions on the right and bottom depict the −IP and −EA limits where proton reduction is thermodynamically feasible.

Bottom left corner. The limits for this region were −IP more negative or equal to −6 eV and −EA more negative or equal to −4.3 eV. In this region the most dominant building block on the A and B sites differ, as can be seen from Table 2. The most common A building block is shown in Fig. 9b and occurs 10 times on the A site and 33 times on the B site. The building block shown in Fig. 9c occurs most often on the B site in this region. Again, the latter occurred more often on the B site (34, 19%) than on the A site (8, 0.4%). The lower percentages of dyes with these building blocks occurring in this region relative to the case for the top right corner is in part the result of the fact that the bottom left corner region contains only 129 dyes in total. The very electron poor nature of the building blocks themselves is in line with the deep −IP and −EA of the resulting dyes.

Middle region. For this region, where −EA lies between −3.3 and −4.3 eV, two slices of the −IP range were taken, −5.3 to −4.8 eV and −6.0 to −5.3 eV (see Table 2). The most often occurring building blocks are shown above in Fig. 9d–f. For the first slice, containing 9926 dyes, the most common A and B, Fig. 9d occurs 140 times (84%) on the A site and 169 times (93%) on the B site and the latter occurring 147 times (82%) on the A site and 170 (95%) on the B site. Within the second −IP slice 6485 dyes reside of which the most common building block on the A site is shown in Fig. 9e, which occurs 89 times (50%) on the A site and 124 times (69%) on the B site. The most common B building block shown in Fig. 9f occurs 138 times (77%) on the B site and 87 times (49%) on the A site. As can be seen from the percentages most of the dyes containing these building blocks are found within this region. However, this is to be expected since such a large proportion of all the ABCBA dyes are contained in this region. The nature of the building blocks themselves, less electron rich than the most common building blocks for the top right corner and less electron poor than the most common building blocks in the bottom left corner, is in line with the properties of the resulting dyes.

Dye-sensitized proton-reduction and DSSC regions. Finally, we focus in on the −IP and −EA region relevant to dye-sensitized proton reduction and dye-sensitized solar cells using the experimental TiO₂ conduction band edge and solution potential values discussed above. These values translate into boundary values relative to vacuum of −IP more negative than −5.13 eV and −EA more positive than −4.14 eV for dye-sensitized proton reduction, and −IP more negative than −4.74 eV and −EA more positive than −3.74 eV in the case of TiO₂-based DSSCs.

Within this dye-sensitized proton reduction region lie 10 941 CHON dyes, with 118 unique building blocks in the A position and 113 in the B position. There are 6 dominant A building blocks and 5 dominant B building blocks (see Fig. 11) each occurring 105 and 116 times, respectively out of the 121 unique CHON building blocks in this truncated dataset. Two of these building blocks are both dominant on the A position and in the B site. In line with previous observations the most common building blocks for either the A or the B site occur a larger number of times on the B site – this is observed for every building block in Fig. 11. For example, building block (vi) in Fig. 11a occurs 105 times on the A site and 111 times on the B site. Building block (iii) in Fig. 11b occurs 103 times on the A site and 116 times on the B site. Even where the frequency of occurrence on the A site and B site are closest, for building block (iii) in Fig. 11a, 105 times on the A site and 109 times on the B site, qualitatively it can be seen that the convex hulls for the B site span a more compact region of the plot (see Fig. 10). Structurally, the most common building blocks in this region overlap with the most common building blocks found for the middle region discussed above (see Table 2(d)). This is perhaps not surprising as the regions also overlap. In line with what is observed for the middle region, at least one pyridinic nitrogen is present in these building blocks in almost all cases, making these all electron poor structures.

Fig. 11 Most common building blocks on (a) the A and (b) B sites for the ABCBA dyes in the dye-sensitized proton reduction region (explicitly shown hydrogen atoms, other than those connected to nitrogen atoms, indicate carbon atoms where building blocks can be connected to other building blocks in the dyes).

In the case of ACA′ dyes, the dye-sensitized proton reduction region contains 6526 dyes. Of the 121 building blocks considered, only 3 of these are not found in the ACA′ dyes in this region. The two most dominant building blocks for ACA′ dyes in the proton reduction region are benzene and 1,6-naphthyridine. The convex hulls for ACA′ dyes based on these two building blocks are also shown in Fig. 10 (labelled as A for benzene and A′ for 1,6-naphthyridine) and have a similar spread of data points.

In general, there appears to be a trend in which the B site on the ABCBA dyes has a greater influence on the overall properties of the dye. This can be inferred from (a) the convex hull plots, in which most of the time the A (yellow) convex hull spans a larger area than the B (blue) convex hull, (b) from the frequency of occurrence of a particular building block within the highlighted regions and (c) from the comparison of the scatter plots of all highest occurring building blocks per grid section on the A site and the B site; the plot of the latter shows the points more localised and separate from each other whereas in the analogous plot for the A position the points are much more spread out and less obviously split up from each other.

Within the DSSC region lie 8952 ABCBA CHON dyes, with 119 and 107 unique building blocks on the A site and B site, respectively. While there is one most common monomer on the A site, pyrrole, there are four dominant monomers on the B site (see Fig. 12). Pyrrole occurs 95 times on the A site and 99 times on the B site. Each of the dominant monomers on the B sites occurs 116 times on the B sites and, in line with our observations discussed above, in all cases fewer times on the A site. In terms of ACA′ dyes, there are 5812 CHON dyes in the DSSC region, containing a total of 119 unique building blocks out of the 121 possible CHON building. The two most common building blocks are 9H-carbozole and difuro[3,2-b:2′,3′-d]furan, the convex hulls of which are shown in Fig. 13 in yellow and blue, respectively, occupying very similar regions of chemical space.

Fig. 12 Most common building blocks on B sites for the ABCBA dyes in the dye-sensitized solar cell region (explicitly shown hydrogen atoms, other than those connected to nitrogen atoms, indicate carbon atoms where building blocks can be connected to other building blocks).

Fig. 13 Convex hulls for selected building blocks in the dye-sensitized solar cell region. Left, building block (i) in Fig. 12 occurring on the A (yellow) and B (blue) sites of ABCBA dyes in this region. Right, for the most common building blocks in the ACA′ CHON dyes in this region (yellow = 9H-carbozole, blue = difuro[3,2-b:2′,3′-d]furan). The unshaded regions depict the −IP and −EA limits where charge injection from the dye into the TiO₂ and oxidation of I⁻ to I₃⁻ is possible.

Conclusions

In this work, we have demonstrated the transferability of our previously developed (sTDA/IPEA-)xTB-based high-throughput virtual screening approach to dye structures. Although the use of IPEA-xTB, followed by calibration to DFT results, was non-problematic for −IP and −EA calibration, we encountered problems with the optical gap calculations using sTDA-xTB for a sub-set of sulfur containing dyes, where we found the optical gaps for such dyes calculated with sTDA-xTB relatively poorly correlated with those calculated by TD-DFT.

The property results post-calibration showed that the ABCBA, ACA and ACA′ families of dyes occupy the same region of property space, although the ABCBA dyes occupy a larger part of it. The properties of the dyes were found to be correlated with the properties of their constituent building blocks, as well as in the case of the ABCBA and ACA′ dyes with those of the simpler AACAA and ACA dyes. While we only consider DPP dyes, we hypothesize that similar correlations exist for dyes with other cores. We further found that a fraction of ACA′ dyes have an optical and/or fundamental gap that is smaller than their ACA/A′CA′ counterparts and that those dyes tend to have D–π–A character. We also demonstrate that a model originally developed for co-polymers, and which takes the −IP and −EA values of the ACA/A′CA′ dyes as input, successfully predicts which ACA′ dyes are likely to have smaller gaps than their ACA/A′CA′ counterparts.

Our analysis of the building blocks that most commonly occur in dyes in particular areas of property space revealed that the deepest −IPs and −EAs can be accessed by including electron poor building blocks in dyes, with the opposite being true for shallow −IPs and −EAs, as expected. We also observe that ABCBA dyes that share a common building block on the B position lie closer together in property space than dyes that share a common building block on the A position, indicating that the B building block is more influential in terms of the overall dye properties than the A building block. We speculate that the closer proximity of B to the core is the cause of this. Finally, in the regions of property space where proton reduction in the presence of ascorbic acid as a sacrificial electron donor is optically and thermodynamically possible, and where the dyes have the right −IP and −EA for dye-sensitized solar cells, slightly less than half of all ABCBA and ACA′ dyes are found. The most common building block on the B site for ABCBA dyes in the dye-sensitized proton reduction region all possess at least one pyridinic nitrogen, which are absent in the most common building blocks for ABCBA dyes suitable for use in dye-sensitized solar cells.

Author contributions

IHA and DVO performed the calculations. LW, IHA and MAZ conceived the study. MAZ supervised the work. IHA, LW, KEJ and MAZ contributed to the preparation of the manuscript. All authors have approved the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The UK Engineering and Physical Sciences Research Council (EPSRC) is kindly acknowledged for funding (EP/N004884/1). KEJ acknowledges the Royal Society for a University Research Fellowship and the ERC through grant agreement number 758370 (ERC-StG-PE5-CoMMaD) for funding. D.V.O acknowledges the CDT in Theory and Simulation of Materials at Imperial College, funded through EPSRC grant EP/L015579/1, for a summer studentship. Dr Michal Kochman is acknowledged for his help with the LRC-TD-TB-DFT calculations.

References

1. D. G. Farnum, G. Mehta, G. G. I. Moore and F. P. Siegal, Attempted Reformatskii Reaction of Benzonitrile, 1,4-Diketo-3,6-Diphenylpyrrolo[3,4-C]Pyrrole. A Lactam Analogue of Pentalene, Tetrahedron Lett., 1974, 15(29), 2549–2552,  DOI:10.1016/S0040-4039(01)93202-2.
2. E. D. Głowacki, H. Coskun, M. A. Blood-Forsythe, U. Monkowius, L. Leonat, M. Grzybowski, D. Gryko, M. S. White, A. Aspuru-Guzik and N. S. Sariciftci, Hydrogen-Bonded Diketopyrrolopyrrole (DPP) Pigments as Organic Semiconductors, Org. Electron. Phys. Mater. Appl, 2014, 15(12), 3521–3528,  DOI:10.1016/j.orgel.2014.09.038.
3. J. Seixas De Melo, A. P. Moura and M. J. Melo, Photophysical and Spectroscopic Studies of Indigo Derivatives in Their Keto and Leuco Forms, J. Phys. Chem. A, 2004, 108(34), 6975–6981,  DOI:10.1021/jp049076y.
4. K. R. Justin Thomas, J. T. Lin, Y. C. Hsu and K. C. Ho, Organic Dyes Containing Thienylfluorene Conjugation for Solar Cells, Chem. Commun., 2005,(32), 4098–4100,  10.1039/b506732d.
5. S. L. Li, K. J. Jiang, K. F. Shao and L. M. Yang, Novel Organic Dyes for Efficient Dye-Sensitized Solar Cells, Chem. Commun., 2006, 2(26), 2792–2794,  10.1039/b603706b.
6. H. Tian, X. Yang, R. Chen, Y. Pan, L. Li, A. Hagfeldt and L. Sun, Phenothiazine Derivatives for Efficient Organic Dye-Sensitized Solar Cells, Chem. Commun., 2007,(36), 3741–3743,  10.1039/b707485a.
7. P. Qin, H. Zhu, T. Edvinsson, G. Boschloo, A. Hagfeldt and L. Sun, Design of an Organic Chromophore for P-Type Dye-Sensitized Solar Cells, J. Am. Chem. Soc., 2008, 130(27), 8570–8571,  DOI:10.1021/ja8001474.
8. F. Guo, S. Qu, W. Wu, J. Li, W. Ying and J. Hua, Synthesis and Photovoltaic Performance of New Diketopyrrolopyrrole (DPP) Dyes for Dye-Sensitized Solar Cells, Synth. Met., 2010, 160(15–16), 1767–1773,  DOI:10.1016/j.synthmet.2010.06.017.
9. L. Le Pleux, A. L. Smeigh, E. Gibson, Y. Pellegrin, E. Blart, G. Boschloo, A. Hagfeldt, L. Hammarström and F. Odobel, Synthesis, Photophysical and Photovoltaic Investigations of Acceptor-Functionalized Perylene Monoimide Dyes for Nickel Oxide p-Type Dye-Sensitized Solar Cells, Energy Environ. Sci., 2011, 4(6), 2075–2084,  10.1039/c1ee01148k.
10. E. Kozma, I. Concina, A. Braga, L. Borgese, L. E. Depero, A. Vomiero, G. Sberveglieri and M. Catellani, Metal-Free Organic Sensitizers with a Sterically Hindered Thiophene Unit for Efficient Dye-Sensitized Solar Cells, J. Mater. Chem., 2011, 21(36), 13785–13788,  10.1039/c1jm12181b.
11. S. Qu, B. Wang, F. Guo, J. Li, W. Wu, C. Kong, Y. Long and J. Hua, New Diketo-Pyrrolo-Pyrrole (DPP) Sensitizer Containing a Furan Moiety for Efficient and Stable Dye-Sensitized Solar Cells, Dyes Pigm., 2012, 92(3), 1384–1393,  DOI:10.1016/j.dyepig.2011.09.009.
12. J. Warnan, J. Gardner, L. Le Pleux, J. Petersson, Y. Pellegrin, E. Blart, L. Hammarström and F. Odobel, Multichromophoric Sensitizers Based on Squaraine for NiO Based Dye-Sensitized Solar Cells, J. Phys. Chem. C, 2014, 118(1), 103–113,  DOI:10.1021/jp408900x.
13. J. F. Lefebvre, X. Z. Sun, J. A. Calladine, M. W. George and E. A. Gibson, Promoting Charge-Separation in p-Type Dye-Sensitized Solar Cells Using Bodipy, Chem. Commun., 2014, 50(40), 5258–5260,  10.1039/c3cc46133e.
14. D. Joly, L. Pellejà, S. Narbey, F. Oswald, J. Chiron, J. N. Clifford, E. Palomares and R. Demadrille, A Robust Organic Dye for Dye Sensitized Solar Cells Based on Iodine/Iodide Electrolytes Combining High Efficiency and Outstanding Stability, Sci. Rep., 2014, 4, 1–7,  DOI:10.1038/srep04033.
15. G. Pepe, J. M. Cole, P. G. Waddell and S. McKechnie, Molecular Engineering of Cyanine Dyes to Design a Panchromatic Response in Co-Sensitized Dye-Sensitized Solar Cells, Mol. Syst. Des. Eng., 2016, 1(1), 86–98,  10.1039/c6me00014b.
16. G. S. Selopal, H. P. Wu, J. Lu, Y. C. Chang, M. Wang, A. Vomiero, I. Concina and E. W. G. Diau, Metal-Free Organic Dyes for TiO2 and ZnO Dye-Sensitized Solar Cells, Sci. Rep., 2016, 6(January), 1–12,  DOI:10.1038/srep18756.
17. G. Pepe, J. M. Cole, P. G. Waddell and J. R. D. Griffiths, Molecular Engineering of Fluorescein Dyes as Complementary Absorbers in Dye Co-Sensitized Solar Cells, Mol. Syst. Des. Eng., 2016, 1(4), 402–415,  10.1039/c6me00075d.
18. Y. Farré, M. Raissi, A. Fihey, Y. Pellegrin, E. Blart, D. Jacquemin and F. Odobel, A Blue Diketopyrrolopyrrole Sensitizer with High Efficiency in Nickel-Oxide-Based Dye-Sensitized Solar Cells, ChemSusChem, 2017, 10(12), 2618–2625,  DOI:10.1002/cssc.201700468.
19. Z. Yang, C. Liu, K. Li, J. M. Cole, C. Shao and D. Cao, Rational Design of Dithienopicenocarbazole-Based Dyes and a Prediction of Their Energy-Conversion Efficiency Characteristics for Dye-Sensitized Solar Cells, ACS Appl. Energy Mater., 2018, 1(4), 1435–1444,  DOI:10.1021/acsaem.7b00154.
20. J. M. Ji, H. Zhou and H. K. Kim, Rational Design Criteria for D-π-A Structured Organic and Porphyrin Sensitizers for Highly Efficient Dye-Sensitized Solar Cells, J. Mater. Chem. A, 2018, 6(30), 14518–14545,  10.1039/c8ta02281j.
21. F. Li, K. Fan, B. Xu, E. Gabrielsson, Q. Daniel, L. Li and L. Sun, Organic Dye-Sensitized Tandem Photoelectrochemical Cell for Light Driven Total Water Splitting, J. Am. Chem. Soc., 2015, 137(28), 9153–9159,  DOI:10.1021/jacs.5b04856.
22. H. C. Chen, R. M. Williams, J. N. H. Reek and A. M. Brouwer, Robust Benzo[g, h, i ]Perylenetriimide Dye-Sensitized Electrodes in Air-Saturated Aqueous Buffer Solution, Chem.–Eur. J., 2016, 22(16), 5489–5493,  DOI:10.1002/chem.201505146.
23. B. Van Den Bosch, J. A. Rombouts, R. V. A. Orru, J. N. H. Reek and R. J. Detz, Nickel-Based Dye-Sensitized Photocathode: Towards Proton Reduction Using a Molecular Nickel Catalyst and an Organic Dye, ChemCatChem, 2016, 8(7), 1392–1398,  DOI:10.1002/cctc.201600025.
24. E. A. Gibson, Dye-Sensitized Photocathodes for H2 Evolution, Chem. Soc. Rev., 2017, 46(20), 6194–6209,  10.1039/c7cs00322f.
25. J. Warnan, J. Willkomm, J. N. Ng, R. Godin, S. Prantl, J. R. Durrant and E. Reisner, Solar H2 Evolution in Water with Modified Diketopyrrolopyrrole Dyes Immobilised on Molecular Co and Ni Catalyst-TiO2 Hybrids, Chem. Sci., 2017, 8(4), 3070–3079,  10.1039/c6sc05219c.
26. D. L. Ashford, M. K. Gish, A. K. Vannucci, M. K. Brennaman, J. L. Templeton, J. M. Papanikolas and T. J. Meyer, Molecular Chromophore–Catalyst Assemblies for Solar Fuel Applications, Chem. Rev., 2015, 115(23), 13006–13049,  DOI:10.1021/acs.chemrev.5b00229.
27. E. D. Głowacki, G. Voss, L. Leonat, M. Irimia-Vladu, S. Bauer and N. S. Sariciftci, Indigo and Tyrian Purple - From Ancient Natural Dyes to Modern Organic Semiconductors, Isr. J. Chem., 2012, 52(6), 540–551,  DOI:10.1002/ijch.201100130.
28. M. Irimia-Vladu, E. D. Gåowacki, P. A. Troshin, G. Schwabegger, L. Leonat, D. K. Susarova, O. Krystal, M. Ullah, Y. Kanbur and M. A. Bodea, et al., Indigo - A Natural Pigment for High Performance Ambipolar Organic Field Effect Transistors and Circuits, Adv. Mater., 2012, 24(3), 375–380,  DOI:10.1002/adma.201102619.
29. Q. Liu, S. E. Bottle and P. Sonar, Developments of Diketopyrrolopyrrole-Dye-Based Organic Semiconductors for a Wide Range of Applications in Electronics, Adv. Mater., 2020, 32(4), 1–46,  DOI:10.1002/adma.201903882.
30. S. W. Eaton, S. A. Miller, E. A. Margulies, L. E. Shoer, R. D. Schaller and M. R. Wasielewski, Singlet Exciton Fission in Thin Films of Tert -Butyl-Substituted Terrylenes, J. Phys. Chem. A, 2015, 119(18), 4151–4161,  DOI:10.1021/acs.jpca.5b02719.
31. E. A. Margulies, C. E. Miller, Y. Wu, L. Ma, G. C. Schatz, R. M. Young and M. R. Wasielewski, Enabling Singlet Fission by Controlling Intramolecular Charge Transfer in π-Stacked Covalent Terrylenediimide Dimers, Nat. Chem., 2016, 8(12), 1120–1125,  DOI:10.1038/nchem.2589.
32. A. K. Le, J. A. Bender and S. T. Roberts, Slow Singlet Fission Observed in a Polycrystalline Perylenediimide Thin Film, J. Phys. Chem. Lett., 2016, 7(23), 4922–4928,  DOI:10.1021/acs.jpclett.6b02320.
33. K. J. Fallon, P. Budden, E. Salvadori, A. M. Ganose, C. N. Savory, L. Eyre, S. Dowland, Q. Ai, S. Goodlett and C. Risko, et al., Exploiting Excited-State Aromaticity to Design Highly Stable Siglet Fission Materials, J. Am. Chem. Soc., 2019, 141(35), 13867–13876,  DOI:10.1021/jacs.9b06346.
34. A. Hagfeldt, G. Boschloo, L. Sun, L. Kloo and H. Pettersson, Dye-Sensitized Solar Cells, Chem. Rev., 2010, 110(11), 6595–6663,  DOI:10.1021/cr900356p.
35. S. Grimme, C. Bannwarth and P. Shushkov, A Robust and Accurate Tight-Binding Quantum Chemical Method for Structures, Vibrational Frequencies, and Noncovalent Interactions of Large Molecular Systems Parametrized for All Spd-Block Elements (Z = 1–86), J. Chem. Theory Comput., 2017, 13(5), 1989–2009,  DOI:10.1021/acs.jctc.7b00118.
36. V. Ásgeirsson, C. A. Bauer and S. Grimme, Quantum Chemical Calculation of Electron Ionization Mass Spectra for General Organic and Inorganic Molecules, Chem. Sci., 2017, 8(7), 4879–4895,  10.1039/c7sc00601b.
37. S. Grimme and C. Bannwarth, Ultra-Fast Computation of Electronic Spectra for Large Systems by Tight-Binding Based Simplified Tamm-Dancoff Approximation (STDA-XTB), J. Chem. Phys., 2016, 145(5), 054103,  DOI:10.1063/1.4959605.
38. L. Wilbraham, R. S. Sprick, K. E. Jelfs and M. A. Zwijnenburg, Mapping Binary Copolymer Property Space with Neural Networks, Chem. Sci., 2019, 10(19), 4973–4984,  10.1039/c8sc05710a.
39. C. Zhao, Y. Guo, Y. Zhang, N. Yan, S. You and W. Li, Diketopyrrolopyrrole-Based Conjugated Materials for Non-Fullerene Organic Solar Cells, J. Mater. Chem. A, 2019, 7(17), 10174–10199,  10.1039/c9ta01976f.
40. L. Turcani, E. Berardo and K. E. Jelfs, Stk: A Python Toolkit for Supramolecular Assembly, J. Comput. Chem., 2018, 39(23), 1931–1942,  DOI:10.1002/jcc.25377.
41. Supramolecular-toolkit, https://github.com/supramolecular-toolkit/stk, accessed Oct 30, 2018.
42. The RDKit Documentation, http://www.rdkit.org/docs/, accessed Oct 30, 2018.
43. S. Riniker and G. A. Landrum, Better Informed Distance Geometry: Using What We Know to Improve Conformation Generation, J. Chem. Inf. Model., 2015, 55(12), 2562–2574,  DOI:10.1021/acs.jcim.5b00654.
44. T. A. Halgren, Merck Molecular Force Field. I. Basis, Form, Scope, Parameterization, and Performance of MMFF94, J. Comput. Chem., 1996, 17(5–6), 490–519,  DOI:10.1002/(SICI)1096-987X(199604)17:5/6<490::AID-JCC1>3.0.CO;2-P.
45. C. Bannwarth and S. Grimme, A Simplified Time-Dependent Density Functional Theory Approach for Electronic Ultraviolet and Circular Dichroism Spectra of Very Large Molecules, Comput. Theor. Chem., 2014, 1040–1041, 45–53,  DOI:10.1016/j.comptc.2014.02.023.
46. xtb - An extended tight-binding semi-empirical program package, https://www.chemie.uni-bonn.de/pctc/mulliken-center/software/xtb/xtb, accessed Oct 30, 2018.
47. sTDA - A simplified Tamm-Dancoff density functional approach for electronic excitation spectra, https://www.chemie.uni-bonn.de/pctc/mulliken-center/software/stda/stda, accessed Oct 30, 2018.
48. A. Humeniuk and R. Mitrić, DFTBaby: A Software Package for Non-Adiabatic Molecular Dynamics Simulations Based on Long-Range Corrected Tight-Binding TD-DFT(B), Comput. Phys. Commun., 2017, 221, 174–202,  DOI:10.1016/j.cpc.2017.08.012.
49. S. H. Vosko, L. Wilk and M. Nusair, Accurate Spin-Dependent Electron Liquid Correlation Energies for Local Spin Density Calculations: A Critical Analysis, Can. J. Phys., 1980, 58(8), 1200–1211,  DOI:10.1139/p80-159.
50. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37(2), 785–789,  DOI:10.1103/PhysRevB.37.785.
51. A. D. Becke, Density-Functional Thermochemistry. III. The Role of Exact Exchange, J. Chem. Phys., 1993, 98(7), 5648–5652,  DOI:10.1063/1.464913.
52. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields, J. Phys. Chem., 1994, 98(45), 11623–11627,  DOI:10.1021/j100096a001.
53. J. D. Chai and M. Head-Gordon, Systematic Optimization of Long-Range Corrected Hybrid Density Functionals, J. Chem. Phys., 2008, 128(8), 084106,  DOI:10.1063/1.2834918.
54. M. J. G. Peach, P. Benfield, T. Helgaker and D. J. Tozer, Excitation Energies in Density Functional Theory: An Evaluation and a Diagnostic Test, J. Chem. Phys., 2008, 128(4), 044118,  DOI:10.1063/1.2831900.
55. D. Jacquemin, B. Moore, A. Planchat, C. Adamo and J. Autschbach, Performance of an Optimally Tuned Range-Separated Hybrid Functional for 0-0 Electronic Excitation Energies, J. Chem. Theory Comput., 2014, 10(4), 1677–1685,  DOI:10.1021/ct5000617.
56. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, et al., Gaussian 16 Revision C.01, 2016.
57. L. Wilbraham, E. Berardo, L. Turcani, K. Jelfs and M. Zwijnenburg, A High-Throughput Screening Approach for the Optoelectronic Properties of Conjugated Polymers, J. Chem. Inf. Model., 2018, 58(12), 2450–2459,  DOI:10.1021/acs.jcim.8b00256.
58. L. Wilbraham, D. Smajli, I. Heath-Apostolopoulos and M. A. Zwijnenburg, Mapping the Optoelectronic Property Space of Small Aromatic Molecules, Commun. Chem., 2020, 3(1), 1–9,  DOI:10.1038/s42004-020-0256-7.
59. P. Guiglion, C. Butchosa and M. A. Zwijnenburg, Polymeric Watersplitting Photocatalysts; a Computational Perspective on the Water Oxidation Conundrum, J. Mater. Chem. A, 2014, 2(30), 11996–12004,  10.1039/C4TA02044H.
60. R. S. Sprick, C. M. Aitchison, E. Berardo, L. Turcani, L. Wilbraham, B. M. Alston, K. E. Jelfs, M. A. Zwijnenburg and A. I. Cooper, Maximising the Hydrogen Evolution Activity in Organic Photocatalysts by Co-Polymerisation, J. Mater. Chem. A, 2018, 6(25), 11994–12003,  10.1039/c8ta04186e.
61. R. S. Sprick, L. Wilbraham, Y. Bai, P. Guiglion, A. Monti, R. Clowes, A. I. Cooper and M. A. Zwijnenburg, Nitrogen Containing Linear Poly(Phenylene) Derivatives for Photo-Catalytic Hydrogen Evolution from Water, Chem. Mater., 2018, 30, 5733–5742,  DOI:10.1021/acs.chemmater.8b02501.
62. D. H. Macartney and N. Sutin, The Oxidation of Ascorbic Acid by Tris(2,2′-Bipyridine) Complexes of Osmium(III), Ruthenium(III) and Nickel(III) in Aqueous Media: Applications of the Marcus Cross-Relation, Inorg. Chim. Acta, 1983, 74(C), 221–228,  DOI:10.1016/S0020-1693(00)81430-9.
63. X. Wang, L. Chen, S. Y. Chong, M. A. Little, Y. Wu, W.-H. Zhu, R. Clowes, Y. Yan, M. A. Zwijnenburg and R. S. Sprick, et al., Sulfone-Containing Covalent Organic Frameworks for Photocatalytic Hydrogen Evolution from Water, Nat. Chem., 2018, 10(12), 1180–1189,  DOI:10.1038/s41557-018-0141-5.
64. M. Grätzel, Photoelectrochemical Cells, Nature, 2001, 414(6861), 338–344,  DOI:10.1038/35104607.
65. G. Redmond and D. Fitzmaurice, Spectroscopic Determination of Flatband Potentials for Polycrystalline TiO2 Electrodes in Nonaqueous Solvents, J. Phys. Chem., 1993, 97(7), 1426–1430,  DOI:10.1021/j100109a029.
66. G. Boschloo and A. Hagfeldt, Characteristics of the Iodide/Triiodide Redox Mediator in Dye-Sensitized Solar Cells, Acc. Chem. Res., 2009, 42(11), 1819–1826,  DOI:10.1021/ar900138m.
67. L. Zhang and J. M. Cole, Anchoring Groups for Dye-Sensitized Solar Cells, ACS Appl. Mater. Interfaces, 2015, 7(6), 3427–3455,  DOI:10.1021/am507334m.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0se00985g

---