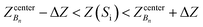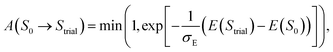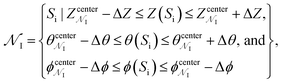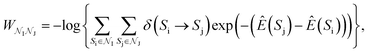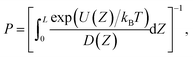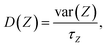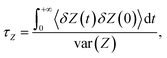Open Access Article
Open Access ArticleRationalizing the generation of broad spectrum antibiotics with the addition of a positive charge†
Nandan
Haloi‡
 a,
Archit Kumar
Vasan‡
a,
Emily J.
Geddes
bc,
Arjun
Prasanna
cd,
Po-Chao
Wen
a,
Archit Kumar
Vasan‡
a,
Emily J.
Geddes
bc,
Arjun
Prasanna
cd,
Po-Chao
Wen
 a,
William W.
Metcalf
cd,
Paul J.
Hergenrother
a,
William W.
Metcalf
cd,
Paul J.
Hergenrother
 bc and
Emad
Tajkhorshid
bc and
Emad
Tajkhorshid
 *a
*a
aTheoretical and Computational Biophysics Group, NIH Center for Macromolecular Modeling and Bioinformatics, Beckman Institute for Advanced Science and Technology, Department of Biochemistry, Center for Biophysics and Quantitative Biology, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA. E-mail: emad@illinois.edu
bDepartment of Chemistry, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA
cCarl R. Woese Institute for Genomic Biology, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA
dDepartment of Microbiology, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA
First published on 14th October 2021
Abstract
Antibiotic resistance of Gram-negative bacteria is largely attributed to the low permeability of their outer membrane (OM). Recently, we disclosed the eNTRy rules, a key lesson of which is that the introduction of a primary amine enhances OM permeation in certain contexts. To understand the molecular basis for this finding, we perform an extensive set of molecular dynamics (MD) simulations and free energy calculations comparing the permeation of aminated and amine-free antibiotic derivatives through the most abundant OM porin of E. coli, OmpF. To improve sampling of conformationally flexible drugs in MD simulations, we developed a novel, Monte Carlo and graph theory based algorithm to probe more efficiently the rotational and translational degrees of freedom visited during the permeation of the antibiotic molecule through OmpF. The resulting pathways were then used for free-energy calculations, revealing a lower barrier against the permeation of the aminated compound, substantiating its greater OM permeability. Further analysis revealed that the amine facilitates permeation by enabling the antibiotic to align its dipole to the luminal electric field of the porin and form favorable electrostatic interactions with specific, highly-conserved charged residues. The importance of these interactions in permeation was further validated with experimental mutagenesis and whole cell accumulation assays. Overall, this study provides insights on the importance of the primary amine for antibiotic permeation into Gram-negative pathogens that could help the design of future antibiotics. We also offer a new computational approach for calculating free-energy of processes where relevant molecular conformations cannot be efficiently captured.
Introduction
Gram-negative bacteria are becoming increasingly resistant to available antibiotics, and the development of new antibiotics targeting these bacteria has been slow.1,2 A major difficulty is designing antibiotics that can readily permeate the dense outer membrane (OM) of Gram-negative bacteria.3,4 Due to the impermeability of the OM, effective antibiotics typically permeate through OM porins, which have evolved to allow diffusion of various substrates necessary for bacterial survival.3,4 Limited knowledge on physicochemical properties that enable permeation of antibiotics through the OM porins, however, has severely hindered the development of new antibiotics for several decades.5,6 Without an understanding of these properties to motivate intelligent antibiotic design, even an expansive screening of millions of compounds typically does not provide advanceable lead compounds.7 Recently, we were able to identify general determinants for antibiotic permeation by directly measuring the accumulation in E. coli for a collection of hundreds of diverse compounds.8 These determinants, coined as the eNTRy rules,9 were low flexibility, low globularity, and the presence of an ionizable nitrogen, typically a primary amine.The eNTRy rules provide guidelines for a drug development framework to convert Gram-positive only antibiotics to broad spectrum antibiotics through the addition of a primary amine to compounds meeting the flexibility and globularity parameters.8 This approach was used to convert 6-deoxynybomycin (6DNM),10 a natural product derivative exclusively active against Gram-positive bacteria, into an antibiotic also effective against Gram-negative pathogens by appending an amino methyl group (6DNM-NH3)8 (Fig. 1A). Compared to 6DNM, 6DNM-NH3 shows significantly enhanced accumulation in E. coli and a 64-fold increase in antibacterial activity.8 More importantly, 6DNM-NH3 has antibacterial activity against a diverse panel of multidrug resistant Gram-negative pathogens such as A. baumannii, K. pneumonia and E. cloacae.8 This same approach has been used to expand the activity of additional Gram-positive only antibiotics,11–18 including Debio-1452 and Ribocil C, into Gram-negative active derivatives, Debio-1452-NH3 and Ribocil C-PA.11,12
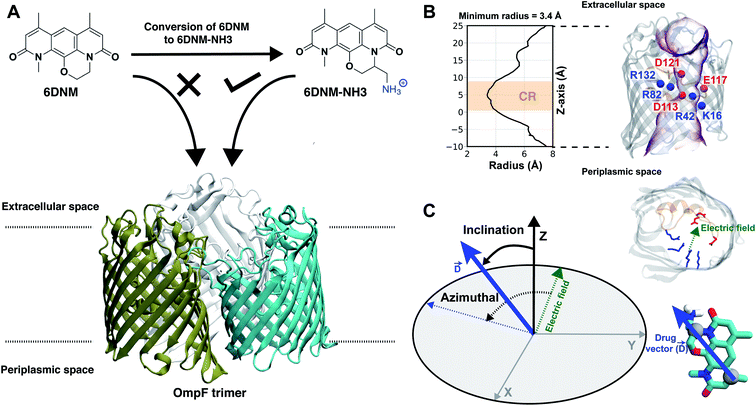 | ||
Fig. 1 Selective permeability of antibiotics across the E. coli porin, OmpF. (A) The conversion of 6DNM to 6DNM-NH3 by introducing a primary amine enhances permeation of the compound through OmpF (each monomer colored differently).8 (B, top, left) The radius profile (calculated using HOLE39) of the crystal structure of an OmpF monomer along the membrane normal (Z-axis) relative to the membrane center of mass (C. O. M). The constriction region (CR), defined based on a pore radius <4 Å, is highlighted in orange. The CR spans z-coordinates from 1 to 8 Å. (B, top, right) Side view of an OmpF monomer, highlighting internal loop L3 in orange and the Cα atoms of acidic and basic residues within the CR in red and blue, respectively. Purple surface depicts the pore radius profile of OmpF, calculated with the program HOLE.39 (B, bottom, right) Top-down view of OmpF, depicting the electric field vector (in green dotted arrow), projected onto the membrane plane (XY), generated due to the arrangement of the charged CR residues. The electric field was evaluated using the dipole of all the water molecules within the CR (in 100 ns of equilibrium MD simulation of membrane-embedded OmpF), following a previously described protocol.25 (C) Representation of the orientation of 6DNM-NH3 in spherical coordinates. To calculate the orientation angles, a drug vector 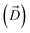 is defined between two carbon atoms (gray spheres), such that the vector points towards the primary amine group. The inclination (θ) is the angle between is defined between two carbon atoms (gray spheres), such that the vector points towards the primary amine group. The inclination (θ) is the angle between 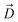 and the membrane normal (Z-axis); ϕ is the angle between the projections of and the membrane normal (Z-axis); ϕ is the angle between the projections of 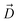 and the electric field vector onto the XY plane. The vector for 6DNM is defined using the same two carbon atoms and the angles are calculated using the same manner. and the electric field vector onto the XY plane. The vector for 6DNM is defined using the same two carbon atoms and the angles are calculated using the same manner. | ||
The major proteins responsible for permeating 6DNM-NH3 through the OM of E. coli were identified through porin-knockout studies of two trimeric general diffusion β-barrel OM porins: outer membrane porin F (OmpF) and OmpC.8 In this study, we use OmpF as a model system to investigate how appending a primary amine to 6DNM can significantly enhance its permeation through the OM of E. coli using molecular dynamics (MD) simulations and free energy calculations.
The main determinant for the enhanced permeation of 6DNM-NH3 is most likely the favorable interaction of the antibiotic with the porin, especially within the constriction region (CR, Fig. 1B),19 a significantly narrowed location within the pore that acts as a bottleneck for antibiotic permeation.20–31 Additionally, the CR contains many charged residues including ladders of acidic and basic residues on the L3 loop (a long, internally folded loop) and on the inner barrel wall (Fig. 1B), respectively; these residues have been suggested to interact with antibiotics to influence permeation in previous MD simulation and experimental mutagenesis studies.20–30,32–35 The arrangement of these charged residues generates a transverse electric field across the CR (Fig. 1C), and alignment of the dipole of antibiotics with this electric field has been suggested to aid in crossing the CR.24,25,29,36–38
Despite previous MD simulation studies of antibiotic permeation through OmpF,20–30,32–35,37,38 a direct comparison between aminated and amine-free antibiotics and the mechanisms by which the primary amine group aids permeation are lacking. While our previous steered molecular dynamics (SMD) simulations of 6DNM-NH3 translocation through OmpF suggested that addition of the amine group enables interactions with the negatively charged residues of the porin, potentially assisting passage of the antibiotic,8 due to the non-equilibrium nature of SMD and the limited simulation timescale, the findings from these simulations were limited, not allowing for a quantitative description of the process. Therefore, to more comprehensively characterize the molecular mechanisms facilitating permeation of aminated antibiotics, we determined the free-energy landscape associated with translocation of 6DNM and 6DNM-NH3 through OmpF using MD simulations. Calculating these free energies, however, was challenging, because adequately sampling multiple conformations of the drug in the permeation processes using equilibrium or conventional enhanced sampling MD simulations is still computationally intractable. To overcome this challenge, we developed a novel, computationally efficient algorithm, combining Monte Carlo and graph theory, to more efficiently probe the high dimensional permeation pathways of the two antibiotics through OmpF. The resulting pathways were then used for one dimensional bias exchange umbrella sampling (1D-BEUS) simulations.
From 1D-BEUS simulations, we evaluated the free-energy of permeation for 6DNM-NH3 and 6DNM which reveals a lower energetic barrier and greater permeability for the aminated antibiotic through OmpF, in accord with our previous experiments.8 Further analysis revealed that the amine facilitates permeation by enabling 6DNM-NH3 to align its dipole to the luminal electric field of the porin and by forming favorable electrostatic interactions with charged residues while hopping along the pore. The importance of these key interactions in permeation of 6DNM-NH3 was further validated by experimental mutagenesis and whole-cell accumulation assays.
Methods
Computational methods
Here we first provide an overview of our computational approach to obtain free energy landscapes of antibiotic permeation. In principle, free energies can be evaluated from equilibrium MD trajectory data by measuring the probability of the antibiotic along the pore (Z) axis. However, drug permeation occurs on timescales40 that may not be sampled sufficiently using equilibrium MD simulations. Therefore, it is necessary to adopt a more rigorous enhanced sampling method such as bias-exchange umbrella sampling (BEUS),41–45 metadynamics,46 or adaptive biasing force.47 Theoretically, these methods can enhance sampling of all relevant slow degrees of freedoms (DOFs), i.e., those DOFs that cannot be sufficiently sampled by equilibrium MD. However, in practice, multi-dimensional enhanced sampling simulations are computationally prohibitive, and reaching convergence is challenging.34,35,45,48–50 Typically, in an enhanced-sampling simulation, a bias is applied only along the most relevant slow DOF, with the assumption that other orthogonal slow DOFs will be properly sampled during the simulation. A break in this assumption is especially apparent when studying antibiotic permeation through porins. Enhanced sampling methods typically only bias the translational coordinate of the antibiotic along the pore axis (Z);34,35 however, this does not allow sufficient sampling of other orthogonal slow DOFs, e.g., the drug orientation, since the narrow CR of these porins restricts reorientation. Insufficient sampling of other slow DOFs would provide an incomplete picture of the drug permeation process. Our approach to account for multiple slow DOFs is to use a heuristic algorithm to exhaustively sample the high dimensional conformational space and then use this sampling to determine an optimal initial pathway. This pathway will then serve to generate seeds for one dimensional BEUS (1D-BEUS) simulations. As 1D-BEUS does not exhaustively sample orthogonal slow DOFs, having a proper initial pathway will ensure that the energetics we derive are physically meaningful. A simple approach to generate such an optimal initial pathway is to perform multiple independent steered MD (SMD) simulations and use the lowest nonequilibrium work run.44,45 However, unless a very large number of SMD runs are performed, conformational space will be still insufficiently sampled and the resulting pathway will be based on an incomplete data set.To address this issue we developed a step-wise approach: (1) create a dataset of discrete poses of the antibiotic by exhaustively exploring the translational and rotational DOFs within the porin using a grid-based workflow;51 (2) use this dataset to determine multiple energetically favorable permeation trajectories from extracellular to periplasmic space using our novel Monte Carlo based pathway search (MCPS) algorithm; (3) determine the most likely permeation pathway sampled in our MCPS trajectories using Dijkstra's algorithm; and (4) use this most likely pathway to determine energetics of the permeation process using BEUS.41–45 Details of these steps are discussed in the following sections.
Creation of a dataset with discrete antibiotic poses
A workflow (Fig. 2A), similar to the one developed by us previously,51 was designed to exhaustively explore the translational and rotational DOFs of 6DNM and 6DNM-NH3, independently, within the pore of the crystal structure of OmpF (PDB ID: 3POX).52 To improve the computational efficiency of our approach, each pose was generated in vacuum and with monomeric OmpF; however, once the optimal initial pathway is obtained, we refine it using 1D-BEUS in a more realistic, fully solvated membrane-embedded protein–drug system with trimeric OmpF (see below). We will describe this workflow using 6DNM-NH3 as an example; the same procedure was used for 6DNM.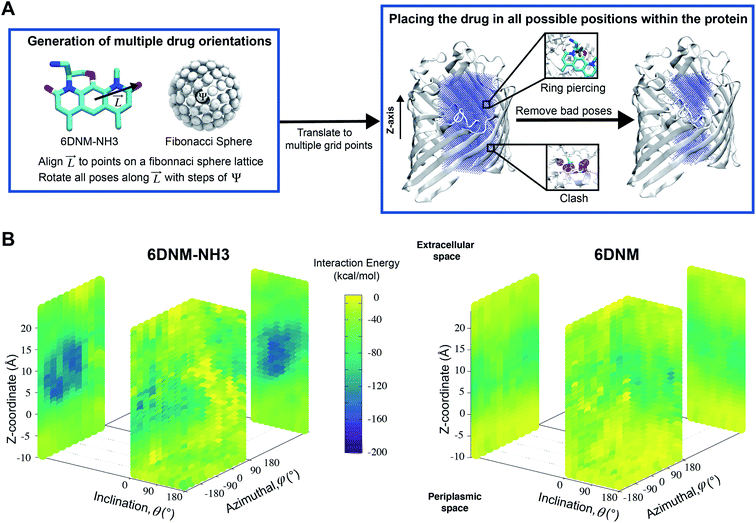 | ||
Fig. 2 A workflow to create a dataset of discrete antibiotic poses by exhaustively exploring the translational and rotational DOFs within the pore of an OM porin and to evaluate the antibiotic–protein interaction energy (IE) for each pose. (A, left) A set of poses of 6DNM-NH3 with multiple antibiotic orientations was generated by mapping the antibiotic along its longest axis from its C. O. M. 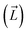 onto a Fibonacci spherical lattice (FSL).58 Each of the generated antibiotic poses was further rotated along onto a Fibonacci spherical lattice (FSL).58 Each of the generated antibiotic poses was further rotated along 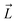 , with an interval of Ψ. (A, right) The set of 6DNM-NH3 orientations was placed at every point of a 3-dimensional rectangular grid. During this placement, poses with clashes between the antibiotic and the protein or ring piercings were removed. The same process was applied to generate 6DNM poses within OmpF. (B) IE between the protein and poses of 6DNM-NH3 (left) or 6DNM (right), projected along the Z-coordinate, inclination (θ) and azimuthal (ϕ) of the antibiotic. , with an interval of Ψ. (A, right) The set of 6DNM-NH3 orientations was placed at every point of a 3-dimensional rectangular grid. During this placement, poses with clashes between the antibiotic and the protein or ring piercings were removed. The same process was applied to generate 6DNM poses within OmpF. (B) IE between the protein and poses of 6DNM-NH3 (left) or 6DNM (right), projected along the Z-coordinate, inclination (θ) and azimuthal (ϕ) of the antibiotic. | ||
First, the residues E296, D312, and D127 in the OmpF crystal structure were protonated based on previous pKa calculations.53 We note that D312 was speculated in one study to be deprotonated,54 but this suggestion was only based on indirect inference from the crystal structure. Protonating these three residues in OmpF has been a standard practice in the literature for the past decade.26,27,36,38,55–57 Then, using the center of the CR residues (Lys16, Tyr40, Arg42, Arg82, Arg132, Tyr102, Tyr106, Asp113, Met114, Leu115, Pro116, Glu117, Phe118, Gly119 and Gly120) as the origin, a 16 × 16 × 34 search grid (1 Å spacing) was defined (Fig. 2A). Copies of 6DNM-NH3 were first placed at every grid point, and then each copy was rotated by mapping a vector, 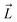 (longest axis from the C. O. M of 6DNM-NH3 to the furthest atom, the oxygen of carbonyl2 [Fig. 4B]) onto a Fibonacci spherical lattice (FSL)58 of 25 points, generating multiple orientations at each grid point. During rotation, the C. O. M of 6DNM-NH3 was set to be at the center of the FSL, while the C. O. M of the oxygen of carbonyl2 was arranged on the FSL. Each of the 25 generated orientations at each grid point was then self-rotated along
(longest axis from the C. O. M of 6DNM-NH3 to the furthest atom, the oxygen of carbonyl2 [Fig. 4B]) onto a Fibonacci spherical lattice (FSL)58 of 25 points, generating multiple orientations at each grid point. During rotation, the C. O. M of 6DNM-NH3 was set to be at the center of the FSL, while the C. O. M of the oxygen of carbonyl2 was arranged on the FSL. Each of the 25 generated orientations at each grid point was then self-rotated along 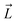 , with an interval of Ψ = 45°, creating a total of 200 poses at each grid point. We reason that this approach would evenly survey possible orientations of 6DNM-NH3. This strategy resulted in a total of 1.7 million distinct drug–protein poses.
, with an interval of Ψ = 45°, creating a total of 200 poses at each grid point. We reason that this approach would evenly survey possible orientations of 6DNM-NH3. This strategy resulted in a total of 1.7 million distinct drug–protein poses.
During our grid-based orientation search process, bad contacts between protein/drug occurred in several poses. These bad contacts were either drug–protein clashes or piercings of the protein into the rings of 6DNM-NH3 (Fig. 2A). Clashes were defined if within a pose, 6DNM-NH3 had a contact distance of <1.0 Å with at least 4 heavy atoms of the protein. Ring piercings were defined by first decomposing rings into triangles and nearby bonds from protein into line segments, and then applying a geometric test to determine if line segments intersected any triangles. Poses associated with clashes and ring piercings were removed, resulting in a total of about 700![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 distinct poses.
000 distinct poses.
Each pose was subjected to 200 steps of energy minimization to relax to an energetically favorable state. Minimization was performed using the generalized Born implicit solvent (GBIS) module implemented in NAMD2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 59,60 to account for the effect of solvation on interactions between the drug and protein without including explicit solvent. GBIS calculates molecular electrostatics in solvent by representing water as a dielectric continuum as described by the Poisson Boltzmann equation. The elimination of explicit solvent greatly accelerates modeling efficiency. During minimization, the protein side chains and the drug were allowed to move, while protein backbone was kept fixed in order to allow the drug to relax in its environment without causing a significant conformational change in the protein. We chose to maintain the global conformation of the protein, because the X-ray structure of OmpF is already the widest state of the porin, as we have shown in a seperate study.61 Therefore, the pathway of the antibiotic through this open conformation should be the most optimum. Furthermore, when we re-ran the pose generation step without fixing the protein backbone and used our pathway search protocol (described below) to find a new pathway; we noticed a significant RMSD of L3 due to minimization alone (Fig. S7†), which is indicative of unphysical perturbation to the protein structure caused by placement of the antibiotic. Also, the drug–protein interaction energy along the new pathway is less favorable than for the original one (Fig. S7†).
59,60 to account for the effect of solvation on interactions between the drug and protein without including explicit solvent. GBIS calculates molecular electrostatics in solvent by representing water as a dielectric continuum as described by the Poisson Boltzmann equation. The elimination of explicit solvent greatly accelerates modeling efficiency. During minimization, the protein side chains and the drug were allowed to move, while protein backbone was kept fixed in order to allow the drug to relax in its environment without causing a significant conformational change in the protein. We chose to maintain the global conformation of the protein, because the X-ray structure of OmpF is already the widest state of the porin, as we have shown in a seperate study.61 Therefore, the pathway of the antibiotic through this open conformation should be the most optimum. Furthermore, when we re-ran the pose generation step without fixing the protein backbone and used our pathway search protocol (described below) to find a new pathway; we noticed a significant RMSD of L3 due to minimization alone (Fig. S7†), which is indicative of unphysical perturbation to the protein structure caused by placement of the antibiotic. Also, the drug–protein interaction energy along the new pathway is less favorable than for the original one (Fig. S7†).
Monte Carlo based pathway search (MCPS) algorithm
We used the minimized poses (Si) obtained from the previous step to probe potential permeation pathways from the extracellular to periplasmic space using Monte Carlo (MC). To use MC, we first generated an energy landscape by calculating the drug–protein interaction energy (IE) for each pose (E(Si)) by evaluating the sum of van der Waals (vdW) and electrostatic interaction energies using NAMD2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 59,60 (Fig. 2B). We then walk through this energy landscape along the membrane normal (Z) to determine favorable pathways connecting extracellular and periplasmic spaces while also exploring orientation space.
59,60 (Fig. 2B). We then walk through this energy landscape along the membrane normal (Z) to determine favorable pathways connecting extracellular and periplasmic spaces while also exploring orientation space.
To do this, we first divide the Z-coordinate space from the extracellular to the periplasmic space into N 1 Å bins, 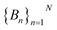 (Fig. 3A and B). Then, we assign poses to these bins, according to the Z-coordinate of the C. O. M. of the drug in each pose. That is, a pose, Si, is assigned to a bin, Bn, if
(Fig. 3A and B). Then, we assign poses to these bins, according to the Z-coordinate of the C. O. M. of the drug in each pose. That is, a pose, Si, is assigned to a bin, Bn, if
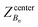 , ΔZ and Z(Si) refer to the center of Bn, the half-width of Bn (=0.5 Å) from
, ΔZ and Z(Si) refer to the center of Bn, the half-width of Bn (=0.5 Å) from 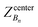 , and the Z-coordinate of the center of mass (C. O. M.) of the antibiotic at a particular pose, respectively. Then, a random pose (S1) from a bin closest to the extracellular space, B1, is selected as the starting point of the trajectory. Now, we need to identify a new pose in the next bin to serve as the next step in the trajectory towards the periplasmic space (decreasing Z by 1 Å). Since we are interested in modeling a chemically relevant permeation trajectory, we also need to ensure that the orientation of the antibiotic, defined by the inclination (θ) and azimuthal (ϕ) angles, does not change substantially in the next step (mechanistically unlikely), since these angular spaces are slow DOFs. To calculate the orientation angles, a drug vector
, and the Z-coordinate of the center of mass (C. O. M.) of the antibiotic at a particular pose, respectively. Then, a random pose (S1) from a bin closest to the extracellular space, B1, is selected as the starting point of the trajectory. Now, we need to identify a new pose in the next bin to serve as the next step in the trajectory towards the periplasmic space (decreasing Z by 1 Å). Since we are interested in modeling a chemically relevant permeation trajectory, we also need to ensure that the orientation of the antibiotic, defined by the inclination (θ) and azimuthal (ϕ) angles, does not change substantially in the next step (mechanistically unlikely), since these angular spaces are slow DOFs. To calculate the orientation angles, a drug vector 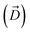 is defined (Fig. 1C), such that the vector points towards the positively charged primary amine group. Then θ is calculated as the angle between
is defined (Fig. 1C), such that the vector points towards the positively charged primary amine group. Then θ is calculated as the angle between 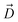 and the membrane normal (Z-axis), while ϕ is the angle between the projections of
and the membrane normal (Z-axis), while ϕ is the angle between the projections of  and the electric field vector of the protein onto the XY plane (Fig. 1C).
and the electric field vector of the protein onto the XY plane (Fig. 1C).
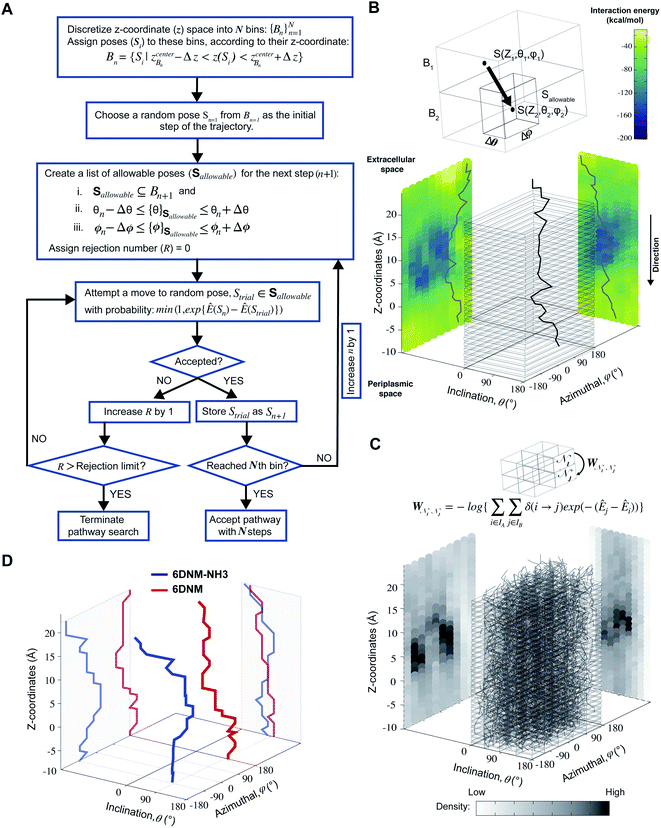 | ||
Fig. 3 Determination of the most likely antibiotic permeation pathways through OM porins using the dataset whose generation is described in Fig. 2. (A) Flowchart describing the Monte Carlo based pathway search (MCPS) algorithm. (B) A representative MCPS trajectory of 6DNM-NH3. To run MCPS, briefly, we first discretize the Z-coordinate space into N bins 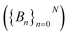 to which we assign the poses generated in Fig. 2A. Then, Monte Carlo (MC) moves are used to walk through the IE landscape generated in Fig. 2B to determine favorable trajectories connecting extracellular and periplasmic spaces. In each MC move, limited change in antibiotic orientation and position are allowed. (C) Generation of a connected graph using multiple MCPS trajectories. Boltzmann weighted densities of the 2000 trajectories are projected along the Z-coordinate, inclination (θ) and azimuthal (ϕ) of the antibiotic. (D) The most likely permeation pathway for 6DNM (red) and 6DNM-NH3 (blue), evaluated using Dijkstra's algorithm.62 to which we assign the poses generated in Fig. 2A. Then, Monte Carlo (MC) moves are used to walk through the IE landscape generated in Fig. 2B to determine favorable trajectories connecting extracellular and periplasmic spaces. In each MC move, limited change in antibiotic orientation and position are allowed. (C) Generation of a connected graph using multiple MCPS trajectories. Boltzmann weighted densities of the 2000 trajectories are projected along the Z-coordinate, inclination (θ) and azimuthal (ϕ) of the antibiotic. (D) The most likely permeation pathway for 6DNM (red) and 6DNM-NH3 (blue), evaluated using Dijkstra's algorithm.62 | ||
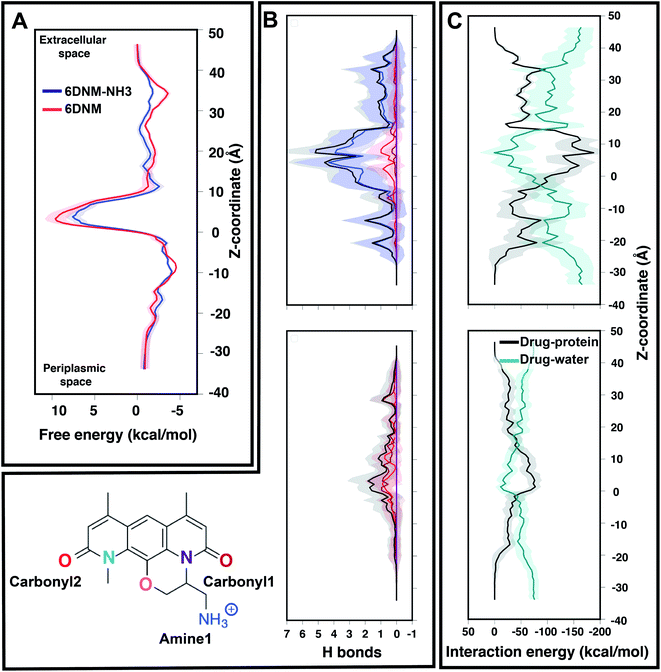 | ||
| Fig. 4 Comparison of the energetics of permeation for 6DNM-NH3 and 6DNM through OmpF. (A) Mean (solid) and standard deviation (shaded) of the free-energy for permeation of 6DNM-NH3 (blue) and 6DNM (red). Free energies were calculated using all the MCPS-BEUS windows and projected along the Z-coordinate of the antibiotic C. O. M. (B) Mean and standard deviation of the number of hydrogen bonds between any protein residue and each functional group in the drug (colored differently according to chemical structure shown in bottom, left) of 6DNM-NH3 (top) and 6DNM (bottom, right) at different Z-positions. The total number of hydrogen bonds for each drug is colored in black. The nomenclature and color code for each electronegative atom are shown in the bottom left panel. (C) Mean and standard deviation of the drug–protein and drug–water interaction energy at different Z-positions for 6DNM-NH3 (top) and 6DNM (bottom). | ||
To transition to the next step, we compile an allowable list of poses in the next bin (B2) with θ and ϕ within a range (Δθ = 18° and Δϕ = 36°, respectively) of θ(S0) and ϕ(S0). Within the compiled list, a trial pose, Strial is chosen randomly and a move is attempted. The move is accepted with probability:
Identifying the most likely pathway
We generated 2000 MCPS trajectories to exhaustively search for the possible pathways the antibiotic can take to permeate through OmpF. These trajectories resulted in exhaustive and convergent sampling of the conformational space (Fig. S8 and S9†). Then, to determine the most likely pathway (that will be used to generate seeds for BEUS simulations) from these trajectories, we build a directed graph and apply Dijkstra's algorithm.62 In the directed graph, each node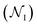 is defined as a set of poses such that:
is defined as a set of poses such that:where
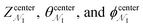 refer to the center of
refer to the center of 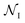 in the Z, θ, and ϕ coordinates, respectively, and ΔZ, Δθ, and Δϕ represent the range from their respective centers (Fig. 3C). Once nodes are defined, edge weights between any two nodes
in the Z, θ, and ϕ coordinates, respectively, and ΔZ, Δθ, and Δϕ represent the range from their respective centers (Fig. 3C). Once nodes are defined, edge weights between any two nodes 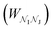 are determined by calculating the negative logarithm of transition counts (each transition weighted by the Boltzmann factor of the two connected poses making up the transition):
are determined by calculating the negative logarithm of transition counts (each transition weighted by the Boltzmann factor of the two connected poses making up the transition):where
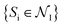 is the set of all poses within node
is the set of all poses within node 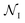 , δ(Si → Sj) is 1 if a transition occurs between Si and Sj (otherwise it is 0) and Ê(Si) is the standardized energy of pose Si. The negative logarithm was taken because Dijkstra's algorithm determines the pathway with the lowest total edge weight from source to sink node. Sink and source nodes are defined as two virtual nodes, V1 (source) and V2 (sink), each connected to the set of nodes with maximum (extracellular set) and minimum (periplasmic set)
, δ(Si → Sj) is 1 if a transition occurs between Si and Sj (otherwise it is 0) and Ê(Si) is the standardized energy of pose Si. The negative logarithm was taken because Dijkstra's algorithm determines the pathway with the lowest total edge weight from source to sink node. Sink and source nodes are defined as two virtual nodes, V1 (source) and V2 (sink), each connected to the set of nodes with maximum (extracellular set) and minimum (periplasmic set) 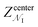 , respectively. Each connection was initially assigned an arbitrary edge weight. We then used Dijkstra's algorithm to compute the pathway connecting V1 and V2 with the lowest overall edge weight, resulting in the most likely pathway from extracellular to periplasmic space with N nodes:
, respectively. Each connection was initially assigned an arbitrary edge weight. We then used Dijkstra's algorithm to compute the pathway connecting V1 and V2 with the lowest overall edge weight, resulting in the most likely pathway from extracellular to periplasmic space with N nodes: 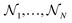 , whose centers are separated by 1 Å along the Z-coordinate.
, whose centers are separated by 1 Å along the Z-coordinate.
It is important to note that the search step for the most likely pathway, by definition, outputs only one most optimal pathway and might miss additional, equally optimal pathways. Therefore, to check other possible pathways, we utilized a method commonly used in transition path theory,63 where the bottleneck transition weight of the top pathway is subtracted from it in the connected graph in order to generate a new graph. Then, Dijkstra's algorithm is re-run to obtain the next optimal pathway. This protocol can be repeated multiple times to obtain additional pathways (4 additional pathways here). We observe that the majority of these new pathways adopt similar configurations to our original top pathway (Fig. S10†). Only one of these pathways is structurally distinct from the original one (termed here “the distinct pathway”), but it has a significantly lower transition weight (54.6) than the original one (230.7) (Fig. S10†), indicating its significantly smaller contribution to the permeation dynamics of the antibiotic. Furthermore, this distinct pathway has a significantly less favorable interaction energy at the region of the greatest permeation barrier (Fig. S11†), indicative of the likely unfavorable free energy profile in this region. We only used the original top pathway for further energetic characterization.
Free-energy calculations using MCPS derived pathways
To investigate the energetics of permeation of 6DNM-NH3 and 6DNM, the lowest energy poses in the nodes along the most likely pathways for each drug were used to serve as windows in 2 independent 1D-BEUS simulations.41–45 The most likely path contains poses with Z-values ranging from −10 to 24 Å (relative to the midplane of the membrane) of 1 Å width; to obtain reference free energies, we extended the number of windows in the extracellular and periplasmic spaces such that the terminal windows are at least 10 Å away from any atom of the protein. To ensure adequate histogram overlap in BEUS, additional windows were added in between the original windows starting from the entrance to the exit of the CR (Z = −3 to 12 Å) such that the window width was 0.5 Å within this region. In total, 94 windows were used spanning 80 Å from the extracellular (Z = 46 Å) to the periplasmic (Z = −34 Å) space.To take into account the biologically relevant configuration of the system, for each window we built a trimeric, membrane-embedded protein–drug system. To do this, we first aligned the backbone atoms of the β-barrel residues of the monomeric protein of each window to those of a single monomer of the X-ray structure of trimeric OmpF (PDB ID: 3POX).52 Then, we merged the resulting coordinates of the aligned antibiotic-monomer system with the two additional monomers of the trimeric OmpF. In the generated trimer for each window, residues E296, D312, and D127 were protonated.36,54,55 The windows were then embedded in a symmetric membrane composed of 1,2-dimyristoyl-sn-glycero-3-phosphocholine (DMPC) lipid molecules in each leaflet generated using the Membrane Builder module of CHARMM-GUI.64 We did not use an OM composition containing lipopolysaccharides (LPS) since the membrane composition is unlikely to influence the dynamics of the drug inside the pore. Each window was solvated with TIP3P water65 and buffered in 0.15 M NaCl to generate systems containing ∼140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms with dimensions of 120 × 120 × 100 Å3.
000 atoms with dimensions of 120 × 120 × 100 Å3.
Before performing 1D-BEUS simulations, each drug-bound, membrane-embedded trimer was minimized using 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps of the steepest descent algorithm, and then the molecular system was allowed to relax at the center of each window during a 1 ns MD simulation while the drug and heavy atoms of the protein were restrained with a force constant of 1 kcal mol−1 Å−2. This was followed by 35 ns of 1D-BEUS simulations (until the convergence of the free-energy, Fig. S13†) using the distance along the membrane normal (Z-axis) between the drug's C. O. M and the C. O. M of the antibiotic-containing monomer as the collective variable. The force constant of each window was chosen such that the exchange ratio for each window was between 0.15 and 0.3.66 The resultant force constants were 2.0 kcal mol−1 Å−2 for all windows except for windows from the entrance to exit of the CR, which had force constants of 7.0 kcal mol−1 Å−2. As shown in Fig. S12,† using these force constants resulted in good window overlap for each drug. The first 20 ns of each window were discarded as equilibration, and the rest of the trajectories were used in evaluating the free-energy. A non-parametric variation of the weighted histogram analysis method (WHAM),67 proposed by Bartels68 and implemented by Moradi and Tajkhorshid45 was used to estimate the free-energy profile from the BEUS simulations.
000 steps of the steepest descent algorithm, and then the molecular system was allowed to relax at the center of each window during a 1 ns MD simulation while the drug and heavy atoms of the protein were restrained with a force constant of 1 kcal mol−1 Å−2. This was followed by 35 ns of 1D-BEUS simulations (until the convergence of the free-energy, Fig. S13†) using the distance along the membrane normal (Z-axis) between the drug's C. O. M and the C. O. M of the antibiotic-containing monomer as the collective variable. The force constant of each window was chosen such that the exchange ratio for each window was between 0.15 and 0.3.66 The resultant force constants were 2.0 kcal mol−1 Å−2 for all windows except for windows from the entrance to exit of the CR, which had force constants of 7.0 kcal mol−1 Å−2. As shown in Fig. S12,† using these force constants resulted in good window overlap for each drug. The first 20 ns of each window were discarded as equilibration, and the rest of the trajectories were used in evaluating the free-energy. A non-parametric variation of the weighted histogram analysis method (WHAM),67 proposed by Bartels68 and implemented by Moradi and Tajkhorshid45 was used to estimate the free-energy profile from the BEUS simulations.
Steered molecular dynamics (SMD)
To compare the free energies for 6DNM and 6DNM-NH3 along MCPS-derived pathways to those along pathways derived using steered molecular dynamics (SMD), SMD simulations were performed and their trajectories were used to generate windows for two additional 1D-BEUS simulations for each drug. To perform SMD, drug–protein systems were built by first embedding the X-ray structure of trimeric OmpF (PDB ID: 3POX)52 in a symmetric membrane composed of DMPC lipids generated using the Membrane Builder module of CHARMM-GUI.64 In each monomer, residues E296, D312, and D127 were protonated.36,54,55 Each system was solvated with TIP3P water65 and neutralized in 0.15 M NaCl to generate systems each containing ∼140![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms with dimensions of 120 × 120 × 100 Å3. Ten replicas of each drug were then placed at the pore mouth with different initial orientations, resulting in a total of 20 independent drug–protein systems.
000 atoms with dimensions of 120 × 120 × 100 Å3. Ten replicas of each drug were then placed at the pore mouth with different initial orientations, resulting in a total of 20 independent drug–protein systems.
The systems were then minimized using the steepest descent algorithm for 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps, followed by an initial equilibration of 1 ns, during which the heavy atoms of the protein and the drug were harmonically restrained using a force constant of 1.0 kcal mol−1 Å−2. Then, a harmonic spring with a force constant of 10 kcal mol−1 Å−2 was attached to the C. O. M. of each drug, to pull it along the Z-coordinate from the pore mouth on the extracellular side to periplasmic space through a monomer of OmpF at a constant velocity of 0.5 Å ns−1. To avoid structural deformation of the protein due to the strong non-equilibrium nature of SMD, protein heavy atoms were harmonically restrained using a force constant of 1.0 kcal mol−1 Å−2.
000 steps, followed by an initial equilibration of 1 ns, during which the heavy atoms of the protein and the drug were harmonically restrained using a force constant of 1.0 kcal mol−1 Å−2. Then, a harmonic spring with a force constant of 10 kcal mol−1 Å−2 was attached to the C. O. M. of each drug, to pull it along the Z-coordinate from the pore mouth on the extracellular side to periplasmic space through a monomer of OmpF at a constant velocity of 0.5 Å ns−1. To avoid structural deformation of the protein due to the strong non-equilibrium nature of SMD, protein heavy atoms were harmonically restrained using a force constant of 1.0 kcal mol−1 Å−2.
The SMD trajectory for each drug associated with the lowest non-equilibrium work was then used to generate 1 Å windows, except for the region between the extracellular entrance and the exit of the CR (Z = −3 to 12), where 0.5 Å windows were used to ensure adequate histogram overlap. To obtain reference free energies, additional windows were added by extending the lowest-work SMD trajectory of each drug towards the water in the extracellular and periplasmic spaces such that terminal windows were at least 10 Å away from any atom of the protein. In total, 94 windows were generated along the Z-coordinate for each drug–protein system. Then, two independent 1D-BEUS simulations were performed using the same protocol described above. This protocol resulted in a good exchange ratio (between 0.15 and 0.3) for each window as suggested previously66 and good window overlap (Fig. S2†). Free energy of each drug was then evaluated using the non-parametric WHAM.45,67,68
MD simulation protocol
MD simulations in this study were performed using NAMD2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 59,60 utilizing CHARMM36m69 and CHARMM36
59,60 utilizing CHARMM36m69 and CHARMM36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 70 force field parameters for proteins and lipids, respectively. The force field parameters for both drugs were generated using the CHARMM General Force Field (CGenFF)71–73 with the ParamChem server. Bonded and short-range nonbonded interactions were calculated every 2 fs, and periodic boundary conditions were employed in all three dimensions. The particle mesh Ewald (PME) method74 was used to calculate long-range electrostatic interactions every 4 fs with a grid density of 1 Å−3. A force-based smoothing function was employed for pairwise nonbonded interactions at a distance of 10 Å with a cutoff of 12 Å. Pairs of atoms whose interactions were evaluated were searched and updated every 20 fs. A cutoff (13.5 Å) slightly longer than the nonbonded cutoff was applied to search for the interacting atom pairs. Constant pressure was maintained at a target of 1 atm using the Nosé–Hoover Langevin piston method.75,76 Langevin dynamics maintained a constant temperature of 310 K with a damping coefficient, γ, of 0.5 ps−1 applied to all atoms. Simulation trajectories were collected every 10 ps.
70 force field parameters for proteins and lipids, respectively. The force field parameters for both drugs were generated using the CHARMM General Force Field (CGenFF)71–73 with the ParamChem server. Bonded and short-range nonbonded interactions were calculated every 2 fs, and periodic boundary conditions were employed in all three dimensions. The particle mesh Ewald (PME) method74 was used to calculate long-range electrostatic interactions every 4 fs with a grid density of 1 Å−3. A force-based smoothing function was employed for pairwise nonbonded interactions at a distance of 10 Å with a cutoff of 12 Å. Pairs of atoms whose interactions were evaluated were searched and updated every 20 fs. A cutoff (13.5 Å) slightly longer than the nonbonded cutoff was applied to search for the interacting atom pairs. Constant pressure was maintained at a target of 1 atm using the Nosé–Hoover Langevin piston method.75,76 Langevin dynamics maintained a constant temperature of 310 K with a damping coefficient, γ, of 0.5 ps−1 applied to all atoms. Simulation trajectories were collected every 10 ps.
Antibiotic permeability calculation
The antibiotic permeability (P) was calculated by treating the antibiotic translocation process as a one-dimensional diffusion-drift problem:24,77,78where U(Z) is the free-energy (calculated as described above) and D(Z) is the diffusion coefficient along the pore axis (Z); L is the length of the pore and kBT is the thermodynamic temperature.
To calculate D(Z), a set of independent simulations were initiated from the same seeds used for BEUS simulations, during which the Z position of the antibiotic was restrained by means of a harmonic potential with a force constant of 10 kcal mol−1 Å−2 (as suggested by Lee et al.78). Each simulation was performed for 10 ns. From these simulations, D(Z) was calculated in the framework of an overdamped harmonic oscillator,78–80
where, δZ(t) = Z(t) − 〈Z〉.
Analysis
System visualization and analyses were carried out using VMD.81 Drug–protein interaction energy (vdW + electrostatic) was calculated using the NAMDENERGY plugin of VMD. A hydrogen bond was counted between an electronegative atom with a hydrogen atom (H) covalently bound to it (the donor, D), and another electronegative atom (the acceptor, A), provided that the distance D–A was less than 3 Å and the angle D–H–A was more than 120°.Experimental methods
Mutant construction
E. coli ompF mutants were constructed as described before.82 Briefly, plasmids carrying the desired mutation were used to replace the wild-type (WT) ompF allele in E. coli BW25113.83 To do this, the mutagenic plasmids were moved from E. coli WM6026![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 84 donors to BW25113 recipients via conjugation with selection for exconjugants on LB agar with kanamycin (50 μg ml−1). Because the plasmids are incapable of replication in E. coli BW25113, these exconjugants arise by integration into the recipient chromosome via homologous recombination, creating partial diploids of the ompF region, with one WT and one mutant allele separated by the plasmid vector. Kanamycin-sensitive recombinants that had resolved the partial diploid state were then selected by growth on a modified LB medium that lacked NaCl and that contained 5% sucrose. The presence of the desired mutation was verified by DNA sequencing of ompF PCR products. E. coli WM8633 (lacIq, rrnB3, Δlac4787, hsdR514, Δ(araBAD)567, Δ(rhaBAD)568, rph-1, ompF(D113F)) was constructed via allele exchange using plasmid pAP002. E. coli WM8636 (lacIq, rrnB3, Δlac4787, hsdR514, Δ(araBAD)567, Δ(rhaBAD)568, rph-1, ompF(D113V)) was constructed via allele exchange using plasmid pAP003. The mutagenic plasmids carrying the ompF mutations are derivatives of pHC001A.85 These plasmids were constructed by HiFi DNA assembly (New England Biolabs, Ipswich, MA) using NotI-digested pHC001A and a mutagenized ompF allele produced by overlap-extension PCR. Plasmid pAP002 was constructed using the following primers: ompF-F: CCGGGGGATCCACTAGTTCTAGAGCGGCCGCACGTAACTGGCGTGCAAAAC; ompF-R: AAAGCTGGAGCTCCACCGCGGTGGCGGCCGCAGCGGCGGTAATGTTCTCAA; ompF(D113V)F: TTCGCGGGTCTTAAATACGCTGTTGTTGGTTCTTTCGATTACGGCCGTAA; and ompF(D113V)R: TTACGGCCGTAATCGAAAGAACCAACAACAGCGTATTTAAGACCCGCGAA. Plasmid pAP003 was constructed using ompF-F; ompF-R; ompF(D113F)F: TTCGCGGGTCTTAAATACGCTTTCGTTGGTTCTTTCGATTACGGCCGTAA; and ompF(D113F)R: TTTACGGCCGTAATCGAAAGAACCAACGAAAGCGTATTTAAGACCCGCGAA. Bold sequences in primers ompF-F and ompF-R represent homology to pHC001A required for HiFi assembly, whereas those in ompF(D113V)F, ompF(D113V)R, ompF(D113F)F, and ompF(D113F)R represent the codon changed to produce the desired mutation.
84 donors to BW25113 recipients via conjugation with selection for exconjugants on LB agar with kanamycin (50 μg ml−1). Because the plasmids are incapable of replication in E. coli BW25113, these exconjugants arise by integration into the recipient chromosome via homologous recombination, creating partial diploids of the ompF region, with one WT and one mutant allele separated by the plasmid vector. Kanamycin-sensitive recombinants that had resolved the partial diploid state were then selected by growth on a modified LB medium that lacked NaCl and that contained 5% sucrose. The presence of the desired mutation was verified by DNA sequencing of ompF PCR products. E. coli WM8633 (lacIq, rrnB3, Δlac4787, hsdR514, Δ(araBAD)567, Δ(rhaBAD)568, rph-1, ompF(D113F)) was constructed via allele exchange using plasmid pAP002. E. coli WM8636 (lacIq, rrnB3, Δlac4787, hsdR514, Δ(araBAD)567, Δ(rhaBAD)568, rph-1, ompF(D113V)) was constructed via allele exchange using plasmid pAP003. The mutagenic plasmids carrying the ompF mutations are derivatives of pHC001A.85 These plasmids were constructed by HiFi DNA assembly (New England Biolabs, Ipswich, MA) using NotI-digested pHC001A and a mutagenized ompF allele produced by overlap-extension PCR. Plasmid pAP002 was constructed using the following primers: ompF-F: CCGGGGGATCCACTAGTTCTAGAGCGGCCGCACGTAACTGGCGTGCAAAAC; ompF-R: AAAGCTGGAGCTCCACCGCGGTGGCGGCCGCAGCGGCGGTAATGTTCTCAA; ompF(D113V)F: TTCGCGGGTCTTAAATACGCTGTTGTTGGTTCTTTCGATTACGGCCGTAA; and ompF(D113V)R: TTACGGCCGTAATCGAAAGAACCAACAACAGCGTATTTAAGACCCGCGAA. Plasmid pAP003 was constructed using ompF-F; ompF-R; ompF(D113F)F: TTCGCGGGTCTTAAATACGCTTTCGTTGGTTCTTTCGATTACGGCCGTAA; and ompF(D113F)R: TTTACGGCCGTAATCGAAAGAACCAACGAAAGCGTATTTAAGACCCGCGAA. Bold sequences in primers ompF-F and ompF-R represent homology to pHC001A required for HiFi assembly, whereas those in ompF(D113V)F, ompF(D113V)R, ompF(D113F)F, and ompF(D113F)R represent the codon changed to produce the desired mutation.
Accumulation assay
The accumulation assay8,86 was performed in triplicate, with tetracycline as a positive control. The strain E. coli BW25113 (WT) and two strains containing single mutants in ompF, E. coli ompFD113V and E. coli ompFD113F, were used for these experiments. For each replicate, 2.5 ml of an overnight culture of E. coli was diluted into 250 ml of fresh Luria Bertani broth (Lennox). Cultures were grown at 37 °C with shaking to an optical density at a wavelength of 600 nm (OD600) of 0.55–0.60. The bacteria were pelleted at 3220 RCF for 10 min at 4 °C, and the supernatant was discarded. The pellets were resuspended in 40 ml phosphate buffered saline (PBS) and pelleted as before, and the supernatant was discarded. The pellets were resuspended in 8.8 ml fresh PBS and aliquoted into 1.7 ml Eppendorf tubes (875 μl each). The number of colony-forming units (CFUs) was determined by a calibration curve. The samples were equilibrated at 37 °C with shaking for 5 min, then compound was added (final concentration = 50 μM) and samples were incubated at 37 °C with shaking for 10 min. A 10 min time point was chosen because it is longer than the predicted amount of time required to reach a steady-state concentration,87 but short enough to minimize metabolic and growth changes (no changes in OD600 or CFU count observed). After incubation, 800 μl of the cultures was carefully layered on 700 μl of silicone oil (9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 AR20 (Acros; catalogue number: 174665000)/Sigma High Temperature (Sigma–Aldrich; catalogue number: 175633), cooled to −78 °C). Bacteria were pelleted through the oil by centrifuging at 13
1 AR20 (Acros; catalogue number: 174665000)/Sigma High Temperature (Sigma–Aldrich; catalogue number: 175633), cooled to −78 °C). Bacteria were pelleted through the oil by centrifuging at 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RCF for 2 min at room temperature (with the supernatant remaining above the oil). The supernatant and oil were then removed by pipetting. To lyse the samples, each pellet was resuspended in 200 μl water, and then subjected to three freeze–thaw cycle of 3 min in liquid nitrogen followed by 3 min in a water bath at 65 °C. The lysates were pelleted at 13
000 RCF for 2 min at room temperature (with the supernatant remaining above the oil). The supernatant and oil were then removed by pipetting. To lyse the samples, each pellet was resuspended in 200 μl water, and then subjected to three freeze–thaw cycle of 3 min in liquid nitrogen followed by 3 min in a water bath at 65 °C. The lysates were pelleted at 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RCF for 2 min at room temperature and the supernatant was collected (180 μl). The debris were resuspended in 100 μl methanol and pelleted as before. The supernatants were removed and combined with the previous supernatants collected. Finally, the remaining debris were removed by centrifuging at 20
000 RCF for 2 min at room temperature and the supernatant was collected (180 μl). The debris were resuspended in 100 μl methanol and pelleted as before. The supernatants were removed and combined with the previous supernatants collected. Finally, the remaining debris were removed by centrifuging at 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 RCF for 10 min at room temperature.
000 RCF for 10 min at room temperature.
Supernatants were analyzed with the QTRAP 5500 LC/MS/MS system (Sciex) in the Metabolomics Laboratory of the Roy J. Carver Biotechnology Center, University of Illinois at Urbana-Champaign. Software Analyst 1.6.2 was used for data acquisition and analysis. The 1200 Series HPLC System (Agilent Technologies) used included a degasser, an autosampler and a binary pump. The liquid chromatography separation was performed on an Agilent Zorbax SB-Aq column (4.6 mm × 50 mm; 5 μm) with mobile phase A (0.1% formic acid in water) and mobile phase B (0.1% formic acid in acetontrile). The flow rate was 0.3 ml min−1. The linear gradient was as follows: 0–3 min: 100% A; 10–15 min: 2% A; 16–20.5 min: 100% A. The autosampler was set at 15 °C. The injection volume was 1 μl. Mass spectra were acquired under positive electrospray ionization with a voltage of 5500 V. The source temperature was 450 °C. The curtain gas, ion source gas 1, and ion source gas 2 were 33, 65 and 60 psi, respectively. Multiple reaction monitoring was used for quantitation with external calibration.
Results and discussion
Free energies along the SMD-derived pathways do not support experimental results
To understand the increased permeability of 6DNM-NH3 relative to 6DNM through OmpF,8 we first attempted to evaluate the energetics of permeation of each drug by performing independent 1D-BEUS simulations seeded by SMD simulations biasing the translational coordinate of the antibiotics along the pore axis (Z-axis). We performed multiple (10) SMD simulations for each drug from which an optimal permeation pathway was selected from the SMD trajectory with the lowest non-equilibrium work value (Fig. S1†). A slow pulling velocity (0.5 Å ns−1) was employed to minimize potential hysteresis and perturbations by the drug's induced translocation to the protein elements. The resulting pathway in each case was used to generate initial seeds for 1D-BEUS simulation for a total of 3.3 μs. As expected, lack of sufficient sampling of the antibiotic orientation at the CR was apparent in the resulting 1D-BEUS simulations (Fig. S4†).Although the 1D-BEUS simulations for each drug produced apparently converging free energies (Fig. S5†), a higher permeation barrier for 6DNM-NH3 was observed compared to 6DNM (Fig. S6†), in disagreement with our experimental finding that 6DNM-NH3 reaches higher accumulation inside E. coli.8 This discrepancy between computation and experiment may arise because the initial pathways for BEUS, derived from SMD runs, may not have captured the most likely permeation pathway for the antibiotics. A proper assessment for the optimal initial pathway would require a more aggressive sampling of the orientation space that was not achieved in our SMD runs (Fig. S3†). Although a large number of SMD runs could theoretically sample orientation space comprehensively, performing an adequate number of SMD simulations for such a complex molecular system would be computationally prohibitive.
Free-energy along the MCPS-derived pathway supports experimental results
Since SMD-seeded BEUS simulations failed to sufficiently sample other slow DOFs such as orientations of the antibiotic (specifically at the narrow CR), we sought to first use a heuristic method to probe the multi-dimensional space more extensively, and then use this sampling to develop a better initial pathway for free energy calculations.To enhance sampling of the orientation and translational DOFs of 6DNM and 6DNM-NH3, we developed a systematic and computationally efficient algorithm named Monte Carlo based pathway search (MCPS). MCPS determines multiple permeation trajectories through OmpF from the extracellular to periplasmic side using an energetic descriptor of the system. To run MCPS, we first generate a dataset containing hundreds of thousands of discrete drug–protein poses to exhaustively explore translational and rotational DOFs of the drug (Fig. 2A). This dataset is then used to construct a multidimensional drug–protein interaction energy (IE) landscape for the translation (Z-coordinate) and orientation (inclination angle, θ, and azimuthal angle, ϕ) (Fig. 2B). It is not trivial, however, to just use a rugged multi-dimensional potential energy landscape to determine the most likely pathway.88,89 Additionally, the IE landscape lacks definitive start and end states for antibiotic permeation. Therefore, we used our MCPS algorithm to walk through the IE landscape using Monte Carlo (MC) moves to determine favorable trajectories connecting extracellular and periplasmic spaces (Fig. 3). The starting point within a trajectory is randomly selected from the poses closest to the extracellular space.
To comprehensively sample all possible pathways in our defined space, we obtained 2000 MCPS trajectories that demonstrated exhaustive and convergent sampling of the conformational space (Fig. S8 and S9†). Then, we used these trajectories to build a connected graph to be used in Dijkstra's algorithm to determine the most favorable permeation pathway (Fig. 3C and D). A detailed description for each step is provided in the Methods section. Our search algorithm shows an excellent computational efficiency of ∼100 folds over 100 SMD runs (≈92 vs. 10 k node-hours; Table 1), realizing that even this many SMD runs might fail to sufficiently sample orientation space of the drug. Although estimating the overall wall clock time for calculating free energies would largely depend on the computational resources utilized, the present approach allows one to achieve a full free energy profile for an antibiotic in a few days on commonly used clusters.
| MCPS steps | Node-hour |
|---|---|
| Conformational search | 1.1 |
| Minimization and IE calculation | 90.5 |
| MCPS | 0.0042 |
| Most likely pathway calculation | 0.02 |
| Total | 91.6 |
For 6DNM-NH3, the most likely pathway derived from MCPS is largely different from the one derived from the lowest-work SMD run; however, for 6DNM, the pathways derived from either approach are similar (Fig. S15†). The MCPS-derived pathways were then used as initial seeds for two independent 1D-BEUS simulations for either drug to obtain free-energy profiles.
The free-energy profiles revealed that within the CR, both drugs face high permeation energetic barriers, similar to the SMD-derived 1D-BEUS; however, the overall free-energy barrier for 6DNM-NH3 is significantly less than 6DNM (by 2 kcal mol−1), (Fig. 4A). The barrier arises likely because: (i) the narrowness of the CR causes a loss in entropy, which has been shown to contribute to the free-energy barrier for other antibiotics' translocations through OmpF in previous MD simulation studies;20 and (ii) the loss of drug–water interactions at the CR leads to a large desolvation enthalpic penalty (Fig. 4C), which has been shown to contribute to the overall free-energy barrier in several biological processes such as protein folding,90 and protein-ligand binding.91 However, the lower free-energy barrier for 6DNM-NH3 can be attributed to the increased protein–drug interactions enabled by the positively charged amino group (amine1) (Fig. 4B and C), which offers more enthalpic compensation to the entropic and desolvation costs within the CR for the aminated compound.
We then used the MCPS-BEUS free-energy profiles combined with our computed diffusion coefficients along the pore axis to determine permeability of either drug through OmpF. Our calculations showed a 30-fold greater permeability for the aminated drug (1.1 × 10−3 cm s−1 for 6DNM-NH3 vs. 3.3 × 10−5 cm s−1 for 6DNM), substantiating the increased accumulation of 6DNM-NH3 into E. coli we observed experimentally.8
Notably, for 6DNM-NH3, a significant decrease (by ≈3 kcal mol−1) in the energetic barrier was observed in the free-energy profile derived using MCPS-BEUS compared to the one derived using SMD-BEUS. For 6DNM, the barrier calculated by the two approaches are rather similar, possibly because the initial pathways derived from these approaches are similar (Fig. S14† and S15†).
Permeation mechanism of 6DNM-NH3 through OmpF
To understand the mechanisms by which the primary amine group (amine1; Fig. 4B) enhances the permeability of 6DNM-NH3, we determined the most likely permeation pathway through the newly generated free-energy landscape for each drug. As we are mainly interested in the translocation of the antibiotics through the CR, we performed further analysis of the frames within the entrance, top, bottom, and exit of the CR along the resulting pathways. At each location, θ, ϕ and hydrogen bonding pattern with protein residues were analyzed (Fig. 5 and 6).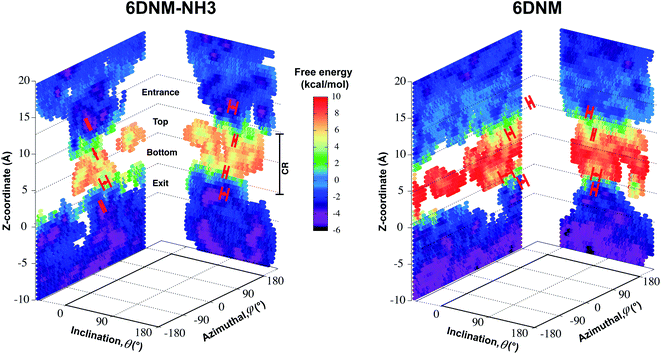 | ||
| Fig. 5 Mechanism of antibiotic permeation through OmpF. Free-energy landscapes for permeation of 6DNM-NH3 and 6DNM (calculated using all respective MCPS-BEUS windows), projected along the Z-coordinate, inclination (θ) and azimuthal (ϕ) angle of the antibiotic. All free-energy values were calculated relative to the free energy in bulk solution. Mean and standard deviation of θ and ϕ of the antibiotic in the CR at (1) the entrance (Z = 9–12 Å), (2) top (Z = 5–8 Å), (3) bottom (Z = 1–4 Å), and 4) exit (Z = −3–0 Å) of the CR, along the most likely pathway are highlighted in red. | ||
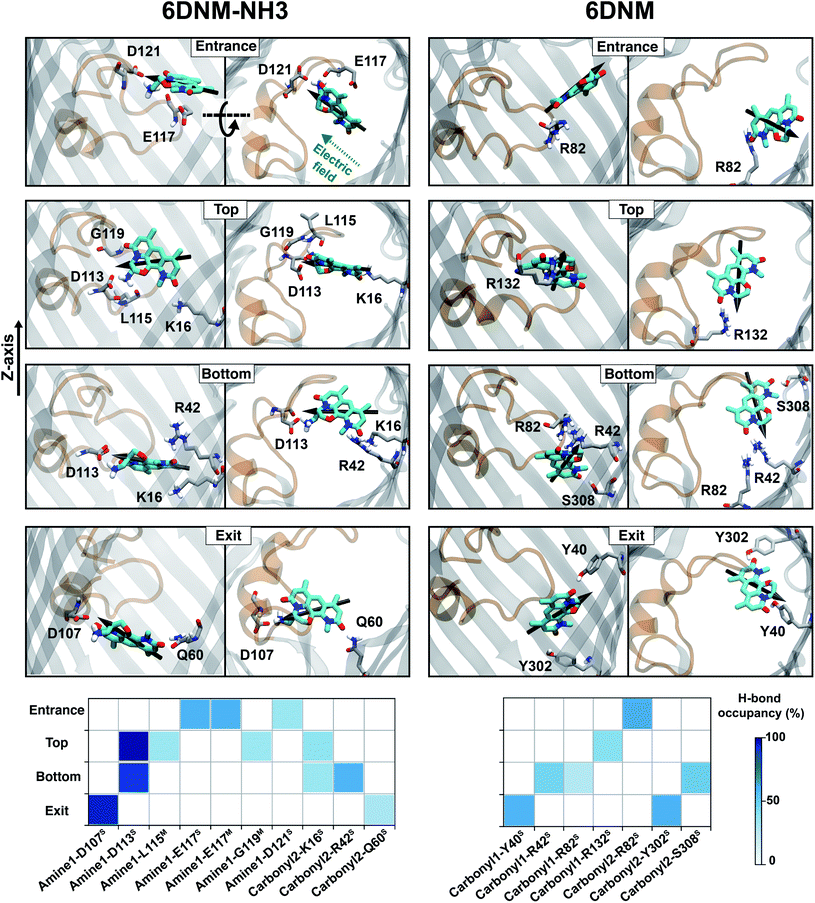 | ||
| Fig. 6 Key interactions along the antibiotic permeation pathway. (Top) Snapshots of both drugs at different locations along the CR, highlighting key interacting residues. (Bottom) Hydrogen bonding between the different functional groups of 6DNM-NH3 and 6DNM and protein elements at different locations along the CR. The interactions shown have hydrogen bond probability greater than 20%. Nomenclature for the antibiotic functional groups is provided in Fig. 4. Superscripts S and M represent side- and main-chain of protein residues, respectively. | ||
We find that upon entering the CR, 6DNM-NH3 orients such that its vector (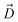 , approximately aligned with the drug's dipole moment with a magnitude of 19 Debye), aligns with the transverse electric field in the CR (θ = 94.0 ± 9.2° and ϕ = −5.1 ± 7.7°) and maintains this orientation throughout the entire CR (from entrance to exit, Fig. 5). The observed alignment of the dipole of 6DNM-NH3 with the protein's electric field may compensate the reduced entropy of the drug within the CR, as illustrated by the appearance of a local affinity site at the CR entrance (Fig. 5). This affinity site helps to stabilize 6DNM-NH3 within the CR, which could increase the probability of the drug passing through the porin. Accordingly, previous MD simulation studies have suggested that electric field alignment of the dipole of other antibiotics and the resulting affinity sites to be beneficial in permeation through OmpF.20,24,25,27 In contrast, for 6DNM, no such local affinity site was observed at the CR entrance since the dipole moment of 6DNM is significantly weaker (8 Debye) than that of 6DNM-NH3 (Fig. 5). As a result, throughout the CR, the free energy for 6DNM in both projections is calculated to be significantly greater than that of 6DNM-NH3 (Fig. 5).
, approximately aligned with the drug's dipole moment with a magnitude of 19 Debye), aligns with the transverse electric field in the CR (θ = 94.0 ± 9.2° and ϕ = −5.1 ± 7.7°) and maintains this orientation throughout the entire CR (from entrance to exit, Fig. 5). The observed alignment of the dipole of 6DNM-NH3 with the protein's electric field may compensate the reduced entropy of the drug within the CR, as illustrated by the appearance of a local affinity site at the CR entrance (Fig. 5). This affinity site helps to stabilize 6DNM-NH3 within the CR, which could increase the probability of the drug passing through the porin. Accordingly, previous MD simulation studies have suggested that electric field alignment of the dipole of other antibiotics and the resulting affinity sites to be beneficial in permeation through OmpF.20,24,25,27 In contrast, for 6DNM, no such local affinity site was observed at the CR entrance since the dipole moment of 6DNM is significantly weaker (8 Debye) than that of 6DNM-NH3 (Fig. 5). As a result, throughout the CR, the free energy for 6DNM in both projections is calculated to be significantly greater than that of 6DNM-NH3 (Fig. 5).
The particular orientation of 6DNM-NH3 within the CR also poses amine1 to interact with acidic residues of L3 and carbonyl2 to interact with residues of the basic ladder located at the barrel wall (Fig. 5 and 6). At the CR entrance, amine1 interacts with the side chain of D121 and side/main chain of E117, located near the extracellular terminal of L3; another factor (in addition to dipole alignment) contributing to the appearance of a local affinity site at this location (Fig. 5). Within the CR, however, amine1 breaks these interactions to interact with the side chain of D113 and main chains of L115 and G119. At this location, carbonyl2 also interacts with the side chains of K16 and R42, further stabilizing the drug in the CR. Notably, the downward movement of the antibiotic towards the periplasmic space is accompanied with a drug rotation (monitored by 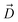 ), while amine1 and carbonyl2 maintain similar interactions along the pore axis; this rotation is expected to help the bulky body of the drug to advance through the narrow CR. The drug exits the CR with no further reorientation; however, interactions are broken as amine1 and carbonyl2 interact with the side chains of D107 and Q60, respectively. Overall, our analysis shows that 6DNM-NH3 permeates through the CR via a stepwise mechanism as the drug hops in order for amine1 and carbonyl2 to interact with residues along the pore. In contrast, for 6DNM, significantly fewer hydrogen bonds and a completely different orientation was observed because this antibiotic lacks a primary amine and carries a weaker dipole moment (Fig. 5 and 6).
), while amine1 and carbonyl2 maintain similar interactions along the pore axis; this rotation is expected to help the bulky body of the drug to advance through the narrow CR. The drug exits the CR with no further reorientation; however, interactions are broken as amine1 and carbonyl2 interact with the side chains of D107 and Q60, respectively. Overall, our analysis shows that 6DNM-NH3 permeates through the CR via a stepwise mechanism as the drug hops in order for amine1 and carbonyl2 to interact with residues along the pore. In contrast, for 6DNM, significantly fewer hydrogen bonds and a completely different orientation was observed because this antibiotic lacks a primary amine and carries a weaker dipole moment (Fig. 5 and 6).
Our molecular rationalization for the increased permeation through addition of a primary amine could be generalized to the addition of other positively charged groups. In fact, we have previously shown that the addition of other positively charged nitrogen groups, namely N-alkyl guanidiniums and pyridiniums also significantly increases the accumulation of small molecules in E. coli.92 Furthermore, our mechanism could also be generalized to other general-diffusion porins of bacteria, such as OmpC (E. coli), OmpK36 (K. pneumoniae) and OmpE36 (E. cloacae), since these porins have a similar architecture to OmpF and conserve several key residues involved in the permeation process (Fig. S16†).94,95
D113 mutation decreases 6DNM-NH3 accumulation inside E. coli
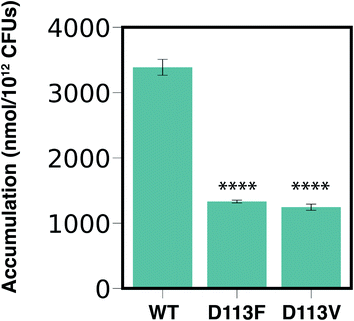
Our computational analysis showed that amine1-D113 is the most persistent interaction along the entire CR (Fig. 5 and 6). To validate the importance of this interaction in permeation of 6DNM-NH3 through OmpF, we compared experimentally the accumulation of 6DNM-NH3 in E. coli BW25113 (parental strain) with two strains containing single mutants in OmpF, E. coli OmpFD113V and E. coli OmpFD113F. Based on our simulation results, we expect cells expressing D113V- and D113F-OmpF to accumulate 6DNM-NH3 to a lesser extent than cells expressing WT-OmpF, because substitution of D113 with uncharged amino acids can disrupt favorable interactions with amine1 at the CR, which would enthalpically compensate for the entropic loss of the drug in this region. The loss of this favorable interaction is therefore expected to decrease the rate of permeation through the porin in the designed OmpF mutants. In accordance with our expectations, we observed a 2.5 fold decrease in the accumulation for cells expressing either mutant (Fig. 7). Furthermore, we provide experimental evidence of a direct relation between accumulation in the bacteria and permeation through porins; this relation has only been shown theoretically previously.93Concluding remarks
MD simulations can provide important structural/dynamic information on molecular processes that can not be obtained using typical experimental methods due to their inherently limited temporal/spatial resolutions. However, despite the ever-increasing capability of supercomputers, the typical timescale of atomistic MD simulations is insufficient to adequately sample configuration space for slow molecular processes. This prevents an accurate description of processes such as membrane transport which occur on long timescales (milliseconds or longer) and include slow degrees of freedoms (DOFs). To alleviate this problem enhanced sampling methods that can bias sampling along the most relevant DOFs are used; however, sufficient sampling of configuration space still remains daunting unless additional simplifications are made.One such simplification is to focus the calculations on a pathway that describes the most relevant DOFs during a structural transition. Identifying this transition pathway using conventional methods can still be computationally expensive; therefore, we have developed an efficient, heuristic approach using a combination of Monte Carlo simulation and graph theory. Within this approach, we first create a dataset of discrete energy minimized molecular states using a grid-based workflow.51 This dataset could be created for any system by exploring the states along all the relevant DOFs and approximately calculating the energy associated with each state. We then use the resulting dataset to determine multiple energetically favorable trajectories along the molecular process of interest using our novel Monte Carlo based pathway search (MCPS) algorithm. Finally, we determine the most likely pathway sampled in our MCPS trajectories using Dijkstra's algorithm and use this pathway to determine the free-energy underlying the molecular process with established enhanced sampling techniques such as BEUS. It is important to note that the resulting pathways could also be used to improve the quality of other enhanced sampling methods such as metadynamics and ABF.
We applied our approach to investigate antibiotic permeation through outer membrane (OM) porins of Gram-negative bacteria; a process that involves multiple slow DOFs, most importantly translation and orientation of the drug. This application is highly biomedically relevant since these pathogens are becoming increasingly resistant to currently available antibiotics, and the development of new antibiotics targeting them has been slow.1 Specifically, we investigated the molecular basis for the conversion of Gram-positive-only to broad-spectrum antibiotics with the addition of a primary amine group as observed in our previous experiments. We found that the free-energy barrier for permeation was significantly lower for the aminated derivative corresponding to a greater permeability through OM porins. Further analysis revealed that the added amino group facilitates favorable antibiotic permeation through porins by enabling the drug molecule to align its dipole to the intrinsic electric field of the porin and by forming interactions with several charged residues. The importance of these interactions, which appear to be conserved among different species, to effective permeation across the outer membrane of Gram-negative bacteria was further validated with experimental mutagenesis and whole-cell accumulation assays. In general, the structural insights offered by this study on the mechanisms by which the primary amine enhances permeation of antibiotics could help to convert other Gram-positive-only antibiotics into broad-spectrum antibiotics. Furthermore, our novel computational method could be generalized to sample better other long-timescale molecular processes involving slow DOFs.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Code availability
Simulation trajectories were collected using NAMD. Visualization and analysis were performed using VMD and Python. All of these software packages are publicly available. Code for the MCPS algorithm were written in Python, C++, and Tcl, and available for public use at https://github.com/nandanhaloi123/MonteCarloPathwaySearch.Author contributions
N. H., A. K. V., P. C. W., P. J. H., and E. T. designed research; N. H., A. K. V., E. J. G., and A. P. performed research; N. H. and A. K. V., E. J. G., and W. W. M. analyzed data; and N. H., A. K. V., and E. T. wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is supported by National Institutes of Health grants R01-AI136773 (to WWM, ET and PJH), R01-HL131673 (to ET), and P41-GM104601 (to ET). Simulations in this study have been performed using allocations at National Science Foundation Supercomputing Centers (XSEDE grant number MCA06N060 to ET) and the Blue Waters supercomputer of National Center for Supercomputing Applications at University of Illinois at Urbana-Champaign.References
- M. Gasser, W. Zingg, A. Cassini and A. Kronenberg, Attributable deaths and disability-adjusted life-years caused by infections with antibiotic-resistant bacteria in Switzerland, Lancet Infect. Dis., 2019, 19, 17–18 CrossRef.
- CDC, Antibiotic resistance threats in the United States, 2019. Atlanta, GA: U.S.A; US Department of Health and Human Services, Centers for Disease Control and Prevention 2019.
- H. Nikaido, Molecular basis of bacterial outer membrane permeability revisited, Microbiol. Mol. Biol. Rev., 2003, 67, 593–656 CrossRef CAS PubMed.
- W. Vollmer, Bacterial outer membrane evolution via sporulation?, Nat. Chem. Biol., 2011, 8, 14–18 CrossRef PubMed.
- D. G. Brown, T. L. May-Dracka, M. M. Gagnon and R. Tommasi, Trends and exceptions of physical properties on antibacterial activity for Gram-positive and Gram-negative pathogens, J. Med. Chem., 2014, 57, 10144–10161 CrossRef CAS PubMed.
- R. ÓShea and H. E. Moser, Physicochemical properties of antibacterial compounds: implications for drug discovery, J. Med. Chem., 2008, 51, 2871–2878 CrossRef PubMed.
- D. J. Payne, M. N. Gwynn, D. J. Holmes and D. L. Pompliano, Drugs for bad bugs: confronting the challenges of antibacterial discovery, Nat. Rev. Drug Discovery, 2007, 6, 29–40 CrossRef CAS PubMed.
- M. F. Richter, B. S. Drown, A. P. Riley, A. Garcia, T. Shirai, R. L. Svec and P. J. Hergenrother, Predictive compound accumulation rules yield a broad-spectrum antibiotic, Nature, 2017, 545, 299–304 CrossRef CAS PubMed.
- M. F. Richter and P. J. Hergenrother, The challenge of converting Gram-positive-only compounds into broad-spectrum antibiotics, Ann. N. Y. Acad. Sci., 2019, 1435, 18 CrossRef CAS PubMed.
- E. I. Parkinson, J. S. Bair, B. A. Nakamura, H. Y. Lee, H. I. Kuttab, E. H. Southgate, S. Lezmi, G. W. Lau and P. J. Hergenrother, Deoxynybomycins inhibit mutant DNA gyrase and rescue mice infected with fluoroquinolone-resistant bacteria, Nat. Commun., 2015, 6, 1–9 Search PubMed.
- S. E. Motika, R. J. Ulrich, E. J. Geddes, H. Y. Lee, G. W. Lau and P. J. Hergenrother, Gram-negative antibiotic active through inhibition of an essential riboswitch, J. Am. Chem. Soc., 2020, 142, 10856–10862 CrossRef CAS PubMed.
- E. N. Parker, B. S. Drown, E. J. Geddes, H. Y. Lee, N. Ismail, G. W. Lau and P. J. Hergenrother, Implementation of permeation rules leads to a FabI inhibitor with activity against Gram-negative pathogens, Nat. Microbiol., 2020, 5, 67–75 CrossRef CAS PubMed.
- Y. Li, J. J. Gardner, K. R. Fortney, I. V. Leus, V. Bonifay, H. I. Zgurskaya, A. A. Pletnev, S. Zhang, Z.-Y. Zhang and G. W. Gribble, et al., First-generation structure-activity relationship studies of 2, 3, 4, 9-tetrahydro-1H-carbazol-1-amines as CpxA phosphatase inhibitors, Bioorg. Med. Chem. Lett., 2019, 29, 1836–1841 CrossRef PubMed.
- L. D. Andrews, T. R. Kane, P. Dozzo, C. M. Haglund, D. J. Hilderbrandt, M. S. Linsell, T. Machajewski, G. McEnroe, A. W. Serio and K. B. Wlasichuk, et al., Optimization and mechanistic characterization of pyridopyrimidine inhibitors of bacterial biotin carboxylase, J. Med. Chem., 2019, 62, 7489–7505 CrossRef CAS PubMed.
- T. Lukežič, A. A. Fayad, C. Bader, K. Harmrolfs, J. Bartuli, S. Groß, U. Lešnik, F. Hennessen, J. Herrmann and v. Pikl, et al., Engineering atypical tetracycline formation in Amycolatopsis sulphurea for the production of modified chelocardin antibiotics, ACS Chem. Biol., 2019, 14, 468477 CrossRef PubMed.
- F. Cohen, J. B. Aggen, L. D. Andrews, Z. Assar, J. Boggs, T. Choi, P. Dozzo, A. N. Easterday, C. M. Haglund and D. J. Hildebrandt, et al., Optimization of LpxC inhibitors for antibacterial activity and cardiovascular safety, ChemMedChem, 2019, 14, 1560–1572 CrossRef CAS PubMed.
- D. Masci, C. Hind, M. K. Islam, A. Toscani, M. Clifford, A. Coluccia, I. Conforti, M. Touitou, S. Memdouh and X. Wei, et al., Switching on the activity of 1, 5-diaryl-pyrrole derivatives against drug-resistant ESKAPE bacteria: Structure-activity relationships and mode of action studies, Eur. J. Med. Chem., 2019, 178, 500–514 CrossRef CAS PubMed.
- Y. Hu, H. Shi, M. Zhou, Q. Ren, W. Zhu, W. Zhang, Z. Zhang, C. Zhou, Y. Liu and X. Ding, et al., Discovery of pyrido [2, 3-b] indole derivatives with Gram-negative activity targeting both DNA gyrase and topoisomerase IV, J. Med. Chem., 2020, 63, 9623–9649 CrossRef CAS PubMed.
- S. W. Cowan, T. Schirmer, G. Rummel, M. Steiert, R. Ghosh, R. A. Pauptit, J. N. Jansonius and J. P. Rosenbusch, Crystal structures explain functional properties of two E. coli porins, Nature, 1992, 358, 727–733 CrossRef CAS PubMed.
- A. Kumar, E. Hajjar, P. Ruggerone and M. Ceccarelli, Molecular simulations reveal the mechanism and the determinants for ampicillin translocation through OmpF, J. Phys. Chem. B, 2010, 114, 9608–9616 CrossRef CAS PubMed.
- C. Danelon, E. M. Nestorovich, M. Winterhalter, M. Ceccarelli and S. M. Bezrukov, Interaction of zwitterionic penicillins with the OmpF channel facilitates their translocation, Biophys. J., 2006, 90, 1617–1627 CrossRef CAS PubMed.
- H. Bajaj, S. Acosta Gutierrez, I. Bodrenko, G. Malloci, M. A. Scorciapino, M. Winterhalter and M. Ceccarelli, Bacterial outer membrane porins as electrostatic nanosieves: exploring transport rules of small polar molecules, ACS Nano, 2017, 11, 5465–5473 CrossRef CAS PubMed.
- J. A. Bafna, E. Sans-Serramitjana, S. Acosta-Gutierrez, I. V. Bodrenko, D. Hörömpöli, A. Berscheid, H. Broetz-Oesterhelt, M. Winterhalter and M. Ceccarelli, Kanamycin uptake into Escherichia coli is facilitated by OmpF and OmpC porin channels located in the outer membrane, ACS Infect. Dis., 2020, 6, 1855–1865 CrossRef CAS PubMed.
- S. Acosta-Gutiérrez, L. Ferrara, M. Pathania, M. Masi, J. Wang, I. Bodrenko, M. Zahn, M. Winterhalter, R. A. Stavenger and J.-M. Pagès, et al., Getting drugs into Gram-negative bacteria: rational rules for permeation through general porins, ACS Infect. Dis., 2018, 4, 1487–1498 CrossRef PubMed.
- S. Acosta-Gutierrez, M. A. Scorciapino, I. Bodrenko and M. Ceccarelli, Filtering with electric field: the case of E. coli porins, J. Phys. Chem. Lett., 2015, 6, 1807–1812 CrossRef CAS PubMed.
- V. K. Golla, E. Sans-Serramitjana, K. R. Pothula, L. Benier, J. A. Bafna, M. Winterhalter and U. Kleinekathöfer, Fosfomycin permeation through the outer membrane porin OmpF, Biophys. J., 2019, 116, 258–269 CrossRef CAS PubMed.
- T. Mach, P. Neves, E. Spiga, H. Weingart, M. Winterhalter, P. Ruggerone, M. Ceccarelli and P. Gameiro, Facilitated permeation of antibiotics across membrane channels- interaction of the quinolone moxifloxacin with the OmpF Channel, J. Am. Chem. Soc., 2008, 130, 13301–13309 CrossRef CAS PubMed.
- K. R. Mahendran, E. Hajjar, T. Mach, M. Lovelle, A. Kumar, I. Sousa, E. Spiga, H. Weingart, P. Gameiro and M. Winterhalter, et al., Molecular basis of enrofloxacin translocation through OmpF, an outer membrane channel of Escherichia coli when binding does not imply translocation, J. Phys. Chem. B, 2010, 114, 5170–5179 CrossRef CAS PubMed.
- M. A. Scorciapino, S. Acosta-Gutierrez, D. Benkerrou, T. Agostino, G. Malloci, S. Samanta, I. Bodrenko and M. Ceccarelli, Rationalizing the permeation of polar antibiotics into Gram-negative bacteria, J. Phys.: Condens. Matter, 2017, 29, 113001 CrossRef PubMed.
- K. R. Pothula, C. J. Solano and U. Kleinekathöefer, Simulations of outer membrane channels and their permeability, Biochim. Biophys. Acta, Biomembr., 2016, 1858, 1760–1771 CrossRef CAS PubMed.
- J. Vergalli, I. V. Bodrenko, M. Masi, L. Moynié, S. Acosta-Gutiérrez, J. H. Naismith, A. Davin-Regli, M. Ceccarelli, B. Van den Berg and M. Winterhalter, et al., Porins and small-molecule translocation across the outer membrane of Gram-negative bacteria, Nat. Rev. Microbiol., 2020, 18, 164176 Search PubMed.
- F. Yoshimura and H. Nikaido, Diffusion of beta-lactam antibiotics through the porin channels of Escherichia coli K-12, Antimicrob. Agents Chemother., 1985, 27, 84–92 CrossRef CAS PubMed.
- E. M. Nestorovich, C. Danelon, M. Winterhalter and S. M. Bezrukov, Designed to penetrate: time-resolved interaction of single antibiotic molecules with bacterial pores, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 9789–9794 CrossRef CAS PubMed.
- J. D. Prajapati, C. J. Fernńdez Solano, M. Winterhalter and U. Kleinekathöfer, Characterization of ciprofloxacin permeation pathways across the porin OmpC using metadynamics and a string method, J. Chem. Theory Comput., 2017, 13, 4553–4566 CrossRef CAS PubMed.
- J. D. Prajapati, C. J. F. Solano, M. Winterhalter and U. Kleinekathöfer, Enrofloxacin permeation pathways across the porin OmpC, J. Phys. Chem. B, 2018, 122, 1417–1426 CrossRef CAS PubMed.
- W. Im and B. Roux, Ions and counterions in a biological channel: a molecular dynamics study of OmpF porin from Escherichia coli in an explicit membrane with 1 M KCl aqueous salt solution, J. Mol. Biol., 2002, 319, 1177–1197 CrossRef CAS.
- K. M. Robertson and D. P. Tieleman, Orientation and interactions of dipolar molecules during transport through OmpF porin, FEBS Lett., 2002, 528, 53–57 CrossRef CAS.
- S. Pezeshki, C. Chimerel, A. Bessenov, M. Winterhalter and U. Kleinekathöfer, Understanding ion conductance on a molecular level: An all-atom modeling of the bacterial porin OmpF, Biophys. J., 2009, 97, 1898–1906 CrossRef CAS PubMed.
- O. S. Smart, J. G. Neduvelil, X. Wang, B. Wallace and M. S. Sansom, HOLE: a program for the analysis of the pore dimensions of ion channel structural models, J. Mol. Graphics, 1996, 14, 354–360 CrossRef CAS PubMed.
- K. R. Mahendran, M. Kreir, H. Weingart, N. Fertig and M. Winterhalter, Permeation of antibiotics through Escherichia coli OmpF and OmpC porins: screening for influx on a single-molecule level, J. Biomol. Screening, 2010, 15, 302–307 CrossRef CAS PubMed.
- G. M. Torrie and J. P. Valleau, Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella Sampling, J. Comput. Phys., 1977, 23, 187–199 CrossRef.
- Y. Sugita and Y. Okamoto, Replica-exchange molecular dynamics method for protein folding, Chem. Phys. Lett., 1999, 314, 141–151 CrossRef CAS.
- Y. Sugita, A. Kitao and Y. Okamoto, Multidimensional replica-exchange method for free-energy calculations, J. Chem. Phys., 2000, 113, 6042–6051 CrossRef CAS.
- M. Moradi and E. Tajkhorshid, Mechanistic picture for conformational transition of a membrane transporter at atomic resolution, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 18916–18921 CrossRef CAS PubMed.
- M. Moradi and E. Tajkhorshid, Computational recipe for efficient description of large-scale conformational changes in biomolecular systems, J. Chem. Theory Comput., 2014, 10, 2866–2880 CrossRef CAS PubMed.
- A. Barducci, G. Bussi and M. Parrinello, Well-Tempered Metadynamics: A Smoothly Converging and Tunable Free-Energy Method, Phys. Rev. Lett., 2008, 100, 020603 CrossRef PubMed.
- J. Comer, J. C. Gumbart, J. Hénin, T. Lelièvre, A. Pohorille and C. Chipot, The adaptive biasing force method: Everything you always wanted to know but were afraid to ask, J. Phys. Chem. B, 2015, 119, 1129–1151 CrossRef CAS PubMed.
- A. Laio and F. L. Gervasio, Metadynamics: a method to simulate rare events and reconstruct the free energy in biophysics, chemistry and material science, Rep. Prog. Phys., 2008, 71, 126601 CrossRef.
- A. Barducci, M. Bonomi and M. Parrinello, Metadynamics, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 826–843 CAS.
- G. Bussi and D. Branduardi, et al., Free-energy calculations with metadynamics: Theory and practice, Rev. Comput. Chem., 2015, 28, 1–49 CAS.
- J. A. Coleman, D. Yang, Z. Zhao, P.-C. Wen, C. Yoshioka, E. Tajkhorshid and E. Gouaux, Serotonin transporter-ibogaine complexes illuminate mechanisms of inhibition and transport, Nature, 2019, 569, 141–145 CrossRef CAS PubMed.
- R. Efremov and L. Sazanov, Structure of Escherichia coli OmpF porin from lipidic mesophase, J. Struct. Biol., 2012, 178, 311–318 CrossRef CAS PubMed.
- A. Karshikoff, V. Spassov, S. Cowan, R. Ladenstein and T. Schirmer, Electrostatic properties of two porin channels from Escherichia coli, J. Mol. Biol., 1994, 240, 372–384 CrossRef CAS PubMed.
- S. Varma, S.-W. Chiu and E. Jakobsson, The influence of amino acid protonation states on molecular dynamics simulations of the bacterial porin OmpF, Biophys. J., 2006, 90, 112–123 CrossRef CAS PubMed.
- W. Im and B. Roux, Ion permeation and selectivity of OmpF Porin: A theoretical study based on Molecular Dynamics, Brownian Dynamics, and Continuum Electrodiffusion theory, J. Mol. Biol., 2002, 322, 851–869 CrossRef CAS PubMed.
- M. Ceccarelli, C. Danelon, A. Laio and M. Parrinello, Microscopic Mechanism of Antibiotics Translocation through Porin, Biophys. J., 2004, 87, 58–64 CrossRef CAS PubMed.
- N. Modi, P. R. Singh, K. R. Mahendran, R. Schulz, M. Winterhalter and U. Kleinekathöfer, Probing the transport of ionic liquids in aqueous solution through nanopores, J. Phys. Chem. Lett., 2011, 2, 2331–2336 CrossRef CAS.
- R. Marques, C. Bouville, M. Ribardière, L. P. Santos and K. Bouatouch, Spherical Fibonacci point sets for illumination integrals, Comput. Graph. Forum, 2013, 32, 134–143 CrossRef.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Schulten, Scalable molecular dynamics with NAMD, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS PubMed.
- J. C. Phillips, et al., Scalable molecular dynamics on CPU and GPU architectures with NAMD, J. Chem. Phys., 2020, 153, 044130 CrossRef CAS PubMed.
- A. K. Vasan, N. Haloi, R. J. Ulrich, M. E. Metcalf, P.-C. Wen, W. W. Metcalf, P. J. Hergenrother, D. Shukla and E. Tajkhorshid, Investigation of gating in outer membrane porins provides new perspectives on antibiotic resistance mechanisms, bioRxiv, 2021 DOI:10.1101/2021.09.09.459668.
- E. W. Dijkstra, A note on two problems in connexion with graphs, Numer. Math., 1959, 1, 269–271 CrossRef.
- P. Metzner, C. Schütte and E. Vanden-Eijnden, Transition path theory for Markov jump processes, Multiscale Model. Simul., 2009, 7, 1192–1219 CrossRef CAS.
- S. Jo, T. Kim, V. G. Iyer and W. Im, CHARMM-GUI: a Web-based Graphical User Interface for CHARMM, J. Comput. Chem., 2008, 29, 1859–1865 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- K. Lam and E. Tajkhorshid, Membrane Interactions of Cy3/Cy5 Fluorophores and Their Effects on Membrane Protein Dynamics, Biophys. J., 2020, 119, 24–34 CrossRef CAS PubMed.
- S. Kumar, D. Bouzida, R. H. Swendsen, P. A. Kollman and J. M. Rosenberg, THE weighted histogram analysis method for free-energy calculations on biomolecules. I. The method, J. Comput. Chem., 1992, 13, 1011–1021 CrossRef CAS.
- C. Bartels, Analyzing biased Monte Carlo and molecular dynamics simulations, Chem. Phys. Lett., 2000, 331, 446–454 CrossRef CAS.
- J. Huang, S. Rauscher, G. Nawrocki, T. Ran, M. Feig, B. L. de Groot, H. Grubmüller and A. D. MacKerell Jr, CHARMM36m: An improved force field for folded and intrinsically disordered proteins, Nat. Methods, 2017, 14, 71–73 CrossRef CAS PubMed.
- J. B. Klauda, R. M. Venable, J. A. Freites, J. W. O'Connor, D. J. Tobias, C. Mondragon-Ramirez, I. Vorobyov, A. D. MacKerell Jr and R. W. Pastor, Update of the CHARMM all-atom additive force field for lipids: Validation on six lipid types, J. Phys. Chem. B, 2010, 114, 7830–7843 CrossRef CAS PubMed.
- K. Vanommeslaeghe and A. D. MacKerell Jr, Automation of the CHARMM General Force Field (CGenFF) I: bond perception and atom typing, J. Chem. Inf. Model., 2012, 52, 3144–3154 CrossRef CAS PubMed.
- K. Vanommeslaeghe, E. P. Raman and A. D. MacKerell Jr, Automation of the CHARMM General Force Field (CGenFF) II: assignment of bonded parameters and partial atomic charges, J. Chem. Inf. Model., 2012, 52, 3155–3168 CrossRef CAS PubMed.
- K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes, I. Vorobyov and A. D. MacKerell Jr, CHARMM General Force Field: a force field for drug-like molecules compatible with the CHARMM all-atom additive biological force fields, J. Comput. Chem., 2010, 31, 671–690 CAS.
- T. Darden, D. York and L. Pedersen, Particle mesh Ewald: an Nlog(N) method for Ewald sums in large systems, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- G. J. Martyna, D. J. Tobias and M. L. Klein, Constant pressure molecular dynamics algorithms, J. Chem. Phys., 1994, 101, 4177–4189 CrossRef CAS.
- S. E. Feller, Y. Zhang and R. W. Pastor, Constant pressure molecular dynamics simulation: the Langevin piston method, J. Chem. Phys., 1995, 103, 4613–4621 CrossRef CAS.
- I. Ghai, A. Pira, M. A. Scorciapino, I. Bodrenko, L. Benier, M. Ceccarelli, M. Winterhalter and R. Wagner, General method to determine the flux of charged molecules through nanopores applied to β-lactamase inhibitors and OmpF, J. Phys. Chem. Lett., 2017, 8, 1295–1301 CrossRef CAS PubMed.
- C. T. Lee, J. Comer, C. Herndon, N. Leung, A. Pavlova, R. V. Swift, C. Tung, C. N. Rowley, R. E. Amaro, C. Chipot, Y. Wang and J. C. Gumbart, Simulation-based approaches for determining membrane permeability of small compounds, J. Chem. Inf. Model., 2016, 56, 721–733 CrossRef CAS PubMed.
- J. Henin, E. Tajkhorshid, K. Schulten and C. Chipot, Diffusion of glycerol through Escherichia coli aquaglyceroporin GlpF, Biophys. J., 2008, 94, 832–839 CrossRef CAS PubMed.
- G. Hummer, Position-dependent diffusion coefficients and free energies from Bayesian analysis of equilibrium and replica molecular dynamics simulations, New J. Phys., 2005, 7, 34 CrossRef.
- W. Humphrey, A. Dalke and K. Schulten, VMD: visual molecular dynamics, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- W. W. Metcalf, W. Jiang, L. L. Daniels, S.-K. Kim, A. Haldimann and B. L. Wanner, Conditionally replicative and conjugative plasmids carrying lacZα for cloning, mutagenesis, and allele replacement in bacteria, Plasmid, 1996, 35, 1–13 CrossRef CAS PubMed.
- K. A. Datsenko and B. L. Wanner, One-step inactivation of chromosomal genes in Escherichia coli K-12 using PCR products, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 6640–6645 CrossRef CAS PubMed.
- J. A. Blodgett, P. M. Thomas, G. Li, J. E. Velasquez, W. A. Van Der Donk, N. L. Kelleher and W. W. Metcalf, Unusual transformations in the biosynthesis of the antibiotic phosphinothricin tripeptide, Nat. Chem. Biol., 2007, 3, 480–485 CrossRef CAS PubMed.
- S. A. Borisova, H. D. Christman, M. M. Metcalf, N. A. Zulkepli, J. K. Zhang, W. A. Van Der Donk and W. W. Metcalf, Genetic and biochemical characterization of a pathway for the degradation of 2-aminoethylphosphonate in Sinorhizobium meliloti 1021, J. Biol. Chem., 2011, 286, 22283–22290 CrossRef CAS PubMed.
- E. J. Geddes, Z. Li and P. J. Hergenrother, A LC-MS/MS assay and complementary web-based tool to quantify and predict compound accumulation in E. coli, Nat. Protoc., 2021, 16, 4833–4854 CrossRef CAS PubMed.
- D. Williamson, K. Brown, R. Luddington, C. Baglin and T. Baglin, Factor V Cambridge: a new mutation (Arg306 → Thr) associated with resistance to activated protein C, Blood, 1998, 91, 1140–1144 CrossRef CAS PubMed.
- H. Fu, H. Chen, X. Wang, H. Chai, X. Shao, W. Cai and C. Chipot, Finding an optimal pathway on a multidimensional free-energy landscape, J. Chem. Inf. Model., 2020, 60, 5366–5374 CrossRef CAS PubMed.
- E. Vanden-Eijnden, et al., Transition-path theory and path-finding algorithms for the study of rare events, Annu. Rev. Phys. Chem., 2010, 61, 391–420 CrossRef PubMed.
- Z. Liu and H. S. Chan, Desolvation is a likely origin of robust enthalpic barriers to protein folding, J. Mol. Biol., 2005, 349, 872–889 CrossRef CAS PubMed.
- R. O. Dror, A. C. Pan, D. H. Arlow, D. W. Borhani, P. Maragakis, Y. Shan, H. Xu and D. E. Shaw, Pathway and mechanism of drug binding to G-protein-coupled receptors, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 13118–13123 CrossRef CAS PubMed.
- S. J. Perlmutter, E. J. Geddes, B. S. Drown, S. E. Motika, M. R. Lee and P. J. Hergenrother, Compound Uptake into E. coli Can Be Facilitated by N-Alkyl Guanidiniums and Pyridiniums, ACS Infect. Dis., 2021, 7, 162–173 CrossRef CAS PubMed.
- S. Acosta-Gutiérrez, I. V. Bodrenko and M. Ceccarelli, The Influence of Permeability through Bacterial Porins in Whole-Cell Compound Accumulation, Antibiotics, 2021, 10, 635 CrossRef PubMed.
- F. Sieversi, A. Wilm, D. Dineen, T. J. Gibson, K. Karplus, W. Li, R. Lopez, H. McWilliam, M. Remmert, J. Söding, J. D. Thompson and D. G. Higgins, Fast, scalable generation of high-quality protein multiple sequence alignments using Clustal Omega, Mol. Syst. Biol., 2011, 7, 539 CrossRef PubMed.
- The UniProt Consortium, UniProt: a worldwide hub of protein knowledge, Nucleic Acids Res., 2019, 47, D506–D515 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc04445a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |