Unravelling the last milliseconds of an individual graphene nanoplatelet before impact with a Pt surface by bipolar electrochemistry

Abstract

Contactless interactions of micro/nano-particles near electrochemically or chemically active interfaces are ubiquitous in chemistry and biochemistry. Forces arising from a convective field, an electric field or chemical gradients act on different scales ranging from few microns down to few nanometers making their study difficult. Here, we correlated optical microscopy and electrochemical measurements to track at the millisecond timescale the dynamics of individual two-dimensional particles, graphene nanoplatelets (GNPs), when approaching an electrified Pt micro-interface. Our original approach takes advantage of the bipolar feedback current recorded when a conducting particle approaches an electrified surface without electrical contact and numerical simulations to access the velocity of individual GNPs. We evidenced a strong deceleration of GNPs from few tens of μm s⁻¹ down to few μm s⁻¹ within the last μm above the surface. This observation reveals the existence of strongly non-uniform forces between tens of and a thousand nanometers from the surface.

---

Introduction

Interaction between particles and surfaces is ubiquitous in biology and chemistry.^1–4 Forces controlling the approach of a single platelet from a blood vessel or a single active metal nanoparticle from an electrode control strongly the efficiency of the interaction and thus need to be precisely understood.^5,6 Observation of both close- and long-range forces on individual particles with dynamics of few ms is an extraordinarily challenging task. Single entity electrochemistry proved to be a powerful method to study individual nanoparticles.^7–12 The high temporal resolution of electrochemical measurements allows probing dynamics of electro-catalysis,^13–17 electrolysis,^18–23 electro-nucleation and growth,^24–30 as well as motion of individual particles.^31–35 For example, several groups showed that Ag nanoparticles (Ag NP) may rebound several times on the surface of the electrode before being completely oxidized.^20,21,23 White and coworkers showed that the dynamics of the rebound controls the overall kinetic of Ag NP oxidation and can be tuned by adjusting the viscosity of the solution.³⁶ These works revealed the potential complexity of nanoparticle dynamics near a surface.

Uncovering the complexity of nanoparticle dynamics often necessitates the combination of electrochemistry with optical techniques. Among the different optical techniques used so far are 3D super-resolution holography,¹⁸ surface plasmonic resonance microscopy,^37,38 backside absorbing layer microscopy (BALM),³² fluorescent microscopy,¹⁹ dark-field microscopy,^39,40 and many others.^12,41 For example, Tschulik and coworkers combined dark-field microscopy and hyperspectral imaging with electrochemistry to study the oxidation of single Ag NP in the presence of chloride ion.³⁹ They observed that the intensity decrease of the optical signal is caused by the reversible formation of AgCl rather than by Ag dissolution. Kanoufi and coworkers utilized BALM to image the reduction dynamics of single silver halide NP and visualized that the NP conversion proceeds to completion through the formation of multiple inclusions rather than by the classical core-shrinking mechanism.³²

Recently, Thorgaard and Lemay's groups observed complex toroidal trajectories of fluorescent particles revealing electro-osmotic flow near an ultra-microelectrode (UME) under supporting electrolyte of low concentrations.^33,34 We also showed that two-dimensional (2D) graphene nanoplatelets (GNPs) collide on the surface of a UME with a preferential up-right orientation and then, rotate at few ° per ms to lay flat on the electrode surface.³⁵ Up to now monitoring dynamics of individual nanoparticles by single entity electrochemistry required electrical contact and thus could only provide indirect information on particle motion when this latter is not in contact with the surface of the electrode.

In this article, we combined time-resolved bright-field microscopy and electrochemistry with finite element simulation to investigate in a contactless mode the motion of individual GNPs at few μm above the surface of a UME. The contact-less tracking of GNPs is based on a novel concept of transient bipolar feedback. We investigated the effect of viscosity on the velocity of GNP approaching the UME and determined velocity profiles of single GNPs with a time resolution of ms and spanning from a couple of microns to solely few tens of nanometers away from the surface of a Pt micro-interface.

Results and discussion

Fig. 1A shows a typical SEM image of a GNP ca. 15 nm thick and 3.2 ± 2.0 μm long (see Fig. S3†). Fig. 1B shows the experimental setup used to monitor the approach of individual GNPs toward the surface of the Pt UME. The UME is facing downward with its surface positioned 300 μm above a coverslip closing the bottom of the opto-electrochemical cell. A two-electrode setup is used to apply a potential and measure the current. The Pt UME is biased at 0.4 V to drive mass-transfer limited oxidation of 1,1′-ferrocenedimethanol (FcDM). The camera and the ammeter are synchronized externally and the data is collected at 1 kHz and 2 kHz, respectively (see Fig. S5†). Fig. 1C shows a typical chronoamperogram starting with a steady-state current of 4.702 nA corresponding to the oxidation of FcDM on Pt. At 0.772 s, the current starts to rise reaching 5.18 nA at 1.5 s (red trace). Afterwards, the rise is followed by decay after 1.500 s. Such current transients are never observed in absence of GNP (see Fig. S6†). Fig. 1D shows simultaneous optical micrographs of the Pt disk, and the full movie is provided in Movie S1.† The Pt disk looks dark while the GNP looks bright. At 0.500 s a white shadow appears on the top left side of the micrographs. Progressively the edges of an individual GNP can be distinguished. At 2.000 s the GNP lays down on the Pt surface and does not move anymore allowing to capture a sharp image of the edges of the GNP (the contour of the GNP is highlighted by the yellow dashed line). The red points on all the micrographs were incrusted to evidence that the top side of the GNP appears sharp and does not move anymore after ca. 1.500 s. At that time the top edge of the GNP is touching the Pt surface while the rest of the GNP is still in solution, out of focus. We recently explained how the rotation of a GNP, once in contact with the UME, can lead via area amplification to current decays such as the one observed after 2.000 s (blue portion of the curve shown in Fig. 1C).³⁵ However, a far more surprising observation here is the increase of current before the GNP enters in contact with the UME.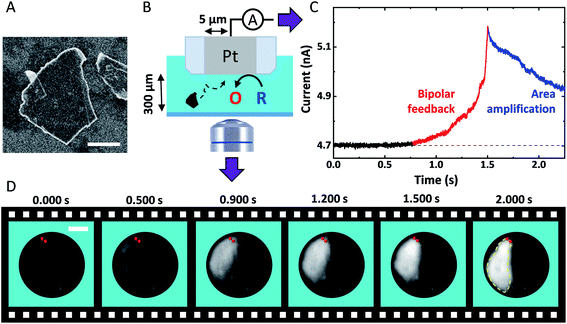

Fig. 1 (A) SEM image of a GNP adsorbed on a Si substrate. The scale bar represents 1 μm. (B) Scheme of the opto-electrochemical cell used to simultaneously record a video of the surface of a 5 μm radius Pt UME and the current passing through this latter. O and R represent FcDM⁺ and FcDM, respectively. (C) Chronoamperogram recorded at 2 kHz with the Pt UME biased at 0.4 V vs. Ag/AgCl 3.4 M KCl in presence of 3.5 mM FcDM, 0.01% v/v PSS and 0.43 mg mL⁻¹ GNP. The supporting electrolyte is 10 μM NaOH. (D) Bright-field optical micrographs of the Pt surface recorded in synchronization with the chronoamperogram in (C). The red points and yellow dashed lines are manually drawn to indicate the position where the GNP first touches the Pt surface and then the edges of the GNP, respectively. The simultaneous movie and current trace is provided in Movie S1.†

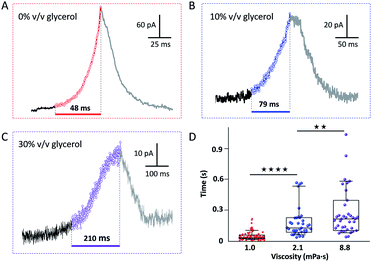
Fig. 2(A–C) show representative current spikes recorded for different GNP suspensions having different viscosity. The viscosity was varied from 1.0 to 8.8 mPa s by the addition of glycerol (see Fig. S7†). Fig. 2D shows the average rise time of the current spike as a function of the viscosity of the solution. Higher viscosity leads to a longer current rise time. Since the motion of the GNP is directly affected by the viscosity of the solution, we conclude that the rise of the current transient and the motion of the GNP are correlated.

Fig. 2 Representative current transients in the presence of (A) 0, (B) 10 and (C) 30% v/v glycerol, with a viscosity of 1.0, 2.1 and 8.8 mPa s, respectively. (D) Statistical analysis of the average duration of the current rise. (**p < 0.01, ****p < 0.0001).

To explain our observation, we propose the existence of the positive feedback mechanism powered by bipolar electrochemistry, as shown in Fig. 3A. The GNP behaves as a bipolar electrode. FcDM (species “R” in Fig. 3A) is oxidized at the extremity of the GNP the furthest in solution while FcDM⁺ (species “O” in Fig. 3A) is being reduced back to FcDM at the extremity of the GNP closest from the UME. The regenerated FcDM can diffuse to the UME and be oxidized again hence increasing the anodic current. Positive feedback has been evidenced with SECM tips approaching unbiased conducting substrates^42–44 as well as networks of micro-ring electrodes at the bottom of a well in proximity with a high-area gold layer that is not electrically connected to the ring electrodes and left floating at the potential of the solution.^45,46

Fig. 3 (A) Schematic illustration of the bipolar feedback mechanism on a “model” spheroidal GNP of length L and width W positioned at a distance d from the UME. (B) Concentration profile of FcDM⁺ near the UME at a steady state where the black lines represent the normal flux of FcDM⁺. (C) Potential profile calculated from the concentration profile in (B) via Nernst equation. The scale bar represents 2 μm. (D) Potential along the z-axis of symmetry and the arc length of the GNP (schematically shown on top). The actor 1.05 comes from the difference between the length and the cord of a spheroid. The green and black traces are obtained for a conducting GNP and an insulating analog, respectively. (E) The driving force (black trace on the left axis) generated from the potential difference in (D) allows passing a current density shown on the right axis. The anodic and cathodic current densities are plotted in red and blue, respectively. The total bipolar current flowing through the GNP is 331 pA.

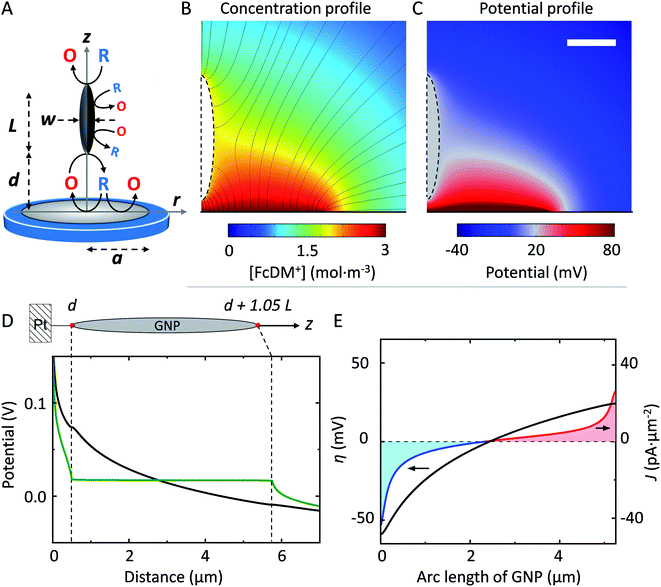
To support our hypothesis, we performed 2D axial numerical simulations describing the oxidation of FcDM on the UME in presence of a spheroidal conducting GNP, as depicted in Fig. 3A. We choose a prolate ellipsoid shape of GNP to allows for 2D simulations, while preserving the trends expected for a 3D system (see ESI†). The presence of a conducting GNP locally disturbs the concentration profile of FcDM⁺ (see Fig. 3B). These changes are not observed in presence of an insulating analog (see Fig. S10A†). Interestingly the concentration of FcDM⁺ and FcDM remains constant (orange color) over the entire surface of the GNP, and the flux of FcDM⁺ increases strongly between the bottom of the GNP and the UME (higher concentration of flux lines) indicating positive feedback for the UME in agreement with our observation. Fig. 3C presents the potential map calculated from the concentration profile via the Nernst equation. The variation of [O]/[R] in the diffusion layer by 2–3 order of magnitudes produces a difference of potential on the order of 120–180 mV near the Pt surface. A fraction of this potential difference will provide the electromotive force to drive faradaic reactions at both ends of the GNP in an attempt to locally reach chemical equilibrium. The equilibrium is reached when the concentrations at both ends are equal. As found in our simulation the potential within the GNP is constant and floats at about 17 mV (vs. E°_FcDM⁺/FcDM) (gray color in Fig. 3C).

The potential along the arc length of the GNP is plotted in green in Fig. 3D, while the potential computed for an insulating analog is in black. The difference between both potentials provides the driving force for the oxidation/reduction of FcDM/FcDM⁺ at the surface of GNP. The computed driving force (η, defined as the potential of the GNP vs. E°_FcDM⁺/FcDM) for the oxidation/reduction of FcDM/FcDM⁺ at the GNP surface is plotted in Fig. 3E (black trace on the left axis). It follows a logarithm relationship with the position along the GNP because of the non-linear concentration profile of FcDM/FcDM⁺ in the diffusion layer of the UME. Importantly, the sign of the driving force changes near the center of the GNP. As a result, both anodic and cathodic currents are expected to flow on the same object, as shown in red and blue traces on the right axis in Fig. 3E, respectively. The integration of the anodic and cathodic current densities along the entire surface of the GNP leads to no net charging of the GNP (as imposed in our model).

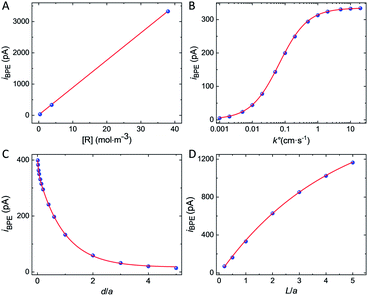
The simulated bipolar current, i_BPE, flowing through the GNP is a function of multiple experimental parameters. It depends on the concentration of the redox species, the kinetics of electron transfer, the distance between the GNP and the UME, as well as the size of the GNP. We computed i_BPE as a function of the initial concentration of [R] as well as the initial bulk [O]/[R] ratio in solution. The bipolar current is proportional to the initial concentration of [R] (see Fig. 4A) but independent of the initial bulk [O]/[R] ratio (see Fig. S11†). In practice, it is advantageous to maximize the current at the UME by using a high concentration of redox species. The presence of the other form of the redox couple (FcDM⁺ in our case) does not affect the bipolar current since the driving force for bipolar electrochemistry does not depend on the bulk [O]/[R] ratio at a certain position but the difference between the bulk [O]/[R] ratio and the local [O]/[R] controlled by electrochemical transformation at the surface of the electrode. On the other hand, the choice of the redox couple can drastically influence the kinetics of the electron transfer and in return i_BPE. Fig. 4B shows i_BPE as a function of k°. For a nernstian system (like FcDM⁺/FcDM), i_BPE is limited by mass transfer. As k° decreases below 0.01 cm s⁻¹, i_BPE decreases by two orders of magnitude. Sluggish electrochemical reactions (i.e. oxidation of hydrazine on carbon⁴⁷) should thus be avoided. A fast redox couple such as metallocene compounds is best suited.

Fig. 4 The blue points are experimental data while the red lines are curves fitted on the data to guide the eye. Simulated bipolar current, i_BPE, as a function of (A) the initial concentration of [R] and (B) the standard electron transfer rate constant k°. The fits in (A) and (B) correspond to the equations Y(x) = 88x (R² = 0.9999) and Y(x) = 334.2 × x/(0.067 + x) (R² = 0.9999), respectively. (C) Bipolar current simulated for L = 5 μm tall and W = 1 μm large spheroidal GNP positioned at d above the surface of a = 5 μm radius UME. The red line corresponds to the equation Y(x) = 57.8 e^−x/0.033 + 346.6 exp^−x/0.94 + 15.4 (R² = 0.9998). (D) Bipolar current simulated for a W = 1 μm large spheroidal GNP positioned at d = 0.5 μm above the surface of a = 5 μm radius UME as a function of the length L of the GNP. The red line corresponds to the equation Y(x) = −1717.8 e^−x/4.3 + 1698.2 (R² = 0.9988).

We will now examine how the size and position of the GNP affect the bipolar feedback current. Fig. 4C shows the bipolar current as a function of the GNP-UME distance normalized by the radius of the UME, denoted as d/a. The bipolar current follows a bi-exponential decay as the GNP is further away from the surface of the UME. Bipolar current is on the order of hundreds of pA when the GNP is closer than one electrode's radii from the surface. Fig. 4D shows the bipolar current as a function of the length of the GNP relative to the size of the UME, denoted as L/a. The distance between the bottom of the GNP and the surface of the UME is constant (0.5 μm). The longer is the GNP and the higher is the bipolar current. This latter tends toward a plateau when the length of the GNP equals about five times the radius of the UME. The variation of driving force at the GNP explains this trend. When the GNP is small compared to the size of the diffusion layer at the UME (proportional to the radius of the UME), the potential gradient explored by the two extremities of the GNP is small and so is the driving force. On the other hand, once the GNP explores most of the diffusion layer (95% of the concentration gradient is contained within two UME's radius) no significant gain in driving force is possible.

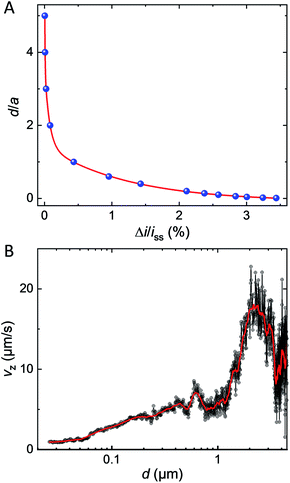
As a matter of fact, only a fraction of this bipolar current will lead to a positive feedback current at the UME. Fig. 5A shows the simulated bipolar feedback current (relative to its value in absence of GNP) at various adimensional distances, d/a, from the UME. The red line is a combination of exponential functions adjusted on the blue dots. As the GNP is approaching the UME at less than one electrode's radius the feedback rises from 0.1% up to a couple of % at 50 nm from the UME. The closer the GNP the stronger is the feedback current. This trend is caused by two phenomena. First, as the GNP is further away in solution the bipolar current decreases (see Fig. 4C). Indeed, the driving force drops as the concentration gradient fades away in solution. Second, as the GNP is further away in solution the collection efficiency decreases (see Fig. S12†).

Fig. 5 (A) Simulated bipolar feedback current (blue dots) versus normalized distance between the UME and the GNP. The red line results from the adjustments of the function Y(x) = −0.4 + 7.7 e^−x/1.23 + 17.8 e^−x/0.005 + 11.1 e^−x/0.07, R2 = 0.9998. (B) Velocity profile of the GNP obtained by calculating the time-derivative of the GNP-UME distance found from the simulated approach curve in (A). The red line is smooth of the black points (adjacent-averaging window 205 points, reflect boundary).

This bipolar feedback mechanism is expected to occur for extremely small objects as long as these latter are good electrical conductors. We performed a numerical simulation for a nanoscale GNP (L = 20 nm, W = 4 nm) positioned at 10 nm above the surface of a 20 nm radius electrode hence keeping the proportions similar to the micrometric GNP. A detailed discussion is provided in ESI (see Section 12†). The simulated current feedback drops to 0.1 pA, a value on the same order of magnitude than the noise level (for a state-of-the-art electrochemical setup with a bandwidth of a ca. kHz). A low noise setup in combination with a nanoelectrode should enable the detection of objects down to few tens of nanometers with a temporal resolution of the order of few ms.

We used the red line in Fig. 5A as a simulated approach curve to deduce the distance between the GNP and the UME at every time during the chronoamperogram shown in Fig. 1C (red part) and then, calculated the derivative with respect to time to obtain the instantaneous velocity of the GNP along the direction normal to the surface (V_z). The velocity V_z is plotted in Fig. 5B in black as a function of d (on a semi-log scale). At several μm from the surface of the electrode, the GNP seems to accelerate and then, at d = 2 μm decelerate from 15–20 μm s⁻¹ to few μm s⁻¹. Another velocity profile obtained for a different GNP and showing a similar trend is provided in Fig. S13.† The movie is provided in Movie S2.† While the uncertainty on the measurement is large far from the UME, the process of deceleration benefits from the high sensitivity of positive feedback at short distances. A deceleration indicates that the resulting forces acting on the GNP are not constant. At 1–2 μm from the surface of the electrode, the Peclet number, Pe, equals ca. 10 (see ESI† for details about the calculation). A value of Pe larger than unity indicates that advection predominates over diffusion. Recent work showed that electro-osmotic flow (EOF) should occur under low ionic strength condition, 10 μM, as the case in the present work (ionic strength = 10 μM).^33,34 The GNP is expected to behave as a tracer reflecting the direction and speed of this convective EOF. Interestingly the simulated velocity profile of EOF presents a decrease of tangential velocity when the liquid coming from above the electrode turns just above the surface in agreement with our observations. However, as the GNP decelerates reaching a distance of ca. 100 nm from the surface, the Pe value drops down to Pe = 0.2. Such a low value indicates that diffusion becomes predominant near the end of the velocity profile. At that stage, the deceleration may result from the reduction of the diffusion coefficient caused by the viscous drag from the nearby electrode's surface (known as near-wall hindered diffusion).⁴⁸

Conclusions

In conclusion, we developed a contactless electrochemical method with ms time resolution to monitor the velocity of individual conducting particles, just before impact on an electrode. We provided a detailed explanation of the key parameters affecting the magnitude and shape of the current transient based on a physical model and numerical simulations. We found that an individual GNP experiences a strong deceleration (10 to 1 μm s⁻¹) between 1 μm and 100 nm from the surface of the electrode. These observations could be discussed regarding physical phenomena occurring only near surfaces (convective electro-osmotic flow and near-wall hindered diffusion). We predict based on numerical simulations that our method is applicable to particles as small as few tens of nanometers. Those particles, to name but a few, could potentially be graphene nanosheet, carbon nanotube, thin metal chalcogenides (i.e. MoS₂, WS₂, and PtS₂),⁴⁹ and Mxenes (i.e. Ti₂AlC, Ti₃AlC₂, and Ta₄AlC₃).⁵⁰

Experimental

Chemicals

1,1′-Ferrocendimethanol (FcDM), sodium hydroxide, poly(4-styrene sulfonic acid) (PSS), and poly(allylamine hydrochloride) (PAA) were purchased from Sigma-Aldrich and used without further purification. DI-water (18.2 MΩ cm) was produced with an Elix Milli-Q water station (Millipore).

Graphene nanoplatelet suspension

The suspension of GNPs (5 μm particle size, 15 nm thickness, Sigma-Aldrich) was prepared by mixing 10 mg of GNP powder in 100 mL of a 0.01% v/v PSS solution, sonicating for 30 min, and then centrifugation. The first centrifugation of 1 min at 11 000g was used to remove the large GNPs. Only the supernatant was kept. The two following centrifugations were performed 10 min at 5000g and the supernatant was discarded to remove the small fragments of GNP. The GNP suspension was sonicated 5 min between each centrifugation to help re-dispersing the GNPs. The concentration of GNP used in this work was measured by UV-visible adsorption (Cary 50 Scan, Variant). The details are provided in Fig. S1.†

Electrode fabrication

Pt ultramicroelectrode (inlaid disk) was fabricated by heat sealing a 10 μm Pt wire (Goodfellow, hard temper) in a borosilicate glass capillary (2 mm o.d., 1.16 mm i.d.) using a heating coil. The side of the wire is exposed by polishing the capillary with sandpaper and then alumina slurry (down to 0.1 μm, Buehler) until obtaining a mirror-like surface. The ultra-microelectrode (UME) is sharpened by manually polishing the side of the capillary on sandpaper until achieving an RG = 15 (see Fig. S2†).

Opto-electrochemical setup

The opto-electrochemical setup consists of an inverted microscope (ix73×, Olympus, 40× objective) and a correlated electrochemical setup housed in a Faraday cage. A two-electrode setup is used to measure the current and apply a potential versus an Ag/AgCl 3.4 M KCl reference electrode. The cell is placed onto an inverted microscope to acquire bright-field videos in reflectance. The camera and the ammeter are synchronized externally and data is collected at 1 kHz and 2 kHz, respectively. Additional experimental details about the apparatus are provided in Fig. S5.†

Numerical simulation

The simulations were performed with COMSOL Multiphysics 5.3a in 2D axial geometry with the stationary solution. The diffusion of FcDM molecules is governed by Fick's law (transport of diluted species module), the potential inside the GNP is governed by Ohm's law (electric currents module), and the electron transfer kinetics at the surface of the UME and GNP is governed by Butler–Volmer equation. The bipolar current passing through GNP and the current at the Pt electrode is simulated by integrating the total normal flux to the GNP surface and the electrode surface under steady-state simulation conditions, respectively. The details are provided in the ESI.†

Data availability

Source data are provided with this article and have been uploaded as part of the ESI.†

Author contributions

All authors performed experiments, built finite element simulations, and collected/processed data. The manuscript was written through the contributions of all authors. All authors have approved the final version of the manuscript. C. R. supervised the project.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is support by the CNRS, the Agence Nationale de la Recherche (ANR-17-CE09-0034-01, “SEE”) and the China Scholarship Council (201706370055). We thank “Institute for Health Innovation & Technology” at NUS for permitting us to use the simulation workstation.

Notes and references

1. A. E. Nel, L. Mädler, D. Velegol, T. Xia, E. M. Hoek, P. Somasundaran, F. Klaessig, V. Castranova and M. Thompson, Nat. Mater., 2009, 8, 543–557.
2. C.-Y. Wu, W. J. Wolf, Y. Levartovsky, H. A. Bechtel, M. C. Martin, F. D. Toste and E. Gross, Nature, 2017, 541, 511–515.
3. M. J. Limo, A. Sola-Rabada, E. Boix, V. Thota, Z. C. Westcott, V. Puddu and C. C. Perry, Chem. Rev., 2018, 118, 11118–11193.
4. J. F. Lemineur, J. M. Noël, D. Ausserré, C. Combellas and F. Kanoufi, Angew. Chem., Int. Ed., 2018, 57, 11998–12002.
5. H. Ma, J. F. Chen, H. F. Wang, P. J. Hu, W. Ma and Y. T. Long, Nat. Commun., 2020, 11, 2307.
6. L. Nicolai, K. Schiefelbein, S. Lipsky, A. Leunig, M. Hoffknecht, K. Pekayvaz, B. Raude, C. Marx, A. Ehrlich and J. Pircher, Nat. Commun., 2020, 11, 1–16.
7. X. Xiao and A. J. Bard, J. Am. Chem. Soc., 2007, 129, 9610–9612.
8. X. Xiao, F.-R. F. Fan, J. Zhou and A. J. Bard, J. Am. Chem. Soc., 2008, 130, 16669–16677.
9. Y. G. Zhou, N. V. Rees and R. G. Compton, Angew. Chem., Int. Ed., 2011, 50, 4219–4221.
10. V. Brasiliense, P. Berto, C. Combellas, G. Tessier and F. d. r. Kanoufi, Acc. Chem. Res., 2016, 49, 2049–2057.
11. L. A. Baker, J. Am. Chem. Soc., 2018, 140, 15549–15559.
12. W. Wang, Chem. Soc. Rev., 2018, 47, 2485–2508.
13. Z. p. Xiang, H. q. Deng, P. Peljo, Z. y. Fu, S. l. Wang, D. Mandler, G. q. Sun and Z. x. Liang, Angew. Chem., Int. Ed., 2018, 130, 3522–3526.
14. M. V. Evers, M. Bernal, B. Roldan Cuenya and K. Tschulik, Angew. Chem., Int. Ed., 2019, 58, 8221–8225.
15. M. Zhou, S. Bao and A. J. Bard, J. Am. Chem. Soc., 2019, 141, 7327–7332.
16. Z. Jin and A. J. Bard, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 12651–12656.
17. P. Choo, T. Liu and T. W. Odom, J. Am. Chem. Soc., 2021, 143, 4550–4555.
18. V. Brasiliense, A. N. Patel, A. Martinez-Marrades, J. Shi, Y. Chen, C. Combellas, G. Tessier and F. Kanoufi, J. Am. Chem. Soc., 2016, 138, 3478–3483.
19. R. Hao, Y. Fan and B. Zhang, J. Am. Chem. Soc., 2017, 139, 12274–12282.
20. W. Ma, H. Ma, J. F. Chen, Y. Y. Peng, Z. Y. Yang, H. F. Wang, Y. L. Ying, H. Tian and Y. T. Long, Chem. Sci., 2017, 8, 1854–1861.
21. S. M. Oja, D. A. Robinson, N. J. Vitti, M. A. Edwards, Y. Liu, H. S. White and B. Zhang, J. Am. Chem. Soc., 2017, 139, 708–718.
22. D. A. Robinson, Y. Liu, M. A. Edwards, N. J. Vitti, S. M. Oja, B. Zhang and H. S. White, J. Am. Chem. Soc., 2017, 139, 16923–16931.
23. J. Ustarroz, M. Kang, E. Bullions and P. R. Unwin, Chem. Sci., 2017, 8, 1841–1853.
24. S. Li, Y. Du, T. He, Y. Shen, C. Bai, F. Ning, X. Hu, W. Wang, S. Xi and X. Zhou, J. Am. Chem. Soc., 2017, 139, 14277–14284.
25. S. R. German, M. A. Edwards, H. Ren and H. S. White, J. Am. Chem. Soc., 2018, 140, 4047–4053.
26. J. F. Lemineur, J. M. Noel, D. Ausserre, C. Combellas and F. Kanoufi, Angew. Chem., Int. Ed., 2018, 57, 11998–12002.
27. Q. Chen, Y. Liu, M. A. Edwards, Y. Liu and H. S. White, Anal. Chem., 2020, 92, 6408–6414.
28. R. Gao, M. A. Edwards, Y. Qiu, K. Barman and H. S. White, J. Am. Chem. Soc., 2020, 142, 8890–8896.
29. J. M. Noel, M. Miranda Vieira, V. Brasiliense, J. F. Lemineur, C. Combellas and F. Kanoufi, Nanoscale, 2020, 12, 3227–3235.
30. J. F. Lemineur, P. Ciocci, J. M. Noel, H. Ge, C. Combellas and F. Kanoufi, ACS Nano, 2021, 15, 2643–2653.
31. S. E. Fosdick, M. J. Anderson, E. G. Nettleton and R. M. Crooks, J. Am. Chem. Soc., 2013, 135, 5994–5997.
32. J. F. Lemineur, J. M. Noel, A. Courty, D. Ausserre, C. Combellas and F. Kanoufi, J. Am. Chem. Soc., 2020, 142, 7937–7946.
33. T. Moazzenzade, X. Yang, L. Walterbos, J. Huskens, C. Renault and S. G. Lemay, J. Am. Chem. Soc., 2020, 142, 17908–17912.
34. S. N. Thorgaard, S. Jenkins and A. R. Tarach, Anal. Chem., 2020, 92, 12663–12669.
35. A. D. Pendergast, Z. Deng, F. Maroun, C. Renault and J. E. Dick, ACS Nano, 2021, 15, 1250–1258.
36. D. A. Robinson, M. A. Edwards, Y. Liu, H. Ren and H. S. White, J. Phys. Chem. C, 2020, 124, 9068–9076.
37. L. Sun, W. Wang and H. Y. Chen, ChemElectroChem, 2018, 5, 2995–2999.
38. H. B. Chen, D. Jiang, X. L. Zhou, C. Qian, Y. Yang and X. W. Liu, Anal. Chem., 2020, 92, 13327–13335.
39. K. Wonner, M. V. Evers and K. Tschulik, J. Am. Chem. Soc., 2018, 140, 12658–12661.
40. V. Sundaresan, J. W. Monaghan and K. A. Willets, J. Phys. Chem. C, 2018, 122, 3138–3145.
41. J.-M. Noël and J.-F. Lemineur, Curr. Opin. Electrochem., 2020, 100647.
42. H. Xiong, J. Guo and S. Amemiya, Anal. Chem., 2007, 79, 2735–2744.
43. A. I. Oleinick, D. Battistel, S. Daniele, I. Svir and C. Amatore, Anal. Chem., 2011, 83, 4887–4893.
44. T. Sun, D. Wang and M. V. Mirkin, Faraday Discuss., 2018, 210, 173–188.
45. A. Oleinick, J. Yan, B. Mao, I. Svir and C. Amatore, ChemElectroChem, 2016, 3, 487–494.
46. D. He, J. Yan, F. Zhu, Y. Zhou, B. Mao, A. Oleinick, I. Svir and C. Amatore, Anal. Chem., 2016, 88, 8535–8541.
47. Z. Deng, F. Maroun, J. E. Dick and C. Renault, Electrochim. Acta, 2020, 355, 136805.
48. E. Kätelhön and R. G. Compton, Chem. Sci., 2014, 5, 4592–4598.
49. J. Zhou, J. Lin, X. Huang, Y. Zhou, Y. Chen, J. Xia, H. Wang, Y. Xie, H. Yu and J. Lei, Nature, 2018, 556, 355–359.
50. M. Naguib, V. N. Mochalin, M. W. Barsoum and Y. Gogotsi, Adv. Mater., 2014, 26, 992–1005.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc03646g

‡ Present address: Institute for Health Innovation & Technology, National University of Singapore, Singapore 117599, Singapore.

---