Vesicular release dynamics are altered by the interaction between the chemical cargo and vesicle membrane lipids

Abstract

The release of the cargo from soft vesicles, an essential process for chemical delivery, is mediated by multiple factors. Among them, the regulation by the interaction between the chemical cargo species and the vesicular membrane, widely existing in all vesicles, has not been investigated to date. Yet, these interactions hold the potential to complicate the release process. We used liposomes loaded with different monoamines, dopamine (DA) and serotonin (5-HT), to simulate vesicular release and to monitor the dynamics of chemical release from isolated vesicles during vesicle impact electrochemical cytometry (VIEC). The release of DA from liposomes presents a longer release time compared to 5-HT. Modelling the release time showed that DA filled vesicles had a higher percentage of events where the time for the peak fall was better fit to a double exponential (DblExp) decay function, suggesting multiple kinetic steps in the release. By fitting to a desorption–release model, where the transmitters adsorbed to the vesicle membrane, the dissociation rates of DA and 5-HT from the liposome membrane were estimated. DA has a lower desorption rate constant, which leads to slower DA release than that observed for 5-HT, whereas there is little difference in pore size. The alteration of vesicular release dynamics due to the interaction between the chemical cargo and vesicle membrane lipids provides an important mechanism to regulate vesicular release in chemical and physiological processes. It is highly possible that this introduces a fundamental chemical regulation difference between transmitters during exocytosis.

---

Introduction

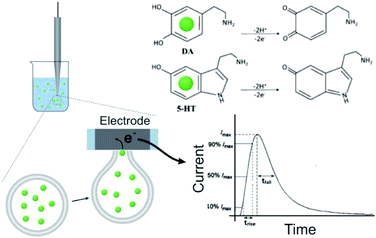
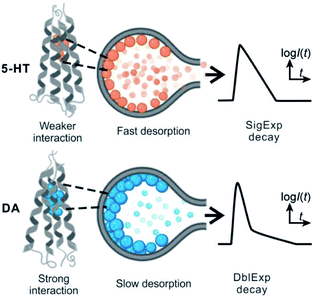
The release of the cargo from soft vesicles is an essential step for chemical delivery related to various processes, including liposome drug delivery, exosome-mediated cell signaling, vesicular transport, intracellular vesicular trafficking, exocytosis, etc. Among these, exocytosis, with a key role in cell communication and possibly a therapeutic target for disease of the nervous or endocrine system, has attracted increasing attention even though its mechanism and dynamics have been investigated for decades.^1–6 Electrochemical techniques, especially amperometry in combination with ultramicroelectrodes, have been developed as an approach to monitor the release of the chemical cargo during the exocytotic event with high sensitivity and spatial–temporal resolution.^7–12 The experimental signals of monitoring exocytosis, in the form of amperometric “spikes,” usually contain complex information about vesicle geometry, cargo quantity, and release dynamics through the exocytotic pore driven and controlled by the SNARE protein complex, actin, and dynamin.^13,14 For those vesicles isolated from cells, we can also trigger their cargo release (simulate exocytosis) and record the release signal again as “spikes” with our previously reported approach, called vesicle impact electrochemical cytometry (VIEC).^15,16 However, some difficulties still exist in the dynamic analysis of these spike signals, especially for those involving complex release processes which are difficult to quantitatively describe.

Usually, the exocytotic spike is observed as an asymmetrical peak, different in the rising and falling time. The spike decay lasts a longer time and for some spikes this current decay can be fit to a single exponential (I = Ae^−αt), whereas for other spikes to a double exponential (I = A₁e^−αt + A₂e^−βt) function.^17,18 The single exponential (SigExp) decay can be easily explained with a diffusion model where the release pore is static.^19–22 In contrast, the widely observed double exponential (DblExp) decay events during exocytotic release appear to indicate that additional processes besides simple diffusion are involved. Trouillon et al.^19,20 and Yue et al.²³ suggested that the DblExp mode of vesicular release might result from the exocytotic pore closing mediated by membrane proteins. Oleinick et al. showed that the interaction of catecholamines with the protein dense core matrix in vesicles can lead to spikes with DblExp in the latter part of the spike.¹⁸ The interaction between the chemical cargo and vesicle dense core is certainly important,²⁴ however, interactions have been shown between the chemical cargo and membranes^25–27 and these might play a broader role in vesicle release dynamics. These interactions could be broadly applicable as they will be observed in all vesicles, not only in the vesicles with a dense core. To the best of our knowledge this has not been investigated to date.

The interaction between the chemical cargo and the membrane, i.e. an adsorption–desorption process, adds an element of complication to the release process model and provides a mechanism of biological regulation. Numerical approaches, represented by the finite element simulation, provide a powerful tool for solving the problems related to complex processes which are difficult with direct analytical approaches. Based on the numerical analysis of the spike signals recorded through the VIEC technique, we can reconstruct the physical model of the entire vesicle release process²⁸ and include an inverse estimation of the relative specific physical parameters,^29,30 such as the vesicular pore size, diffusion coefficient of cargo chemicals, desorption rate constant, etc. These parameters can clearly describe the dissociation of the cargo from the membrane and how it alters general vesicle release dynamics.

In this paper, we used similarly sized liposomes but containing different monoamines, dopamine (DA) and serotonin (5-HT) to simulate vesicular release, and further assessed the release dynamics regulated by the different affinities of DA and 5-HT to the lipid membrane. The use of liposomes avoids the influence of the vesicular dense core.^31–34 We observed statistically different dynamics of release for the different monoamines. A finite element method, combined with Monte Carlo optimization, was adopted to estimate the dynamic parameters for the release of monoamines from the liposomes during VIEC. We provide evidence that these amines differentially adsorb to the membrane lipids in the liposomes or vesicles changing the release dynamics by which they exit the vesicle, which has not been shown. By fitting to a desorption model, we calculated the desorption rate constants of these two monoamines from the vesicular membrane lipids. DA has a lower desorption rate constant from the liposome membrane, which leads to slower DA release than that observed for 5-HT, while there is little difference in pore size. Although this work describes the desorption–release process for transmitters exiting vesicles during VIEC, the fundamental aspects can be applied to many aspects of chemical or biological vesicle transport. The results experimentally indicate that the process of vesicular release is complicated by the interaction between the chemical cargo and the vesicular membrane, thereby altering exocytotic release dynamics.^25,26,35,36

Results and discussion

Preparation and release dynamics for amine-loaded liposomes

In order to simulate the cargo–membrane interaction of different neurotransmitters within bio-vesicles, and further compare the difference of their effects on the release dynamics, we chose similarly sized dopamine-loaded liposomes (DLL) and serotonin-loaded liposomes (SLL) as the models of biological vesicles without the protein dense core and cargo with different membrane adsorption properties. These two monoamines are major species of neurotransmitters and widely distributed in the nervous systems of mammals. DA was chosen as a representative of common catecholamine neurotransmitters, including also epinephrine and norepinephrine, because of the similarity of their chemical structure and affinity to lipid molecules.²⁷ Serotonin is a representative indoleamine.

Meanwhile, a mixture of 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC), 1,2-dioleoyl-sn-glycero-3-phosphethanolamine (DOPE) and cholesterol was adopted to simulate the composition of bio-vesicle membranes, as these lipids are the major components of pre-synaptic vesicles.^37,38 The preparation process of DLL and SLL followed our previous work.³³ Briefly, the mixed solution of phospholipids in chloroform was dried and formed a lipid film in a round-bottom flask. The lipid film was then hydrated in a hydration solution containing 150 mM DA or 5-HT, to prepare a population of DLL or SLL but still in various sizes. The sizes of vesicles were further narrowed by use of reciprocating extrusion through double polycarbonate filter membranes in the same hydration solution and were measured to be 188 nm (polydispersity index = 0.13) as the average radius via dynamic light scattering (see more details in the ESI†).

The DLL or SLL is stable in isotonic solution. To trigger and record the release of contents, VIEC was used according to that described previously³³ (see Fig. 1, and more details in the ESI†). When a vesicle settles on the electrode, the high electric field near the surface induces electroporation of the liposome membrane allowing the contents to diffuse out through the pore in the membrane at the electrode surface. Released DA and 5-HT are rapidly electrooxidized at the electrode generating a spike shaped current signal. Using Faraday's law, the charge passed for each current spike (Q, the charge) is proportional to the number of molecules oxidised. In addition, the dynamic parameters of each spike, including the rise time (t_rise), fall time (t_fall), and width at half spike height (t_half) can be used to evaluate release dynamics.¹⁷

Fig. 1 Schematic showing the VIEC principle: attachment of the liposomes onto an electrode, electrooxidation of the released monoamines, and convection to a typical amperometric spike for peak analysis. The inset shows the electrooxidation of DA and 5-HT.

Comparison of the release dynamics of DLL and SLL

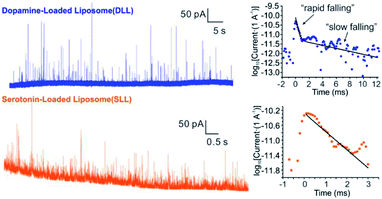
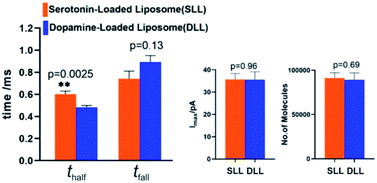
By applying the VIEC approach to each group of DLL and SLL, the dynamics of release from the vesicles in each group were statistically analysed (2182 spikes for DLL and 2301 spikes for SLL, 10 traces for each, see details in the ESI†). Typical amperometry traces for DLL and SLL and the spike analysis parameters are shown in Fig. 2 and Fig. 3, respectively. The results reveal that the average quantities of both monoamine molecules within each individual liposome and the height of the spike (I_max) of both groups are similar, while a significant increase in t_half and also a relative decrease in fall time (t_fall) are observed in the SLL compared to the DLL. Typical spikes (in the form of logarithmic dimensionless current) for each of DLL and SLL are shown on the right side of Fig. 2. The decay of the DLL spike has been fit to a rapid decay (∼1 ms) and subsequent slow long decay (∼10 ms), and it is better fit to a DblExp decay function than a SigExp function, whereas the spike of SLL fits better to only a SigExp function. We further compared the number of spikes having DblExp vs. SigExp decay for all spikes from DLL and SLL. Indeed, when the ratio of χ²(single)/χ²(double) > 1 is set as a cutoff, the percentage of spikes that have a better fit to DblExp decay in the DLL group (∼70%) is higher than for the SLL group (∼60%). This result shows that dopamine release from the liposomes is more complex and generally slower than 5-HT, which might result from the slower desorption of DA from membrane lipids (liposomes have no dense core).

Fig. 2 Traces for VIEC of DLL (blue line) and SLL (orange line) with a typical spike for each blown up to the right (with log₁₀ Y axis, blue dots for DLL, orange dots for SLL), showing the difference in spike shape. The best-fit simulation result (see the simulation method below) for the decay of each spike was drawn as the solid line. The simulation result for DLL follows a DblExp while that for the SLL is a SigExp.

Fig. 3 Comparison of DLL vs. SLL VIEC data showing means for dynamic data: t_half, t_fall, I_max, and the number of molecules observed in each. The fall time is defined as 90–10% of the backside of each current transient. Data sets have been compared with a two-tailed Mann–Whitney rank-sum test; **, p < 0.01.

Desorption–release processes of DA and 5-HT from liposomes

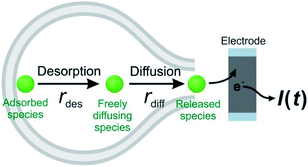
Theoretically, as discussed previously,^17,22,39 the dynamics of release from liposomes (or vesicles) is thought to be mainly controlled by the product of diffusional flux and the pore area. In contrast to exocytosis where pore opening and closing are driven by the cell, the liposome pore cannot close under a constant strong electric field.⁴⁰ Thus, the outflow flux should fit to a SigExp decay following the diffusion model of Cottrell.²² But if a rate-limiting desorption process is added before release through the pore, the entire release rate becomes a combination of desorption rate and diffusion (via pore) rate, and both can be fit to SigExp decay with different scaling factors. If the desorption rate is faster, the release rate will be controlled only by the slower diffusion rate and fit to a single exponential decay (similar to the apparent rate of a multi-step reaction controlled by the rate-determining step). This is shown conceptually in Fig. 4. However, when the rates of the two processes are similar, the apparent rate of the combined process will be expressed as a DblExp mode.

Fig. 4 A schematic of the desorption–release process. The adsorbed species dissociate from the lipid membrane creating freely diffusing species. These species are free to exit via the pore as released species. This mechanism is analogous to a 1^st order chemical reaction or one that is further combined as two consecutive reactions and the rate limiting step determines the apparent rate and whether the fall time is a single or double exponential. The r_des is the desorption rate of adsorbed species. The r_diff is the diffusion rate (i.e. flux) of freely diffusing species.

In order to estimate the desorption rate, we first constructed a finite element model to simulate this desorption–release process. The finite element model depicts a spherical liposome (radius 188 nm, experimental average) with a round pore in its membrane. On the other side, the total quantity of the chemical cargo was set as 151 000 molecules (according to the average experimental current spikes of charge Q = 48 fC), but divided into adsorbed species (Q_s, where s indicates the membrane inner surface) and freely diffusing species (Q_f, f indicates the freely moving species). Species need to reach an adsorption–desorption equilibrium before release. If we pre-set parameters describing the adsorption–desorption process, such as the adsorption rate constant (k_ads), of adsorbed molecules in the saturated state (Γ_s), then the Q_s and Q_f can be calculated by use of Langmuir's adsorption equation and converted into an initial concentration on the membrane (C_s,0) and in the liposome cavity (C_f,0). After pore generation, the freely diffusing species exit the pore, while the adsorbed species require time to dissociate from the membrane and transfer into the solution phase. The flux of molecules flowing out of the pore is converted into current that is then used to fit to the experimental spike and estimate the key parameters in the desorption–release process, including the desorption rate constant (k_des) and radius of the pore (R_p). The Monte Carlo optimization method was used to facilitate these estimates owing to its advantages such as high efficiency to solve complex problems and exemption of any a priori hypothetical relationship between current spikes and initial parameters (see the calculation protocol and details in the ESI†).

Four groups of typical DA and 5-HT spikes were analyzed by the finite element simulation. A pair of the experimental spikes and their best fit results are shown in Fig. 2. The DLL spikes show a better fit with a DblExp decay, whereas the SLL spikes fit better to a SigExp decay. By comparing the estimated desorption rate constant (k_des) and pore radius (R_p) corresponding to DA or 5-HT spikes, the pore sizes of both groups (see Table 1) cover a similar range (40–90 nm for DLL vs. 40–80 nm for SLL), while the k_des of DA is obviously smaller than that of 5-HT (10^2.3–3.0 s⁻¹ for DA vs. 10^3.5–5.1 s⁻¹ for 5-HT). This smaller k_des leads to a slower desorption rate (r_des) and longer time to end the release, which is consistent with a longer decay for DLL spikes.

Table 1 The estimated results of 4 pairs of spikes from DLL and SLL

No.	DLL		SLL
	log10 kdes (s^−1)	R p (nm)	log10 kdes (s^−1)	R p (nm)
1	2.31	43	3.93	43
2	3.05	64	3.48	56
3	2.77	93	4.43	47
4	2.90	74	5.12	80

---

Experimental and theoretical studies of the interaction between DA/5HT and lipids have shown that there is a strong electrostatic interaction – “salt bridge” – between the DA/5-HT ammonium group and the phosphate group of the lipids, and also a weaker interaction – hydrogen bonds (H-bonds) – between the DA/5-HT hydroxyl group and polar atoms of the lipids, and the latter seems to play a more important role among them.^41–44 Hence, the smaller k_des of DA might result more from the greater number of H-bonds (∼3 bonds) formed between DA and the polar neutral lipid compared to 5-HT which can form only 2, and the higher free energy of DA to lipid binding (∼21 kJ mol⁻¹) compared to 5-HT (∼14 kJ mol⁻¹) makes it harder for DA to dissociate.²⁷

These results support our assumption that different desorption rates alter the release dynamics between these two different monoamines (Fig. 5). It also provides a new perspective for the DblExp decay in the study of bio-vesicular release by the VIEC experiment or exocytosis measured by single cell amperometry. However, it is worth noting that, in the VIEC analysis of native biological vesicles, the proportion of DblExp fitting (empirically 30–60%)⁴⁵ is much higher than that of liposomes (empirically <10%, when the ratio of χ²(single)/χ²(double) > 2 is set as the cutoff). This phenomenon likely indicates that the dense core in the bio-vesicles still plays an important role in regulating release from the vesicle.^18,46–49

Fig. 5 Proposed mechanism showing the different dissociation rates for DA and 5-HT from the vesicular membrane and change in the dynamics of the VIEC event leading to DblExp and SigExp decay for the decay of spikes.

Conclusions

In summary, we employed the VIEC technique to monitor the differential dynamics of chemical cargo release from liposomes loaded with two different electroactive neurotransmitters (DA and 5-HT). Liposomes were used to simulate bio-vesicles without a dense core or proteins. A finite element simulation with Monte Carlo optimization was adopted to estimate the kinetic parameters of chemical desorption and suggests that the rate constant of DA desorbing from the lipids inside the vesicle is smaller than that for 5-HT. The slower desorption alters the release rate as recognized by a mode of best fit (SigExp or DblExp) for spike signal decay. Our models suggest this might be induced by a stronger interaction between the cargo and vesicle membrane lipids, consistent with some previous studies on the interaction, as more hydrogen bonding between DA and membrane lipid molecules can occur than for 5-HT. Hence, the existence of adsorption–desorption behaviour for transmitter molecules and the lipid membrane could be a basic component of the vesicular release process. Although the dense core might also play a crucial role in regulating chemical release from the cells having vesicles containing protein dense cores, regulation via adsorption–desorption from the vesicle wall can occur in all biological vesicles with or without a dense core. A better understanding of the interaction between transmitters and the vesicle membrane might provide strategies to regulate neurotransmitter, hormone, protein or drug release related to cellular communication, intracellular vesicular transport, and controlled delivery of liposomal drugs.^50,51

Data availability

Raw data is available upon request to the corresponding author.

Author contributions

F. Asadpour and X. Zhang contributed equally. A. E. suggested the liposome model and initial idea. F. A. carried out the liposome preparation and VIEC measurements; X. Z. carried out the simulation and parameter estimation; F. A. and X. Z. also proposed the mechanism and drafted the manuscript; M. M. carried out the data acquisition and statistical analysis; M. M. A., S. M., and A. E. were involved in funding acquisition, supervising, discussions of data interpretation, and outlining and editing the manuscript. All authors have given approval to the final version of the manuscript.

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

The European Research Council (ERC Advanced Grant Project No. 787534 NanoBioNext), Knut and Alice Wallenberg Foundation, and the Swedish Research Council (VR Grant No. 2017-04366) are acknowledged for financial support. FA and MMA wish to thank the Yazd University Research Council and the Iran National Science Foundation (INSF) for financial support of this research.

References

1. R. Jahn and T. C. Südhof, Annu. Rev. Biochem., 1999, 68, 863–911.
2. R. C. Lin and R. H. Scheller, Annu. Rev. Cell Dev. Biol., 2000, 16, 19–49.
3. M. Vakilian, Y. Tahamtani and K. Ghaedi, Gene, 2019, 706, 52–61.
4. N. T. N. Phan, X. Li and A. G. Ewing, Nat. Rev. Chem., 2017, 1, 0048.
5. R. S. Zucker, Neuron, 1996, 17, 1049–1055.
6. R. D. Burgoyne and A. Morgan, Physiol. Rev., 2003, 83, 581–632.
7. C. Amatore, S. Arbault, M. Guille and F. Lemaitre, Chem. Rev., 2008, 108, 2585–2621.
8. W. Wang, S. H. Zhang, L. M. Li, Z. L. Wang, J. K. Cheng and W. H. Huang, Anal. Bioanal. Chem., 2009, 394, 17–32.
9. R. M. Wightman, J. A. Jankowski, R. T. Kennedy, K. T. Kawagoe, T. J. Schroeder, D. J. Leszczyszyn, J. A. Near, E. J. Diliberto and O. H. Viveros, Proc. Natl. Acad. Sci. U. S. A., 1991, 88, 10754–10758.
10. A. Schulte and W. Schuhmann, Angew. Chem., Int. Ed., 2007, 46, 8760–8777.
11. P. Sun, F. O. Laforge, T. P. Abeyweera, S. A. Rotenberg, J. Carpino and M. V. Mirkin, Proc. Natl. Acad. Sci. U. S. A., 2008, 105, 443–448.
12. H. K. McCormick and J. E. Dick, Anal. Bioanal. Chem., 2021, 413, 17–24.
13. R. Jahn, T. Lang and T. C. Südhof, Cell, 2003, 112, 519–533.
14. T. C. Sudhof and J. E. Rothman, Science, 2009, 323, 474–477.
15. J. Dunevall, H. Fathali, N. Najafinobar, J. Lovric, J. Wigstr, A. Cans and A. G. Ewing, J. Am. Chem. Soc., 2015, 137, 4344–4346.
16. J. Dunevall, S. Majdi, A. Larsson and A. Ewing, Curr. Opin. Electrochem., 2017, 5, 85–91.
17. E. V. Mosharov and D. Sulzer, Nat. Methods, 2005, 2, 651–658.
18. A. Oleinick, R. Hu, B. Ren, Z. Tian, I. Svir and C. Amatore, J. Electrochem. Soc., 2016, 163, H3014–H3024.
19. R. Trouillon and A. G. Ewing, ChemPhysChem, 2013, 14, 2295–2301.
20. R. Trouillon and A. G. Ewing, ACS Chem. Biol., 2014, 9, 812–820.
21. X. Li, A. S. Mohammadi and A. G. Ewing, J. Electroanal. Chem., 2016, 781, 30–35.
22. C. Amatore, A. I. Oleinick and I. Svir, ChemPhysChem, 2010, 11, 149–158.
23. Q. Yue, X. Li, F. Wu, W. Ji, Y. Zhang, P. Yu, M. Zhang, W. Ma, M. Wang and L. Mao, Angew. Chem., Int. Ed., 2020, 59, 11061–11065.
24. R. M. Wightman, K. P. Troyer, M. L. Mundorf and R. Catahan, Ann. N. Y. Acad. Sci., 2002, 971, 620–626.
25. K. Jodko-Piorecka and G. Litwinienko, ACS Chem. Neurosci., 2013, 4, 1114–1122.
26. G. H. Peters, C. Wang, N. Cruys-Bagger, G. F. Velardez, J. J. Madsen and P. Westh, J. Am. Chem. Soc., 2013, 135, 2164–2171.
27. P. A. Postila, I. Vattulainen and T. Róg, Sci. Rep., 2016, 6, 19345.
28. A. Datta, C. L. Haynes and V. H. Barocas, Integr. Biol., 2017, 9, 248–256.
29. C. Gu, X. Zhang and A. G. Ewing, Anal. Chem., 2020, 92, 10268–10273.
30. R. Trouillon, Y. Lin, L. J. Mellander, J. D. Keighron and A. G. Ewing, Anal. Chem., 2013, 85, 6421–6428.
31. W. Cheng and R. G. Compton, Angew. Chem., Int. Ed., 2014, 53, 13928–13930.
32. W. Cheng and R. G. Compton, ChemElectroChem, 2016, 3, 2017–2020.
33. J. Lovric, N. Najafinobar, J. Dunevall, S. Majdi, I. Svir, A. Oleinick, C. Amatore and A. G. Ewing, Faraday Discuss., 2016, 193, 65–79.
34. A. S. Cans, N. Wittenberg, R. Karlsson, L. Sombers, M. Karlsson, O. Orwar and A. Ewing, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 400–404.
35. C. Wang, F. Ye, G. F. Velardez, G. H. Peters, P. Westh and T. P. Abeyweera, J. Phys. Chem. B, 2011, 115, 196–203.
36. G. Taugner and A. Wahler, Naunyn-Schmiedeberg's Arch. Pharmacol., 1974, 282, 279–293.
37. S. Mokkila, P. A. Postila, S. Rissanen, H. Juhola, I. Vattulainen and T. Róg, ACS Chem. Neurosci., 2017, 8, 1242–1250.
38. P. A. Postila and T. Rog, Mol. Neurobiol., 2020, 57, 910–925.
39. C. Amatore, A. I. Oleinick and I. Svir, ChemPhysChem, 2010, 11, 159–174.
40. A. O. Bilska, K. A. DeBruin and W. Krassowska, Bioelectrochemistry, 2000, 51, 133–143.
41. K. Jodko-Piorecka and G. Litwinienko, ACS Chem. Neurosci., 2013, 4, 1114–1122.
42. S. Azouzi, H. Santuz, S. Morandat, C. Pereira, F. Cote, O. Hermine, K. K. El, Y. Colin, C. Le Van Kim, C. Etchebest and P. Amireault, Biophys. J., 2017, 112, 1863–1873.
43. A. Orlowski, M. Grzybek, A. Bunker, M. Pasenkiewicz-Gierula, I. Vattulainen, P. T. Mannisto and T. Rog, J. Neurochem., 2012, 122, 681–690.
44. B. P. Josey, F. Heinrich, V. Silin and M. Losche, Biophys. J., 2020, 118, 1044–1057.
45. X. W. Zhang, A. Hatamie and A. G. Ewing, J. Am. Chem. Soc., 2020, 142, 4093–4097.
46. J. D. Machado, J. Diaz-Vera, N. Dominguez, C. M. Alvarez, M. R. Pardo and R. Borges, Cell. Mol. Neurobiol., 2010, 30, 1181–1187.
47. R. Borges, J. Díaz Vera, N. Domínguez, M. R. Arnau and J. D. Machado, J. Neurochem., 2010, 114, 335–343.
48. R. Hu, B. Ren, C. Lin, A. Oleinick, I. Svir, Z. Tian and C. Amatore, J. Electrochem. Soc., 2016, 163, H853–H865.
49. N. Dominguez, J. Estevez-Herrera, R. Borges and J. D. Machado, FASEB J., 2014, 28, 4657–4667.
50. D. L. Le, Ferdinandus, C. K. Tnee, T. T. Vo Doan, S. Arai, M. Suzuki, K. Sou and H. Sato, ACS Appl. Mater. Interfaces, 2018, 10, 37812–37819.
51. K. Sou, D. L. Le and H. Sato, Small, 2019, 15, e1900132.

---

Footnotes

† Electronic supplementary information (ESI) available: Detailed experimental procedures and materials; Fig. S1 and Table S1. See DOI: 10.1039/d1sc02247d

‡ These authors contributed equally.

---