“Anti-electrostatic” halogen bonding in solution

Abstract

Halogen-bonded (XB) complexes between halide anions and a cyclopropenylium-based anionic XB donor were characterized in solution for the first time. Spontaneous formation of such complexes confirms that halogen bonding is sufficiently strong to overcome electrostatic repulsion between two anions. The formation constants of such “anti-electrostatic” associations are comparable to those formed by halides with neutral halogenated electrophiles. However, while the latter usually show charge-transfer absorption bands, the UV-Vis spectra of the anion–anion complexes examined herein are determined by the electronic excitations within the XB donor. The identification of XB anion–anion complexes substantially extends the range of the feasible XB systems, and it provides vital information for the discussion of the nature of this interaction.

---

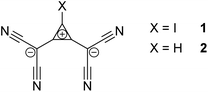
Halogen bonding (XB) is an attractive interaction between a Lewis base (LB) and a halogenated compound, exhibiting an electrophilic region on the halogen atom.¹ It is most commonly related to electrostatic interaction between an electron-rich species (XB acceptor) and an area of positive electrostatic potential (σ-holes) on the surface of the halogen substituent in the electrophilic molecule (XB donor).² Provided that mutual polarization of the interacting species is taken into account, the σ-hole model explains geometric features and the variation of stabilities of XB associations, especially in the series of relatively weak complexes.³ Based on the definition of halogen bonding and its electrostatic interpretation, this interaction is expected to involve either cationic or neutral XB donors. Electrostatic interaction of anionic halogenated species with electron-rich XB acceptors, however, seems to be repulsive, especially if the latter are also anionic. Yet, computational analyses predicted that halogen bonding between ions of like charges, called “anti-electrostatic” halogen bonding (AEXB),⁴ can possibly be formed^5–12 and the first examples of AEXB complexes formed by different anions, i.e. halide anions and the anionic iodinated bis(dicyanomethylene)cyclopropanide derivatives 1 (see Scheme 1) or the anionic tetraiodo-p-benzoquinone radical, were characterized recently in the solid state.^13,14 The identification of such complexes substantially extends the range of feasible XB systems, and it provides vital information for the discussion of the nature of this interaction. Computational results, however, significantly depend on the used methods and applied media (gas phase vs. polar environment and solvation models) and the solid state arrangements of the XB species might be affected by crystal forces and/or counterions. Unambiguous confirmation of the stability of the halogen-bonded anion–anion complexes and verification of their thermodynamic characteristics thus requires experimental characterization of the spontaneous formation of such associations in solution. Still, while the solution-phase complexes formed by hydrogen bonding between two anionic species were reported previously,^15–17 there is currently no example of “anti-electrostatic” XB in solution.

Scheme 1 Structures of the XB donor 1 and its hydrogen-substituted analogue 2.

To examine halogen bonding between two anions in solution, we turn to the interaction between halides and 1,2-bis(dicyanomethylene)-3-iodo-cyclopropanide 1 (Scheme 1).‡ Even though this compound features a cationic cyclopropenylium core, it is overall anionic, and calculations have demonstrated that its electrostatic potential is universally negative across its entire surface.¹³ The solution of 1 (with tris(dimethylamino)cyclopropenium (TDA) as counterion) in acetonitrile is characterized by an absorption band at 288 nm with ε = 2.3 × 10⁴ M⁻¹ cm⁻¹ (Fig. 1). As LB, we first applied iodide anions taken as a salt with n-tetrabutylammonium counter-ion, Bu₄NI. This salt does not show absorption bands above 290 nm, but its addition to a solution of 1 led to a rise of absorption in the 290–350 nm range (Fig. 1). Subtraction of the absorption of the individual components from that of their mixture produced a differential spectrum which shows a maximum at about 301 nm (insert in Fig. 1). At constant concentration of the XB donor (1) and constant ionic strength, the intensity of the absorption in the range of 280–300 nm (and hence differential absorbance, ΔAbs) rises with increasing iodide concentration (Fig. S1 in the ESI†). This suggests that the interaction of iodide with 1 results in the formation of the [1, I⁻]-complex which shows a higher absorptivity in this spectral range (eqn (1)):

1 + X⁻ ⇌ [1, X⁻] (1)

Fig. 1 Spectra of acetonitrile solutions with constant concentration of 1 (0.60 mM) and various concentrations of Bu₄NI (6.0, 13, 32, 49, 75, 115 and 250 mM, solid lines from the bottom to the top). The dashed lines show spectra of the individual solutions 1 (c = 0.60 mM, red line) and Bu₄NI (c = 250 mM, blue line). The ionic strength was maintained using Bu₄NPF₆. Insert: Differential spectra of the solutions obtained by subtraction of the absorption of the individual components from the spectra of their corresponding mixtures.

To clarify the mode of interaction between 1 and iodide in the complex, we also performed analogous measurements with the hydrogen-substituted compound 2 (see Scheme 1). The addition of iodide to a solution of 2 in acetonitrile did not increase the absorption in the 280–300 nm spectral range. Instead, some decrease of the absorption band intensity of 2 with the increase of concentration of I⁻ anions was observed (Fig. S2 in the ESI†). Such changes are related to a blue shift of this band resulting from the hydrogen bonding between 2 and iodide (formation of hydrogen-bonded [2, I⁻] complex is corroborated by the observation of the small shift of the NMR signal of the proton of 2 to the higher ppm values in the presence of I⁻ anions, see Fig. S3 in the ESI†).§ Furthermore, since H-compound 2 should be at least as suitable as XB donor 1 to form anion–π complexes with the halide, this finding (as well as solid-state and computational data¶) rules out that any increase in absorption in this region observed with the I-compound 1 may be due to this alternative interaction.

Likewise, the addition of NBu₄I to a solution of TDA cations taken as a salt with Cl⁻ anions did not result in an increase in the relevant region. Hence, we could also rule out anion–π interactions with the TDA counter-ions as source of the observed changes, which is in line with previous reports on the electron-rich nature of TDA.¹⁸

All these observations (supported by the computational analysis, vide infra) indicate that the [1, I⁻] complex (eqn (1)) is formed via halogen bonding of I⁻ with iodine substituents in 1. The changes in the intensities of the differential absorption ΔAbs as a function of the iodide concentration (with constant concentration of XB donor (1) as well as constant ionic strength) are well-modelled by the 1 : 1 binding isotherm (Fig. S1 in the ESI†). The fit of the absorption data produced a formation constant of K = 15 M⁻¹ for the [1, I⁻] complex (Table 1).|| The overlap with the absorption of the individual XB donor hindered the accurate evaluation of the position and intensity of the absorption band of the corresponding complex which is formed upon LB-addition to 1. As such, the values of Δλ_max shown in Table 1 represent a wavelength of the largest difference in the absorptivity of the [1, I⁻] complex and individual anion 1, and Δε reflects the difference of their absorptivity at this point (see the ESI† for the details of calculations).

Table 1 Equilibrium constants and spectral characteristics of the complexes of 1 with halide anions X⁻

Complex^a	K [M^−1]	Δλmax^c [nm]	10^−3Δε^d [M^−1 cm^−1]
a All measurements performed in CH3CN at 22 °C, unless stated otherwise. b In CH2Cl2. c Wavelength of the maximum of the differential spectra. d Differences in extinction coefficients of XB [1, I^−] complex and individual 1 at Δλmax.
1·I^−	15 ± 2	302	9.0
1·I^−^b	8 ± 2	303	8.0
1·Br^−	17 ± 2	302	3.7
1·Cl^−	40 ± 8	302	3.0

---

Since earlier computational studies demonstrated substantial dependence of formation of the AEXB complexes on polarity of the medium,^6–12 interaction between 1 and I⁻ anions was also examined in dichloromethane. The spectral changes in this moderately-polar solvent were analogous to that in acetonitrile (Fig. S4 in the ESI†). ** The values for the formation constants of the [1, I⁻] complex and Δε (obtained from the fitting of the ΔAbs vs. [I⁻] dependence) in CH₂Cl₂ are lower than those in acetonitrile (Table 1). This finding is in line with the computational studies,^6–12 predicting stronger binding in more polar solvents.

The addition of bromide or chloride salts to an acetonitrile solution of 1 caused changes in the UV-Vis range which were generally similar to that observed upon addition of iodide. The variations of the magnitude of the differential absorption intensities with the increase in the bromide or chloride concentrations are less pronounced than that observed upon addition of iodide (in agreement with the results of the DFT computations of the UV-Vis spectra of the complexes, vide infra). Yet, they could also be fitted using 1 : 1 binding isotherms (see Fig. S5 and S6 in the ESI†). The formation constants of the corresponding [1, Br⁻] and [1, Cl⁻] complexes resulted from the fitting of these dependencies are listed in Table 1. The values of K (which correspond to the free energy changes of complex formation in a range of −6 to −8 kJ mol⁻¹) are comparable to those reported for complexes of neutral monodentate bromo- or iodosubstituted aliphatic or aromatic electrophiles with halides.^19–22 Thus, despite the “anti-electrostatic” nature of XB complexes between two anions, the stabilities of such associations are similar to that observed with the most common neutral XB donors.

In contrast to the similarity in thermodynamic characteristics, the UV-Vis spectral properties of the complexes of the anionic XB donor 1 with halides are substantially different from that reported for the analogous associations with the neutral XB donors. Specifically, a number of earlier studies revealed that intermolecular (XB or anion–π) complexes of halide anions are characterized by distinct absorption bands, which could be clearly segregated from the absorption of the interacting species.^21–23 If the same neutral XB donor was used, the absorption bands of the corresponding complexes with chloride were blue shifted, and absorption bands of the complexes with iodide as LB were red shifted as compared to the bands of complexes with bromide. For example, XB complexes of CFBr₃ with Cl⁻, Br⁻ or I⁻ show absorption band maxima at 247 nm, 269 nm and 312 nm, respectively (individual CFBr₃ is characterized by an absorption band at 233 nm).²¹ Within a framework of the Mulliken charge-transfer theory of molecular complexes,²⁴ such an order is related to a rise in the energy of the corresponding HOMO (and electron-donor strength) from Cl⁻ to Br⁻ and to I⁻ anions. In the complexes with the same electron acceptor, this is accompanied by a decrease of the HOMO–LUMO gap, and thus, a red shift of the absorption band. The data in Table 1 shows, however, that the maxima of differential absorption spectra for these systems are observed at roughly the same wavelength. To clarify the reason for this observation, we carried out computational analysis of the associations between 1 and halide anions.

The DFT optimization†† at M06-2X/def2-tzvpp level with acetonitrile as a medium (using PCM solvation model)²⁵ produced thermodynamically stable XB complexes between 1 and I⁻, Br⁻ or Cl⁻ anions (they were similar to the complexes which were obtained earlier via M06-2X/def2-tzvp computations with SMD solvation model¹³). The calculated structure of the [1, I⁻] complex is shown in Fig. 2 and similar structures for the [1, Br⁻] and [1, Cl⁻] are shown in Fig. S7 in the ESI.†

Fig. 2 Optimized geometries of the [1, I⁻] complex with (3, −1) bond critical points (yellow spheres) and the bond path (green line) from the QTAIM analysis. The blue–green disc indicates intermolecular attractive interactions resulting from the NCI treatments (s = 0.4 a.u. isosurfaces, color scale: −0.035 (blue) < ρ < 0.02 (red) a.u.).

QTAIM analysis²⁶ of these structures revealed the presence of the bond paths (shown as the green line) and (3, −1) bond critical points (BCPs) indicating bonding interaction between iodine substituent of 1 and halide anions. Characteristics of these BCPs (electron density of about 0.015 a.u., Laplacians of electron density of about 0.05 a.u. and energy density of about 0.0004 a.u., see Table S1 in the ESI†) are typical for the moderately strong supramolecular halogen bonds.²⁷ The Non-Covalent Interaction (NCI) Indexes treatment²⁸ produced characteristic green–blue discs at the critical points' positions, confirming bonding interaction in all these complexes.

Binding energies, ΔE, for the [1, X⁻] complexes are listed in Table 2. They are negative and their variations are consistent with the changes in experimental formation constants measured with three halide anions in Table 1. The ΔE value for [1, I⁻] calculated in dichloromethane is also negative. Its magnitude is lower than that in acetonitrile, in agreement with the smaller formation constant of [1, I⁻] in less polar dichloromethane.

Table 2 Calculated characteristics of the [1, X⁻] complexes^a

Complex	ΔE, kJ mol^−1	λ max,^c nm	10^−4ε,^c M^−1 cm^−1	Δλmax,^d M^−1 cm^−1	10^−3Δε,^d M^−1 cm^−1
a In CH3CN, if not noted otherwise. b In CH2Cl2. c Extinction coefficient for the lowest-energy absorption band of the complex. d Position and extinction coefficient of the differential absorption (see Fig. 3).
1·I^−	−14.2	252	5.70	255	14
1·I^−^b	−4.7	253	6.07	—	—
1·Br^−	−14.8	252	5.02	253	7.4
1·Cl^−	−16.2	251	4.78	249	5.3

---

The TD DFT calculations of the individual XB donor 1 and its complexes with halides (which were carried at the same level as the optimizations) produced strong absorption bands in the UV range (Fig. 3). The calculated spectrum of the individual anion 1 (λ_max = 252 nm and ε = 4.27 × 10⁴ M⁻¹ cm⁻¹) is characterized by somewhat higher energy and intensity of the absorption band than the experimental one, but the differences of about 0.6 eV in energy and about 0.3 in log ε are common for the TD DFT calculations.

Fig. 3 Calculated spectra of 1 and its complexes (as indicated). The dashed lines show differential absorption obtained by subtraction of absorption of 1 from the absorption of the corresponding complex.

The TD DFT calculations of the XB complexes with all three anions produced absorption bands at essentially the same wavelength as that of the individual XB donor 1, but their intensities were higher (in contrast, the hydrogen-bonded complex of 2 with iodide showed absorption band with slightly lower intensity than that of individual 2). The differential spectra obtained by subtraction of the spectra of individual anion 1 from the spectra of the complexes are shown in Fig. 3, and their characteristics are listed in Table 2. Similarly to the experimental data in Table 1, the calculated values of Δλ_max are very close in complexes with different halides, and values of Δε are increasing in the order 1·Cl⁻ < 1·Br⁻ < 1·I⁻.

An analysis of the calculated spectra of the complexes revealed that the distinction in spectral characteristics of the XB complexes of anionic and neutral XB donors with halides are related to the differences in the molecular orbital energies of the interacting species. Specifically, the energy of the highest occupied molecular orbital (HOMO) of the anionic XB donor 1 is higher than the energies of the HOMOs of I⁻, Br⁻ and Cl⁻, and the energy of the lowest unoccupied molecular orbital (LUMO) of 1 is lower than those of the halides (Table S2 in the ESI†). As such, the lowest-energy electron excitations (with the substantial oscillator strength) in the AEXB complexes involve molecular orbitals localized mostly on the XB donor (see Fig. S8 in the ESI†). Accordingly, the energy of the absorption bands is essentially independent on the halide. Still, due to the molecular orbital interactions between the halides and 1, the small segments of the HOMOs of the complexes are localized on the halides, which affected the intensity of the transitions.‡‡ In contrast, in the XB complexes with the neutral halogenated electrophiles, the energies of the HOMOs and LUMOs of the halides are higher than the energies of the corresponding orbitals of the XB donors. As such, the HOMO of such complexes (as well as the other common molecular complexes) is localized mostly on the XB acceptors (electron donor), and the LUMO on the XB donor (electron acceptor). Accordingly, their lowest energy absorption bands represent in essence charge-transfer transition, and its energy vary with the energies of the HOMO of halides (the TD DFT calculations suggest that similar charge-transfer transitions in complexes of halides with 1 occur at higher energies, and they are overshadowed by the absorption of components).

In summary, combined experimental (UV-Vis spectral) and computational studies of the interaction between halides and 1 demonstrated spontaneous formation of the anion–anion XB complexes in moderately-polar and polar solvents (which attenuate the electrostatic anion–anion repulsion and facilitate close approach of the interacting species§§). To the best of our knowledge, this constitutes the first experimental observation of AEXBs in solution. Stabilities of such “anti-electrostatic” associations are comparable to that formed by halide anions with the common neutral bromo- and iodo-substituted aliphatic or aromatic XB donors. These findings confirm that halogen bonding between our anionic XB donor 1 and halides is sufficiently strong to overcome electrostatic repulsion between two anions. It also supports earlier conclusions²⁹ that besides electrostatics, molecular-orbital (weakly-covalent interaction) play an important role in the formation of XB complexes. Since the HOMO of 1 is higher in energy than those of the halides, the lowest-energy absorption bands in the anion–anion complexes is related mostly to the transition between the XB-donor localized MOs (in contrast to the charge transfer transition in the analogous complexes with neutral XB donors). Therefore, the energies of these transitions are similar in all complexes and the interaction with halides only slightly increase their intensities.

Author contributions

R. W.: compound design, conceptualization; S. M. H., S. V. R.: conceptualization, project supervision; J. M. H.: compounds synthesis and characterization; C. L.: UV-Vis and NMR measurements and data treatment, S. V. R.: data analysis, calculations, manuscript writing. All authors reviewed, discussed, edited and commented on the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

C. L. and S. V. R thank the National Science Foundation (grant CHE-2003603) for financial support of this work. Calculation were done on Ball State University's beowulf cluster, which is supported by The National Science Foundation (MRI-1726017) and Ball State University. Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy – EXC 2033–390677874 – RESOLV. J. M. H. is grateful for financial support by the Studienstiftung des deutschen Volkes. We thank Prof. M. Erdelyi (Uppsala University) for measuring ¹³C NMR spectra.

References

1. (a) L. C. Gilday, S. W. Robinson, T. A. Barendt, M. J. Langton, B. R. Mullaney and P. D. Beer, Chem. Rev., 2015, 115, 7118; (b) G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, Chem. Rev., 2016, 116, 2478.
2. (a) P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2010, 12, 7748; (b) P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2013, 15, 11178.
3. (a) J. S. Murray and P. Politzer, Crystals, 2020, 10, 76; (b) A. Lange, J. Heidrich, M. O. Zimmermann, T. E. Exner and F. M. Boeckler, J. Chem. Inf. Model., 2019, 59, 885; (c) K. E. Riley, J. S. Murray, P. Politzer, M. C. Concha and P. Hobza, J. Chem. Theory Comput., 2009, 5, 155.
4. The term “counter-intuitive” was proposed earlier as an alternative label for the “anti-electrostatic” hydrogen bonding, see: J. S. Murray, Z. P.-I. Shields, P. G. Seybold and P. Politzer, J. Compos. Sci., 2015, 10, 209.
5. C. Wang, Y. Fu, L. Zhang, D. Danovich, S. Shaik and Y. Mo, J. Comput. Chem., 2018, 39, 481.
6. Z. Zhu, G. Wang, Z. Xu, Z. Chen, J. Wang, J. Shi and W. Zhu, Phys. Chem. Chem. Phys., 2019, 21, 15106.
7. Z. Yang, Z. Xu, Y. Liu, J. Wang, J. Shi, K. Chen and W. Zhu, J. Phys. Chem. B, 2014, 118, 14223.
8. G. Wang, Z. Chen, Z. Xu, J. Wang, Y. Yang, T. Cai, J. Shi and W. Zhu, J. Phys. Chem. B, 2016, 120, 610.
9. (a) D. Quiñonero, I. Alkorta and J. Elguero, Phys. Chem. Chem. Phys., 2016, 18, 27939; (b) S. M. Chalanchi, I. Alkorta, J. Elguero and D. Quiñonero, ChemPhysChem, 2017, 18, 3462.
10. Z. Chen, G. Wang, Z. Xu, J. Wang, Y. Yu, T. Cai, Q. Shao, J. Shi and W. Zhu, J. Phys. Chem. B, 2016, 120, 8784.
11. Y. Li, L. Meng and Y. Zeng, ChemPlusChem, 2021, 86, 232.
12. K. Ghosh, A. Frontera and S. Chattopadhyay, CrystEngComm, 2021, 23, 1429.
13. J. M. Holthoff, E. Engelage, R. Weiss and S. M. Huber, Angew. Chem., Int. Ed., 2020, 59, 11150.
14. T. Maxson, A. S. Jalilov, M. Zeller and S. V. Rosokha, Angew. Chem., 2020, 132, 17350.
15. A. Knorr, P. Stange, K. Fumino, F. Weinhold and R. Ludwig, ChemPhysChem, 2016, 17, 458.
16. A. Strate, T. Niemann, D. Michalik and R. Ludwig, Angew. Chem., Int. Ed., 2017, 56, 496.
17. A. E. Khudozhitkov, P. Stange, B. Golub, D. Paschek, A. G. Stepanov, D. I. Kolokolov and R. Ludwig, Angew. Chem., Int. Ed., 2017, 56, 14310.
18. R. Weiss, T. Brenner, F. Hampel and A. Wolski, Angew. Chem., Int. Ed., 1995, 34, 439.
19. (a) M. G. Sarwar, B. Dragisic, L. J. Salsberg, C. Gouliaras and M. S. Taylor, J. Am. Chem. Soc., 2010, 132, 1646; (b) T. M. Beale, M. G. Chudzinski, M. G. Sarwar and M. S. Taylor, Chem. Soc. Rev., 2013, 42, 1667.
20. (a) F. Biedermann and H.-J. Schneider, Chem. Rev., 2016, 116, 5216; (b) D. von der Heiden, A. Vanderkooy and M. Erdélyi, Coord. Chem. Rev., 2020, 407, 213147.
21. S. V. Rosokha and A. Traversa, Phys. Chem. Chem. Phys., 2015, 17, 4989.
22. B. Watson, O. Grounds, W. Borley and S. V. Rosokha, Phys. Chem. Chem. Phys., 2018, 20, 21999.
23. S. Kepler, M. Zeller and S. V. Rosokha, J. Am. Chem. Soc., 2019, 141, 9338.
24. R. S. Mulliken and W. B. Pearson, Molecular complexes: A Lecture and Reprint Volume, Wiley, New York, NY, 1969.
25. (a) Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215; (b) J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999.
26. R. F. W. Bader, Chem. Rev., 1991, 91, 893.
27. (a) E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529; (b) S. J. Grabowski, Phys. Chem. Chem. Phys., 2013, 15, 7249; (c) S. J. Grabowski, J. Phys. Chem. A, 2012, 116, 1838.
28. (a) E. R. Johnson, S. Keinan, P. Mori-Sánchez, J. Contreras-García, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498; (b) J. Contreras-García, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625.
29. (a) S. V. Rosokha, I. S. Neretin, T. Y. Rosokha, J. Hecht and J. K. Kochi, Heteroat. Chem., 2006, 17, 449; (b) L. P. Wolters and F. M. Bickelhaupt, ChemistryOpen, 2012, 1, 96; (c) C. Wang, D. Danovich, Y. Mo and S. Shaik, J. Chem. Theory Comput., 2014, 10, 3726; (d) J. Thirman, E. Engelage, S. M. Huber and M. Head-Gordon, Phys. Chem. Chem. Phys., 2018, 20, 905.
30. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision E01, Gaussian, Inc, Wallingford, CT, USA, 2009.
31. (a) T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580; (b) W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc01863a

‡ Syntheses of 1 and 2 were reported earlier.¹³ Due to intrinsic synthetic limitations, only salts with tris(dimethylamino)cyclopropenium cations are currently available.

§ Orientating attempts to obtain a formation constant for the iodide complex of 2via NMR titrations yielded only very small shifts. We estimate that this constant is at least two orders of magnitude lower than the one involving XB donor 1 (see Fig. S3 in the ESI†).

¶ This conclusion is consistent with the absence of any indication for anion–π interaction within the crystal structures of 1 with iodide and chloride.¹³ It is also supported by the DFT calculations, which showed that the hypothetical anion–π complexes of XB donor 1 with I⁻, Br⁻ or Cl⁻ have positive (unfavourable) binding energies. In addition, the observed stability trends of complexes of 1 with different halides (with the chloride complex being least stable) and the UV characteristics of such complexes (featuring almost identical λ_max and ε, see Table S3 in the ESI†) do not match the experimental findings (Table 1).

|| The equilibria constants K in Table 1 were obtained by averaging values from the fitting of several (3–5) series of measurements (and the errors were obtained from the variations of these values), each series included 10–18 solutions with constant concentration of 1 and ionic strength, and different concentrations of the halide anions (see ESI† for details).

** Note that the study of complex formation in the low-polarity solvents were hindered by the limited solubility of halide salts in such media.

†† Geometries of the XB complexes and their components were optimized without constrains using Gaussian 09 suite of program.³⁰ The binding energies were determined as: ΔE = E_comp − (E₁ + E_X) + BSSE, where E_comp, E₁ and E_X are sums of the electronic and ZPE of the complex, optimized 1 and halide and BSSE is a basis set superposition error. AIM and NCI analyses were performed and visualized using Multiwfn and VMD programs, respectively.³¹ Details of the calculations, energies, geometric and spectral characteristics of HB and XB complexes as well as atomic coordinates of the calculated complexes are listed in the ESI.†

‡‡ The closer is the energy of HOMO of halide to that of 1, the more effective is their interaction. This probably explains the fact that the difference between absorption band intensities of the individual 1 and its complex with halide is increasing from chloride to bromide and iodide. Besides, the most pronounced effects observed in complexes with iodide is probably related to involvement of the MO residing mostly on the XB acceptor in the excited state responsible for the appearance of the absorption band (see Fig. S7 in the ESI†).

§§ Electrostatic interaction energy between iodide and XB donor 1 estimated using ESP atomic charges (which are fitted to reproduce the molecular electrostatic potential) and atomic coordinates of the optimized AEXB 1·I⁻ complex afforded values of 102 kJ mol⁻¹ in the gas phase and 2.8 kJ mol⁻¹ in acetonitrile. Such changes are comparable to the reported earlier¹³ shift of the calculated binding energy in 1·I⁻ from 108 kJ mol⁻¹ in the gas phase to −10 kJ mol⁻¹ in acetonitrile.

---