Towards multistate multimode landscapes in singlet fission of pentacene: the dual role of charge-transfer states

Abstract

Singlet fission duplicates triplet excitons for improving light harvesting efficiency. The presence of the interaction between electronic and nuclear degrees of freedom complicates the interpretation of correlated triplet pairs. We report a quantum chemistry study on the significance and subtleties of multistate and multimode pathways in forming triplet pair states of the pentacene dimer through a six-state vibronic-coupling Hamiltonian derived from many-electron adiabatic wavefunctions of an ab initio density matrix renormalization group. The resulting spin values of the singlet manifolds on each pentacene center are computed, and the varying spin nature can be distinguished clearly with respect to dimer stacking and vibronic progression. Our monomer spin assignments reveal the coexistence of both lower-lying weak and higher-lying strong charge transfer states which interact vibronically with the triplet pair state, providing important implications for its generation and separation occurring in vibronic regions. This work conveys the importance of the many-electron process requiring close low-lying singlet manifolds to determine the subtle fission details, and represents an important step for understanding vibronically resolved spin states and conversions underlying efficient singlet fission.

---

1 Introduction

Singlet fission (SF), a process in which a singlet exciton of higher energy splits into two triplets of lower energy, is potentially promising in applications of third-generation photonic devices. In SF chromophores, these two triplets are born coupled into a low-lying singlet state which makes the SF process spin allowed.^1,2 This “two-for-one” potential for the photon-to-electron conversion enables an interesting pathway to surpass the Shockley–Queisser conversion limit (33.7%) for a single p–n junction solar cell.^3,4

A set of general theoretical guidelines was proposed for the low-lying excited states of SF chromophores, i.e., E(S) − 2E(T) ≥ 0 to make the whole process isoergic (or slightly exoergic), and E(T₂) − 2E(T) > 0 to compete with an inverse phenomenon, triplet–triplet annihilation.⁵ A few organic compounds have been identified to produce triplet yields more than 100%, such as polyacenes (anthracene, tetracene, pentacene, and hexacene), 1,3-diphenylisobenzofuran, perylene derivatives, and biradicaloids.^6–9

As pointed out by Casanova in a recent seminal review article,¹⁰ “in singlet fission, it is commonly assumed that if the optical state is not the lowest excited singlet (S₁), the system rapidly decays to S₁ (Kasha's rule) before it undergoes fission, …”. The most interesting state in these electronically excited molecules for SF applications is the low-lying state which has a predominant double excitation character. This state is vaguely understood as a composition of two triplets (on different monomers) coupled in a singlet and usually called a correlated triplet pair state as ¹TT, that is generated at an ultrafast time scale (∼100 fs) and has a tendency to split into two distinct triplets.¹¹ Although the energetic criteria for pentacene and other SF chromophores have already been clearly established,^12,13 a quantitative understanding of the photophysical nature of TT states arising in SF materials has been difficult from experiments alone, which causes confusion in unambiguous assignments and proper analysis of TT spectral signatures, and complicates the interpretation of the SF mechanism.¹⁴

Pentacene is the smallest polyacene that undergoes exoergic SF and has thus been extensively investigated in both theoretical^12,15–20 and experimental SF studies.^11,21–27 These studies have demonstrated diverse mechanistic pathways in the SF generation process which require an active interaction between single- and multi-excitonic states in one way or another, such as the inter-conversion of a local excitation (LE) singlet S₁ state with a nearby dark state through the excimer formation,¹⁶ a superexchange mechanism via a virtual charge-transfer (CT) state,²⁸ and an indirect quantum coherent mechanism involving low-lying CT and multiexcitonic diabatic states.^19,29,30 Although the CT-mediated mechanism appears to be the largely accepted explanation for SF in tetracene and pentacene crystals,¹⁰ more detailed studies have also revealed various vibronic origins for making a coherent TT population, ranging from a single vibrational mode³¹ through a collection of vibrations in both low- and high-frequency regions,^32,33 to the vibrational coherency.^34–36 Interestingly, the vibronic coupling (VC) between two CT states has been shown to enhance SF dynamics by reducing the two CTs' destructive interference.³⁷ The crystalline polarizable environment was deduced to stabilize vibronically tuned CT states, causing a significant acceleration in SF generation rates with a slight diminution in the TT yield.³⁸

Conceptually, the presence of strongly correlated triplet pairs in SF chromophores requires a high-level ab initio multiconfigurational wavefunction^39,40 for which the number of significant determinants grows exponentially with correlated electrons. Dealing with such strongly correlated systems becomes intractable, which limits correlation to only a small number of electrons in these molecules, leaving many profound questions unresolved despite already intriguing findings. For instance, the part of the molecule which can be statically correlated with traditional complete active space self-consistent field (CASSCF) methods remains very small in large molecules particularly in acenes larger than naphthalene and these methods may not provide an accurate picture of the SF pathway involving two or more such coupled chromophores. Although the ideal CASSCF-based calculations should treat complete π-valence electrons, due to the aforementioned challenges, a practical choice of active space should be at least sufficiently large to account for most valence π → π* excitation spectra of SF chromophores. The use of ab initio density matrix renormalization group (ab-DMRG) method provides a way of correlating a larger number of excited electrons in only polynomial costs, particularly effective in obtaining numerically exact wavefunctions for strongly correlated one- and quasi-one-dimensional systems,^41,42e.g., molecules such as polyenes and metallic hydrogen chains by using up to (100o, 100e) active spaces.⁴³

In this work, we applied the ab-DMRG algorithm to correlate a large part of the π-valence space and investigate the low-lying excited states of pentacene. These electronic states in the pentacene dimer are characterized using state-average density matrix renormalization group self-consistent field (DMRGSCF)⁴⁴ calculations. Furthermore, we implemented an extensive wavefunction analysis tool based on DMRG one- and two-particle state and transition density matrices to reveal the role of these low-lying adiabatic states in explaining the essence of the SF mechanism. Specifically, we used DMRG wavefunctions to calculate the projected local spin distribution for monomer fragments in the dimer system, the multipole couplings to quantify the role of intermediate CT states electrostatically, and a VC analysis to understand molecular vibrations facilitating SF state conversion. This study serves to not only reconcile the need of multiple excitonic states and vibrational modes which are shown to be critical to revealing the SF mechanistic details in pentacene, but also to extend a general high-level computational approach and modeling tool for systematically analyzing potential candidates that harvest efficient SF.

2 Computational details

We implemented our wavefunction analysis in the quantum chemistry program package PySCF⁴⁵ based on one- and two-particle state/transition density matrices of low-lying states from the DMRG-BLOCK program.^46–50 The static correlation was treated using the state-average DMRGSCF wavefunctions by giving equal weights to the states included in the calculations and the dynamic correlation is accounted for using the second-order N-electron valence state perturbation (NEVPT2) method. The adiabatic states of the pentacene dimer were computed using the dimer that was built by combining the CASSCF(12π, 12e)/cc-pVTZ monomer geometry. The normal vibrational modes for the pentacene monomer were calculated using hybrid density functional M062X⁵¹ with the Gaussian 16 program.⁵² All vibronic couplings were computed by displacing the dimer structure prepared by combining the M062X/cc-pVTZ monomer geometry. For comparison of energetics for choice of DMRG active space, we used the DFT-based GW/BSE (GW approximation with the Bethe–Salpeter equation using DFT orbitals) method implemented in the BerkeleyGW program⁵³ to characterize the low-lying electronic states of pentacene solid using the plane wave basis. All DMRG computations were performed using the cc-pVTZ basis set.⁵⁴ We chose the number of renormalized states M = 1000 in our DMRG calculations, which is accurate enough for our system (see Table S1†).

In what follows, to avoid ambiguity, the mechanistic discussions on the formation and separation of the correlated triplet–triplet (TT) pair state are differentiated, while the abbreviation “SF” is generally applied to the whole process, as recommended by Smith and Michl.⁵ Moreover, we denote the lowest adiabatic excited singlet manifold as the dimeric S₁ without linking to its character, the next singlet state as the dimeric S₂ and so on, as recommended by Casanova.¹⁰

3 Results and discussion

3.1 Nature of low-lying electronic states in the pentacene dimer

A minimal morphology model of at least two chromophores is required to study the SF process. We used a pentacene dimer (Fig. 1) constructed by combining optimized CASSCF/12π12e S₀ structures for the pentacene monomer, replicating a similar structure with the pentacene polymorph in fiber thin films.⁵⁵ Similar SF models have been well employed in SF investigations depicting a close relationship with the real crystal structures.^15,19,56 Our monomer calculations adopting an active space of (10–14)π-orbitals/electrons yield accurate estimation of singlet–triplet gaps, replicating such previous literature results.^57,58 This follows the fact that at least an active space of 20π-electrons should be considered to treat a significant static correlation associated with the pentacene dimer for DMRGSCF computations.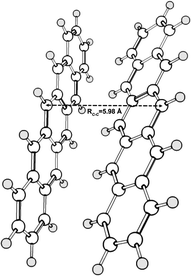

Fig. 1 The reference dimer geometry for SF applications: two monomers are used to form the dimer model similar to the crystal structure in pentacene polymorphs.

An analysis of the DMRGSCF/NEVPT2 energetics of the dimer model over a range of orbitals reveals that the (22π,22e) active space is suitable to effectively replicate excited state energies of low-lying singlets as compared to those from the GW/BSE method. The DMRGSCF(22π,22e)/NEVPT2 results account for the CAS-based static correlation, corrected with the NEVPT2 dynamic correlations on top of the DMRGSCF(12π,12e) wavefunction due to the complexity of NEVPT2 calculations for the cc-pVTZ basis set at the DMRG(22π,22e) reference wavefunction. These energies for the first five excited singlet states of the pentacene dimer and solid are listed in Table 1. The detailed analyses of excited state energies and the choice of active space in both the monomer and dimer are given in Section S1 of the ESI.† The first four excited states of the pentacene dimer are close-lying within an energy window of ∼0.3 eV, indicating that the wavefunction delocalizes over the dimer when two monomers approach each other. Similar excited state energies were obtained by Zimmerman et al. using the restricted active space double spin-flip (RAS-2SF) method for a pentacene dimer, where R_C–C = 5.65 Å.¹⁸ The delocalization of the wavefunction is more enhanced in a crystal environment and this energy window further reduces to ∼0.2 eV.

Table 1 The excited state energies (eV) of low-lying states of the pentacene dimer [DMRGSCF(22π,22e)/NEVPT2] and pentacene crystal [GW/BSE]. The characters and local spin square 〈Ŝ²〉 values are assigned to DMRG states in the dimer based on DMRG local spin analysis

State	Dimer (22π,22e)	Pentacene crystal	Character	〈Ŝ^2〉
S1	1.85	1.86	TT	1.82
S2	1.93	1.88	CT1	0.29
S3	1.99	1.97	LE	0.00
S4	2.16	2.05	CT2	0.62
S5	2.84	2.06	LE	0.00

---

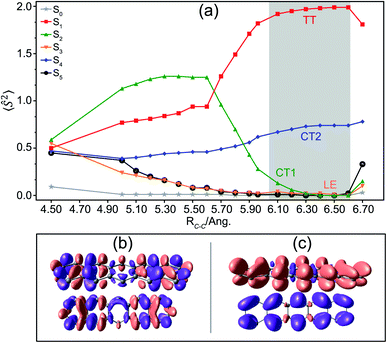
These SF states in the dimer possess distinct spin and spatial characteristics and interact with one another differently. Luzanov et al. determined the spin nature for various dimers of SF relevance (e.g., 1,3-diphenylisobenzofuran (DPBF) and tetracene) based on the weights of LE, charge-resonance (CR) and TT spin-adapted configurations employing a fragment spin-correlator.⁵⁹ In this work, we reformulate the well-established^60–62 local spin decomposition of total spin square operator 〈Ŝ²〉 in terms of the local one- and two-particle density matrices for exact adiabatic wavefunctions (see eqn (S3) in the ESI†). Fig. 2(a) shows the 〈Ŝ²〉 distribution for a fragment in the pentacene dimer as a function of inter-dimer separations. 〈Ŝ²〉 is quite sensitive to the overlap between monomers; at smaller separations, the spin is equally distributed as the wavefunctions on two fragments overlap very strongly. However, as the monomers drift apart from each other, the spin changes rapidly, the S₁ state shows considerable TT character with 〈Ŝ²〉 = ∼2.0 at separations >5.90 Å and behaves as a pure TT configuration at ∼6.10–6.50 Å. We will show later that this TT state is further stabilized and becomes bound with respect to free triplets upon vibronic stretching, which provides computational evidence supporting previous experimental findings for the pentacene dimer.⁶³ The S₂ state has an 〈Ŝ²〉 value of >0.75 on each fragment and is expected to retain some TT character at small separations. However, the spin drops rapidly at larger distances and this state can be primarily termed as a weak CT state (CT1). The S₄ excited state remains a strong CT (CT2) state irrespective of the distance and behaves as a pure CT state at >5.90 Å (where the TT formation begins for S) with a significant doublet character (〈Ŝ²〉 = 0.75). The distinction in the extent of charge transfer is clearly evident for CT1 and CT2 states in their corresponding density difference plots in Fig. 2(b) and (c) (see Fig. S5† for natural transition orbital analysis). The moderate energetic separation of 0.23 eV and the drastic difference in character between the two CT states arise due to the asymmetric alignment in the dimer (Fig. 1).^19,64 On the other hand, it has also been argued that the energy gap of “CT” states (diabatic) can be further substantially reduced from dimeric 0.8 eV to crystalline 0.04 eV due to the balance between the charge–quadrupole interaction and the crystalline dielectric environment.^65,66

Fig. 2 The local spin square 〈Ŝ²〉 distribution for the fragment in the pentacene dimer as a function of inter-dimer distance (a), the difference density for the S₂ (CT1) state (b) and S₄ (CT2) state (c). The spin values predict a TT pair formation in a range of dimer stacking distances, as shown by the grey colored area. S₂ and S₃ are weak CT1 and LE states, respectively. S₄ behaves as a pure doublet state CT2.

S₃ and S₅ primarily remain locally excited states termed as LE (see Section S2 in the ESI† for mathematical details). Although the overall local spin density for each of these states is zero because of their singlet characters, the spin densities on fragments can be projected. One thing of particular interest is that the spin of many electronic states except S₄ drops rapidly as soon as the S₁ state acquires a pure TT phenomenon, implying that the spin wavefunctions in this system interact in a way to maximize the population in the S₁ state. It also suggests that the interaction between S₁ and S₄, i.e., TT–CT2 interaction, should be investigated more carefully as the spin manifold for only the S₄ state survives during triplet pair formation. The local molecular orbitals employed in this spin analysis are visualized in Fig. S4.†

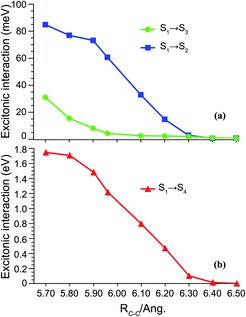
To quantify the overall intermolecular electron–electron interactions, we extract the important coulombic interactions among these SF states from multipolar moments such as dipole, quadrupole, hexapole and octupole moments using DMRG one-particle transition density matrices.^67–69 The detailed mathematical expressions are included in Section S3 of the ESI.† These interactions drop rapidly as the inter-dimer separation approaches the TT formation region as predicted by the spin analysis. Most of the states weakly couple with each other, except for S₁ → S₄ (TT–CT2) interactions with an effective magnitude of 100–400 meV in the region of interest (Fig. 3(b)). The other CT1 state couples weakly with the TT state and the S₁ → S₂ couplings drop rapidly with inter-dimer separation. Other couplings of the ground and LE states with the TT state are much smaller in magnitude because of the two-electron nature of these transitions, validating the previous findings that these interactions are smaller in comparison to one-electron transitions (Fig. 3(a)).^1,19 It should also be noted that the multipolar moments are one-electron operators and cannot reflect the true multielectronic nature of the SF states. Our analysis reveals strong couplings, particularly for TT–CT2 interactions, as compared to previously reported values of <200 meV at the Hartree–Fock level of theory.²⁸ Such interactions are restored by employing DMRG ansätze which enables the coulombic coupling of the multireference electronic density among a larger number of π-electrons by the inclusion of higher-order multipolar contributions. For instance, at R_C–C = 6.30 Å, more than 22% of the total coulombic coupling of the S₁ → S₄ transition originates from hexapole based interactions between the monomers.

Fig. 3 Significant coulombic couplings between the low-lying excited states of the dimer along with the inter-dimer distance. Note that the energy scales in (a) and (b) are quite different from each other.

Although direct electron–electron coulombic couplings exist between adiabatic S₁ and S₂/S₄ states, these coulombic couplings do not seem to be very relevant to the formation of the TT character in S₁. This is clearly seen by comparing Fig. 2 and 3: for R_C–C = 6.1–6.5 Å, S₁ states exhibit increasingly perfect TT characters with respect to increasing distance, while S₁–S₄ coulombic couplings are rapidly attenuated to zero at R_C–C = 6.5–6.6 Å; at shorter R_C–C ≤ 5.9 Å, on the other hand, the S₁–S₄ coulombic couplings are significantly intensified and surprisingly destroy the TT nature by creating a strong CT character.

3.2 The influence of vibronic interactions in pentacene

The discussion till now considered only the electrostatic contribution to the interaction between SF singlet states and showed that the lack of strong couplings between LE and TT/CT2 states excludes the possibility of any direct and CT-mediated SF. In this section, we calculate the DMRG-based Holstein (HCs) and Peierls couplings (PCs) for the pentacene dimer system.^70,71 In general, HCs,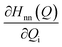 , derived from the natural difference density, represents the geometry relaxations in an excited state n, and PCs, 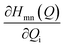, derived from transition density between two states m and n, relates to the vibronic coupling modulation between two electronic states. Further mathematical details for the calculation of VCs are given in Section S4 of the ESI.† We calculated the vibrational modes for the monomer and here consider two ways for the superposition of these modes to mimic the normalized vibrational motion of the dimer: the (i) out-of-phase and (ii) in-phase superposition. During in-phase motion, the atoms in both fragments reach their respective maximum positive (negative) vibrational displacement at the same time. However, the atoms in different fragments vibrate in opposite vibrational directions during the out-of-phase motion (Fig. S10†), i.e., the phase differs by π. The vibronic analysis using the vibrational modes obtained from the optimal dimer geometry is not suitable as this dimer structure is drastically different in inter-dimer separation and dihedral angle from the original herringbone orientation. The higher frequencies at >2000 cm⁻¹ corresponding to the C–H vibrational modulations are not included in this analysis, as in real applications the C–H bonds in pentacene are replaced in silico.⁷²

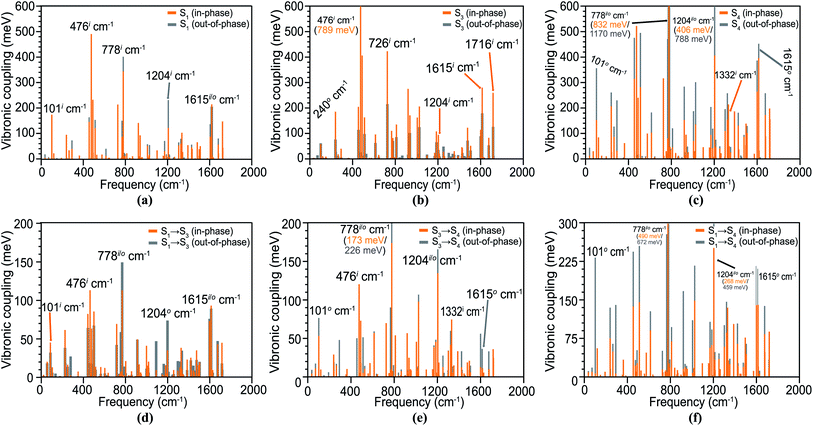
In the spectrum, hereafter, the in-phase and out-of-phase vibrations are distinguished with superscripts i and o, respectively. First, we analyze the Holstein vibronic signatures of the S₁ (TT) state from the active tuning modes by considering the difference density of its parent S₁ state. The calculated HCs are shown in Fig. 4(a), indicating large HCs depending upon the vibrational modulation in each monomer and a few significant peaks are observed at in-phase vibrations of 101ⁱ cm⁻¹, 476ⁱ cm⁻¹, 778^o cm⁻¹, 1204^o cm⁻¹ and 1615ⁱ cm⁻¹ with amplitudes of 175, 491, 403, 233 and 215 meV, respectively. This significant geometric relaxation is a result of in-plane ring bending, in-plane ring breathing, out-of-plane ring breathing, out-of-plane C=C stretching and in-plane C=C stretching motions. In principle, the VCs for out-of-phase modes should vanish in a perfect TT state as previously reported in a slip-stacked tetracene dimer by Ito et al.⁷³ However, the pentacene units in our dimer are not parallel and tilted to an angle resembling more the crystal structure of pentacene in solid films. A recent study by Schnedermann et al.⁷⁴ observed strong vibrational coherence in the frequency region >1000 cm⁻¹ for the intramolecular pentacene SF system, with a perfect intensity match for the 1207 cm⁻¹ mode. Interestingly, our calculations reveal a near-perfect energy matching for both in- and out-of-phase modes at 1204 cm⁻¹ with HCs of 123 and 233 meV, respectively, which can effectively compensate for the energy difference [E(TT) – E(LE)] of 100–200 meV in pentacene or tetracene.

Fig. 4 The Holstein couplings (HCs) of the S₁ (TT) (a), S₃ (LE) (b), and S₄ state (CT2) (c) and the Peierls couplings of the S → S₃ (d), S₃ → S₄ (e), and S → S₄ (f) transitions in the pentacene dimer; the ‘in-phase’ and ‘out-of-phase’ vibrations are represented separately, in orange and grey colors, respectively. The superscripts ‘i’ and ‘o’ represent the ‘in-phase’ and ‘out-of-phase’ vibrations, respectively.

In a locally excited state S₃, the majority of similar vibronic patterns originates from in-phase vibronic interactions, validating the non-CT nature of these electronic states (Fig. 4(b)). A few significant HCs for the S₄ state are observed at 476 cm⁻¹, 1204 cm⁻¹ and 1615 cm⁻¹, similar frequencies to the S₁ state. The large HCs in S₄ are attributed to its strong CT nature modulated by evident interactions through out-of-phase vibronic motion. The strong couplings of 356 meV, 1170 meV and 788 meV originate from very large out-of-plane interactions at 101^o cm⁻¹, 778^o cm⁻¹ and 1204^o cm⁻¹, respectively, and appears to activate the very crucial CT-channel (Fig. 4(c)).

The PC spectra for the significant transitions in the dimer are shown in Fig. 4(d)–(f), which relates to the vibronic modulation from the coupling modes between electronic states, i.e., S₁ → S₃ (TT–LE), S₃ → S₄ (LE–CT2) and S₁ → S₄ (TT–CT2). Our calculations establish the importance of PCs (∼100–300 meV) for the pentacene dimer, which is linked to the small energy differences of these low-lying states derived from DMRG/NEVPT2 computation, as well as the herringbone geometry. This is in sharp contrast to negligible PCs (<50 meV) for a model tetracene as compared to HCs in previous vibronic exciton modeling.^73,75 We realize that the importance of the Peierls-type interaction is highly controversial and sensitive to the dimer packing geometry and crystalline bulk environment.³⁵ The importance of PCs associated with an intermolecular mode was discovered early for the pentacene dimer by Zimmerman et al.,¹⁸ and an intramolecular mode of the covalent dimer was also proposed to facilitate SF via a direct coupling mechanism.⁷⁶ In some other simulations, PCs were entirely neglected for pentacene,^77,78 and also found to be much weaker than HCs by at least an order of magnitude in a recent DFT/MM study in which more surrounding pentacene units were included.²¹ Although the role of PCs appears debatable due to model approximations,^31,37 there exists strong experimental evidence pointing to the significance of symmetry-breaking intermolecular modes leading to considerable couplings between singlet and TT manifolds.^32,79,80

The PCs for the S₁ → S₃ transition have large peaks for many out-of-plane modes at 101ⁱ cm⁻¹, 476ⁱ cm⁻¹, 778^i/o cm⁻¹, 1204ⁱ cm⁻¹ and 1615^i/o cm⁻¹ with amplitudes of 0.05–0.2 eV. The PCs for S₃ → S₄ and S₁ → S₄ transitions have strong PCs at similar vibrational modes; however, the spectra in these cases are dominated by several out-of-phase couplings as shown in Fig. 4(e) and (f). In all the vibronic spectra involving the strong CT2 state, we observe a characteristic peak at 1332 cm⁻¹ for a C=C ring stretching vibrational mode; indeed, it has been shown that crystalline pentacene has a similar fundamental vibrational frequency at 1380 cm⁻¹ contributing towards the VC,⁸¹ in the condensed phase. A VC density (VCD) analysis is performed to understand the microscopic origin or VCs in Section S5† and the important normal modes are sketched in Fig. S11 of the ESI.† The other significant HCs and PCs are plotted in Fig. S8 and S9 of the ESI,† respectively.

3.3 The mixing of SF excitons: an effective Holstein–Peierls Hamiltonian

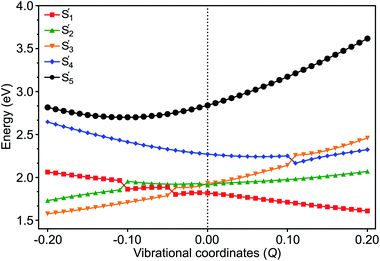
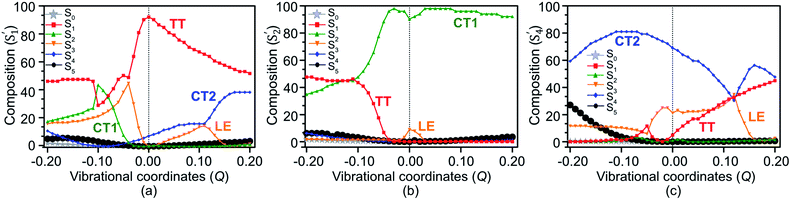
The electronic and Holstein–Peierls interactions are further coupled to construct a six-state vibronic Hamiltonian matrix on the basis of these low-lying SF adiabatic states in pentacene dimer, where (i) the Holstein couplings from all vibrational modes add to the DMRG excited state energy in diagonal Hamiltonian elements, and (ii) the Peierls and multipolar couplings correspond to the corrections in off-diagonal Hamiltonian elements. Here we add vibronic modulations on top of electronic interactions to resemble e–ph couplings and provide a complete picture of the interactions in SF chromophores (see Section S6 of the ESI† for details). This vibronic Hamiltonian is diagonalized with respect to the cumulative vibrational coordinates Q from all the in-phase and out-of-phase modes of the dimer. These eigenvectors denoted by S′_m, where m = 0, 1, …, 5, represent new electronic states as a linear combination of SF basis states. The resulting excited state energies shown as a function of Q in Fig. 5 largely depend on the nature of vibrations. At Q = 0.0, where only coulombic corrections are activated for reasons described in Section S6,† the CT1 (S′₂) becomes totally degenerate with the LE (S′₃) state. However, along with the vibronic motion the energy of the electronic states changes due to the corrections from effective VCs. At large vibronic modulations, S′₂ and S′₄ drift apart and their energy difference becomes large, which reflects the asymmetrical alignment between two monomers.⁶⁴

Fig. 5 The excited state energies of SF states in the pentacene dimer along the vibrational coordinates showing the stabilization/destabilization originating from strong multistate–multimode interactions. The vibrational coordinate, Q (in Å), represents the cumulative contributions from all the in-phase and out-of-phase vibrations of the dimer. The characters (and colors) of the states are assigned by the eigenvector analysis.

According to the theoretical analysis by Feng et al.,⁵⁶ a multiexcitonic state can be populated via either nonadiabatic transition from a source state or by coherently creating the population in the target state, both of which are governed by nonadiabatic couplings. While nonadiabatic transition is commonly promoted at the geometry where two adiabatic states intersect, coherent population can take place in any region where nonadiabatic couplings are strong. Hence the vibrational modes for promoting nonadiabatic transition may be different from the modes strengthening nonadiabatic couplings. In our vibronic coupling analysis, these modes associated with intensive PCs are therefore expected to play a major role in coherently admixing the TT configuration with CT1 and CT2 states, and these modes with intensive HCs are much more meaningful in helping tune the energies of crossing states than well separated states, depending on the symmetries of vibrational modes and the states involved (see Table S4† for the herringbone pentacene dimer).

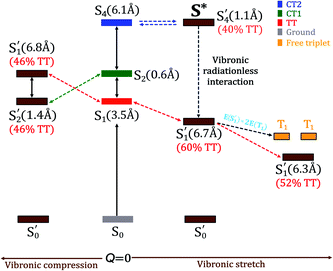
The population transfer is evident in the composition of final SF states shown in Fig. 6, as a result of interstate VCs. At Q = 0.10, the population of the LE basis state in S′₁ drops (Fig. 6(a)), while the contribution from the CT2 basis state rises rapidly with a concomitant rise of TT in S′₄ (Fig. 6(c)). Consequently, a significant TT population is observed not only in S′₁ but in S′₄ as well. In contrast to this, the CT1 contribution to S′₂ plays a crucial role when the dimer is compressed along with the vibronic modulation. The TT basis state destabilizes as a result of the crossing with the CT1 state at about Q = −0.11 and LE state at Q = −0.05 (Fig. 5) and a rather strong mixing among electronic states becomes evident at these displaced geometries (Fig. 6(a)). At Q = −0.11, the overall TT character is mainly distributed among S′₁ (46%), S′₂ (46%) and S′₃ (5%), in which TT, CT1 and LE basis states are admixed (Fig. 6). This paves two indirect pathways for SF in the regions of vibrational stretching and compression, with the former being energetically favorable. The S′₅ does not appear to play any significant role in SF in any region.

Fig. 6 The composition of S′₁ (a), S′₂ (b) and S′₄ (c) states on the basis of the SF states S₀ (ground), S₁ (TT), S₂ (CT1), S₃ (LE), S₄ (CT2) and S₅. A strong “TT–LE–CT” mixing is evident as a result of effective mixing between electronic states with respect to vibrational coordinates Q.

Upon the vibronic stretching, the TT of the S₁ state stabilizes as E(S′₁) = ∼1.71 eV at Q = +0.10 and E(S′₁) = ∼1.61 eV at Q = +0.20, which becomes energetically bound from a free triplet pair (2 E(T₁) = 2 × 0.83 eV of the pentacene monomer⁸²). The TT stabilization also accounts for the evident exothermicity of ∼110 meV in the formation of the correlated triplet pair in pentacene.⁸³ As shown in Fig. 5 and 8, this stabilization of the TT state is a result of vibronic mixing of LE (in S′₃) and CT2 (in S′₄) configurations, which has also been observed for pentacene and other polyenes.^63,84,85 At Q = +0.10, the CT2 and LE states cross each other (Fig. 5 and 6(c)), indicating a rapid population transfer between LE and CT2 manifolds by nonadiabatic transition.

Miyata et al. also observed a similar phenomenon of TT stabilization (destabilization) in the corresponding regions of vibrational stretching (compression) for the tetracene dimer and related it to an interpolated reaction coordinate (Q_SF), which is dominated by the presence of high-frequency C=C stretching modes.⁸⁰ Interestingly, the S′₁ state does not present any possibility of state crossings (or avoided crossings) with other states in the stretching region, indicating that the coherent channel involving S′₁ alone dominates the SF pathway of TT radiationless conversion. As a result, at Q = +0.10, the two states, S′₁ and S′₄, retain a significant TT population of ∼60% and ∼40%, respectively. This indicates that the strong coherent PC interaction admixing the high-lying CT2 and TT characters leads to a multimode vibronic relaxation in S′₁ (Fig. 5) by the stretching modes, towards forming a bound triplet pair state. Our computational evidence implies that the TT dissociation channel can be tuned and facilitated independently from intermolecular interactions.⁸⁶

Although our dimer essentially incorporates the most significant electronic and structural features for SF, yet the mixing between electronic states in crystalline pentacene can be different owing to other solid state effects and different dielectric environments. Keeping this in mind, we adapt a similar approach to construct an effective e–ph interaction Hamiltonian for the pentacene crystal using the GW/BSE method (see Section S7 of the ESI† for computational details). The e–ph interactions in the pentacene crystal further stabilize the S₁ state to ∼1.6 eV (Table S5†), so that this state becomes near-degenerate with the 2 × E(T₁) for pentacene, similar to the phenomenon observed in the vibronic stretching regions of the pentacene dimer to reduce the binding energy of a TT pair along with the vibrational modulation. Although there is an evident difference in how different SF basis states mix with each other between the dimer and the crystal (see Fig. S12 of the ESI† for SF mixing in the pentacene crystal), it is straightforward to identify S′₁ and high-lying S* states with a considerable TT population, provided the fact that the basis S₁ state bears a TT pair in both the dimer and crystal environments. Such an S* state has been interpreted as a geometrically twisted conformation of the TT state in carotenoids.⁸⁷ Kobori et al. highlighted the conformational changes in the covalent pentacene dimer as a result of the vibronic interactions induced by low-frequency modes.⁸⁸

3.4 Implications on TT formation and separation

A loosely bound high-lying state with considerable TT character has been discussed in various experimental observations to be associated with a tightly bound TT state.^89,90 In covalently linked pentacene dimers, a tightly bound TT state is evident from pump–probe spectroscopic investigations.⁹¹ Similarly, our calculations (see Section S8 of the ESI† for further details) predict a tightly bound low-lying S′₁ and a relatively loosely bound high-lying S′₄ state with exciton sizes of 3.46 and 6.12 Å, respectively, at Q = 0.0 merely due to coulombic couplings. As a result of out-of-plane VC modulation, the extent of delocalization in S′₁ increases, while the exciton in S′₄ becomes more localized. The exciton of the S′₂ state remains localized due to its weaker CT character (Fig. 7). It is straightforward to note that the strong out-of-phase Holstein and Peierls VCs between S₁ and S₄ basis states (Fig. 4(c) and (f)) stabilize the new S′₁ state in the vibronic stretching region. It is highly likely that S′₁ would dissociate into two distinct triplets in these regions favored by larger exciton sizes and the insufficient binding energy to couple the two triplets together. It is worth noting that both the S′₃ → S′₄ and S′₁ → S′₄ population transfers are significantly delocalized over two monomers to facilitate a LE–CT–TT modulation, with the exciton sizes of >6.0 Å caused by the out-of-phase vibronic motion (Fig. S13†). Recent electron spin polarization probes on thin films of 6,13-bis(triisopropylsilylethynyl)-pentacene have concluded that the presence of such high-frequency vibronic modulations instigates the depletion of orbital overlap between the two fragments in the dimer leading to the delocalization of the initial exciton.⁹² Overall, the TT formation and separation are driven by multistate interactions activated vibronically, as illustrated in Fig. 8. The Holstein and Peierls modulation through multimode pathways further stabilizes the S′₁ state to generate a loosely bound TT pair with reduced TT binding energy. In contrast to the out-of-phase progression, the exciton for S′₁ shrinks from in-phase vibronic interactions in similar regions (Fig. S14 of the ESI†).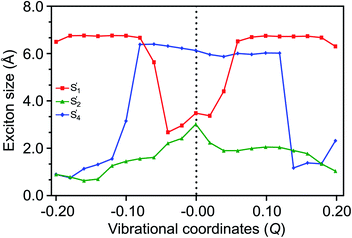

Fig. 7 The exciton sizes for SF states, representing the delocalization of the S′₁ state caused by out-of-phase vibronic modulations.

Fig. 8 Multimode vibronic interactions resulting in the LE ⇔ CT ⇔ TT mixing in the pentacene dimer which further induces the distribution of the TT pair population in two states: a low-lying singlet state S′₁ and another singlet state S* associated with S′₁. Along with the vibronic stretching, the local spin analysis and vibronic Hamiltonian results point to the increasingly loose (delocalized) and tight (localized) TT pair character emerging in S′₁ and S*, respectively. The bound TT is stabilized with respect to the initial singlet states and free triplet pairs. The brown color represents vibronically modified SF states. The exciton sizes (Å) are given in parentheses. The free triplet states (yellow) do not relate to Q.

4 Conclusions

We have presented a comprehensive ab initio molecular quantum chemical study for a pentacene-based SF system. The inclusion of large active electrons in DMRG-based methods treats strongly correlated singlet TT states accurately with computationally feasible calculations. By solving an ongoing puzzle to accurately predict the energy level and nature of excited states in pentacene chromophores, we show that the singlet TT, LE, weak CT1 and strong CT2 characters of low-lying states can be accurately identified and distinguished according to local spin analyses based on a DMRG two-particle descriptor.

The prevailing intermediate mechanism mediating TT generation is not justified in the pentacene dimer. The TT character merely results from the superposition of adiabatic electronic configurations associated with double electron excitations, without assuming an intermediate state model. The direct electron–electron coulombic interaction exists between adiabatic S₁ (TT) and S₂ (weak CT)/S₄ (strong CT) states. However, coulombic interaction is not found to be strongly relevant to the formation of TT pair state S₁, since the S₁ state of perfect TT character also appears in the pentacene dimer at a larger range of intermolecular distances (6.3–6.6 Å) where interstate coulombic interaction is rapidly attenuated to zero, while at short intermolecular distances where coulombic interaction is intensified, the singlet TT nature is annihilated with a strong charge-transfer character created.

To reveal the vibronic details of the SF process, we further include vibronic interactions in our multistate–multimode Hamiltonian, revealing that there are significant indirect couplings between the electronic states, as compared to the limited direct coupling involving states of local excitation. Through various wavefunction analyses, it is found that the initial bright singlet state exhibits the character of low-lying weak CT1 which however does not favor strong SF through the CT-mediated coherent pathway alone. Both CT1 and CT2 states must be effectively engaged in SF through a vibronic state admixture with TT pair states, causing significant TT population transfer to CT1 and CT2 states in the vibrational region of compression and stretching, respectively. The vibronic compression makes local TT characters photophysically accessible by mixing with the lower-lying weak CT1, and the vibronic stretching facilitates substantial delocalization and stabilization of TT pair states in an effective mixture with the higher-lying strong CT2. Moreover, the presence of strong VCs with some low-frequency vibrational modes provides qualitative evidence for a thermally activated SF process. The vibrational motion can be tuned by structural modification to achieve enhanced admixture between electronic states for desirable TT character and exciton energies. A comparison between the pentacene dimer and crystal environments highlights the structural features and provides a link between the crystal and vibronically tuned dimer structure. These findings brick a multistate–multimode landscape for understanding the fundamental and complex SF process in pentacene.

Data availability

Computational techniques and additional data are available in the ESI.†

Author contributions

R. W. and J. Y. designed and developed the theoretical framework. R. W. implemented the methodologies and analyzed the data. Z. D. performed the GW/BSE calculations. All authors discussed the results and contributed to the final manuscript. R. W. and J. Y. wrote the manuscript. J. Y. supervised and conceived the whole project.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the funding support from the Hong Kong Research Grants Council (GRF17308618 and ECS27307517), the Major Program of Guangdong Basic and Applied Research (2019B030302009) and the Science, Technology, and Innovation Commission of Shenzhen Municipality (JCYJ20170412140251576 and JCYJ20180508162429786). J. Y. acknowledges the research program of the AIR@InnoHK cluster from the Innovation and Technology Commission of Hong Kong SAR of China. The computations were partially performed using research computing facilities offered by Information Technology Services, the University of Hong Kong.

References

1. M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936.
2. M. A. Green, Prog. Photovoltaics, 2001, 9, 123–135.
3. National Renewable Energy Laboratory, Singlet fission holds two-for-one potential in solar cells, United States, 2012.
4. W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510.
5. M. B. Smith and J. Michl, Annu. Rev. Phys. Chem., 2013, 64, 361–386.
6. A. Akdag, Z. Havlas and J. Michl, J. Am. Chem. Soc., 2012, 134, 14624–14631.
7. A. F. Schwerin, J. C. Johnson, M. B. Smith, P. Sreearunothai, D. Popović, J. Černý, Z. Havlas, I. Paci, A. Akdag, M. K. MacLeod, U. Chen, D. E. David, M. A. Ratner, J. R. Miller, A. J. Nozik and J. Michl, J. Phys. Chem. A, 2010, 114, 1457–1473.
8. N. Renaud, P. A. Sherratt and M. A. Ratner, J. Phys. Chem. Lett., 2013, 4, 1065–1069.
9. T. Zeng, N. Ananth and R. Hoffmann, J. Am. Chem. Soc., 2014, 136, 12638–12647.
10. D. Casanova, Chem. Rev., 2018, 118, 7164–7207.
11. A. Rao, M. B. Wilson, J. M. Hodgkiss, S. Albert-Seifried, H. Bässler and R. H. Friend, J. Am. Chem. Soc., 2010, 132, 12698–12703.
12. I. Paci, J. C. Johnson, X. Chen, G. Rana, D. Popović, D. E. David, A. J. Nozik, M. A. Ratner and J. Michl, J. Am. Chem. Soc., 2006, 128, 16546–16553.
13. A. M. Müller, Y. S. Avlasevich, W. W. Schoeller, K. Müllen and C. J. Bardeen, J. Am. Chem. Soc., 2007, 129, 14240–14250.
14. K. Miyata, F. S. Conrad-Burton, F. L. Geyer and X.-Y. Zhu, Chem. Rev., 2019, 119, 4261–4292.
15. T. S. Kuhlman, J. Kongsted, K. V. Mikkelsen, K. B. Møller and T. I. Sølling, J. Am. Chem. Soc., 2010, 132, 3431–3439.
16. P. M. Zimmerman, Z. Zhang and C. B. Musgrave, Nat. Chem., 2010, 2, 648–652.
17. R. Havenith, H. D. de Gier and R. Broer, Mol. Phys., 2012, 110, 2445–2454.
18. P. M. Zimmerman, F. Bell, D. Casanova and M. Head-Gordon, J. Am. Chem. Soc., 2011, 133, 19944–19952.
19. T. Zeng, R. Hoffmann and N. Ananth, J. Am. Chem. Soc., 2014, 136, 5755–5764.
20. F. A. Schröder, D. H. Turban, A. J. Musser, N. D. Hine and A. W. Chin, Nat. Commun., 2019, 10, 1–10.
21. T. Nagami, T. Tonami, K. Okada, W. Yoshida, H. Miyamoto and M. Nakano, J. Chem. Phys., 2020, 153, 134302.
22. K. T. Munson, J. Gan, C. Grieco, G. S. Doucette, J. E. Anthony and J. B. Asbury, J. Phys. Chem. C, 2020, 124, 23567–23578.
23. C. Hetzer, B. S. Basel, S. M. Kopp, F. Hampel, F. J. White, T. Clark, D. M. Guldi and R. R. Tykwinski, Angew. Chem., 2019, 131, 15407–15411.
24. S. N. Sanders, E. Kumarasamy, A. B. Pun, M. L. Steigerwald, M. Y. Sfeir and L. M. Campos, Chem, 2016, 1, 505–511.
25. S. N. Sanders, E. Kumarasamy, A. B. Pun, M. L. Steigerwald, M. Y. Sfeir and L. M. Campos, Angew. Chem., 2016, 55, 3373–3377.
26. S. N. Sanders, E. Kumarasamy, A. B. Pun, M. T. Trinh, B. Choi, J. Xia, E. J. Taffet, J. Z. Low, J. R. Miller, X. Roy, X.-Y. Zhu, M. L. Steigerwald, M. Y. Sfeir and L. M. Campos, J. Am. Chem. Soc., 2015, 137, 8965–8972.
27. B. S. Basel, J. Zirzlmeier, C. Hetzer, B. T. Phelan, M. D. Krzyaniak, S. R. Reddy, P. B. Coto, N. E. Horwitz, R. M. Young, F. J. White, F. Hampel, T. Clark, M. Thoss, R. R. Tykwinski, M. R. Wasielewski and D. M. Guldi, Nat. Commun., 2017, 8, 15171.
28. T. C. Berkelbach, M. S. Hybertsen and D. R. Reichman, J. Chem. Phys., 2013, 138, 114103.
29. W.-L. Chan, M. Ligges, A. Jailaubekov, L. Kaake, L. Miaja-Avila and X.-Y. Zhu, Science, 2011, 334, 1541–1545.
30. W.-L. Chan, T. C. Berkelbach, M. R. Provorse, N. R. Monahan, J. R. Tritsch, M. S. Hybertsen, D. R. Reichman, J. Gao and X.-Y. Zhu, Acc. Chem. Res., 2013, 46, 1321–1329.
31. R. Tempelaar and D. R. Reichman, J. Chem. Phys., 2018, 148, 244701.
32. H.-G. Duan, A. Jha, X. Li, V. Tiwari, H. Ye, P. K. Nayak, X.-L. Zhu, Z. Li, T. J. Martinez, M. Thorwart and R. J. D. Miller, Sci. Adv., 2020, 6, eabb0052.
33. J. D. Schultz, J. Y. Shin, M. Chen, J. P. O'Connor, R. M. Young, M. A. Ratner and M. R. Wasielewski, J. Am. Chem. Soc., 2021, 2049–2058.
34. A. J. Musser, M. Liebel, C. Schnedermann, T. Wende, T. B. Kehoe, A. Rao and P. Kukura, Nat. Phys., 2015, 11, 352–357.
35. N. Renaud and F. C. Grozema, J. Phys. Chem. Lett., 2015, 6, 360–365.
36. T. Nagami, T. Tonami, K. Okada, W. Yoshida, H. Miyamoto and M. Nakano, J. Chem. Phys., 2020, 153, 134302.
37. M. A. Castellanos and P. Huo, J. Phys. Chem. Lett., 2017, 8, 2480–2488.
38. T. Nagami, H. Miyamoto, R. Sakai and M. Nakano, J. Phys. Chem. C, 2021, 125, 2264–2275.
39. J. Hachmann, J. J. Dorando, M. Avilés and G. K.-L. Chan, J. Chem. Phys., 2007, 127, 134309.
40. L. V. Slipchenko and A. I. Krylov, J. Chem. Phys., 2002, 117, 4694.
41. S. R. White, Phys. Rev. Lett., 1992, 69, 2863.
42. G. K.-L. Chan and S. Sharma, Annu. Rev. Phys. Chem., 2011, 62, 465–481.
43. J. Hachmann, W. Cardoen and G. K.-L. Chan, J. Chem. Phys., 2006, 125, 144101.
44. Q. Sun, J. Yang and G. K.-L. Chan, Chem. Phys. Lett., 2017, 683, 291–299.
45. Q. Sun, X. Zhang, S. Banerjee, P. Bao, M. Barbry, N. S. Blunt, N. A. Bogdanov, G. H. Booth, J. Chen, Z.-H. Cui, J. J. Eriksen, Y. Gao, S. Guo, J. Hermann, M. R. Hermes, K. Koh, P. Koval, S. Lehtola, Z. Li, J. Liu, N. Mardirossian, J. D. McClain, M. Motta, B. Mussard, H. Q. Pham, A. Pulkin, W. Purwanto, P. J. Robinson, E. Ronca, E. R. Sayfutyarova, M. Scheurer, H. F. Schurkus, J. E. T. Smith, C. Sun, S.-N. Sun, S. Upadhyay, L. K. Wagner, X. Wang, A. White, J. D. Whitfield, M. J. Williamson, S. Wouters, J. Yang, J. M. Yu, T. Zhu, T. C. Berkelbach, S. Sharma, A. Y. Sokolov and G. K.-L. Chan, J. Chem. Phys., 2020, 153, 024109.
46. G. K.-L. Chan and M. Head-Gordon, J. Chem. Phys., 2002, 116, 4462–4476.
47. G. K.-L. Chan, J. Chem. Phys., 2004, 120, 3172–3178.
48. D. Ghosh, J. Hachmann, T. Yanai and G. K.-L. Chan, J. Chem. Phys., 2008, 128, 144117.
49. S. Sharma and G. K.-L. Chan, J. Chem. Phys., 2012, 136, 124121.
50. R. Olivares-Amaya, W. Hu, N. Nakatani, S. Sharma, J. Yang and G. K.-L. Chan, J. Chem. Phys., 2015, 142, 034102.
51. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
52. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc. Wallingford CT, 2016.
53. J. Deslippe, G. Samsonidze, D. A. Strubbe, M. Jain, M. L. Cohen and S. G. Louie, Comput. Phys. Commun., 2012, 183, 1269–1289.
54. T. H. Dunning, J. Chem. Phys., 1989, 90, 1007.
55. S. Schiefer, M. Huth, A. Dobrinevski and B. Nickel, J. Am. Chem. Soc., 2007, 129, 10316–10317.
56. X. Feng, A. V. Luzanov and A. I. Krylov, J. Phys. Chem. Lett., 2013, 4, 3845–3852.
57. Y. Kurashige and T. Yanai, Bull. Chem. Soc. Jpn., 2014, 1071–1073.
58. P. B. Coto, S. Sharifzadeh, J. B. Neaton and M. Thoss, J. Chem. Theory Comput., 2015, 11, 147–156.
59. A. V. Luzanov, D. Casanova, X. Feng and A. I. Krylov, J. Chem. Phys., 2015, 142, 224104.
60. A. E. Clark and E. R. Davidson, J. Chem. Phys., 2001, 115, 7382–7392.
61. E. Ramos-Cordoba, E. Matito, I. Mayer and P. Salvador, J. Chem. Theory Comput., 2012, 8, 1270–1279.
62. A. Martín Pendás and E. Francisco, Phys. Chem. Chem. Phys., 2021, 23, 8375–8392.
63. C. K. Yong, A. J. Musser, S. L. Bayliss, S. Lukman, H. Tamura, O. Bubnova, R. K. Hallani, A. Meneau, R. Resel, M. Maruyama, S. Hotta, L. M. Herz, D. Beljonne, J. E. Anthony, J. Clark and H. Sirringhaus, Nat. Commun., 2017, 8, 15953.
64. D. Beljonne, H. Yamagata, J. L. Brédas, F. C. Spano and Y. Oliver, Phys. Rev. Lett., 2013, 110, 226402.
65. P. Petelenz, M. Snamina and G. Mazur, J. Phys. Chem. C, 2015, 119, 14338–14342.
66. M. Snamina and P. Petelenz, ChemPhysChem, 2017, 18, 149–155.
67. B. Błasiak, M. Maj, M. Cho and R. W. Góra, J. Chem. Theory Comput., 2015, 11, 3259–3266.
68. A. Olaya-Castro and G. D. Scholes, Int. Rev. Phys. Chem., 2011, 30, 49–77.
69. V. May and O. Kühn, Charge and Energy Transfer Dynamics in Molecular Systems, Wiley-VCH Verlag, Weinheim, Germany, 3rd edn, 2011.
70. K. Tokunaga, T. Sato and K. Tanaka, J. Chem. Phys., 2006, 124, 154303.
71. T. Sato, K. Tokunaga and K. Tanaka, J. Chem. Phys., 2006, 124, 024314.
72. E. Kumarasamy, S. N. Sanders, A. B. Pun, S. A. Vaselabadi, J. Z. Low, M. Y. Sfeir, M. L. Steigerwald, G. E. Stein and L. M. Campos, Macromolecules, 2016, 49, 1279–1285.
73. S. Ito, T. Nagami and M. Nakano, J. Phys. Chem. Lett., 2015, 6, 4972–4977.
74. C. Schnedermann, A. M. Alvertis, T. Wende, S. Lukman, J. Feng, F. A. Y. N. Schröder, D. H. P. Turban, N. D. M. H. Jishan Wu, N. C. Greenham, A. W. Chin, A. Rao, P. Kukura and A. J. Musser, Nat. Commun., 2019, 10, 4207.
75. A. F. Morrison and J. M. Herbert, J. Phys. Chem. Lett., 2017, 8, 1442–1448.
76. E. G. Fuemmeler, S. N. Sanders, A. B. Pun, E. Kumarasamy, T. Zeng, K. Miyata, M. L. Steigerwald, X.-Y. Zhu, M. Y. Sfeir and L. M. Campos, et al. , ACS Cent. Sci., 2016, 2, 316–324.
77. L. Wang, Y. Olivier, O. V. Prezhdo and D. Beljonne, J. Phys. Chem. Lett., 2014, 5, 3345–3353.
78. T. C. Berkelbach, M. S. Hybertsen and D. R. Reichman, J. Chem. Phys., 2014, 141, 074705.
79. A. A. Bakulin, S. E. Morgan, T. B. Kehoe, M. W. Wilson, A. W. Chin, D. Zigmantas, D. Egorova and A. Rao, Nat. Chem., 2016, 8, 16–23.
80. K. Miyata, Y. Kurashige, K. Watanabe, T. Sugimoto, S. Takahashi, S. Tanaka, J. Takeya, T. Yanai and Y. Matsumoto, Nat. Chem., 2017, 9, 983–989.
81. N. J. Hestand, H. Yamagata, B. Xu, D. Sun, Y. Zhong, A. R. Harutyunyan, G. Chen, H.-L. Dai, Y. Rao and F. C. Spano, J. Phys. Chem. C, 2015, 119, 22137–22147.
82. E. Heinecke, D. Hartmann, R. Müller and A. Hese, J. Chem. Phys., 1998, 109, 906–911.
83. N. Monahan and X.-Y. Zhu, Annu. Rev. Phys. Chem., 2015, 66, 601–618.
84. P. Tavan and K. Schulten, Phys. Rev. B: Condens. Matter Mater. Phys., 1987, 36, 4337–4358.
85. A. J. Musser, M. Al-Hashimi, M. Maiuri, D. Brida, M. Heeney, G. Cerullo, R. H. Friend and J. Clark, J. Am. Chem. Soc., 2013, 135, 12747–12754.
86. M. T. Trinh, Y. Zhong, Q. Chen, T. Schiros, S. Jockusch, M. Y. Sfeir, M. Steigerwald, C. Nuckolls and X. Zhu, J. Phys. Chem. C, 2015, 119, 1312–1319.
87. D. Niedzwiedzki, J. F. Koscielecki, H. Cong, J. O. Sullivan, G. N. Gibson, R. R. Birge and H. A. Frank, J. Phys. Chem. B, 2007, 111, 5984–5998.
88. Y. Kobori, M. Fuki, S. Nakamura and T. Hasobe, J. Phys. Chem. B, 2020, 124, 9411–9419.
89. C. C. Gradinaru, J. T. M. Kennis, E. Papagiannakis, I. H. M. van Stokkum, R. J. Cogdell, G. R. Fleming, R. A. Niederman and R. van Grondelle, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 2364–2369.
90. E. Papagiannakis, J. T. M. Kennis, I. H. M. van Stokkum, R. J. Cogdell and R. van Grondelle, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 6017–6022.
91. M. T. Trinh, A. Pinkard, A. B. Pun, S. N. Sanders, E. Kumarasamy, M. Y. Sfeir, L. M. Campos, X. Roy and X.-Y. Zhu, Sci. Adv., 2017, 3, e1700241.
92. S. Matsuda, S. Oyama and Y. Kobori, Chem. Sci., 2020, 11, 2934–2942.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc01703a

---