Open Access Article
Open Access ArticleCatalyst design in C–H activation: a case study in the use of binding free energies to rationalise intramolecular directing group selectivity in iridium catalysis†
William J.
Kerr
 *,
Gary J.
Knox
*,
Gary J.
Knox
 ,
Marc
Reid
,
Marc
Reid
 * and
Tell
Tuttle
* and
Tell
Tuttle

Department of Pure & Applied Chemistry, WestCHEM, University of Strathclyde, Glasgow G1 1XL, Scotland, UK. E-mail: w.kerr@strath.ac.uk; marc.reid.100@strath.ac.uk
First published on 20th April 2021
Abstract
Remote directing groups in a bifunctional molecule do not always behave independently of one another in C–H activation chemistries. A combined DFT and experimental mechanistic study to provide enhanced Ir catalysts for chemoselective C–H deuteration of bifunctional aryl primary sulfonamides is described. This provides a pharmaceutically-relevant and limiting case study in using binding energies to predict intramolecular directing group chemoselectivity. Rational catalyst design, guided solely by qualitative substrate–catalyst binding free energy predictions, enabled intramolecular discrimination between competing ortho-directing groups in C–H activation and delivered improved catalysts for sulfonamide-selective C–H deuteration. As a result, chemoselective binding of the primary sulfonamide moiety was achieved in the face of an intrinsically more powerful pyrazole directing group present in the same molecule. Detailed DFT calculations and mechanistic experiments revealed a breakdown in the applied binding free energy model, illustrating the important interconnectivity of ligand design, substrate geometry, directing group cooperativity, and solvation in supporting DFT calculations. This work has important implications around attempts to predict intramolecular C–H activation directing group chemoselectivity using simplified monofunctional fragment molecules. More generally, these studies provide insights for catalyst design methods in late-stage C–H functionalisation.
Introduction
The evolving synergy between experimental and computational chemistry is central to the study of organometallic reactions, and now permeates most aspects of catalysis, mechanistic studies, ligand design, and chemoinformatics.1–7 Among the areas of organometallic chemistry capitalising on this contemporary investigative approach, C–H activation is notably prevalent.8,9 However, while the use of theory to rationalise and analyse experimental results is increasingly common, application of these methods to the prediction and design of new catalysts remains less so.An understanding of site selectivity is vital for the implementation of late-stage C–H functionalisation methods in organic synthesis.10–12 Yet, relative to the number of synthetic developments, fundamental studies on site selectivity in complex molecules are rare.13–21 In our laboratories,18,22–25 we have explored iridium-catalysed C–H activation and hydrogen isotope exchange (HIE) protocols26–31 for application in pharmaceutically-relevant labelling studies. Importantly, such studies also serve as an insightful proxy for determining site selectivity in other C–H functionalisation processes.32–38 In relation to this, we recently reported a rare example of ortho-C–H activation and deuteration of aryl primary (1°) sulfonamides.24 In the course of these studies, when labelling bifunctional sulfa drug 1→3, sterically-distinct precatalysts 2a and 2b labelled 1 with dramatically different selectivities, with neutral NHC/Cl catalyst 2a directing labelling ortho to the sulfonamide, and cationic NHC/phosphine catalyst 2b leading to deuterium incorporation ortho to the pyrazole unit (Scheme 1).
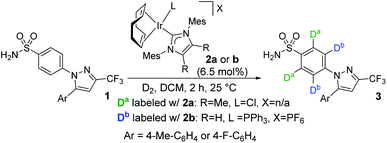 | ||
| Scheme 1 Catalyst-enabled switching of directing group chemoselectivity in the deuterium labelling of sulfa drugs. | ||
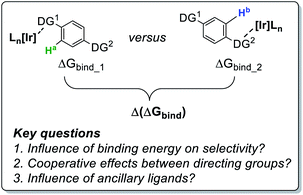
Mechanistic analysis led to an enhanced understanding of this intramolecular ortho-directing group (DG) selectivity. Specifically, it was found that, in the face of energetically similar C–H activation barriers proceeding via sigma-complex assisted metathesis, the substrate–catalyst binding event (through either sulfonamide or pyrazole ortho-directing groups) was found to be the product-determining step.24 Furthermore, the choice of catalyst 2a or 2b was sufficient to completely alter the observed labelling chemoselectivity from one directing group to the other. Crucially, directing group selectivity in these bifunctional molecules could not be predicted on the basis of competition experiments with the individual sulfonamide and pyrazole fragments.24 We have therefore undertaken practical and theoretical studies to further develop the qualitative (semi-quantitative) understanding of intramolecular directing group selectivity in the context of rational catalyst design for ortho-C–H activation with aryl 1° sulfonamides (Scheme 2).
Computational details
Consistent with previous studies on related systems,24,25 the vast majority of calculations employed the M06 density functional in conjunction with the 6-31G* basis set for main group non-metal atoms and the Stuttgart RSC effective core potential along with the associated basis set for Ir. This level of theory – with and without solvation – has been employed successfully by our group,24,25,39 and others,13 in previous reports for related systems, serving as the minimum viable level of theory to produce qualitative direction for experimental catalyst design strategies. Additional calculations employing the Polarization Continuum Model40 for DCM solvation have been included and stated explicitly where it has been relevant to highlight the limitations of the predictive binding free energy model under investigation. As detailed in the Results section, our original aim was not to provide a high-level quantitative model, but rather a simple qualitative predictor of labelling selectivity via examination of differences in directing group binding free energy alone. This approach is based on findings from our previous publication, wherein combined binding and transition state calculations showed that binding free energy differences alone could be semi-quantitative predictors of directing group chemoselectivity in the presence of various catalysts.24 While the energy of the transition state will have an effect on the rate and efficacy of a reaction, the aforementioned previous investigations have shown that the transition state energy, in the Ir C–H activation catalyst types under consideration, is not strongly affected by the directing groups. Therefore, the relative energy difference between the initial bound states of each available directing group in the substrate creates an effective higher activation energy for the weaker bound complex, which invites the assumption that the difference in binding free energy is product determining. Free energy differences for Δ(ΔGbind) displayed herein are as a result of manually exploring reasonable conformational substrate–catalyst binding space and calculating Boltzmann distributions where appropriate. All calculated conformations were found to exist within approximately 10–15 kcal mol−1 of the global minimum. The Boys–Bernardi counterpoise scheme was employed for the exploration of electronic binding energies deconstructed into favourable and distorting interactions between catalyst and substrate fragments. All counterpoise calculations were conducted using geometries previously optimised in either gas phase or DCM, as appropriate. Importantly, counterpoise calculations themselves possess no information on free energy, and contain only electronic energy contributions. Full details of and references to the theoretical methods are contained within the ESI†.Results
Understanding bifunctional substrate properties
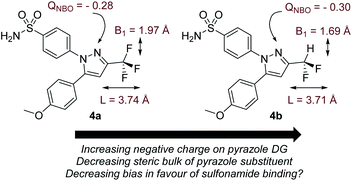
Before commencing our investigations and as delineated in the Computational details section, it was hypothesised that the simple thermodynamic parameter Δ(ΔGbind) (Scheme 2; computationally less demanding than transition state calculations) may serve as a useful qualitative indicator of overall intramolecular directing group selectivity, assuming similar ortho-C–H activation kinetic barriers for reaction at either directing group.24 However, we also recognised that computational predictions and observed selectivities reported in our earlier work may have been biased – in favour of sulfonamide selectivity – by both the steric encumbrance and electron-withdrawing power of the trifluoromethyl (CF3) substituent in drug series 1 (Scheme 1).24 Specifically, the CF3 group directly attenuates the binding ability of the competing pyrazole directing group. However, the CF3 group only indirectly influences the remote sulfonamide in the same molecule. The CF3 group may, then, exaggerate the observed sulfonamide over pyrazole directing group chemoselectivity differences between catalysts 2a and 2b (Scheme 1). Indeed, calculation of Sterimol41 (steric) and NBO42 charge (electronic) differences in methoxy analogues of 1, 4a (CF3 pyrazole substituent) and 4b (CF2H pyrazole substituent), supports this view (Scheme 3).The CF3 group is calculated to be distinctly larger (in two dimensions) than CF2H in the analogous molecule. Not surprisingly, CF3 also withdraws more electron density from the Lewis basic pyrazole nitrogen relative to the CF2H analogue.
Using qualitative binding free energy calculations to explore product-determining directing group chemoselectivity and sulfonamide-selective catalyst design
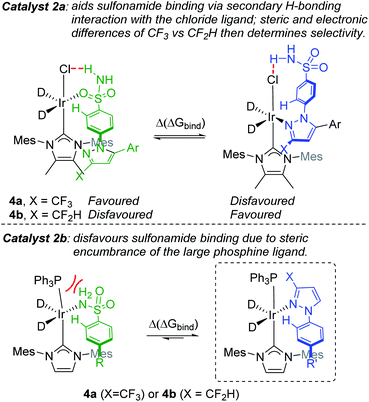
With the aforementioned observations in mind, we aimed initially to answer two key questions in the current study: (i) can intramolecular directing group selectivity be more generally (within the realms of Ir-catalysed C–H activation) predicted via qualitative Δ(ΔGbind) calculations alone, and (ii) to what extent do electronic and steric effects in the competing pyrazole directing group (i.e. CF3 derivative 4avs. CF2H derivative 4b) influence sulfonamide binding when employing less encumbered catalyst 2a? Furthermore, in the course of these investigations, we also established the deuterium labelling profiles with further derivatives of drug series 1, and evaluated the broader ability of binding free energy calculations to qualitatively guide rational catalyst design for enhanced sulfonamide-selective C–H deuteration.Our hypothesis on the combined influences of catalyst and substrate structure on directing group chemoselectivity is shown in Scheme 4. For the smaller catalyst 2a, we showed previously that sulfonamide selectivity was consistent with the binding model that harnesses secondary hydrogen bonding between the chloride ligand and the sulfonamide directing group (Scheme 4, top left).24 It was theorised that this preference would switch to pyrazole binding upon a switch of CF3 for CF2H substitution (Scheme 4, top right). Conversely, the more rigid and sterically encumbered ligand sphere in catalyst 2b is more discerning between these directing groups on the basis of directing group size. The planar pyrazole binds preferentially over the larger tetrahedral sulfonamide, regardless of CF3 or CF2H substitution on the pyrazole ring (Scheme 4, bottom). Indeed, catalyst 2b is unable to efficiently label even simple aryl 1° sulfonamides.24 Based on all of this, the switchable directing group chemoselectivity is predicted to be unique to NHC/Cl precatalyst 2a (cf. 2b).
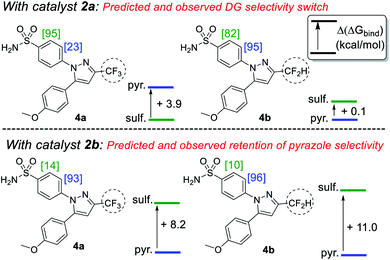
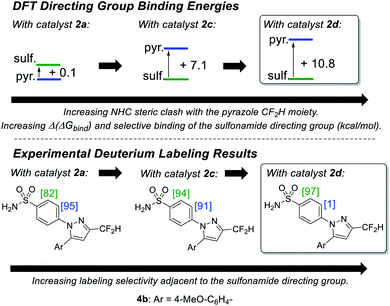
Building on our initial hypothesis, our investigations towards catalysts of enhanced effectiveness for sulfonamide-directed C–H activation and labelling began by assessing the relative binding energies of drug derivatives 4a and 4b to the activated Ir(III) dideuteride forms of Ir(I) precatalysts 2a and 2b (Scheme 5). For bulky catalyst 2b, pyrazole binding was predicted to dominate in both drug derivatives, 4a (CF3) and 4b (CF2H); Scheme 5 (bottom). In the case of smaller catalyst 2a, however, the sulfonamide and pyrazole directing group binding energies were relatively balanced, with sulfonamide binding favoured in CF3 derivative 4a, but pyrazole binding dominating in CF2H derivative 4b; Scheme 5 (top).
Encouragingly, consideration of the sulfonamide and pyrazole binding energies was sufficient to qualitatively understand and predict the experimentally observed labelling, and thus directing group chemoselectivity (in binary terms), in all cases (Scheme 5). Remarkably, it appeared that qualitative binding free energy calculations were able to capture directing group selectivity switching (Scheme 5, top) and selectivity retention (Scheme 5, bottom) for each combination of substrate and catalyst. This comparison of theoretical directing group binding energies Δ(ΔGbind) versus experimentally observed deuterium labelling selectivity highlighted the apparent qualitative and predictive use of these simple calculations in discriminating intramolecular directing groups (Scheme 5). This was consistent with a number of previous observations emerging from our own laboratories,18,22,24,25,39 as well as those reported by Derdau and co-workers.13 As a result, these observations presented an opportunity to redesign catalyst 2a in an attempt to reinstate high sulfonamide directing group chemoselectivity in CF2H derivative 4b, even in the face of the intrinsically favoured competitor pyrazole directing group present in the same substrate.
Redesigning catalyst 2a towards improved sulfonamide selectivity
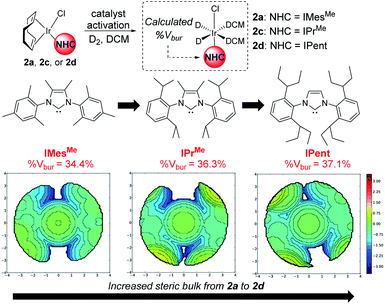
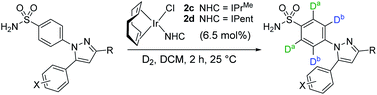
From our previous studies with catalysts such as 2a, alteration of the NHC ligand size had the most marked impact on catalyst activity across the various design parameters considered.24 Accordingly, percent buried volume (%Vbur) calculations43–45 suggested that new catalysts 2c, [(COD)Ir(IPrMe)(Cl)], and 2d, [(COD)Ir(IPent)(Cl)], progressively more sterically encumbered analogues of 2a (Scheme 6), would provide a steric clash with the CF2H substituent that would diminish deuterium labelling via the pyrazole unit.Indeed, on comparing Δ(ΔGbind) and experimentally observed deuterium labelling selectivities in substrate 4b with catalysts 2a, 2c, and 2d, sulfonamide selectivity was restored with progressive efficacy using larger catalysts 2c then 2d (Scheme 7). Table 1 (vide infra) reveals the broader effectiveness, synthetic utility, and limits of redesigned catalyst 2d (the most encumbered in the series), demonstrating previously unattainable chemoselectivity for the sulfonamide directing group in the face of the competing pyrazole.
Kinetic analysis of intramolecular directing group chemoselectivity across the evolving catalyst series
Importantly, the vastly improved sulfonamide directing group chemoselectivity with catalyst 2dversus catalyst 2a is consistent with differences in the temporal profiles of deuterium labelling ortho to each directing group in substrate 4b using catalysts 2a, 2c, and 2d in the series (Scheme 8). More specifically, kinetic profiling showed that there were modest relative rate differences in labelling next to the sulfonamide versus pyrazole directing groups when catalyst 2a or 2c was used (Scheme 8, left and middle panels). However, with catalyst 2d, the C–H positions ortho to the sulfonamide in 4b were labelled over 400 times faster than those C–H positions adjacent to the pyrazole (Scheme 8, rightmost panel). Catalyst 2d was also the only catalyst in the series to enable high levels of sulfonamide selectivity to be maintained throughout the entire time period in which the profile was monitored (Scheme 8, right). This selectivity differs from that of catalyst 2c, where selectivity for sulfonamide over pyrazole labelling was eroded over the monitored time course. Finally, it should be noted that the kinetic results qualitatively agree with the single-point deuteration results reported for reactions with 4b (Scheme 7).46 The direction of selectivity remains the same across all cases in Schemes 7 and 8, and differences in absolute %D are likely due to the different scale and vessel shape required to capture the kinetic information reported in Scheme 8.53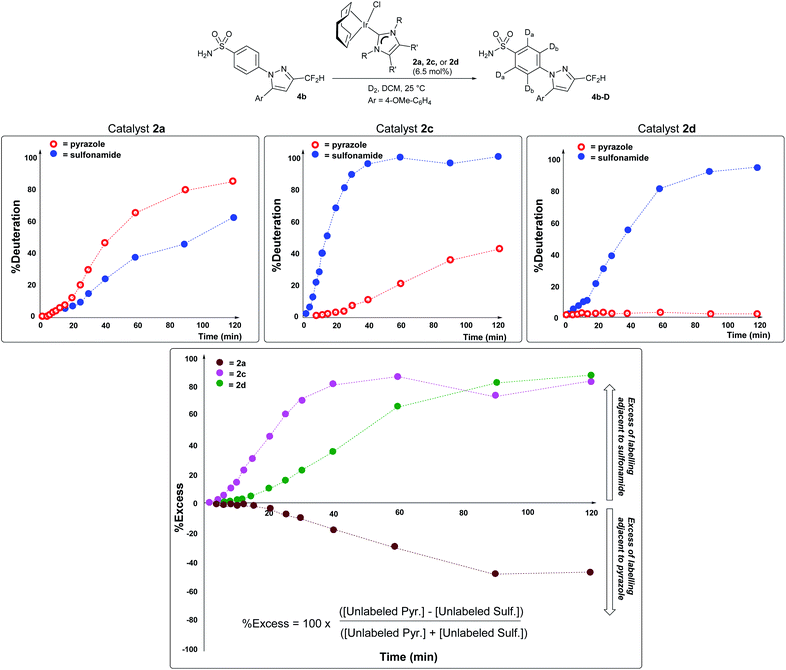 | ||
| Scheme 8 Top row, left to right: time course plots evidencing increased kinetic selectivity for labelling adjacent to the sulfonamide over the pyrazole directing group as the catalyst becomes more sterically encumbered. The visible induction period in each time course reflects the precatalyst Ir(I) → Ir(III) activation process, a simplified representation of which is shown at the top of Scheme 6. Bottom panel: dynamic selectivity for labelling adjacent to the sulfonamide directing group over the pyrazole as a function of time, expressed as a percentage excess, with the positive y-values denoting a preference for sulfonamide over pyrazole. Each series of points and dashed lines represents a different catalyst employed. | ||
Probing the possible non-innocence of a distal directing group in a bifunctional substrate
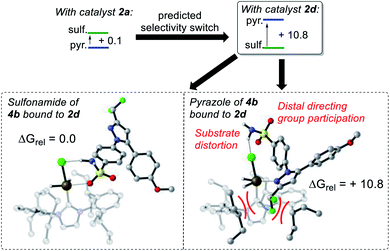
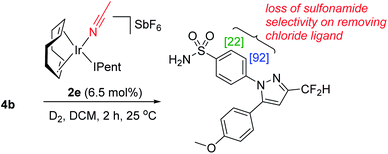
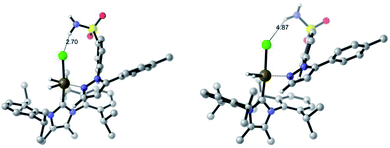
In the IPrMe47 or IPent48 ligands of 2nd and 3rd generation precatalysts 2c and 2d, respectively, the enhanced steric interaction with the CF2H group on the pyrazole of substrate 4b appeared to be manifested in Δ(ΔGbind), and is exemplified in the resultant DFT-calculated structures for the interaction of 4b and 2d (Scheme 9). Crucially, when the pyrazole of 4b is bound to the iridium centre (Scheme 9, right), our standard and precedented gas phase calculation protocol suggested that the distal sulfonamide is not innocent. Whilst the pyrazole binds to the metal centre, the gas phase calculation shows the sulfonamide binding via a NH–Cl hydrogen bond, resulting in an unfavourable distortion of the bound substrate. This apparent distortion is in addition to the steric clash between the CF2H substituent and the NHC ligand. Using the Δ(ΔGbind) method and our standard level of theory in DFT calculations, the secondary interaction of the distal sulfonamide would appear to suggest that directing groups within the same molecule cannot be assumed to be acting independently of one another (Scheme 9, right).24 In this case, and despite their apparent spatial separation, intramolecular directing group reactivity could be considered coupled, and thus suggest that secondary interactions emerging from the binding event can influence a given directing group binding mode. Note that no such secondary interaction is apparent from gas phase calculations that have the sulfonamide participating as the main directing group bound directly to the metal (Scheme 9, left).It is important to note that the evolution towards catalyst 2d was considered in concert with maintaining the chloride as a partner ligand. Indeed, the employment of IPent in 2d is rendered obsolete if the chloride is replaced with a weakly-coordinating MeCN ligand (Scheme 10). Accordingly, the result of chloride abstraction is to reverse the directing group chemoselectivity back to the pyrazole. This result might be interpreted as removing the key additional interaction in substrate binding apparent in the DFT calculations (Scheme 9, right). The result in Scheme 10 may alternatively be interpreted as a change in catalyst speciation facilitated by the abstraction of chloride.
Up to this point in the investigation, all experimental observations supported the initial hypothesis in which simple Δ(ΔGbind) calculations could be used as a qualitative predictor of intramolecular directing group chemoselectivity, and thus serve as a guiding tool for enhanced sulfonamide-selective catalyst design. To test the generality of the DFT-guided catalyst design strategy, catalysts 2c and 2d were applied to the labelling of 4 additional celecoxib derivatives (Table 1). Consistent with results first noted in Scheme 7, complex 2d was shown to provide good to excellent sulfonamide selectivity for 3 of the 4 additional substrates (entries 4, 6, and 8). Only when substitution was removed from the pyrazole (R = H, entries 9 and 10) was it shown that catalyst 2d was unable to maintain sulfonamide selectivity. Overall, these results appeared to demonstrate the power of rational catalyst design in overcoming intrinsic directing group chemoselectivity (Scheme 1). As well as enhancing our understanding of site-selective C–H activation, this ability to control deuterium incorporation and isotope distribution in a medicinal candidate represents a key resource for metabolic studies in early-stage drug design.49,50
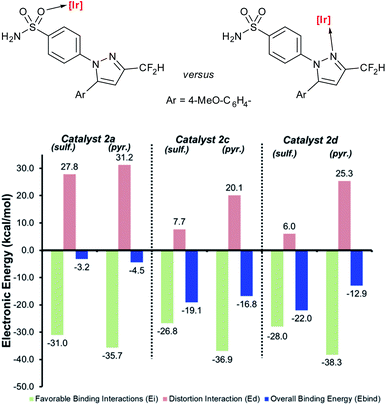
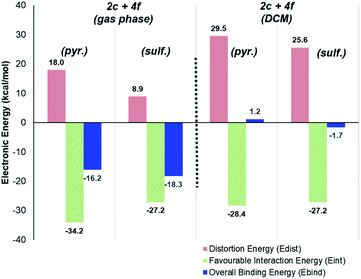
Deconstructing binding energies to probe the structural origins of improved sulfonamide directing group chemoselectivity with catalysts 2c and 2d
Having demonstrated the qualitative a priori catalyst design strategy with Δ(ΔGbind), the underlying cause of differences in directing group binding free energies was investigated. Any difference in the directing group binding electronic energies (Ebind) represents the combined impact of favourable substrate–catalyst interactions (Eint) and unfavourable structural distortions (Edist), as in eqn (1):| Ebind = Eint + Edist | (1) |
Limitations of the Δ(ΔGbind) catalyst design strategy
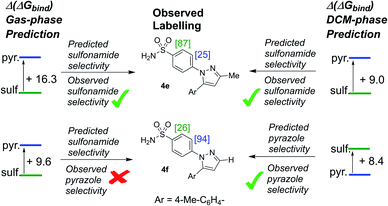
To this stage, our attempts to design a catalyst for enhanced sulfonamide directing group chemoselectivity had been met with a somewhat compelling and consistent design strategy in both Δ(ΔGbind) and deconstructed electronic energies via the counterpoise method. However, having found the experimental limit in which bulky catalysts 2c and 2d fails to deliver sulfonamide selective deuterium labelling (Table 1, entry 10, substrate 4f), it was important to revisit Δ(ΔGbind) to probe whether the method was able to predict the switch back to pyrazole selectivity on moving to the unsubstituted pyrazole-containing substrate 4f. Interestingly, our original Δ(ΔGbind) method and chosen level of theory failed to account for the observed switch back to pyrazole selectivity for substrate 4f and catalyst 2c (used as the less computationally demanding variant of catalyst 2d; Scheme 12).When the breakdown of the Δ(ΔGbind) method was investigated further, it was found that inclusion of a DCM continuum solvation model in the binding energy calculations caused crucial structural changes that switched the calculated order of directing group binding strength for substrate 4f. Specifically, in the pyrazole bound state, the supposed secondary interaction of the sulfonamide with the chloride ligand via the hydrogen bond NH–Cl, found in the earlier gas phase calculation, was lost in the re-optimised DCM-solvated structure (Scheme 13). This, in turn, had the knock-on effect of reducing the substrate distortion for the pyrazole bound conformer. Ultimately, inclusion of DCM solvation in geometry optimisations and thermal calculations corrected the Δ(ΔGbind) prediction, but served as an illustrative case of where gas-phase binding energy calculations as descriptors of intramolecular directing group chemoselectivity can break down.
Perhaps more strikingly, when the DCM-solvated structures from Scheme 13 were investigated via the counterpoise electronic energy decomposition method (Scheme 14), the predicted binding electronic energies did not match the revised Δ(ΔGbind) values from DCM re-optimisation, and therefore did not match the experimental outcome. It is worth re-emphasising that the counterpoise method is one that requires single point gas-phase structures, even if those structures were found using solvated optimisation methods.
For methyl-substituted substrate 4e, rigorous (Boys–Bernardi) binding energies calculated from both gas-phase and DCM-solvated structures matched the experimental directing group chemoselectivity; both gas-phase and DCM-solvated methods predicted majority deuterium labelling adjacent to the sulfonamide directing group (see ESI†). However, for unsubstituted pyrazole substrate 4f, using either gas-phase or DCM-solvated structures, were unable to predict the experimental outcome via the counterpoise method (Scheme 14). Only when free energies were considered, inclusive of all thermal corrections to electronic energies, were the binding energy differences between sulfonamide and pyrazole in full agreement with observed ortho-labelling outcomes (Scheme 12).
Conclusions
In conclusion, this case study has shown the use and limitations of directing group binding energy calculations to guide the development of new iridium-based complexes which deliver enhanced chemoselectivity in the C–H activation and deuteration of 1° aryl sulfonamides in the face of a competing directing group. Additionally, these endeavours have revealed several important findings of immediate relevance to the broader C–H activation community:1. For substrates bearing two directing groups, ground state (thermodynamic) Δ(ΔGbind) calculations can serve as a simple, qualitative measure for directing group chemoselectivity, without requirement for detailed transition state calculations, so long as the use or absence of solvation is carefully considered.
2. The inclusion of solvation in Δ(ΔGbind) calculations can lead to notable inconsistencies in conclusions drawn from more detailed binding energy deconstructions, as facilitated by, for example, the counterpoise method.
In sum, the identification of catalyst 2d has the potential to deliver direct applications in the isotopic labeling community. Further, we also believe that the mechanistic findings of this study will be of interest as part of emerging late-stage C–H functionalisation strategies as applied to densely functionalised molecules. The consequences of these outputs on labelling and C–H functionalisation are the subjects of further investigation in our laboratories.
Abbreviations
| COD | Cyclooctadiene |
| DFT | Density functional theory |
| DG | Directing group |
| HIE | Hydrogen isotope exchange |
| IPent | 1,3-bis(2,6-di(pentan-3-yl)phenyl)imidazol-2-ylidene) |
| IPrMe | 1,3-bis(2,6-di-iso-propylphenyl)-4,5-dimethylimidazol-2-ylidene |
| Mes | Mesityl |
| NHC | N-Heterocyclic carbene |
| NBO | Natural Bond Orbital |
Author contributions
WJK – conceptualization, funding acquisition, project administration, resources, supervision, writing – review & editing. GJK – data curation, investigation, visualization. MR – conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, visualization, writing – original draft, writing – reviewing & editing. TT – project administration, resources, supervision, validation.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank the Carnegie Trust for the Universities of Scotland and the Leverhulme Trust for funding (M. R.), and the EPSRC UK National Mass Spectrometry Facility at Swansea University for analyses.Notes and references
- G.-J. Cheng, X. Zhang, L. W. Chung, L. Xu and Y.-D. Wu, J. Am. Chem. Soc., 2015, 137, 1706–1725 CrossRef CAS PubMed.
- G. Jindal, H. K. Kisan and R. B. Sunoj, ACS Catal., 2015, 5, 480–503 CrossRef CAS.
- I. Fernández and F. M. Bickelhaupt, Chem. Soc. Rev., 2014, 43, 4953–4967 RSC.
- A. S.-K. Tsang, I. A. Sanhueza and F. Schoenebeck, Chem. Eur. J., 2014, 20, 16432–16441 CrossRef CAS PubMed.
- J. Jover and N. Fey, Chem.–Asian J., 2014, 9, 1714–1723 CrossRef CAS PubMed.
- A. G. Maldonado and G. Rothenberg, Chem. Soc. Rev., 2010, 39, 1891–1902 RSC.
- K. N. Houk and P. H.-Y. Cheong, Nature, 2008, 455, 309–313 CrossRef CAS PubMed.
- D. Balcells, E. Clot and O. Eisenstein, Chem. Rev., 2010, 110, 749–823 CrossRef CAS PubMed.
- H. M. L. Davies and D. Morton, J. Org. Chem., 2016, 81, 343–350 CrossRef CAS PubMed.
- T. Cernak, K. D. Dykstra, S. Tyagarajan, P. Vachal and S. W. Krska, Chem. Soc. Rev., 2016, 45, 546–576 RSC.
- J. Yamaguchi, A. D. Yamaguchi and K. Itami, Angew. Chem., Int. Ed., 2012, 51, 8960–9009 CrossRef CAS PubMed.
- L. McMurray, F. O'Hara and M. J. Gaunt, Chem. Soc. Rev., 2011, 40, 1885–1898 RSC.
- M. Valero, T. Kruissink, J. Blass, R. Weck, S. Güssregen, A. T. Plowright and V. Derdau, Angew. Chem., Int. Ed., 2020, 59, 5626–5631 CrossRef CAS PubMed.
- Y. Dong, X. Zhang, J. Chen, W. Zou, S. Lin and H. Xu, Chem. Sci., 2019, 10, 8744–8751 RSC.
- G. B. Boursalian, W. S. Ham, A. R. Mazzotti and T. Ritter, Nat. Chem., 2016, 8, 810–815 CrossRef CAS PubMed.
- J. M. Curto and M. C. Kozlowski, J. Am. Chem. Soc., 2015, 137, 18–21 CrossRef CAS PubMed.
- S. R. Neufeldt, G. Jiménez-Osés, J. R. Huckins, O. R. Thiel and K. N. Houk, J. Am. Chem. Soc., 2015, 137, 9843–9854 CrossRef CAS PubMed.
- J. Devlin, W. Kerr, D. Lindsay, T. McCabe, M. Reid and T. Tuttle, Molecules, 2015, 20, 11676–11698 CrossRef CAS PubMed.
- A. G. Green, P. Liu, C. A. Merlic and K. N. Houk, J. Am. Chem. Soc., 2014, 136, 4575–4583 CrossRef CAS PubMed.
- Y. Ma, J. Liang, D. Zhao, Y. Chen, J. Shen and B. Xiong, RSC Adv., 2014, 4, 17262–17264 RSC.
- W. M. C. Sameera, S. Maeda and K. Morokuma, Acc. Chem. Res., 2016, 49, 763–773 CrossRef CAS PubMed.
- W. J. Kerr, G. J. Knox, M. Reid, T. Tuttle, J. Bergare and R. A. Bragg, ACS Catal., 2020, 10, 11120–11126 CrossRef CAS PubMed.
- W. J. Kerr, M. Reid and T. Tuttle, Angew. Chem., Int. Ed., 2017, 56, 7808–7812 CrossRef CAS PubMed.
- W. J. Kerr, M. Reid and T. Tuttle, ACS Catal., 2015, 5, 402–410 CrossRef CAS.
- J. A. Brown, A. R. Cochrane, S. Irvine, W. J. Kerr, B. Mondal, J. A. Parkinson, L. C. Paterson, M. Reid, T. Tuttle, S. Andersson and G. N. Nilsson, Adv. Synth. Catal., 2014, 356, 3551–3562 CrossRef CAS.
- M. Reid, in Topics in Organometallic Chemistry, Springer Berlin Heidelberg, Berlin, Heidelberg, 2020, pp. 1–32 Search PubMed.
- J. Atzrodt, V. Derdau, W. J. Kerr and M. Reid, Angew. Chem., Int. Ed., 2018, 57, 3022–3047 CrossRef CAS PubMed.
- W. J. S. Lockley, A. McEwen and R. Cooke, J. Labelled Compd. Radiopharm., 2012, 55, 235–257 CrossRef CAS.
- P. H. Allen, M. J. Hickey, L. P. Kingston and D. J. Wilkinson, J. Labelled Compd. Radiopharm., 2010, 53, 731–738 CrossRef CAS.
- G. N. Nilsson and W. J. Kerr, J. Labelled Compd. Radiopharm., 2010, 53, 662–667 CrossRef CAS.
- R. Salter, J. Labelled Compd. Radiopharm., 2010, 53, 645–657 CrossRef CAS.
- M. Parmentier, T. Hartung, A. Pfaltz and D. Muri, Chem.–Eur. J., 2014, 20, 11496–11504 CrossRef CAS PubMed.
- M. C. Lehman, J. B. Gary, P. D. Boyle, M. S. Sanford and E. A. Ison, ACS Catal., 2013, 3, 2304–2310 CrossRef CAS.
- J. Zhou and J. F. Hartwig, Angew. Chem., Int. Ed., 2008, 47, 5783–5787 CrossRef CAS PubMed.
- C. A. Swift and S. Gronert, Angew. Chem., Int. Ed., 2015, 54, 6475–6478 CrossRef CAS PubMed.
- J. L. Rhinehart, K. A. Manbeck, S. K. Buzak, G. M. Lippa, W. W. Brennessel, K. I. Goldberg and W. D. Jones, Organometallics, 2012, 31, 1943–1952 CrossRef CAS.
- V. M. Iluc, A. Fedorov and R. H. Grubbs, Organometallics, 2012, 31, 39–41 CrossRef CAS.
- C. M. Yung, M. B. Skaddan and R. G. Bergman, J. Am. Chem. Soc., 2004, 126, 13033–13043 CrossRef CAS PubMed.
- W. J. Kerr, D. M. Lindsay, P. K. Owens, M. Reid, T. Tuttle and S. Campos, ACS Catal., 2017, 7, 7182–7186 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093 CrossRef CAS PubMed.
- K. C. Harper, E. N. Bess and M. S. Sigman, Nat. Chem., 2012, 4, 366–374 CrossRef CAS PubMed.
- A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746 CrossRef CAS.
- L. Falivene, Z. Cao, A. Petta, L. Serra, A. Poater, R. Oliva, V. Scarano and L. Cavallo, Nat. Chem., 2019, 11, 872–879 CrossRef CAS PubMed.
- H. Clavier and S. P. Nolan, Chem. Commun., 2010, 46, 841–861 RSC.
- A. Poater, B. Cosenza, A. Correa, S. Giudice, F. Ragone, V. Scarano and L. Cavallo, Eur. J. Inorg. Chem., 2009, 2009, 1759–1766 CrossRef.
- The necessary change in glassware to facilitate kinetic experiments (versus single point experiments) is presumed to modify the surface area and overall concentration of deuterium gas present in the system relative to substrate concentration.
- S. Gaillard, X. Bantreil, A. M. Z. Slawin and S. P. Nolan, Dalton Trans., 2009, 6967 RSC.
- M. Pompeo, R. D. J. Froese, N. Hadei and M. G. Organ, Angew. Chem., Int. Ed., 2012, 51, 11354–11357 CrossRef CAS PubMed.
- J. Atzrodt, V. Derdau, W. J. Kerr and M. Reid, Angew. Chem., Int. Ed., 2018, 57, 1758–1784 CrossRef CAS PubMed.
- J. Atzrodt and V. Derdau, J. Labelled Compd. Radiopharm., 2010, 53, 674–685 CrossRef CAS.
- K. N. Kirschner, J. B. Sorensen and J. P. Bowen, J. Chem. Educ., 2007, 84, 1225 CrossRef.
- S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- J. Luo, Y. Wu, H. S. Zijlstra, D. A. Harrington and J. S. McIndoe, Mass transfer and convection effects in small-scale catalytic hydrogenation, Catal. Sci. Technol., 2017, 7, 2609–2615 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc01509e |
| This journal is © The Royal Society of Chemistry 2021 |