Open Access Article
Open Access ArticleReaction-based machine learning representations for predicting the enantioselectivity of organocatalysts†
Simone
Gallarati‡
 a,
Raimon
Fabregat‡
a,
Raimon
Fabregat‡
 a,
Rubén
Laplaza
a,
Rubén
Laplaza
 ab,
Sinjini
Bhattacharjee
ab,
Sinjini
Bhattacharjee
 ac,
Matthew D.
Wodrich
ac,
Matthew D.
Wodrich
 ab and
Clemence
Corminboeuf
ab and
Clemence
Corminboeuf
 *abd
*abd
aLaboratory for Computational Molecular Design, Institute of Chemical Sciences and Engineering, Ecole Polytechnique Fédérale de Lausanne (EPFL), 1015 Lausanne, Switzerland. E-mail: clemence.corminboeuf@epfl.ch
bNational Center for Competence in Research-Catalysis (NCCR-Catalysis), Ecole Polytechnique Fédérale de Lausanne (EPFL), 1015 Lausanne, Switzerland
cIndian Institute of Science Education and Research, Dr Homi Bhabha Rd, Ward No. 8, NCL Colony, Pashan, Pune, Maharashtra 411008, India
dNational Center for Computational Design and Discovery of Novel Materials (MARVEL), Ecole Polytechnique Fédérale de Lausanne (EPFL), 1015 Lausanne, Switzerland
First published on 3rd April 2021
Abstract
Hundreds of catalytic methods are developed each year to meet the demand for high-purity chiral compounds. The computational design of enantioselective organocatalysts remains a significant challenge, as catalysts are typically discovered through experimental screening. Recent advances in combining quantum chemical computations and machine learning (ML) hold great potential to propel the next leap forward in asymmetric catalysis. Within the context of quantum chemical machine learning (QML, or atomistic ML), the ML representations used to encode the three-dimensional structure of molecules and evaluate their similarity cannot easily capture the subtle energy differences that govern enantioselectivity. Here, we present a general strategy for improving molecular representations within an atomistic machine learning model to predict the DFT-computed enantiomeric excess of asymmetric propargylation organocatalysts solely from the structure of catalytic cycle intermediates. Mean absolute errors as low as 0.25 kcal mol−1 were achieved in predictions of the activation energy with respect to DFT computations. By virtue of its design, this strategy is generalisable to other ML models, to experimental data and to any catalytic asymmetric reaction, enabling the rapid screening of structurally diverse organocatalysts from available structural information.
Introduction
Society's growing need for pharmaceuticals, agricultural chemicals, and materials requires a continuous push in the development of asymmetric catalytic methods.1,2 In particular, enantioselective organocatalysis has emerged as a powerful strategy for the stereocontrolled assembly of structurally diverse molecules3–5 with constant effort placed in making chemical transformations more selective, efficient, or generally applicable.6 Although the computational design of highly selective catalysts has long been viewed as a “Holy Grail” in chemistry,7,8 it is generally still more efficient to experimentally screen a range of potential organocatalysts for a given reaction than to assess their performance in silico.9 That is because e.e. (enantiomeric excess) values, estimated as the ratio between the competitive reaction rates leading to the two enantiomeric products,10 are relatively computationally expensive and challenging to predict accurately with standard electronic structure computations. The energy difference between the transition states (TSs) leading to the major and minor enantiomers can be quite small (<2 kcal mol−1) and multiple diastereomeric transition states, stemming from the large conformational space of flexible organocatalysts, can yield the same enantiomer.7,11 As the relation between rate constants and computed selectivity is exponential, minor errors in computed energies can lead to major errors in stereochemical outcome prediction. These factors pose a monumental challenge for traditional quantum mechanical (QM) methods, in terms of both accuracy and cost,12,13 especially if many conformers and substrate-catalyst combinations have to be computed. While the intrinsic error of the quantum chemical level is often addressed in comprehensive benchmark studies,10,14–17 automated toolkits,18,19 such as AARON20 and CatVS,21 have been developed to streamline the tedious and error-prone task of optimising hundreds of thermodynamically accessible stereocontrolling transition states. Starting from user-defined libraries, multiple conformations and configurations of TS structures are located and optimised. Although such accelerated prediction of selectivity is enticing for the prospect of computational catalyst design,9 the applicability of QM-based tools such as AARON remains limited either by the cost of the quantum mechanical computations, which quickly become prohibitive, or by the inherent difficulty of locating all transition state structures. On the other hand, tools using QM-derived molecular mechanics force fields (Q2MM), like CatVS, require the development of an MM force field for each new reaction type considered, a major limitation to their widespread application.11An alternative approach pioneered by Norrby22 and Pradhan23 and popularised by Sigman and co-workers is to fit experimental reaction outcomes to computationally- and experimentally-derived physical organic molecular descriptors.24–26 The difference in free energies at the stereocontrolling transition states27 can be expressed as a polynomial function of global or local steric and electronic parameters, such as Sterimol values, natural bond orbital charges, IR frequencies, HOMO/LUMO energies, and polarisabilities.28–34 In principle, the resulting statistical model allows for extrapolation to out-of-sample examples,35,36 however, like all QSSR-type methods,37 such multivariate linear regressions are not easily transferable and most suitable only for closely related analogues of the training set, given that a set of appropriate molecular descriptors must be redefined for every new regression.21
Nonlinear regression models (e.g., artificial neural networks, random forest, kernel methods)38 have demonstrated the potential to overcome some of the previous limits in catalyst screening and constitute an alternative to multilinear regressions with parameters derived from chemical knowledge and mechanistic hypotheses (e.g., Hammett constants, Tolman cone angles, percent buried volume, vibrational frequencies, pKa values).39–45 Recently, the organic synthetic community has exploited these artificial intelligence-based approaches for predicting ΔΔG‡,27 e.e., the activation energy, the product distribution, or the yield of (asymmetric) catalytic reactions. These models rely on the identification of a large set of system-specific molecular descriptors (e.g., physical organic descriptors like Charton or Sterimol values, NBO charges, NMR chemical shifts, bond distances and angles, HOMO–LUMO gaps, local electro/nucleophilicity, or RDKit descriptors46) used as the input from which an algorithm can “learn” while being “supervised” by the reaction outcome (output, i.e. ΔΔG‡, e.e., or yield).47–62 While the reaction outcome is often obtained from experiment (i.e., phenomenological models), alternatives based on computed data are highly valuable as well.63–67 Indeed, so-called quantum (or atomistic) ML models, which map a three-dimensional molecular structure (called molecular representations, e.g. CM,68 SLATM,69 SOAP70) to a representative target computed quantum chemically, constitute an appealing complementary strategy owing to its broad applicability and dependence on the laws of physics.69,71,72 While these approaches provide a favourable combination of efficiency, scalability, accuracy, and transferability for predicting energetic and more complex molecular properties,71 identifying enantioselective organocatalysts requires precise predictions of the relative energy barriers for the stereocontrolling transition states, a target currently beyond their accuracy. Recently, SOAP features of isolated reactants were used to train a machine learning classifier and predict transition state barriers of regioselective arene C–H functionalization. In this work, a large number of molecular fingerprints were combined with the SOAP features to improve the regression, and the resulting model was outperformed in out-of-sample predictions by a random forest model using chemical descriptors with physical organic basis (PhysOrg).73
Here, we provide a stepwise route to improve such QML approaches to reach sufficient accuracy for subtle properties such as those associated with asymmetric catalysis (i.e., e.e.). This objective is achieved by rationally designing a reaction-based representation (vide infra) that is a more faithful fingerprint of the enantiodetermining TS energy. The performance of the approach is demonstrated through accurately predicting the DFT-computed enantiomeric excess of Lewis base-catalysed propargylation reactions directly from the structure of the catalytic cycle intermediates. Unlike other ML models trained on (absolute) experimental e.e.'s,35,36 our model is able to predict the absolute configuration of the excess product, because it is trained on the activation energy of the enantiodetermining step for each pair of enantiomers (pro-(R) and pro-(S) intermediates) independently.
Methods
Reaction and organocatalysts database
Asymmetric allylations75–78 and propargylations79 of aromatic aldehydes are key C–C bond forming transformations, providing access to optically enriched homoallylic and homopropargylic alcohols, respectively, which serve as valuable building blocks for the synthesis of complex chiral molecules.80 Catalysts that are selective for allylations are generally not highly stereoselective for propargylations, which has led to a dearth of stereoselective propargylation catalysts.81–85 Tools to screen dozens of allylation catalysts to find promising candidates for propargylation reactions are therefore highly valuable.9 To this end, Wheeler and co-workers have investigated 76 Lewis base organocatalysts (Scheme 1)74 and used the computational toolkit AARON20 to build a database of 760 stereocontrolling transition states to predict their enantioselectivity in the propargylation of benzaldehyde (Scheme 2).14,74,86 Large databases of kinetic data for asymmetric catalysis generated in silico are scarce.63 Therefore, this library constitutes an ideal training and validation set for the development of an atomistic ML model with reaction-based representations capable of predicting the e.e. of organocatalysts readily from the structures of intermediates. Note that the workflow presented below would improve the ML performance independently of the size of the training data. The target of the ML model is the DFT-computed relative forward activation energy (Ea, i.e., the energy difference between the TS and the preceding intermediate) associated with each of the 10 (R)- or (S)-ligand arrangements (see Fig. S1†) of the enantiodetermining TS in Scheme 2 for the 76 catalysts in Scheme 1 (11 catalysts of type 1, 16 of type 2, 15 3, 11 4, 13 5, and 10 catalysts of type 6), yielding a total of 754 Ea values.87 e.e. values are computed from Ea (vide infra), thus accurate predictions of Ea lead to accurate e.e. predictions.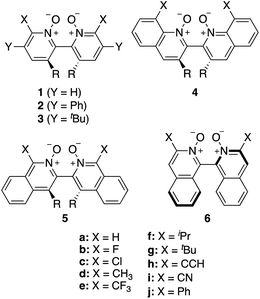 | ||
| Scheme 1 Library of axially chiral bipyridine N,N′-dioxide organocatalysts. R = H or Me. Adapted from ref. 74. | ||
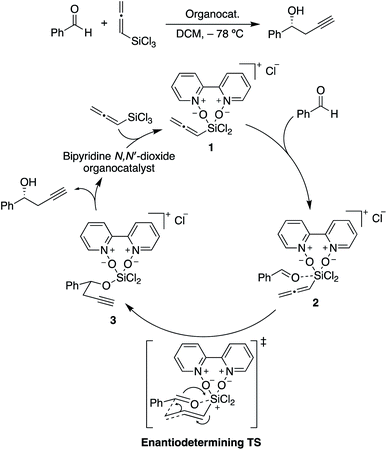 | ||
| Scheme 2 Catalytic cycle for the propargylation of benzaldehyde with allenyltrichlorosilane, showing the rate-limiting and stereocontrolling transition state. Adapted from ref. 85. | ||
General ML workflow
The general workflow exploited and improved herein relies on a physics-based ML model for the prediction of the e.e. of the asymmetric catalytic reactions, as illustrated in Scheme 3 and described hereafter. It comprises two parts: part (1) is a training procedure that relies on the following steps: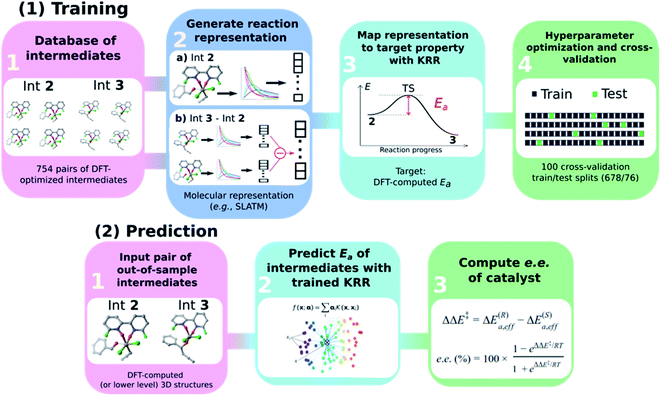 | ||
| Scheme 3 Graphical overview of the workflow used to build an atomistic ML model for e.e. prediction. | ||
(1) Database construction: a library of 3D geometries and energies of catalytic cycle intermediates is curated. Here, the structures of 754 pairs of intermediates 2 and 3 are optimised with DFT (see the next section) and used to train the ML model. As shown in our previous work,43 accurate geometries are not necessarily needed as inputs for atomistic ML models; thus, rough-coordinate estimates (e.g., obtained directly from SMILES strings) or low-cost DFTB structures could potentially be used to generate suitable molecular representations.
(2) Generation of molecular representations: information intrinsically contained within the 3D structure of each intermediate is transformed into a suitable molecular representation. Here we build different variants based on the Spectral London and Axilrod-Teller-Muto (SLATM)69 representation. SLATM is composed of two- and three-body potentials, which are derived from the atomic coordinates and contain most of the relevant information to predict molecular properties.70,88–94
(3) Training of the model: input representations are mapped onto the corresponding target values (Ea, computed at the DFT level, see the next section) using Kernel Ridge Regression (KRR)95 with a Gaussian kernel. Note that even if target values based on DFT are used here to train the ML model, the strategy proposed hereafter is expected to perform equally well on experimental or more accurate quantum chemical data.
(4) Hyperparameter optimisation and cross-validation: the full dataset is split randomly 100 times into 90/10 training/test sets (678/76 datapoints) to optimise the KRR hyperparameters and obtain the learning curves.
In part (2), the trained ML model is used to predict the activation energy of out-of-sample organocatalysts. The model requires as input the 3D structures of 2 and 3 and delivers the corresponding Ea value. Using the energy of 2 as reference, the relative energies of the enantiodetermining (R)- and (S)-TSs can be calculated, and the e.e. of the catalyst under investigation computed (vide infra).
Computational details
Quantum chemistry
Catalytic cycle intermediates 2 and 3 were optimised at the B97-D/TZV(2p,2d) level of theory,96–98 accounting for solvent effects (dichloromethane, ε = 8.93) using the polarizable continuum model (PCM)99–101 with Gaussian16,102,103 in analogy with the study by Wheeler and co-workers.74 Density fitting techniques were used throughout. The structures of 1508 intermediates were obtained via intrinsic reaction coordinate calculations (IRC)104 from the TS database curated by Wheeler et al.74 754 target Ea values (11 catalysts of type 1, 16 type 2, 15 3, 11 4, 13 5, and 10 of type 6, each in 5 distinct pro-(R) and pro-(S) ligand arrangements)87 were computed (relative to the lowest-lying intermediate 2 ligand arrangement) at the same level, which was shown to provide the best compromise between accurate predictions of low-lying TS energies and stereoselectivities for allylation and propargylation reactions.14 e.e. values were not predicted from Gibbs free energy barriers, but rather from relative energy barriers (i.e., electronic energies plus solvation free energies), since they have been found to be more reliable than those based on either relative enthalpies or free energy barriers for this reaction.14 The symbol Ea was therefore used to indicate the energy (electronic plus solvation) difference between the TS and the preceding intermediate. For each C2-symmetric catalyst (Scheme 1), 10 distinct ligand arrangements around a hexacoordinate Si centre are possible (BP1–5, (R)- and (S)-, Fig. S1†).84–86 Since each of these can lead to thermodynamically accessible reaction pathways, and the stereoselectivity is largely a consequence of which ligand arrangement is low-lying for a particular catalyst, all diastereomeric TSs were considered viable and the e.e. calculated from a Boltzmann weighting of the relative energy barriers.74 In eqn (1)–(3), ΔEa,eff is the relative Boltzmann-weighted activation energy of each (R)- or (S)-species, ΔΔE‡ is the difference between the (R)- and (S)-Boltzmann-weighted activation energies, R is the ideal gas constant, and T is the propargylation reaction temperature (195 K).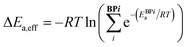 | (1) |
| ΔΔE‡ = ΔE(R)a,eff – ΔE(S)a,eff | (2) |
| e.e. (%) = 100 × (1 − eΔΔE‡/RT)/(1 + eΔΔE‡/RT) | (3) |
Machine learning
The Python package QML105 was used to construct standard SLATM representations. Feature selection and the construction of the reaction-based representations SLATMDIFF and SLATMDIFF+ were done using the Python package Scikit-learn.106 To generate the learning curves and the e.e. predictions, a cross-validation scheme was used with 100 different 90/10 training/test sets (678/76). The KRR hyperparameters (the width of the Gaussian kernel σ and the ridge regularization λ) were optimised for each train/test split, systematically obtaining essentially the same results for each split (see the ESI†). From the 100 train/test splits, the Ea of each intermediate pair (2 and 3) was predicted approximately 10 times; these test predictions were then averaged to obtain one final prediction. The standard deviation from the ∼10 test predictions were used to generate the error bars. The final average prediction of the Ea value was used to calculate the Boltzmann-weighted ΔEa,eff values (eqn (1)) and the ΔΔE‡ of each (R)- and (S)-pair (eqn (2)), and so the e.e. value of each organocatalyst (eqn (3)). The out-of-sample predictions were done with the same SLATMDIFF+ models trained in the cross-validation scheme. Additionally, out-of-sample predictions were done re-training the model on the entire dataset (see Fig. S6†), although this did not lead to noticeable improvement. While simpler representations (e.g., CM,68 BoB107) were tested, SLATM performs significantly better (see Fig. S2†).Results and discussion
Molecular representations
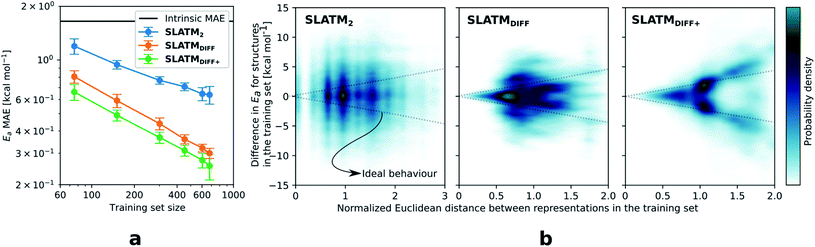
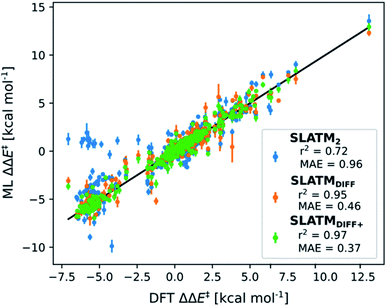
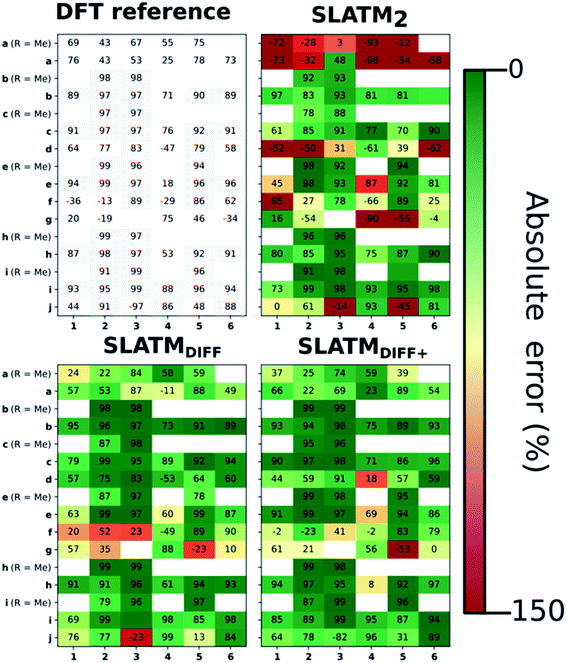
The key step of the workflow presented above is generating a molecular representation, which is mapped onto the target value (i.e., the activation energy Ea) and used as a fingerprint of the enantiodetermining TS. Representations can be constructed from single molecules and more recently as “ensemble representations”: instead of associating one fixed configuration of atoms to a single-point geometry energetic target value, information from multiple structures can be combined to generate a representation for an ensemble property, such as the free energy of solvation (ΔGsol).108 This has recently been achieved by calculating the ensemble average of the FCHL19 representations109,110 of a set of configurational snapshots obtained through MD sampling.108 Here, we propose an alternative approach that goes beyond standard QML representations (i.e., KRR using one given gas-phase geometry)108 by describing the chemical transformation occurring during the enantiodetermining step of an asymmetric reaction through the comparison of the representations of the two catalytic cycle intermediates preceding and following the stereocontrolling TS. This allows us to generate a “reaction-based” representation, which can be closely mapped to the activation energy of the enantiodetermining step, as discussed later. We rely on “dissimilarity” plots as a diagnostic tool to determine whether a particular representation can adequately characterize the stereocontrolling step. By dissimilarity plots, we refer to histograms of the Euclidean distance between any two representations vs. the difference in their target property, which in this case is Ea. For a particular representation to be effective, small distances between structures must correspond to small differences between target properties, as the Euclidean distance is used to measure the similarity of two molecular representations. Similar plots have previously been exploited to analyse the behaviour of molecular representations,70,111 but only parenthetically. Here, we highlight their importance as a fundamental analytical tool to understand the performance of molecular representations in kernel methods for asymmetric catalysis and demonstrate their utility for constructing reliable ML models.Before discussing our proposed representation variants, we report in Fig. 1a the performance of the standard SLATM representation using the structure of a single intermediate (e.g., 2). Due to the structural similarities between 2 and the enantiodetermining TS (in both, the Si atom has 6 coordination sites occupied, whereas the coordination number is only 5 or 4 in intermediate 3), intermediate 2 was first chosen to construct the input representation. The learning curve for the prediction of Ea using SLATM (blue) of intermediate 2 (denoted SLATM2) reaches a Mean Absolute Error (MAE) of 0.54 ± 0.06 kcal mol−1 for the prediction of Ea with 90% of the data used for training (i.e., 680 structures). Considering the exponential relationship between relative activation energies and e.e. values, which implies a dramatic propagation of errors, the accuracy of this approach is insufficient. This is further demonstrated in Fig. 2, which shows the correlation between the predicted and reference ΔΔE‡ values (MAE = 0.96 kcal mol−1), and in Fig. 3, where the e.e. values obtained from SLATM2 are compared to the reference quantities: the large number of red-coloured cells indicates large deviations between ML-predicted and DFT-computed e.e. values. The rather poor mapping between SLATM2 and the Ea of the stereocontrolling step (associated with the key 2 → 3 transition state) is evident from the visual inspection of Fig. 3, where the large number of red-coloured cells associated with catalysts bearing substituents a, d, e, g, f and j indicates inaccurate predictions of e.e. values, and from the analysis of the corresponding dissimilarity plot in Fig. 1b (left). In the latter, the large scattering of points lying outside the area delimited by the dotted lines, particularly when the Euclidean distance tends to zero, means that two different structures might be considered equal by the kernel (distance ≈ 0) albeit leading to very different Ea values. Thus, the shape of the dissimilarity plot of SLATM2 deviates considerably from ideal one, indicated by the dotted straight lines.70 Note that the MAE for Ea increases up to 0.77 ± 0.05 kcal mol−1 (see Fig. S2†) if starting from the SLATM representation of 3, the intermediate following the enantiodetermining step in the catalytic cycle (Scheme 2). The higher accuracy achieved using the representation of 2vs.3 could be attributed to the reaction step being exergonic and, according to the Hammond Postulate,112 the enantiodetermining TS resembling 2 more closely. In any case, neither the structure of 2 or 3 provides sufficiently good fingerprints of Ea on their own.
Unlike other intrinsic molecular properties that depend on the structure of a single molecule,108 enantioselectivity is determined by electronic and/or steric effects stabilising or destabilising one enantiomeric TS to a greater or lesser degree than the other. In that sense, it is to be expected that our target accuracy for Ea, well below 1 kcal mol−1, cannot be reached using only one structure that does not adequately describe the stereocontrolling transition state as an input. To improve the model performance, an alternative representation is constructed by comparing the representations of both intermediates. Knowing that neither the structure of 2 or 3 are uniquely related to the corresponding activation energies, we can generate such a “reaction-based” representation that draws information from both structures, subtracting the global SLATM of 2 from 3. This is reminiscent of binary reaction fingerprints (obtained by subtracting the products' from the reactants' RDKit46 fingerprints), which reflect changes in molecular features over reaction processes.113 The resulting representation (denoted SLATMDIFF) accounts for the differences between the two intermediates and is thus more sensitive to the structural changes occurring during the enantiodetermining step. By subtracting “reactant” from “product”, the global features that do not change during the catalytic cycle step are eliminated from the representation, and the structural changes between intermediates are highlighted. In this way, we obtain a more faithful representation of the reaction step, which corresponds to a more unique fingerprint of Ea. Although the construction of SLATMDIFF requires the SLATM representations of both intermediates (2 and 3), the computational cost associated with its generation is negligible.
As depicted in the dissimilarity plot (Fig. 1b, middle), the reaction-based representation (SLATMDIFF) is significantly better than SLATM2: the difference in Ea values tends to zero as the Euclidean distance between their representations tends to zero. In line with this observation, the learning curve (shown by the orange line in Fig. 1a) is significantly improved. The MAE of SLATMDIFF is reduced to 0.31 ± 0.2 kcal mol−1, roughly 50% better than SLATM2 and up to 60% better than that of SLATM3 using 90% of the data for training (i.e., 680 structures) in the train/test splits of the cross-validation scheme. Given the rationality of the approach leading to the construction of SLATMDIFF, its gain in accuracy is encouraging. As shown in Fig. 2 and 3, the halved MAE leads to a very notable improvement in the prediction of e.e. values. Nevertheless, we note again that very small errors in Ea are amplified when e.e. values are calculated, and therefore even a small accuracy gain can be significant.
The high probability density of normalised Euclidean distances between 0.5 and 0.75 seen in Fig. 1b (middle, SLATMDIFF) indicates that the shape adopted by the dissimilarity histogram of SLATMDIFF is not yet ideal, and that further improvement is possible. To achieve higher accuracy, we focus on improving the shape of this dissimilarity plot. Notice that in our ML model, the Euclidean distance is used as a measure of similarity between representations. This means that features with high variance (i.e., that change the most between molecules) dominate the notion of similarity, as they contribute the most to the Euclidean distance between representations. By feature, we mean each of the terms in the molecular representation, which, for SLATM, consist of two- (London dispersion) and three- (Axilrod–Teller–Muto) body potentials computed on groups of atoms closer than a certain cut-off (here, 4.8 Å). The results of these potentials are averaged over their atom-type sets (e.g., all C–C interactions for the two-body terms, all the C–C–C for the three-body terms), which are then concatenated to generate the SLATM vector. The size of the SLATM representation depends on the existing atom-type sets in the database. Given that our dataset contains the elements C, H, O, N, F, Cl and Si, the total number of features of the SLATM representations is 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 827.
827.
In SLATMDIFF, features with high variance dominate the notion of similarity, measured through the Euclidean distance. However, we are using SLATM to predict a property that is very different from the single-molecule properties for which it was originally designed. Consequently, features with high variance in SLATM are not necessarily the most important fingerprints of Ea. In pursuit of the best possible fingerprint of the activation energy, we assign importance scores to each feature and attempt to focus on the most relevant ones. The linear correlation coefficient (r2) between each feature and the target property is used as an estimate of the importance of the different terms in the representation. The results, presented in Fig. 4, show that in SLATMDIFF there are only a few high-variance features, while the computed importance scores are spread over many other features that have relatively small variances. Simply put, the variances in the features of the SLATMDIFF representation are not well correlated with their real importance in this application.
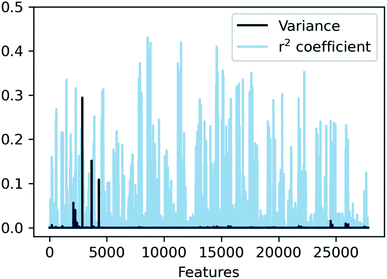 | ||
Fig. 4 Variance and correlation coefficient with the target value for each of the 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 827 features of the SLATMDIFF representation in the dataset. 827 features of the SLATMDIFF representation in the dataset. | ||
Based on this observation, an improved representation, labelled SLATMDIFF+, is generated by selecting only the Nf most important features of SLATMDIFF (specifically, Nf = 500) and discarding the rest. This feature selection was done using only the training data at each train/test split of the cross-validation step, as otherwise it could lead to severe overfitting. Nevertheless, the importance scores were consistent across the cross-validation splits thanks to the robustness of the linear regressions. An improved relationship between representation and target distances (Fig. 1b, right) is obtained with the SLATMDIFF+ representation, in spite of its reduced size. This simple feature selection leads to a noticeable improvement in accuracy, with a cross-validated MAE of 0.25 ± 0.4 kcal mol−1 (see the green curve in Fig. 1a). Using the SLATMDIFF+ representation, the resulting cross-validated correlation coefficients for the difference between (R)- and (S)-activation energies (ΔΔE‡, Fig. 2) in the test set are greatly improved (r2 > 0.95). The quality of our fitted model far supersedes previously reported approaches. Good qualitative and even quantitative agreement is achieved between predicted and reference e.e. values computed using the test data splits from the cross-validation runs (Fig. 3).
Since linear correlation constitutes a very limited notion of relevance, other methods, such as nonlinear mutual information criteria,114 were tested as feature importance estimators, but the resulting models showed similar or even worse performance (see the ESI†). Similarly, methods based on metric learning111,115 did not lead to any improvement, as the high dimensionality of the problem led to severe overfitting. Ceriotti et al.116 suggested the use of principal covariates regression (PCovR) to solve similar issues.117 PCovR is a supervised feature selection method that interpolates between principal component analysis (PCA) and linear regression. Herein, because the variance of the features is completely unrelated to the importance scores, the addition of PCA would not offer any advantage. Nevertheless, these findings highlight the importance of adapting molecular representations to the application at hand, while still preserving the overall generality of the approach.
Chemical insight on asymmetric propargylation catalysts
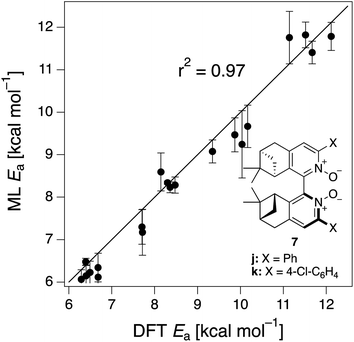
The ML model is able to reproduce the main trends in e.e. observed across the different catalysts from the 100 different random train/test splits (Fig. 3, top left table). For example, using SLATMDIFF+ (Fig. 3, bottom right table), which gives the best predictions with respect to the reference data, catalysts built on scaffold 4 (Scheme 1) are revealed to be outliers, yielding e.e.'s that are significantly different to those obtained with other scaffolds, for a given substituent a–j. This is due to the different placement of the substituent X on the organocatalysts' scaffold. Excluding 4, the effect of different substituents on the e.e. is qualitatively the same across all scaffolds, with the exception of f (iPr) and j (Ph). The introduction of a phenyl group on the organocatalysts' scaffold leads to highly varied e.e. values, from −97 (S) to 91 (R). This variation, which is due to the presence of favourable π-stacking and CH/π interactions stabilising some (S)-TSs and degrading the enantioselectivity,74 is nicely captured by SLATMDIFF+. Overall, the high enantioselectivity displayed by (most) catalysts in the library can be attributed to the favourable electrostatic interaction between the formyl C–H of benzaldehyde and one of the chlorines bound to Si, which is present in the lowest-lying (R)-ligand arrangement, and absent in the (S)-structures.74In their computational screening with AARON,74 Wheeler and co-workers identified derivatives of 6 as promising candidates for propargylation reactions. However, these catalysts are difficult to synthesize stereoselectively.81,118 Recently, Malkov et al. reported the synthesis of a set of terpene-derived atropisomeric bipyridine N,N′-dioxides 7 (Fig. 5) as easily-separated diastereoisomers.119 Aromatically-substituted catalysts 7j and 7k were shown to be highly active and selective (e.e. of 96 and 97, respectively); additionally, the TS structures for 7 were computationally shown to be nearly identical to the corresponding substituted forms of 6.119 Prompted by these results, we decided to test the ML model with SLATMDIFF+ to predict the activation energy of the 10 distinct ligand arrangements afforded by 7j and 7k. The out-of-sample results are shown in Fig. 5. Despite scaffold 7 and substituent k not being in the original training set, excellent correlation between predicted and reference Ea values is obtained (r2 = 0.97). Thus, the enantioselectivity of these out-of-sample catalysts is qualitatively reproduced, despite not achieving exact quantitative agreement between DFT and ML predicted ΔΔE‡ values (1.2 and 1.3 for 7j and 7k, respectively, vs. 0.2 and 0.5 kcal mol−1).
In summary, we provide a logical route to improve atomistic ML methods for enantioselectivity prediction of asymmetric catalytic reactions, which are limited by both the required accuracy and the small amount of data generally available. Firstly, the intermediates associated with the enantiodetermining step (2 and 3 in Scheme 2) must be identified, and their SLATM representations generated. Secondly, using the difference between the two SLATM representations (SLATMDIFF) as input, a set of features that map the activation energy accurately can be obtained. Finally, feature engineering can be used to improve SLATMDIFF, keeping only the most relevant features that relate to the target property. The results show that the ML workflow presented herein is able to accurately predict enantioselectivity from the molecular structures of catalytic cycle intermediates.
Conclusions
In this work, we have developed an atomistic machine learning model to predict the DFT-computed e.e. of Lewis base-catalysed propargylation reactions (Scheme 2). The use of dissimilarity plots allowed us to rationally develop and progressively improve a reaction-based representation that can be adequately mapped onto the activation energy of the stereocontrolling step. We identified two fundamental limitations of many standard physics-based molecular representations for subtle catalytic properties. First, we have shown that neither the structure of the preceding nor that of the following catalytic cycle intermediate is a fine fingerprint of the energy of the stereocontrolling transition state. This issue can be circumvented by using a reaction-based molecular representation derived from both structures. Finally, we have demonstrated how feature selection can be used to fine-tune this representation.The resulting model can accurately predict the DFT-computed enantioselectivity of asymmetric propargylations from the structure of catalytic cycle intermediates. Thus, it constitutes a valuable tool to quickly identify potentially selective propargylation organocatalysts. By design, the model is well-balanced between computational cost, generality and accuracy. It is easy to implement for a wide region of chemical space and seamlessly compatible with experimental (e.g., X-ray structures of stable intermediates) and computational data alike. Our results prove that semi-quantitative predictions of e.e. values in asymmetric catalysis can be achieved by accurately predicting Ea.
We conclude that atomistic ML models with adequately tailored molecular representations can be a practical and accurate alternative to both traditional quantum chemical computations of relative rate constants and multivariate linear regression with physical organic molecular descriptors. The stepwise improvement to the model described in this work opens the door to more complex reaction-based and catalytic cycle-based representations. Indeed, ensemble representations, which were recently introduced for properties very sensitive to conformational freedom, such as the free energy of solvation ΔGsol,108 are a promising path to go beyond the single structure-to-property paradigm and allow for further generalisation, once combined with the approach discussed herein. Such methodologies will be explored in future work for the accurate screening of enantioselective catalysts in asymmetric reactions.
Author contributions
S. G. performed DFT computations and analyzed the results. R. F. trained and improved the ML models. S. G. and R. F. jointly wrote the manuscript with help from R. L. M. D. W. and R. L. provided feedback on the DFT and ML components, respectively. S. B. and M. D. W. ran preliminary computations initiating this work. All authors discussed the results and commented on the manuscript. C. C. conceived the project with M. D. W., provided supervision and wrote the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to the EPFL for financial support. S. G., R. F. and C. C. acknowledge funding from the European Research Council (ERC, Grant Agreement No. 817977) within the framework of European Union's H2020. The National Centre of Competence in Research (NCCR) “Sustainable chemical process through catalysis (Catalysis)” of the Swiss National Science Foundation (SNSF) is acknowledged for financial support of R. L. S. B. acknowledges the NCCR “Materials' Revolution: Computational Design and Discovery of Novel Materials (MARVEL)” for providing a “INSPIRE” master fellowship. The authors thank Benjamin Meyer for helpful discussions at the origin of the project.References
- M. S. Taylor and E. N. Jacobsen, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 5368–5373 CrossRef CAS PubMed.
- R. E. Gawley and J. Aubé, in Principles of Asymmetric Synthesis, ed. R. E. Gawley and J. Aubé, Elsevier, Oxford, 2nd edn, 2012, pp. 63–95 Search PubMed.
- D. W. C. MacMillan, Nature, 2008, 455, 304–308 CrossRef CAS PubMed.
- P. I. Dalko and L. Moisan, Angew. Chem., Int. Ed., 2001, 40, 3726–3748 CrossRef CAS PubMed.
- P. I. Dalko, in Enantioselective Organocatalysis, John Wiley & Sons, Ltd, 2007, pp. 1–17 Search PubMed.
- S.-H. Xiang and B. Tan, Nat. Commun., 2020, 11, 3786 CrossRef CAS PubMed.
- C. Poree and F. Schoenebeck, Acc. Chem. Res., 2017, 50, 605–608 CrossRef CAS PubMed.
- K. N. Houk and F. Liu, Acc. Chem. Res., 2017, 50, 539–543 CrossRef CAS PubMed.
- S. E. Wheeler, T. J. Seguin, Y. Guan and A. C. Doney, Acc. Chem. Res., 2016, 49, 1061–1069 CrossRef CAS PubMed.
- Q. Peng, F. Duarte and R. S. Paton, Chem. Soc. Rev., 2016, 45, 6093–6107 RSC.
- E. Hansen, A. R. Rosales, B. Tutkowski, P.-O. Norrby and O. Wiest, Acc. Chem. Res., 2016, 49, 996–1005 CrossRef CAS PubMed.
- K. H. Hopmann, Int. J. Quantum Chem., 2015, 115, 1232–1249 CrossRef CAS.
- A. S. K. Tsang, I. A. Sanhueza and F. Schoenebeck, Chem.–Eur. J., 2014, 20, 16432–16441 CrossRef CAS PubMed.
- D. Sepúlveda, T. Lu and S. E. Wheeler, Org. Biomol. Chem., 2014, 12, 8346–8353 RSC.
- D. Balcells, E. Clot, O. Eisenstein, A. Nova and L. Perrin, Acc. Chem. Res., 2016, 49, 1070–1078 CrossRef CAS.
- P. H. Cheong, C. Y. Legault, J. M. Um, N. Celebi-Olcum and K. N. Houk, Chem. Rev., 2011, 111, 5042–5137 CrossRef CAS PubMed.
- T. Sperger, I. A. Sanhueza, I. Kalvet and F. Schoenebeck, Chem. Rev., 2015, 115, 9532–9586 CrossRef CAS PubMed.
- M. Foscato and V. R. Jensen, ACS Catal., 2020, 10, 2354–2377 CrossRef CAS.
- V. M. Ingman, A. J. Schaefer, L. R. Andreola and S. E. Wheeler, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, e1510 Search PubMed.
- Y. Guan, V. M. Ingman, B. J. Rooks and S. E. Wheeler, J. Chem. Theory Comput., 2018, 14, 5249–5261 CrossRef CAS PubMed.
- A. R. Rosales, J. Wahlers, E. Limé, R. E. Meadows, K. W. Leslie, R. Savin, F. Bell, E. Hansen, P. Helquist, R. H. Munday, O. Wiest and P.-O. Norrby, Nat. Catal., 2019, 2, 41–45 CrossRef CAS.
- J. D. Oslob, B. Akermark, P. Helquist and P. O. Norrby, Organometallics, 1997, 16, 3015–3021 CrossRef CAS.
- K. B. Lipkowitz and M. Pradhan, J. Org. Chem., 2003, 68, 4648–4656 CrossRef CAS PubMed.
- K. C. Harper and M. S. Sigman, Science, 2011, 333, 1875 CrossRef CAS PubMed.
- M. S. Sigman, K. C. Harper, E. N. Bess and A. Milo, Acc. Chem. Res., 2016, 49, 1292–1301 CrossRef CAS PubMed.
- J. P. Reid and M. S. Sigman, Nat. Rev. Chem., 2018, 2, 290–305 CrossRef CAS.
- ΔΔG‡, calculated from the experimental enantioselectivity using Gibbs's free energy equation (ΔΔG‡ = −RT
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln|e.r.|, e.r. = enantiomeric ratio)..
ln|e.r.|, e.r. = enantiomeric ratio).. - K. C. Harper and M. S. Sigman, J. Org. Chem., 2013, 78, 2813–2818 CrossRef CAS PubMed.
- C. B. Santiago, J. Y. Guo and M. S. Sigman, Chem. Sci., 2018, 9, 2398–2412 RSC.
- D. J. Durand and N. Fey, Chem. Rev., 2019, 119, 6561–6594 CrossRef CAS PubMed.
- A. Milo, E. N. Bess and M. S. Sigman, Nature, 2014, 507, 210–214 CrossRef CAS PubMed.
- S. E. Denmark, N. D. Gould and L. M. Wolf, J. Org. Chem., 2011, 76, 4337–4357 CrossRef CAS.
- A. Milo, A. J. Neel, F. D. Toste and M. S. Sigman, Science, 2015, 347, 737 CrossRef CAS PubMed.
- E. N. Bess, A. J. Bischoff and M. S. Sigman, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 14698 CrossRef CAS PubMed.
- J. Werth and M. S. Sigman, J. Am. Chem. Soc., 2020, 142, 16382–16391 CrossRef CAS PubMed.
- J. P. Reid and M. S. Sigman, Nature, 2019, 571, 343–348 CrossRef CAS PubMed.
- A. F. Zahrt, S. V. Athavale and S. E. Denmark, Chem. Rev., 2020, 120, 1620–1689 CrossRef CAS PubMed.
- J. B. O. Mitchell, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 468–481 CAS.
- I. Funes-Ardoiz and F. Schoenebeck, Chem, 2020, 6, 1904–1913 CAS.
- J. R. Kitchin, Nat. Catal., 2018, 1, 230–232 CrossRef.
- W. Yang, T. T. Fidelis and W.-H. Sun, ACS Omega, 2020, 5, 83–88 CrossRef CAS PubMed.
- Z. Li, S. Wang and H. Xin, Nat. Catal., 2018, 1, 641–642 CrossRef.
- B. Meyer, B. Sawatlon, S. Heinen, O. A. von Lilienfeld and C. Corminboeuf, Chem. Sci., 2018, 9, 7069–7077 RSC.
- M. Cordova, M. D. Wodrich, B. Meyer, B. Sawatlon and C. Corminboeuf, ACS Catal., 2020, 10, 7021–7031 CrossRef CAS.
- M. D. Wodrich, A. Fabrizio, B. Meyer and C. Corminboeuf, Chem. Sci., 2020, 11, 12070–12080 RSC.
- RDKit: open-source chemoinformatics and machine learning, http://www.rdkit.org Search PubMed.
- A. F. Zahrt, J. J. Henle, B. T. Rose, Y. Wang, W. T. Darrow and S. E. Denmark, Science, 2019, 363, eaau5631 CrossRef CAS.
- J. J. Henle, A. F. Zahrt, B. T. Rose, W. T. Darrow, Y. Wang and S. E. Denmark, J. Am. Chem. Soc., 2020, 142, 11578–11592 CrossRef CAS PubMed.
- A. Tomberg, M. J. Johansson and P.-O. Norrby, J. Org. Chem., 2019, 84, 4695–4703 CrossRef CAS PubMed.
- S. Singh, M. Pareek, A. Changotra, S. Banerjee, B. Bhaskararao, P. Balamurugan and R. B. Sunoj, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 1339–1345 CrossRef CAS PubMed.
- J. Chen, W. Jiwu, L. Mingzong and T. You, J. Mol. Catal. A: Chem., 2006, 258, 191–197 CrossRef CAS.
- Y. Amar, A. M. Schweidtmann, P. Deutsch, L. Cao and A. Lapkin, Chem. Sci., 2019, 10, 6697–6706 RSC.
- S. Banerjee, A. Sreenithya and R. B. Sunoj, Phys. Chem. Chem. Phys., 2018, 20, 18311–18318 RSC.
- W. Beker, E. P. Gajewska, T. Badowski and B. A. Grzybowski, Angew. Chem., Int. Ed., 2019, 58, 4515–4519 CrossRef CAS PubMed.
- S. M. Maley, D.-H. Kwon, N. Rollins, J. C. Stanley, O. L. Sydora, S. M. Bischof and D. H. Ess, Chem. Sci., 2020, 11, 9665–9674 RSC.
- V. Dhayalan, S. C. Gadekar, Z. Alassad and A. Milo, Nat. Chem., 2019, 11, 543–551 CrossRef CAS PubMed.
- D. T. Ahneman, J. G. Estrada, S. Lin, S. D. Dreher and A. G. Doyle, Science, 2018, 360, 186 CrossRef CAS PubMed.
- M. K. Nielsen, D. T. Ahneman, O. Riera and A. G. Doyle, J. Am. Chem. Soc., 2018, 140, 5004–5008 CrossRef CAS PubMed.
- K. Jorner, T. Brinck, P.-O. Norrby and D. Buttar, Chem. Sci., 2021, 12, 1163–1175 RSC.
- F. Sandfort, F. Strieth-Kalthoff, M. Kühnemund, C. Beecks and F. Glorius, Chem, 2020, 6, 1379–1390 CAS.
- J. M. Granda, L. Donina, V. Dragone, D.-L. Long and L. Cronin, Nature, 2018, 559, 377–381 CrossRef CAS PubMed.
- C. W. Coley, W. Jin, L. Rogers, T. F. Jamison, T. S. Jaakkola, W. H. Green, R. Barzilay and K. F. Jensen, Chem. Sci., 2019, 10, 370–377 RSC.
- P. Friederich, G. dos Passos Gomes, R. De Bin, A. Aspuru-Guzik and D. Balcells, Chem. Sci., 2020, 11, 4584–4601 RSC.
- S. Heinen, G. F. von Rudorff and O. A. von Lilienfeld, arXiv:2009.13429, 2020.
- G. F. von Rudorff, S. N. Heinen, M. Bragato and O. A. von Lilienfeld, arXiv:2006.00504, 2020.
- M. Bragato, G. F. von Rudorff and O. A. von Lilienfeld, Chem. Sci., 2020, 11, 11859–11868 RSC.
- G. Skoraczyński, P. Dittwald, B. Miasojedow, S. Szymkuć, E. P. Gajewska, B. A. Grzybowski and A. Gambin, Sci. Rep., 2017, 7, 3582 CrossRef PubMed.
- M. Rupp, A. Tkatchenko, K.-R. Müller and O. A. von Lilienfeld, Phys. Rev. Lett., 2012, 108, 058301 CrossRef PubMed.
- B. Huang and O. A. von Lilienfeld, Nat. Chem., 2020, 12, 945–951 CrossRef CAS PubMed.
- S. De, A. P. Bartók, G. Csányi and M. Ceriotti, Phys. Chem. Chem. Phys., 2016, 18, 13754–13769 RSC.
- O. A. von Lilienfeld, K.-R. Müller and A. Tkatchenko, Nat. Rev. Chem., 2020, 4, 347–358 CrossRef.
- O. A. von Lilienfeld and K. Burke, Nat. Commun., 2020, 11, 4895 CrossRef CAS PubMed.
- X. Li, S. Q. Zhang, L. C. Xu and X. Hong, Angew. Chem., Int. Ed., 2020, 59, 13253–13259 CrossRef CAS PubMed.
- A. C. Doney, B. J. Rooks, T. Lu and S. E. Wheeler, ACS Catal., 2016, 6, 7948–7955 CrossRef CAS.
- S. E. Denmark, D. M. Coe, N. E. Pratt and B. D. Griedel, J. Org. Chem., 1994, 59, 6161–6163 CrossRef CAS.
- S. E. Denmark and J. Fu, J. Am. Chem. Soc., 2000, 122, 12021–12022 CrossRef CAS.
- S. E. Denmark and T. Wynn, J. Am. Chem. Soc., 2001, 123, 6199–6200 CrossRef CAS PubMed.
- S. E. Denmark and G. L. Beutner, Angew. Chem., Int. Ed., 2008, 47, 1560–1638 CrossRef CAS.
- C.-H. Ding and X.-L. Hou, Chem. Rev., 2011, 111, 1914–1937 CrossRef CAS PubMed.
- J. A. Marshall, J. Org. Chem., 2007, 72, 8153–8166 CrossRef CAS PubMed.
- M. Nakajima, M. Saito, M. Shiro and S.-i. Hashimoto, J. Am. Chem. Soc., 1998, 120, 6419–6420 CrossRef CAS.
- M. Nakajima, M. Saito and S. Hashimoto, Tetrahedron: Asymmetry, 2002, 13, 2449–2452 CrossRef CAS.
- J. Chen, B. Captain and N. Takenaka, Org. Lett., 2011, 13, 1654–1657 CrossRef CAS.
- T. Lu, M. A. Porterfield and S. E. Wheeler, Org. Lett., 2012, 14, 5310–5313 CrossRef CAS.
- B. J. Rooks, M. R. Haas, D. Sepúlveda, T. Lu and S. E. Wheeler, ACS Catal., 2015, 5, 272–280 CrossRef CAS.
- T. Lu, R. Zhu, Y. An and S. E. Wheeler, J. Am. Chem. Soc., 2012, 134, 3095–3102 CrossRef CAS PubMed.
- 4 intermediates (1f_S_bp2 int 2, 3e_R_bp1 int 3, 3e_S_bp1 int 3, and 3j_S_bp2 int 3) could not be converged, therefore the corresponding enantiomeric TS structures were removed from the original database of 760 TSs..
- K. Vu, J. C. Snyder, L. Li, M. Rupp, B. F. Chen, T. Khelif, K.-R. Müller and K. Burke, Int. J. Quantum Chem., 2015, 115, 1115–1128 CrossRef CAS.
- K. Hansen, G. Montavon, F. Biegler, S. Fazli, M. Rupp, M. Scheffler, O. A. von Lilienfeld, A. Tkatchenko and K.-R. Müller, J. Chem. Theory Comput., 2013, 9, 3404–3419 CrossRef CAS PubMed.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, J. Chem. Theory Comput., 2015, 11, 2087–2096 CrossRef CAS PubMed.
- D. Hu, Y. Xie, X. Li, L. Li and Z. Lan, J. Phys. Chem. Lett., 2018, 9, 2725–2732 CrossRef CAS PubMed.
- J. Westermayr, F. A. Faber, A. S. Christensen, O. A. von Lilienfeld and P. Marquetand, Mach. Learn.: Sci. Technol., 2020, 1, 025009 CrossRef.
- Q. V. Nguyen, S. De, J. Lin and V. Cevher, Int. J. Quantum Chem., 2019, 119, e25872 CrossRef.
- S. N. Pozdnyakov, M. J. Willatt, A. P. Bartók, C. Ortner, G. Csányi and M. Ceriotti, Phys. Rev. Lett., 2020, 125, 166001 CrossRef CAS.
- R. Tibshirani and J. Friedman, The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Springer, 2001 Search PubMed.
- A. D. Becke, J. Chem. Phys., 1997, 107, 8554–8560 CrossRef CAS.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS.
- E. Cancès and B. Mennucci, J. Math. Chem., 1998, 23, 309–326 CrossRef.
- E. Cancès, B. Mennucci and J. Tomasi, J. Chem. Phys., 1997, 107, 3032–3041 CrossRef.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, Wallingford, CT, 2016 Search PubMed.
- Because the original TS database was computed with Gaussian09, the fine (75
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 302) integration grid (default of Gaussian09) was used instead of the ultrafine (99
302) integration grid (default of Gaussian09) was used instead of the ultrafine (99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 590) grid (default of Gaussian16)..
590) grid (default of Gaussian16).. - K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- A. S. Christensen, F. A. Faber, B. Huang, L. A. Bratholm, A. Tkatchenko, K. R. Muller and O. A. von Lilienfeld, QML : A Python Toolkit for Quantum Machine Learning, 2017 Search PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- K. Hansen, F. Biegler, R. Ramakrishnan, W. Pronobis, O. A. von Lilienfeld, K.-R. Müller and A. Tkatchenko, J. Phys. Chem. Lett., 2015, 6, 2326–2331 CrossRef CAS PubMed.
- J. Weinreich, N. J. Browning and O. A. von Lilienfeld, arXiv:2012.09722, 2020.
- A. S. Christensen, L. A. Bratholm, F. A. Faber and O. Anatole von Lilienfeld, J. Chem. Phys., 2020, 152, 044107 CrossRef CAS PubMed.
- F. A. Faber, A. S. Christensen, B. Huang and O. A. von Lilienfeld, J. Chem. Phys., 2018, 148, 241717 CrossRef.
- G. S. Na, H. Chang and H. W. Kim, Phys. Chem. Chem. Phys., 2020, 22, 18526–18535 RSC.
- G. S. Hammond, J. Am. Chem. Soc., 1955, 77, 334–338 CrossRef CAS.
- G. Skoraczynski, P. Dittwald, B. Miasojedow, S. Szymkuc, E. P. Gajewska, B. A. Grzybowski and A. Gambin, Sci. Rep., 2017, 7, 3582 CrossRef CAS.
- B. C. Ross, PLoS One, 2014, 9, e87357 CrossRef.
- Q. W. Kilian and T. Gerald, presented in part at the Eleventh International Conference on Artificial Intelligence and Statistics, 2007/03/11, 2007 Search PubMed.
- B. A. Helfrecht, R. K. Cersonsky, G. Fraux and M. Ceriotti, arXiv:2002.05076, 2020.
- B. A. Helfrecht, R. K. Cersonsky, G. Fraux and M. Ceriotti, Mach. Learn.: Sci. Technol., 2020, 1, 045021 CrossRef.
- A. V. Malkov, M.-M. Westwater, A. Gutnov, P. Ramírez-López, F. Friscourt, A. Kadlčíková, J. Hodačová, Z. Rankovic, M. Kotora and P. Kočovský, Tetrahedron, 2008, 64, 11335–11348 CrossRef CAS.
- V. Y. Vaganov, Y. Fukazawa, N. S. Kondratyev, S. A. Shipilovskikh, S. E. Wheeler, A. E. Rubtsov and A. V. Malkov, Adv. Synth. Catal., 2020, 362, 5467–5474 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1sc00482d |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |