Open Access Article
Open Access ArticleMolecular mechanism of secreted amyloid-β precursor protein in binding and modulating GABABR1a†
Mei
Feng‡
ae,
Yi
Song‡
a,
Serena H.
Chen
 b,
Yuanzhao
Zhang
c and
Ruhong
Zhou
b,
Yuanzhao
Zhang
c and
Ruhong
Zhou
 *ad
*ad
aInstitute of Quantitative Biology, Shanghai Institute for Advanced Study, College of Life Sciences, Department of Physics, Zhejiang University, Hangzhou 310027, China. E-mail: rhzhou@zju.edu.cn
bComputational Sciences and Engineering Division, Oak Ridge National Laboratory, Oak Ridge, TN 37830, USA
cCenter for Applied Mathematics, Cornell University, Ithaca, NY 14583, USA
dDepartment of Chemistry, Columbia University, New York, NY 10027, USA
eLanzhou Center for Theoretical Physics, Key Laboratory of Theoretical Physics of Gansu Province, Lanzhou University, Lanzhou, Gansu 730000, China
First published on 16th March 2021
Abstract
A recent phenomenal study discovered that the extension domain of secreted amyloid-β precursor protein (sAPP) can bind to the intrinsically disordered sushi 1 domain of the γ-aminobutyric acid type B receptor subunit 1a (GABABR1a) and modulate its synaptic transmission. The work provided an important structural foundation for the modulation of GABABR1a; however, the detailed molecular interaction mechanism, crucial for future drug design, remains elusive. Here, we further investigated the dynamical interactions between sAPP peptides and the natively unstructured sushi 1 domain using all-atom molecular dynamics simulations, for both the 17-residue sAPP peptide (APP 17-mer) and its minimally active 9 residue segment (APP 9-mer). We then explored mutations of the APP 9-mer with rigorous free energy perturbation (FEP) calculations. Our in silico mutagenesis studies revealed key residues (D4, W6, and W7) responsible for the binding with the sushi 1 domain. More importantly, one double mutation based on different vertebrate APP sequences from evolution exhibited a stronger binding (ΔΔG = −1.91 ± 0.66 kcal mol−1), indicating a potentially enhanced GABABR1a modulator. These large-scale simulations may provide new insights into the binding mechanism between sAPP and the sushi 1 domain, which could open new avenues in the development of future GABABR1a-specific therapeutics.
Introduction
Amyloid-β peptide is the main component of senile plaques found in the brains of patients with Alzheimer's disease (AD) and is derived from normal proteolytic cleavage of the amyloid-β precursor protein (APP).2 APP is a single-pass type I membrane protein with a large amino-terminal ectodomain and a short carboxyl-terminal cytoplasmic domain.3 Mature APP goes through ectodomain shedding via α-, β-, or η-secretase to release secreted APP (sAPPα, sAPPβ, or sAPPη, respectively).4,5 The synaptic function of APP6–12 is performed by sAPP13,14 and is mediated by cell-surface receptors.14–16 Unraveling these sAPP functions and their binding partners has not been trivial, because APP undergoes complex processing, and this results in numerous fragments, which have different and sometimes opposing functional properties. Interestingly, a very recent phenomenal study by De Wit and coworkers has shown that the γ-aminobutyric acid type B receptor subunit 1a (GABABR1a) is also a synaptic receptor for sAPP1, which might open new avenues to treat AD – not only through targeting Aβ but also by strengthening alternate routes of cleaving APP and utilizing nonamylogenic pathways.GABABR is a metabotropic receptor of the central inhibitory neurotransmitter γ-aminobutyric acid (GABA). It is composed of two subunits: GABABR1 and GABABR2, which supply the GABA binding site and allow the heterotrimeric G protein activation. The isoform of GABABR1, GABABR1a, has potential therapeutic significance to a number of neurological disorders which implicate GABABR signaling.17 GABABR1a contains two protein interaction motifs known as sushi domains in the amino-terminal extracellular region.18–22 The sushi 1 domain of GABABR1a is natively unstructured, and it interacts with the flexible, partially structured extension domain (ExD) in the linker region of sAPP. This interaction induces a conformational change in the sushi 1 domain, which leads to increased short-term facilitation in mouse hippocampal synapses and decreased neuronal activity via inhibition of neurotransmitter release. A short peptide within the sAPP ExD, the APP 17-mer, functionally mimics sAPP1. This work discovered a surprising role of the sushi 1 domain of GABABR1a as a new binding partner for sAPP and also provided a preliminary complex structure involving these intrinsically disordered protein domains (NMR structure, more below); however, the detailed molecular interaction mechanism still remains elusive, which is crucial for future potential drug design on this important sushi-containing neurotransmitter receptor.
Here, we undertake extensive all-atom molecular dynamics (MD) simulations and free energy perturbation (FEP) calculations to characterize the effect of the APP 17-mer and its minimal 9-amino acid sequence, the APP 9-mer, in binding to the sushi 1 domain of GABABR1a.1 FEP calculations can supplement experiments in investigating the complicated binding between biomolecules such as protein–protein interaction, ligand–receptor binding, protein–DNA/RNA binding, as well as solvation free energy calculations.23–34 A large number of FEP calculations have achieved excellent agreements with the difficult and expensive experimental measurements in antigen–antibody, protein–ligand, and protein–protein binding affinities.7,8,10,27,29,30,32,35,36 In this study, we found that the APP 9-mer is sufficient to bind GABABR1a and stabilize the sushi 1 domain, in agreement with the previous experimental investigation.1 The stacking interaction between W6 in the APP 9-mer and T20 in the sushi 1 is crucial to preserve the strong binding. A single mutation of W6A can cause a decrease in binding affinity by ΔΔG = 4.90 ± 0.45 kcal mol−1. Moreover, the hydrophobic interactions between W7 in the APP 9-mer and the hydrophobic pocket of the sushi 1 consisting of G16, G17, V43, C44, and R45 also contribute substantially to the App 9 mer–sushi 1 association, as indicated by the significant loss of binding affinity (ΔΔG = 3.45 ± 0.60 kcal mol−1) due to a single mutation of W7A. Meanwhile, D4A mutation results in a binding affinity loss of ΔΔG = 2.19 ± 0.25 kcal mol−1, due to the loss of favorable electrostatic interactions, in particular the loss of a salt-bridge between D4 and R25 of sushi 1 domain. Most interestingly, we found that one double mutation based on different vertebrate APP sequences from evolution has a stronger binding (ΔΔG = −1.91 ± 0.66 kcal mol−1), indicating a potentially enhanced GABABR1a modulator. These findings not only reveal key interactions between the sushi 1 domain and the ExD of APP, but also provide insights for the future development of GABABR1a therapeutics.
Simulation methods
Molecular dynamics simulations
We performed all-atom MD simulations on complexes of the APP 17-mer and 9-mer peptides4 bound to the sushi 1 domain of GABABR1a.§ The complexes were solvated in water boxes using the TIP3P37 water model. Na+ and Cl− were added to neutralize the systems and we set the ion concentration to be 0.15 M. Each system was energy minimized for 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps, equilibrated for 10 ns, followed by a 300 ns production run. All MD simulations were carried out with NAMD38 using the CHARMM force field.39 Long-range electrostatic interactions were calculated using the particle-mesh Ewald (PME) method,40,41 and van der Waals (vdW) interactions were calculated using a cutoff distance of 12 Å. All production runs were performed with the NPT ensemble at 1 atm pressure and 310 K temperature. The covalent bonds with hydrogen atoms were constrained at their equilibrium values by the LINCS algorithm,42 which allows a time step of 2 fs.
000 steps, equilibrated for 10 ns, followed by a 300 ns production run. All MD simulations were carried out with NAMD38 using the CHARMM force field.39 Long-range electrostatic interactions were calculated using the particle-mesh Ewald (PME) method,40,41 and van der Waals (vdW) interactions were calculated using a cutoff distance of 12 Å. All production runs were performed with the NPT ensemble at 1 atm pressure and 310 K temperature. The covalent bonds with hydrogen atoms were constrained at their equilibrium values by the LINCS algorithm,42 which allows a time step of 2 fs.
FEP protocol
The in silico mutagenesis studies were carried out with the FEP calculations.24,26,43–45 The binding free energy change ΔG caused by a mutation can be calculated as:ΔGλ = −kT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln〈exp(−β[V(λ + Δλ) − V(λ)])〉λ, ln〈exp(−β[V(λ + Δλ) − V(λ)])〉λ, | (1) |
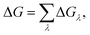 | (2) |
| ΔΔG = ΔGB − ΔGA = ΔG1 − ΔG2 | (3) |
We calculated the free energy changes for the same mutation(s) in both the bound state and the free state. In this case, for every mutation, five independent runs were started from different initial configurations randomly chosen from the MD simulations for improved sampling. The simulation time for each run was 6 ns, amounting to 60 ns (6 ns × 5 runs × 2 states) of FEP calculations for each mutation.
Following the protocols in our previous studies,46,47 we also performed the decomposition of binding affinity into its van der Waals and electrostatic components, since it offers useful information about the contributions of various physical interactions involved in the sAPP peptides–sushi 1 domain binding. Of course, the free energy decomposition might be path-dependent (turning on van der Waals interactions first or electrostatic interactions first).48–51 In this study, we use a straightforward decomposition in FEP by collecting van der Waals and electrostatic interaction contributions separately, i.e., V(λ) = V(λ)elec + V(λ)vdW, in the same ensemble with full interactions in eqn (1) (see above). Due to the nonlinearity of the FEP formulation, there might be a small coupling term in this approach as the total binding free energy ΔΔG is not additive from the two components.51
Results and analyses
Key residues for sAPP–GABABR1a binding
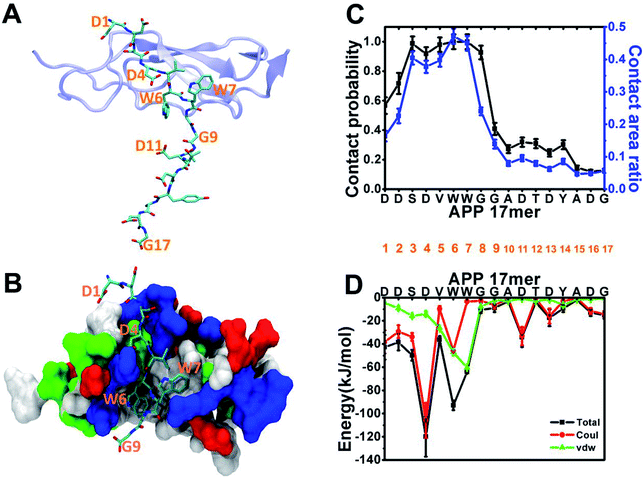
Following the experiment,1 we began our analysis with the structure of the sushi 1 domain of GABABR1a (PDB ID: 6HKC) bound to a short peptide from the ExD of sAPP in two forms: a 17-amino acid peptide (DDSDVWWGGADTDYADG) and a truncated 9-amino acid peptide (DDSDVWWGG). To characterize ExD peptide–sushi 1 binding, we perform 300 ns all-atom MD simulation for each bound complex (APP 17 mer–sushi 1 and APP 9 mer–sushi 1).As illustrated in Fig. 1A and B, both the APP 17-mer and 9-mer bind to a shallow groove of the sushi 1 domain. The per-residue contact probabilities and contact area ratios between the APP 17-mer and the sushi 1 domain are shown in Fig. 1C. A residue of the APP 17-mer is considered to be in contact with sushi 1 domain if any heavy atom is within 4 Å from any heavy atom of sushi 1. The contact probability is calculated as the ratio of the residue contact time to the total 300 ns simulation time. The contact area ratio is defined as the ratio between the residue surface area in contact with sushi 1 domain and the total solvent-accessible surface area (SASA) of that residue. The first nine residues of the 17-mer maintain high contact probabilities and high contact area ratios with the sushi 1 domain. Fig. 1D shows the average interaction energy between each residue of the APP 17-mer and the sushi 1 domain. Again, the interaction energy is dominated by contributions from the first nine amino acids (Fig. 1D).
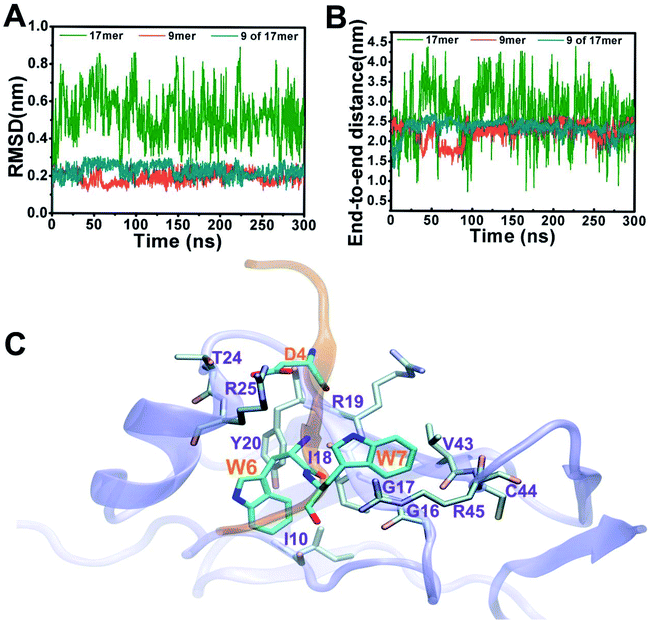
Fig. 2 depicts structural fluctuations of the APP 9-mer and 17-mer during the 300 ns MD simulations. The APP 9-mer was relatively stable, as indicated by the root-mean-square deviations (RMSD) of the backbone atoms which saturates at around 0.21 nm. In contrast, the APP 17-mer is less stable, whose RMSD fluctuates between 0.22 nm and 0.89 nm (with an average of 0.53 nm), although the first nine of the 17 residues are as stable as the APP 9-mer.
To better characterize the conformation of APP 17-mer and APP 9-mer in complex with the sushi 1 domain, we calculated their end-to-end distance, the time-dependent distance between the C atoms of the terminal residues (D1 and G17 for APP 17-mer; D1 and G9 for APP 9-mer), in Fig. 2B. Our analysis illustrates that the end-to-end distance of APP 17-mer fluctuates drastically between 0.74 nm and 4.41 nm (averaged at 2.74 nm), while the first nine of the 17 residues were more stable with an average end-to-end distance around 2.36 nm, close to that of APP 9-mer (2.25 nm). This suggests that the conserved, minimal 9-amino acid sequence fits well into the shallow groove of the sushi 1 domain, while the remaining 8 residues extends into the solution and move freely in large. No stable contacts were observed between these remaining 8 residues and sushi 1 domain. Only temporary contacts were made occasionally by residues like Asp11 through “salt-bridge-like” short range electrostatic interactions with basic residues such as Arg25 and Lys29 on the sushi 1 domain (see Fig. S2 and descriptions in ESI†).
The binding interface between APP 9-mer and sushi 1 domain is presented in Fig. 2C, which reveals three key residues: (i) D4, which forms hydrogen bonds with R19 and Y20 of sushi 1, and the side chain of D4 forms electrostatic interactions with T24 and R25 of sushi 1 (salt-bridge between D4 and R25) (also shown in more details in Fig. 3A, left); (ii) W6, which stacks with the side chain of Y20, establishes hydrogen bonds with G17 and I18, and forms hydrophobic interactions with G17, I18 and I10 (Fig. 3B, left); (iii) W7, making contacts with the hydrophobic pocket of sushi 1 consisting of G16, G17, V43, C44 and R45 (Fig. 3C, left).
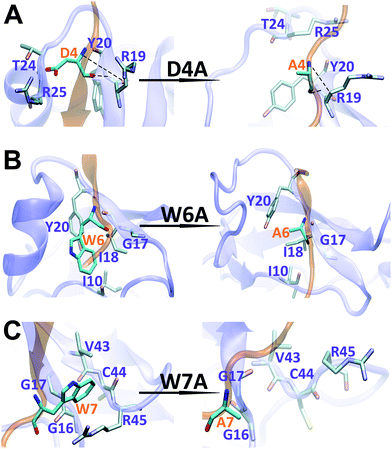 | ||
| Fig. 3 Structural comparison of sushi 1 domain bound to WT APP 9-mer (left) and mutated APP 9-mer's (right) at the end of 300 ns of MD simulation: (A) for D4A mutation; (B) for W6A; (C) for W7A. | ||
Structural analysis of the mutants
To further characterize the binding between APP 9-mer and sushi 1, we separately mutated several central sites on APP 9-mer and ran additional MD simulations. The three residues with the highest interaction energy were chosen for alanine scan mutations, including residues D4, W6, and W7. Fig. 4 presents the RMSD results for the WT and the three mutants. These RMSD profiles demonstrate that alanine scan mutations in APP 9-mer give rise to significant conformational changes in the sushi 1 domain—the average RMSD of the sushi 1 domain in the case of D4A (0.37 nm) and W6A (0.38 nm) was much higher than that of WT (0.27 nm). In comparison, we also analyzed the trajectories of a system containing the sushi 1 domain alone (Fig. S3†), whose RMSD saturates at around 0.38 nm (Fig. S3C†). The RMSD profiles reveal that binding by APP 9-mer stabilized the sushi 1 domain, while D4A and W6A mutations in APP 9-mer destabilized binding of APP 9-mer to sushi 1 domain and made the sushi 1 domain less stable. The structure of the binding complexes (Fig. 4E–H) further support the RMSD calculations, showing the shallow groove of sushi 1 (marked by the red circle) lost its native structure when interacting with mutant APP 9-mer's (especially for D4A and W6A mutations). The secondary structure analysis shows the same conclusion with D4A and W6A mutants lost most of the helices within residues 16–35 in the wild-type after a few nanoseconds while the W7A mutant maintained a significant portion of the helical content during the simulation length (Fig. S4†).The final binding site conformations for the mutant D4A, W6A, and W7A systems at the end of simulations are also shown in Fig. 3 (right part as compared the wild-type on the left). In the D4A system, despite A4 being still hydrogen-bonded with R19 and Y20, the electrostatic interactions with T24 and R25 were completely disrupted (Fig. 3A, right). For the W6A system (Fig. 3B), the stacking interaction with Y20 was sundered (Fig. 3B, right). In both cases, APP 9-mer can no longer bound to or stabilized the shallow groove of the sushi 1 domain (Fig. 4F and G). For the W7A system (Fig. 3C), since the mutant A7 lacks an aromatic ring, the binding interaction with the hydrophobic pocket (G16, G17, V43, C44 and R45) was mostly lost, and only weak hydrophobic interactions with residues G16 and G17 remain (Fig. 3C, right). Since V43, C44, and R45 are not in the binding groove, the mutation has little effect on APP 9-mer stabilizing the sushi 1 domain, and the conformational change of the sushi 1 domain is not significant (Fig. 4H).
FEP in silico mutagenesis study
We further explored the effect of mutations in APP 9-mer through free energy perturbation (FEP) calculations.24,26,43–45 As detailed in the Methods section, we calculated the free energy changes for the same mutation(s) in both the bound state and the free state. For every mutation, five independent runs were started from different initial configurations randomly chosen from the MD simulation trajectories for improved sampling. The results of a complete alanine scan mutation on the first nine residues are summarized in Table 1. Our rigorous FEP calculations reveal a dramatic decrease in the binding affinity for mutation W6A (ΔΔG = 4.90 ± 0.45 kcal mol−1). The free energy decomposition shows that this decrease is mainly contributed by the vdW interaction (5.29 ± 0.39 kcal mol−1). There are also significant reductions in the binding affinity for the mutations D4A (ΔΔG = 2.19 ± 0.25 kcal mol−1), with majority contribution from the electrostatic interaction (1.97 ± 0.49 kcal mol−1); V5A (ΔΔG = 2.96 ± 0.20 kcal mol−1), with majority contribution from the vdW interaction (2.95 ± 0.20 kcal mol−1); and W7A (ΔΔG = 3.45 ± 0.60 kcal mol−1), with majority contribution from the vdW interaction (5.25 ± 0.59 kcal mol−1). The effect of mutations at the other five residues are relatively mild or neutral.| Mutation | ΔΔG (kcal mol−1) | ΔΔGelec (kcal mol−1) | ΔΔGvdW (kcal mol−1) | ΔΔGcoupling (kcal mol−1) |
|---|---|---|---|---|
| D1A | 0.62 ± 0.63 | 0.33 ± 0.39 | 0.52 ± 0.38 | −0.23 ± 0.05 |
| D2A | 0.04 ± 0.38 | −0.05 ± 0.43 | 0.14 ± 0.43 | −0.05 ± 0.10 |
| S3A | 1.14 ± 0.23 | 1.82 ± 0.59 | −0.53 ± 0.49 | −0.15 ± 0.05 |
| D4A | 2.19 ± 0.25 | 1.97 ± 0.49 | 0.67 ± 0.41 | −0.44 ± 0.15 |
| V5A | 2.96 ± 0.20 | 0.007 ± 0.083 | 2.95 ± 0.20 | 0.006 ± 0.003 |
| W6A | 4.90 ± 0.45 | −0.37 ± 0.17 | 5.29 ± 0.39 | −0.02 ± 0.03 |
| W7A | 3.45 ± 0.60 | −1.68 ± 0.14 | 5.25 ± 0.59 | −0.12 ± 0.04 |
| G8A | 0.10 ± 0.14 | 0.07 ± 0.04 | 0.02 ± 0.14 | 0.006 ± 0.004 |
| G9A | −0.03 ± 0.04 | 0.01 ± 0.01 | −0.04 ± 0.04 | −0.001 ± 0.001 |
Design novel peptides for enhanced binding
In order to better understand the binding mechanism between APP 9-mer and sushi 1 domain, we designed single or double mutations for possible stronger binding. As shown in Table 2, we first examined two single mutations D1E and D2E through our previous experiences,46,47 However, this conservative mutation of similar size and charge had little influence on the binding affinity, with ΔΔG = 1.12 ± 0.74 kcal mol−1 (D1E) and ΔΔG = 0.29 ± 0.56 kcal mol−1 (D2E). We also observed slight reduction in the binding affinity by the single mutation S3M (ΔΔG = 0.44 ± 0.28 kcal mol−1). The D4E mutation at the binding interface results in a somewhat modest reduction in binding affinity ΔΔG = 2.79 ± 0.90 kcal mol−1, similar to D4A (ΔΔG = 2.19 ± 0.25 kcal mol−1). For V5, we examined three different mutations: V5I (ΔΔG = 0.12 ± 0.28 kcal mol−1), V5A (ΔΔG = 2.96 ± 0.20 kcal mol−1), and V5D (ΔΔG = 4.82 ± 1.11 kcal mol−1), which revealed the importance of hydrophobic interactions. For the target site W6, the conservative mutation W6F (ΔΔG = 0.28 ± 0.27 kcal mol−1) had a much smaller effect than the mutation W6A (ΔΔG = 4.90 ± 0.45 kcal mol−1), which indicates the importance of the stacking interaction. The double mutation V5W + W6V resulted in a significant reduction in binding affinity, ΔΔG = 9.72 ± 3.11 kcal mol−1. For the target site W7, two other different mutations were also tested: the conservative mutation W7F had little influence on the binding affinity (ΔΔG = 0.70 ± 0.73 kcal mol−1), while W7I caused a more significant decrease (ΔΔG = 3.09 ± 0.85 kcal mol−1), similar to W7A (ΔΔG = 3.45 ± 0.60 kcal mol−1). These FEP calculations indicate that the APP-9 peptide is well conserved and optimized.| Mutation | ΔΔG (kcal mol−1) | ΔΔGelec (kcal mol−1) | ΔΔGvdW (kcal mol−1) | ΔΔGcoupling (kcal mol−1) |
|---|---|---|---|---|
| D1E | 1.12 ± 0.74 | 0.51 ± 0.49 | 0.54 ± 0.75 | 0.07 ± 0.36 |
| D2E | 0.29 ± 0.56 | −0.46 ± 0.46 | 0.94 ± 0.52 | −0.19 ± 0.23 |
| D2N | −1.14 ± 0.51 | −0.85 ± 0.64 | −0.12 ± 0.71 | −0.17 ± 0.17 |
| S3M | 0.44 ± 0.28 | 0.11 ± 0.72 | 0.66 ± 0.72 | −0.33 ± 0.12 |
| D4E | 2.79 ± 0.90 | 1.41 ± 0.76 | 1.09 ± 0.55 | 0.30 ± 0.26 |
| V5I | 0.12 ± 0.28 | −0.08 ± 0.03 | 0.22 ± 0.28 | −0.01 ± 0.01 |
| V5D | 4.82 ± 1.11 | 4.33 ± 1.00 | 0.66 ± 0.67 | −0.17 ± 0.12 |
| V5A | 2.96 ± 0.20 | 0.007 ± 0.083 | 2.95 ± 0.20 | 0.006 ± 0.003 |
| W6F | 0.28 ± 0.27 | −0.31 ± 0.08 | 0.48 ± 0.26 | 0.12 ± 0.03 |
| W7F | 0.70 ± 0.73 | −1.10 ± 0.10 | 1.92 ± 0.76 | −0.12 ± 0.03 |
| W7I | 3.09 ± 0.85 | −1.06 ± 0.32 | 4.30 ± 0.72 | −0.15 ± 0.03 |
| V5W + W6V | 9.72 ± 3.11 | 0.29 ± 0.40 | 9.24 ± 2.84 | 0.19 ± 0.13 |
| D1A + D2N | −1.91 ± 0.66 | −1.43 ± 1.61 | −0.03 ± 1.42 | −0.45 ± 0.89 |
We then explored the APP sequences from other species trying to learn from the evolution. The first nine residues among different vertebrate APP sequences, APP_human, APP_pig, APP_chicken, APP_rat, APP_mouse, APP_frog, APPa_fish, and APPb_fish are highly conserved1 (see Table 3). Only APP_frog 9-mer (DDSDAWWGG) and APPb_fish 9-mer (ANSDVWWGG) are different from the others (DDSDVWWGG). APP_frog 9-mer can be regarded as single mutation V5A of APP_human 9-mer, and APPb_fish can be regarded as a double mutation D1A + D2N of APP_human 9-mer. Our FEP calculations show that the double mutation D1A + D2N enhanced the binding affinity by ΔΔG = −1.91 ± 0.66 kcal mol−1 (see Table 3; also included in Table 2 for completeness), with majority of the contribution from electrostatic interactions (−1.43 kcal mol−1), indicating the two consecutive acidic residues D1 and D2 in the APP 9-mer might not be optimal for binding in this case. As we already learned from above that the single mutation D1A is not favorable (ΔΔG = 0.62 ± 0.63 kcal mol−1), we further investigated the single mutation D2N (also included in Table 2 for completeness), which turned out to enhance the binding affinity by ΔΔG = −1.14 ± 0.51 kcal mol−1, with majority of the contribution also from electrostatic interactions (−0.85 kcal mol−1). A closer look indicates that there exists about −1.39 kcal mol−1 “synergy” in the double D1A + D2N mutation as compared to the sum of the two single mutations (−1.91 − 0.62 − (−1.14) = −1.39 kcal mol−1), and the free energy decomposition shows the synergy consists of contributions of −0.91 kcal mol−1 in electrostatic and (a meaningful) −0.43 kcal mol−1 in van der Waals interactions, with the remaining in coupling terms. Fig. 5 further illustrates the structural changes due to the double mutation, which clearly shows the strong repulsion between D1 and D2 in the wild-type peptide, with both D1 and D2's negatively charged sidechains sticking into solvent (Fig. 5, left), thus less binding to the sushi 1 domain. On the other hand, the double mutant A1N2 displays a backbone hydrogen bond between N2 and Gly22 in the sushi 1 domain, and meanwhile, both A1 and N2 residues are pushed closer to the sushi 1 domain, with 5 residues in close proximity (defined as within 6 Å from the first two APP residues) as compared to only 4 in the wild-type (Fig. 5, right), which explains the meaningful synergy contributions from both electrostatic and van der Waals interactions (−0.91 and −0.43 kcal mol−1, respectively). Either D1A or D2N single mutation cannot generate strong enough hydrophobic force to push the first two APP 9-mer residues to be in “tight binding” with sushi 1 domain. All these analyses confirm our earlier suspicion that the two consecutive acidic residues D1 and D2 in the APP 9-mer might not be optimal for binding in this case. Even though the double mutant (APPb_fish peptide) is not overwhelmingly stronger in terms of binding affinity (∼3kT at room temperature), we believe this new peptide learned from evolution can potentially serve as an enhanced GABABR1a modulator. Further experimental validation on our in silico prediction is highly desired.
| Species | 9-mer sequence | ΔΔG (kcal mol−1) |
|---|---|---|
| APP_human | DDSDVWWGG | — |
| APP_pig | DDSDVWWGG | 0 |
| APP_chicken | DDSDVWWGG | 0 |
| APP_rat | DDSDVWWGG | 0 |
| APP_mouse | DDSDVWWGG | 0 |
| APP_frog | DDSDAWWGG | 2.96 ± 0.20 |
| APPa_fish | DDSDVWWGG | 0 |
| APPb_fish | ANSDVWWGG | −1.91 ± 0.66 |
Conclusion
In this work, we investigated the binding dynamics and underlying molecular mechanism of the App 17-mer (and its minimal 9-amino acid sequence) in binding with the sushi 1 domain of GABABR1a. Our MD simulations revealed important structural binding patterns and major driving forces that sAPP peptides utilize to stabilize the natively unstructured sushi 1 domain. Contact and energy analyses identified three key binding residues in the APP 9-mer peptide (D4, W6, and W7), which were further examined through in silico mutagenesis studies. We found that the stacking interaction between W6 of the APP-9 mer and T20 of the sushi 1 domain is crucial to the strong binding between the two. Our FEP calculations suggest that W6A mutation will cause a significant decrease in binding affinity (ΔΔG = 4.90 ± 0.45 kcal mol−1). In addition, the hydrophobic interaction between W7 (APP-9 mer) and the hydrophobic pocket (sushi 1) is also important, as evidenced by the significant loss of binding affinity (ΔΔG = 3.45 ± 0.60 kcal mol−1) due to a single W7A mutation. Finally, we designed single and double mutations for potentially stronger binding and found that a double mutation (D1A + D2N) learned from evolution shows a stronger binding (ΔΔG = −1.91 ± 0.66 kcal mol−1), indicating a potentially enhanced GABABR1a modulator. Our current work reveals novel insights into App 9-mer–sushi 1 domain binding, which might provide new targets for the development of GABABR1a isotype-specific therapies that are associated with many neurological diseases involving GABABR signaling.Author contributions
R. Z. conceived and designed the study. M. F. and S. H. C. performed the molecular dynamics simulations. Y. S. carried out the free energy perturbation calculations. M. F., Y. S. and Y. Z. performed computational analysis and wrote the manuscript with support from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We would like to thank Prof. Joris De Wit for sending us the NMR structure of APP 9-mer bound with sushi-1 domain (PDB coordinates). We also thank Wei Song, David Bell, Binquan Luan, and Zonglin Gu for help with the manuscript. This work is partially supported by the National Natural Science Foundation of China (grants U1967217 and 11574224) and China Postdoctoral Science Foundation (grant 2019M652052). R. Z. also acknowledges the financial support from W. M. Keck Foundation (grant award 2019-2022) and National Independent Innovation Demonstration Zone Shanghai Zhangjiang Major Projects (ZJZX2020014).References
- H. C. Rice, D. de Malmazet, A. Schreurs, S. Frere, I. Van Molle, A. N. Volkov, E. Creemers, I. Vertkin, J. Nys, F. M. Ranaivoson, D. Comoletti, J. N. Savas, H. Remaut, D. Balschun, K. D. Wierda, I. Slutsky, K. Farrow, B. De Strooper and J. de Wit, Secreted amyloid-beta precursor protein functions as a GABA(B)R1a ligand to modulate synaptic transmission, Science, 2019, 363(6423), 143 CrossRef PubMed.
- T. E. Golde, S. Estus, L. H. Younkin, D. J. Selkoe and S. G. Younkin, Processing of the amyloid protein-precursor to potentially amyloidogenic derivatives, Science, 1992, 255(5045), 728–730 CrossRef CAS.
- J. Kang, H. G. Lemaire, A. Unterbeck, J. M. Salbaum, C. L. Masters, K. H. Grzeschik, G. Multhaup, K. Beyreuther and B. Mullerhill, The precursor of Alzheimer's-disease amyloid-a4 protein resembles a cell-surface receptor, Nature, 1987, 325(6106), 733–736 CrossRef CAS PubMed.
- C. Haass, C. Kaether, G. Thinakaran and S. Sisodia, Trafficking and Proteolytic Processing of APP, Cold Spring Harbor Perspect. Med., 2012, 2(5), a006270 Search PubMed.
- M. Willem, S. Tahirovic, M. A. Busche, S. V. Ovsepian, M. Chafai, S. Kootar, D. Hornburg, L. D. B. Evans, S. Moore, A. Daria, H. Hampel, V. Mueller, C. Giudici, B. Nuscher, A. Wenninger-Weinzierl, E. Kremmer, M. T. Heneka, D. R. Thal, V. Giedraitis, L. Lannfelt, U. Mueller, F. J. Livesey, F. Meissner, J. Herms, A. Konnerth, H. Marie and C. Haass, eta-Secretase processing of APP inhibits neuronal activity in the hippocampus, Nature, 2015, 526(7573), 443–+ CrossRef CAS.
- L. Yang, Z. Wang, B. Wang, N. J. Justice and H. Zheng, Amyloid Precursor Protein Regulates Ca(v)1.2 L-type Calcium Channel Levels and Function to Influence GABAergic Short-Term Plasticity, J. Neurosci., 2009, 29(50), 15660–15668 CrossRef CAS PubMed.
- G. R. Seabrook, D. W. Smith, B. J. Bowery, A. Easter, T. Reynolds, S. M. Fitzjohn, R. A. Morton, H. Zheng, G. R. Dawson, D. J. S. Sirinathsinghji, C. H. Davies, G. L. Collingridge and R. G. Hill, Mechanisms contributing to the deficits in hippocampal synaptic plasticity in mice lacking amyloid precursor protein, Neuropharmacology, 1999, 38(3), 349–359 CrossRef CAS.
- G. R. Dawson, G. R. Seabrook, H. Zheng, D. W. Smith, S. Graham, G. O'Dowd, B. J. Bowery, S. Boyce, M. E. Trumbauer, H. Y. Chen, L. H. T. Van der Ploeg and D. J. S. Sirinathsinghji, Age-related cognitive deficits, impaired long-term potentiation and reduction in synaptic marker density in mice lacking the beta-amyloid precursor protein, Neuroscience, 1999, 90(1), 1–13 CrossRef CAS.
- S. M. Fitzjohn, R. A. Morton, F. Kuenzi, C. H. Davies, G. R. Seabrook and G. L. Collingridge, Similar levels of long-term potentiation in amyloid precursor protein-null and wild-type mice in the CA1 region of picrotoxin treated slices, Neurosci. Lett., 2000, 288(1), 9–12 CrossRef CAS PubMed.
- S.-H. Tyan, A. Y.-J. Shih, J. J. Walsh, H. Maruyama, F. Sarsoza, L. Ku, S. Eggert, P. R. Hof, E. H. Koo and D. L. Dickstein, Amyloid precursor protein (APP) regulates synaptic structure and function, Mol. Cell. Neurosci., 2012, 51(1–2), 43–52 CrossRef CAS PubMed.
- B. Wang, Z. Wang, L. Sun, L. Yang, H. Li, A. L. Cole, J. Rodriguez-Rivera, H.-C. Lu and H. Zheng, The Amyloid Precursor Protein Controls Adult Hippocampal Neurogenesis through GABAergic Interneurons, J. Neurosci., 2014, 34(40), 13314–13325 CrossRef CAS PubMed.
- M. Chen, J. Wang, J. Jiang, X. Zheng, N. J. Justice, K. Wang, X. Ran, Y. Li, Q. Huo, J. Zhang, H. Li, N. Lu, Y. Wang, H. Zheng, C. Long and L. Yang, APP modulates KCC2 expression and function in hippocampal GABAergic inhibition, Elife, 2017, 6, e20142 CrossRef PubMed.
- B. G. Mockett, M. Richter, W. C. Abraham and U. C. Mueller, Therapeutic Potential of Secreted Amyloid Precursor Protein APPs alpha, Front. Mol. Neurosci., 2017, 10, 30 Search PubMed.
- U. C. Mueller, T. Deller and M. Korte, Not just amyloid: physiological functions of the amyloid precursor protein family, Nat. Rev. Neurosci., 2017, 18(5), 281–298 CrossRef CAS PubMed.
- T. Saitoh, M. Sundsmo, J. M. Roch, N. Kimura, G. Cole, D. Schubert, T. Oltersdorf and D. B. Schenk, Secreted form of amyloid-beta protein-precursor is involved in the growth-regulation of fibroblasts, Cell, 1989, 58(4), 615–622 CrossRef CAS PubMed.
- C. Reinhard, M. Borgers, G. David and B. De Strooper, Soluble amyloid-beta precursor protein binds its cell surface receptor in a cooperative fashion with glypican and syndecan proteoglycans, J. Cell Sci., 2013, 126(21), 4856–4861 CAS.
- J.-P. Pin and B. Bettler, Organization and functions of mGlu and GABA(B) receptor complexes, Nature, 2016, 540(7631), 60–68 CrossRef CAS PubMed.
- R. Vigot, S. Barbieri, H. Brauner-Osborne, R. Turecek, R. Shigemoto, Y.-P. Zhang, R. Lujan, L. H. Jacobson, B. Biermann, J.-M. Fritschy, C.-M. Vacher, M. Mueller, G. Sansig, N. Guetg, J. F. Cryan, K. Kaupmann, M. Gassmann, T. G. Oertner and B. Bettler, Differential compartmentalization and distinct functions of GABA(B) receptor variants, Neuron, 2006, 50(4), 589–601 CrossRef CAS PubMed.
- P. C. Waldmeier, K. Kaupmann and S. Urwyler, Roles of GABA(B) receptor subtypes in presynaptic auto- and heteroreceptor function regulating GABA and glutamate release, J. Neural Transm., 2008, 115(10), 1401–1411 CrossRef CAS PubMed.
- B. Biermann, K. Ivankova-Susankova, A. Bradaia, S. A. Aziz, V. Besseyrias, J. P. Kapfhammer, M. Missler, M. Gassmann and B. Bettler, The Sushi Domains of GABA(B) Receptors Function as Axonal Targeting Signals, J. Neurosci., 2010, 30(4), 1385–1394 CrossRef CAS PubMed.
- M. Gassmann and B. Bettler, Regulation of neuronal GABA(B) receptor functions by subunit composition, Nat. Rev. Neurosci., 2012, 13(6), 380–394 CrossRef CAS PubMed.
- S. Hannan, K. Gerrow, A. Triller and T. G. Smart, Phospho-dependent Accumulation of GABABRs at Presynaptic Terminals after NMDAR Activation, Cell Rep., 2016, 16(7), 1962–1973 CrossRef CAS PubMed.
- B. L. Tembe and J. A. McCammon, Ligand receptor interactions, Comput. Chem., 1984, 8(4), 281–283 CrossRef CAS.
- W. L. Jorgensen, Free-energy calculations - a breakthrough for modeling organic-chemistry in solution, Acc. Chem. Res., 1989, 22(5), 184–189 CrossRef CAS.
- P. Kollman, Free-energy calculations - applications to chemical and biochemical phenomena, Chem. Rev., 1993, 93(7), 2395–2417 CrossRef CAS.
- Y. Deng and B. Roux, Calculation of standard binding free energies: Aromatic molecules in the T4 lysozyme L99A mutant, J. Chem. Theory Comput., 2006, 2(5), 1255–1273 CrossRef CAS PubMed.
- T. Simonson, G. Archontis and M. Karplus, Free energy simulations come of age: Protein-ligand recognition, Acc. Chem. Res., 2002, 35(6), 430–437 CrossRef CAS PubMed.
- A. Warshel, P. K. Sharma, M. Kato and W. W. Parson, Modeling electrostatic effects in proteins, Biochim. Biophys. Acta Protein Proteonomics, 2006, 1764(11), 1647–1676 CrossRef CAS PubMed.
- R. Zhou, P. Das and A. K. Royyuru, Single Mutation Induced H3N2 Hemagglutinin Antibody Neutralization: A Free Energy Perturbation Study, J. Phys. Chem. B, 2008, 112(49), 15813–15820 CrossRef CAS PubMed.
- P. Das, J. Li, A. K. Royyuru and R. Zhou, Free Energy Simulations Reveal a Double Mutant Avian H5N1 Virus Hemagglutinin with Altered Receptor Binding Specificity, J. Comput. Chem., 2009, 30(11), 1654–1663 CrossRef CAS PubMed.
- S. H. Chen, S.-g. Kang, J. Luo and R. Zhou, Charging nanoparticles: increased binding of Gd@C-82(OH)(22) derivatives to human MMP-9, Nanoscale, 2018, 10(12), 5667–5677 RSC.
- Z. Xia, H. Tien, S.-G. Kang and R. Zhou, Free-Energy Simulations Reveal that Both Hydrophobic and Polar Interactions Are Important for Influenza Hemagglutinin Antibody Binding, Biophys. J., 2012, 102(6), 1453–1461 CrossRef CAS PubMed.
- M. Feng, D. R. Bell, H. Kang, Q. Shao and R. Zhou, Exploration of HIV-1 fusion peptide-antibody VRC34.01 binding reveals fundamental neutralization sites, Phys. Chem. Chem. Phys., 2019, 21(34), 18569–18576 RSC.
- B. Luan, G. Xu, M. Feng, L. Cong and R. Zhou, Combined Computational-Experimental Approach to Explore the Molecular Mechanism of SaCas9 with a Broadened DNA Targeting Range, J. Am. Chem. Soc., 2019, 141(16), 6545–6552 CrossRef CAS PubMed.
- J. Wang, Y. Deng and B. Roux, Absolute binding free energy calculations using molecular dynamics simulations with restraining potentials, Biophys. J., 2006, 91(8), 2798–2814 CrossRef CAS PubMed.
- M. Almlof, J. Aqvist, A. O. Smalas and B. O. Brandsdal, Probing the effect of point mutations at protein-protein interfaces with free energy calculations, Biophys. J., 2006, 90(2), 433–442 CrossRef PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, Comparison of simple potential functions for simulating liquid water, J. Chem. Phys., 1983, 79(2), 926–935 CrossRef CAS.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Schulten, Scalable molecular dynamics with NAMD, J. Comput. Chem., 2005, 26(16), 1781–1802 CrossRef CAS PubMed.
- A. D. MacKerell, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin and M. Karplus, All-atom empirical potential for molecular modeling and dynamics studies of proteins, J. Phys. Chem. B, 1998, 102(18), 3586–3616 CrossRef CAS PubMed.
- T. Darden, D. York and L. Pedersen, Particle mesh Ewald - an n.log(n) method for Ewald sums in large systems, J. Chem. Phys., 1993, 98(12), 10089–10092 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, A smooth particle mesh Ewald method, J. Chem. Phys., 1995, 103(19), 8577–8593 CrossRef CAS.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. Fraaije, LINCS: A linear constraint solver for molecular simulations, J. Comput. Chem., 1997, 18(12), 1463–1472 CrossRef CAS.
- S. Boresch, F. Tettinger, M. Leitgeb and M. Karplus, Absolute binding free energies: A quantitative approach for their calculation, J. Phys. Chem. B, 2003, 107(35), 9535–9551 CrossRef CAS.
- D. L. Mobley, J. D. Chodera and K. A. Dill, On the use of orientational restraints and symmetry corrections in alchemical free energy calculations, J. Chem. Phys., 2006, 125(8), 084902 CrossRef PubMed.
- B. Luan, H. Tien and R. Zhou, Complete wetting of graphene by biological lipids, Nanoscale, 2016, 8(10), 5750–5754 RSC.
- P. Das, J. Li, A. K. Royyuru and R. Zhou, Free energy simulations reveal a double mutant avian H5N1 virus hemagglutinin with altered receptor binding specificity, J. Comput. Chem., 2009, 30(11), 1654–1663 CrossRef CAS PubMed.
- R. Zhou, P. Das and A. K. Royyuru, Single mutation induced H3N2 hemagglutinin antibody neutralization: a free energy perturbation study, J. Phys. Chem. B, 2008, 112(49), 15813–15820 CrossRef CAS PubMed.
- A. E. Mark and W. F. Vangunsteren, Decomposition of the free-energy of a system in terms of specific interactions - Implications for theoretical and experimental studies, J. Mol. Biol., 1994, 240(2), 167–176 CrossRef CAS PubMed.
- S. Boressch and M. Karplus, The meaning of component analysis - Decomposition of the free-energy in terms of specific interactions, J. Mol. Biol., 1995, 254(5), 801–807 CrossRef PubMed.
- G. P. Brady and K. A. Sharp, Decomposition of interaction free-energies in proteins and other complex-systems, J. Mol. Biol., 1995, 254(1), 77–85 CrossRef CAS PubMed.
- M. Bren, J. Florian, J. Mavri and U. Bren, Do all pieces make a whole? Thiele cumulants and the free energy decomposition, Theor. Chem. Acc., 2007, 117(4), 535–540 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc06946a |
| ‡ These authors contributed equally. |
| § The initial NMR structure of the APP 9-mer bound with sushi-1 domain (complex PDB coordinates) was obtained from Prof. Joris De Wit's group. |
| This journal is © The Royal Society of Chemistry 2021 |