Reversible Pt^II–CH₃ deuteration without methane loss: metal–ligand cooperation vs. ligand-assisted Pt^II-protonation

Abstract

Di(2-pyridyl)ketone dimethylplatinum(II), (dpk)Pt^II(CH₃)₂, reacts with CD₃OD at 25 °C to undergo complete deuteration of Pt–CH₃ fragments in ∼5 h without loss of methane to form (dpk)Pt^II(CD₃)₂ in virtually quantitative yield. The deuteration can be reversed by dissolution in CH₃OH or CD₃OH. Kinetic analysis and isotope effects, together with support from density functional theory calculations indicate a metal–ligand cooperative mechanism wherein DPK enables Pt–CH₃ deuteration by allowing non-rate-limiting protonation of Pt^II by CD₃OD. In contrast, other model di(2-pyridyl) ligands enable rate-limiting protonation of Pt^II, resulting in non-rate-limiting C–H(D) reductive coupling. Owing to its electron-poor nature, following complete deuteration, DPK can be dissociated from the Pt^II-centre, furnishing [(CD₃)₂Pt^II(μ-SMe₂)]₂ as the perdeutero analogue of [(CH₃)₂Pt^II(μ-SMe₂)]₂, a commonly used Pt^II-precursor.

---

Introduction

Homogeneous catalytic functionalization of methane is one of the biggest challenges of organometallic chemistry. Even 50 years¹ after Shilov's discovery of Pt^II-mediated methane functionalization,² no industrially-viable processes³ exist for the conversion of methane to value-added commodity chemicals. Efforts towards addressing this challenge have focussed, in part, on developing new metal–ligand platforms for methane activation,^4,5 a critical step in the overall goal of methane functionalization.

The suitability of a new metal–ligand platform in methane activation is often inferred from mechanistic investigation of the microscopic reverse: methane reductive elimination from critical Pt^IV(CH₃)(H) intermediates supported by new ligands. Pioneering studies by Puddephatt,^6,7 Tilset,⁸ Bercaw⁹ and others focussed on the protonation of dimethyl–Pt^II complexes (e.g.A, Scheme 1) with strong acids (HX) leading to the formation of Pt^IV(CH₃)₂(H) intermediates such as B, and rate-limiting but fast methane elimination to form C, presumably via the formation of a transient Pt^II–σ(CH₄) complex. In these representative examples, the neutral κ²-(L,L) ligands such as 2,2′-bipyridine (BPY), diimines or di(2-pyridyl)ketone (DPK) etc. serve as spectator ligands throughout the reaction. When facially chelating anionic ligands such as tris(pyrazolyl)borate (Tp),¹⁰ di(2-pyridyl)methanesulfonate (DPMS)¹¹ or di(2-pyridyl)borates (DPB)^12–15 are employed, the anionic complexes such as A′ can be protonated by weak acids such as water or methanol leading to the formation of B′ and MOR (M = Na, K etc.; R = H, Me). The Pt^IV-centres in B′ are stabilized by κ³-(L,L,Y) coordination modes. Methane loss from B′ depends on the coordinating ability of the pseudo-axial donor (Y), since the formation of 5-coordinate Pt^IV-centres is a prerequisite for reductive elimination. For example, owing to the strongly coordinating pyrazolyl fragment, the Tp-supported analogue of B′ is resistant to methane elimination and can be isolated.¹⁶

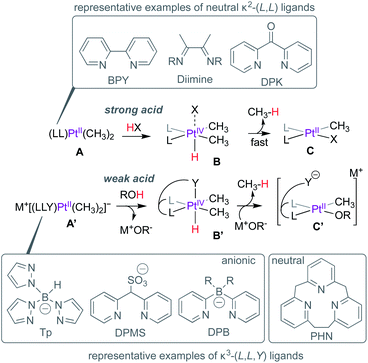Scheme 1 Protonation and methane reductive elimination from Pt-centres supported by κ²-(L,L) and κ³-(L,L,Y) ligands.

On the other hand, while the DPMS-analogue of B′ featuring a moderately coordinating sulfonate arm can be isolated,¹¹ slow methane loss was also observed. In contrast, the DPB-analogue of B′, featuring weaker agostic B(C–H)→Pt^IV interactions cannot be observed and rapid methane loss leads to C′.^13,14 Cationic analogues of B′, such as the [2.1.1]-(2,6)-pyridinophane (PHN)-supported complex can also be directly observed,^17,18 albeit requiring stronger acids such as triflic acid to afford protonation of the neutral (PHN)Pt^II(CH₃)₂-precursor.

H/D exchange studies provide critical insight into the C–H reductive elimination event (the microscopic reverse of C–H activation), especially in cases where Pt^IV(CH₃)(H) intermediates such as B or B′ (Scheme 1) cannot be observed or isolated. When protonation of Pt^II–CH₃ complexes such as A or A′ are performed with deuterated acids, the concomitant Pt^IV(CH₃)(D) intermediates can undergo H/D scrambling via reversible C–H(D) reductive coupling prior to methane loss (reductive elimination), resulting in the observation of methane isotopologues (CH_4−nD_n).

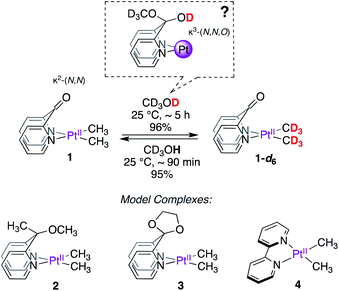
As the search for new metal–ligand platforms for methane functionalization continues, we sought to investigate the κ²-(N,N) DPK-supported dimethylplatinum(II) complex, 1 (Scheme 2) from the perspective of exploiting the ability of the keto fragment of DPK to undergo reversible addition of protic molecules leading to potential κ³-(N,N,O) coordination modes. Although widely explored in organometallic chemistry,^19–33 to the best of our knowledge, such involvement has not been investigated in the context of C–H reductive elimination from Pt^IV, despite the demonstrated ability of κ²-(N,N)-DPK-supported Pt^II complexes to activate C–H bonds.^34–36

Scheme 2 Complexes investigated for Pt^II–CH₃ deuteration.

Here, we report that the DPK-supported dimethylplatinum(II) complex (1, Scheme 2), upon dissolution in CD₃OD, undergoes fast and reversible Pt^II–CH₃ deuteration (reductive coupling) at room temperature without methane loss (reductive elimination). Mechanistic insights gained from kinetics, analyses of isotope effects, reactivity of model complexes (2–4, Scheme 2) and DFT calculations suggest that DPK enables non-rate-limiting Pt^II-protonation via a novel cooperative mechanism between the metal and the ligand. Although widely explored in other areas of organometallic chemistry,³⁷ examples of metal–ligand cooperation in the context of C–H activation/reductive elimination at Pt are scarce.³⁸

Results and discussion

Synthesis and deuteration of Pt^II(CH₃)₂ complexes

Complexes 1–4 (Scheme 2) were synthesized in virtually quantitative yields by reacting [(CH₃)₂Pt^II(μ-SMe₂)]₂ with 2 equiv. of the corresponding κ²-(N,N) ligands (see ESI†). We selected complex 1 for initial study. Upon dissolution in CD₃OD, the Pt^II–CH₃ fragments of 1 were found to undergo fast deuteration without loss of methane. Although not unprecedented,^17,39,40 complexes that undergo C–H(D) reductive coupling without undergoing reductive elimination are exceedingly rare and are particularly interesting, since the σ(methane) intermediates^41,42 presumed to form immediately before methane loss, have never been observed for Pt^II.

The deuteration of the Pt^II–CH₃ fragments of 1 was found to be complete in 5 h at 25 °C and removal of CD₃OD furnished 1-d₆ in 96% yield. The ¹H NMR spectra of 1 (Fig. 1a) and 1-d₆ (Fig. 1b) in CD₃CN differ only in the presence or absence of the resonances of the Pt^II(CH₃)₂ fragment, respectively, appearing as a singlet (δ = 0.72 ppm) with ¹⁹⁵Pt-satellites (²J_H–Pt = 84 Hz) for 1. The reaction could be reversed: upon dissolution of the isolated 1-d₆ in CD₃OH (or CH₃OH), complex 1 could be isolated in 95%, leading to a round-trip recovery of 91%.

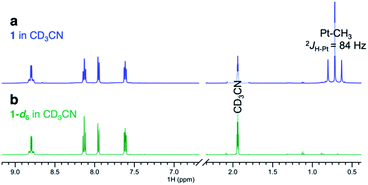Fig. 1 ¹H NMR spectra of (a) (dpk)Pt^II(CH₃)₂, complex 1 and (b) (dpk)Pt^II(CD₃)₂, complex 1-d₆ in CD₃CN.

Upon monitoring the reaction of 1 with CD₃OD by ¹H NMR spectroscopy, sequential deuteration of Pt^II–CH₃ fragments was observed, as shown in Fig. 2. The ¹H NMR resonances of the Pt^II–CH₃, Pt^II–CH₂D, and Pt^II–CHD₂ fragments appear as a singlet (δ = 0.78 ppm, ²J_H–Pt ∼ 84 Hz, ²J_H–D ∼ 1.5 Hz), 1 : 1 : 1 triplet (δ = 0.76 ppm, ²J_H–Pt ∼ 84 Hz, ²J_H–D ∼ 1.5 Hz) and 1 : 2 : 3 : 2 : 1 quintet (δ = 0.74 ppm, ²J_H–Pt ∼ 84 Hz, ²J_H–D ∼ 1.5 Hz), respectively, in CD₃OD. The conversion of 1 to 1-d₆ in neat CD₃OD follows pseudo-first-order kinetics with an initial rate constant k_D = 8.4(2) × 10⁻³ min⁻¹ at 25 °C. From Eyring analyses of initial rates observed in the range 25–55 °C, the activation free energy for the reaction of 1 with CD₃OD was found to be ΔG^‡_{298 K} = 22.7 ± 1.0 kcal mol⁻¹.

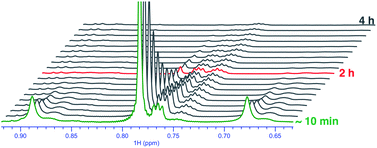Fig. 2 Sequential deuteration of Pt^II–CH₃ fragments of complex 1 in neat CD₃OD as seen by ¹H NMR spectroscopy over the course of 4 h.

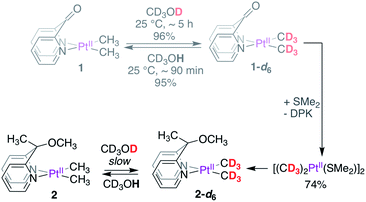
We next explored the reactivity of complexes 2–4 with CD₃OD. We expected complexes 2 and 3, featuring potential κ³-(N,N,O) coordination modes built-in within the ligand motif, to also undergo deuteration of Pt^II–CH₃ fragments. In contrast, complex 4 was not expected to undergo facile deuteration of its Pt^II–CH₃ fragments. Consistent with these expectations, complex 2 was found to undergo Pt^II–CH₃ deuteration in neat CD₃OD, while no deuteration of the Pt^II–CH₃ fragment of 4 was observed at 25 °C in the course of 24 h. Complex 3 was found to be unstable in CD₃OD owing to progressive ligand degradation (presumably due to methanolysis of the ketal fragment) and was thus excluded from further studies. In contrast to 1, the reaction of 2 with CD₃OD was found to be much slower, with an initial pseudo first order rate constant of k_D = 4.5(1) × 10⁻⁴ min⁻¹ at 25 °C. From Eyring analyses of initial rates observed in the range 25–55 °C, the activation free energy for the reaction of 2 with CD₃OD was found to be ΔG^‡_{298 K} = 24.4 ± 1.3 kcal mol⁻¹.

Determination of isotope effects

The deuteration of Pt^II–CH₃ fragments without methane loss (reductive elimination) presented a unique opportunity to investigate kinetic isotope effects associated with the reductive coupling event. To this end, we synthesized the Pt^II(CD₃)₂ analogues 1-d₆ and 2-d₆, as shown in Scheme 3. While 1-d₆ could be isolated in high yields (96%) in a fast and straightforward manner by simple dissolution of 1 in CD₃OD, the reaction of 2 with CD₃OD was slow at 25 °C, taking days to reach completion, warranting the synthesis of 2-d₆via an alternate strategy. Gratifyingly, the perdeutero-analogue of the Pt^II-precursor, i.e. [(CD₃)₂Pt^II(μ-SMe₂)]₂ could be obtained in modest yields (74%) by reacting 1-d₆ with SMe₂, which in turn was used to synthesize 2-d₆. Despite demetallation being unexpected for a κ²-(N,N) chelating ligand,⁴³ the facility with which DPK undergoes substitution by SMe₂ may be ascribed to the high trans effect of the Pt^II-bound CH₃ fragments, the strong coordinating ability of SMe₂, and last but not the least, the electron-poor nature of the DPK-ligand. Indeed, while the DPK ligand was found to also undergo dissociation upon dissolution of complex 1 in DMSO-d₆ at 25 °C (see Section S3.4 of the ESI†), both complexes 2 and 4 were found to be resilient and no demetallation from the κ²-(N,N) chelate was observed over the course of ∼3 days at 25 °C. The synthetic route illustrated in Scheme 3 is a convenient alternative to the use of expensive methyl-d₃ lithium or magnesium reagents for the synthesis of [(CD₃)₂Pt^II(μ-SMe₂)]₂.⁴⁴

Scheme 3 Synthesis of Pt^II(CD₃)₂ complexes for determination of isotope effects.

With complexes 1-d₆ and 2-d₆ in hand, we monitored protonation reactions with CD₃OH at 25 °C. The protonation of 1-d₆ was found to follow pseudo-first-order kinetics⁴⁵ with an initial rate constant k_H = 2.2(3) × 10⁻² min⁻¹ at 25 °C, resulting in an observed KIE of k_H/k_D = 2.6 ± 0.4.

In sharp contrast, the protonation of 2-d₆ was found to follow pseudo-first-order kinetics with an initial rate constant k_H = 6.0(2) × 10⁻³ min⁻¹ at 25 °C, resulting in an observed KIE of k_H/k_D = 13.3 ± 0.7. These differences in isotope effects suggest a difference in mechanism^46,47 by which complexes 1 and 2 undergo Pt^II–CH₃ deuteration, warranting further investigation of fundamental steps, discussed as follows.

Mechanistic and computational studies

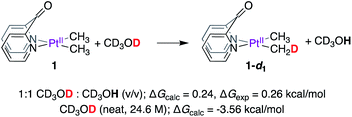
We performed mechanistic studies and DFT calculations to (1) gain insight into the reactions of 1 and 2 with CD₃OD, (2) explain why methane loss is not observed en route to Pt^II–CH₃ deuteration, and (3) benchmark the kinetic isotope effects observed for complexes 1 and 2. DFT calculations were performed using the M06 functional⁴⁸ and def2-tzvp basis⁴⁹ set for all elements (default ECPs for Pt) as implemented in the Gaussian 16 package.⁵⁰ All structures were fully optimized in solvent (methanol) using the SMD model.⁵¹ Free energies of ‘deuterated’ structures were calculated by performing frequency calculations on appropriately ‘deuterated’ structures in solvent. Since neat methanol serves both as solvent and reactant, the free energy was corrected to account for the change in standard state (24.6 M for CD₃OD and 24.7 M for CD₃OH as reactants, see Table S1† in the Computational Section of the ESI†), while no correction was applied for all other solutes. For accurate determination of fully-formed solvent-separated ion pairs (i.e. cationic complexes and methoxide counter-anion), the free energy of methoxide in methanol solution was calculated by adding the free energy of solvation of the methoxide ion (ΔG_solvation = −107.6 kcal mol⁻¹,⁵² see Table S1† in the Computational Section of the ESI†) to the free energy of methoxide calculated by DFT in the gas-phase. Despite exhaustive attempts, transition states involving Pt^II-protonation with methanol could not be located, owing to inadequate solvation of the emerging methoxide by implicit solvation models. This limitation was circumvented by using acetic acid (vide infra).

We first investigated the thermodynamics of the reaction of 1 with CD₃OD to afford 1-d₁, as shown in Scheme 4. According to DFT calculations, when concentrations of CD₃OD (12.31 M) and CD₃OH (12.36 M) are virtually identical, the formation of 1-d₁ is endergonic by 0.24 kcal mol⁻¹ (see Table S2† in the Computational Section of the ESI†).

Scheme 4 Thermodynamics of deuteration of 1 with CD₃OD.

Experimentally, this value was determined to be 0.26 kcal mol⁻¹⁵³ by calculating the relative amounts of Pt^II–CH₃, Pt^II–CH₂D, and Pt^II–CHD₂ isotopologues in an equilibrium mixture obtained by dissolving 1 in 1 : 1 (v/v) CD₃OD : CD₃OH (virtually equimolar) solution. When reactions of 1 are performed in neat CD₃OD (24.6 M), the aforementioned endergonicity is offset by dilution of the CD₃OH formed as a result of H/D exchange, corresponding to a calculated exergonicity of 3.56 kcal mol⁻¹ (see Table S2† in the Computational Section of the ESI†). Indeed, a similar rationale can explain why the reverse reaction (i.e., reaction of 1-d₆ with neat CD₃OH) also goes to completion: here, the CD₃OD produced as a result of H/D scrambling undergoes immediate dilution in neat CD₃OH.

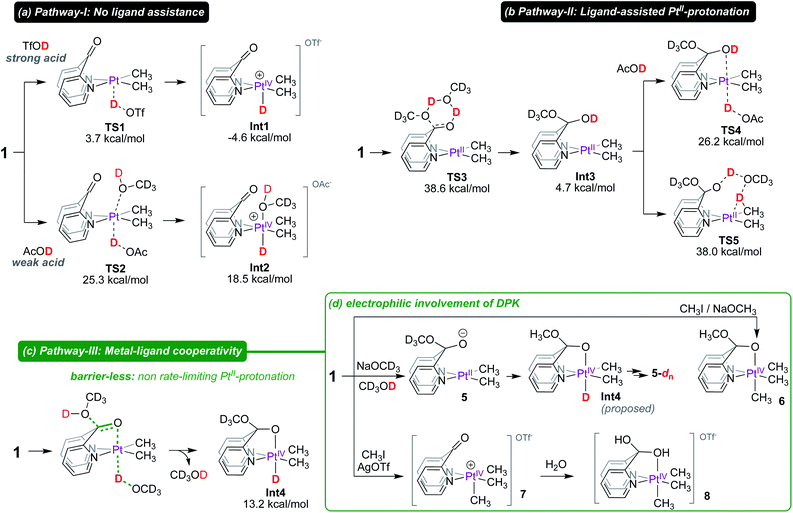
Following up on the reported intermediacy of Pt^IV(CH₃)(D) complexes en route to deuteration of Pt^II–CH₃ fragments (as previously discussed in Scheme 1), we next investigated mechanistic pathways (pathways I, II and III in Scheme 5) by which such intermediates could be formed.

Scheme 5 Mechanistic pathways for the formation of Pt^IV–D intermediates: Pt^II-protonation via: (a) no ligand assistance, (b) ligand-assisted and (c) metal–ligand cooperativity, and (d) experimental support for electrophilic involvement of the keto fragment of DPK.

In Pathway-I (Scheme 5a), DPK serves as an innocent κ²-(N,N) ligand and does not assist in the Pt^II-protonation event. When a strong acid such as triflic acid-d is used, no assistance is necessary and a low-lying transition state (TS1) with an associated barrier of only 3.7 kcal mol⁻¹ leads to the Pt^IV–D intermediate Int1, the formation of which is exergonic by 4.6 kcal mol⁻¹. As a consequence, concomitant C–H reductive coupling and methane elimination are expected to be fast, indeed as observed by Puddephatt.⁷

In contrast, protonation of the Pt^II-centre of 1 by a weak acid such as acetic acid-d₁ (AcOD) is endergonic. Importantly, the protonation of the Pt^II-centre of 1 with AcOD requires assistance by a solvent molecule (with corresponding entropic penalty) which stabilizes the emerging Pt^IV-centre by coordinating at the pseudo-axial site. Since the barrier associated with TS2 (ΔG^‡ = 25.3 kcal mol⁻¹) is already high, this pathway was ruled out as a viable pathway for Pt^II–CH₃ deuteration in CD₃OD, especially since methanol is a much weaker acid than acetic acid. This mechanistic argument is also in favour of the reluctance of complex 4 to undergo deuteration with CD₃OD (as previously discussed in Scheme 2), which would also require assistance from an external solvent molecule (with corresponding entropic penalty) to form the corresponding Pt^IV–D intermediate.

In Pathway-II, we anticipated that the formation of the hemiketal intermediate (Int3) might assist in Pt^II-protonation by coordinating to the emerging octahedral Pt^IV-centre. Arguably, Int3 is an analogue of complex 2, which also undergoes Pt^II–CH₃ deuteration (vide infra for mechanism). Although the formation of Int3 is not significantly endergonic (4.7 kcal mol⁻¹ relative to 1), the barrier for its formation (TS3; ΔG^‡ = 38.6 kcal mol⁻¹) is inaccessible.

Consistent with these calculations, complex 1 in CD₃OD persists in CD₃OD solutions, evident from the resonance at 190 ppm in the ¹³C NMR spectrum corresponding to the C=O fragment of the ‘native keto’ form (see Fig. S13 in the ESI† for ¹³C NMR spectra). Even upon prolonged storage, no evidence for the formation of Int3 was observed. Furthermore, even if other low-energy pathways exist for the formation of Int3, concomitant ligand-assisted pathways for Pt^II-protonation (viaTS4, ΔG^‡ = 26.2 kcal mol⁻¹) or direct Pt^II–CH₃ protonation (viaTS5, ΔG^‡ = 38.0 kcal mol⁻¹) are both inaccessible under reaction conditions. Thus, Pathway-II, where formation of the hemiketal intermediate precedes Pt^II-protonation, was ruled out.

In Pathway-III, we propose a mechanism in which protonation of the Pt^II-centre of 1 and capture of the methoxide occur in a concerted fashion, leading directly to the neutral Pt^IV–D intermediate Int4, the formation of which is endergonic by 13.2 kcal mol⁻¹. Indeed, capture of hydroxide or methoxide, respectively, by the alkali metal cations (M⁺) in complexes A′ (Scheme 1) was, in part, ascribed to observation of the facile protonation of their Pt^II-centres^11–14,54 by water or methanol. In support of this mechanism, a barrier-less pathway where both Pt^II-protonation and attack of methanol to the keto fragment of DPK occurs in a concerted manner was found (see animation of trajectory in the ESI†). This hypothesis implies that the keto fragment of DPK only begins to participate as the Pt^II-centre undergoes protonation. Although the same methanol molecule does not undergo O–H(D) cleavage across the metal and ligand, since proton hopping is an extremely fast process,⁵⁵ from a stoichiometric perspective, the direct formation of Int4, via pathway-III can be described as metal–ligand cooperation. To further support this hypothesis, we conducted mechanistic tests, as shown in Scheme 5d.

Firstly, we found that treatment of 1 with 5-fold excess NaOCD₃ in CD₃OD leads to the formation of 5in situ. According to ¹³C NMR spectroscopy, the resonance corresponding to the keto fragment (δ ∼190 ppm) had disappeared and a new resonance at 104 ppm assigned to the (py)₂C-bridge appeared (see Fig. S30 in the ESI†). Interestingly, complex 5 was also found to undergo slow deuteration of the Pt^II–CH₃ fragments to form 5-d_n, arguing in favour of the purported intermediacy of Int4. Moreover, as shown in Scheme 5d, we found that reaction of 1 with CH₃I, followed by subsequent treatment with sodium methoxide leads to the formation of 6 where the Pt^IV-octahedron is locked by an anionic κ²-(N,N,O) coordination mode of the ligand. Complex 6 may be considered an analogue of Int4.

We also found that the trimethyl–Pt^IV complex 7 undergoes immediate addition of water to form the cationic complex 8 which was characterized by ¹H and ¹³C NMR spectroscopy and X-ray diffraction (see Fig. 3). It is noteworthy that while the DPK ligand in the Pt^II complex 1 might not directly undergo addition of methanol (Scheme 5b), the keto fragments of the DPK ligand in both the supported Pt^II or Pt^IV complexes readily undergo nucleophilic attack by methoxide.

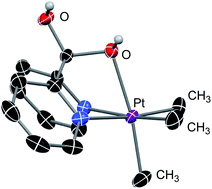Fig. 3 ORTEP representation of 8 at 50% probability level. Hydrogen atoms (except for the OH fragments), triflate counter-anion and disordered molecules are omitted for clarity.

Presumably, as the Pt^II-centre of 1 is undergoing protonation by CD₃OD, the concomitant methoxide can readily be trapped by the keto fragment leading to Int4, as shown in Scheme 6. This mechanistic hypothesis (i.e. barrier-less formation of Int4via metal–ligand cooperation) leads to the corollary that C–D reductive elimination is the rate-limiting step (vide infra).

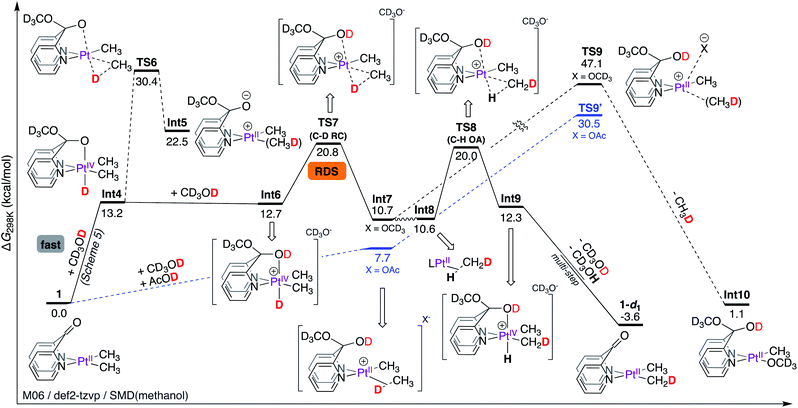Scheme 6 Gibbs free energy profile for the reaction of complex 1 with CD₃OD: rate-limiting C–D reductive coupling.

As shown in Scheme 6, in Int4, the octahedral Pt^IV-centre is locked by a strongly coordinating pseudoaxial^10,13,54 O-donor. According to NBO⁵⁶ analysis, Int4 exhibits a strong donation (E⁽²⁾ = 64.7 kcal mol⁻¹) of electrons from the O lone pair to the σ* orbital of the Pt^IV–H fragment (Table 1), manifesting in a short O–Pt bond length of 2.18 Å. Thus, C–D reductive coupling from Int4 occurs with a very high barrier of 17.2 kcal mol⁻¹ (relative to Int4) associated with TS6 leading to the zwitterionic Pt^II–σ(CH₃D) complex, Int5. Since TS6 corresponds to an overall reaction activation free energy of 30.4 kcal mol⁻¹, it is not accessible under reaction conditions.

Table 1 NBO analysis of coordination strengths of pseudoaxial O-donors in Int4 and Int6 manifesting in proportional barriers associated with C–H reductive coupling

Complex	O(lp) → (σ*)Pt^IV–H, E^(2) (kcal mol^−1)	r(O–Pt) Å	ΔG^‡C–H RC (kcal mol^−1)
Int4	64.7	2.18	17.2
Int6	30.3	2.35	8.1

---

On the other hand, protonation of the pseudo-axial O-donor of Int4 by CD₃OD can lead to the formation of the cationic intermediate Int6. Not only is this step virtually thermo-neutral, the coordinating ability of the pseudoaxial O-donor in Int6 is dramatically decreased, evident from a significantly weaker donation of electrons from the O lone pair to the σ*(Pt^IV–H) orbital (E⁽²⁾ = 30.3 kcal mol⁻¹), consistent with both an elongation of the O–Pt bond length (2.35 Å) and a lower barrier of 8.1 kcal mol⁻¹ (relative to Int6) for C–D reductive coupling leading to Int7. Thus, the barrier associated with TS7 corresponds to an overall reaction activation free energy of 20.8 kcal mol⁻¹.

Since oxidative cleavage of the σ-coordinated C–D fragment of Int7 can only lead back to the starting materials, the coordinated methane fragment must undergo tumbling to form Int8 (an isotopomer of Int7 featuring Pt^II–σ(H–CH₂D)). Int8 can then undergo C–H oxidative addition of the σ-coordinated C–H fragment viaTS8 with an associated barrier of 20.0 kcal mol⁻¹ leading to the formation of Int9, which is an isotopomer of Int6. A sequential deprotonation of the OD and Pt^IV–H fragments of Int9 (not shown, since they are the microscopic reverse of the previously discussed steps leading from 1 to Int4) leads to the formation of 1-d₁, the mono-deuterated isotopologue of complex 1.

Given the scarcity of complexes that do not undergo methane loss en route to C–H(D) reductive coupling,^39,40 we performed NBO analysis (Table 2) to gain insight into nature of interactions between the Pt^II-centre and the σ-coordinated CH₄ fragment in Int7 and compared the same interactions to other related Pt^II(CH₃)σ(CH₄) intermediates such as those featuring DPMS,¹¹ DPB,^12–14 and DPK⁷ ligands (all of which undergo methane loss).

Table 2 Comparative NBO analysis of Int7 and other putative Pt^II–σ(CH₄) intermediates that undergo loss of methane

Complex	σ(C–H)→Pt^II, E^(2) (kcal mol^−1)	Pt^II(lp)→σ*(C–H), E^(2) (kcal mol^−1)	Methane-loss
Int7	36.0	5.3	No
		4.7
[(dpms)Pt^II(CH3)σ(CH4)]	36.8	6.3	Yes
		4.2
[(dpb)Pt^II(CH3)σ(CH4)]	34.1	5.7	Yes
		4.4
[(dpk)Pt^II(CH3)σ(CH4)]^+	37.1	6.9	Yes

---

As shown in Table 2, the cationic Int7 exhibits a moderate (E⁽²⁾ = 36.0 kcal mol⁻¹) donation of electrons from the σ(C–H) fragment to the Pt^II-centre and two much weaker interactions corresponding to back-donation of electrons (E⁽²⁾ = 5.3, 4.7 kcal mol⁻¹) from the Pt^II-centre to the coordinated σ*-orbital of the C–H fragment. The magnitude of these interactions are comparable to those in the [(dpms)Pt^II(CH₃)σ(CH₄)], [(dpb)Pt^II(CH₃)σ(CH₄)], and [(dpk)Pt^II(CH₃)σ(CH₄)]⁺ intermediates, suggesting that loss of methane might not entirely be correlated to the strength by which methane is coordinated to the Pt^II-centre, arguing against a dissociative mechanism.⁵⁷

Thus, we considered an associative mechanism of methane loss, especially since Int7 does not feature strongly trans influencing ligands that facilitate dissociation of the σ-coordinated CH₄ fragment.^58–60 According to our calculations, the transition state (TS9) for associative loss of methane corresponds to a very high barrier of 47.1 kcal mol⁻¹, ruling out the possibility for the formation of Int10. Realizing that the calculated free energy of the transition state TS9 (where methoxide serves as the incoming nucleophile) likely suffers from inadequate solvation of methoxide by implicit solvation, we also considered acetate as the incoming nucleophile.⁶¹ According to our calculations, the transition state for associative loss of methane TS9′ with an associated barrier of 30.5 kcal mol⁻¹ (relative to Int7, X = OAc), is inaccessible under reaction conditions. In support of this hypothesis, we found that although complex 1 undergoes deuteration of Pt–CH₃ fragments with AcOD in THF-d₈ (see Section S3.6.4 of the ESI†), no loss of methane was observed.

Thus, according to the mechanism discussed in Scheme 6, the C–D reductive coupling step viaTS7 is the rate determining step (RDS) for the deuteration of 1 with CD₃OD. The calculated barrier of 20.8 kcal mol⁻¹ is in good agreement with the reaction activation energy of 22.7 ± 1.0 kcal mol⁻¹ observed experimentally. With these results in hand, we next calculated isotope effects, as shown in Scheme 7. Scheme 7a is an excerpt from Scheme 6 illustrating that in the reaction of 1 with CD₃OD, the C–D reductive coupling (TS7; ΔG^‡_{C–D RC} = 20.77 kcal mol⁻¹) is the rate determining step, since the barrier associated with C–H oxidative addition (TS8; ΔG^‡_{C–D OA} = 20.00 kcal mol⁻¹) is lower than that associated with C–D reductive coupling. On the other hand, in the reverse (i.e., protonation of 1-d₆ with CD₃OH) reaction, C–D oxidative addition and not C–H reductive coupling becomes the rate determining step. As shown in Scheme 7b, the calculated barrier for C–H reductive coupling (TS10; ΔG^‡_{C–H RC} = 19.66 kcal mol⁻¹) is lower than the barrier for C–D oxidative addition (TS11; ΔG^‡_{C–D OA} = 20.37 kcal mol⁻¹). Comparing these barriers, the k_H/k_D ratio was calculated to be 2.0, which is reasonably close to the experimentally observed value of 2.6 under initial rate conditions. It should be noted here that the observed k_H/k_D ratio here is not true primary kinetic isotope effect, since the latter would require comparison of the rates of reactions of 1-d₁ with CD₃OH (for k_H) and CD₃OD (for k_D).^46,47

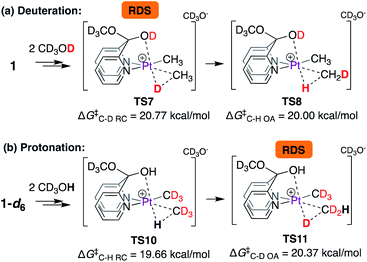Scheme 7 Calculation of isotope effects in (a) deuteration of 1 with CD₃OD and (b) protonation of 1-d₆ with CD₃OH.

Rate-limiting Pt^II-protonation

In contrast to complex 1 where non-rate-limiting Pt^II-protonation leads to the observation of rate-limiting C–D reductive elimination, the rate-limiting step for the Pt^II–CH₃ deuteration of 2 is the protonation of its Pt^II-centre. This is because the ligand cannot participate in metal–ligand cooperation and only assists in the protonation step by coordination to the emerging octahedral Pt^IV-centre.

As shown in Scheme 8, the C_s-symmetric complex 2 exists in solution as two isomers, featuring the OCH₃ fragment positioned either endo (2) or exo (2′) to the Pt^II-centre. Interconversion of these isomers is fast, evident from NOE interactions of the Pt^IICH₃ fragments with both the CH₃ (for 2′) and OCH₃ fragments (for 2) (see Fig. S7† in the ESI†). According to DFT calculations, the barrier for the interconversion of 2 and 2′ associated with TS12 is 11.9 kcal mol⁻¹, similar to that reported for other related square-planar complexes.^13,54,62,63 Since complexes 2 and 2′ are square-planar Pt^II complexes, the orientation of the OCH₃ fragment confers no energetic advantage, and thus, 2 and 2′ are virtually isoergonic. The endo OCH₃ fragment, however, can enable protonation of the Pt^II-centre of 2 by CD₃OD to form Int11.

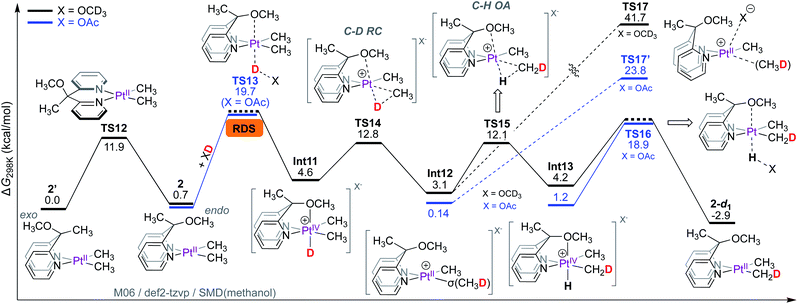Scheme 8 Gibbs free energy profile for reaction of complex 2 with CD₃OD: rate-limiting Pt^II-protonation.

Despite extensive attempts, transition states for the protonation of the Pt^II-centre of 2 with methanol (X = OCD₃) could not be located. As a workaround, the barrier for protonation of Pt^II was estimated with acetic acid-d₁ (X = OAc), furnishing a barrier of 19.7 kcal mol⁻¹ associated with TS13. In the transition state TS13, the endo OCH₃ fragment can be clearly seen to coordinate to the emerging Pt^IV-centre (see animation in the ESI†). The isomer 2′ with the OCH₃ fragment positioned exo to the Pt^II-centre cannot confer such advantage (as previously discussed in Scheme 5a).

The formation of Pt^IV-D intermediate Int11 (X = OCD₃) is endergonic by only 4.6 kcal mol; consequently, the transition state for reductive coupling (TS14) has an associated barrier of only 12.8 kcal mol⁻¹, leading to the Pt^II–σ(CH₃D) intermediate Int12. The Pt^II-bound σ-coordinated CH₃D can undergo tumbling (similar to that discussed in Scheme 6), followed by oxidative C–H cleavage viaTS15 with an associated barrier of 12.1 kcal mol⁻¹. Since the concomitant Pt^IV–H intermediate Int13 is an isotopomer of the Pt^IV–D intermediate Int11, it can undergo deprotonation of the Pt^IV–H fragment leading to the 2-d₁ as the monodeuterated isotopologue of complex 2. The transition state corresponding to deprotonation of the Pt^IV–H fragment TS16 was estimated with X = OAc as the base, furnishing a barrier of 18.9 kcal mol⁻¹.

Since methane loss is also not observed in the reaction of 2 with CD₃OD, we next calculated the barriers associated with transition states for methane loss with both X = OCD₃ (TS17, ΔG^‡ = 41.7 kcal mol⁻¹) and X = OAc⁶⁴ (TS17′, ΔG^‡ = 23.8 kcal mol⁻¹). Regardless of whether X = OAc or OCD₃, the transition states for methane loss have barriers that are significantly higher than those for both C–H(D) oxidative cleavage and Pt^II-protonation. This implies that Int12 will prefer to undergo transformation into either the Pt^IV–D intermediate Int11 or the Pt^IV–H intermediate Int13 over methane loss.

Thus, according to the mechanism presented in Scheme 8, the rate-limiting step for the reaction of 2 with CD₃OD is the protonation of the Pt^II-centre. The isotope effects were calculated as shown in Scheme 9. Scheme 9a is an excerpt from Scheme 8 illustrating the rate-limiting step: protonation of the Pt^II-centre of 2 with AcOD with an activation free energy of 19.73 kcal mol⁻¹ associated with TS13. In the reverse reaction, i.e., in the protonation of 2-d₆ with AcOH (Scheme 7b), the barrier associated with TS18 was found to be 18.63 kcal mol⁻¹. Comparing these values, the k_H/k_D ratio was calculated to be 6.1. This discord between the calculated and experimentally observed value was presumed to be due to the exclusion of tunnelling in our calculations, which can cause drastic enhancements in k_H/k_D ratios^9,65,66 when the rate-limiting step involves protonation at the Pt^II-centre.

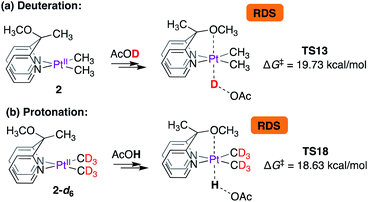Scheme 9 Calculated isotope effects associated with rate-limiting protonation of the Pt^II-centres of (a) complex 2 and (b) complex 2-d₆ with acetic acid.

Moreover, if the C–H(D) reductive coupling (or oxidative addition) steps were indeed the rate-limiting steps, then a k_H/k_D ratio similar to that observed for complex 1 might be expected, as shown in Scheme 10. Scheme 10a illustrates the barrier associated with the C–D reductive coupling (viaTS14, ΔG^‡ = 12.87 kcal mol⁻¹) and C–H oxidative addition (viaTS15, ΔG^‡ = 12.14 kcal mol⁻¹) steps. For the reverse reaction, i.e. the reaction of 2-d₆ with CD₃OH, as shown in Scheme 10b, the barrier associated with C–H reductive coupling (viaTS19, ΔG^‡ = 11.79 kcal mol⁻¹) is lower than that for the C–D oxidative addition step (viaTS20, ΔG^‡ = 12.55 kcal mol⁻¹). Accordingly, the calculated k_H/k_D ratio is 1.73, similar to that observed experimentally for complex 1.

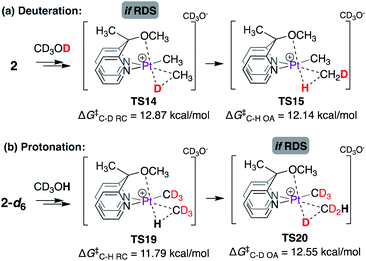Scheme 10 Calculated isotope effects associated with the C–H(D) reductive coupling (or oxidative addition) step in the reaction of (a) 2 with CD₃OD and (b) 2-d₆ with CD₃OH.

Conclusions

In conclusion, we report the first examples of neutral dimethylplatinum(II) complexes that undergo reversible deuteration of Pt^II–CH₃ fragments upon reaction with CD₃OD without methane loss. This happens due to a combination of (1) ligand participation allowing Pt^II-protonation and (2) formation of a strong base (methoxide) in situ allowing Pt^IV–H(D) deprotonation in preference to methane loss. In the case of di(2-pyridyl)ketone (DPK) as supporting ligand, this reactivity was utilized to synthesize [(CD₃)₂Pt^II(μ-SMe₂)]₂, which is otherwise conventionally synthesized by using expensive methyl-d₃ lithium or magnesium reagents. Mechanistic inferences drawn from kinetics, analysis of isotope effects, DFT calculations and reactivity of model complexes suggest that a unique metal (Pt)–ligand (DPK) cooperative behaviour is responsible for fast (non-rate-limiting) protonation of the supported Pt^II-centre. Although DPK-supported Pt^II complexes have been employed in C–H activation, they have not been investigated from the perspective of metal ligand cooperativity. While efforts to utilize this platform for C–H functionalization of benzene and methane are currently being undertaken, we believe that DPK can be an excellent ligand in other fields of organometallic chemistry as well, especially those operating in green solvents such as water or methanol where metal–ligand cooperativity proposed herein might be exploited towards novel reactivity.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The American Chemical Society Petroleum Research Fund (ACS PRF no. 53316-ND3 awarded to J. A. L.) and JSPS KAKENHI (Grant Numbers JP15K21707 and JP15H05796 awarded to K. N.) in “Precisely Designed Catalysts with Customized Scaffolding”, for partial financial support of this work. This research was enabled in part by the University of British Columbia, NSERC (Discovery and Research Tools and Instrumentation grants), and the Canada Foundation for Innovation. Computations were performed using Research Centre for Computational Science, Okazaki, Japan. The authors thank Assoc. Prof. Takanori Iwasaki (U-Tokyo) for X-ray analysis of complex 8 and Dr Eric G. Bowes for assistance with DFT calculations. Dr Dimitrios G. Liakos (Max Planck Institute for Chemical Energy Conversion, Mülheim), Prof. Josefredo R. Pliego Jr. (Federal University of São João del-Rei, Brazil), Prof. Julia Khusnutdinova (Okinawa Institute of Science and Technology, Japan), Dr Addison Desnoyer and Takuya Higashi are thanked for helpful discussions.

Notes and references

1. A. Shteinman, J. Organomet. Chem., 2015, 793, 34–40.
2. A. E. Shilov and G. B. Shulpin, Chem. Rev., 1997, 97, 2879–2932.
3. N. J. Gunsalus, A. Koppaka, S. H. Park, S. M. Bischof, B. G. Hashiguchi and R. A. Periana, Chem. Rev., 2017, 117, 8521–8573.
4. M. Lersch and M. Tilset, Chem. Rev., 2005, 105, 2471–2526.
5. J. A. Labinger and J. E. Bercaw, J. Organomet. Chem., 2015, 793, 47–53.
6. G. S. Hill, L. M. Rendina and R. J. Puddephatt, Organometallics, 1995, 14, 4966–4968.
7. F. Zhang, E. M. Prokopchuk, M. E. Broczkowski, M. C. Jennings and R. J. Puddephatt, Organometallics, 2006, 25, 1583–1591.
8. B. J. Wik, M. Lersch and M. Tilset, J. Am. Chem. Soc., 2002, 124, 12116–12117.
9. J. E. Bercaw, G. S. Chen, J. A. Labinger and B. L. Lin, Organometallics, 2010, 29, 4354–4359.
10. M. P. Jensen, D. D. Wick, S. Reinartz, P. S. White, J. L. Templeton and K. I. Goldberg, J. Am. Chem. Soc., 2003, 125, 8614–8624.
11. A. N. Vedernikov, J. C. Fettinger and F. Mohr, J. Am. Chem. Soc., 2004, 126, 11160–11161.
12. E. Khaskin, P. Y. Zavalij and A. N. Vedernikov, J. Am. Chem. Soc., 2006, 128, 13054–13055.
13. S. Pal, P. Y. Zavalij and A. N. Vedernikov, Organometallics, 2015, 34, 5183–5190.
14. S. Pal, P. Y. Zavalij and A. N. Vedernikov, Chem. Commun., 2014, 50, 5376–5378.
15. E. Khaskin, D. L. Lew, S. Pal and A. N. Vedernikov, Chem. Commun., 2009, 6270–6272.
16. S. A. O'Reilly, P. S. White and J. L. Templeton, J. Am. Chem. Soc., 1996, 118, 5684–5689.
17. A. N. Vedernikov and K. G. Caulton, Chem. Commun., 2003, 3, 358–359.
18. A. N. Vedernikov, M. Pink and K. G. Caulton, Inorg. Chem., 2004, 43, 3642–3646.
19. W. Oloo, P. Y. Zavalij, J. Zhang, E. Khaskin and A. N. Vedernikov, J. Am. Chem. Soc., 2010, 132, 14400–14402.
20. W. N. Oloo, P. Y. Zavalij and A. N. Vedernikov, Organometallics, 2013, 32, 5601–5614.
21. C. G. Efthymiou, C. P. Raptopoulou, A. Terzis, R. Boča, M. Korabic, J. Mrozinski, S. P. Perlepes and E. G. Bakalbassis, Eur. J. Inorg. Chem., 2006, 2236–2252.
22. G. S. Papaefstathiou and S. P. Perlepes, Comments Inorg. Chem., 2002, 23, 249–274.
23. M. Toyama, M. Nakahara and N. Nagao, Bull. Chem. Soc. Jpn., 2007, 80, 937–950.
24. G. Annibale, L. Canovese, L. Cattalini, G. Natile, M. Biagini-Cingi, A.-M. Manotti-Lanfredi and A. Tiripicchio, J. Chem. Soc., Dalton Trans., 1981, 2280–2287.
25. E. Abada, P. Y. Zavalij and A. N. Vedernikov, J. Am. Chem. Soc., 2017, 139, 643–646.
26. J. R. Khusnutdinova, L. L. Newman and A. N. Vedernikov, J. Organomet. Chem., 2011, 696, 3998–4006.
27. F. Zhang, M. E. Broczkowski, M. C. Jennings and R. J. Puddephatt, Can. J. Chem., 2005, 83, 595–605.
28. G. Bandoli, A. Dolmella, T. I. A. Gerber, J. G. H. du Preez and H. J. Kemp, Inorg. Chim. Acta, 1994, 217, 141–147.
29. K. N. Crowder, S. J. Garcia, R. L. Burr, J. M. North, M. H. Wilson, B. L. Conley, P. E. Fanwick, P. S. White, K. D. Sienerth and R. M. Granger, Inorg. Chem., 2004, 43, 72–78.
30. K. R. Pellarin, M. S. McCready and R. J. Puddephatt, Organometallics, 2012, 31, 6388–6394.
31. K. R. Pellarin, M. S. McCready and R. J. Puddephatt, Dalton Trans., 2013, 42, 10444–10453.
32. T. C. Stamatatos, C. G. Efthymiou, C. C. Stoumpos and S. P. Perlepes, Eur. J. Inorg. Chem., 2009, 3361–3391.
33. A. C. Komor and J. K. Barton, J. Am. Chem. Soc., 2014, 136, 14160–14172.
34. A. J. Hickman, J. M. Villalobos and M. S. Sanford, Organometallics, 2009, 28, 5316–5322.
35. B. A. McKeown, H. E. Gonzalez, T. Michaelos, T. B. Gunnoe, T. R. Cundari, R. H. Crabtree and M. Sabat, Organometallics, 2013, 32, 3903–3913.
36. K. J. Bonnington, F. Zhang, M. M. A. R. Moustafa, B. F. T. Cooper, M. C. Jennings and R. J. Puddephatt, Organometallics, 2012, 31, 306–317.
37. J. R. Khusnutdinova and D. Milstein, Angew. Chem., Int. Ed., 2015, 54, 12236–12273.
38. T. Higashi, H. Ando, S. Kusumoto and K. Nozaki, J. Am. Chem. Soc., 2019, 141, 2247–2250.
39. H. C. Lo, A. Haskel, M. Kapon and E. Keinan, J. Am. Chem. Soc., 2002, 124, 3226–3228.
40. M. A. Iron, H. C. Lo, J. M. L. Martin and E. Keinan, J. Am. Chem. Soc., 2002, 124, 7041–7054.
41. W. H. Bernskoetter, C. K. Schauer, K. I. Goldberg and M. Brookhart, Science, 2009, 326, 553–556.
42. S. D. Pike, A. L. Thompson, A. G. Algarra, D. C. Apperley, S. A. Macgregor and A. S. Weller, Science, 2012, 337, 1648–1651.
43. J. J. R. Fraústo Da Silva, J. Chem. Educ., 1983, 60, 390–392.
44. E. G. Bowes, S. Pal and J. A. Love, J. Am. Chem. Soc., 2015, 137, 16004–16007.
45. The reaction of 1-d₆ with CD₃OH was found to slow down over the course of ∼15 minutes. For a qualitative discussion, see Section S3.5 of the ESI.†.
46. W. D. Jones, Acc. Chem. Res., 2003, 36, 140–146.
47. G. Parkin, Acc. Chem. Res., 2009, 42, 315–325.
48. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
49. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
50. Gaussian 16, Revision C.01. Gaussian, Inc., Wallingford CT, 2016. For full citation of the Gaussian 16 program package, see the Computational Section of the ESI†.
51. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
52. N. F. Carvalho and J. R. Pliego, Phys. Chem. Chem. Phys., 2015, 17, 26745–26755.
53. Based on integrations of Pt–CH₃, Pt–CH₂D and Pt–CHD₂ resonances (see section S3.1 of the ESI†) in the ¹H NMR spectra, the equilibrium constants for Pt(CH₃) + CD₃OD → Pt(CH₂D) + CD₃OH and Pt(CH₂D) + CD₃OD → Pt(CHD₂) + CD₃OH reactions were calculated to be 0.64 and 0.72, corresponding to free energy changes of 0.26 and 0.20 kcal mol⁻¹, respectively..
54. S. Pal, B. O. Patrick and J. A. Love, Faraday Discuss., 2019, 220, 317–327.
55. S. Cukierman, Biochim. Biophys. Acta, Bioenerg., 2006, 1757, 876–885.
56. E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2013, 34, 1429–1437.
57. The potential energy surface obtained by scanning the Pt–C distance in the Pt–(CH₃D) fragment of Int7 revealed no saddle-point (see Fig. S42† in the ESI†) but progressive increase in energy exceeding the barrier associated with TS8, suggesting that even if a dissociative mechanism is valid, Int7 will undergo preferential oxidative C–H(D) cleavage..
58. M. R. Plutino, L. M. Scolaro, R. Romeo and A. Grassi, Inorg. Chem., 2000, 39, 2712–2720.
59. J. Cooper and T. Ziegler, Inorg. Chem., 2002, 41, 6614–6622.
60. H. Zhu and T. Ziegler, Organometallics, 2009, 28, 2773–2777.
61. Compared to methoxide, acetate is less susceptible to errors associated implicit solvation. For example, see: F. Ding, J. M. Smith and H. Wang, J. Org. Chem., 2009, 74, 2679–2691.
62. M. K. Pennington-Boggio, B. L. Conley, M. G. Richmond and T. J. Williams, Polyhedron, 2014, 84, 24–31.
63. S. Pal, M. W. Drover, B. O. Patrick and J. A. Love, Eur. J. Inorg. Chem., 2016, 2403–2408.
64. Since TS17 is likely to suffer from errors associated with inadequate solvation of the incoming methoxide, we calculated TS17′ with OAc as the incoming nucelophile, which is less susceptible to errors associated with implicit solvation (see ref. 61)..
65. J. E. Bercaw, G. S. Chen, J. A. Labinger and B. L. Lin, J. Am. Chem. Soc., 2008, 130, 17654–17655.
66. A. Datta, D. A. Hrovat and W. T. Borden, J. Am. Chem. Soc., 2008, 130, 2726–2727.

---

Footnotes

† Electronic supplementary information (ESI) available: Details of syntheses, characterization of ligands and complexes, kinetic analyses and DFT calculations (PDF), crystallographic data CCDC 2027312 and a ZIP-archive containing molecular structures (MOL2) and animations (GIF) for transition states. CCDC 2027312. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc06518h

‡ Present Address: Department of Chemistry, The University of Calgary, 2500 University Dr. NW, Calgary, Alberta T2N 1N4 Canada.

---