How metallylenes activate small molecules

Abstract

We have studied the activation of dihydrogen by metallylenes using relativistic density functional theory (DFT). Our detailed activation strain and Kohn–Sham molecular orbital analyses have quantified the physical factors behind the decreased reactivity of the metallylene on going down Group 14, from carbenes to stannylenes. Along this series, the reactivity decreases due to a worsening of the back-donation interaction between the filled lone-pair orbital of the metallylene and the σ*-orbital of H₂, which, therefore, reduces the metallylene–substrate interaction and increases the reaction barrier. As the metallylene ligand is varied from nitrogen to phosphorus to arsenic a significant rate enhancement is observed for the activation of H₂ due to (i) a reduced steric (Pauli) repulsion between the metallylene and the substrate; and (ii) less activation strain, as the metallylene becomes increasingly more predistorted. Using a rationally designed metallylene with an optimal Group 14 atom and ligand combination, we show that a number of small molecules (i.e. HCN, CO₂, H₂, NH₃) may also be readily activated. For the first time, we show the ability of our H₂ activated designer metallylenes to hydrogenate unsaturated hydrocarbons. The results presented herein will serve as a guide for the rational design of metallylenes toward the activation of small molecules and subsequent reactions.

---

Introduction

Originating with the seminal work of Philip P. Power in 2010,¹ the activation of small molecules by main-group elements, a field traditionally dominated by transition metal chemistry, has fascinated chemists. A class of main-group species that has received recent attention are carbenes and their heavier Group 14 analogs (metallylenes).² Owing to their large singlet–triplet energy gap, metallylenes have an sp²-hybridized lone pair orbital in the plane of the molecule and a vacant p-type orbital perpendicular to the molecular plane, which resemble the filled and empty nd and ns orbitals found in transition metal catalysts.¹ As a result, these molecular species are able to participate in similar chemistry as their transition metal analogs.³

Recently, Group 14 metallylenes have been shown to activate a number of small molecules, such as H₂, by oxidative insertion into the respective bond of the molecule.^4–7 The reactivity of these metallylenes is commonly ascribed to the HOMO–LUMO gap of this species. It has been postulated that metallylenes possessing a small HOMO–LUMO gap are more active towards bond activation since a correlation has been found between the magnitude of the metallylene's band gap and the height of the reaction barrier corresponding to the activation of a chemical bond.^4,6b,6c The energies of the HOMO and LUMO of these metallylenes, and hence their activity in small molecule activation, can be tuned by (i) narrowing the angle between the ligands around the central Group 14 metallylene atom; and (ii) changing the nature of the ligands.^2a On the contrary, Ess et al. showed, by applying an energy decomposition analyses based on absolutely localized molecular orbitals (ALMO-EDA) on transition state structures, that the reaction barrier height for the activation of H₂ by metallylenes, as well as the differences in reaction barriers between carbenes, silylenes, and germylenes, arise from the activation strain accompanied by the stretch of the H–H bond, which, in turn, is controlled by intermolecular electron repulsion.⁸ Furthermore, Ess revealed that carbenes act, in analogy with transition metal catalysts, as amphiphiles towards H₂ activation, where both the back-donation HOMO_metallylene–LUMO_H2 and donation LUMO_metallylene–HOMO_H2 interaction are in play. Silylenes and germylenes, on the other hand, react as nucleophiles and hence predominantly feature a back-donation HOMO_metallylene–LUMO_H2 interaction.

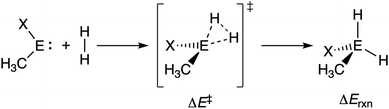
Herein, we have performed a systematic computational study on the activation of dihydrogen by various metallylenes using relativistic density functional theory (DFT) at ZORA-BP86/TZ2P level,^9–11 as implemented in the Amsterdam Density Functional (ADF) program.¹² To this end, we have selected the model singlet metallylene H₃C–E–X (CEX), where E = C, Si, Ge, Sn; and X = NMe₂, PMe₂, AsMe₂ (see Scheme 1), as it resembles the metalyllenes previously used in both experiment and theory.^4a,6b,8 The effect of varying the Group 14 central atom E, as well as changing the Group 15 ligand X, on the activation of H₂ has been analyzed using the activation strain model (ASM)¹³ of reactivity in combination with quantitative Kohn–Sham molecular orbital (KS-MO) theory and a matching canonical energy decomposition analysis (EDA) scheme.¹⁴ In addition, we show that the rationale found behind the trends in reactivity of our model systems can be extrapolated to explain the reactivity trends in experimentally used metallylenes. Furthermore, we highlight the applicability of the H₂ activated metallylene species to efficiently hydrogenate unsaturated bonds.

Scheme 1 The activation of H₂ by a singlet metallylene (CEX; where E = C, Si, Ge, Sn, and X = NMe₂, PMe₂, AsMe₂).

Results and discussion

Reaction profiles

Table 1 summarizes the reaction barriers, ΔE^‡, and reaction energies, ΔE_rxn, of the activation of H₂ by various singlet metallylenes with varying Group 15 ligands, denoted as CEX, where E = C, Si, Ge, Sn, and X = NMe₂, PMe₂, AsMe₂ (see Fig. S1† in the ESI for transition state structures). Two distinct trends can be observed. In the first place, varying the central atom E of CEX by going down Group 14, i.e., from C to Sn, while keeping the ligand X consistent increases the reaction barrier and makes the reaction less exergonic. An exception is the series with the AsMe₂ ligand. In this series, the reaction barrier slightly lowers from carbon to silicon and increases again from silicon to germanium to tin. The reaction energy along this series, however, becomes steadily less exergonic. Secondly, variation of the Group 15 ligand X from NMe₂ to PMe₂ to AsMe₂ while keeping the central atom E constant stabilizes, for all studied metallylenes, the reaction barrier significantly and makes the reaction more exergonic. The computed trends in reactivity at ZORA-BP86/TZ2P agree well with those calculated in apolar and polar solvent (COSMO(toluene) and COSMO(water)),¹⁵ the meta-hybrid and dispersion-corrected exchange-correlation functionals ZORA-M06-2X¹⁶/TZ2P//ZORA-BP86/TZ2P, ZORA-BP86-D3(BJ)¹⁷/TZ2P, and ZORA-M06-2X/TZ2P//ZORA-BP86-D3(BJ)/TZ2P, and the more accurate DLPNO-CCSD(T)/def2-QZVPP//ZORA-BP86/TZ2P (Tables S1–S6†). Statistical analyses revealed that ZORA-BP86/TZ2P performs equally as well as ZORA-M06-2X/TZ2P//ZORA-BP86/TZ2P and slightly better than ZORA-BP86-D3(BJ)/TZ2P and ZORA-M06-2X/TZ2P//ZORA-BP86-D3(BJ)/TZ2P relative to the DLPNO-CCSD(T)¹⁸/def2-QZVPP¹⁹//ZORA-BP86/TZ2P data (see Table S7†).

Table 1 Electronic reaction barriers (ΔE^‡) and reaction energies (ΔE_rxn) (in kcal mol⁻¹) of the activation of H₂ by H₃C–E–X (CEX) metallylenes^a

E	X	ΔE^‡^b	ΔErxn^b
a Computed at ZORA-BP86/TZ2P. b Gibbs free energies are given in parenthesis.
C	NMe2	12.2 (21.3)	−58.3 (−41.8)
C	PMe2	8.3 (17.6)	−80.1 (−63.2)
C	AsMe2	5.5 (14.7)	−95.6 (−78.7)
Si	NMe2	23.4 (31.6)	−35.8 (−25.1)
Si	PMe2	8.5 (18.6)	−44.5 (−32.4)
Si	AsMe2	2.4 (12.5)	−50.0 (−37.8)
Ge	NMe2	38.0 (45.8)	−12.9 (−2.6)
Ge	PMe2	18.4 (28.3)	−26.2 (−14.3)
Ge	AsMe2	13.1 (22.5)	−30.7 (−19.1)
Sn	NMe2	48.6 (55.8)	1.5 (10.1)
Sn	PMe2	29.0 (38.0)	−12.1 (1.7)
Sn	AsMe2	25.0 (33.5)	−15.2 (−5.4)

---

Variation along group 14 metallylene central atom

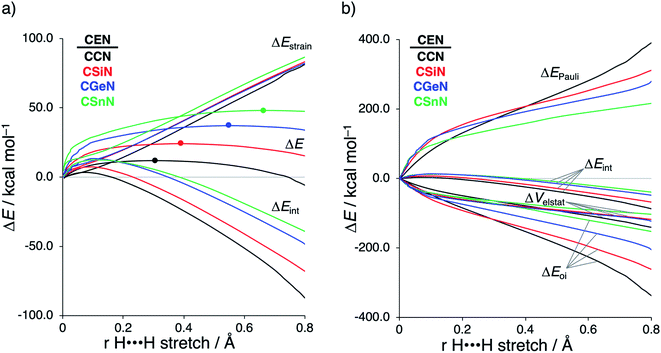
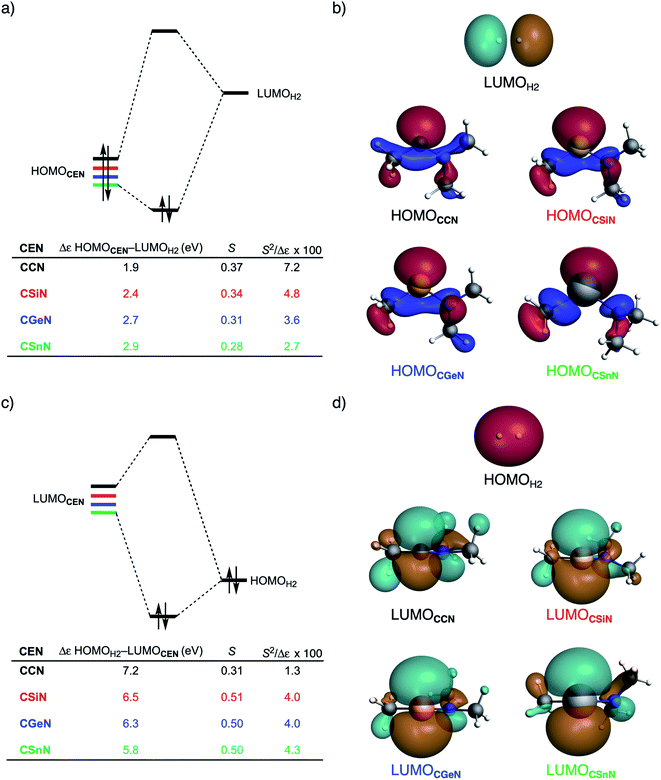
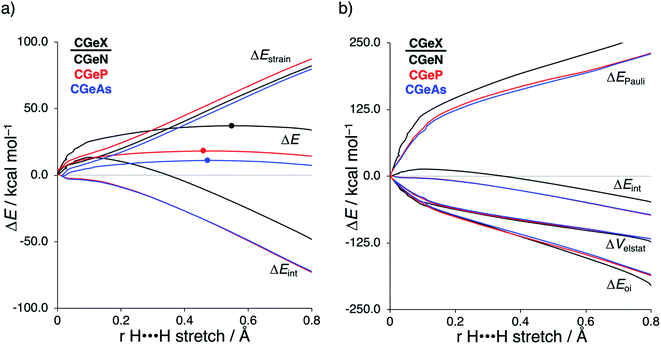
Next, we turn to the activation strain model (ASM)¹³ of reactivity to gain quantitative insight into the physical factors leading to the changes in reactivity upon varying the metallylene central atom and the ligand. This model involves decomposing the electronic energy (ΔE) into two distinct energy terms, namely, the strain energy (ΔE_strain) that results from the deformation of the individual reactants and the interaction energy (ΔE_int) between the deformed reactants along the reaction coordinate, defined, in this case, by the stretch of the activated H–H bond. This critical reaction coordinate undergoes a well-defined change throughout the reaction and has successfully been used in the past for the analysis of similar reactions.²⁰ First, we focus on the effect of changing the central Group 14 atom E on the activation of H₂. In Fig. 1, we show the activation strain diagram of the CEN series for which the effects are the largest. Note that the activation strain diagrams of all other CEX series (CEP and CEAs, respectively) possess the same, only less pronounced characteristics (Fig. S2 and S3†). The increase of the reaction barrier on going from CCN to CSnN is mainly dictated by a consistently less stabilizing interaction energy. In other words, the reaction with CCN goes, along the entire reaction coordinate, with the most stabilizing interaction energy and hence the lowest reaction barrier.²¹ The reaction with CSnN, on the contrary, experiences the least stabilizing interaction energy and, therefore, the highest reaction barrier. On top of that, the former reaction also encounters the least destabilizing strain energy, which again lowers the reaction barrier. The important role of the interaction energy on the observed reactivity trend prompted the analysis of the different contributors to the interaction energy using the canonical energy decomposition analysis (EDA).¹⁴ Our canonical EDA decomposed the ΔE_int between the reactants into three physically meaningful energy terms: classical electrostatic interaction (ΔV_elstat), (steric) Pauli repulsion (ΔE_Pauli) which, in general, arises from the two-center four-electron repulsion between the closed-shell orbitals of both reactants, and stabilizing orbital interactions (ΔE_oi) that account, among others, for HOMO–LUMO interactions. By performing the EDA, we establish that the trend in ΔE_int is predominantly determined by the orbital interactions, ΔE_oi, which are, in analogy with the trend in ΔE_int, the most stabilizing for CCN and the least for CSnN (see Table S12† for analysis at consistent geometry). The Pauli repulsion, ΔE_Pauli, and electrostatic interaction, ΔV_elstat, on the other hand, have a small or even opposite effect (ΔE_Pauli is more destabilizing for CCN) on the interaction energy.²¹

Fig. 1 (a) Activation strain analysis and (b) energy decomposition analysis of the H₂ bond activation by metallylenes CEN with variating Group 14 central atom (E = C, Si, Ge, Sn), where the transition states are indicated with a dot and the energies are projected onto the H⋯H bond stretch of H₂, computed at ZORA-BP86/TZ2P.

To further probe the key orbital interactions involved in the H₂ activation by metallylenes, we analyze the orbitals participating in these interactions using a Kohn–Sham molecular orbital analysis on consistent geometries with a H⋯H bond stretch of 0.47 Å at ZORA-BP86/TZ2P.^14b,22,23 The consistent geometry of a H⋯H bond stretch of 0.47 Å was judiciously selected because it provided transition state-like geometries with energies that differ no more than 2 kcal mol⁻¹ compared to the respective transition state. Analysis at this point on the reaction coordinate (near all transition states), rather than the transition state alone, ensured that the results are not skewed by the position of the transition state (i.e., early- or late-transition state).^13c In contrast with the work of Ess et al.,⁸ we find that two major orbital interaction mechanisms are playing a role in all bond activation reactions, namely, the back-donation interaction, where the lone pair orbital of the metallylene (HOMO_CEN) donates electrons into the σ*-orbital of H₂ (LUMO_H2) (Fig. 2a and b), and the donation interaction, where the empty p-type orbital on the central atom E of the metallylene (LUMO_CEN) accepts electrons from the σ-orbital of H₂ (HOMO_H2) (Fig. 2c and d).

Fig. 2 (a) Molecular orbital diagram with the key orbital energy gap and overlap of the HOMO_CEN–LUMO_H2 back-donation interaction, (b) key orbitals contributing to the back-donation interaction (isovalue = 0.03 Bohr^−3/2), (c) Molecular orbital diagram with the key orbital energy gap and overlap of the HOMO_H2–LUMO_CEN donation interaction, and (d) key orbitals contributing to the donation interaction (isovalue = 0.03 Bohr^−3/2) of the H₂ bond activation by CEN metallylenes with variating Group 14 central atom (E = C, Si, Ge, Sn) computed using ZORA-BP86/TZ2P on consistent geometries with a H⋯H bond stretch of 0.47 Å.

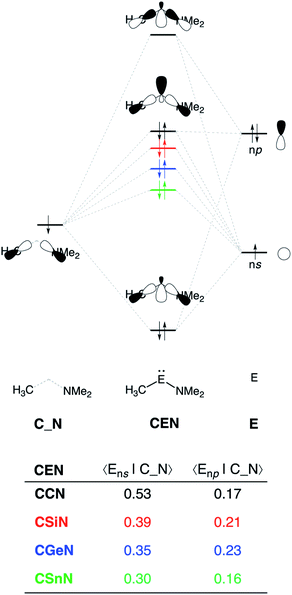
The reduction in stabilizing ΔE_oi (and thus the increasing reaction barrier), when going from CCN to CSnN, can be ascribed to the weakening of the back-donation interaction. Along this series, the HOMO_CEN goes down in energy and becomes more diffuse, i.e., increased spatial extent of the lone pair orbital on E, which leads to a less favorable (larger) HOMO–LUMO gap and a poorer orbital overlap. For the back-donation interaction (Fig. 2a and b), CCN, the most reactive metallylene, has the smallest HOMO_CEN–LUMO_H2 orbital energy gap (1.9 eV) and the largest orbital overlap (S = 0.37). As we go down Group 14, the HOMO_CEN–LUMO_H2 orbital energy gap increases from 1.9 eV for CCN to 2.9 eV for CSnN, due to a more stable CEN HOMO. In order to understand why the HOMO_CEN lowers in energy (i.e., stabilizes) when descending in Group 14, we perform an additional Kohn–Sham molecular orbital analysis where the construction of the HOMO_CEN from the interaction between the ns atomic orbital (AO) of E and the in-phase C_N ligand orbitals is examined (see Fig. 3). Note that the in-phase C_N orbital is the σ-orbital in the CEN plane responsible for the formation of the C–E and E–N bonds. We found that the stabilization of the HOMO_CEN, going down in Group 14, is caused by the reduced antibonding character originating from the interaction between the ns AO of E and the in-phase C_N ligand orbitals. The CEN HOMO arises from both the antibonding interaction between the ns AO of E and the C_N ligand orbital, which destabilizes the CEN HOMO, and the bonding interaction between the np AO of E and the C_N ligand orbital, which stabilizes the CEN HOMO. The antibonding E_ns–C_N interaction becomes, going from CCN to CSnN, consistently weaker, as the overlap reduces from 〈C_2s|C_N〉 = 0.53 to 〈Sn_5s|C_N〉 = 0.30. As a result, the CEN HOMO experiences less antibonding character, and hence lowers in energy (stabilizes). Additionally, along this series, the bonding E_np–C_N interaction becomes more pronounced, which also contributes to the stabilization of the CEN HOMO. Note that the 〈Sn_5p|C_N〉 orbital overlap is slightly less compared to the other Group 14 analogs, due to the diffuseness of the Sn 5p orbital that extends past the nodal surface of the C_N ligand orbital and, therefore, reduces the orbital overlap. Besides an increased HOMO_CEN–LUMO_H2 energy gap, there is also a continuous decrease in orbital overlap upon going from CCN to CSnN. Along this series, the increasing diffuseness of the HOMO_CEN, as the AOs of E becomes larger, gives rise to a spatial mismatch with the LUMO_H2, resulting in a less favorable HOMO_CEN–LUMO_H2 orbital overlap.

Fig. 3 Schematic representation of the construction of the CEN HOMO (E = C, Si, Ge, Sn) and orbital overlap between the atomic orbitals of E (E_ns and E_np) and the in-phase ligand orbital (C_N), computed using ZORA-BP86/TZ2P level at consistent geometries with a H⋯H bond stretch of 0.47 Å.

The stronger donation interaction between the LUMO_CEN–HOMO_H2 of CGeN and CSnN, on the other hand, will partly, but not completely, compensate their weaker back-donation interaction compared to CCN and CSiN (Fig. 2c and d). Despite the fact that almost all orbital overlaps between LUMO_CEN–HOMO_H2 are larger compared to HOMO_CEN–LUMO_H2 (S = 0.31 for CCN, S = 0.51 for CSiN, S = 0.50 for CGeN, and S = 0.50 for CSnN), the donation orbital interaction mechanism is not able to overrule the trend dictated by the back-donation interaction, because the LUMO_CEN–HOMO_H2 energy gaps, ranging from 7.1 eV for CCN to 5.8 eV for CSnN, are significantly larger than the HOMO_CEN–LUMO_H2 analogs. Thus, it can be concluded that the strong back-donation orbital interaction of CCN induces a significant stabilizing orbital interaction energy, which manifests in a more favorable interaction energy and hence a lower reaction barrier. The back-donation orbital mechanism becomes, going down Group 14, less prominent, resulting in reduced orbital interactions and, as a consequence, a higher reaction barrier.

Variation along group 15 ligand

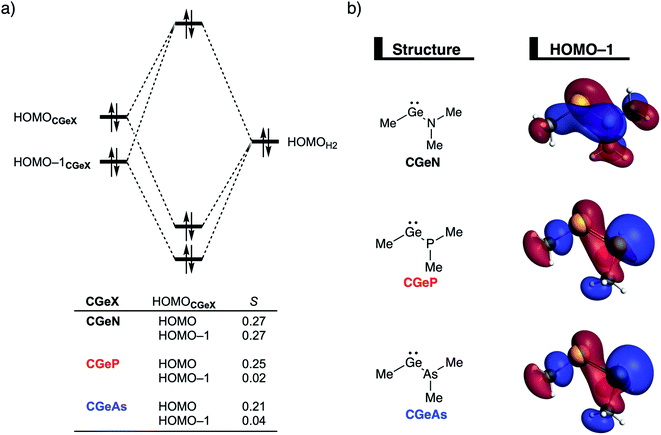
After establishing the trends in reactivity upon changing the central Group 14 metallylene atom, we analyze the role of the Group 15 ligand on the reactivity of the metallylene towards the activation of H₂. Here, we solely discuss the reactivity trend of CGeX, which resembles metallylenes used experimentally.^6b The activation strain diagram of all other metallylenes (CCX, CSiX, and CSnX) show similar characteristics and are shown in Fig. S5–S7 in the ESI.† The activation strain analysis (ASA) provided in Fig. 4a clearly shows that the reaction barriers lower when varying the Group 15 ligand from NMe₂ to PMe₂ to AsMe₂, which is, as we will discuss later, originating from both a reduced Pauli-repulsive orbital overlap between the reactants and less activation strain in the germylene. The high CGeN reaction barrier is solely caused by a less stabilizing interaction energy that is even repulsive at an early stage of the reaction. By applying the energy decomposition analysis, we established that the more destabilizing Pauli repulsion between the filled orbitals of CGeN and H₂ is the causal actor behind the less stabilizing interaction energy and hence the higher reaction barrier (Fig. 4b). The electrostatic and orbital interactions are, on the other side, equal or even more stabilizing compared to CGeP and CGeAs, and, therefore, not decisive for the observed trend in reactivity.²¹ The difference between CGeP and CGeAs can be ascribed to their difference in strain energy, and this appears to be due to the favorable pre-distortion of the ligand in the latter. The PMe₂ ligand of CGeP is, in the equilibrium geometry of the germylene, trigonal planar, due to a strong hyperconjugation interaction between the empty 4p atomic orbital of germanium and the filled 3p atomic orbital of phosphorus (〈4p_Ge|3p_P〉 = 0.27) (Fig. S9†). Along the course of the reaction, however, the phosphorus ligand must pyrimidalize which leads to the loss of the stabilizing hyperconjugation interaction. On the contrary, the arsenic ligand of CGeAs is, in the equilibrium geometry of the metallylene, already pyramidal (i.e., favorably predistorted) and, therefore, benefits from a less destabilizing activation strain.

Fig. 4 (a) Activation strain analysis and (b) energy decomposition analysis of the H₂ bond activation by germylenes CGeX with variating Group 15 ligands (X = NMe₂, PMe₂, AsMe₂), where the transition states are indicated with a dot and the energies are projected onto the H⋯H bond stretch of H₂, computed at ZORA-BP86/TZ2P.

To understand the origin of the more destabilizing Pauli repulsion for the H₂ activation using CGeN compared to CGeP and CGeAs, which causes the intrinsic differences in their reactivity, we perform a Kohn–Sham molecular orbital (KS-MO) analysis.^14b,22 The occupied molecular orbitals of CGeX and H₂, that determine the underlying differences in Pauli repulsion, were quantified on consistent geometries with a H⋯H bond stretch of 0.47 Å (Fig. 5a). The most important occupied MOs of CGeX involved in the two-center four-electron interaction are the HOMO and HOMO−1, which are the lone pair orbital of the germylene and the hyperconjugation between the empty 4p-type orbital on the central Ge atom and the filled np lone pair orbital of Group 15 ligand. The difference in Pauli repulsion between the reactions with the three different CGeX germylenes is predominantly caused by the HOMO−1_CGeX–HOMO_H2 interaction, going from S = 0.27 for CGeN to S = 0.02 and 0.04 for CGeP and CGeAs, respectively. Interestingly, the interaction between the lone pair orbital of Ge and the filled σ-orbital of H₂ (HOMO_CGeX–HOMO_H2) is the main responsible factor for the magnitude of the Pauli repulsion but only has a small contribution to the underlying trend in Pauli repulsion between the different germylenes. The large difference in repulsive occupied–occupied orbital overlap can be explained by looking at the pyramidalization of the Group 15 ligand. In their equilibrium geometry, the NMe₂ and PMe₂ ligands of CGeN and CGeP, respectively, are trigonal planar due to hyperconjugation between the empty 4p-type orbital of Ge and the filled np orbital of the Group 15 ligand (vide supra; Fig. S7†). To reduce steric repulsion with the incoming H₂, the Group 15 ligand of CGeP and CGeAs deforms from trigonal planar to trigonal pyramidal which goes with the loss of hyperconjugation (CGeP: 〈4p_Ge|3p_P〉 = 0.02, CGeAs: 〈4p_Ge|5p_As〉 = 0.01; in the consistent geometries used in Fig. 4). This effectively polarizes the HOMO−1_CGeX away from the central germanium atom and results in a well-defined np lone pair orbital lobe on the Group 15 ligand, for CGeP and CGeAs, respectively (see blue lobe on the right side of Fig. 5b), which in turn leads to less orbital amplitude pointing towards the incoming H₂. The Group 15 ligand of the CGeN gemylene, on the other hand, deforms only little over the course of the reaction and retains the hyperconjugation interaction (CGeN: 〈4p_Ge|2p_N〉 = 0.15), which leads to a large HOMO−1_CGeN orbital amplitude on Ge and, consequently, a larger orbital overlap with H₂ (Fig. 5b). In summary, the loss of hyperconjugation interaction upon pyramidalization of the Group 15 ligand results in less 〈HOMO−1_CGeX|HOMO_H2〉 overlap and ultimately, to a less destabilizing Pauli repulsion and a lower reaction barrier, for CGeP and CGeAs compared to CGeN.

Fig. 5 (a) Molecular orbital diagram of the most important occupied–occupied orbital overlap of the H₂ bond activation by germylenes with various Group 15 ligands (CGeX) and (b) key metallylene occupied orbitals (isovalue = 0.03 Bohr^−3/2) computed at ZORA-BP86/TZ2P on consistent geometries with a H⋯H bond stretch of 0.47 Å.

Validating the model metallylene species

To validate our model metallylenes and check whether our computed reactivity trends are a good representation of the experimentally used metallylenes, we take a retrosynthesis approach and build in the molecular complexity of the metallylene step-by-step. Two experimentally viable germylene species (CGeN–4 and CGeP–4) were selected to evaluate the trend in reactivity upon changing the Group 15 ligand.^6b These two germylene species are chosen for their resemblance to the model germylene, having a germanium central metallylene atom, one carbon and one nitrogen or phosphorus bearing ligand. In Fig. 6, we show the transition state structures of the H₂ activation using the model germylene of the first part of this study (CGeX–TS1), two intermediate germylenes (CGeX–TS3 and CGeX–TS2), and the complete germylene species (CGeX–TS4). Because the position of the transition state, along the reaction coordinate, remains relatively constant upon increasing the molecular complexity of the germylene's ligands, we perform an ASA on the transition states. The reaction barrier for both germylenes, CGeN and CGeP, slightly increases when going from the model germylene CGeX–1 to the realistic germylene CGeX–4. This effect can predominantly be ascribed to a less stabilizing interaction energy, which, in turn, is caused by a more destabilizing Pauli repulsion between the increasingly bulkier ligands and H₂ (Table S13†). The electrostatic and orbital interaction, on the other hand, become more stabilizing when the molecular complexity of the metallylene increases. In addition, for a few instances, an enhancement of destabilizing activation strain also contributes to the increase in reaction barrier, due to the increased rigidity of the ligands.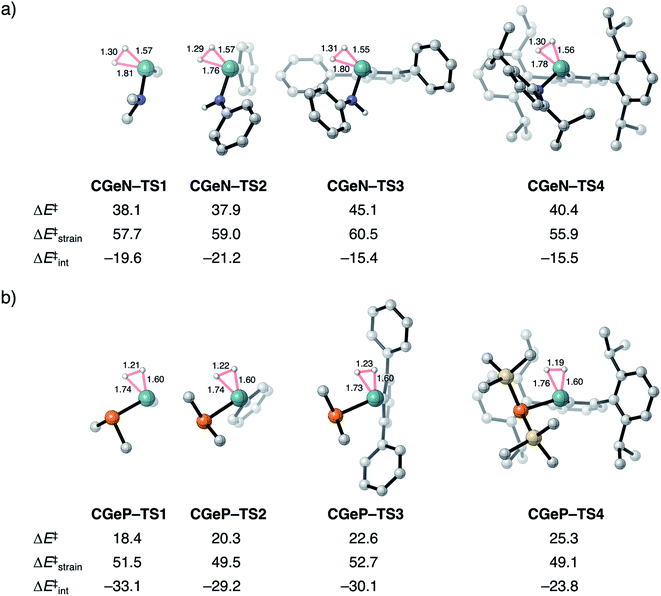

Fig. 6 Transition structures with key geometrical information (in Å), computed electronic reaction barriers (ΔE^‡), strain (ΔE^‡_strain), and interaction energies (ΔE^‡_int) (in kcal mol⁻¹) for the H₂ activation by the synthesizable germylene species^6b (a) CGeN–4 and (b) CGeP–4 and the, in three steps, simplified analogs, computed at ZORA-BP86/TZ2P. Hydrogen atoms are not shown.

The analysis performed here also shows that the reactivity trends observed for our model metallylenes agree with, and therefore are a faithful representation of. the realistic, synthesizable metallylenes. All trends in reactivity, going from the model germylene CGeX–1 to the realistic germylene CGeX–4, are identical, namely, the reaction barrier of CGeN is always higher in energy than the CGeP analog. In line with our detailed analysis displayed in Fig. 4, we find that the more destabilizing Pauli repulsion and, therefore, less favorable interaction energy is the main actor behind the higher reaction barrier of CGeN compared to CGeP (Table S13†).

Expanding the substrate scope

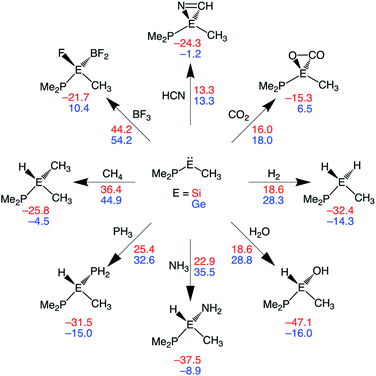
In this section, we assess the ability of our rationally designed metallylenes to activate other small molecules, such as HCN, CO₂, H₂O, NH₃, PH₃, CH₄, and BF₃. CSiP and CGeP are selected, where the former (CSiP) exhibits a low reaction barrier for activation of H₂ and a not too exergonic reaction energy, while the latter (CGeP) metallylene, as we prior showed, closely resembles an experimentally feasible metallylene.^6b In Fig. 7, we show the Gibbs free reaction barriers and reaction energies for the activation of the aforementioned small molecules. Note that, starting with HCN activation, the processes systematically increase in reaction barrier when following the processes in the wind-rose scheme in a clockwise direction. Interestingly, we find that both HCN and CO₂ have a lower reaction barrier than our model substrate H₂. This likely originates from the fact that for the former two substrates only a π-bond is broken, but for the latter, a strong σ-bond is dissociated, which goes with a high activation strain. The activation of H₂O, NH₃, and PH₃ go with reaction barriers that are in the same range as the one for H₂, making them, as shown in the literature,^5a,6a–c,7b possible candidates to be activated by metallylenes. In contrast, the reaction barriers for the activation of CH₄ and BF₃ are relatively high and, therefore, require further optimization to become suitable targets for activation by metallylenes. Furthermore, in analogy with the activation of H₂, the activation using CSiP goes with a lower reaction barrier than and more stable product compared to CGeP. One exception is the activation of HCN, for which the reaction barriers of CSiP and CGeP are identical. These results highlight that the herein used tailor-made metallylenes can be extrapolated to the activation of a wide range of different small molecules.

Fig. 7 Gibbs free energy reaction barriers (ΔG^‡; next to arrow) and reaction energies (ΔG_rxn; below product) (in kcal mol⁻¹) of the activation of various small molecules by CEP metallylenes, where E = Si, Ge (red, blue values). All data computed at ZORA-BP86/TZ2P.

Hydrogenation of unsaturated bonds

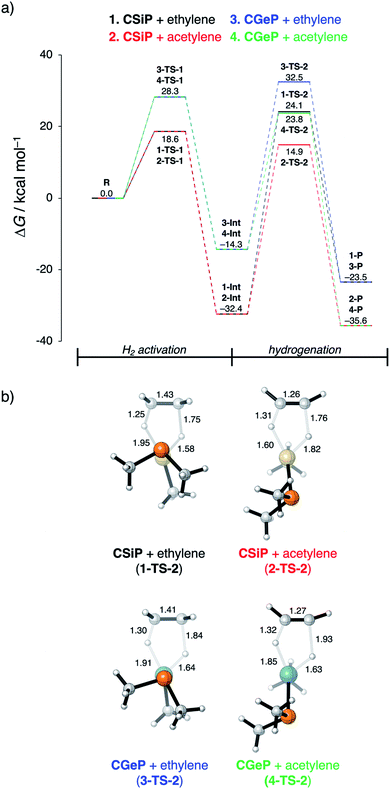
In the last section, we study the viability of the H₂ activated metallylene species to react in subsequent transformations. As discussed above, several studies solely focus on the activation of H₂ and other small molecules by metallylenes and do not consider any follow up reactions. Recently, Bertrand et al.^4d showed that activated carbene species can hydrogenate terminal alkynes to alkenes. However, up to our knowledge, very little is actually known concerning the hydrogenation of unsaturated bonds by H₂ activated metallylenes.

In Fig. 8, we show the reaction profiles of the activation of H₂ by CSiP or CGeP and the subsequent hydrogenation of ethylene or acetylene to ethane and ethylene, respectively. As previously discussed in detail, the activation of H₂ by CSiP goes with a significantly lower reaction barrier (TS-1) than the activation by CGeP (ΔΔG^‡ = 9.7 kcal mol⁻¹). Furthermore, the former reaction is also more exergonic compared to the latter, resulting in a more stable intermediate (ΔΔG_Int = 18.1 kcal mol⁻¹), which is, as we will show later, of great importance for the follow-up hydrogenation reaction. As shown in Fig. 8b, all hydrogenation reactions occur in a concerted asynchronous fashion, where one newly formed C–H bond forms ahead of the other. The reaction barrier of the hydrogenation step (TS-2), relative to the intermediate Int, is for all metallylenes higher in energy than the H₂ activation step

In addition, it can be seen that, in contrast with the H₂ activation barriers, the hydrogenation reaction barriers are higher for CSiP than for CGeP.

Fig. 8 (a) Gibbs free energy profile (in kcal mol⁻¹) for H₂ activation and subsequent hydrogenation of ethylene or acetylene by CEP metallylenes (E = Si, Ge) computed at ZORA-BP86/TZ2P. (b) Transition state structures with key bond lengths (in Å) for the hydrogenation of ethylene or acetylene.

These results indicate that metallylenes, which can efficiently activate H₂ with a low reaction barrier, are not by definition good metallylenes for hydrogenation. A highly exergonic H₂ activation reaction, in this mechanism, goes hand in hand with strong E–H bonds in CEXH₂. Breaking these strong E–H bonds, in a subsequent hydrogenation step, will give rise to a high activation strain and hence a high hydrogenation reaction barrier. Thus, one must consider both the H₂ activation barrier along with the associated reaction energies and ensure that the latter are only moderately exergonic so that the follow-up hydrogenation barrier is not prohibitively high.

Conclusion

Our quantum chemical exploration, based on the activation strain model and Kohn–Sham molecular orbital theory, highlight the factors that determine the trends in reactivity of the H₂ activation by various metallylenes H₃C–E–X (CEX: E = C, Si, Ge, Sn, and X = NMe₂, PMe₂, AsMe₂). Upon changing the central metallylene atom down in Group 14, from carbon to tin, while keeping the ligand consistent, systematically increases the H₂ activation barrier. In contrast, varying the ligand X, from NMe₂ to PMe₂ to AsMe₂, while keeping the central atom E constant results in a significant lowering of the reaction barrier.

We found that the increasing reaction barrier, on going from C to Sn, is caused by a reduced metallylene–H₂ interaction that was traced back to less stabilizing orbital interactions. Along this series, the back-donation interaction between filled lone-pair orbital of the metallylene and the σ*-orbital of H₂, i.e., HOMO_CEX–LUMO_H2, becomes progressively weaker, due to both an increased orbital energy gap, as the CEX HOMO goes up in energy (destabilized), as well as a reduced orbital overlap. Furthermore, the destabilization of the reaction barrier, as a response to changing the ligand down in Group 15, can be ascribed to two factors, namely, (i) reduced Pauli repulsive occupied–occupied orbital overlap between the reactants, because the ligand becomes more pyramidal and, therefore, polarizes the HOMO amplitude away from the incoming H₂; and (ii) less activation strain, as the degree of pyramidalization of the ligand, upon reacting, becomes increasingly smaller.

At last, we extended our work to demonstrate, for the first time, that H₂ activated metallylenes might be utilized in subsequent reactions. We exhibited that the rationally designed metallylenes are able, after the activation of H₂, to hydrogenate ethylene and acetylene in one concerted asynchronous reaction step to ethane and ethylene, respectively. The reaction barrier corresponding to this reaction step is, however, higher in energy than the H₂ activation step and additional tuning of the metallylene is necessary. Thus, to realize the full potential of metallylenes, one must carefully tune the exergonicity of the bond activation step, to reduce the strength of the E–H bonds, and also the reaction barrier of the subsequent reaction step, such as the hydrogenation reaction of unsaturated bonds.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

We thank the Netherlands Organization for Scientific Research (NWO) and the Dutch Astrochemistry Network (DAN) for financial support. This work was carried out on the Dutch national e-infrastructure with the support of SURF Cooperative. Furthermore, we thank Kevin van Dommelen of the Vrije Universiteit Amsterdam for helpful discussions.

Notes and references

1. P. P. Power, Nature, 2010, 463, 171.
2. (a) D. Bourissou, O. Guerret, F. P. Gabbai and G. Bertrand, Chem. Rev., 2000, 100, 39; (b) Y. Mizuhata, T. Sasamori and N. Tokitoh, Chem. Rev., 2009, 109, 3479.
3. See, for instance: (a) D. Martin, M. Soleihavoup and G. Bertrand, Chem. Sci., 2011, 2, 389; (b) C. Weetman and S. Inoue, ChemCatChem, 2018, 10, 4213; (c) T. J. Hadlington, M. Driess and C. Jones, Chem. Soc. Rev., 2018, 47, 4176; (d) F. Hanush, L. Groll and S. Inoue, Chem. Sci. 10.1039/d0sc03192e.
4. For carbenes, see for instance: (a) D. G. Frey, V. Lavallo, B. Donnadieu, W. W. Schoeller and G. Bertrand, Science, 2007, 316, 439; (b) T. Hudnall, J. P. Moerdyk and C. W. Bielawski, Chemm. Commun., 2010, 46, 4288; (c) M. P. Doyle, R. Duffy, M. Ratnikov and L. Zhou, Chem. Rev., 2010, 110, 704; (d) D. R. Tolentino, S. E. Neale, C. P. Isaac, S. A. Macgregor, M. K. Whittlesey, R. Jazzar and G. Bertrand, J. Am. Chem. Soc., 2019, 141, 9823.
5. For silylenes, see for instance: (a) A. V. Protchenko, K. H. Birjkumar, D. Dange, A. D. Schwarz, D. Vidovic, C. Jones, N. Kaltsoyannis, P. Mountford and S. Aldridge, J. Am. Chem. Soc., 2012, 134, 6500; (b) A. V. Protchenko, A. D. Schwarz, M. P. Blake, C. Jones, N. Kaltsoyannis, P. Mountford and S. Aldridge, Angew. Chem. Int. Ed., 2013, 52, 568 ( Angew. Chem. , 2013 , 125 , 596 ); (c) D. Wendel, A. Porzelt, F. A. D. Herz, D. Sakar, C. Jandl, S. Inoue and B. Rieger, J. Am. Chem. Soc., 2017, 139, 8134; (d) S. Fujimori and S. Inoue, Eur. J. Inorg. Chem., 2020, 3131.
6. For germylenes, see for instance: (a) Y. Peng, J.-D. Guo, B. D. Ellis, Z. Zhu, J. C. Fettinger, S. Nagase and P. P. Power, J. Am. Chem. Soc., 2009, 131, 16272; (b) M. Usher, A. V. Protchenko, A. Rit, J. Campos, E. L. Kolychev, R. Tirfoin and S. Aldridge, Chem. –Eur. J., 2016, 22, 11685; (c) K. L. Gullet, T. Y. Lai, C.-Y. Chen, J. C. Fettinger and P. P. Power, Organometallics, 2019, 38, 1425; (d) R. J. Mangan, A. Rit, C. P. Sindlinger, R. Tirfoin, J. Campos, J. Hicks, K. E. Christensen, H. Niu and S. Aldridge, Chem. –Eur. J., 2020, 26, 306.
7. For stannylenes, see for instance: (a) Y. Peng, B. D. Ellis, X. Wang and P. P. Power, J. Am. Chem. Soc., 2008, 130, 12268; (b) J. W. Dube, Z. D. Brown, C. Caputo, P. P. Power and P. J. Ragogna, Chem. Comm., 2014, 50, 1944; (c) A. V. Protchenko, J. I. Bates, L. M. A. Saleh, M. P. Blake, A. D. Schwarz, E. L. Kolychev, A. L. Thompson, C. Jones, P. Mountford and S. Aldridge, J. Am. Chem. Soc., 2016, 138, 4555.
8. D. Devarajan, C. E. Doubleday and D. H. Ess, Inorg. Chem., 2013, 52, 8820.
9. (a) E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597; (b) E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783.
10. E. van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142.
11. (a) A. D. Becke, Phys. Rev. A, 1988, 38, 3098; (b) J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822.
12. (a) G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931; (b) C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391; (c) ADF2018.104, SCM Theoretical Chemistry, Vrije Universiteit, Amsterdam (Netherlands), 2018, http://www.scm.com.
13. For a step-by-step protocol, see: (a) P. Vermeeren, S. C. C. van der Lubbe, C. Fonseca Guerra, F. M. Bickelhaupt and T. A. Hamlin, Nat. Protoc., 2020, 15, 649. For reviews, see: (b) F. M. Bickelhaupt, J. Comp. Chem., 1999, 20, 114; (c) I. Fernández and F. M. Bickelhaupt, Chem. Soc. Rev., 2014, 43, 4953; (d) F. M. Bickelhaupt and K. N. Houk, Angew. Chem. Int. Ed., 2017, 56, 10070 ( Angew. Chem. , 2017 , 129 , 10204 ); (e) D. Ess and K. Houk, J. Am. Chem. Soc., 2007, 129, 10646; (f) D. Ess and K. Houk, J. Am. Chem. Soc., 2008, 130, 10187.
14. (a) F. M. Bickelhaupt and E. J. Baerends, in Reviews in Computational Chemistry, ed. K. B. Lipkowitz and D. B. Boyd, Wiley, Hoboken, 2000, pp. 1–86; (b) R. van Meer, O. V. Gritsenko and E. J. Baerends, J. Chem. Theory Comput., 2014, 10, 4432; (c) K. Morokuma, J. Chem. Phys., 1971, 55, 1236; (d) K. Kitaura and K. Morokuma, Int. J. Quantum Chem., 1976, 10, 325; (e) T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1558; (f) T. Ziegler and A. Rauk, Inorg. Chem., 1979, 18, 1755.
15. (a) A. Klamt and G. Schüürmann, J. Chem. Soc. Perkin Trans., 1993, 2, 799; (b) A. Klamt, J. Phys. Chem., 1995, 99, 22245; (c) A. Klamt and V. Jonas, J. Chem. Phys., 1996, 105, 9972; (d) C. C. Pye and T. Ziegler, Theor. Chem. Acc., 1999, 101, 396.
16. (a) Y. Zhao and D. G. Truhlar, J. Chem. Phys., 2006, 125, 194101; (b) Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215.
17. (a) S. Grimme, J. Antony, S. Ehrlich and H. A. Krieg, J. Chem. Phys., 2010, 132, 154104; (b) S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456.
18. (a) F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327; (b) C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101.
19. (a) F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297; (b) F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057.
20. (a) W. J. van Zeist, A. H. Koers, L. P. Wolters and F. M. Bickelhaupt, J. Chem. Theory Comput., 2008, 4, 920; (b) P. Vermeeren, X. Sun and F. M. Bickelhaupt, Sci. Rep., 2018, 8, 10729; (c) J. J. Cabrera-Trujillo and I. Fernández, Chem. –Eur. J., 2020, 26, 11806.
21. The same general conclusions are obtained at ZORA-BP86/TZ2P and at ZORA-M06-2X/TZ2P//ZORA-BP86/TZ2P, see Fig. S4 and S8.†.
22. T. A. Albright, J. K. Burdett and W. H. Wangbo, Orbital Interactions in Chemistry, Wiley, New York, 2013.
23. The HOMO–LUMO energy gaps computed at ZORA-BP86/TZ2P are almost as accurate as those computed at SAOP/TZ2P//ZORA-BP86/TZ2P (SAOP is a good approximation to the exact KS potential) and significantly more accurate than the HOMO–LUMO energy gaps computed at ZORA-M06-2X/TZ2P//ZORA-BP86/TZ2P (Tables S8–S11).†.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc05987k

---