Open Access Article
Open Access ArticleTailoring the cavities of hydrogen-bonded amphidynamic crystals using weak contacts: towards faster molecular machines†
Armando
Navarro-Huerta
 a,
Marcus J.
Jellen
b,
Jessica
Arcudia
a,
Marcus J.
Jellen
b,
Jessica
Arcudia
 c,
Simon J.
Teat
c,
Simon J.
Teat
 d,
Rubén A.
Toscano
d,
Rubén A.
Toscano
 a,
Gabriel
Merino
a,
Gabriel
Merino
 *c and
Braulio
Rodríguez-Molina
*c and
Braulio
Rodríguez-Molina
 *a
*a
aInstituto de Química, Universidad Nacional Autónoma de México, Circuito Exterior, Ciudad Universitaria, 04510, Ciudad de México, Mexico. E-mail: brodriguez@iquimica.unam.mx
bDepartment of Chemistry and Biochemistry, University of California, Los Angeles, California 90095, USA
cDepartamento de Física Aplicada, Centro de Investigación y de Estudios Avanzados, Unidad Mérida, Km 6 Antigua Carretera a Progreso, Apdo. Postal 73, Cordemex, Mérida, 97310, Yucatán, Mexico. E-mail: gmerino@cinvestav.mx
dAdvanced Light Source, Lawrence Berkeley National Laboratory, Berkeley, California 94720-8229, USA
First published on 14th December 2020
Abstract
This work describes the use of C–H⋯F–C contacts in the solid-state from the stator towards the rotator to fine-tune their internal motion, by constructing a set of interactions that generate close-fitting cavities in three supramolecular rotors 1–3I. The crystal structures of these rotors, determined by synchrotron radiation experiments at different temperatures, show the presence of such C–H⋯F–C contacts between extended carbazole stators featuring fluorinated phenyl rings and the 1,4-diazabicyclo[2.2.2]octane (DABCO) rotator. According to the 2H NMR results, using deuterated samples, and periodic density functional theory computations, the rotators experience fast angular displacements (preferentially 120° jumps) due to their low rotational activation energies (Ea = 0.8–2.0 kcal mol−1). The higher rotational barrier for 1 (2.0 kcal mol−1) is associated with a larger number of weak C–H⋯F–C contacts generated by the stators. This strategy offers the possibility to explore the correlation among weak intermolecular forces, cavity shape, and internal dynamics, which has strong implications in the design of future fine-tuned amphidynamic crystals.
Introduction
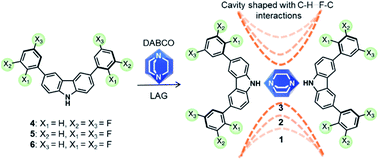
Artificial molecular machines are designed compounds that show the segmental motion of their components, where each element performs a specific task to facilitate motion at nanoscale.1–4 Such motions can be realized either in solution (i.e. rotaxanes)5–7 or in the solid-state (i.e. crystalline host–guest complexes).8,9 The main purpose is to harness the motion of each molecular component to produce a particular function, mimicking the collective dynamics of complex biomolecular machines such as ATP synthase. The work in crystalline molecular rotors from pioneering groups10–13 has pushed the boundaries of this field towards the supramolecular assembly of artificial systems to enable very fast internal motion. However, facilitating the motion of specific components in the solid-state remains challenging, mostly by the unfavorable intermolecular interactions that result from densely packed crystalline solids. To circumvent this, the proper assemblage of at least two molecular components is required: a bulky constituent, that dictates the lattice and creates a cavity (stators), linked to a highly symmetrical mobile component that should rotate rapidly (rotators).14 These tailored compounds are termed amphidynamic crystals because they encompass ultrafast molecular dynamics within their rigid frameworks.15Several amphidynamic crystals, with low rotational activation energies (Ea), have been recently reported based on the supramolecular approach,16,17 by forming cocrystals between a globular rotator, preferably 1,4-diazabicyclo[2.2.2]octane (DABCO) because this framework can form halogen (N⋯X, X = I, Br) or hydrogen bonds (N⋯HX, X = O, N),18 and bulky molecules as the stators (e.g. trityl groups,19 triptycyl diacids,20 or carbazole heterocycles21). However, to the best of our knowledge, the stator has been only used to create the sufficient space around the rotary part, and large efforts have been paid to try to avoid interactions with the rotator because they are considered as deleterious for the motion. Therefore, it would be interesting if fast dynamics could be regulated with the interplay between the rotator and the stator, after matching the proper molecular components.
Herein we propose that carbazole heterocycles can be bestowed with haloaromatic rings on their periphery to afford new supramolecular rotors with favorable stator–rotator contacts. We hypothesize that the interactions between the halogen atoms in the stator and the aliphatic methylenes in DABCO would transform the shape and size of the empty space around the rotator and thus change its motion. To generate the envisioned compounds in a supramolecular way, we postulate that the rotor's framework should be created first, taking advantage of the typically robust N–H⋯N hydrogen bonds between carbazole and DABCO. Subsequently, halogen atoms in the outer part of the stator might produce subtle changes in their conformations and induce the formation of weaker attractive contacts around the rotator. Fluorine atoms were selected as the appropriate substituents, due to their strong electron-withdrawing nature and small size, two favorable characteristics that may facilitate the interaction with hydrogen atoms of DABCO. This design is inspired by the fact that the C–H⋯F–C contacts in some crystalline structures lead to changes in the properties of the solid.22 It is also known that the ground state of a fluorinated rotator could be destabilized by steric interactions with the stator, causing an additional reduction of the rotational barriers.23
We succeed in this approach by synthesizing three molecular rotors 1–3I with fitted cavities. The rotors obtained through cocrystallization of DABCO with one of three difluorophenylcarbazole regioisomers (4–6). The strong N–H⋯N hydrogen bonds creates the expected triad and the halogen atoms formed weak hydrogen contacts within the crystals (Scheme 1). The structures of these crystalline rotors were resolved by a combination of variable temperature synchrotron radiation and in-house X-ray diffraction experiments. Fast angular trajectories (3-fold jumps) of DABCO in these rotors were determined by VT 2H solid-state NMR studies using isotopically enriched analogues, whereas periodic density functional theory (DFT) computations, using the Nudged-Elastic Band method (NEB), provided a description of the rotational profiles. Finally, the activation parameters for 1–3I were experimentally obtained with 1H T1 relaxometry experiments.
It is apparent that the higher activation energies to the rotation, i.e. rotor 1 (Ea = 2.0 kcal mol−1) result from larger, less symmetric cavities but with a higher number of C–H⋯F–C interactions. When more cylindrical cavities and less C–H⋯F–C intermolecular contacts are created, lower barriers are observed, i.e. rotors 2 (Ea = 0.84 kcal mol−1) and 3I (Ea = 0.80 kcal mol−1). These results show that the dynamics of the DABCO can be regulated by the combination of the symmetrical cavity and the intermolecular interactions from the stator towards the rotator.
Results and discussion
Synthesis and X-ray diffraction studies of rotors 1–3
The difluorinated regioisomers 4, 5, and 6, which allowed us to explore the positional effects of the halogen atom, were prepared in a two-step process: oxidative iodination of carbazole and subsequent Suzuki coupling with selected boronic acids (see ESI†). 2D NMR experiments were performed for all compounds to assign the 1H and 13C signals in the collected spectra (Fig. S2–S13†). A preliminary evaluation of the interaction between the carbazole derivatives 4–6 and DABCO was carried out in CDCl3 solution at room temperature. Changes in the chemical shift of the NH protons (Δδ = 0.11–0.25 ppm) indicate that the N–H⋯N interactions are present in solution and could be formed in the solid-state. Additionally, similar recognition experiments were performed using 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixtures of the components. The 1H spectra (Fig. S20–S22†) also indicated changes in the NH proton chemical shifts, suggesting the possibility to obtain asymmetric rotors; however, the crystals of these compounds were not obtained.
1 mixtures of the components. The 1H spectra (Fig. S20–S22†) also indicated changes in the NH proton chemical shifts, suggesting the possibility to obtain asymmetric rotors; however, the crystals of these compounds were not obtained.
Given the high solubility of the components in chloroform, only minute crystals were acquired from the evaporation of these solutions. One form of rotor 3 (named 3II) was initially diffracted by synchrotron radiation. However, we were not able to reproduce the crystallization of such form neither by slow evaporation nor LAG method, therefore, the crystallographic data is provided only in the ESI (Table S7)† and no detailed description is provided in this manuscript.
Other solvent systems were explored to produce single crystals suitable for synchrotron diffraction. Crystals of the rotors 1–3I and their deuterated analogs for dynamic studies (1-d10, 2-d10 and 3I-d10) were grown using a mixture of hexane/ethyl acetate (9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v). The most relevant crystallographic parameters are compiled in Tables S3–S6 in the ESI.† A derivative without fluorine atoms was also prepared for comparison purposes, but the structure refinement revealed that this compound crystallized only with a 1
1 v/v). The most relevant crystallographic parameters are compiled in Tables S3–S6 in the ESI.† A derivative without fluorine atoms was also prepared for comparison purposes, but the structure refinement revealed that this compound crystallized only with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (carbazole
1 (carbazole![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DABCO) relationship (compound 7s) in a P21/c monoclinic system, despite the initial 2
DABCO) relationship (compound 7s) in a P21/c monoclinic system, despite the initial 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometry, and therefore it is not discussed in detail here (Table S8†). This latter result highlights one additional advantage of adding the fluorine atoms in the carbazoles, which is to increase the availability of the NH proton towards DABCO to form the desired triads.
1 stoichiometry, and therefore it is not discussed in detail here (Table S8†). This latter result highlights one additional advantage of adding the fluorine atoms in the carbazoles, which is to increase the availability of the NH proton towards DABCO to form the desired triads.
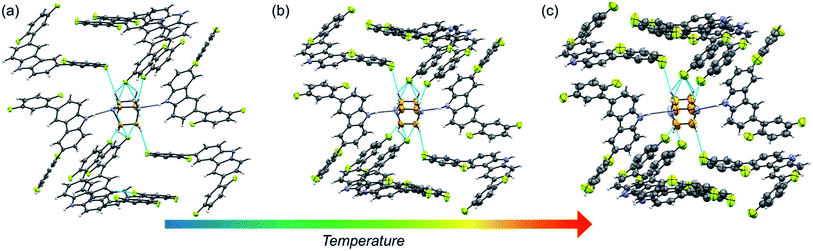
Molecular rotor 1 displays a temperature-dependent klassengleiche phase transition upon cooling: Cc – k2, −b, a, c → P21 producing two crystal forms with a high crystal packing similarity (RMS = 0.483154 for 14/15 molecules) calculated with Mercury.40 At low temperature (1-LT), the crystal was solved and refined in space group P21 with Z′ = 2 comprising two complete rotors. In contrast, at 300 K (1-HT) the crystal was solved and refined in the space group Cc, with Z′ = 1 consisting of only one molecular rotor (Fig. 1a). The changes in the lattice parameters and the average bond lengths are minimal with the main differences occurring in the orientation of the difluorophenyl substituents (Table S4†). In 1-LT, there are four N–H⋯N bonds with DA distances between 2.826(2) and 2.876(2) Å and angles closer to linearity (173 and 177°), whereas in 1-HT the distances are 2.87(3) and 2.88(3) Å, but the angles departed more from the expected linearity (163.7 and 163.6°). In these structures, DABCO does not show disorder at all the temperatures explored displaying an approximate C3 symmetry while its surroundings remained very similar (Table S9 and Fig. S24†), showing only a significant increase in the size of the Anisotropic Displacement Parameters (ADPs).
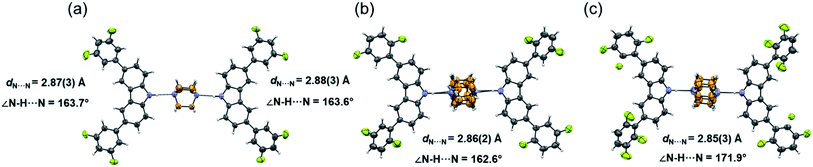 | ||
| Fig. 1 Molecular structure and hydrogen bond parameters of cocrystals at 300 K: (a) rotor 1, (b) rotor 2, and (c) rotor 3I. Ellipsoids are drawn at 50% probability level. | ||
Since rotors 2 and 3I give rise to isomorphous crystals, they are discussed together. The similarity between their cell parameters is remarkable, with values of a = 6.6761(5) Å, 15.0587(11) Å, 21.4293(14) Å, β = 94.9412(17)° for rotor 2 and a = 6.8192(8) Å, 14.6728(18) Å, 21.461(3) Å, β = 95.452(4)° for rotor 3I (both at 300 K). The structures of these rotors have hydrogen bonds with comparable distances of 2.86(3) Å (2) and 2.85(3) (3I) and angles of 162.6 and 171.9°, respectively (Fig. 1a and b). Regarding the mobile component, in both crystals, the DABCO molecules occupy a special crystallographic position, which leads to a disordered molecule with 50/50 occupancies by symmetry and makes impossible to remove the disorder even at low-temperature experiments (100 K). Regarding the crystal arrays, note that the difluorophenyl rings in rotors 2 and 3I have a more twisted conformation compared to those in rotor 1, which is attributed to the presence of the fluorine atoms in the ortho position. The torsion of the phenyl groups is essential because due to these conformational differences, the cavity around DABCO in 2 and 3I turned out to be smaller (vide infra).
The fluorine atoms in all stators are in contact with DABCO of neighboring rotors. These sought-after C–H⋯F–C contacts could be regarded as weak hydrogen interactions, as discussed by Taylor.24,25 To assess their influence on the internal dynamics, the interactions around DABCO for the three rotors were counted at 100 K (dH⋯F < 3 Å) using both Mercury® and the optimized structures used for the periodic DFT studies. The analysis reveals that in 1 more than 40 C–F⋯H–C interactions exist, whereas rotors 2 and 3I present almost half of these C–F⋯H–C interactions (Fig. S26–S28†). These interactions remain in rotor 2 at three different measured temperatures (Fig. 2). For consistency, the same analysis was performed at room temperature for all three rotors, affording similar results (Tables S9–S11†). Note that despite the phase transition in rotor 1, this cocrystal has a higher number of interactions at any given temperature.
Dynamic characterization by solid state NMR and periodic DFT computations
After achieving those weak interactions between the stators and rotators, it was necessary to correlate their structure and dynamics by means of the solid-state 13C and 2H NMR, using natural abundance and deuterated analogs, respectively. Fresh crystalline samples were rapidly prepared by using the Liquid-Assisted Grinding (LAG) technique, which produced the designed rotors in minutes. The phase purity of the powders obtained using LAG was higher than those produced by the slow evaporation method, according to powder X-ray diffraction (PXRD) analyses (Fig. S29–S31†). Therefore, this was the preferred method to yield large quantities of the rotors (100 mg).The LAG approach was also used to explore the synthesis of new asymmetric rotors, grinding two different stators of the fluorinated carbazoles with one equivalent of DABCO in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 relationship. The PXRD studies of the resulting powders indicated the preferred formation of the symmetric rotors 1–3I, and thus, no further experiments were performed to achieve those mixed rotors.
1 relationship. The PXRD studies of the resulting powders indicated the preferred formation of the symmetric rotors 1–3I, and thus, no further experiments were performed to achieve those mixed rotors.
After verifying the phase of rotors 1–3I, 13C Cross-Polarization Magic Angle Spinning (CPMAS) experiments at 300 K were used to identify small differences in the spectra among them and with the starting materials. For instance, the signals belonging to the C–F atoms always have higher intensity in the rotors than the stators, which is attributed to a better cross-polarization from the highly protonated DABCO molecules to the neighboring carbazole derivatives (Fig. S32–S34†).
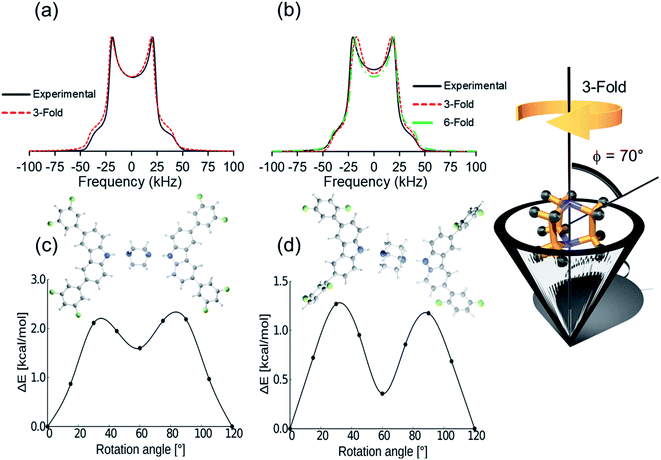
Deuterium solid-state NMR, a common technique to describe frequencies and angular displacements of isotopically enriched mobile components,26,27 was used next to study the three deuterated rotors 1-d10, 2-d10, and 3I-d10 from 300 K to 150 K. The line shapes were successfully fitted using NMR Weblab,28 proposing a model that involves 120° jumps (3-fold) in the fast exchange, with a Quadrupolar Coupling Constant (QCC) of 170 kHz and a cone angle of 70°. As an example, the agreement between the experimental and simulated spectra in rotor 2 shows that DABCO experience very fast rotations (Fig. 3a). A second model involving jumps of 60° (6-fold) could also match the experimental spectra. Due to the fast regime of the rotation, the difference between the trajectories was latter supported with DFT computations.29 Similar results were collected for all rotors, confirming that the globular rotators experience motions with frequencies beyond the timescale of this technique (>107 Hz) even at the lowest temperatures available in the spectrometer; and therefore, it was insufficient to fully establish the effects of the weak C–H⋯F–C contacts in the inner dynamics, prompting us to seek a computational approach.
First, the DFT computations for molecular rotor 1 were carried out using the X-ray structures at 100 K, 200 K and 300 K to determine if the phase transformation causes some changes in the dynamics. The data obtained imply that compound 1 experiences 120° jumps with very similar barriers in the two crystal forms, Ea = 2.4 kcal mol−1 (1-LT) and Ea = 2.3 kcal mol−1 (1-HT). There is a shallow minimum at 60° in both forms, and the phase transition does not significantly change the barrier to rotation, although the potential is slightly modified (see ESI, Fig. S39†). Note that the computed angular displacements and the low rotational barriers are in excellent agreement with the first dynamic model proposed from the simulated 2H NMR data. The computed results and the fact that the 2H line shape did not change at low temperatures, indicated that the class phase transition has minor effects in the dynamics of DABCO in 1.
By comparison, DFT computations for isostructural rotors 2 and 3I yielded lower values, Ea = 1.3 kcal mol−1 and 1.4 kcal mol−1, respectively. Although the computed rotational profiles have a shape similar to the previous rotor, the local minimum at 60° is more pronounced (Fig. 3d). Even though the motion is mainly 3-fold in 2 and 3I (120° jumps), the structural modifications in the stator afforded subtle changes in the environment around DABCO rotators. This not only affects the position of the maxima but may also allow motions with shorter angular displacements (6-fold), which could also be responsible for the observed deuterium line shape of this rotor (Fig. 3b, dotted green line).
Intramolecular dynamics by 1H spin–lattice relaxometry
Previous works30 have documented that very fast dynamics with low rotational barriers could be measured by studying their 1H T1 relaxation times. It has also been reported that the motion of fast rotational moving fragments such as DABCO are the principal contributor to the relaxation in these crystalline rotors.31 Therefore, 1H T1 saturation-recovery experiments were carried out to support the DFT values. As the motion of DABCO in these rotors is a temperature-dependent process that follows an Arrhenius behavior, the activation energy (Ea) and preexponential factor (A = τ0−1) of the process can be calculated from the experimental T1 times. The shortest T1 value should be achieved at the temperature when the rotational frequency of DABCO matches the 1H Larmor frequency (600 MHz). The relaxation data can then be fitted to the Kubo–Tomita expression32 (eqn (1)), which provides the correlation time τc that is employed to extract the Ea (eqn (2)):| T1−1 = C[τc(1 + ω02τc2)]−1 + 4τc(1 + 4ω02τc2)−1 | (1) |
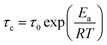 | (2) |
Those experiments revealed essential differences in the dynamic behavior of all molecular rotors reported here. For example, the minimum relaxation value was only observed in 1, but no minimum was observed in rotors 2 or 3I even at 150 K (Fig. 4a–c), indicating that lower temperatures than those available in the spectrometer are needed to reduce the rotation of DABCO in the latter rotors. The minimum T1 for molecular rotor 1 is surprisingly close at room temperature (ca. 280 K). The barrier obtained by the Kubo–Tomita fitting process is the highest one among the three rotors (Ea = 2.0 kcal mol−1). For rotors 2 (Ea = 0.84 kcal mol−1) and 3I (0.80 kcal mol−1), their barriers to rotation were estimated from the slope of the T1 data, as reported elsewhere.33,34 Although the rotational barriers achieved from 1H T1 experiments are not identical to those from periodic DFT computations, there is an excellent agreement in the values and their relative position, given that the Ea in rotor 1 three times larger than those of rotors 2 and 3I.
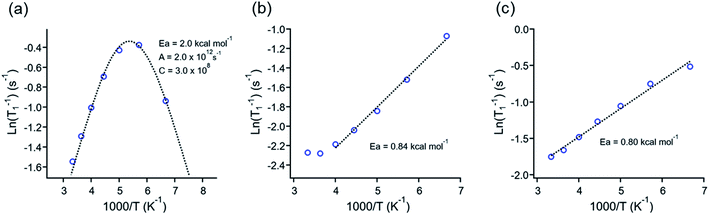 | ||
| Fig. 4 1H T1 data fitting of rotors (a) 1, (b) 2 and (c) 3I. The Arrhenius parameters for the rotors presented are inserted in each plot. | ||
Shape of the internal cavity by Hirshfeld and NCIs analyses
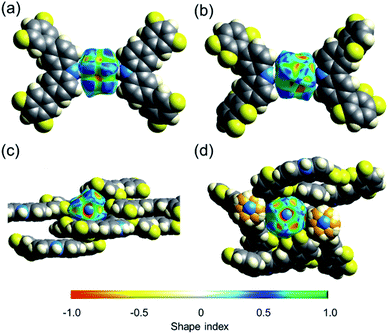
The collected data prompted us to consider if the differences in the shape of the cavity and the number of weak hydrogen contacts could be responsible for the distinctive barriers. One way to estimate how dense these molecular crystals are is by calculating their packing coefficient (Ck),35 whose values are from 0.65 (loose packing) to 0.80 (densely packed).36 The Ck values at room temperature of rotors 1 (0.67), 2 (0.69), and 3I (0.71) are relatively low, but it is clear that the largest cavities are present in 1. However, although the packing coefficient is very useful, additional voids in the structure could contribute to this value, and thus, further analyses were carried out.The interactions of the fluorine atoms over the rotator and the shape of the surface were also evaluated by Hirshfeld analyses.37,38 This tool afforded valuable insights about the type and intensity of intermolecular interactions around DABCO at 100 K and 300 K. Attention was paid to the shape index values, which could adopt values between −1 and +1. Negative values are denoted by a concave surface (red) due to closer intermolecular interactions.39 Conversely, positive values imply a protruding surface (blue), indicating weaker interactions. The mean value in rotor 1-HT (0.278) is larger than the mean values for rotors 2 and 3I of (0.222 and 0.217, respectively). A visual comparison of the shape index of rotors 1 and 3I is presented in Fig. 5. These differences are maintained at low temperatures, as compiled in Table 1.
| Rotor | C k (100 K/300 K) | Shape index (100 K/300 K) | Globularity (100 K/300 K) |
|---|---|---|---|
| a Calculated using Mercury 4.3.1.40 b Calculated using CrystalExplorer 17.41 c The space group at 100 K is P21. Values for shape index and globularity were calculated as the mean value of both DABCO fragments in the asymmetric unit. d The space group at 300 K is Cc. | |||
| 1 | 0.69/0.67 | 0.274/0.278 | 0.887/0.891 |
| 2 | 0.71/0.69 | 0.231/0.222 | 0.917/0.920 |
| 3I | 0.73c/0.71d | 0.211c/0.217d | 0.913c/0.917d |
To further pinpoint the nature of the intramolecular interactions, we also used the Non-Covalent Interactions (NCI) index. For a better visual inspection, we considered pairs of carbazole–DABCO–carbazole moieties formed by the first neighbors of each rotor (see Fig. S42–S45†). In general, there are four different types of contacts in all crystals: (1) the stacking CH⋯CH and π⋯H–C, that is, interactions between the difluorinated phenyls and DABCO, and interactions between the ring of the fluorinated phenyl and carbazole, (2) the C–F⋯H–C contacts that take place between neighboring carbazoles, (3) the hydrogen bonds, namely, the expected N⋯H between rotator and stator, and to a lesser extent (4) some F⋯H between carbazoles. In addition, for the case of 1-LT, there are some F⋯F contacts between neighboring stators (Fig. S42†). From the optimized structures, it is clear that the number of C–H⋯F–C interactions between the methylene of the rotator and the fluorine atoms in the stators is twice the number in rotor 1 than those observed in rotors 2 and 3I (Fig. S26–S28†).
Finally, a measure of the symmetry of the cavity around DABCO in the rotors can be obtained by calculating the globularity index. This parameter can take values from 0 to 1 after considering the intermolecular interactions around the portion of interest. Values closer to 1 denote a more spherical shape. The rotator in 1 has the lowest globularity, in comparison with the isostructural rotors 2 and 3 (Table 1). It is also notorious that the closest stators in rotor 3I built a more rounded cavity around the rotator, thus producing a more symmetrical environment.
The detailed X-ray structural analyses together with the 1H T1 relaxation data explain that even though rotor 1 has a larger cavity and its rotator could, at least in principle, experience more rotational freedom, it has the higher barrier to rotation. In contrast, lower barriers are found in rotors 2 and 3I, both with smaller cavities. This fact can be rationalized because the higher number of C–H⋯F–C interactions from the stators towards DABCO in rotor 1 dampens the rotational frequency and at the same time, produces a less symmetrical cavity, as revealed by DFT computations and Hirshfeld analyses. It has been described that the symmetry of the rotator plays an essential role in the height of the rotational barriers, as stated by Howe et al.42 It has also been stated that the ‘crystal fluidity’, i.e. the freedom of the lattice, may also facilitate to the inner dynamics. However, in the supramolecular rotors presented here, the use of secondary interactions from the stator towards the rotator defines the activation barriers to rotation ultimately.
Conclusions
In summary, we synthesized three fast molecular rotors 1–3I through a supramolecular design. Their molecular structures and packing arrays were characterized by synchrotron radiation experiments at 100 K, 200 K and 300 K and by in-house X-ray studies. The desired rotor triads were generated thanks to the strong N–H⋯N hydrogen bonds between halogen-functionalized carbazole stators and DABCO rotators. The fluorinated stators establish weak hydrogen bonds with neighboring rotators. The highest number of these interactions are present in rotor 1, whereas almost half of those interactions are observed in 2 and 3I. Deuterium NMR experiments of isotopically enriched samples, periodic DFT computations and 1H spin–lattice relaxation studies, offer a comprehensive perspective of the inner dynamics of the rotors. Rotor 1 shows an activation energy to rotation (Ea = 2.0 kcal mol−1) that is three times higher than the other rotors. Conversely, rotors 2 and 3I, with smaller cavities and less C–H⋯F–C interactions, have lower barriers (Ea = 0.84 and 0.80 kcal mol−1, respectively). It allows us to establish that the rotation of DABCO is reduced in the rotor with the highest number of attractive hydrogen bonds with the fluorinated stator, as well as the more asymmetrical cavity. This new approach can be used in the future to fine-tune the rotation in new amphidynamic crystals.Conflicts of interest
The authors declare no competing interests.Acknowledgements
This work was supported by CONACYT A1-S-32820. A. N.-H. thanks CONACYT for a MSc scholarship (957838). J. A. thanks CONACYT for support through her PhD fellowship. We acknowledge the UCLA Department of Chemistry and Biochemistry for solid-state 2H NMR experiments (NSF DMR-1700471 and MRI-1532232) and the technical assistance from E. Huerta Salazar (NMR), M. C. Garcia Gonzalez, F. J. Pérez Flores (MS), M. A. Peña González (NMR), Rocío Patiño (IR) and F. Ruiz Ruiz (PXRD). We thank Abraham Colin-Molina and Sarahi Vázquez-García for valuable scientific contributions. This research used resources of the Advanced Light Source, which is a DOE Office of Science User Facility under contract no. DE-AC02-05CH11231. The CGSTIC (Xiuhcoatl) is acknowledged for allocation of computational resources. The authors thank UNAM for support related to UNAM's BGSI node.Notes and references
- V. Balzani, A. Credi, F. M. Raymo and J. F. Stoddart, Angew. Chem., Int. Ed., 2000, 39, 3348–3391 CrossRef CAS.
- S. Kassem, T. van Leeuwen, A. S. Lubbe, M. R. Wilson, B. L. Feringa and D. A. Leigh, Chem. Soc. Rev., 2017, 46, 2592–2621 RSC.
- D. Dattler, G. Fuks, J. Heiser, E. Moulin, A. Perrot, X. Yao and N. Giuseppone, Chem. Rev., 2020, 120, 310–433 CrossRef CAS.
- V. Balzani, M. Venturi and A. Credi, Molecular Devices and Machines. Concepts and Perspectives for the Nanoworld, Wiley-VCH, Weinheim, Germany, 2nd edn, 2008 Search PubMed.
- A. Goujon, T. Lang, G. Mariani, E. Moulin, G. Fuks, J. Raya, E. Buhler and N. Giuseppone, J. Am. Chem. Soc., 2017, 139, 14825–14828 CrossRef CAS.
- Y. Wu, M. Frasconi, W.-G. Liu, R. M. Young, W. A. Goddard III, M. R. Wasielewski and J. F. Stoddart, J. Am. Chem. Soc., 2020, 142, 11835–11846 CrossRef CAS.
- N. D. Suhan, S. J. Loeb and S. H. Eichhorn, J. Am. Chem. Soc., 2013, 135, 400–408 CrossRef CAS.
- T. Matsuno, K. Fukunaga, S. Sato and H. Isobe, Angew. Chem., Int. Ed., 2019, 58, 12170–12174 CrossRef CAS.
- T. Matsuno, M. Fujita, K. Fukunaga, S. Sato and H. Isobe, Nat. Commun., 2018, 9, 3779–3886 CrossRef.
- A. Rodríguez-Fortea, E. Canadell, P. Wzietek, C. Lemouchi, M. Allain, L. Zorina and P. Batail, Nanoscale, 2020, 12, 8294–8302 RSC.
- A. Comotti, S. Bracco, T. Ben, S. Qiu and P. Sozzani, Angew. Chem., Int. Ed., 2014, 53, 1043–1047 CrossRef CAS.
- I. Liepuoniute, M. J. Jellen and M. A. Garcia-Garibay, Chem. Sci., 2020 10.1039/D0SC04495D.
- S. Simonov, L. Zorina, P. Wzietek, A. Rodríguez-Fortea, E. Canadell, C. Mézière, G. Bastien, C. Lemouchi, M. A. García-Garibay and P. Batail, Nano Lett., 2018, 18, 3780–3784 CrossRef CAS.
- G. S. Kottas, L. I. Clarke, D. Horinek and J. Michl, Chem. Rev., 2005, 105, 1281–1376 CrossRef CAS.
- M. A. García-Garibay, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10771–10776 CrossRef.
- J. Perego, S. Bracco, M. Negroni, C. X. Bezuidenhout, G. Prando, P. Carretta, A. Comotti and P. Sozzani, Nat. Chem., 2020, 12, 845–851 CrossRef CAS.
- Y. Yoshida, Y. Kumagai, M. Mizuno, K. Isomura, Y. Nakamura, H. Kishida and G. Saito, Cryst. Growth Des., 2015, 15, 5513–5518 CrossRef CAS.
- L. Catalano, S. Perez-Estrada, G. Terraneo, T. Pilati, G. Resnati, P. Metrangolo and M. A. Garcia-Garibay, J. Am. Chem. Soc., 2015, 137(49), 15386–15389 CrossRef CAS.
- L. Catalano, S. Perez-Estrada, H.-H. Wang, A. J.-L. Ayitou, S. I. Khan, G. Terraneo, P. Metrangolo, S. Brown and M. A. Garcia-Garibay, J. Am. Chem. Soc., 2017, 139, 843–848 CrossRef CAS.
- X. Jiang, H.-B. Duan, M. J. Jellen, Y. Chen, T. S. Chung, Y. Liang and M. A. Garcia-Garibay, J. Am. Chem. Soc., 2020, 141(42), 16802–16809 CrossRef.
- A. Colin-Molina, D. P. Karothu, M. J. Jellen, R. A. Toscano, M. A. Garcia-Garibay, P. Naumov and B. Rodríguez-Molina, Matter, 2019, 1, 1033–1046 CrossRef.
- K. Reichenbächer, H. I. Süss and J. Hulliger, Chem. Soc. Rev., 2005, 34, 22–30 RSC.
- I. Liepuoniute, C. M. Huynh, S. Perez-Estrada, Y. Wang, S. I. Khan, K. N. Houk and M. A. Garcia-Garibay, J. Phys. Chem. C, 2020, 124, 15391–15398 CrossRef CAS.
- R. Taylor, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2017, 73, 474–488 CrossRef CAS.
- R. Taylor, Cryst. Growth Des., 2016, 16, 4165–4168 CrossRef CAS.
- C. A. Fyfe, Solid State NMR for Chemists, CFC Press, Guelph, Ontario, Canada, 1983 Search PubMed.
- K. Zhu, N. Vukotic, C. A. O'Keefe, R. W. Schurko and S. J. Loeb, J. Am. Chem. Soc., 2014, 136, 7403–7409 CrossRef CAS.
- V. Macho, L. Brombacher and H. W. Spiess, Appl. Magn. Reson., 2001, 20, 405–432 CrossRef CAS.
- N. C. Burtch, A. Torres-Knoop, G. S. Foo, J. Leisen, C. Sievers, B. Ensing, D. Dubbeldam and K. S. Walton, J. Phys. Chem. Lett., 2015, 6, 812–816 CrossRef CAS.
- P. Beckmann, C. I. Ratcliffe and B. A. Dunell, J. Magn. Reson., 1978, 32, 391–402 CAS.
- S. D. Karlen, H. Reyes, R. E. Taylor, S. I. Khan, M. F. Hawthorne and M. A. Garcia-Garibay, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 14973–14977 CrossRef CAS.
- R. Kubo and K. A. Tomita, J. Phys. Soc. Jpn., 1954, 9, 888–919 CrossRef CAS.
- A. Colin-Molina, M. J. Jellen, J. Rodriguez-Hernández, M. E. Cifuentes-Quintal, J. Barroso, R. A. Toscano, G. Merino and B. Rodriguez-Molina, Chem.–Eur. J., 2020, 26, 11727–11733 CrossRef CAS.
- C. Lemouchi, C. S. Vogelsberg, L. Zorina, S. Simonov, P. Batail, S. Brown and M. A. García-Garibay, J. Am. Chem. Soc., 2011, 133, 6371–6379 CrossRef CAS.
- A. Gavezzotti, J. Am. Chem. Soc., 1983, 105, 5220–5225 CrossRef CAS.
- M. Kaźmierczak and A. Katrusiak, J. Phys. Chem. C, 2013, 117, 1441–1446 CrossRef.
- A. Saha, S. A. Rather, D. Sharada and B. K. Saha, Cryst. Growth Des., 2018, 18, 6084–6090 CrossRef CAS.
- M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19–32 RSC.
- J. J. Koenderink and A. J. van Doorn, Image Vis Comput., 1992, 10, 557–564 CrossRef.
- C. F. Macrae, I. Sovago, S. J. Cottrell, P. T. A. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, J. Appl. Crystallogr., 2020, 53, 226–235 CrossRef CAS.
- M. J. Turner, J. J. McKinnon, S. K. Wolff, D. J. Grimwood, P. R. Spackman, D. Jayatilaka and M. A. Spackman, CrystalExplorer17, University of Western Australia, Perth, Australia, 2017 Search PubMed.
- M. E. Howe and M. A. Garcia-Garibay, J. Org. Chem., 2019, 84, 9835–9849 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Materials and methods, synthetic procedures, VT solid-state 2H NMR spectra, 1H T1 data, final crystallographic refinement parameters, Hirshfeld surface maps and DFT computational details. CCDC 2022170–2022187. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/d0sc05899h |
| This journal is © The Royal Society of Chemistry 2021 |