Open Access Article
Open Access ArticleDetermination and perturbation of the electronic potentials of solid catalysts for innovative catalysis
Xingyu
Qi
 ,
Tatsuya
Shinagawa
,
Tatsuya
Shinagawa
 ,
Fuminao
Kishimoto
and
Kazuhiro
Takanabe
,
Fuminao
Kishimoto
and
Kazuhiro
Takanabe
 *
*
Department of Chemical System Engineering, School of Engineering, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo, Japan. E-mail: takanabe@chemsys.t.u-tokyo.ac.jp
First published on 8th December 2020
Abstract
Concerns about energy and the environment are motivating a reexamination of catalytic processes, aiming to achieve more efficient and improved catalysis compatible with sustainability. Designing an active site for such heterogeneous catalytic processes remains a challenge leading to a next level breakthrough. Herein, we discuss a fundamental aspect of heterogeneous catalysis: the chemical potential of electrons in solid catalysts during thermal catalysis, which directly reflects the consequent catalytic reaction rate. The use of electrochemical tools during thermal catalysis allows for the quantitative determination of the ill-defined chemical potentials of solids in operando, whereby the potential–rate relationship can be established. Furthermore, the electrochemical means can also introduce the direct perturbation of catalyst potentials, in turn, perturbing the coverage of adsorbates functioning as poison, promoters, or reactants. We collect selected publications on these aspects, and provide a viewpoint bridging the fields of thermal- and electro-catalysis.
Introduction
For centuries, our society has relied on catalytic processes in industry.1,2 Historically, economic growth had been the primary concern, linked with the large production of commodity chemicals, which is, however, required to balance with its impact on the environment.3 Building upon the fundamental understanding of catalysis hitherto established, it is imperative to revisit catalytic systems, to achieve more efficient catalytic systems and more advanced characterization. Determination of the electronic state or Fermi level of the catalyst, especially during catalysis, is one of the key factors to scale its performance.4,5 On this basis, we envisage that the determination and active perturbation of the catalyst potential can pave the way for sustainable alternatives.The past few decades have witnessed much research activity on determining the electronic state of a substance as well as its chemical manipulation by the addition of a foreign component.6–8 In the field of surface science, for instance, Kiskinova et al. experimentally measured the work function (WF) of Pt(111) under vacuum to be 5.9 eV by using ultra-violet photoemission spectroscopy.9 These authors observed that the addition of potassium at a coverage of 0.17 on Pt(111) changed its WF to 1.3 eV, resulting in an increased electron back donation to the 2π* orbital of chemisorbed CO with stronger Pt–C and weaker C–O bonds.9 Another representative study using a Kelvin probe force microscope examined WF at the surface of Au nanoparticles deposited on an n-doped Si substrate and found that the WF of nano-sized Au decreased when in contact with n-Si, indicative of electron transfer from n-Si to Au.10 Additionally, the electronic and molecular structures of the solid–liquid interface also attract attention, which is considered as key to the development of catalytic reactions.11 In 2009, the group of Domen demonstrated the direct probing of the Fermi level of Pt metal nanoparticles on a GaN wafer in water under ultraviolet irradiation using the application of in situ attenuated total reflection surface-enhanced infrared absorption spectroscopy (ATR-SEIRAS).12 By correlating the vibrational frequency of probe molecules (CO) on Pt with the electrochemical applied potential, the potential shift of Pt on a self-standing Pt/GaN photocatalyst under light illumination was estimated by following the CO vibrational frequency, which shows a good example of revealing the electronic states of catalysts involved at the solid–liquid interfaces.12 Notably, the recent development of computational tools corroborated these experimental studies.5 The group of Nørskov theoretically studied the electronic structure and reactivity trends of transition and noble metal surfaces by performing density functional theory (DFT) calculations.13 Particularly, they addressed the centre of the d-bands of metals that reflects the interaction between metal electrons and an unoccupied state of the adsorbate, such as 2π* for chemisorbed CO, and computationally demonstrated that the coupling between these orbitals, to a large extent, determines the chemisorption energy.13
By applying this fundamental understanding, we can detail the so-called “metal–support interaction” (MSI) and “promoter effect” in the field of catalysis.14–17 When an active metal particle is supported on some oxides, such as SrTiO3 (ref. 14) and CeO2,17 with a distinct Fermi level or physically in contact with elements having a lower WF, such as alkali,16 alkali-earth,18 or rare-earth18 elements, it exhibited facile dissociative adsorption of reactants, such as N2, and thus a higher reaction rate.16,17 We can account for the rate enhancement by the electron transfer between the substances, whereby the catalyst attains an electrochemical potential distinct from its pristine state. A recent study “counting” the number of electrons transferred between the Pt catalyst and CeO2(111) support by resonant photoemission spectroscopy and X-ray photoelectron spectroscopy (XPS) further validated the quantitative description of the Fermi level of the supported metal catalysts.19 Advances in synchrotron radiation XPS and electrochemical infrared spectroscopy also helped observe the change of the electronic state of the metal at the interface with oxide supports.20 The consequence of the change in the catalyst potential is the alteration of its binding strength to the surface adsorbate21,22 and thereby the reaction rate.
From a different perspective, in the field of electrochemistry, the electric potential is the primary parameter to control the rate of electrode reactions, measured as current.23 By applying more positive [negative] potentials, anodic [cathodic] reaction rates kinetically increase.24,25 More precisely, the application of external bias causes the chemical potential of the reactants and products of the electrode reaction to deviate from their original equilibrium state.26 Consequently, the activation energy of the reaction changes, resulting in the alteration of the reaction rate, as evidenced both experimentally27 and computationally.28
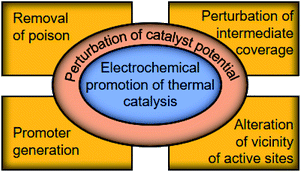
These studies provide insights into how the electrochemical potential plays a decisive role in the reactivity of metal catalysts. However, these surface science techniques require either demanding experimental conditions19 or advanced equipment,20 which cannot universally reveal the catalyst potential during the reaction in operando. In what follows, by bridging the fields of thermal- and electro-catalysis, we elaborate the correlation between the potential of a thermal catalyst and its catalytic performance in an electrochemical manner, quantitatively detailing the fundamental aspects of catalytic reactions,29,30 and review studies on the in operando determination of the catalyst potential using electrochemical tools. Subsequently, we discuss the perturbation of the catalyst potential using electrochemical tools that induce the generation of the promoter, removal of poison, perturbation of intermediate-coverage on the surface, and local alteration of the vicinity of active sites, as illustrated in Fig. 1, aiming at providing a refined view into the electrochemical promotion of thermal catalytic reactions.
Electrochemical potential determination of a solid catalyst during thermal catalytic reactions
To quantitatively measure the potential of solids in operando, the material of interest can be fabricated into a working electrode (WE) in contact with an adequate electrolyte environment. Using a three-electrode setup, the WE potential is scaled relative to a reference electrode (RE) even under open-circuit conditions, i.e., no current flow,31 which directly corresponds to the Fermi level of the WE. With concurrent detection of substances produced by thermal catalysis as a measure of the reaction rate, the potential–performance correlation can be established.32,33 Obviously, the limitation of this application is only for materials to be conductive enough to achieve electronic circuits. The employed electrochemical setup therein does not necessarily require well-defined clean systems such as single crystals, and thus would be tolerant to some impurities to the same extent as industrialized electrochemical processes.The Marin group33 measured the (thermal) oxidation rate of methyl α-D-glucopyranoside with O2 catalysed by 3.3 wt% Pt/graphite, while monitoring the catalyst potential in operando. These authors observed a continuous shift of the open-circuit potential (OCP) with time to a more positive potential as the reaction rate decreased. The oxidation rate decreased from 2.5 mmol kgcat−1 s−1 to the steady-state value of 0.5 mmol kgcat−1 s−1, which coincided with the OCP shift from 0.4 V vs. the reversible hydrogen electrode (RHE) to, finally, 0.9 V vs. RHE.33 The Marin group proposed that upon exposure to the O2 reactant, the OCP changed due to an increase in the Oad coverage, followed by the gradual formation of inactive O in the sublayer to reach a more positive potential, and further built a Langmuir–Hinshelwood type of kinetic model to describe the reaction over a board range of conditions.33 In 2014, Tao et al.4 corroborated this view by quantitatively determining the surface adsorbate by infrared spectroscopy while measuring the OCP and the reaction rate for the reaction between CO and pre-oxidized Pt. These studies demonstrate the measurements of the potential during catalysis as a powerful tool to rationalize the surface state, which in turn dictates the catalytic performance.
Such determination of the electronic potential of the catalyst in the working state can also be a powerful tool to elucidate the reaction mechanism. In one example, according to the mixed potential theory,34,35 each catalyst particle functions as a short-circuit electrochemical cell, where both electrochemical half-reactions, i.e., reduction and oxidation reactions, occur at the same rate, leading to the unified potential. By analysing the overall rate and each half-reaction rate, controversial mechanisms can be elucidated whether there is internal faradaic charge transfer or not in a thermal-catalytic reaction.
Approaches to alter the potential of a solid catalyst for heterogeneous reactions
We now discuss active perturbation of the solid potential by applying an electrochemical setup to alter the thermal-catalytic reaction rate in a distinct manner from the electrocatalytic process. Such electrochemical promotion of the catalyst changes the reaction rate and is therefore only applicable to steady-state reactions with ΔG < 0 at a given reaction temperature, which contrasts with electrocatalytic processes.26,36 In electrocatalysis, electric power acts as energy input to polarize the electrode potential beyond the equilibrium potential, thereby making the reaction thermodynamically allowed to proceed.26 The electrochemical promotion of the active sites can directly alter the structure of the activated complex at the transition state, or influence the coverage of species on the surface that function as a promoter, reaction intermediate, or poison. The following are some examples of the promotion effects of thermal catalysis.The group of Vayenas37,38 reported the pioneering work of promoted catalysis induced by altering the potential with electrochemical tools, and named it non-faradaic electrochemical modification of catalytic activity (NEMCA) or electrochemical promotion of catalysis (EPOC). As shown in Fig. 2a, their system is composed of a solid electrolyte, whose one side is decorated with the catalyst film prepared with commercial metal paste and functions as a WE, while the other side plays the role of a counter electrode (CE). By externally applying a voltage between the WE and CE, the promoted catalytic rate consisting of the rate at the OCP (rOCP), faradaic rate (rI), and extra rate of promotion (rP) can be observed, as illustrated in Fig. 2b. The mechanism accounting for such improvement is that the charge carriers in the solid electrolyte “spill-over” the surface of the supported catalyst and the spilled-over species alters the WF of the catalyst, and thereby functions as a promoter, as schematically illustrated in Fig. 2c.36 Such a change in the WF alters the activation energy of the reaction, resulting in improved thermal-catalytic performance in a reversible manner compared to that without the applied voltage.39–42 As one example, the hydrogenation of CO2 over Ru deposited on a proton-conducting oxide (BaZr0.85Y0.15O3−α + 1 wt% NiO) has been investigated.41,43 Their study showed that positively polarizing the WF removed the proton promoter and, in turn, enhanced thermal-catalytic CH4 formation and suppressed the CO formation rate, while negatively polarizing the WF resulted in an opposite manner.41,43 A similar promotion effect was also observed in a liquid phase for the H2 + O2 reaction, demonstrating the applicability of NEMCA to various reactions.44–47
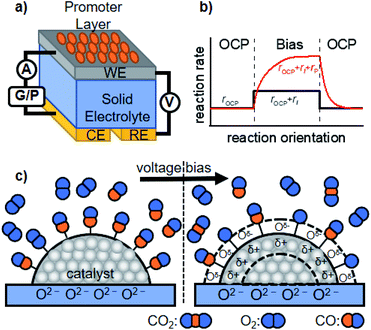 | ||
| Fig. 2 Schematic representation of the (a) basic experimental setup for NEMCA, (b) typical transient NEMCA curve showing the reaction rate at the OCP (rOCP), faradaic reaction rate (rI) and extra rate of promotion (rP) caused by bias application, and (c) spilling-over of the promoter on the surface of the supported catalyst induced by external voltage bias and its consequent change of adsorption of reactants using CO oxidation as an example. The figure was drawn based on ref. 36. | ||
In a distinct mechanism, externally applying electric potentials onto the catalyst tunes its WF as in the electrochemical process, and facilitates the formation or consumption of the surface adsorbate that is otherwise considerably slow in the thermal-catalytic manner.48–51 More specifically, a change in the WF of the solid catalyst leads to subsequent alteration of its binding energy to surface species, and thereby the adsorption energy is changed. According to the Brønsted–Evans–Polanyi relationship, the activation energy Ea linearly scales with the adsorption energy ΔE:52
| Ea = αΔE + β | (1) |
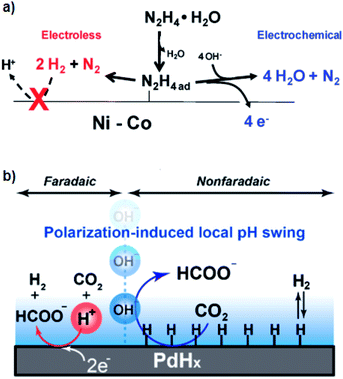 | ||
| Fig. 3 Mechanism of (a) electrochemically promoted formation of N2H4ad that acts as the shared intermediate for both electro- and thermal-pathways48 and (b) improved thermal catalysis of CO2 hydrogenation by polarization-induced local pH swing.53 Reprinted (adapted) with permission from ref. 48 and 53. Copyright 2011 American Chemical Society. Copyright 2020 American Chemical Society. | ||
From a more general perspective, the direct application of potential can tune the coverage of adsorbed species on the surfaces. More precisely, by pinning the potential of solids during the thermal-catalytic reaction with an electrochemical means, we can control the surface state of a solid, e.g., to keep the surface clean from passivation or poisoning. This interesting approach was reported in 2018 by the group of Lercher for the hydrogenation of benzaldehyde over a Ni catalyst.49 The Ni surface was inert for hydrogenation of benzaldehyde at the OCP due to the strong binding of Oad species on the surface, which, however, became active upon the application of a potential negative enough to reduce Ni–O species.49
The electrochemical promotion system in the liquid phase might additionally benefit from the “polarization-induced local pH swing”.53 Ryu et al.53 observed that the hydrogenation rate of CO2 over a Pd catalyst in the aqueous phase was positively correlated with the alkalinity of the reaction media. Building on the correlation, they cathodically polarized the system to induce local alkaline environments in an electrochemical manner.53 Consequently, as schematically illustrated in Fig. 3b, this electrochemical perturbation resulted in the promotion of the thermal-catalytic CO2 hydrogenation reaction.53
The electrochemical promotion, in principle, can be achieved for all steady-state reactions with ΔG < 0, and should only have kinetic effects unless a substantial external current is applied. Electronic consequences caused by classical promotion (e.g., promoters and MSI) are, after all, similar phenomena to the EPOC, which is however driven by different devices.36,46 Compared to conventional promotion, electrochemical promotion can manipulate the potential of the solid catalyst more precisely by utilizing external electrochemical devices. However, targeted electrochemical promotion effects can only be realized when certain sufficient criteria are met. Firstly, the system must achieve a delicate balance that allows the back-spillover of the promoter to be faster than its desorption or consumption, i.e., slow kinetics of promoter destruction.36,54 By appropriate catalyst–electrode design as well as appropriate choice of electrolyte that can maintain the effective promoter layer, the above criterion can be met,36 and investigations on better combinations for targeted chemical reactions can be one of the directions for the research of this aspect. Secondly, it is important to control the contribution of the non-faradaic reaction relative to that of the faradaic one when the EPOC is operational.36 Maximizing the apparent electrochemical promotion effect thus requires optimizing not only the catalyst materials but also reaction conditions, e.g., applied external potentials. Another challenging issue for gas reactions performed in a liquid system is the slow diffusion of gas reactants caused by low solubility, which limits the total reaction rate in practical applications. Such a mass-transport limitation can be mitigated by the use of membrane–electrode assembly, which allows the direct supply of gas reactants to the catalyst surfaces without diffusion limitations. Designing better experimental setups for more pronounced promotion effects is surely another target that researchers are going to pay attention to.
Lastly, we address how to quantify the active sites of the targeted reactions, which might be one of the major concerns of researchers. In some electrochemical promotion systems, the number of active sites would remain unchanged when the external potential/current is applied, since the application of electric field basically induces the supply of a promoter without restructuring the catalyst surface. This type of simple system allows for quantification of the active sites by the conventional means such as the chemisorption and desorption of appropriate probe molecules ex situ under unpromoted conditions.55 However, in some other systems where the reconstruction of the catalyst and/or the removal of poisoning occurs when the external potential/current is applied, and the number of active sites changes, the quantification requires the employment of sophisticated in situ or operando characterization, for instance, stripping of adsorbed probe species56 or infrared spectroscopy.57
Outlook for other innovative catalysis
From the viewpoint of electrochemically promoting thermal-catalytic reactions, one novel approach has been reported by the group of Sekine.58,59 These authors applied voltage to the particulate catalyst of 9.9 wt% Cs/5.0 wt% Ru/SrZrO3 for ammonia synthesis, distinct from the disk-shaped electrode employed for the NEMCA.58 Its consequence was also the lowered activation energy of reaction and improved catalytic rates, accompanying a change in the reaction mechanism from dissociative to associative.58 The origin of this improvement remains elusive. However, the reaction path mediated by the surface proton is proposed as the plausible one.58 In addition, the applied voltage would form an electric field in the vicinity of the surfaces, which itself also impacts the catalysis.60 Interested readers are referred to the recent report by the group of Sekine.59 In another example, a DFT study by Jafarzadeh et al. found that Cu favors physisorption of CO2, which, when placed in an electric field, switches to chemisorption by bending CO2 molecules.61Lastly, based on the understanding of the decisive role of the potential in catalysis, we can now revisit the “MSI” for innovative catalysis. Upon light illumination, the photon-induced charge transfer of the excited carriers between the metal particle and semiconductor support can provide a steady-state potential shift of the active surfaces, resulting in different thermal catalytic reactivity.62 For instance, choosing n- or p-type semiconductors as the support can determine the type of contact, either Schottky or ohmic, which additionally dictate the charge transfer at the interface.63 Using Pt supported on p- or n-GaN as a model, the groups of Lercher and Stutzmann studied the variation in the electronic structure of Pt.64 Its resultant catalysis was also altered; higher activity for thermal CO oxidation over Pt/n-GaN than over Pt/p-GaN was observed.62 The electride is another non-conventional support, where, according to the research of Hosono's group, by the electron donation from the support to the metal, the catalyst can not only lower the activation energy of ammonia synthesis over a Ru catalyst, but also suppress the poisoning of the Ru surface caused by H adatoms.65 The application of such novel materials to the support would open a new frontier of supported metal catalysis.
Summary
In this minireview, we highlighted how the catalyst potential plays a decisive role in catalytic reactions. First, we reviewed the determination of the catalyst potential with various experimental tools while concurrently measuring the reaction rate, which allows for quantitatively establishing the potential–rate relationship. Next, we showed that the active perturbation of the potential by electrochemical methods alters the catalyst WF and thereby the surface coverage of the adsorbate that functions as a promoter, poison, or reactant. Toward the end, we shared other examples that utilize an electric field or non-conventional catalyst–support, adding another viewpoint to the promoted thermal-catalytic reactions. Herein we provide a view bridging the field of thermal- and electro-catalysis, paving the way for innovative catalysis.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by JSPS KAKENHI Grant Number 19H02510 and 20K15084.References
- S. L. Foster, S. I. P. Bakovic, R. D. Duda, S. Maheshwari, R. D. Milton, S. D. Minteer, M. J. Janik, J. N. Renner and L. F. Greenlee, Nat. Catal., 2018, 1, 490–500 CrossRef.
- J. Sun and Y. Wang, ACS Catal., 2014, 4, 1078–1090 CrossRef CAS.
- K.-i. Shimizu and A. Satsuma, Energy Environ. Sci., 2011, 4, 3140–3153 RSC.
- Q. Tao, Y.-L. Zheng, D.-C. Jiang, Y.-X. Chen, Z. Jusys and R. J. Behm, J. Phys. Chem. C, 2014, 118, 6799–6808 CrossRef CAS.
- J. Greeley, J. K. Nørskov and M. Mavrikakis, Annu. Rev. Phys. Chem., 2002, 53, 319–348 CrossRef CAS.
- D. C. Koningsberger, J. de Graaf, B. L. Mojet, D. E. Ramaker and J. T. Miller, Appl. Catal., A, 2000, 191, 205–220 CrossRef CAS.
- P. Li, X. Duan, Y. Kuang, Y. Li, G. Zhang, W. Liu and X. Sun, Adv. Energy Mater., 2018, 8, 1703341 CrossRef.
- J. L. Gland and G. A. Somorjai, Surf. Sci., 1973, 38, 157–186 CrossRef CAS.
- M. Kiskinova, G. Pirug and H. P. Bonzel, Surf. Sci., 1983, 133, 321–343 CrossRef CAS.
- Y. Zhang, O. Pluchery, L. Caillard, A.-F. Lamic-Humblot, S. Casale, Y. J. Chabal and M. Salmeron, Nano Lett., 2015, 15, 51–55 CrossRef CAS.
- F. Zaera, Chem. Rev., 2012, 112, 2920–2986 CrossRef CAS.
- M. Yoshida, A. Yamakata, K. Takanabe, J. Kubota, M. Osawa and K. Domen, J. Am. Chem. Soc., 2009, 131, 13218–13219 CrossRef CAS.
- A. Ruban, B. Hammer, P. Stoltze, H. L. Skriver and J. K. Nørskov, J. Mol. Catal. A: Chem., 1997, 115, 421–429 CrossRef CAS.
- M. Qureshi, A. T. Garcia-Esparza, G. Jeantelot, S. Ould-Chikh, A. Aguilar-Tapia, J.-L. Hazemann, J.-M. Basset, D. Loffreda, T. Le Bahers and K. Takanabe, J. Catal., 2019, 376, 180–190 CrossRef CAS.
- T. W. van Deelen, C. Hernández Mejía and K. P. de Jong, Nat. Catal., 2019, 2, 955–970 CrossRef CAS.
- K. Aika, A. Ohya, A. Ozaki, Y. Inoue and I. Yasumori, J. Catal., 1985, 92, 305–311 CrossRef CAS.
- A. Bruix, J. A. Rodriguez, P. J. Ramírez, S. D. Senanayake, J. Evans, J. B. Park, D. Stacchiola, P. Liu, J. Hrbek and F. Illas, J. Am. Chem. Soc., 2012, 134, 8968–8974 CrossRef CAS.
- K.-i. Aika, T. Takano and S. Murata, J. Catal., 1992, 136, 126–140 CrossRef CAS.
- Y. Lykhach, S. M. Kozlov, T. Skála, A. Tovt, V. Stetsovych, N. Tsud, F. Dvořák, V. Johánek, A. Neitzel, J. Mysliveček, S. Fabris, V. Matolín, K. M. Neyman and J. Libuda, Nat. Mater., 2016, 15, 284–288 CrossRef CAS.
- F. Faisal, C. Stumm, M. Bertram, F. Waidhas, Y. Lykhach, S. Cherevko, F. Xiang, M. Ammon, M. Vorokhta and B. Šmíd, Nat. Mater., 2018, 17, 592–598 CrossRef CAS.
- S. A. Wasileski, M. J. Weaver and M. T. M. Koper, J. Electroanal. Chem., 2001, 500, 344–355 CrossRef CAS.
- S. A. Wasileski, M. T. M. Koper and M. J. Weaver, J. Chem. Phys., 2001, 115, 8193–8203 CrossRef CAS.
- M. Tsionsky, A. J. Bard and M. V. Mirkin, J. Phys. Chem., 1996, 100, 17881–17888 CrossRef CAS.
- M. Navarro, W. F. De Giovani and J. R. Romero, J. Mol. Catal. A: Chem., 1998, 135, 249–256 CrossRef CAS.
- A. Funakawa, I. Yamanaka, S. Takenaka and K. Otsuka, J. Am. Chem. Soc., 2004, 126, 5346–5347 CrossRef CAS.
- A. J. Bard and L. R. Faulkner, Electrochemical Methods: Fundamentals and Applications, John Wiley & Sons, Inc., New York, 2nd edn, 2001 Search PubMed.
- V. S. Protsenko and F. I. Danilov, J. Electroanal. Chem., 2011, 651, 105–110 CrossRef CAS.
- A. B. Anderson and T. V. Albu, Electrochem. Commun., 1999, 1, 203–206 CrossRef CAS.
- Y. Wei, K. F. Hsueh and G.-W. Jang, Polymer, 1994, 35, 3572–3575 CrossRef CAS.
- G. Horanyi, Catal. Today, 1994, 19, 285–311 CrossRef CAS.
- J. A. S. Roberts and R. M. Bullock, Inorg. Chem., 2013, 52, 3823–3835 CrossRef CAS.
- L. Jelemensky, B. F. M. Kuster and G. B. Marin, Ind. Eng. Chem. Res., 1997, 36, 3065–3074 CrossRef CAS.
- J. H. Vleeming, B. F. M. Kuster and G. B. Marin, Ind. Eng. Chem. Res., 1997, 36, 3541–3553 CrossRef CAS.
- T. Mallat and A. Baiker, Catal. Today, 1995, 24, 143–150 CrossRef CAS.
- A. Mills, Chem. Soc. Rev., 1989, 18, 285–316 RSC.
- C. G. Vayenas, S. Bebelis, C. Pliangos, S. Brosda and D. Tsiplakides, Electrochemical activation of catalysis: promotion, electrochemical promotion, and metal–support interactions, Springer Science & Business Media, 2001 Search PubMed.
- M. Stoukides and C. G. Vayenas, J. Catal., 1981, 70, 137–146 CrossRef CAS.
- A. Katsaounis, J. Appl. Electrochem., 2010, 40, 885–902 CrossRef CAS.
- A. de Lucas-Consuegra, J. González-Cobos, Y. García-Rodríguez, A. Mosquera, J. L. Endrino and J. L. Valverde, J. Catal., 2012, 293, 149–157 CrossRef CAS.
- I. Kalaitzidou, M. Makri, D. Theleritis, A. Katsaounis and C. G. Vayenas, Surf. Sci., 2016, 646, 194–203 CrossRef CAS.
- A. Kotsiras, I. Kalaitzidou, D. Grigoriou, A. Symillidis, M. Makri, A. Katsaounis and C. G. Vayenas, Appl. Catal., B, 2018, 232, 60–68 CrossRef CAS.
- D. Poulidi and I. S. Metcalfe, Chem. Eng. Sci., 2010, 65, 446–450 CrossRef CAS.
- I. Kalaitzidou, A. Katsaounis, T. Norby and C. G. Vayenas, J. Catal., 2015, 331, 98–109 CrossRef CAS.
- S. G. Neophytides, D. Tsiplakides, P. Stonehart, M. M. Jaksic and C. G. Vayenas, Nature, 1994, 370, 45–47 CrossRef CAS.
- S. G. Neophytides, D. Tsiplakides, P. Stonehart, M. Jaksic and C. G. Vayenas, J. Phys. Chem., 1996, 100, 14803–14814 CrossRef CAS.
- D. Labou and S. G. Neophytides, Top. Catal., 2007, 44, 451–460 CrossRef CAS.
- E. Ruiz-López, A. Caravaca, P. Vernoux, F. Dorado and A. de Lucas-Consuegra, Chem. Eng. J., 2020, 396, 125217 CrossRef.
- J. Sanabria-Chinchilla, K. Asazawa, T. Sakamoto, K. Yamada, H. Tanaka and P. Strasser, J. Am. Chem. Soc., 2011, 133, 5425–5431 CrossRef CAS.
- Y. Song, U. Sanyal, D. Pangotra, J. D. Holladay, D. M. Camaioni, O. Y. Gutiérrez and J. A. Lercher, J. Catal., 2018, 359, 68–75 CrossRef CAS.
- E. Lamy-Pitara, S. El Mouahid and J. Barbier, Electrochim. Acta, 2000, 45, 4299–4308 CrossRef CAS.
- F. Cai, D. Gao, H. Zhou, G. Wang, T. He, H. Gong, S. Miao, F. Yang, J. Wang and X. Bao, Chem. Sci., 2017, 8, 2569–2573 RSC.
- T. Bligaard, J. K. Nørskov, S. Dahl, J. Matthiesen, C. H. Christensen and J. Sehested, J. Catal., 2004, 224, 206–217 CrossRef CAS.
- J. Ryu and Y. Surendranath, J. Am. Chem. Soc., 2020, 142, 13384–13390 CrossRef CAS.
- S. Brosda, C. G. Vayenas and J. Wei, Appl. Catal., B, 2006, 68, 109–124 CrossRef CAS.
- L. J. Burcham, L. E. Briand and I. E. Wachs, Langmuir, 2001, 17, 6164–6174 CrossRef CAS.
- D. Malko, A. Kucernak and T. Lopes, Nat. Commun., 2016, 7, 1–7 Search PubMed.
- C. M. Gunathunge, J. Li, X. Li and M. M. Waegele, ACS Catal., 2020, 10, 11700–11711 CrossRef CAS.
- R. Manabe, H. Nakatsubo, A. Gondo, K. Murakami, S. Ogo, H. Tsuneki, M. Ikeda, A. Ishikawa, H. Nakai and Y. Sekine, Chem. Sci., 2017, 8, 5434–5439 RSC.
- Y. Sekine and R. Manabe, Faraday Discuss., 2020 10.1039/C9FD00129H.
- F. Che, J. T. Gray, S. Ha, N. Kruse, S. L. Scott and J.-S. McEwen, ACS Catal., 2018, 8, 5153–5174 CrossRef CAS.
- A. Jafarzadeh, K. M. Bal, A. Bogaerts and E. C. Neyts, J. Phys. Chem. C, 2020, 124, 6747–6755 CrossRef CAS.
- S. M. Kim, D. Park, Y. Yuk, S. H. Kim and J. Y. Park, Faraday Discuss., 2013, 162, 355–364 RSC.
- H. Zhong, Z. Liu, G. Xu, Y. Fan, J. Wang, X. Zhang, L. Liu, K. Xu and H. Yang, Appl. Phys. Lett., 2012, 100, 122108 CrossRef.
- S. Schäfer, S. A. Wyrzgol, R. Caterino, A. Jentys, S. J. Schoell, M. Hävecker, A. Knop-Gericke, J. A. Lercher, I. D. Sharp and M. Stutzmann, J. Am. Chem. Soc., 2012, 134, 12528–12535 CrossRef.
- M. Kitano, Y. Inoue, Y. Yamazaki, F. Hayashi, S. Kanbara, S. Matsuishi, T. Yokoyama, S.-W. Kim, M. Hara and H. Hosono, Nat. Chem., 2012, 4, 934–940 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |