Open Access Article
Open Access ArticleBridging photochemistry and photomechanics with NMR crystallography: the molecular basis for the macroscopic expansion of an anthracene ester nanorod†
Kevin R.
Chalek
a,
Xinning
Dong
a,
Fei
Tong
a,
Ryan A.
Kudla
a,
Lingyan
Zhu
a,
Adam D.
Gill
b,
Wenwen
Xu
e,
Chen
Yang
a,
Joshua D.
Hartman
 a,
Alviclér
Magalhães
a,
Alviclér
Magalhães
 c,
Rabih O.
Al-Kaysi
c,
Rabih O.
Al-Kaysi
 d,
Ryan C.
Hayward
d,
Ryan C.
Hayward
 e,
Richard J.
Hooley
e,
Richard J.
Hooley
 a,
Gregory J. O.
Beran
a,
Gregory J. O.
Beran
 a,
Christopher J.
Bardeen
a,
Christopher J.
Bardeen
 *a and
Leonard J.
Mueller
*a and
Leonard J.
Mueller
 *a
*a
aDepartment of Chemistry, University of California-Riverside, Riverside, CA 92521, USA. E-mail: leonard.mueller@ucr.edu; christopher.bardeen@ucr.edu
bDepartment of Biochemistry, University of California-Riverside, Riverside, CA 92521, USA
cDepartment of Organic Chemistry, Institute of Chemistry, Federal University of Rio de Janeiro, Rio de Janeiro, RJ 21941-909, Brazil
dCollege of Science and Health Professions-3124, King Saud Bin Abdulaziz University for Health Sciences, King Abdullah International Medical Research Center, Ministry of National Guard Health Affairs, Riyadh 11426, Kingdom of Saudi Arabia
eDepartment of Chemical and Biological Engineering, University of Colorado Boulder, 3415 Colorado Ave., Boulder, CO 80303, USA
First published on 30th October 2020
Abstract
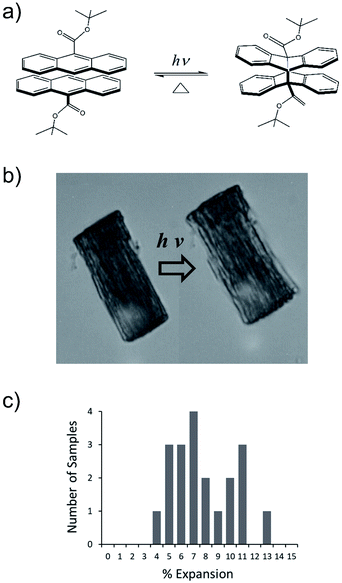
Crystals composed of photoreactive molecules represent a new class of photomechanical materials with the potential to generate large forces on fast timescales. An example is the photodimerization of 9-tert-butyl-anthracene ester (9TBAE) in molecular crystal nanorods that leads to an average elongation of 8%. Previous work showed that this expansion results from the formation of a metastable crystalline product. In this article, it is shown how a novel combination of ensemble oriented-crystal solid-state NMR, X-ray diffraction, and first principles computational modeling can be used to establish the absolute unit cell orientations relative to the shape change, revealing the atomic-resolution mechanism for the photomechanical response and enabling the construction of a model that predicts an elongation of 7.4%, in good agreement with the experimental value. According to this model, the nanorod expansion does not result from an overall change in the volume of the unit cell, but rather from an anisotropic rearrangement of the molecular contents. The ability to understand quantitatively how molecular-level photochemistry generates mechanical displacements allows us to predict that the expansion could be tuned from +9% to −9.5% by controlling the initial orientation of the unit cell with respect to the nanorod axis. This application of NMR-assisted crystallography provides a new tool capable of tying the atomic-level structural rearrangement of the reacting molecular species to the mechanical response of a nanostructured sample.
1. Introduction
The creation of new stimuli-responsive materials is a central goal in chemistry. Although many such materials are based on polymers, over the last decade molecular crystals have become recognized as dynamic, mechanically responsive structures.2 Dramatic examples of this dynamic nature involve photomechanical effects, where crystals composed of photochemically reactive molecules undergo a variety of mechanical deformations when exposed to light, including bending,3–15 twisting,16–18 peeling,19,20 and rotational/translational motion.21–24 In most cases, the photomechanical effect can be understood as resulting from the formation of a bimorph structure within the crystal: spatially distinct regions of incommensurate reactant and product phases lead to interfacial strain that drives the shape change. If the crystal is transformed from 100% reactant to 100% product, there is no interfacial strain and thus no bending.25,26Reactant-product interfacial stress is not the only way to obtain photomechanical motion: a complete single-crystal-to-single-crystal transformation can generate even greater amounts of work via expansion. There are many examples of single crystal polymorphic phase transformations that lead to shape changes and mechanical motion.27–30 These mechanically active crystal transitions usually rely on heat or mechanical stimuli to drive the change in crystal packing arrangements – no actual chemical change takes place, just a shifting of the molecules within the crystal lattice. An analogous phase change can be achieved in a molecular crystal during a photochemical reaction. In this case, molecular photoisomerization changes the local crystal packing, which in turn drives large-scale changes in crystal shape. From a practical standpoint, a negative photochromic system is required in order to achieve full reaction so that the photoproduct does not absorb the incoming light.31–33 Furthermore, crystal fracture and disintegration are common in macroscopic photoreactive crystals, necessitating the use of micro- or nanoscale crystals in order to limit internal strain build-up.34–37
We have developed a family of 9-anthracene esters that undergo a [4 + 4] photodimerization reaction in crystal form,38 for which 9-tert-butyl-anthracene ester (9TBAE) is the most studied example. When grown as single-crystal nanorods, the 9TBAE crystal-to-crystal photodimerization reaction (Fig. 1a) leads to a unique crystal phase – the solid-state reacted dimer (SSRD) – and large expansion along the rod axis with a slight contraction across its diameter. The large directional expansion has the potential to perform linear actuation, similar to the anisotropic expansion of piezoelectric crystals that allows them to function as mechanical actuators. The photoinduced expansion of 9TBAE nanorods was first observed in 2006,39 but exactly how the molecular-level geometry changes yield the observed expansion has remained a mystery. In many photomechanical systems, a unit cell expansion/contraction is invoked to qualitatively describe bending phenomena derived from reactant/produce interfacial strain. However, the 9TBAE system provides a unique case of 100% conversion, so in principle knowledge of the reactant and product crystal structures should allow us to quantitatively predict the expansion. But previous attempts to rationalize the observed photochemical transformation in 9TBAE nanorods based on changes in the unit cell volume incorrectly predicted that nanorods should shrink by 1.2%, rather than expand by 8%.40 Clearly, knowledge of the reactant and product crystal structures is not sufficient to predict the photomechanical response of the material.
In favorable cases, traditional single-crystal X-ray diffraction methods can be used to determine the structural rearrangements induced by photodimerization. But the useful photomechanical response only occurs in 9TBAE nanorods. Larger crystals fragment and disintegrate due to the buildup of internal strain, so a structural characterization method that can be adapted to the nanorod sample is necessary. Furthermore, it is vital to be able to connect crystal structure changes with the photochemical reaction progress. NMR is often used to monitor chemical changes, and although 13C-labeling is usually required to increase sensitivity, it can also be used to assess crystal packing and orientation. In this article, we describe a new approach that combines ensemble oriented-crystal NMR spectroscopy and first-principles computational chemistry to determine the absolute unit cell orientations relative to the shape change in a photoreactive, molecular crystal, 9TBAE nanorod. Solid-state NMR (SSNMR) has been used to study a number of solid-state photochemical transformations,25,38,40–52 and foundational work by Nieuwendaal, Hayes and coworkers53 demonstrated how single-crystal NMR could be used to determine the relative orientation of the reactant and product in the single-crystal to single-crystal topochemical photoreaction of trans-cinnamic acid. Our work builds on this approach and for the first time uses SSNMR to tie the atomic-level structural rearrangement of the reacting molecular species to the mechanical response of a nanostructured sample. We deduce the absolute monomer and dimer crystal orientations within the 9TBAE nanorods and develop a quantitative molecular-level model of the photochemical reaction that predicts a macroscopic elongation of 7.4%, in good agreement with the experimental value. Our analysis demonstrates that both the molecular shape change of the reacting unit and the molecular reorientation relative to the nanoscale crystal must be considered.54 Based on these observations, we predict that tailoring the alignment of the 9TBAE monomer crystal unit cell with respect to the nanorod axis can tune the mechanical response from a 9% expansion to a 9.5% contraction. The results demonstrate how the synergistic combination of SSNMR spectroscopy, X-ray diffraction, and first-principles computational chemistry – an integrated approach often referred to as NMR-assisted crystallography55–69 – can provide crucial insights for engineering new crystal-based responsive materials.
2. Results and discussion
2.1. Nanorod expansion
The expansion of 9TBAE nanorods grown in an AAO template is a general phenomenon, but there is some variability in the magnitude of the effect, even within a single sample. The photodimerization reaction is illustrated in Fig. 1a. Optical microscopy images of a bundle of rods before and after 365 nm irradiation are shown in Fig. 1b, and a histogram of the expansion for individual nanorods is shown in Fig. 1c. The average expansion is 8 ± 2%, with some expanding as much as 13% and others as little as 5%. Both PXRD and SSNMR measurements have confirmed that the solid-state photodimerization occurs in the AAO growth templates as well, and previous SEM images showed that the nanorods expand vertically even when confined in the template.39 Therefore, we assume that any insights gained from studies on 9TBAE nanorods aligned in the AAO template are relevant to the dynamics occurring in individual nanorods as well.2.2. Unit cell orientations from NMR crystallography
Given that the nanorods expand, the next task is to establish the orientation of the 9TBAE unit cells with respect to the shape change. SSNMR provides one approach for determining absolute crystal orientation based on the inherent spatial anisotropy of the interactions.1,70,71 NMR observables such as chemical shift and dipolar coupling depend not only on the local molecular and electronic structure, but also on molecular orientation with respect to the laboratory-frame magnetic field. Measuring chemical shifts as a function of crystal orientation is a classic way to obtain molecular chemical shift tensors and orient them with respect to the crystal and molecular frames.72 Conversely, if the magnitude and positioning of the relevant tensors within the molecular frame are known, then single-crystal NMR spectra can be used to align the unit cell relative to the magnetic field.53Our previous determination of the monomer and SSRD crystal structures40 allows the required dipolar and chemical shift tensors to be obtained. Dipolar tensors can be placed directly on the molecular frame based on the molecular coordinates,1 while chemical shift tensors can be predicted very accurately from the three-dimensional geometry using first-principles computational methods.73 We recently reported first-principles chemical shifts for the 9TBAE monomer and SSRD species in the solid state, calculated using DFT.40,73 These computationally predicted shifts showed good agreement with the experimentally measured isotropic chemical shifts (monomer and SSRD) and chemical shift tensors (SSRD). The tensor components for monomeric 9TBAE were not part of the previous study, so select tensors were measured and are compared to the first-principles values in the ESI.† The dipolar and shift tensor values are summarized in the ESI† for each of the asymmetric units in the monomer and SSRD unit cells.
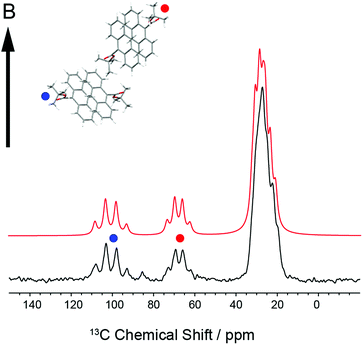
In order to establish the dynamic molecular features necessary to model the NMR spectrum, we first investigated a large single crystal of 9TBAE prepared 13C labeled on the ester moiety t-butyl group (13C4-t-Bu-9TBAE). The 13C solid-state NMR spectrum of this bulk single crystal in Fig. 2 shows two magnetically inequivalent t-butyl groups, corresponding to two distinct arrangements of the asymmetric unit relative to the magnetic field. Note that the sample yields a well-resolved spectrum without the customary magic angle spinning because it is a single crystal as opposed to a randomly oriented powder. The spectrum is consistent with fast rotation of the t-butyl group about the O–C ester bond, leading to three dynamically-equivalent methyl carbons (centered at 30 ppm) and a simplified multiplet pattern for the two magnetically inequivalent quaternary carbons (centered at 70 and 100 ppm, respectively) that each show an average dipolar coupling to their respective three methyl carbons with a roughly 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3
3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 intensity pattern. The methyl resonances in these spectra are more complicated because they are modulated not only by the dipolar coupling back to the quaternary carbon, but also by the 13C dipolar couplings between the three methyl groups; unlike J-couplings between magnetically-equivalent sites, these methyl group dipolar couplings do alter the spectrum. Full numerical density matrix simulations of this four-spin system (vide infra) support these interpretations.
1 intensity pattern. The methyl resonances in these spectra are more complicated because they are modulated not only by the dipolar coupling back to the quaternary carbon, but also by the 13C dipolar couplings between the three methyl groups; unlike J-couplings between magnetically-equivalent sites, these methyl group dipolar couplings do alter the spectrum. Full numerical density matrix simulations of this four-spin system (vide infra) support these interpretations.
Knowledge of the chemical shift and dipolar tensors for 9TBAE allows this spectrum to be used to uniquely align the crystal relative to the laboratory frame magnetic field. Fig. 3 shows the predicted quaternary carbon NMR spectrum as a function of the unit cell orientation in the laboratory frame, defined by Euler angles β and γ using an active rotation convention.71 The methyl carbons are omitted for clarity. By scanning these angles to find the best match with experiment, the orientation of the single crystal in the magnetic field can be determined; in this case the crystal frame is rotated from initial alignment with the laboratory frame by Euler angles β = 19.2° and γ = 73.8° to give its final orientation in the magnetic field. The full dynamically-averaged CSA and dipolar tensors were considered in the four-spin numerical density matrix simulations used to predict the best-fit spectrum shown in Fig. 2.
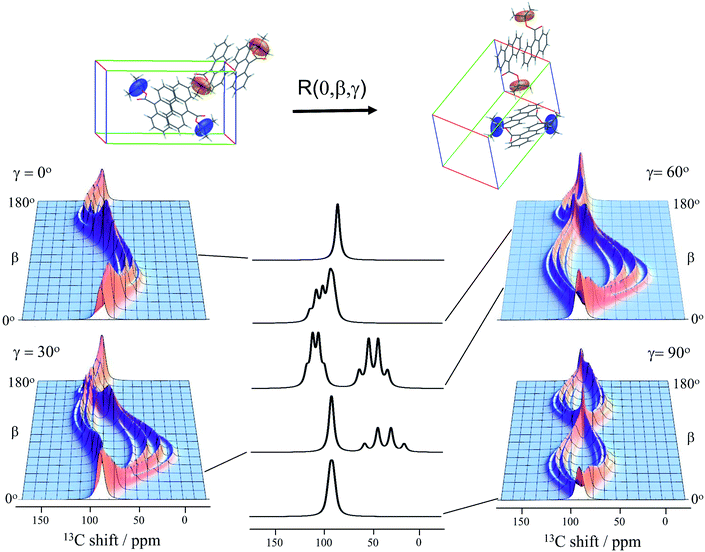 | ||
| Fig. 3 The predicted 13C4-t-Bu-9TBAE single crystal 13C solid-state NMR spectrum as a function of unit cell orientation relative to laboratory frame magnetic field. In these simulations, only the quaternary carbon resonances are shown and strong coupling effects are neglected. The dipolar and chemical shielding tensors used to generate these simulations were determined via first-principle calculations as described in the text and are fixed relative to the unit cell. As the unit cell rotates, the resulting spectral parameters are modulated, giving rise to orientation-dependent spectra. The magnetically equivalent chemical shift tensors for asymmetric units related by inversion symmetry are shown in the same color, while the magnetically inequivalent tensors are colored independently. Molecules and tensors are rendered in TensorView1.4.1 | ||
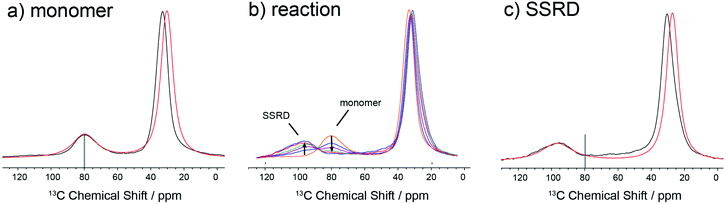
The data in Fig. 3 show how it is possible to use SSNMR spectra to obtain the absolute orientation of a 9TBAE crystal with respect to the magnetic field. However, the 9TBAE nanorods are too small to be studied individually with single-crystal NMR. Rather, a bulk ensemble of uniformly oriented single-crystal nanorods was left within the AAO growth template and placed into a flat coil NMR probe with their rod axes aligned parallel to the static magnetic field. As the nanorods grow normal to the disk-shaped template surface,39 this uniform alignment was accomplished by positioning the disk perpendicular to the field (Fig. S2†). Fig. 4a shows the resulting 13C solid-state NMR spectrum of the 13C4-t-Bu-9TBAE monomeric nanorods. Although each crystalline nanorod within the template can potentially have a distinct azimuthal displacement, the observed NMR spectrum is insensitive to this angle when the rod axis is aligned along the magnetic field, giving spectra with reasonably good resolution. That a single axis of alignment allows for high resolution NMR studies is well-known in other contexts, such as oriented bilayer systems.74
There are several qualitative differences between the single crystal and nanorod spectra. First, the NMR resonances of the nanorod sample are broadened compared to those of the bulk single crystal. This broadening cannot be ascribed to (orientation-dependent) intermolecular dipole–dipole couplings between the 13C-labeled moieties in this static solid as the single crystal spectrum in Fig. 2 was acquired with the same labeling density and shows no such broadening; additional experiments performed on nanorods prepared using 10% labeled monomer confirm this and show this same broad set of resonances (Fig. S10†). Rather, these line widths can be reproduced by assuming a Gaussian distribution of alignment angles with a standard deviation of ±3.6° as detailed in the ESI.† Second, only a single resonance is observed for the quaternary carbons. This places restrictions on the alignment of the monomer unit cells, which must have the previously distinct quaternary carbons in magnetically equivalent orientations. This is confirmed when the unit cells are rigorously oriented with respect to the magnetic field by once more tracking the agreement between the experimental and predicted quaternary carbon spectral frequencies. The error surface (residuals squared) for this analysis is shown in Fig. S7 (ESI†), and the best-fit spectrum in Fig. 4a (red trace) corresponds to an 84.4° rotation of the unit cell along the crystallographic b axis with Euler angles β = 84.4° and γ = 180°. For reference, the closest Miller plane perpendicular to the rod axis is (13,0,−1), which is tilted 4° from the (1,0,0) Miller plane and has a normal 5.6° off the real space [1,0,0] axis.
Fig. 4b shows the evolution of the SSNMR spectrum during the photodimerization reaction. After each irradiation period, the sample is removed from the light and placed in the NMR spectrometer to obtain a 13C spectrum. There is a clear transition from the monomer to the SSRD, with the quaternary carbon shifting downfield and broadening slightly, and an isosbestic point is observed, consistent with a two-state single-crystal-to-single-crystal reaction model. While acquisition of these spectra is time-consuming (9 h. each), the integrated NMR signals are proportional to the chemical concentrations (within certain limits under cross-polarization75,76) at the end of the irradiation periods, which allows us to quantitatively follow the course of the dimerization reaction. Fig. 4c shows the spectrum of the fully converted SSRD nanorods. As with the monomer, only a single quaternary resonance is observed, signaling that the sites remain magnetically equivalent. Again, the orientation-dependent spectra can be predicted and scanned to determine the alignment of the dimer unit cell in the magnetic field and therefore relative to the rod axis. The error surface for this scan is given in Fig. S8 (ESI†) and the best-fit agreement (red trace, Fig. 4c) corresponds to a 144.5° rotation of the unit cell along the crystallographic a axis (Euler angles β = 144.5° and γ = 90.0°). For reference, the nearest low index Miller plane is (0,1,−2), which is tilted 2.3° off of this plane, while the [0,1,−1] real space axis is 2° off of the plane normal.
To confirm the crystal orientations deduced from the SSNMR experiments, GIWAXS measurements were also undertaken on the oriented AAO templates. The GIWAXS experiment acquires diffraction information across a range of angles, so it is sensitive to crystal planes with different orientations with respect to the surface plane. The GIWAXS results show a good match with SSNMR, with absolute alignments differing by only 5.6° for the monomer and 2° for the dimer. The full details of the GIWAXS experiments and their analysis are given in the ESI.†
2.3. Connecting photochemical structural rearrangement to photochemical crystal expansion
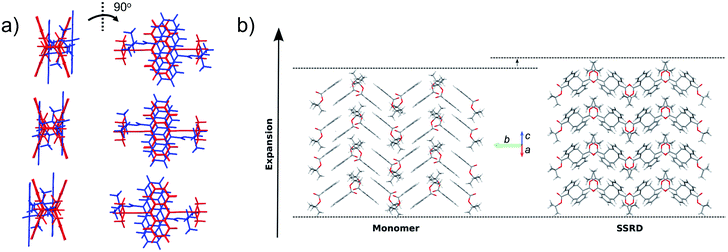
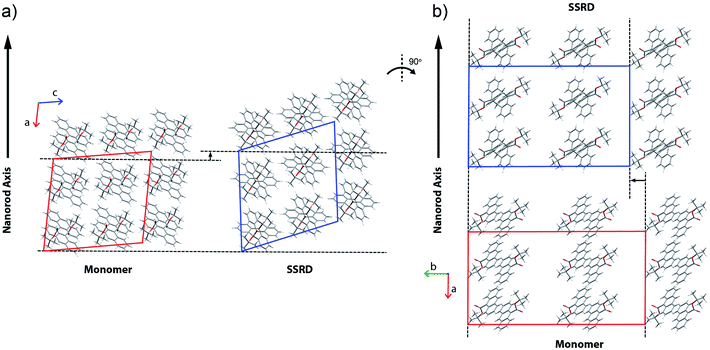
Given the absolute crystal orientations before and after the photochemical reaction, the molecular-level basis for the macroscopic response of the 9TBAE nanorods can be delineated. Our starting point is atomic, focusing on the how photodimerization alters the bonding and structural arrangements. Fig. 5a shows the overlay of the molecular contents in the oriented monomer and SSRD unit cells. While the overall molecular positions overlap almost perfectly, the solid-state [4 + 4] photocycloaddition reaction generates several key atomic displacements that drive the photomechanical response. Note that initially the monomer anthracene rings are packed slightly offset. As the photoreaction occurs, the newly formed carbon–carbon bonds pull the rings into registry, while at the same time the planes bend out to accommodate the new sp3 hybridization at the central carbons. This “butterfly” motion opens up space above and below the dimers that allows adjacent pairs to stack more efficiently along the direction of the anthracene rings. During this reconfiguration, the t-butyl ester groups remain essentially fixed with respect to the anthracene core; this is in contrast to their 180° outward rotation for the polymorph crystallized out of solution.38 Overall, this minimum displacement reaction pathway is consistent with the topochemical principle – the solid-state monomers dimerize with minimal disruption to the crystal packing/ester side chain conformations.77–79 Moving one level out, the effect of these molecular geometry changes on the crystal packing can be seen most clearly by looking at a single layer of herringbone pairs. Fig. 5b shows how the atomic-level reconfiguration translates into a net expansion as the now protruding phenyl groups push the herringbone pairs apart.The nanorods are three-dimensional macroscopic objects, and the final step is to understand how the herringbone pair expansion projects into this space. Fig. 6 shows the absolute molecular orientations of the monomer and SSRD relative to the nanorod axis, which are key to understanding the photomechanical response. The molecular expansion identified in Fig. 5b lies along the diagonal of the monomer unit cell ac plane, but as seen in Fig. 6a only a component of this expansion falls along the nanorod axis. The elongation of the nanorod is aided, however, by a slight tilt of the dimer unit cell as each successive layer of dimers adjusts its position to partially compensate for the expansion of the neighboring herringbone pair. This layer shift also leads to a significant contraction perpendicular to the rod axis (Fig. 6b). We had previously observed this contraction but could not absolutely quantify it due to the small feature size (it is harder to resolve a 9% change in 200 nm than an 8% change over 60 μm). According to this analysis, molecular shape change and spatial/unit cell rotation are both operative in the 9TBAE photomechanical response.
The qualitative observations above on crystal packing changes and mechanical displacements can be quantified in a unit cell based model of the photomechanical single-crystal to single-crystal transformation. During the crystal reconfiguration, the monomer unit cell axes (am, bm, and cm) morph into the transformed dimer unit cell axes 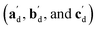 . For a general photoreaction, the transformed axes do not necessarily correspond to the minimum unit cell obtained from a standard XRD analysis, which due to unique symmetries could be drawn quite differently for two species. Rather, the transformed unit cell is chosen to provide a 1-to-1 atom mapping of the monomer to dimer transformation, which facilitates comparisons between the crystal forms; these are the axes shown in Fig. 6. Using this approach, the displacement upon photoreaction of any point in the monomer crystal can be determined by first representing it in fractional coordinates of the monomer unit cell
. For a general photoreaction, the transformed axes do not necessarily correspond to the minimum unit cell obtained from a standard XRD analysis, which due to unique symmetries could be drawn quite differently for two species. Rather, the transformed unit cell is chosen to provide a 1-to-1 atom mapping of the monomer to dimer transformation, which facilitates comparisons between the crystal forms; these are the axes shown in Fig. 6. Using this approach, the displacement upon photoreaction of any point in the monomer crystal can be determined by first representing it in fractional coordinates of the monomer unit cell
| r = uam + vbm + wcm | (1) |
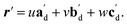 | (2) |
As noted above, the broadened NMR resonances for the monomer nanorods can be fit to a Gaussian distribution of alignment angles with a standard deviation of 3.6° for the unit cell relative to the nanorod axis (Fig. S11, ESI†). Based on the assumptions that the relative orientation of the monomer and SSRD unit cells is fixed during the photochemical reaction, this same distribution in the initial orientation of the monomer unit cell would predict a spread (95% confidence limits) in the expansion of 7.4 ± 1.5%. The experimental and theoretical predictions for the distribution in the expansion therefore also agree to within experimental error. The variable crystal alignment most likely results from small variations in the growth direction along the AAO pore channels. It is possible that more uniform channels would lead to more aligned nanorods and less variability in the expansion. The ability to characterize this distribution with atomic resolution in inhomogeneous samples is a salient feature of NMR-assisted crystallography.
2.4. Roadmap for engineered photomechanical response
Our results demonstrate how knowledge of the relative orientations of the 9TBAE monomer and dimer unit cells makes it possible to quantitatively predict the magnitude of the photomechanical crystal shape change. This result presents a novel opportunity: if the initial alignment of the monomer unit cell relative to the nanorod axis could be controlled, either through self-assembly or by precision cutting from bulk single crystals,80 a variable mechanical response could be engineered. Using the model developed here, we systematically explored different starting unit cell orientations, and found that a maximum expansion of 9% could be obtained for rods in which the monomer is arranged with its crystallographic c axis 15° off of the nanorod axis (Euler angles {β = 75°, γ = 0°}). This orientation nearly aligns the full butterfly expansion axis (the ac face diagonal in Fig. 5) along the rod axis. Alternatively, a contraction of 9.5% was found for nanorods in which the monomer crystallographic b axis was initially aligned along the nanorod axis. This corresponds to a rotation of the crystal in Fig. 5b by 90° about the axis perpendicular to the page.Crystal engineering concentrates on controlling the local molecular packing within a crystal to yield desired material properties, often by varying the molecular structure through synthetic modification. The results here suggest an alternative approach – controlling the molecular orientation with respect to the macroscopic crystal shape. For 9TBAE, our results suggest that such an approach can yield a dynamic range of nearly 20% in length change. Crystal shape engineering may be a fruitful avenue to produce photomechanical materials that generate extraordinarily large strains, even for standard photochromes that show little response in their natural habit.
Conceivably, one might hope to engineer the combination of molecular structure, crystal packing, and orientation to achieve a material with a specific dynamic range of motion. Given how even small changes in molecular structure can lead to completely different packing motifs, computational crystal structure prediction could be helpful.81 Crystal structure prediction has recently been employed to discover materials with desired porosity82 or organic semiconducting properties,83,84 for example. The photomechanical materials described here would provide an even stiffer challenge, since knowledge of the crystal structure before and after the photochemical reaction is required. Crystal structure prediction for the reactant species would be relatively straightforward. On the other hand, structure prediction for the photodimer product is complicated by the fact that the crystal-to-crystal photochemical transformation can produce polymorphs that are substantially less stable than those that occur under traditional crystallization conditions.85 This makes it hard to identify the correct photodimer product structure from the many hypothetical higher-energy crystal structures typically generated in a structure prediction study.86 On the other hand, it might be possible to identify the photodimer structure by comparing the relationships between potential photodimer crystal packings with that of the unreacted monomer crystal. Once the crystal structures are known, one would determine the optimal crystal orientation for achieving the desired dynamic range and then design an experimental strategy for producing the crystals accordingly.
3. Conclusion
A combined solid-state NMR, diffraction, and computational approach has been used to establish the atomic-resolution, molecular mechanism for the macroscopically-observed photomechanical expansion of 9TBAE nanorods. Key to its success was the determination of the absolute orientations of the monomer and SSRD unit cells relative to the nanorod axis. For the first time, we can precisely map out how photochemical changes shift both molecular alignment and packing in a photomechanical crystal, allowing us to predict an expansion of 7.4%, in very good quantitative agreement with the experimental value of 8%. Packing defects and disorder will affect the observed expansion of individual rods but do not appear to play a dominant role. Thus it should be possible to develop quantitative structure–function relations that can be used to optimize molecular crystal photomechanical systems. The results in this paper also point to a need for more sophisticated theoretical approaches that enable the a priori prediction of crystal photomechanical motions. A combination of theory and experiment should enable the design of crystalline photomechanical materials with greater energy densities and higher strains, leading to applications in photon-powered actuators from smart materials to medicine.87 Finally, this approach points to a new use of NMR-assisted crystallography that moves beyond the description of static structures to the characterization of chemical reactivity and mechanism, a theme shared by concomitant development and emerging applications of NMR-assisted crystallography in biological chemistry.69,88,894. Experimental
4.1. Preparation of 9TBAE nanorods inside AAO templates
The 9TBAE crystalline nanorods were grown using the solvent annealing method.36,39 5 mg of 9TBAE was dissolved in 100 μL of HPLC grade tetrahydrofuran. The solution was deposited on an anodized aluminum oxide (AAO) template (Whatman Anodisc, 13 mm diameter, 60 μm thickness, 200 nm pore diameter) which was supported by a Teflon ring to allow for vapor circulation. The template and Teflon holder were then covered by a glass bell-jar along with a cotton ball saturated by THF. At room temperature, the solvent evaporated slowly inside bell jar and allowed the 9TBAE to recrystallize inside AAO channels. After 24 hours, the template was totally dry. A 1500 grit sandpaper was used to polish away residual 9TBAE on the template surface.4.2. Preparation of 13C labeled 9TBAE
9TBAE was prepared with two separate 13C labeling patterns as described in the ESI.† The first was 13C labeled on the ester moiety t-butyl groups (13C4-t-Bu-9TBAE) and the second on the ester carbonyl group (13C15-9TBAE).4.3. 9TBAE nanorod expansion
Isolated nanorods and bundles were prepared by dissolving the AAO templates containing 9TBAE nanorods in 30% phosphoric acid with 0.2 wt% SDS, leaving an aqueous suspension that could be deposited on a microscope slide. The nanorod suspension was irradiated by a 365 nm light source in an Olympus IX-70 microscope with 20 mW cm−2 average intensity. Nanorod expansion was observed after several seconds, and the expansion was measured by analysis of the optical images before and after irradiation.4.4. First-principles geometries and chemical shift calculations
First-principles refined solid-state structures and chemical shifts for the 9TBAE monomer73 and SSRD40 were previously reported as part of benchmarking and NMR-assisted crystallographic studies, respectively. In brief, solid-state geometry optimizations were first performed using the freely available Quantum Espresso (QE) software package,90 using the PBE density functional and the D2 dispersion correction,91 ultrasoft pseudopotentials with a plane wave cut off of 80 Ry, and a 3 × 3 × 3 Monkhorst–Pack k-point grid. The pseudopotentials H.pbe-rrkjus.UPF, C.pbe-rrkjus.UPF, and O.pbe-rrkjus.UPF from http://www.quantum-espresso.org were used. These structures were used for NMR chemical shift calculations, performed using a fragment-based cluster approach with fragmentation carried out using a hybrid many-body interaction code92 and including pair-wise contributions from all molecules (asymmetric units) lying within 6 Å. Individual shielding tensor calculations were performed using Gaussian09 at the PBE0/6-311+G(2d,p) level and employing the mixed basis scheme previously reported.73,93 In these calculations, electrostatic point-charge embedding was employed out to a radius of 30 Å. Calculated 13C chemical shieldings (σ) were converted to chemical shifts (δ) using the linear rescaling relation73,93δ[TMS(l)] = (−0.9674)σcalc + 179.5. Benchmarking studies have demonstrated good agreement between experimental and computationally-predicted chemical shifts, with root-mean-square-errors (RMSE) of 1.4 ppm for isotropic shifts, 3.2 ppm for aliphatic and aromatic shift tensor components, and 9.2 ppm for tensor components of sp2 carbons directly bonded to oxygen and nitrogen atoms.73,93The crystal information files (CIF) for the 9TBAE monomer and SSRD structures are included in the ESI,† along with a summary of the chemical shift and dipolar tensors for the relevant sites.
4.5. Oriented-crystal NMR
Solid-state 13C NMR spectra of the ensemble-oriented 9TBAE monomer and solid-state reacted dimer crystals were acquired at 9.4 T (400.37 MHz 1H, 100.68 MHz 13C) on a Bruker AVANCE III spectrometer equipped with a homebuilt double resonance solid-state NMR probe fitted with a static flat coil (Fig. S2†). The coil was wound in 4 turns from 2 mm wide high-oxygen free copper flat wire, with overall coil dimensions of 14 mm × 14 mm × 3 mm. The coil was positioned with the largest side perpendicular to the magnetic field and could be shimmed to a 13C line width of 3 ppm on a static sample of adamantane powder. Cross-polarization was implemented using a spin lock field of 25 kHz on 1H and a ramped field of 21–29 kHz on 13C, with a 2 ms contact time; excitation and decoupling powers on 1H were 40 kHz. The 13C spectra shown consist of the sum of 8192 transients acquired with a relaxation delay of 4 s, for a total acquisition time of 9.1 h. 13C chemical shifts were referenced indirectly to neat TMS via an external solid-state sample of adamantane with the downfield-shifted peak set to 38.48 ppm.94The nanorods were oriented with their long axes parallel to the magnetic field by leaving them within the disk-shaped AAO templates and placing the disks within the flat-coil NMR probe perpendicular to the magnetic field (Fig. S2†). The nanorods grow with their rod axes normal to the disk surface,39 so this arrangement of the coil and disk aligns the rods along the static magnetic field.
4.6. Density matrix simulations of NMR spectra
13C solid-state NMR spectra were simulated using a four-spin numerical density matrix approach implemented within the Mathematica™ programming environment.95 The 13C4-labeled t-butyl group was modeled as a strongly-coupled spin system with dipolar and scalar coupling interactions between all sites. Full details are given in the ESI.†4.7. Grazing incidence wide-angle X-ray scattering
Grazing incidence wide-angle X-ray diffraction (GIWAXS) experiments were performed using a Ganesha SAXS-LAB instrument at room temperature. X-rays (λ = 1.54 Å, Cu Kα radiation) were incident at an angle of 2° with respect to the sample surface. A slice of 9TBAE-filled AAO template (3 mm × 1 mm) was mounted on a Thorlabs rotation Stage (MSRP01). A Pilatus 300 K detector was used to collect the 2D diffraction pattern. All the GIWAXS raw data were processed using SAXSGUI software. The monomer crystals were illuminated with 365 nm light (20 mW cm−2) for 6 h to convert into dimer crystals.Author contributions
All authors have contributed to this work with primary contributions in the follow areas. Overall research direction: Mueller, Bardeen, Beran; NMR spectroscopy: Chalek, Kudla, Yang, Magalhães, Mueller; nanorod preparation and characterization: Dong, Tong, Zhu, Al-Kaysi, Bardeen; first-principles computational chemistry: Hartman, Beran; synthetic organic chemistry: Gill, Al-Kaysi, Hooley; GIWAXS: Xu, Hayward.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Research reported in this publication was supported by the United States National Science Foundation (DMR-1810514 to CJB, CHE-1708019 to RJH, CHE-1665212 and CHE-1955554 to GJB, CHE-1710671 to LJM), the US National Institutes of Health (GM097569 to LJM), the Office of Naval Research (MURI on Photomechanical Material Systems; ONR N00014-18-1-2624 to CJB and RCH), and KSAU-HS/KSIMRC (RC10/104 to ROK). Supercomputer time from XSEDE (TG-CHE110064 to GJB) is acknowledged and additional computations were performed using the computer clusters and data storage resources of the UCR HPCC, which were funded by grants from NSF (MRI-1429826) and NIH (1S10OD016290-01A1). The flat-coil NMR probe was constructed with the assistance of Albert Wu and the UCSD Center for Magnetic Resonance and the Imaging of Proteins supported by NIH grant P41EB002031.References
- R. P. Young, C. R. Lewis, C. Yang, L. Wang, J. K. Harper and L. J. Mueller, Magn. Reson. Chem., 2019, 57, 211–223 CrossRef CAS.
- P. Naumov, S. Chizhik, M. K. Panda, N. K. Nath and E. Boldyreva, Chem. Rev., 2015, 115, 12440–12490 CrossRef CAS.
- S. Chizhik, A. Sidelnikov, B. Zakharov, P. Naumov and E. B. ab, Chem. Sci., 2018, 9, 2319–2335 RSC.
- P. Naumov, J. Kowalik, K. M. Solntsev, A. Baldridge, J.-S. Moon, C. Kranz and L. M. Tolbert, J. Am. Chem. Soc., 2010, 132, 5845–5857 CrossRef CAS.
- H. Koshima, H. Nakaya, H. Uchimoto and N. Ojima, Chem. Lett., 2012, 41, 107–109 CrossRef CAS.
- H. Koshima, N. Ojima and H. Uchimoto, J. Am. Chem. Soc., 2009, 131, 6890–6891 CrossRef CAS.
- H. Koshima, K. Takechi, H. Uchimoto, M. Shiro and D. Hashizume, Chem. Commun., 2011, 47, 11423–11425 CAS.
- D. Kitagawa, K. Kawasaki, R. Tanaka and S. Kobatake, Chem. Mater., 2017, 29, 7524–7529 CAS.
- D. Kitagawa and S. Kobatake, Photochem. Photobio. Sci., 2014, 13, 764–769 RSC.
- D. Kitagawa, R. Tanaka and S. Kobatake, Crystengcomm, 2016, 18, 7236–7240 RSC.
- M. Morimoto and M. Irie, J. Am. Chem. Soc., 2010, 132, 14172–14178 CrossRef CAS.
- S. Ohshima, M. Morimoto and M. Irie, Chem. Sci., 2015, 6, 5746–5752 RSC.
- O. S. Bushuyev, A. Tomberg, T. Friscic and C. J. Barrett, J. Am. Chem. Soc., 2013, 135, 12556–12559 CrossRef CAS.
- H. Wang, P. Chen, Z. Wu, J. Zhao, J. Sun and R. Lu, Angew. Chem., Int. Ed., 2017, 56, 9463–9467 CrossRef CAS.
- J. Liu, K. Ye, Y. Shen, J. Peng, J. Sun and R. Lu, J. Mater. Chem. C, 2020, ASAP Search PubMed.
- D. Kitagawa, H. Nishi and S. Kobatake, Angew. Chem., Int. Ed., 2013, 52, 9320–9322 CrossRef CAS.
- D. Kitagawa, H. Tsujioka, F. Tong, X. Dong, C. J. Bardeen and S. Kobatake, J. Am. Chem. Soc., 2018, 140, 4208–4212 CrossRef CAS.
- L. Zhu, R. O. Al-Kaysi and C. J. Bardeen, J. Am. Chem. Soc., 2011, 133, 12569–12575 CrossRef CAS.
- J. M. Cole, J. d. J. Velazquez-Garcia, D. J. Gosztola, S. G. Wang and Y.-S. Chen, Chem. Mater., 2019, 31, 4927–4935 CrossRef CAS.
- F. Tong, M. Al-Haidar, L. Zhu, R. O. Al-Kaysi and C. J. Bardeen, Chem. Commun., 2019, 55, 3709–3712 RSC.
- P. Naumov, S. C. Sahoo, B. Z. Zakharov and E. V. Boldyreva, Angew. Chem., Int. Ed., 2013, 52, 9990–9995 CrossRef CAS.
- R. Medishetty, A. Husain, Z. Bai, T. Runceviski, R. E. Dinnebier, P. Naumov and J. J. Vittal, Angew. Chem., Int. Ed., 2014, 53, 5907–5911 CrossRef CAS.
- L. Zhu, R. O. Al-Kaysi and C. J. Bardeen, Angew. Chem., Int. Ed., 2016, 55, 7073–7076 CAS.
- E. Uchida, R. Azumi and Y. Norikane, Nat. Commun., 2015, 6, 7310/7311–7317 Search PubMed.
- T. Kim, L. Zhu, L. J. Mueller and C. J. Bardeen, J. Am. Chem. Soc., 2014, 136, 6617–6625 CrossRef CAS.
- N. K. Nath, L. Pejov, S. M. Nichols, C. Hu, N. Saleh, B. Kahr and P. Naumov, J. Am. Chem. Soc., 2014, 136, 2757–2766 CrossRef CAS.
- G. Liu, J. Liu, Y. Liu and X. Tao, J. Am. Chem. Soc., 2014, 136, 590–593 CrossRef CAS.
- M. K. Panda, T. Runcevski, S. C. Sahoo, A. A. Belik, N. K. Nath, R. E. Dinnebier and P. Naumov, Nat. Commun., 2014, 5, 4811–4818 CrossRef CAS.
- A. Khalil, D. P. Karothu and P. e. Naumov, J. Am. Chem. Soc., 2019, 141, 3371–3375 CrossRef CAS.
- L. Li, P. Commins, M. B. Al-Handawi, D. P. Karothu, J. M. Halabi, S. Schramm, J. Weston, R. Rezgui and P. Naumov, Chem. Sci., 2019, 10, 7327–7332 RSC.
- H. Durr and H. Bouas-Laurent, Photochromism : Molecules and Systems, Elsevier, New York, 1990 Search PubMed.
- A. Shimamura, A. Priimagi, J.-i. Mamiya, T. Ikeda, Y. Yu, C. J. Barrett and A. Shishido, ACS Appl. Mater. Interfaces, 2011, 3, 4190–4196 CrossRef CAS.
- S. Aiken, R. J. L. Edgar, C. D. Gabbutt, B. M. Heron and P. A. Hobson, Dyes Pigm., 2018, 149, 92–121 CAS.
- A. E. Keating and M. A. Garcia-Garibay, in Organic and Inorganic Photochemistry, ed. V. Ramamurthy and K. S. Schanze, Dekker, New York, 1st edn, 1998, vol. 2, pp. 195–248 Search PubMed.
- S. Takahashi, H. Miura, H. Kasai, S. Okada, H. Oikawa and H. Nakanishi, J. Am. Chem. Soc., 2002, 124, 10944–10945 CAS.
- R. O. Al-Kaysi and C. J. Bardeen, Chem. Comm., 2006, 1224–1226 RSC.
- D. K. Bucar and L. R. MacGillivray, J. Am. Chem. Soc., 2007, 129, 32–33 CrossRef CAS.
- L. Zhu, A. Agarwal, J. Lai, R. O. Al-Kaysi, F. S. Tham, T. Ghaddar, L. Mueller and C. J. Bardeen, J. Mater. Chem., 2011, 21, 6258–6268 RSC.
- R. O. Al-Kaysi, A. M. Muller and C. J. Bardeen, J. Am. Chem. Soc., 2006, 128, 15938–15939 CrossRef CAS.
- C. Yang, L. Zhu, R. A. Kudla, J. D. Hartman, R. O. Al-Kaysi, S. Monaco, B. Schatschneider, A. Magalhaes, G. J. O. Beran, C. J. Bardeen and L. J. Mueller, Crystengcomm, 2016, 18, 7319–7329 RSC.
- K. D. M. Harris and J. M. Thomas, J. Solid State Chem., 1991, 94, 197–205 CrossRef CAS.
- S. G. Stitchell, K. D. M. Harris and A. E. Aliev, Struct. Chem., 1994, 5, 327–333 CrossRef CAS.
- K. Takegoshi, S. Nakamura and T. Terao, Solid State Nucl. Magn. Reson., 1998, 11, 189–196 CrossRef CAS.
- A. Hilgeroth, G. Hempel, U. Baumeister and D. Reichert, Solid State Nucl. Magn. Reson., 1999, 13, 231–243 CrossRef CAS.
- M. Bertmer, R. C. Nieuwendaal, A. B. Barnes and S. E. Hayes, J. Phys. Chem. B, 2006, 110, 6270–6273 CrossRef CAS.
- R. O. Al-Kaysi, R. J. Dillon, J. M. Kaiser, L. J. Mueller, G. Guirado and C. J. Bardeen, Macromolecules, 2007, 40, 9040–9044 CrossRef CAS.
- I. Fonseca, S. Hayes, B. Bluemich and M. Bertmer, Phys. Chem. Chem. Phys., 2008, 10, 5898–5907 RSC.
- M. Khan, G. Brunklaus, V. Enkelmann and H. W. Spiess, J. Am. Chem. Soc., 2008, 130, 1741–1748 CrossRef CAS.
- R. C. Nieuwendaal, M. Bertmer and S. E. Hayes, J. Phys. Chem. B, 2008, 112, 12920–12926 CrossRef CAS.
- I. Fonseca, M. Baias, S. E. Hayes, C. J. Pickard and M. Bertmer, J. Phys. Chem. C, 2012, 116, 12212–12218 CrossRef CAS.
- T. Kim, L. C. Zhu, L. J. Mueller and C. J. Bardeen, Crystengcomm, 2012, 14, 7792–7799 RSC.
- T. Kim, L. C. Zhu, L. J. Mueller and C. J. Bardeen, J. Am. Chem. Soc., 2014, 136, 6617–6625 CrossRef CAS.
- R. C. Nieuwendaal, S. J. Mattler, M. Bertmer and S. E. Hayes, J. Phys. Chem. B, 2011, 115, 5785–5793 CrossRef CAS.
- F. Tong, W. Xu, M. Al-Haidar, D. Kitagawa, R. O. Al-Kaysi and C. J. Bardeen, Angew. Chem., Int. Ed., 2018, 57, 7080–7084 CrossRef CAS.
- A. Nayeem and J. P. Yesinowski, J. Chem. Phys., 1988, 89, 4600–4608 CAS.
- J. C. Facelli and D. M. Grant, Nature, 1993, 365, 325–327 CrossRef CAS.
- R. A. Olsen, J. Struppe, D. W. Elliott, R. J. Thomas and L. J. Mueller, J. Am. Chem. Soc., 2003, 125, 11784–11785 CrossRef CAS.
- R. Witter, U. Sternberg, S. Hesse, T. Kondo, F. T. Koch and A. S. Ulrich, Macromolecules, 2006, 39, 6125–6132 CrossRef CAS.
- G. Pintacuda, N. Giraud, R. Pierattelli, A. Bockmann, I. Bertini and L. Emsley, Angew. Chem., Int. Ed., 2007, 46, 1079–1082 CrossRef CAS.
- E. Salager, G. M. Day, R. S. Stein, C. J. Pickard, B. Elena and L. Emsley, J. Am. Chem. Soc., 2010, 132, 2564–2566 CrossRef CAS.
- C. Bonhomme, C. Gervais, F. Babonneau, C. Coelho, F. Pourpoint, T. Azais, S. E. Ashbrook, J. M. Griffin, J. R. Yates, F. Mauri and C. J. Pickard, Chem. Rev., 2012, 112, 5733–5779 CrossRef CAS.
- C. Luchinat, G. Parigi, E. Ravera and M. Rinaldelli, J. Am. Chem. Soc., 2012, 134, 5006–5009 CrossRef CAS.
- M. Baias, J. N. Dumez, P. H. Svensson, S. Schantz, G. M. Day and L. Emsley, J. Am. Chem. Soc., 2013, 135, 17501–17507 CrossRef CAS.
- D. H. Brouwer, S. Cadars, J. Eckert, Z. Liu, O. Terasaki and B. F. Chmelka, J. Am. Chem. Soc., 2013, 135, 5641–5655 CrossRef CAS.
- J. K. Harper, R. Iuliucci, M. Gruber and K. Kalakewich, Crystengcomm, 2013, 15, 8693–8704 RSC.
- L. J. Mueller and M. F. Dunn, Acc. Chem. Res., 2013, 46, 2008–2017 CrossRef CAS.
- C. Martineau, Solid State Nucl. Magn. Reson., 2014, 63–64, 1–12 CrossRef CAS.
- D. L. Bryce, IUCrJ, 2017, 4, 350–359 CrossRef CAS.
- A. Bertarello, L. Benda, K. J. Sanders, A. J. Pell, M. J. Knight, V. Pelmenschikov, L. Gonnelli, I. C. Felli, M. Kaupp, L. Emsley, R. Pierattelli and G. Pintacuda, J. Am. Chem. Soc., 2020, 142, 16757–16765 CrossRef CAS.
- M. Mehring, Principles of high resolution NMR in solids, Springer-Verlag, Berlin ; New York, 1983 Search PubMed.
- L. J. Mueller, Concepts Magn. Reson., Part A, 2011, 38A, 221–235 CrossRef CAS.
- U. Haeberlen, High resolution NMR in solids : selective averaging, Academic Press, New York, 1976 Search PubMed.
- J. D. Hartman, R. A. Kudla, G. M. Day, L. J. Mueller and G. J. O. Beran, Phys. Chem. Chem. Phys., 2016, 18, 21686–21709 RSC.
- S. J. Opella and F. M. Marassi, Chem. Rev., 2004, 104, 3587–3606 CrossRef CAS.
- R. L. Johnson and K. Schmidt-Rohr, J. Magn. Reson., 2014, 239, 44–49 CrossRef CAS.
- S. Radhakrishnan, H. Colaux, C. V. Chandran, D. Dom, L. Verheyden, F. Taulelle, J. Martens and E. Breynaert, Anal. Chem., 2020, 92, 13004–13009 CAS.
- K. Biradha and R. Santra, Chem. Soc. Rev., 2013, 42, 950–967 CAS.
- G. M. J. Schmidt, Pure Appl. Chem., 1971, 27, 647–678 CAS.
- W. Shang, M. B. Hickey, V. Enkelmann, B. B. Snider and B. M. Foxman, CrystEngComm, 2011, 13, 4339–4350 RSC.
- W. Li, J. v. Baren, A. Berges, E. Bekyarova, C. H. Lui and C. J. Bardeen, Cryst. Growth Des., 2020, 20, 1583–1589 CrossRef CAS.
- A. M. Lund, G. I. Pagola, A. M. Orendt, M. B. Ferraro and J. C. Facelli, Chem. Phys. Lett., 2015, 626, 20–24 CrossRef CAS.
- A. Pulido, L. J. Chen, T. Kaczorowski, D. Holden, M. A. Little, S. Y. Chong, B. J. Slater, D. P. McMahon, B. Bonillo, C. J. Stackhouse, A. Stephenson, C. M. Kane, R. Clowes, T. Hasell, A. I. Cooper and G. M. Day, Nature, 2017, 543, 657–664 CrossRef CAS.
- C. Y. Cheng, J. E. Campbell and G. M. Day, Chem. Sci., 2020, 11, 4922–4933 RSC.
- A. N. Sokolov, S. Atahan-Evrenk, R. Mondal, H. B. Akkerman, R. S. Sanchez-Carrera, S. Granados-Focil, J. Schrier, S. C. B. Mannsfeld, A. P. Zoombelt, Z. N. Bao and A. Aspuru-Guzik, Nat. Commun., 2011, 2, 437 CrossRef.
- G. J. O. Beran, Crystengcomm, 2019, 21, 758–764 RSC.
- S. L. Price, D. E. Braun and S. M. Reutzel-Edens, Chem. Commun., 2016, 52, 7065–7077 RSC.
- Photomechanical Materials, Composites, and Systems, ed. T. J. White, Wiley, Hoboken, New Jersey, 2017 Search PubMed.
- B. G. Caulkins, R. P. Young, R. A. Kudla, C. Yang, T. J. Bittbauer, B. Bastin, E. Hilario, L. Fan, M. J. Marsella, M. F. Dunn and L. J. Mueller, J. Am. Chem. Soc., 2016, 138, 15214–15226 CrossRef CAS.
- H. L. Zhang, G. J. Hou, M. M. Lu, J. Ahn, I. J. L. Byeon, C. J. Langmead, J. R. Perilla, I. Hung, P. L. Gor'kov, Z. H. Gan, W. W. Brey, D. A. Case, K. Schulten, A. M. Gronenborn and T. Polenova, J. Am. Chem. Soc., 2016, 138, 14066–14075 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef.
- J. Antony and S. Grimme, Phys. Chem. Chem. Phys., 2006, 8, 5287–5293 RSC.
- G. J. O. Beran, J. Chem. Phys., 2009, 130, 164115 CrossRef.
- J. D. Hartman, S. Monaco, B. Schatschneider and G. J. O. Beran, J. Chem. Phys., 2015, 143, 102809 CrossRef.
- C. R. Morcombe and K. W. Zilm, J. Magn. Reson., 2003, 162, 479–486 CrossRef CAS.
- Mathematica, version 11.2, software for technical computation, Wolfram Research , Inc., Champaign, Illinois, 2017 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d0sc05118g |
| This journal is © The Royal Society of Chemistry 2021 |