Stabilization of hydrated Ac^III cation: the role of superatom states in actinium-water bonding

Abstract

²²⁵Ac-based radiopharmaceuticals have the potential to become invaluable in designated cancer therapy. However, the limited understanding of the solution chemistry and bonding properties of actinium has hindered the development of existing and emerging targeted radiotherapeutics, which also poses a significant challenge in the discovery of new agents. Herein, we report the geometric and electronic structural properties of hydrated Ac^III cations in the [Ac^III(H₂O)_n]³⁺ (n = 4–11) complexes in aqueous solution and gas-phase using density functional theory. We found that nine water molecules coordinated to the Ac^III cation is the most stable complex due to an enhanced hydration Gibbs free energy. This complex adopts a closed-shell 18-electron configuration (1S²1P⁶1D¹⁰) of a superatom state, which indicates a non-negligible covalent character and involves H₂O → Ac^III σ donation interaction between s-/p-/d-type atomic orbitals of the Ac atom and 2p atomic orbitals of the O atoms. Furthermore, potentially existing 10-coordinated complexes need to overcome an energy barrier (>0.10 eV) caused by hydrogen bonding to convert to 9-coordination. These results imply the importance of superatom states in actinide chemistry generally, and specifically in Ac^III solution chemistry, and highlight the conversion mechanism between different coordination numbers.

---

Introduction

Actinium (Ac), as the first member of the actinide (An) family, is often overlooked and considered to be a member of the d-block transition metals (TMs), due to it showing striking similarities to Sc (3d¹4s²), Y (4d¹5s²), and La (5d¹6s²) with respect to the electronic configuration.^1–3 However, recent discoveries tend to support its reassignment as an actual f-block element.^4–7 All isotopes of actinium are unstable and highly radioactive. Specifically, the Ac isotope ²²⁵Ac, as a promising anticancer therapeutic agent, makes targeted radionuclide therapy a powerful cancer treatment strategy.^5–9 The main reasons are that (a) the short half-life of 10 days matches the pharmacokinetics of the final radioactive drug, (b) the isotope is a pure α-emitter with a high energy (100 keV μm⁻¹) and short distance (<100 μm) in biological tissue, (c) the final product (²⁰⁹Bi) from the ²²⁵Ac decay chain leaves with small accumulated energy of 28 meV and is innocuous in vivo. Despite these advantages, many basic science problems are surrounding the coordination and solution chemistry of actinium, and the biological delivery of the ²²⁵Ac isotope remains unresolved.^10,11

From the viewpoint of electronic structure, the electronic configuration of the Ac atom (5f⁰6d¹7s²) is indeed similar to that of TMs (it only involves s- and d-electrons). As a result, some established knowledge of TM chemistry also applies to light actinides, such as the electron-counting rule for characterization of superatomic stability.^12,13 Recently, a host of TM clusters/complexes have been designed and constructed via specific electron-counting rules based on the “Jellium model”, which can mimic the chemical behavior of elements in the periodic table, and hence these clusters and complexes can be regarded as “superatoms”.^14,15 The Jellium model is a critical guiding principle for evaluating new superatom candidates.¹⁵ In this system, all the charges of the nuclei and core electrons in the cluster are uniformly distributed throughout the cluster spheroid. As such, the energy levels for electrons interacting with such a charge distribution correspond to 1S², 1P⁶, 1D¹⁰, 2S², 1F¹⁴, 2P⁶, etc., where the resulting magic numbers are 2, 8, 18, 20, 32, 40, … (to distinguish the electronic shells of atoms, the super shells are depicted as capital letters).

Examples include the famous WAu₁₂ superatom cluster,^16,17 Fe(C₅H₅)₂, Cr(C₆H₆)₂, M(CO)₆ (M = Cr, Mo, W) and M(CO)₈ (M = Ca, Sr, or Ba) complexes,^18–21 whose chemical stability is not only due to the high coordination number and corresponding high cohesive energy for surface atoms, but also mainly on account of the strong relativistic effects and the closed shell 18-electron rule (1S²1P⁶1D¹⁰). Focusing on the actinides, the An@Au₁₄ (An = Ac⁻, Th, Pa⁺), Sg@Au₁₂ clusters, [An(CO)₈]^+/− (An = Th, U) and [Ac(H₂)_n]³⁺ (n = 9–12) complexes^22–25 were also found to be superatom clusters, obeying the 18-electron rule. Even though the 5f electrons of actinides prefer to localize, they were still found to be excited to 6d shells to satisfy the bonding of the 18-electron rule,²⁶ which demonstrated the similarity in the electron-counting rules between the early actinides and transition metals. On the other hand, the An@C₂₈ (An = Th, Pa⁺, U²⁺, Pu⁴⁺), [U@Si₂₀]⁶⁻ and U@B₄₀ superatom clusters^27–29 follow the 32-electron rule (1S²1P⁶1D¹⁰1F¹⁴). Hence, when it comes to the development of thermodynamically stable and kinetically inert actinide cation complexes as part of radiopharmaceuticals, the superatom states play a major role in the coordination and solution chemistry.

It is well known that the Ac atom usually exists in the trivalent oxidation state (i.e. Ac^III with the configuration 5f⁰6d⁰7s⁰), which leads to its invisible nature in spectroscopy and resulting difficulty to characterize.³⁰ Further, because of the highly radioactive nature and limited availability of Ac isotopes, experimental works have been greatly hindered.³¹ For instance, the first Ac bond distance wasn't measured until 2016,³⁰ which means that many basic chelate properties of Ac^III have not been discovered in solution chemistry yet. In this work, a systematic investigation on the superatom chemistry of hydrated Ac^III cations in the [Ac^III(H₂O)_n]³⁺ (n = 4–11) complexes in gas-phase (gas, for short in the following) and aqueous solution (aq, for short in the following) conditions is presented by employing first-principles density functional theory (DFT). This study addresses the superatom states in the optimized geometries of Ac^III aquo complexes, the change of coordination number of the Ac^III cation in solution chemistry, as well as the nature of bonding between Ac^III and oxygen. The analysis of such superatom states of the hydrated Ac^III cation has broad potential to be implicated in the development of a predictive understanding of its solubility, stability, and reactivity.

Results and discussion

Geometry structures

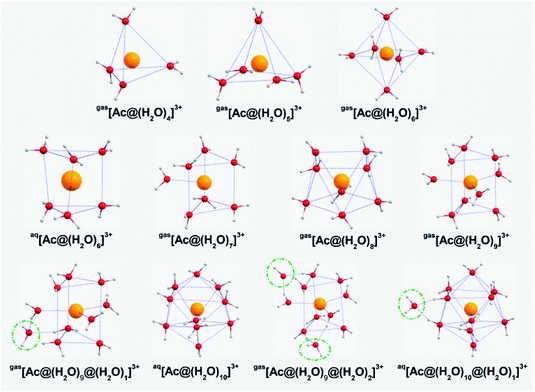
The stable Ac^III aquo complexes were obtained via PBE-D3 optimization, followed by validation with the B3LYP-D3 functional, as shown in Fig. 1 (see the isomers of different initial structures in Table S1 of ESI†). When the coordination numbers (CN) in the first hydration shell are 4, 5, 7, 8, 9, the most stable structures obtained under both gas-phase and aqueous solution conditions are similar. However, when the numbers of water molecule in the first hydration shell of initial structures are 6, 10, 11, the most stable geometries are different between the gas-phase and aqueous solution. Specifically, the coordination geometries of the water molecules for CN = 4 and 5 are trigonal pyramidal and square pyramidal, respectively. For CN = 6, the most stable structures in the gas-phase and aqueous solution are octahedral and trigonal prism (TP), respectively. For CN = 7, the structure formed is equivalent to adding a cap to one side of the TP. Upon adding three caps to the three sides of the TP, the coordination geometry becomes a tricapped trigonal prism (TTP), which correspond to CN = 9. This TTP structure looks similar to those of [U(H₂O)₉]³⁺,³² and [La(H₂O)₉]³⁺.³³ On the contrary, when CN = 8, the Ac^III aquo complex possesses a square antiprism (SAP) structure, instead of a bicapped trigonal prism (BTP). The reason for the sharp change in geometries from BTP → SAP → TTP is that the BTP structure is an intermediate of both the 9 → 8 and 8 ← 9 reactions, whereas the CN = 8 structure rearranges itself to the SAP structure upon reaching a stable state.³⁴

Fig. 1 Optimized geometries of Ac^III aquo complexes under gas-phase (gas) and aqueous solution (aq) conditions at the PBE-D3/TZ2P level of theory. Water molecules marked with green circles belong to the second hydration shell.

Regarding the geometry of the first hydration shell, we further considered using initial starting structures containing 10 or 11 water molecules to coordinate an Ac^III cation. The calculation results show the CNs in the optimized structures always tends to be 10 (Bicapped Square Antiprism) under aqueous solution conditions and 9 (TTP) under gas-phase conditions. Fig. 1 clearly shows that the water molecules marked with green circles have moved into the second hydration shell. Recently, it has been observed experimentally that there are approximately 10.0 ± 0.9 (ref. 36) and 10.9 ± 0.5 (ref. 35) water molecules in the first Ac^III coordination sphere, at an average distance of ∼2.630 Å. Also, the MDDFT (accompanying that work:³⁵ Ac^III cation in a supercell of 64 water molecules), DFT,³⁷ and classical MD³⁸ studies predicted a CN of nine water molecules at a distance of 2.689 ± 0.110 Å, 2.66 ± 0.02 Å, and 2.699 Å, respectively. Based on the above works, it is possible for all three coordination numbers (9, 10 and 11) of Ac cations to actually exist simultaneously. Obviously, we cannot be restricted to the Ac^III cation itself. Instead, we need to also include the hydration properties of other actinide trivalent cations to discuss the coordination chemistry of the Ac^III cation.

Over the last half-century, both experimental and theoretical studies have been devoted to the understanding of the hydration properties of actinoid ions in water. Reported structural parameters of An^III aquo complexes are summarized in Table 1. Compared with the systematic experimental investigations for aqueous trivalent lanthanoids, there are no comprehensive experimental studies in the actinoid series. This is not only because of the difference that arises from partial delocalization of 5f orbitals versus localization of 4f orbitals, but also the higher experimental difficulty in studying these systems owing to the redox instability of the lighter An^III aqua ions. In short, the experimentally observed CNs of trivalent actinide cations (U, Np, Pu, Am, Cm, Bk, and Cf), range from 7.0 to 10.3, which is still not in complete agreement with the theoretically predicted hydration numbers (8 or 9). However, these differences become justified if the following practical issues are considered: (1) different metal and ligand concentrations in the experiments will result in different hydration spheres about the metal ion (see e.g. in “[Pu^III(H₂O)_x]³⁺” Table 1);^42,43 (2) there are many issues in accurately evaluating the coordination number of EXAFS, including the statistical limitations of the EXAFS fitting problem, empirical effects due to sample preparation, and the assumptions made about the physical structure surrounding the absorber in the course of data analysis;^35–38,54 (3) a natural constraint on the quantum mechanics: an increase of the coordination number is directly associated with an An–O lengthening, while the two parameters (bond length and CN) can be fitted separately in EXAFS. In summary, the remaining deviations between theory and experiment appear reasonable, and further studies including the detailed analysis from the perspective of electronic structure and relaxed potential energy surface scanning certainly will help in figuring out the dynamic coordination (9 or 10) for the Ac^III cation.

Table 1 Summary of structural parameters for hydrated, trivalent-actinide ions in aqueous solution

Actinides cation	CN	An–Owater distances	Technique	Solution conditions
a Metal solution concentration: 20 mM. b Metal solution concentration: 20 mM. For [Pu^III(H2O)x]^3+, only one combination (10 mM + 0.01 M, LiCl) is the most reliable, the other two sets of values are listed here for comparison purposes. EXAFS (extended X-ray absorption fine structure); MD (molecular dynamics); CPCM (conductor-like polarizable continuum model); NEMO (non-empirical molecular orbital).
[Ac^III(H2O)x]^3+	10.9 ± 0.5	2.63 ± 0.01	EXAFS	0.11 M, HO3SCF3 (ref. 35)
	10.0 ± 0.9	2.63 ± 0.02	EXAFS	0.05 M, HNO3 (ref. 36)
	9.0	2.699	GGA functional with COSMO^37
	8.9	2.66 ± 0.02	Classical MD^38
	9.0	2.689 ± 0.110	DFT-based MD with PBE functional^35
[Th^III(H2O)x]^3+	9.0	2.682	GGA functional with COSMO^37
[Pa^III(H2O)x]^3+	9.0	2.656	GGA functional with COSMO^37
[U^III(H2O)x]^3+	9.1 ± 0.6	2.52 ± 0.01	EXAFS	pH 0 HCl^39
	9.0	2.636	GGA functional with COSMO^37
	9.0	2.51	Polarizable model^40
[Np^III(H2O)x]^3+	10.0 ± 1.2	2.51 ± 0.01	EXAFS	pH 0 HCl^39
	9.0 ± 1.0	2.48 ± 0.02	EXAFS	1 M, HClO4 (ref. 41)
	9.0	2.617	GGA functional with COSMO^37
	9.0	2.50	Polarizable model^40
[Pu^III(H2O)x]^3+	9.9 ± 0.3	2.49 ± 0.01	EXAFS	pH0 HCl^39
	10.2 ± 1.1	2.51 ± 0.06	EXAFS	0.01 M, LiCl^a^42
	9.2 ± 0.33	2.51 ± 0.06	EXAFS	0.01 M, LiCl^b^43
	5.2 ± 0.33	2.50 ± 0.06	EXAFS	12.3 M, LiCl^b^43
	8.6 ± 0.2	2.50 ± 0.02	EXAFS	1 M, HClO4 (ref. 44)
	9.0 (8.0)	2.599 (2.561)	GGA functional with COSMO^37
	9.0	2.490	Polarizable model^40
[Am^III(H2O)x]^3+	9.5 ± 0.87	2.48 ± 0.01	EXAFS	0.11 M, HO3SCF3 (ref. 30)
	8.3 ± 0.4	2.473 ± 0.004	EXAFS	0.025 M, HClO4 (ref. 45)
	10.3 ± 0.33	2.480 ± 0.06	EXAFS	0.25 M, HCl^43
	8.9 ± 0.8	2.470 ± 0.01	EXAFS	0.05 M, HNO3 (ref. 36)
	9.0 (8.0)	2.582 (2.544)	GGA functional with COSMO^37
	9.0	2.480	Polarizable model^40
[Cm^III(H2O)x]^3+	10.3 ± 0.33	2.450 ± 0.06	EXAFS	0.25 M, HCl^43
	7.0 ± 0.4	2.469 ± 0.007	EXAFS	1 M, HClO4 (ref. 46)
	9.6 ± 0.7	2.470 ± 0.01	EXAFS	0.05 M, HNO3 (ref. 36)
	8.5 ± 0.8	2.477 ± 0.005	EXAFS	0.1 M, HClO4 (ref. 47)
	9.0 (8.0)	2.566 (2.526)	GGA functional with COSMO^37
	9.0 (8.0)	2.473 (2.445)	Hybrid GGA functional with CPCM^48
	9.0	2.460	Polarizable model^40
	8.9	2.550	Polarizable NEMO potential^49
	9.0	2.480	DFT-based MD with PBE functional^50
	9.0	2.520–2.530	Non-polarizable force field^50
[Bk^III(H2O)x]^3+	9.0 ± 0.6	2.430 ± 0.02	EXAFS	1 M, HClO4 (ref. 51)
	9.0 (8.0)	2.551 (2.511)	GGA functional with COSMO^37
	9.0	2.430	Polarizable model^40
[Cf^III(H2O)x]^3+	8.0 ± 0.0	2.420 ± 0.01	EXAFS	0.1 M, HClO4 (ref. 52)
	8.5 ± 1.5	2.420 ± 0.02	EXAFS	1 M, HCl^53
	9.0 (8.0)	2.537 (2.495)	GGA functional with COSMO^37
	8.9	2.420	Polarizable model^40
[Es^III(H2O)x]^3+	9.0 (8.0)	2.524 (2.482)	GGA functional with COSMO^37
	8.5	2.37	Polarizable model^40
[Fm^III(H2O)x]^3+	9.0 (8.0)	2.513 (2.469)	GGA functional with COSMO^37
	8.3	2.35	Polarizable model^40
[Md^III(H2O)x]^3+	9.0 (8.0)	2.502 (2.455)	GGA functional with COSMO^37
	8.1	2.34	Polarizable model^40
[No^III(H2O)x]^3+	9.0 (8.0)	2.490 (2.443)	GGA functional with COSMO^37
	8.0	2.32	Polarizable model^40
[Lr^III(H2O)x]^3+	9.0 (8.0)	2.478 (2.431)	GGA functional with COSMO^37
	8.0	2.31	Polarizable model^40

---

In addition, the Ac–O_water distances for prismatically arranged (O_prism) and capping (O_cap) oxygen atoms in [Ac^III(H₂O)₉]³⁺ (TTP) complex are shown in Table 2 and Table S2 of the ESI† together with those of the others Ac^III aquo complexes. The Ac–O_water distances become longer as the CN increases which is mainly due to the steric effects. The 9- and 10-coordinated Ac^III cation complexes show average distance values of 2.642/2.663 Å and 2.690/2.711 Å at the PBE-D3/B3LYP-D3 levels of theory, respectively. The differences compared with previously reported values are all of the order of ∼1 × 10⁻² Å. For each complex, the average Ac–O_water bond length is shortened or lengthened by ∼1 × 10⁻³ Å when spin-orbit coupling-ZORA (SOC-ZORA) relativistic effects are included in the gas-phase calculations in comparison to scalar relativistic calculations (SR-ZORA). For the SR-ZORA calculations including water solvent effects, the overall average Ac–O_water distance is reduced by ∼4 × 10⁻² Å compared to the corresponding gas-phase calculation. This difference is consistent with that of the equatorial U–OH₂ bond lengths of the [UO₂(H₂O)₅]²⁺·nH₂O complexes (n = 0, 5, 7, 10, 12) in gas phase and solution.⁵⁵

Table 2 Average Ac–O_water distances (Å) in the first hydration shell of Ac^III aquo complexes in both gas-phase and aqueous solution^a

Geometries	PBE-D3			B3LYP-D3
	^gasSR	^gasSOC	^aqSR	^gasSR	^gasSOC	^aqSR
a Both structure a and b are 9-coordinated Ac^III cation complexes and correspond to the c6 and d8 energy points in Fig. 5, respectively.
[Ac^III(H2O)4]^3+	2.524	2.523	2.478	2.545	2.543	2.505
[Ac^III(H2O)5]^3+	2.563	2.563	2.518	2.584	2.584	2.541
^gas[Ac^III(H2O)6]^3+	2.599	2.599	—	2.620	2.618	—
^aq[Ac^III(H2O)6]^3+	—	—	2.552	—	—	2.572
[Ac^III(H2O)7]^3+	2.629	2.631	2.580	2.648	2.647	2.600
[Ac^III(H2O)8]^3+	2.657	2.662	2.610	2.678	2.676	2.630
[Ac^III(H2O)9]^3+	2.690	2.695	2.642	2.706	2.706	2.663
^gas[Ac^III(H2O)9(H2O)1]^3+	2.688	2.691	—	2.704	2.702	—
^aq[Ac^III(H2O)10]^3+	—	—	2.690	—	—	2.711
^gas[Ac^III(H2O)9(H2O)2]^3+	2.690	2.687	—	2.701	2.700	—
^aq[Ac^III(H2O)10(H2O)1]^3+	—	—	2.693	—	—	2.701
^aq[Ac^III(H2O)8(H2O)16]^3+	—	—	2.640	—	—	—
^aq[Ac^III(H2O)9(H2O)18]^3+	—	—	2.648	—	—	—
^aq[Ac^III(H2O)10(H2O)35]^3+	—	—	2.726	—	—	—
^aq[Ac^III(H2O)9(H2O)36]^3+	—	—	2.669^a	—	—	—
^aq[Ac^III(H2O)9(H2O)36]^3+	—	—	2.679^b	—	—	—

---

Hydration Gibbs free energies

Gibbs free energies of appropriate reactions have always been a useful tool for identifying the optimal coordination number.^56,57 Accordingly, the hydration Gibbs free energies of Ac^III cations were calculated in aqueous solution at the PBE-D3 and B3LYP-D3 levels of theory using the following reactions:

Ac³⁺(gas) + n(H₂O)(aq) ↔ [Ac(H₂O)_n]³⁺(aq), ΔG(Ac³⁺) = G([Ac(H₂O)_n]³⁺) − G⁰(Ac³⁺) − nG(H₂O) (R1)

where G and G⁰ are the Gibbs free energies of COSMO-solvated and gas-phase species, respectively, and n denotes the number of water molecules. In (R1), the lowest (most negative) hydration Gibbs free energy represents the most stable complex. As shown in Table 3, the hydration Gibbs free energies of the Ac^III cation gradually decreases with the increase of the number of water molecules (4 → 9). Moreover, although the first hydration shell can hold up to 10 water molecules in aqueous solution, from the energetics point of view, the [Ac^III(H₂O)₉]³⁺ complex is the most stable one.

Table 3 Relative hydration Gibbs free energies (kcal mol⁻¹) of Ac^III cations (reaction (1)) and water addition (reaction (2)) in aqueous solution at the PBE-D3 and B3LYP-D3 levels of theory. The lowest and highest energies are set to zero and used as a reference point for reaction (1) and (2), respectively. Only the water molecules in the first hydration shell are considered here

Geometries	Reaction (1)		Reaction (2)
	PBE-D3	B3LYP-D3	PBE-D3	B3LYP-D3
[Ac^III(H2O)4]^3+	46.60	40.86	−17.16	−11.80
[Ac^III(H2O)5]^3+	31.17	30.05	−11.26	−5.63
[Ac^III(H2O)6]^3+	21.64	25.41	−11.65	−11.58
[Ac^III(H2O)7]^3+	11.72	14.82	−10.73	−11.17
[Ac^III(H2O)8]^3+	2.72	4.64	−4.45	−5.63
[Ac^III(H2O)9]^3+	0.00	0.00	0.00	0.00
[Ac^III(H2O)10]^3+	1.73	0.99	−5.81	−1.00

---

To further probe the preferences in terms of energy for accommodating one additional water molecule in the first coordination shell, we also examined the hydration Gibbs free energies in aqueous solution at the PBE-D3 and B3LYP-D3 levels of theory by using the following reactions:

[Ac(H₂O)_n]³⁺(aq) + H₂O(aq) ↔ [Ac(H₂O)_n+1]³⁺(aq), G([Ac(H₂O)_n]³⁺) = G([Ac(H₂O)_n+1]³⁺) − G(H₂O) (R2)

Table 3 shows that the complexes with (n = 4 → 8, 10) have a stronger ability to accept one additional water molecule than the complex with n = 9. This means that the additional water molecule is most difficult to add to the first hydration shell of the [Ac^III(H₂O)₉]³⁺ complex, i.e. the complex with nine water molecules coordinated to the Ac^III cation is the most stable complex. This result is consistent with the coordination environment of other hydrated trivalent actinide cations.^4,32,46

Electronic structures

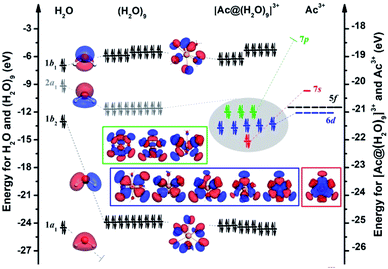
Free energy calculations can only determine the preferred CNs but do not explain the reason why this is the case. To achieve a better understanding of the electronic requirements of the Ac^III aquo complexes, we chose the [Ac^III(H₂O)₉]³⁺ complex as an example. A diagram of the interaction between the Ac^III cation and the 9H₂O ligands is shown in Fig. 2. For actinide complexes in which water molecules act as ligands, it is beneficial to start from the electronic structure of a simple H₂O molecule. To reduce the complexity of the electronic structure, the 1s orbital of the O atom was frozen. As a result, there are only four occupied orbitals (1a₁)²(1b₂)²(2a₁)²(1b₁)² for the isolated H₂O molecule. The lowest energy orbital (1a₁) is (mostly) contributed from the 2s orbitals of the O atom. The three highest occupied orbitals (1b₂ σ-bonding, 2a₁ lone pair electrons, 1b₁ lone pair electrons) are resulting from the 2p atomic orbitals of the O atom and are orthogonal along the x, y, z directions of the oxygen atom. From the molecular orbital (MO) diagram of the [Ac^III(H₂O)₉]³⁺ complex, we found that the 1a₁, 1b₂, 1b₁ MOs of H₂O are MOs without any interaction with the Ac^III cation, and still maintain the character of the isolated H₂O molecule. Contrary to that, the MOs of 2a₁ symmetry of H₂O molecules are hybridized with the Ac^III cation, and all the lone pair (LP) electrons (similar to free electrons) are more or less pointing toward the Ac^III cation, with noticeable deformation of the electron cloud. This implies that the Ac^III–O_water interactions are not completely dominated by electrostatic interactions.

Fig. 2 Electronic structure diagram of the [Ac^III(H₂O)₉]³⁺ complex in gas-phase at the PBE-D3/TZ2P level of theory. The MO energies of the H₂O molecule and (H₂O)₉ fragment correspond to the left Y axis, and the MO energies of the Ac³⁺ cation and [Ac^III(H₂O)₉]³⁺ complex are shown on the right Y axis.

It is well known that the electron configuration of an isolated Ac atom is 6d¹7s², and the positive trivalent Ac^III cation will certainly adopt the electronic configuration (6d⁰7s⁰) of the inert-gas Rn atom, which means that the [Ac^III(H₂O)₉]³⁺ complex could satisfy the closed-shell 18-electron rule (9 × 2 + 0) in the Jellium model. According to the nodal shape of the MOs, as well as the fact that only the 2a₁ LP electrons of the nine water molecules participate in the chemical bonding, we can indeed identify a series of superatomic orbitals within the framework of the Jellium model in the sequence 1S, 1D, 1P that corresponds to the 9 occupied MOs with 18 electrons (see Fig. 2, for the detailed composition of the MOs see Table S3 of ESI†). In order to better understand the valence orbitals of [Ac^III(H₂O)₉]³⁺ as a “18e-superatom” based on the Jellium model, we compared the molecular orbitals of the [Ac^III(H₂O)₉]³⁺ complex and the [Ac@Au₁₄]⁻ cluster (see Fig. S1 of ESI†). Although [Ac^III(H₂O)₉]³⁺ is not a metal cluster, its configuration can be similarly described as 1S²1P⁶1D¹⁰ based on the Jellium model. Very recent research applying the Jellium model also proved that the octacarbonyl metal cation complex [Ba(CO)₈]²⁻ and the metal cluster [BaBe₈]²⁻ strictly satisfy the closed-shell “20e-superatom” configuration of 1S²1P⁶1D¹⁰1F².⁵⁸

Interestingly, the [Ac^III(H₂O)₉]³⁺ “superatom” formulation is different from a number of gold-based superatom clusters, such as An@Au₁₄ (An = Ac⁻, Th, Pa⁺),²² and also different from complexes with other small molecules as ligands, such as M(CO)₈ (M = Ca, Sr, or Ba).²¹ All the electrons in its potential field come from the nine water molecules instead of from both, central atom and water cage. Further insight can be gained from charge transfer analysis, resulting in the charges of the Ac^III cation based on the Voronoi deformation density (VDD), Hirshfeld, and Mulliken charge analysis methods with values of 0.24e, 0.84e, 2.11e and 0.19e, 0.79e, 2.11e under gas-phase and aqueous solution conditions respectively. It is important to note that it is not the absolute values of the charge populations that are important to our analyses here, but rather the trends between the An ions. This indicates that the positive trivalent Ac^III cation has gained electrons from the nine water molecules and has thus attained a charge that is smaller than +3.

To provide detailed insight into the chemical bonding, we analyzed the nature of the Ac–O_water bonds with the natural orbitals for chemical valence (NOCV) combined with the energy decomposition analysis (EDA).⁵⁹ The EDA-NOCV results for the interaction between the Ac^III cation and the (H₂O)₉ ligand (Table 4) show that the attractive contribution to the total interaction energy ΔE_int comes from the electrostatic term ΔE_elstat (57.24%), the orbital term ΔE_orb (42.54%), and the dispersion term ΔE_dis (0.22%). The electrostatic attraction (ΔE_elstat) is responsible for the overall trend, which is also in line with the long-held idea of the strong electrostatic character of the ion–water interaction.^{32,56,60–62} Further, since the ΔE_orb term represents a mixture of orbitals between the two fragments, it can be identified as a covalent contribution to the chemical bond. It should be noted that the strength of the covalent bond is not determined by the value of the ΔE_orb term alone, but rather by the balance between the attractive forces (electrostatic and covalent) and the repulsive exchange (Pauli) term. Therefore, when we considered the explicit second water shell for ^aq[Ac^III(H₂O)₈]³⁺ and ^aq[Ac^III(H₂O)₉]³⁺, the orbital interactions energy (ΔE_orb) representing covalent characteristics still accounts for more than 30% of the total attractive energy (ΔE_elstat+ΔE_orb+ΔE_dis), indicating that there is a non-negligible covalent character (ΔE_orb) between the Ac cation and water molecules (see Table S4 of ESI†).

Table 4 EDA-NOCV results (kcal mol⁻¹) for the [Ac^III(H₂O)₉]³⁺, [Ac^III(NH₃)₉]³⁺, and [Ac^III(PH₃)₉]³⁺ complexes in gas-phase at the PBE-D3/TZ2P level of theory, taking (H₂O)₉, (NH₃)₉, (PH₃)₉ and Ac^III in the singlet state as interacting fragments at the corresponding frozen geometries. Values in parentheses give the percentage of each attractive term with respect to the sum of the attractive terms^a. The 1S, 1P, 1D represent superatomic molecular orbitals

Energy terms	Assignment^b	Interacting fragments
		(H2O)9vs. Ac^III	(NH3)9vs. Ac^III	(PH3)9vs. Ac^III
a ΔEpauli is the Pauli repulsion term; ΔEdis is the dispersion term; ΔEelstat is the classical electrostatic interaction term; ΔEorb is the orbitals interaction term. Within this energy decomposition scheme the attractive and repulsive terms are negative and positive, respectively. “x” denotes the valence acceptor atomic orbitals of Ac atom. b For the [Ac^III(NH3)9]^3+, and [Ac^III(PH3)9]^3+ complexes, we only list the percentage of the nine superatomic molecular orbitals that account for the majority of the total orbital interaction energy.
ΔE int		−474.98	−525.82	−413.81
ΔE pauli		136.70	134.49	113.25
ΔE dis		−1.35 (0.22%)	−2.34 (0.35%)	−3.12 (0.59%)
ΔE elstat		−350.14 (57.24%)	−373.35 (56.55%)	−168.92 (32.05%)
ΔE orb		−260.19 (42.54%)	−284.62 (43.10%)	−355.03 (67.36%)
ΔEorb(1)	[9H2O(2p)] σ donation → [Ac(6d)] (1D)	−26.58 (10.22%)	−33.64 (11.82%)	−44.57 (12.55%)
ΔEorb(2)	[9H2O(2p)] σ donation → [Ac(6d)] (1D)	−26.45 (10.17%)	−33.56 (11.79%)	−44.38 (12.50%)
ΔEorb(3)	[9H2O(2p)] σ donation → [Ac(6d)] (1D)	−24.32 (9.35%)	−31.49 (11.06%)	−43.87 (12.36%)
ΔEorb(4)	[9H2O(2p)] σ donation → [Ac(6d)] (1D)	−24.06 (9.25%)	−30.57(10.74%)	−39.93 (11.25%)
ΔEorb(5)	[9H2O(2p)] σ donation → [Ac(6d)] (1D)	−23.34 (8.97%)	−28.42 (9.99%)	−39.43 (11.11%)
ΔEorb(6)	[9H2O(2p)] σ donation → [Ac(7s)] (1S)	−16.98 (6.53%)	−22.99 (8.08%)	−33.13 (9.33%)
ΔEorb(7)	[9H2O(2p)] σ donation → [Ac(7p)] (1P)	−9.53 (3.66%)	−11.29 (3.97%)	−14.46 (4.07%)
ΔEorb(8)	[9H2O(2p)] σ donation → [Ac(7p)] (1P)	−9.48 (3.64%)	−11.19 (3.93%)	−14.28 (4.02%)
ΔEorb(9)	[9H2O(2p)] σ donation → [Ac(7p)] (1P)	−6.28 (2.41%)	−11.11 (3.90%)	−14.21 (4.00%)
ΔEorb(10)	[9H2O(2p)] σ donation → [Ac(5f)]	−7.67 (2.95%)	—	—
ΔEorb(11)	[9H2O(2p)] σ donation → [Ac(5f)]	−8.14 (3.13%)	—	—
ΔEorb(12)	[9H2O(2p)] σ donation → [Ac(5f)]	−8.06 (3.10%)	—	—
ΔEorb(13)	[9H2O(2p)] σ donation → [Ac(5f)]	−7.92 (3.04%)	—	—
ΔEorb(14)	[9H2O(2p)] σ donation → [Ac(5f)]	−6.13 (2.36%)	—	—
ΔEorb(15)	[9H2O(2p)] π bonding ← [Ac(x)]	−7.17 (2.76%)	—	—
ΔEorb(16)	[9H2O(2p)] π bonding ← [Ac(x)]	−7.17 (2.76%)	—	—
ΔEorb(17)	9H2O polarization	−37.94 (14.58%)	—	—
ΔEorb(18)	Rest	−2.97 (1.14%)	—	—

---

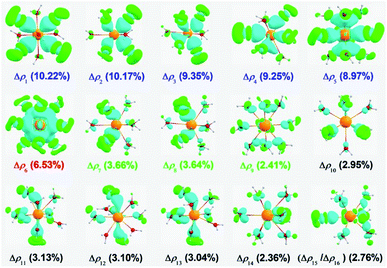
In particular, ΔE_orb can be further split into pairwise orbital interactions. This has been proven very helpful, because it provides a quantitative expression of the frontier molecular orbital model of Fukui⁶³ and the orbital symmetry rules of Woodward and Hoffman.⁶⁴ The shapes of the deformation densities Δρ corresponding to the ΔE_orb contributions are shown in Fig. 3. The first five deformation densities (Δρ₁ to Δρ₅) display a slightly larger charge flow in the direction [9H₂O_(2p)] → [Ac_(6d)]; they correspond to the 1D orbitals of the [Ac^III(H₂O)₉]³⁺ superatom. In a similar way, the following one (Δρ₆) and three deformation densities (Δρ₇ to Δρ₉) correspond to the 1S and 1P orbitals of the [Ac^III(H₂O)₉]³⁺ superatom. Interestingly, we also found that the 5f orbitals could also accept a small amount of 2p electrons (Δρ₁₀ to Δρ₁₄) and the valence acceptor electrons of the Ac atom might also go back via weak π bonding (Δρ₁₅ and Δρ₁₆). In general, the Ac–O_water bonding arises mainly from the [9H₂O_(2p)] to [Ac_(x)] σ donation of the 2p atomic orbitals of the O atom into x, where x denotes the valence acceptor atomic orbitals of the Ac^III cation. This also explains why the Ac^III cation gains electrons, as mentioned above.

Fig. 3 Shapes of deformation densities (isovalue = 0.0005 a.u.) between the interacting fragments of (H₂O)₉ and Ac^III from EDA-NOCV analysis. The cyan and green colors represent density inflow and outflow respectively.

In order to confirm the superatomic formation mechanism of the Ac cation with such a monodentate ligand, we further calculated and analyzed the EDA-NOCV results of the interaction of the positive trivalent Ac cation with nine NH₃ and nine PH₃ molecules. We found the [Ac^III(NH₃)₉]³⁺ and [Ac^III(PH₃)₉]³⁺ complexes, like the [Ac^III(H₂O)₉]³⁺ complex, both obey the 18-electron rule. This is mainly because NH₃ and PH₃ have strong polarity and also can provide LP electrons to coordinate with many metal ions to form coordination complexes (the detailed electronic structure diagrams are shown in Fig. S2 and S3 of ESI†). Specifically, the EDA-NOCV results are very interesting because they demonstrate that there is a non-negligible covalent character (ΔE_orb) between the Ac cation and the monodentate ligands (see Table 4).

The ammonia ligands NH₃ exhibit the largest interaction energy (−525.82 kcal mol⁻¹) with the Ac cation out of all three monodentate ligands. The Pauli repulsion exhibited by the NH₃ ligands (134.49 kcal mol⁻¹) is slightly smaller than for H₂O (136.70 kcal mol⁻¹) and larger than for PH₃ (113.25 kcal mol⁻¹), which leaves the orbital term (ΔE_orb) as a crucial component for the trend of the interaction energies (ΔE_int). Table 4 shows that the ΔE_orb value for PH₃ (−355.03 kcal mol⁻¹) is much larger than for H₂O (−260.19 kcal mol⁻¹) and NH₃ (−284.62 kcal mol⁻¹). The trend can be explained with the hybridization of the σ lone-pair orbital at the P atom, which has a much higher hybrid percentage in PH₃ than in NH₃ and H₂O (see Table S5 of ESI†). The higher hybrid percentage makes the lone-pair orbital to be more delocalized, which yields a larger overlap with the metal nucleus, which in turn is the main component of the electrostatic attraction in Ac-monodentate ligands.

In addition, the electronic structure diagrams of the ^gas[Ac^III(H₂O)₉(H₂O)₁]³⁺, ^aq[Ac^III(H₂O)₁₀]³⁺, ^gas[Ac^III(H₂O)₉(H₂O)₂]³⁺ and ^aq[Ac^III(H₂O)₁₀(H₂O)₁]³⁺ complexes are shown in Fig. 4. All of these complexes obey the 18-electron rule. This includes the 10-coordinated ^aq[Ac^III(H₂O)₁₀]³⁺ and ^aq[Ac^III(H₂O)₁₀(H₂O)₁]³⁺ complexes (with a total of 20e) that have the valence electron configuration 1S²1P⁶1D¹⁰1F², where the 1F orbital is a ligand-only orbital (or nonbonding orbital), which satisfies the 18-electron rule perfectly. The electrons in the 1F² orbital are stabilized by the field effect of the metal on the ligand cage because there is no valence atomic orbital of the s/p/d shells that possesses the same symmetry (geometric structure). Molecular orbital component analysis further proves this point, as the 1F² orbitals in orange circles in Fig. 4 arise from the contribution of the mixing of 2p atomic orbitals of the oxygen atoms (∼99%) and slightly from the 5f shell of Ac^III cation due to the polarization (∼1%). Moreover, the phenomenon of ligand-only superatom orbitals has also recently been discovered in the octacarbonyl complexes M(CO)₈ (M = Ca, Sr, Ba, Sc⁻, Y⁻, La⁻).^21,65 In order to explore the direct relationship between the coordination number of the Ac^III cation hydration layer and the 18-electron rule, we also analyzed the electronic structure of the Ac cation with coordination numbers ranging from 7 to 10, and found that the decrease in the number of water molecules corresponds to the disappearance of the 1D superatom states (see Fig. S4 of ESI†). To be specific, the superatom states based on the Jellium model are 1S²1P⁶1D¹⁰ for 9-coordination (18e), 1S²1P⁶1D⁸ for 8-coordination (16e), 1S²1P⁶1D⁶ for 7-coordination (14e). Therefore, there is indeed a strong connection between coordination number 9 and the 18 electron rule in hydrated Ac^III complexes.

Fig. 4 Electronic structure diagrams of ^gas[Ac^III(H₂O)₉(H₂O)₁]³⁺, ^aq[Ac^III(H₂O)₁₀]³⁺, ^gas[Ac^III(H₂O)₉(H₂O)₂]³⁺, ^aq[Ac^III(H₂O)₁₀(H₂O)₁]³⁺ complexes at the PBE-D3/TZ2P level of theory. The energies of ^aq[Ac^III(H₂O)₁₀]³⁺ and ^aq[Ac^III(H₂O)₁₀(H₂O)₁]³⁺ correspond to the left Y axis, and the energies of ^gas[Ac^III(H₂O)₉(H₂O)₁]³⁺ and ^gas[Ac^III(H₂O)₉(H₂O)₂]³⁺ complex correspond to the right Y axis.

At the conclusion of this section, it should be emphasized that one reviewer remarked that the existence of many known hydrated transition metal complexes is completely unrelated to the 18-electron rule, and this would similarly apply to the hydrated actinide complexes. However, here we summarize two traditional misunderstandings and use this to explain why the rule does indeed apply to the system we are studying: (a) the relevance of the individual atomic orbitals is not just limited to transition metal atoms, it also applies to some alkali earth metal elements and early lanthanide and actinide elements; (b) the “superatom concept” has nothing to do with whether the metal–ligand interactions are weak or strong. Specifically, within the spherical potential field of a superatom cluster, all electrons are separately confined in quantized molecular orbitals. Moreover, the symmetry of the MOs could prevent that the occupied ligand orbitals donate electronic charge into the valences orbitals of the metal and thus contribute to the electron count.^66,67 Regardless of whether the ligand is H₂O, CO or Au, they could all be regarded as a confined outer-shell structure that plays the same role, meaning that they all obey the 18-electron rule. In fact, both H₂O and CO are 2-electron donor ligands, notwithstanding the fact that the latter is also a strong π-acceptor. The discussion of the superatoms concept herein for an actinide metal complex, combined with previous examples (see the above discussion), will facilitate the understanding of superatomic states in solution chemistry and coordination chemistry.

Changes in coordination numbers

As discussed above, despite the use of the same initial structures containing 10 (or more) water molecules and 1 Ac^III cation, the CN always tends to be 10 in aqueous solution and 9 in gas phase. Therefore, considering this geometrical difference between gas phase and aqueous solution, we performed simulations for relaxed potential energy surface (PES) scans for the distance between an O atom and the Ac^III cation in both the complexes. In Fig. 5a, the PES is displayed as a function of the distance between the O atom in the second hydration shell of the ^gas[Ac^III(H₂O)₉(H₂O)₁]³⁺ complex and the Ac^III cation. The initial O⋯Ac distance is 4.470 Å (see a1 in Fig. 5a and 6). This distance is scanned to both sides, to a minimum of 2.300 Å and a maximum of 5.500 Å. Between 4.470 Å and 2.300 Å, there is a significant and sudden drop in the energy, at geometries a2 (O⋯Ac distance: 3.096 Å) and a3 (O⋯Ac distance: 3.077 Å), Fig. 5a. By checking the corresponding structures, we found that the geometries of a2 and a3 have changed dramatically (see Fig. 6). In other words, if we force a water molecule of the second hydration shell to be added to the first hydration shell, it will push one of the nine water molecules in the first hydration shell to the second hydration shell, and bring the geometry of this complex back to the original geometry at the same time. Indeed, the geometries of a1 and a4 are almost similar, Fig. 6. This implies that the coordination geometry with 9 water molecules (CN = 9) is most stable under gas-phase conditions. Besides, we also found that when the O⋯Ac distance reaches 5.122 Å (see a5 in Fig. 5a and 6), the energy has a small discontinuity, which is caused by the breaking of a hydrogen bond.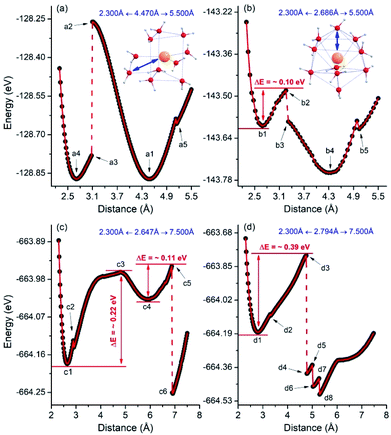

Fig. 5 Relaxed potential energy surface scans for the distance between O atom and Ac^III cation at the PBE-D3/TZ2P level of theory: (a) for ^gas[Ac^III(H₂O)₉(H₂O)₁]³⁺, (b) for ^aq[Ac^III(H₂O)₁₀]³⁺, (c and d) for ^aq[Ac^III(H₂O)₁₀(H₂O)₃₅]³⁺. In the ^aq[Ac^III(H₂O)₁₀(H₂O)₃₅]³⁺ complex, (c and d), two typical O atoms (O8 and O5, see the detailed structural information in Fig. S5 of ESI†) were chosen in the first hydration shell.

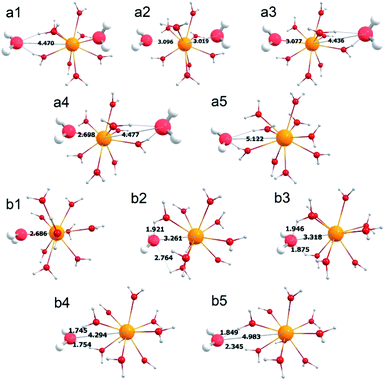Fig. 6 Typical geometries of the relaxed scan for the Ac–O_water bond length in the ^gas[Ac^III(H₂O)₉(H₂O)₁]³⁺ and ^aq[Ac^III(H₂O)₁₀]³⁺ complexes (see Fig. 5).

For the ^aq[Ac^III(H₂O)₁₀]³⁺ complexes, the initial distance between O atom and Ac^III cation is 2.686 Å (see b1 in Fig. 5b and 6). The O⋯Ac distance is scanned in the ranges 2.300 Å ← 2.686 Å → 5.500 Å. As the O⋯Ac distance increases, there is an obvious instantaneous drop in energy, from b2 (O⋯Ac distance: 3.261 Å) to b3 (O⋯Ac distance: 3. 318 Å), which is mainly due to the hydrogen bond forming by the target O atom with a H atom in an adjacent water molecule. Furthermore, when the O⋯Ac distance reaches 4.294 Å (i.e. CN = 9, see b4 in Fig. 5b and 6), the energy of the complex is the lowest. Therefore, even under aqueous conditions, the CN = 9 is more stable than the CN = 10. However, the change in the CNs from 10 to 9 requires crossing an energy barrier of ∼0.10 eV caused by hydrogen bonds.

As is well-known, like all implicit solvent models, COSMO cannot account for explicit interactions and charge transfer between the solute and solvent.^68,69 Herein, we consider an “explicit hydrogen bond model” (EHBM) for the implicit solvent model to simulate a real water environment, using 35 water molecules as the second hydration shell on the periphery of the 10 water molecules in the ^aq[Ac^III(H₂O)₁₀]³⁺ complex, i.e.^aq[Ac^III(H₂O)₁₀(H₂O)₃₅]³⁺ (see the detailed structural information in Fig. S5 of ESI†). Two prototypical O atoms were chosen in the first hydration shell of ^aq[Ac^III(H₂O)₁₀(H₂O)₃₅]³⁺. Similar relaxed PES scans as those above were performed, changing the O⋯Ac distance from 2.300 Å to 7.500 Å (see Fig. 5c and d). In Fig. 5c, the process of changing the CN from 10 to 9 requires crossing an energy barrier of ∼0.22 eV, but the energy of the potential well (see c4 in Fig. 5c) is higher (less negative) than that of the starting point (see c1 in Fig. 5c). Thus, an energy barrier of ∼0.11 eV must again be crossed to reach a more stable potential well (see c6 in Fig. 5c). In Fig. 5d, the process of transferring the CN from 10 to 9 only needs to cross an energy barrier of ∼0.39 eV. Evidently, when the Ac^III cation is in a real water environment, despite the preferred CN of the first hydration of 9, the CN = 10 (or even larger complexes) are also possible to exist. All the various breakpoints of the energy (Fig. 5) are directly related to the breakage and formation of hydrogen bonds. Overall, our research results are consistent with those of a recent DFT-based MD study on the hydrated Th(IV) complexes.⁷⁰ That is, the 9-coordinated complex is stable, and to achieve 10 coordination requires crossing of a non-negligible energy barrier.

Conclusions

In this work, we systematically studied the superatom states and the change of CN of the Ac^III cation in the [Ac^III(H₂O)_n]³⁺ (n = 4–11) complexes under gas-phase and aqueous solution conditions via first-principles DFT. From the geometrical point of view of the first hydration shell, the CN of the Ac^III cation tends to be 9 under gas-phase conditions. This is further verified through PES scans by forcing a tenth water molecule into the first hydration shell which results in one water molecule always being knocked out. However, for the aqueous solution case, the CN tends to be 10 although the 9-coordination exhibits greater stability than the 10-coordination in the first hydration shell and PES scans show a crossing energy barrier of 0.10 eV for the change of CN from 10 to 9. These results are strongly supported by both implicit (COSMO) and explicit (EHBM) solvation models. Moreover, electronic structure analysis reveals that the chemical stability of the [Ac^III(H₂O)₉]³⁺ complex can be attributed to the 18-electron rule (1S²1P⁶1D¹⁰). It primarily involves H₂O → Ac^III σ donation interaction between s-/p-/d-type atomic orbitals of the Ac atom and 2p atomic orbitals of the O atom.

Currently, due to the lack of a deep understanding of the physical and chemical properties of Ac, lanthanides and heavier actinides are often used as stable Ac surrogates.^30,71 However, our and other results show that Ac chemistry cannot be simply predicted from their behavior under comparable circumstances. In these cases, advanced quantum-chemical methods are supposed to help understand and define the bonding properties of actinide valence electrons, thus determine the possible type of bonding (covalent bond, ionic bond, or both). The nature of the Ac–O/N bond is the core of chelating agents, and one can expect similar behavior (18-electron rule, electron donation from ligand to metal) when the Ac cation interacts with oxygen atoms of other ligands. However, more details need to be considered regarding possible similarities and differences when oxygen and nitrogen atoms coordinate together. Hopefully, the results obtained herein for monodentate ligands, combined with previous studies of multidentate ligands (such as DOTA and its derivatives, EDTA, DTPA, PEPA, etc.),^72–74 in this context will facilitate future clinical applications.

Methods

For hydrated complexes containing actinide ions, the Perdew–Burke–Ernzerhof (PBE)⁷⁵ functional can reasonably reproduce the results of high-level ab initio wave-function theory.^55,76 Thus, the spin-polarized generalized gradient approximation (GGA) with empirical dispersion⁷⁷ corrections, PBE-D3, was used throughout this work. Both scalar relativistic (SR) and spin-orbit coupling (SOC) effects within the zeroth-order regular approximation (ZORA) have been considered.^78–81 Moreover, we also performed re-optimized energy calculations at the empirical dispersion corrected Becke-3-Lee-Yang-Parr^82,83 (B3LYP-D3) hybrid functional level based on the PBE-D3 geometries to provide additional evidence for the validity of our method.⁸⁴ A triple-ζ with two polarization functions (TZ2P) uncontracted Slater-type orbital (STO) basis set was used,⁸⁵ with a [1s²–4f¹⁰] frozen core for Ac, a [1s²] frozen core for O, and all electrons for H atoms, respectively.

Considering the effect of water solvent, all the complexes obtained under gas-phase conditions were re-optimized at both the PBE-D3/TZ2P and B3LYP-D3/TZ2P levels by applying the conductor-like screening solvation model (COSMO).^86–89 Since the free energy for each complex was computed at 1 atm pressure, an entropy correction for higher pressure is a simple way to model translational degrees of freedom in the solvent. An effective pressure of p = 1354 atm was used to mimic the condensed phase, which is the pressure obtained from p = ρ_wRT, corresponding to the experimental density of liquid water ρ_w = 997.02 kg m⁻³ at the temperature of 298 K.^55,90

The nature of the Ac–O_water interactions has been investigated employing the EDA-NOCV method, which combines the energy decomposition analysis (EDA) with the natural orbitals for chemical valence (NOCV) approach.⁵⁹ The interaction energy ΔE_int between the fragments is divided into four components:

ΔE_int = ΔE_elstat + ΔE_Pauli + ΔE_orb + ΔE_disp

where the ΔE_elstat term represents the quasi-classical electrostatic interaction between the unperturbed charge distributions of the prepared fragments, and the ΔE_Pauli term is the electron–electron Pauli repulsion due to the orthogonality requirement of the orbitals. The ΔE_orb term explains the process of forming covalent bonds through the inter-fragment mixing of the orbitals, and also explains the polarization within the fragments via intra-fragment orbital mixing. Finally, the ΔE_disp term corresponds to the dispersion (van der Waals) interaction between the fragments. All calculations under gas-phase and aqueous solution conditions are spin restricted. Geometry optimizations have been performed without imposing any symmetric constraints. The optimized structures were analyzed with vibrational frequency calculations at the same level to obtain thermochemical corrections as well as to ensure that all structures correspond to local minima. The calculations were performed using the Amsterdam Density Functional package (ADF 2017).⁹¹

In addition, for the ^aq[Ac^III(H₂O)₁₀(H₂O)₃₅]³⁺ complex in aqueous solution, we considered an “explicit hydrogen bond model” (EHBM) to simulate a real water environment for the implicit COSMO solvent model. Specific steps are as follows: (a) centering on the PBE-based ^aq[Ac^III(H₂O)₁₀]³⁺ complex, we constructed an initial structure of a larger water droplet with a radius of 12 Å. (b) In the Molecular Orbital PACkage (MOPAC 2012),⁹² because there are no available parameters for actinides, the Ac^III cation was temporarily removed. To further obtain a reasonable hydrogen bond network between the first and the second hydration shells, as well as to avoid errors caused by the removal of the Ac^III cation, all ten water molecules in the first hydration shell were frozen, while the remaining water molecules in the droplet were free to move. This large water droplet without Ac^III cation was initially optimized via a semi-empirical method (PM6-D3H4)⁹³ containing water solvent effects using the MOPAC 2012 program. (c) With the idea of being able to completely coat the ^aq[Ac^III(H₂O)₁₀]³⁺ complex but save computational cost, we removed excess water molecules (such that 35 water molecules were left in the second hydration shell) and performed the same optimization as in step (b) again. (d) The ^aq[(H₂O)₁₀(H₂O)₃₅] structure optimized at the semi-empirical method was used and the Ac^III cation was added back as in the initial structure. (e) The final stable complex ^aq[Ac^III(H₂O)₁₀(H₂O)₃₅]³⁺ was then optimized without any constraints at the PBE-D3/TZ2P level of theory (ADF 2017).

Conflicts of interest

The authors declare no competing financial interest.

Acknowledgements

The authors would like to thank Prof. Gernot Frenking for his input and comments. YG acknowledges the support of the National Science Foundation of China (under grant number 11904049) and the Project funded by China Postdoctoral Science Foundation (2019M653365). GS acknowledges funding from the Natural Sciences and Engineering Research Council of Canada (NSERC, Discovery Grant) and the Government of Canada through the New Frontiers in Research Fund – Exploration (NFRF-E) program.

References

1. G. J. P. Deblonde and R. J. Abergel, Nat. Chem., 2016, 8, 1084.
2. https://iupac.org/what-we-do/periodic-table-of-elements/ .
3. W. H. Xu and P. Pyykkö, Phys. Chem. Chem. Phys., 2016, 18, 17351–17355.
4. L. M. Thierer and N. C. Tomson, ACS Cent. Sci, 2017, 3, 153–155.
5. Y. S. Kim and M. W. Brechbiel, Tumor. Biol, 2012, 33, 573–590.
6. M. W. Brechbiel, Dalton Trans., 2007, 4918–4928.
7. D. E. Milenic, K. E. Baidoo, Y. S. Kim, R. Barkley and M. W. Brechbiel, Dalton Trans., 2017, 46, 14591–14601.
8. M. Miederer, D. A. Scheinberg and M. R. McDevitt, Adv Drug Deliver Rev, 2008, 60, 1371–1382.
9. N. A. Thiele and J. J. Wilson, Canc. Biother. Rad., 2018, 33, 336–348.
10. A. K. H. Robertson, C. F. Ramogida, P. Schaffer and V. Radchenko, Curr. Rad., 2018, 11, 156–172.
11. NSAC Isotopes Subcommittee, Meeting Isotope Needs and Capturing Opportunities for the Future: The 2015 Long Range Plan for the DOE-NP Isotope Program, July 2015.
12. P. Jena and Q. Sun, Chem. Rev., 2018, 118, 5755–5870.
13. Y. Gao and Z. Wang, Chin. Phys. B, 2016, 25, 083102.
14. S. N. Khanna and P. Jena, Phys. Rev. Lett., 1992, 69, 1664–1667.
15. W. D. Knight, K. Clemenger, W. A. Deheer, W. A. Saunders, M. Y. Chou and M. L. Cohen, Phys. Rev. Lett., 1984, 52, 2141–2143.
16. X. Li, B. Kiran, J. Li, H. J. Zhai and L. S. Wang, Angew. Chem. Int. Ed., 2002, 41, 4786–4789.
17. P. Pyykkö and N. Runeberg, Angew. Chem. Int. Ed., 2002, 41, 2174–2176.
18. T. J. Kealy and P. L. Pauson, Nature, 1951, 168, 1039–1040.
19. R. Pandey, B. K. Rao, P. Jena and M. A. Blanco, J. Am. Chem. Soc., 2001, 123, 3799–3808.
20. R. Arratia-Perez and C. Y. Yang, J. Chem. Phys., 1985, 83, 4005–4014.
21. X. Wu, L. Zhao, J. Jin, S. Pan, W. Li, X. Jin, G. Wang, M. Zhou and G. Frenking, Science, 2018, 361, 912–916.
22. Y. Gao, B. Wang, Y. Y. Lei, B. K. Teo and Z. G. Wang, Nano Res., 2016, 9, 622–632.
23. G. J. Cao, W. H. Schwarz and J. Li, Inorg. Chem., 2015, 54, 3695–3701.
24. C. Chi, S. Pan, J. Jin, L. Meng, M. Luo, L. Zhao, M. Zhou and G. Frenking, Chem.–Eur. J, 2019, 25, 11772–11784.
25. M. Joshi and T. K. Ghanty, Chem. Commun., 2019, 55, 7788–7791.
26. Y. Gao, W. Jiang, D. Xu and Z. Wang, Adv. Theory Simul., 2018, 1, 1700038.
27. J. P. Dognon, C. Clavaguera and P. Pyykkö, Chem. Sci., 2012, 3, 2843–2848.
28. J. P. Dognon, C. Clavaguéra and P. Pyykkö, J. Am. Chem. Soc., 2009, 131, 238–243.
29. T. R. Yu, Y. Gao, D. X. Xu and Z. G. Wang, Nano Res., 2018, 11, 354–359.
30. M. G. Ferrier, E. R. Batista, J. M. Berg, E. R. Birnbaum, J. N. Cross, J. W. Engle, H. S. La Pierre, S. A. Kozimor, J. S. Lezama Pacheco, B. W. Stein, S. C. Stieber and J. J. Wilson, Nat. Commun., 2016, 7, 12312.
31. M. Salvatores and G. Palmiotti, Prog. Part. Nucl. Phys., 2011, 66, 144–166.
32. C. Apostolidis, B. Schimmelpfennig, N. Magnani, P. Lindqvist-Reis, O. Walter, R. Sykora, A. Morgenstern, E. Colineau, R. Caciuffo, R. Klenze, R. G. Haire, J. Rebizant, F. Bruchertseifer and T. Fanghänel, Angew. Chem. Int. Ed., 2010, 49, 6343–6347.
33. P. D'Angelo and R. Spezia, Chem.–Eur. J, 2012, 18, 11162–11178.
34. M. Duvail, R. Spezia and P. Vitorge, ChemPhysChem, 2008, 9, 693–696.
35. M. G. Ferrier, B. W. Stein, E. R. Batista, J. M. Berg, E. R. Birnbaum, J. W. Engle, K. D. John, S. A. Kozimor, J. S. L. Pacheco and L. N. Redman, ACS Cent. Sci, 2017, 3, 176–185.
36. M. G. Ferrier, B. Stein, S. E. Bone, S. K. Cary, A. S. Ditter, S. A. Kozimor, J. S. Lezama Pacheco, V. Mocko and G. T. Seidler, Chem. Sci., 2018, 9, 7078–7090.
37. J. Wiebke, A. Moritz, X. Cao and M. Dolg, Phys. Chem. Chem. Phys., 2007, 9, 459–465.
38. R. R. Pappalardo, D. Z. Caralampio, J. M. Martinez and E. S. Marcos, Inorg. Chem., 2019, 58, 2777–2783.
39. B. Brendebach, N. L. Banik, C. M. Marquardt, J. Rothe, M. A. Denecke and H. Geckeis, Radiochim. Acta, 2009, 97, 701–708.
40. M. Duvail, F. Martelli, P. Vitorge and R. Spezia, J. Chem. Phys., 2011, 135, 044503.
41. M. R. Antonio, L. Soderholm, C. W. Williams, J. P. Blaudeau and B. E. Bursten, Radiochim. Acta, 2001, 89, 17–25.
42. P. G. Allen, J. J. Bucher, D. K. Shuh, N. M. Edelstein and T. Reich, Inorg. Chem., 1997, 36, 4676–4683.
43. P. G. Allen, J. J. Bucher, D. K. Shuh, N. M. Edelstein and I. Craig, Inorg. Chem., 2000, 39, 595–601.
44. R. Kirsch, D. Fellhauer, M. Altmaier, V. Neck, A. Rossberg, T. Fanghanel, L. Charlet and A. C. Scheinost, Environ. Sci. Technol., 2011, 45, 7267–7274.
45. T. Stumpf, C. Hennig, A. Bauer, M. A. Denecke and T. Fanghanel, Radiochim. Acta, 2004, 92, 133–138.
46. S. Skanthakumar, M. R. Antonio, R. E. Wilson and L. Soderholm, Inorg. Chem., 2007, 46, 3485–3491.
47. P. Lindqvist-Reis, C. Apostolidis, J. Rebizant, A. Morgenstern, R. Klenze, O. Walter, T. Fanghanel and R. G. Haire, Angew. Chem. Int. Ed., 2007, 46, 919–922.
48. T. Yang and B. E. Bursten, Inorg. Chem., 2006, 45, 5291–5301.
49. D. Hagberg, E. Bednarz, N. M. Edelstein and L. Gagliardi, J. Am. Chem. Soc., 2007, 129, 14136–14137.
50. R. Atta-Fynn, E. J. Bylaska, G. K. Schenter and W. A. de Jong, J. Phys. Chem. A, 2011, 115, 4665–4677.
51. M. R. Antonio, C. W. Williams and L. Soderholm, Radiochim. Acta, 2002, 90, 851–856.
52. E. Galbis, J. Hernandez-Cobos, C. den Auwer, C. Le Naour, D. Guillaumont, E. Simoni, R. R. Pappalardo and E. S. Marcos, Angew. Chem. Int. Ed., 2010, 49, 3811–3815.
53. R. Revel, C. Den Auwer, C. Madic, F. David, B. Fourest, S. Hubert, J. F. Le Du and L. R. Morss, Inorg. Chem., 1999, 38, 4139–4141.
54. B. Ravel and S. D. Kelly, AIP Conf. Proc., 2007, 882, 150–152.
55. G. A. Shamov and G. Schreckenbach, J. Phys. Chem. A, 2006, 110, 12072.
56. J. Kuta and A. E. Clark, Inorg. Chem., 2010, 49, 7808–7817.
57. J. Zhang, N. Heinz and M. Dolg, Inorg. Chem., 2014, 53, 7700–7708.
58. K. Wang, C. Xu, D. Li and L. Cheng, Commun. Chem., 2020, 3, 39.
59. M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962–975.
60. C. Terrier, P. Vitorge, M. P. Gaigeot, R. Spezia and R. Vuilleumier, J. Chem. Phys., 2010, 133, 044509.
61. M. Duvail, P. Vitorge and R. Spezia, J. Chem. Phys., 2009, 130, 104501.
62. G. Dupouy, I. Bonhoure, S. D. Conradson, T. Dumas, C. Hennig, C. Le Naour, P. Moisy, S. Petit, A. C. Scheinost, E. Simoni and C. Den Auwer, Eur. J. Inorg. Chem., 2011, 2011, 1560–1569.
63. K. Fukui, Theory of Orientation and Stereoselection, Springer Verlag: Berlin, 1975.
64. R. B. Woodward and R. Hoffmann, Angew. Chem. Int. Ed., 1969, 8, 781–853.
65. J. Jin, T. Yang, K. Xin, G. Wang, X. Jin, M. Zhou and G. Frenking, Angew. Chem. Int. Ed., 2018, 57, 6236–6241.
66. R. Hoffmann, J. M. Howell and E. L. Muetterties, J. Am. Chem. Soc., 1972, 94, 3047–3058.
67. J. Jin, S. Pan, X. Jin, S. Lei, L. Zhao, G. Frenking and M. Zhou, Chem.–Eur. J, 2019, 25, 3229–3234.
68. I. S. Ufimtsev, N. Luehr and T. J. Martinez, J. Phys. Chem. Lett., 2011, 2, 1789–1793.
69. A. van der Vaart and K. M. Merz, J. Am. Chem. Soc., 1999, 121, 9182–9190.
70. R. Spezia, Y. Jeanvoine, C. Beuchat, L. Gagliardi and R. Vuilleumier, Phys. Chem. Chem. Phys., 2014, 16, 5824–5832.
71. S. Cotton, Lanthanide and actinide chemistry, John Wiley & Sons, Ltd, Uppingham, Rutland, UK, 2006.
72. I. A. Davis, K. A. Glowienka, R. A. Boll, K. A. Deal, M. W. Brechbiel, M. Stabin, P. N. Bochsler, S. Mirzadeh and S. J. Kennel, Nucl. Med. Biol., 1999, 26, 581–589.
73. K. A. Deal, I. A. Davis, S. Mirzadeh, S. J. Kennel and M. W. Brechbiel, J. Med. Chem., 1999, 42, 2988–2992.
74. N. A. Thiele, V. Brown, J. M. Kelly, A. Amor-Coarasa, U. Jermilova, S. N. MacMillan, A. Nikolopoulou, S. Ponnala, C. F. Ramogida, A. K. H. Robertson, C. Rodriguez-Rodriguez, P. Schaffer, C. Williams, J. W. Babich, V. Radchenko and J. J. Wilson, Angew. Chem. Int. Ed., 2017, 56, 14712–14717.
75. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
76. M. P. Kelley, J. Su, M. Urban, M. Luckey, E. R. Batista, P. Yang and J. C. Shafer, J. Am. Chem. Soc., 2017, 139, 9901–9908.
77. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
78. E. van Lenthe, A. Ehlers and E.-J. Baerends, J. Chem. Phys., 1999, 110, 8943–8953.
79. E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1993, 99, 4597–4610.
80. E. van Lenthe, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1996, 105, 6505–6516.
81. E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783–9792.
82. C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789.
83. A. D. Becke, J. Chem. Phys, 1993, 98, 5648–5652.
84. G. A. Shamov, G. Schreckenbach and T. N. Vo, Chem.–Eur. J, 2007, 13, 4932–4947.
85. E. van Lenthe and E. J. Baerends, J. Comput. Chem, 2003, 24, 1142–1156.
86. A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805.
87. A. Klamt, J. Chem. Phys, 1995, 99, 2224–2235.
88. A. Klamt and V. Jonas, J. Chem. Phys, 1996, 105, 9972–9981.
89. C. C. Pye and T. Ziegler, Theor. Chem. Acc, 1999, 101, 396–408.
90. R. L. Martin, P. J. Hay and L. R. Pratt, J. Phys. Chem. A, 1998, 102, 3565–3573.
91. G. Te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. Van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem, 2001, 22, 931–967.
92. J. J. Stewart, J. Comput. Aided Mol. Des., 1990, 4, 1–105.
93. J. Rezac and P. Hobza, J. Chem. Theory Comput, 2012, 8, 141–151.

---

Footnote

† Electronic supplementary information (ESI) available: Part 1. Different isomers of Ac^III aquo complexes; part 2. Ac–O_water bond lengths of Ac^III aquo complexes; part 3. Detailed composition of superatom MOs of Ac^III(H₂O)₉]³⁺ complexes; part 4. Molecular orbitals of [Ac^III(H₂O)₉]³⁺ and [Ac@Au₁₄]⁻ based on the Jellium model; part 5. EDA-NOCV results with and without the explicit second water shell; part 6. Electronic structure of [Ac^III(NH₃)₉]³⁺ and [Ac^III(PH₃)₉]³⁺ complexes; part 7. Electronic structure diagrams for the Ac cation with coordination numbers from 7 to 10; part 8. Optimized geometry of the ^aq[Ac^III(H₂O)₁₀(H₂O)₃₅]³⁺ complex. See DOI: 10.1039/d0sc02342f

---