Flow synthesis kinetics for lomustine, an anti-cancer active pharmaceutical ingredient
Received
7th May 2021
, Accepted 19th July 2021
First published on 19th July 2021
Abstract
Continuous flow synthesis of active pharmaceutical ingredients (APIs) can offer access to process conditions that are otherwise hazardous when operated in batch mode, resulting in improved mixing and heat transfer, which enables higher yields and greater reaction selectivity. Reaction kinetic parameter estimation from flow synthesis data is an essential activity for the development of process models for drug substance manufacturing unit operations and systems, facilitating a reduction of experimental effort and accelerating development. The flow synthesis of lomustine, an anti-cancer API, in two flow reactors (carbamylation + nitrosation stages) was recently demonstrated by Jaman et al. (Org. Process Res. Dev., 2019, 23, 334). In this study, we postulate kinetic rate laws based on hereby proposed reaction mechanisms presented for the first time in the literature for this API synthesis. We then perform kinetic parameter regression for the proposed rate laws, on the basis of published data, towards establishing reactor models. For the carbamylation (irreversible reaction), we compare two candidate reaction rate laws, an overall third-order rate law (first-order in each reagent) deriving best fit. For the nitrosation, we propose two substitution reactions on the basis of published mechanisms (a rate-limiting equilibrium step, followed by a fast irreversible reaction) with very good model fit.
Introduction
Background
The number of people living with cancer and the number of cancer-related deaths have increased significantly over the last 30 years1,2 (Fig. 1). Global spending on cancer treatment and prices of anti-cancer drugs have also rapidly increased.3 Although there are many convoluted factors affecting drug prices,4,5 efficient manufacturing can help to reduce the cost of production of medicines with societal and economic impact. Streamlining active pharmaceutical ingredient (API) manufacturing and accelerating process development can significantly reduce development costs towards this end.
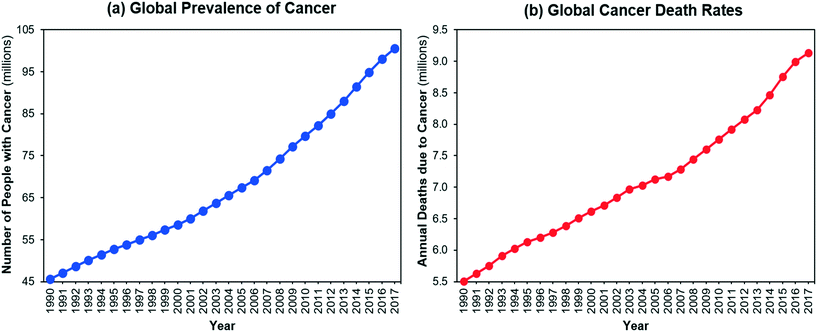 |
| | Fig. 1 (a) Global prevalence of cancer, (b) global death rates due to cancer.2 | |
Flow synthesis of active pharmaceutical ingredients
Flow synthesis demonstrations for a variety of APIs and their intermediates has received significant attention over the past decade. Development of flow technology and flow synthetic routes towards continuous manufacturing has rapidly increased due to the wide variety of chemical processes whose performance (productivity, quality, etc.) can be improved or intensified by switching from batch to continuous operation. There are several reviews documenting the rapid development of flow technology for fine chemical and pharmaceutical products.6–12
Table 1 summarises the various flow synthesis demonstrations of different anti-cancer APIs in the literature. However, deciding whether to operate in batch or continuous mode is non-trivial. For example, reactions with slow kinetics are better suited to batch operation and the existence of multiple phases can limit the benefits of operating in one mode vs. the other.13,14 Moreover, if an existing process route has acceptable performance with respect to yield, scale, process time, purity etc., and can be operated safely, then switching operating mode is not worthwhile. Judicious process selection and design is imperative for successful continuous process implementation.15
Table 1 Literature demonstrations of flow syntheses of APIs used in cancer treatment
| # |
API |
Treatment |
No. reactions |
Intermediate separations? |
Yield [%] |
Capacity [g h−1] |
Ref. |
| 1 |
Imatinib |
Gastrointestinal stromal tumours |
6 |
Y |
69 |
[—] |
16
|
| 2 |
Imatinib |
Gastrointestinal stromal tumours |
3 |
N |
58 |
0.327 |
17
|
| 3 |
Tasisulam |
Breast + ovarian cancer |
3 |
N |
90 |
5.200 |
18, 19 |
| 4 |
Tamoxifen |
Breast cancer |
5 |
N |
84 |
8.287 |
20
|
| 5 |
Lomustine |
Brain tumours Hodgkin's lymphoma |
2 |
Y |
63 |
0.110 |
21
|
| 6 |
Prexasertib |
Acute myeloid leukaemia |
3 |
Y |
75–85 |
0.023 |
22
|
| 7 |
2-Fluoroadenine |
Tumour prevention |
1 |
N |
82 |
120 |
23
|
Reaction modelling to streamline process development
Mathematical modelling and be used to reduce experimental effort involved in process development and design. Despite the widespread adoption of modelling approaches in general, industrial pharmaceutical development is still dominated by experimental approaches; this is in part due to the fact that new projects are constantly being begun and terminated depending on the company's portfolio regarding prioritised assets, challenges in clinical and process development, etc.
Traditionally, the definition of the process optimum and the control strategy are supported by design of experiments (DoE) approaches which are used to construct empirical models.24 Despite their value and the advances in high throughput experimentation technologies,25 they are not always the most suitable approaches to complex nonlinear problems typically encountered in pharmaceutical process systems. Moreover, they are generally resource-intensive.
Mechanistic and first-principles modelling approaches can provide deeper process understanding during development and design stages as well as definition of control strategies. The benefits of developing such models vary depending on the stage of development, but broadly include: (a) enhanced process understanding; (b) reducing experimental effort; (c) aiding process design; (d) sensitivity analysis; (e) design space elucidation; (f) process optimisation; (g) aiding scale-up.
Mechanistic modelling approaches are generally well-developed for reactor design and such models can be the basis of better-designed processes. In order to develop reactor models, it is fundamental to develop an understanding of: (a) reaction mechanisms and kinetics, including rate law parameters as well as interphase mass transfer, equilibria and mixing effects; (b) reaction thermodynamics; (c) dispersion effects and gradients; (d) mass and energy balances. Without these (either specific knowledge or valid assumptions therein), a detailed mechanistic understanding of a reaction remains elusive. Table 2 summarises different literature demonstrations of reaction kinetic parameter estimation for flow reaction model development, specifically for pharmaceutical small molecule synthesis.
Table 2 Examples of reaction kinetic modelling for API flow syntheses in the literature
| # |
API |
Application |
Parameters regressed |
Kinetic modelling benefits |
Ref. |
| 1 |
API |
(—) |
Isothermal rate constant, kR |
Reaction modelling + optimisation, process selection |
26
|
| 2 |
API |
(—) |
Arrhenius pre-exponential factor, k0 Activation energy, Ea |
Reactor design + scaleup |
27
|
| 3 |
Artemether |
Antimalarial |
Arrhenius pre-exponential factor, k0 Activation energy, Ea Rate law |
Reaction modelling + optimisation |
28
|
| 4 |
Ibuprofen |
Analgaesic |
Isothermal rate constant, kR Rate law |
Continuous process simulation + optimisation |
29, 30 |
| 5 |
Artemisinin |
Antimalarial |
Isothermal rate constant, kR |
Continuous process model simulation + optimisation |
31, 32 |
| 6 |
Diphenhydramine |
Antihistamine |
Isothermal rate constant, kR Rate law |
Continuous process model simulation |
33
|
| 7 |
Aziridines |
Cancer therapy |
Arrhenius pre-exponential factor, k0 Activation energy, Ea |
Reaction modelling + optimisation |
34
|
| 8 |
Pyroles |
Precursor |
Arrhenius pre-exponential factor, k0 Activation energy, Ea Rate law |
Minimise number of experiments to characterise kinetic model |
35
|
| 9 |
Int. |
(—) |
Arrhenius pre-exponential factor, k0 Activation energy, Ea |
Reaction modelling + optimisation |
36
|
| 10 |
Abemaciclib |
Anticoagulant |
Arrhenius pre-exponential factor, k0 Activation energy, Ea |
Reaction modelling + optimisation |
37
|
| 11 |
Rufinamide |
Antiepileptic |
Isothermal rate constant, kR |
Continuous process simulation |
38
|
| 12 |
Thiazolidine Int. |
Diabetes |
Arrhenius pre-exponential factor, k0 Activation energy, Ea |
Reaction solvent selection |
39
|
| 13 |
Glitazone |
Diabetes |
Arrhenius pre-exponential factor, k0 Activation energy, Ea |
Reaction solvent selection |
40
|
| 14 |
Tryptophol |
Sleep inducing |
Arrhenius pre-exponential factor, k0 Activation energy, Ea |
Reaction modelling + optimisation |
41
|
| 15 |
Atropine |
Nerve agents + pre-surgical procedures |
Isothermal rate constant, kR Rate law |
Continuous process simulation + optimisation |
42, 43 |
| 16 |
Nevirapine |
Anti-HIV |
Arrhenius pre-exponential factor, k0 Activation energy, Ea |
Continuous process simulation + optimisation |
44
|
| 17 |
Dolutegravir Int. |
Anti-HIV |
Arrhenius pre-exponential factor, k0 Activation energy, Ea |
Enable CFD modelling of flow reactor |
45
|
| 18 |
Atropine |
Nerve agents + pre-surgical procedures |
Arrhenius pre-exponential factor, k0 Activation energy, Ea |
Model predictive control of continuous API manufacturing |
46
|
| 19 |
API |
(—) |
Isothermal rate constant, kR |
Reaction modelling + optimisation |
47
|
This study
One example of an anti-cancer API with demonstrated continuous flow synthesis (Table 1) is lomustine, used for the treatment of brain tumours and Hodgkin's lymphoma.21 Between 2013–2019, the cost of lomustine increased from 50 to 768 USD per capsule.48 Herein, we use the available published reaction data for the lomustine flow synthesis21 in order to postulate reaction mechanisms for each synthetic stage (informed by similar reactions in the literature) and perform kinetic parameter estimation towards reactor modelling for a drug substance manufacturing system model.
The remainder of this paper is structured as follows. First, we describe the published flow synthesis process of lomustine, including the equipment configuration and materials used.21 We then postulate the reaction mechanisms of these steps as a basis for their proposed rate laws. The kinetic parameter estimation problem is then mathematically defined. The regressed kinetic parameters for the proposed rate laws are then presented with critical discussion of the methodology and results, followed by the conclusions of this study.
Lomustine flow synthesis
The demonstrated continuous flow synthesis of lomustine (1-(2-chloroethyl)-3-cyclohexyl-1-nitrosourea) is performed in two flow reactors, with an intermediate purification to change reaction solvents21 – the process flowsheet is shown in Fig. 2.
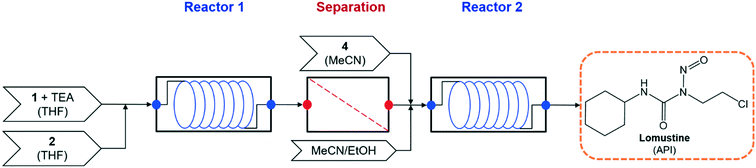 |
| | Fig. 2 Process flowsheet for flow synthesis of lomustine.21 | |
The overall reaction scheme is shown in Fig. 3. First, the carbamylation of cyclohexylamine (1, 0.5 mol L−1, 1 equiv.) by 1-chloro-2-isocyanatoethane (2, 1.4 equiv.) in the presence of triethylamine (TEA, 1 equiv.) occurs in reactor 1 to form 1-(2-chloroethyl)-3-cyclohexylurea intermediate (3); reactor 1 is operated at T = 50 °C with tetrahydrofuran (THF) as the reaction solvent. Reaction data21 is available at residence times, τ1 = {0, 10, 30, 60} s.
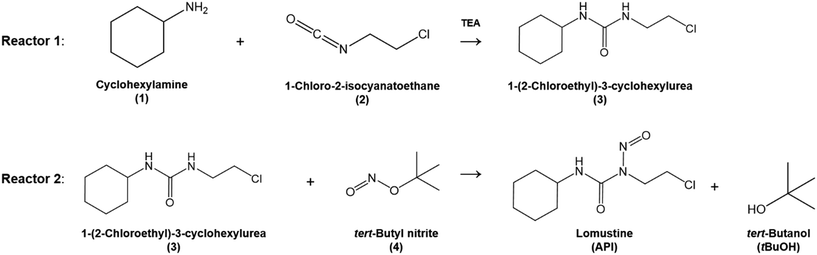 |
| | Fig. 3 Flow reaction scheme for continuous synthesis of lomustine (API).21 | |
In reactor 2, Int. 3 undergoes nitrosation with tert-butyl nitrite (4) to form lomustine (API); Int. 3 (1 equiv., 1 mol L−1) in a mixture of 3.72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 [v/v] acetonitrile/ethanol (MeCN/EtOH) solvent mixture reacts with 4 (3 equiv. in MeCN) at T = 50 °C to form API and tert-butanol (tBuOH) by-product. Reaction data is available at residence times, τ2 = {0, 30, 60, 180, 300, 480} s in the literature demonstration.21 Full details and properties of these key feed materials, intermediates and products involved in the flow synthesis of lomustine are summarised in Table 3.
1 [v/v] acetonitrile/ethanol (MeCN/EtOH) solvent mixture reacts with 4 (3 equiv. in MeCN) at T = 50 °C to form API and tert-butanol (tBuOH) by-product. Reaction data is available at residence times, τ2 = {0, 30, 60, 180, 300, 480} s in the literature demonstration.21 Full details and properties of these key feed materials, intermediates and products involved in the flow synthesis of lomustine are summarised in Table 3.
Table 3 Material properties of components used in lomustine flow synthesis (N.A. = not available)
| Species |
Role |
CAS # |
Formula |
MW [g mol−1] |
Density [g mL−1] |
Melting point [°C] |
Boiling point [°C] |
|
1
|
Reagent |
108-91-8 |
C6H13N |
99.17 |
0.865 |
−17.7 |
134.0 |
|
2
|
Reagent |
1943-83-5 |
C5H6ClNO3 |
163.56 |
1.237 |
N.A. |
135.0 |
| TEA |
Reagent/base |
121-44-8 |
C6H15N |
101.19 |
0.726 |
−114.7 |
89.3 |
|
3
|
Intermediate |
13908-11-7 |
C9H17ClN2O |
204.70 |
1.110 |
N.A. |
N.A. |
| THF |
Solvent |
109-99-9 |
C4H8O |
72.11 |
0.889 |
−108.4 |
66.0 |
|
4
|
Reagent |
463-04-7 |
C4H9NO2 |
103.12 |
0.867 |
N.A. |
62.0 |
| API |
Product |
13010-47-4 |
C9H16ClN3O2 |
233.70 |
1.400 |
90.0 |
N.A. |
| MeCN |
Solvent |
75-05-08 |
C2H3N |
41.05 |
0.786 |
−45.0 |
82.0 |
| EtOH |
Solvent |
64-17-5 |
C2H6O |
46.07 |
0.789 |
−114.1 |
78.4 |
Reaction mechanisms and kinetic model equations
Reaction rate and material balances
The following assumptions are made in the reaction kinetic modelling presented in this study:
(a) Only the considered reactions occur in their corresponding reactors, i.e., carbamylation in reactor 1, nitrosation in reactor 2, in the liquid phase only;21
(b) All reactions are isothermal (both reactors operated at T = 50 °C) as per the demonstrated flow synthesis;21
(c) Ideal mixing is achieved in each reactor, i.e., radial concentration gradients are negligible, as well as axial dispersion and temperature gradients (an appropriate assumption given the scale of the considered experimental flow synthesis demonstration);21
(d) Constant volumetric flowrates in all reactors, i.e., consumption/formation of species due to chemical reaction does not alter the mixture volume;
(e) Isothermal reactor operation is considered, and the requisite heat transfer is assumed perfectly efficient, ensured by appropriate heat transfer media provision and flow (no heat accumulation);
(f) Reactor operating temperatures are kept safely below solvent boiling points – this has indeed been confirmed as per the comparison thereof vs. solvent thermophysical properties (Table 3);
(g) Precipitation of reagents, intermediates and products does not occur, on account of the fact that such phenomena are not reported in the experimental demonstration, rendering this assumption valid.21
The proposed rate laws and regressed kinetic parameters should apply to both batch and flow modes of operation given these assumptions. Upon scale up, care should be taken to ensure that the intrinsic kinetics still hold; they could potentially vary due to other reaction rate-limiting barriers such as heat transfer and gradients within the reactor.
Under the listed assumptions, the general reaction rate equation is given by eqn (1). Here, rR = rate of reaction R, kR = isothermal rate constant of reaction R (at T = 50 °C for both reactors21), NC = total number of species, Ci(τ) = concentration of species i at residence time τl in reactor l for a total Nreactor reactors, αi,R = order of species i in reaction R, Nrxn = total number of reactions, C = vector of species concentrations. The overall order of reaction, αT,R is the sum of the individual species' orders, αi,R, (eqn (2)).
| | 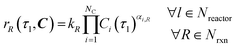 | (1) |
| | 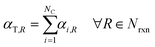 | (2) |
The material balance of an ideally mixed tubular reactor with constant volumetric flowrate is described by a system of ordinary differential equations (ODEs), as per
eqn (3). Here,
vi,R = stoichiometric coefficient of species
i in reaction
R.
| | 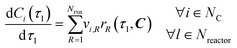 | (3) |
These equations are now expanded in the context of the proposed rate laws for reactions for the considered lomustine flow synthesis.
21
Reactor 1: carbamylation
The mechanism of reaction 1 is illustrated in Fig. 4. The carbamylation (reaction 1) in reactor 1 involves the interaction between a nucleophile (the lone electron pair on the nitrogen atom on 1) and an electrophile (the O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N carbon centre on 2). This then leads to a tetrahedral intermediate, in which proton transfer then occurs from one nitrogen atom (which has a positive charge due to the extra proton) to the other one (which has a free electron from the opening of the C
N carbon centre on 2). This then leads to a tetrahedral intermediate, in which proton transfer then occurs from one nitrogen atom (which has a positive charge due to the extra proton) to the other one (which has a free electron from the opening of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond on 1), resulting in Int. 3.
N bond on 1), resulting in Int. 3.
 |
| | Fig. 4 Carbamylation (reaction 1) mechanism to form Int. 3. | |
There is also the possibility that the lone electron pair on the nitrogen atom of 1 can attack the carbon centre adjacent to the chlorine atom on 2. This would result in HCl formation, which would impede the desired reaction of 1 with 2 to form Int. 3. The role of TEA in the reaction is not explained in the published lomustine flow synthesis,21 but it is possible that the goal is the prevention of the said effect.
Carbamylations are fast and irreversible.49,50 We compare two candidate rate laws: (a) first-order in each of 1 and 2 (i.e., overall second-order, αT,R = 2) and (b) first-order in each of 1, 2 and TEA (i.e., overall third-order, αT,R = 3). Candidate rate law (b) is considered as TEA is in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar equivalent with reagent 1, which is key in facilitating the carbamylation and thus the rate law may be dependent on its concentration51 in addition to the key reagents 1 and 2.
1 molar equivalent with reagent 1, which is key in facilitating the carbamylation and thus the rate law may be dependent on its concentration51 in addition to the key reagents 1 and 2.
| | | Option (a): r1(τ1, C) = k1C1(τ1)C2(τ1) | (4) |
| | | Option (b): r1(τ1, C) = k1C1(τ1)C2(τ1)CTEA(τ1) | (5) |
Expanding
eqn (2), the material balances in reactor 1 are thus described by
eqn (6)–(8). Stoichiometric coefficients and reaction orders for each species are listed in
Table 4.
| | 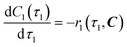 | (6) |
| | 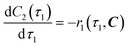 | (7) |
| | 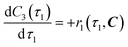 | (8) |
Table 4 Stoichiometric coefficients (v) and reaction orders (α) for different species in rate equations
| Reactor |
Reaction |
|
Species, i |
|
l
|
R
|
|
1
|
2
|
TEA |
3
|
4
|
4a
|
4b
|
API |
tBuOH |
| 1 |
1 (Opt. a) |
v
i,1
|
−1 |
−1 |
−1 |
+1 |
0 |
0 |
0 |
0 |
0 |
|
|
|
α
i,1
|
+1 |
+1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
1 (Opt. b) |
v
i,1
|
−1 |
−1 |
−1 |
+1 |
0 |
0 |
0 |
0 |
0 |
|
|
|
α
i,1
|
+1 |
+1 |
+1 |
0 |
0 |
0 |
0 |
0 |
0 |
| 2 |
2f |
v
i,2f
|
0 |
0 |
0 |
0 |
−1 |
+1 |
+1 |
0 |
0 |
|
|
|
α
i,2f
|
0 |
0 |
0 |
0 |
+1 |
0 |
0 |
0 |
0 |
|
|
2r |
v
i,2r
|
0 |
0 |
0 |
0 |
+1 |
−1 |
−1 |
0 |
0 |
|
|
|
α
i,2r
|
0 |
0 |
0 |
0 |
0 |
+1 |
+1 |
0 |
0 |
|
|
3 |
v
i,3
|
0 |
0 |
0 |
−1 |
0 |
0 |
−1 |
+1 |
+1 |
|
|
|
α
i,3
|
0 |
0 |
0 |
+1 |
0 |
0 |
+1 |
0 |
0 |
Reactor 2: nitrosation
The overall synthesis of API in reactor 2 is the nitrosation involving 3 and 4 in aqueous solution. Detailed kinetic rate law equations of such nitrosation reactions for the considered system are not published in the literature to the best of the authors' knowledge. Here, we propose a reaction mechanism based on other studies for similar nitrosations and postulate the rate law equations, for which kinetic parameters are regressed using the available published experimental data for lomustine synthesis.21
The considered reaction mechanism for the nitrosation of Int. 3 by 4 involves radical disproportionation of 4 to tBuO˙ (Int. 4a) and ˙N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (Int. 4b), which has been reported to occur in aqueous conditions.52,53 Thereafter, Int. 4a interacts with a N–H bond on Int. 3, as illustrated in Fig. 5, forming tBuOH as well as another radical, which subsequently reacts with Int. 4b, in order to form the API (lomustine).
O (Int. 4b), which has been reported to occur in aqueous conditions.52,53 Thereafter, Int. 4a interacts with a N–H bond on Int. 3, as illustrated in Fig. 5, forming tBuOH as well as another radical, which subsequently reacts with Int. 4b, in order to form the API (lomustine).
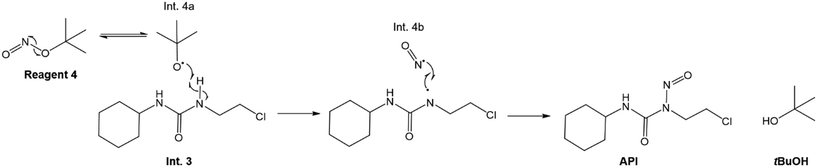 |
| | Fig. 5 Overall nitrosation reaction mechanism in reactor 2 to form API.52 | |
The reaction scheme (Fig. 5) shows the tBuO˙ radical interacting with the N–H bond on the chlorine side of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond on the Int. 3 molecule as opposed to that adjacent to the cyclohexyl group. It is possible that the N–H bond adjacent to the cyclohexyl ring is being stabilised by the said group, leading to the tBuO˙ radical preferentially interacting with the N–H bond on the chlorine side of the C
O bond on the Int. 3 molecule as opposed to that adjacent to the cyclohexyl group. It is possible that the N–H bond adjacent to the cyclohexyl ring is being stabilised by the said group, leading to the tBuO˙ radical preferentially interacting with the N–H bond on the chlorine side of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond. The authors suggest that the proposed reaction mechanisms be corroborated with additional data confirming these hypotheses.
O bond. The authors suggest that the proposed reaction mechanisms be corroborated with additional data confirming these hypotheses.
The radical formation is considered an equilibrium reaction with forward and backward reaction rates, r2f and r2r, respectively, with rate constants, k2f and k2r = k2f/Keq, respectively, where Keq therein has been defined as the radical disproportionation equilibrium constant. Reaction 3 is therefore considered an overall irreversible (forward only) reaction involving Int. 3, Int. 4a and Int. 4b, which proceeds to form the API (lomustine) as well as tBuOH (a by-product), as illustrated in the final stage of Fig. 5. The proposed kinetic rate laws for the foregoing reactions are therefore now described by eqn (9)–(11).
| | | r2f(τ2, C) = k2fC4(τ2) | (9) |
| | 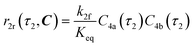 | (10) |
| | | r3(τ2, C) = k3C3(τ2)C4b(τ2) | (11) |
Expanding from
eqn (2), the resulting material balances in reactor 2 are as per
eqn (12)–(14). Stoichiometric coefficients and reaction orders for reactor 2 are listed in
Table 4.
| | 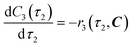 | (12) |
| | 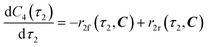 | (13) |
| | 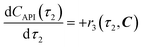 | (14) |
With the proposed reaction mechanisms, we now formulate a parameter estimation problem for reaction kinetic parameter estimation.
Parameter estimation
The regression of reaction kinetic parameters from experimental data is a parameter estimation problem described as the minimisation of the sum of square errors in eqn (15). Here, f = objective function, Nexpt = number of reaction experiments considered, NC = number of species for which data is measured and being predicted by the kinetic model, NP = number of time points at which experimental data is available, Cmodelp,i,j = model prediction of concentration of species i and time p in experiment j, Cexptp,i,j is the corresponding experimental value, τp,j = time p in experiment j, θ = model parameter vector.| | 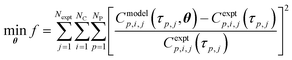 | (15) |
For each reaction, Nexpt = 1. In reactor 1, NC = 3 (species i = reagent 1, reagent 2, Int. 3), NP = 4; in reactor 2, NC = 3 (species i = 3, reagent 4, API), NP = 6. For reaction 1 occurring in reactor 1, the parameter vector in eqn (15) is θ = k1. For Reactions 2 + 3 in reactor 2, the parameter vector in eqn (15) is θ = [k2f, Keq, k3].
The model equations and parameter estimation problem are coded in MATLAB. The system of ODEs is solved using ode15s (stiff ODE solver54) and the parameter estimation problem is solved using lsqnonlin (Levenberg–Marquardt algorithm,55,56 default tolerance = 10−6). Reactor 1 is simulated for a total τ = 60 s and reactor 2 is simulated for a total τ = 480 s, chosen as the maximum time at which reaction data is available in the experimental demonstrations.21 All modelling is performed on an Intel® Core™ i-78665 CPU @ 1.90 GHz processor with 16.0 GB of RAM. In all cases, a single simulation took <1 s and the parameter estimation problem was solved in <10 s.
Results and discussion
Carbamylation (reaction 1)
The model fits for both candidate rate laws (options a and b) for reaction 1 in reactor 1 are shown in Fig. 6; parameter fits are summarised in Table 5 along with fitting confidence interval (CIs) and the corresponding coefficients of determination (R2) for each concentration profile. It can be seen a better fit is obtained for option (b), however option (a) still provides good fit, albeit with lower confidence.
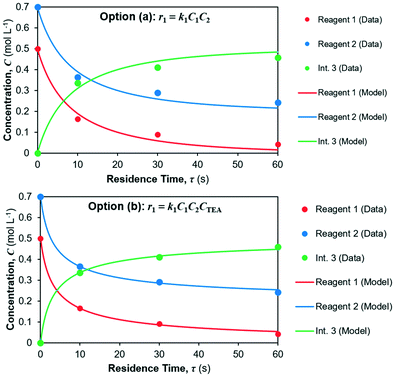 |
| | Fig. 6 Kinetic parameter fit for reaction 1. (a) Overall second-order rate law, (b) overall third-order rate law. | |
Table 5 Regressed kinetic parameter values and model fit quality for carbamylation (reaction 1)
| Parameter θ |
Value |
95% CI |
Units |
Coefficient of determination (R2) |
|
1
|
2
|
3
|
|
k
1 (Opt. a) |
0.1906 |
±16.96% |
[L mol−1 s−1] |
0.9820 |
0.9820 |
0.9820 |
|
k
1 (Opt. b) |
0.9024 |
±6.75% |
[L2 mol−2 s−1] |
0.9988 |
0.9988 |
0.9988 |
Table 6 Regressed kinetic parameter values and model fit quality for nitrosation reaction (reactions 2 + 3)
| Reaction |
Parameter θ |
Value |
95% CI |
Units |
Coefficient of determination (R2) |
|
3
|
4
|
API |
| 2 |
k
2f
|
0.5074 |
±19.00% |
[s−1] |
0.9558 |
0.9715 |
0.9709 |
|
|
K
eq
|
1.1798 × 10−5 |
±16.70% |
[mol L−1] |
| 3 |
k
3
|
100.1360 |
±16.50% |
[L mol−1 s−1] |
The yield of Int. 3 in reaction 1 is calculated as the ratio of molar concentration of Int. 3 at the end of the reaction vs. the initial molar concentration of limiting reagent (= Reagent 1). The assumed rate law thus also results in different yields of Int. 3vs. residence time, shown in Fig. 7; option (a) overpredicts the Int. 3 concentration (see model vs. data in Fig. 6a) compared to option (b), which fits better. Corroboration with additional data is required to confidently distinguish between the options.
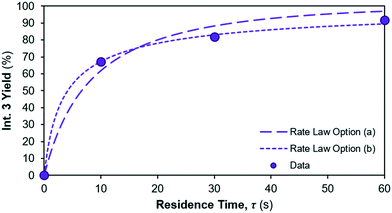 |
| | Fig. 7 Int. 3 yield profile for different reaction 1 rate law assumptions. | |
Nitrosation (reactions 2 + 3)
The model fit for the considered reaction mechanism/rate laws for the reactions occurring in reactor 2 are shown in Fig. 8. Parameter fits are summarised in Table 6. The quality of fit is very high for the considered rate laws, however confidence in the parameter fits (= CI) is lower than for reaction 1. The yield of API from reactions 2 + 3 is calculated as the ratio of product (= API) obtained at the end of the reaction vs. the initial concentration of limiting reagent (= Int. 3). The corresponding API yield profile is shown in Fig. 9.
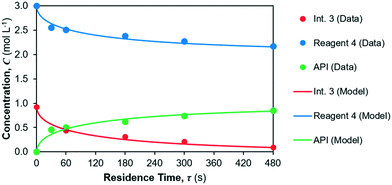 |
| | Fig. 8 Kinetic parameter fit for reactions 2 and 3 in reactor 2. | |
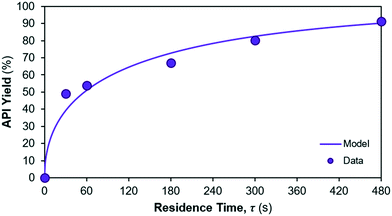 |
| | Fig. 9 API yield profile in reactor 2. | |
As per our hypothesis, the equilibrium constant of reaction 2 is low, i.e., the equilibrium is far to the left and thus reaction 2 is rate limiting with respect to API formation. Reaction 3 then proceeds very fast, as shown by the high value of rate constant k3. This observed behaviour of a rate-limiting equilibrium step followed by a fast reaction is often observed in organic syntheses,57,58 including nitrosation, as is occurring in reactions 2 + 3.59,60
Discussion
The proposed reaction mechanisms and rate laws fit the available data for each reaction very well; corroboration of the proposed rate laws can be accomplished by means of additional experimental effort towards data acquisition, which should ideally address: (a) spectroscopic identification of relevant intermediates for proposed reaction mechanisms, (b) high-resolution dynamic concentration measurements (especially at the onset of reactions, during which concentration gradients are steepest), (c) parametric (e.g. feed flowrates, reactor temperatures) variation. Obtaining such augmented datasets is beyond the scope of our kinetic analysis study; nevertheless, such an effort can certainly enhance our understanding of the reaction mechanisms for this particular API synthetic route.
A kinetic model is most often based on an assumed reaction mechanism whose rate equations are then to be validated via experimental data, possibly via similar reaction literature precedents. This validation does not ensure uniqueness or proof of the postulate, but has predictive value. The quality of fit for model parameters (best assessed by confidence intervals) strongly depends on data quality and quantity, and can indicate whether the assumed mechanism (thus: model structure) is correct, or if an alternative pathway may actually be occurring (assuming the parameter estimation algorithm and solver settings are suitably chosen to safeguard against local minimisation entrapment possibility).
Computational chemistry complements experiments in order to elucidate complex reaction phenomena. Density functional theory (DFT) is an established and efficient methodology61 for studying and analysing mechanisms related to stereoselectivity,62 organocatalysis,63 and provides valuable assistance to spectroscopic64 and other relevant investigations. A DFT approach may provide additional insight, but is beyond the scope of our present study. Various hurdles still remain to allow for its wider applicability and use, including the issue of successful predictions of transition structure geometry65 (which are key to the reaction mechanisms proposed in this study), the selection of appropriate functionals66 and the hazard of errors in kinetic parameter estimations67 (also important in this study). It would be an exciting prospect for this kinetic parameter estimation study to motivate DFT analyses.
Conclusions
The demonstrated flow synthesis of lomustine and available reaction data were used to postulate candidate rate laws based on proposed reaction mechanisms for each synthesis step. For the carbamylation (irreversible reaction), we compare two candidate reaction rate laws, with an overall third-order rate law (first-order in each reagent) showing the best fit. For the nitrosation (in the first reactor), we propose two substitution reactions (one rate-limiting equilibrium step, one fast irreversible step) with very good model fit vs. published experimental data. Corroboration of the proposed mechanisms with computational chemistry (e.g. DFT) methods and/or additional experimentation can enhance understanding of the reaction mechanisms for this API synthetic route. The presented kinetic model can accelerate continuous reactor design, scale-up and optimisation of lomustine production.
Nomenclature
Acronyms
| API | Active pharmaceutical ingredient |
| CI | Confidence interval |
| DFT | Density functional theory |
| DoE | Design of experiments |
| ODE | Ordinary differential equation |
Chemical compounds
|
1
| Cyclohexylamine |
|
2
| 1-Chloro-2-isocyanatoethane |
|
3
| 1-(2-Chloroethyl)-3-cyclohexylurea |
|
4
|
tert-Butyl nitrite |
|
4a
|
tBuO˙ radical |
|
4b
| ˙N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O radical O radical |
| EtOH | Ethanol |
| Int. | Intermediate |
| MeCN | Acetonitrile |
|
tBuOH |
tert-Butanol |
| TEA | Triethylamine |
| THF | Tetrahydrofuran |
Symbols
Latin letters.
|
C
| Concentration [mol L−1] |
|
C
| Vector of species concentrations [mol−1] |
|
E
a
| Activation energy [J mol−1] |
|
f
| Parameter estimation objective function [−] |
|
K
eq
| Equilibrium constant [mol L−1] |
|
k
0
| Pre-exponential factor [LαT−1 molαT−1 s−1] |
|
k
R
| Isothermal rate constant of reaction R [LαT−1 molαT−1 s−1] |
| MW | Molecular weight [g mol−1] |
|
N
C
| Number of components [−] |
|
N
expt
| Number of experiments [−] |
|
N
P
| Number of data points [−] |
|
N
reactor
| Number of reactors [−] |
|
N
rxn
| Number of reactions [−] |
|
R
2
| Coefficient of determination [−] |
|
r
R
| Rate of reaction R [mol L−1 s−1] |
|
T
| Temperature [°C] |
|
v
i,R
| Stoichiometric coefficient of species i in reaction R [−] |
Greek letters.
|
α
i,R
| Reaction order of species i in reaction R [−] |
|
α
T,R
| Overall order of reaction R [−] |
|
τ
| Residence time [s] |
|
θ
| Parameter vector |
Author contributions
Samir Diab: methodology, software, formal analysis, investigation, writing – original draft + review & editing, visualisation. Mateen Raiyat: methodology, software, formal analysis, investigation, writing – original draft, visualisation. Dimitrios I. Gerogiorgis: conceptualisation, methodology, writing – review & editing, visualisation, supervision, project administration, funding acquisition.
Conflicts of interest
There are no conflicts of interest to declare.
Acknowledgements
The authors gratefully acknowledge the Engineering and Physical Sciences Research Council (EPSRC) via a Doctoral Training Partnership PhD Fellowship (Grant #EP/N509644/1) to S. D., the support of the Great Britain Sasakawa and Nagai Foundations and a Royal Society (RS) Short Industrial Fellowship (2020–2021) to D. I. G (SIF\R1\201041). Tabulated and cited literature data suffice for reproduction of all original process simulation and parameter estimation results; no other supporting data are required for reproducibility.
References
- A. Jemal, E. M. Ward, C. J. Johnson, K. A. Cronin, J. Ma, A. B. Ryerson, A. Mariotto, A. J. Lake, R. Wilson, R. L. Sherman, R. N. Anderson, S. J. Henley, B. A. Kohler, L. Penberthy, E. J. Feuer and H. K. Weir, JNCI, J. Natl. Cancer Inst., 2017, 109, djx030 CrossRef PubMed.
-
M. Roser and H. Ritchie, “Cancer”, https://ourworldindata.org/cancer, (Accessed: 18th March 2021).
- P. B. Bach, N. Engl. J. Med., 2009, 360, 626 CrossRef CAS PubMed.
- N. P. Tallapragada, J. Law Biosci., 2016, 3, 238 CrossRef PubMed.
- J. A. DiMasi, H. G. Grabowski and R. W. Hansen, J. Health Econ., 2016, 47, 20 CrossRef PubMed.
- M. Baumann and I. R. Baxendale, Beilstein J. Org. Chem., 2015, 11, 1194 CrossRef CAS PubMed.
- M. B. Plutschack, B. Pieber, K. Gilmore and P. H. Seeberger, Chem. Rev., 2017, 117, 11796 CrossRef CAS PubMed.
- J. Britton and C. L. Raston, Chem. Soc. Rev., 2017, 52, 10159 Search PubMed.
- R. O. M. A. de Souza and P. Watts, J. Flow Chem., 2017, 7, 146 CrossRef CAS.
- L. Malet-Sanz and F. Susanne, J. Med. Chem., 2012, 55, 4062 CrossRef CAS PubMed.
- I. R. Rossetti and M. Compagnoni, Chem. Eng. J., 2016, 296, 56 CrossRef CAS.
- V. R. L. J. Bloemendal, M. A. C. H. Janssen, J. C. M. van Hest and F. P. J. T. Rutjes, React. Chem. Eng., 2020, 5, 1186 RSC.
- J. G. Costandy, T. F. Edgar and M. Baldea, Ind. Eng. Chem. Res., 2019, 58, 13718 CrossRef CAS.
- P. Bana, R. Örkényi, K. Lövei, Á. Lakó, G. I. Túrós, J. Éles, F. Faigl and F. I. Greiner, Bioorg. Med. Chem., 2017, 25, 6180 CrossRef CAS PubMed.
- S. Diab and D. I. Gerogiorgis, Pharmaceutics, 2020, 12, 235 CrossRef CAS PubMed.
- M. D. Hopkin, I. R. Baxendale and S. V. Ley, Chem. Commun., 2010, 46, 2450 RSC.
- W. C. Fu and T. F. Jamison, Org. Lett., 2019, 21, 6112 CrossRef CAS PubMed.
- T. D. White, K. D. Berglund, J. M. Groh, M. D. Johnson, R. D. Miller and M. H. Yates, Org. Process Res. Dev., 2012, 16, 939 CrossRef CAS.
- C. S. Polster, K. P. Cole, C. L. Burcham, B. M. Campbell, A. L. Frederick, M. M. Hansen, M. Harding, M. R. Heller, M. T. Miller, J. L. Phillips, P. M. Pollock and N. Zaborenko, Org. Process Res. Dev., 2014, 18, 1295 CrossRef CAS.
- P. R. D. Murray, D. L. Browne, J. C. Pastre, C. Butters, D. Guthrie and S. V. Ley, Org. Process Res. Dev., 2013, 17, 1192 CrossRef CAS.
- Z. Jaman, T. J. P. Sobreira, A. Mufti, C. R. Ferreira, R. G. Cooks and D. H. Thompson, Org. Process Res. Dev., 2019, 23, 334 CrossRef CAS.
- K. P. Cole, J. M. C. Groh, M. D. Johnson, C. L. Burcham, B. M. Campbell, W. D. Diseroad, M. R. Heller, J. R. Howell, N. J. Kallman, T. M. Koenig, S. A. May, R. D. Miller, D. Mitchell, D. P. Myers, S. S. Myers, J. L. Phillips, C. S. Polster, T. D. White, J. Cashman, D. Hurley, R. Moylan, P. Sheehan, R. D. Spencer, K. Desmond, P. Desmond and O. Gowran, Science, 2017, 356, 1144 CrossRef CAS PubMed.
- N. Salehi Marzijarani, D. R. Snead, J. P. McMullen, F. Lévesque, M. Weisel, R. J. Varsolona, Y. Lam, Z. Liu and J. R. Naber, Org. Process Res. Dev., 2019, 23, 1522 CrossRef CAS.
- N. S. Politis, P. Colombo, G. M. Colombo and D. Rekkas, Drug Dev. Ind. Pharm., 2017, 43, 889–901 CrossRef PubMed.
- S. M. Mennen, C. Alhambra, C. L. Allen, M. Barberis, S. Berritt, T. A. Brandt, A. D. Campbell, J. Castañón, A. H. Cherney, M. Christensen, D. B. Damon, J. Eugenio de Diego, S. García-Cerrada, P. García-Losada, R. Haro, J. Janey, D. C. Leitch, L. Li, F. Liu, P. C. Lobben, D. W. C. MacMillan, J. Magano, E. McInturff, S. Monfette, R. J. Post, D. Schultz, B. J. Sitter, J. M. Stevens, I. I. Strambeanu, J. Twilton, K. Wang and M. A. Zajac, Org. Process Res. Dev., 2019, 23, 1213–1242 CrossRef CAS.
- A. E. Rubin, S. Tummala, D. A. Both, C. Wang and E. J. Delaney, Chem. Rev., 2006, 106, 2794 CrossRef CAS PubMed.
- N. Kockmann and D. Roberge, Chem. Eng. Process, 2011, 50, 1017 CrossRef CAS.
- P. Yaseneva, D. Plaza, X. Fan, K. Loponov and A. Lapkin, Catal. Today, 2015, 239, 90 CrossRef CAS.
- H. G. Jolliffe and D. I. Gerogiorgis, Chem. Eng. Res. Des., 2015, 97, 175 CrossRef CAS.
- H. G. Jolliffe and D. I. Gerogiorgis, Ind. Eng. Chem. Res., 2017, 56, 4357 CrossRef CAS.
- H. G. Jolliffe and D. I. Gerogiorgis, Chem. Eng. Res. Des., 2016, 112, 310 CrossRef CAS.
- H. G. Jolliffe and D. I. Gerogiorgis, Comput. Chem. Eng., 2017, 103, 218 CrossRef CAS.
- S. Diab and D. I. Gerogiorgis, Org. Process Res. Dev., 2017, 21, 924 CrossRef CAS.
- A. Echtermeyer, Y. Amar, J. Zakrzewski and A. Lapkin, Beilstein J. Org. Chem., 2017, 13, 150 CrossRef CAS PubMed.
- K. C. Aroh and K. F. Jensen, React. Chem. Eng., 2018, 3, 94–101 RSC.
- H. Keles, F. Susanne, H. Livingstone, S. Hunter, C. Wade, R. Bourdon and A. Rutter, Org. Process Res. Dev., 2017, 21, 1761 CrossRef CAS.
- M. O. Frederick, M. A. Pietz, D. P. Kjell, R. N. Richey, G. A. Tharp, T. Touge, N. Yokoyama, M. Kida and T. Matsuo, Org. Process Res. Dev., 2017, 21, 1447 CrossRef CAS.
- S. Diab and D. I. Gerogiorgis, Comput. Chem. Eng., 2018, 111, 102 CrossRef CAS.
- R. R. de Oliveira Silva, P. V. C. Calvo, M. Fernandes da Silva, C. Solisio, A. Converti and M. S. Alves Palma, Chem. Eng. Technol., 2019, 42, 465 Search PubMed.
- D. da Pinheiro, R. R. Silva, R. R. de Oliveira, P. V. C. Calvo, M. Fernandes da Silva, A. Converti and M. S. A. Palma, Chem. Eng. Technol., 2018, 41, 1800 CrossRef.
- Y. R. Dubhashe, V. M. Sawant and V. G. Gaikar, Ind. Eng. Chem. Res., 2018, 57, 2787 CrossRef CAS.
- S. Diab, N. Mytis, A. G. Boudouvis and D. I. Gerogiorgis, Comput. Chem. Eng., 2019, 124, 28 CrossRef CAS.
- S. Diab and D. I. Gerogiorgis, AIChE J., 2019, 65, e16738 CrossRef CAS.
- S. Diab, D. T. McQuade, B. F. Gupton and D. I. Gerogiorgis, Org. Process Res. Dev., 2019, 23, 320 CrossRef CAS.
- C. T. Armstrong, C. Q. Pritchard, D. W. Cook, M. Ibrahim, B. K. Desai, P. J. Whitham, B. J. Marquardt, Y. Chen, J. T. Zoueu, M. J. Bortner and T. D. Roper, React. Chem. Eng., 2019, 4, 634 RSC.
-
A. Nikolakopoulou, M. von Andrian and R. D. Braatz, 2020 American Control Conference, 2020, p. 2778 Search PubMed.
- C. J. Taylor, M. Booth, J. A. Manson, M. J. Willis, G. Clemens, B. A. Taylor, T. W. Chamberlain and R. A. Bourne, Chem. Eng. J., 2020, 127017 Search PubMed.
- J. W. Taylor, T. Armstrong, A. H. Kim, M. Venere, A. Acquaye, D. Schrag and P. Y. Wen, Neuro. Oncol., 2019, 21, 1 CrossRef PubMed.
- G. R. Stark, J. Biol. Chem., 1964, 239, 1411 CrossRef CAS.
- D. G. Smyth, J. Biol. Chem., 1967, 242, 1579 CrossRef CAS.
- J. Burés, Top. Catal., 2017, 60, 631 CrossRef.
- A. Dahiya, A. K. Sahoo, T. Alam and B. K. Patel, Chem. – Asian J., 2019, 14, 4454 CrossRef CAS PubMed.
- S. A. Glover, A. Goosen, C. W. McCleland, F. R. Vogel and S. African, J. Chem., 1981, 34, 96 CAS.
-
L. F. Shampine, Numerical Solution of Ordinary Differential Equations, CRC Press, Boca Raton, 1st edn, 1994 Search PubMed.
- K. Levenberg, Q. Appl. Math., 1944, 2, 164 CrossRef.
-
J. J. Moré, in Numerical Analysis, ed. G. A. Watson, Springer Berlin Heidelberg, Berlin, Heidelberg, 1978, p. 105 Search PubMed.
- S.-D. Yoh, D.-Y. Cheong, C.-H. Lee, S.-H. Kim, J.-H. Park, M. Fujio and Y. Tsuno, J. Phys. Org. Chem., 2001, 14, 123 CrossRef CAS.
- T. B. Phan, C. Nolte, S. Kobayashi, A. R. Ofial and H. Mayr, J. Am. Chem. Soc., 2009, 131, 11392 CrossRef CAS PubMed.
- S. S. Mirvish, B. Gold, M. Eagen and S. Arnold, Zeitschrift für Krebsforsch. und Klin. Onkol., 1974, 82, 259 CAS.
- M. J. Crookes and D. L. H. Williams, J. Chem. Soc., Perkin Trans. 2, 1989, 9, 1319 RSC.
- T. Sperger, I. A. Sanhueza and F. Schoenebeck, Acc. Chem. Res., 2016, 49, 1311 CrossRef CAS PubMed.
- S. Moon, S. Chatterjee, P. H. Seeberger and K. G. Gilmore, Chem. Sci., 2021, 12, 2931 RSC.
- P. H.-Y. Cheong, C. Y. Legault, J. M. Um, N. Çelebi-Ölçüm and K. N. Houk, Chem. Rev., 2011, 111, 5042 CrossRef CAS PubMed.
- E. C. Sherer, J. R. Cheeseman and R. T. Williamson, Org. Biomol. Chem., 2015, 13, 4169 RSC.
- L. Simón and J. M. Goodman, Org. Biomol. Chem., 2011, 9, 689 RSC.
- K. N. Houk and F. Liu, Acc. Chem. Res., 2017, 50, 539 CrossRef CAS PubMed.
- O. Engkvist, P.-O. Norrby, N. Selmi, Y. Lam, Z. Peng, E. C. Sherer, W. Amberg, T. Erhard and A. L. Smyth, Drug Discovery Today, 2018, 23, 1203 CrossRef CAS PubMed.
Footnote |
| † Present affiliation: GlaxoSmithKline (GSK), Ware, SG12 0DP, UK. |
|
| This journal is © The Royal Society of Chemistry 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ,
Mateen
Raiyat
and
Dimitrios I.
Gerogiorgis
,
Mateen
Raiyat
and
Dimitrios I.
Gerogiorgis
 *
*



![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 [v/v] acetonitrile/ethanol (MeCN/EtOH) solvent mixture reacts with 4 (3 equiv. in MeCN) at T = 50 °C to form API and tert-butanol (tBuOH) by-product. Reaction data is available at residence times, τ2 = {0, 30, 60, 180, 300, 480} s in the literature demonstration.21 Full details and properties of these key feed materials, intermediates and products involved in the flow synthesis of lomustine are summarised in Table 3.
1 [v/v] acetonitrile/ethanol (MeCN/EtOH) solvent mixture reacts with 4 (3 equiv. in MeCN) at T = 50 °C to form API and tert-butanol (tBuOH) by-product. Reaction data is available at residence times, τ2 = {0, 30, 60, 180, 300, 480} s in the literature demonstration.21 Full details and properties of these key feed materials, intermediates and products involved in the flow synthesis of lomustine are summarised in Table 3.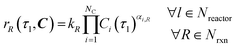
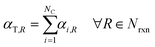
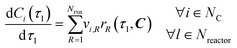
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N carbon centre on 2). This then leads to a tetrahedral intermediate, in which proton transfer then occurs from one nitrogen atom (which has a positive charge due to the extra proton) to the other one (which has a free electron from the opening of the C
N carbon centre on 2). This then leads to a tetrahedral intermediate, in which proton transfer then occurs from one nitrogen atom (which has a positive charge due to the extra proton) to the other one (which has a free electron from the opening of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bond on 1), resulting in Int. 3.
N bond on 1), resulting in Int. 3.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar equivalent with reagent 1, which is key in facilitating the carbamylation and thus the rate law may be dependent on its concentration51 in addition to the key reagents 1 and 2.
1 molar equivalent with reagent 1, which is key in facilitating the carbamylation and thus the rate law may be dependent on its concentration51 in addition to the key reagents 1 and 2.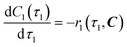
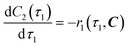
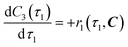
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O (Int. 4b), which has been reported to occur in aqueous conditions.52,53 Thereafter, Int. 4a interacts with a N–H bond on Int. 3, as illustrated in Fig. 5, forming tBuOH as well as another radical, which subsequently reacts with Int. 4b, in order to form the API (lomustine).
O (Int. 4b), which has been reported to occur in aqueous conditions.52,53 Thereafter, Int. 4a interacts with a N–H bond on Int. 3, as illustrated in Fig. 5, forming tBuOH as well as another radical, which subsequently reacts with Int. 4b, in order to form the API (lomustine).
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond on the Int. 3 molecule as opposed to that adjacent to the cyclohexyl group. It is possible that the N–H bond adjacent to the cyclohexyl ring is being stabilised by the said group, leading to the tBuO˙ radical preferentially interacting with the N–H bond on the chlorine side of the C
O bond on the Int. 3 molecule as opposed to that adjacent to the cyclohexyl group. It is possible that the N–H bond adjacent to the cyclohexyl ring is being stabilised by the said group, leading to the tBuO˙ radical preferentially interacting with the N–H bond on the chlorine side of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond. The authors suggest that the proposed reaction mechanisms be corroborated with additional data confirming these hypotheses.
O bond. The authors suggest that the proposed reaction mechanisms be corroborated with additional data confirming these hypotheses.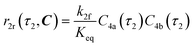
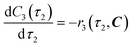
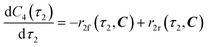
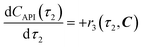
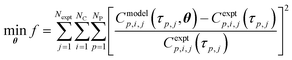

![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O radical
O radical



