Open Access Article
Open Access ArticleMolecular insight into carbon dioxide hydrate formation from saline solution
Chanjuan Liuabcd,
Xuebing Zhouabcd and
Deqing Liang *abcd
*abcd
aChinese Acad Sci, Guangzhou Ctr Gas Hydrate Res, Guangzhou Inst Energy Convers, Guangzhou 510640, Peoples R China. E-mail: liangdq@ms.giec.ac.cn
bCAS Key Lab Gas Hydrate, Guangzhou 510640, Peoples R China
cGuangdong Prov Key Lab New & Renewable Energy Res, Guangzhou 510640, Peoples R China
dState Key Lab Nat Gas Hydrate, Beijing 100028, China
First published on 24th September 2021
Abstract
Carbon dioxide hydrate has been intensively investigated in recent years because of its potential use as gas and heat storage materials. To understand the hydrate formation mechanisms, the crystallization of CO2 hydrate from NaCl solutions was simulated at a molecular level. The influence of temperature, pressure, salt concentration and CO2 concentration on CO2 hydrate formation was evaluated. Results showed that the amount of the newly formed hydrate cages pressure went through a fast linear growth period followed by a relatively stable period. Pressure had little effect on CO2 hydrate formation and temperature had a significant influence. The linear growth rate was greatly reduced as the temperature dropped from 255 to 235 K. The salt ion pairs could inhibit CO2 hydrate formation, suggesting that we should choose the lower salinity areas if we want to storage CO2 as gas hydrates in the seabed sediments. The observations in this study can provide theoretical support for the micro mechanism of hydrate formation, and provide a theoretical reference for the technology of hydrate based CO2 storage.
1. Introduction
Gas hydrates are ice-like compounds that form through a combination of gas and water molecules. Under elevated pressure and low temperature, water molecules form a cage-like host framework connected by hydrogen bonds and gas molecules are trapped inside as guests. The structure of gas hydrate largely depends on the size of the gas molecules.1,2 For example, methane (CH4), carbon dioxide (CO2) and ethane form sI hydrates; propane, nitrogen and tetrahydrofuran form sII hydrates.3 Naturally occurring gas hydrates, mainly CH4 hydrate, are considered as a potential alternative energy due to their huge reserves and wide distribution.4,5 More than 230 gas hydrate deposits have been detected worldwide and the amount of carbon stored in natural gas hydrates is estimated to be twice that of all the other carbon sources combined.6 At the same time, CO2 hydrates are found to be an eco-friendly material for CO2 storage.7–9 Thermodynamic calculations show that CO2 can be stably preserved in the seabed where the water depth is around 250 to 530 m which is more stable in the hydrate phase than CH4 at relevant pressures.10 Therefore, CO2 is suggested to displace CH4 from hydrate phase, releasing CH4 and capturing CO2 in the hydrate bearing sediments, which is expected to impact on both the sustainability of energy system and the global climate change.11–13The gas exchange concept for natural gas production has been confirmed viable technically. In 2011 and 2012, the field test conducted at the Alaska North Slope tried to replace CH4 with a gas mixture of 23 mol% CO2 and 77 mol% N2 from hydrate reservoir and found that a total of 24410 m3 of CH4 was recovered by sequestrating 2247 m3 of N2–CO2 mixtures successfully within 48 days.14 This field test reveals that the gas exchange in hydrate phase is a slow process and is limited by a series of factors. Then revealing the kinetic mechanism and key factors affecting gas exchange become a hotspot in gas hydrate research.15–18 With the recent progress in learning the kinetic features of CH4–CO2 replacement, gas exchange in hydrate phase was found to start with a fast reaction from simple hydrate to mixed hydrate at hydrate surface, then the gas replacement proceeds towards the deep inside of hydrate phase where gas diffusion is limited by the break of hydrate cages.19,20 However, there is a discrepancy lie in the existence of free water molecules in gas exchange. Ota et al.21,22 built a kinetic model by assuming that CH4–CO2 exchange in hydrate phase consist of a series of dissociation and reformation processes. This model provides a well description of the gas exchange in the initial stage and widely used.13,23,24 However, such an assumption is not supported from microscopic level. Magnetic resonance imaging (MRI) and differential scanning calorimeter (DSC) revealed that there was no sign of free water molecules appeared during gas replacement.25–27 Therefore, the gas exchange is suggested to proceed without significant change to host water lattice.
Molecular dynamic (MD) simulation is an effective tool to study the microscopic behavior of gas hydrate and has been widely used to study the kinetic process of gas hydrate.28–34 However, a direct simulation on the gas exchange at hydrate surface lead to different results because of the deviation in computational methods. Liu et al.35 and Tung et al.36 reported that the host lattice was slightly distorted during CH4–CO2 exchange. While Bai et al.37 and Wu et al.38 revealed that the CH4–CO2 exchange pathway started with the melting of CH4 hydrate near hydrate surface and followed by the formation of an amorphous CO2 hydrate layer. Since the CH4–CO2 exchange is closely related to the CH4 dissociation and the CO2 hydrate formation, it will be necessary to characterize the formation and dissociation of gas hydrate individually. Sarupria et al.39 found that CO2 hydrate dissociation rate was dependent on the fractional occupancy of each cage type. Qi et al.40 revealed that gas hydrates was not salt-free and massive salt ions may concentrate on the surface of the hydrates. Yi et al.41 noted that NaCl and MgCl2 decreased the mobility of their surrounding water molecules and inhibited CO2 hydrate growth. He et al.42 suggested that absorbing sufficient CO2 molecules around the CO2 hydration shells and a high aqueous CO2 concentration were the key factors governing the CO2 hydrate nucleation.
Since the CO2 hydrate formation is closely related to the CH4–CO2 exchange in hydrate phase, CO2 hydrate crystallization from NaCl solution was characterized from molecular level in this work. The growth pattern of hydrate cage at the hydrate–liquid interface was recorded. The influence of temperature (235–275 K), pressure (30–100 MPa) and salt concentration (0–20 wt%) on the growth rate of CO2 hydrate was measured. Results of this work is useful to identify the kinetic properties of CO2 hydrate formation from molecular level.
2. Simulation details
2.1 Simulation models and force field
The initial system is a solid–liquid model with the sizes of 73 × 48 × 48 Å3, which include hydrate phase and liquid phase as seen in Fig. 1. The hydrate phase consists of a 2 × 4 × 4 unit cell of sI hydrate structure with CO2 molecules full occupying the hydrate cages. The liquid water phase contains 2944 water molecules, 512 CO2 molecules and a certain amount of sodium chloride ion pairs determined by experimental conditions. MD simulations were performed in the GROMACS software package. The TIP4P/2005 model was used to describe water molecules in liquid phase.43 Zhang model was employed for CO2 molecules, which was better in predicting the self-diffusion at low temperature.44 The potential parameters of water and CO2 molecule used in this work were listed in Table 1.| Molecule | Atom/site | σii (Å) | εii (KJ/Mol) | q (e) | lb (Å) | αc (°) |
|---|---|---|---|---|---|---|
| a The site M of H2O lies in the molecular plane on the bisector of the H–O–H angle, and the distance between atom O and M is 0.1546 Å.b l refers to the bond length.c α refers to the bond angle. | ||||||
| — | O | 3.1589 | 0.774![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 912 912 |
0.0 | lOH = 0.9572 | ∠HOH = 104.52 |
| H2O | H | 0 | 0 | 0.5564 | — | — |
| Ma | 0 | 0 | −1.1128 | — | — | |
| CO2 | C | 2.7918 | 0.239832 | 0.5888 | lCO = 1.163 | ∠OCO = 180 |
| — | O | 3.0 | 0.687244 | −0.2944 | — | — |
The pair additive Lennard–Jones potential model in association with the coulombic charge expression isemployed for non-bonded interactions which can be written in following form the cross interactions between water and guest molecules were calculated according to the Lorentz–Berthelot combining rules45 via.
 | (1) |
 | (2) |
| εij = (εiiεjj)1/2 | (3) |
In this paper, all the simulations were performed by the NPT ensemble. The temperature was coupled by the Nosé–Hoover thermostat with a period constant of 1.0 ps and the pressure was coupled by the Parrinello-Rahman barostat with a period constant of 1.0 ps. In each simulation, energy minimization was initially performed to relax the initial configuration with the steepest descent algorithm. After energy minimization, the system was equilibrated in the NVT ensemble at 255 K, and then the NPT ensemble was set with a temperature of 255 K and a pressure of 30 MPa. The cutoff distance was 10 Å for the Lennard–Jones potential. Periodic boundary conditions were used in all three directions46 and the long-range electrostatic interactions were calculated using the particle mesh Ewald (PME) method with a real space cutoff of 10 Å, spline order of 4, and Fourier spacing of 1.2 Å.47
2.2 Data analysis
The face-saturated incomplete cage analysis method (FSICA) was used to recognize all the face-saturated cages in the system.48 For a standard polyhedron, the cage with both face saturated and edge saturated could be defined as a complete cage (CC). Here, the face saturated means that each edge of a cage is shared by two and only two faces which are water rings that no more than six members. The edge saturated means that each vertex in the polyhedron is shared by three edges at least. In brief, the face-saturated cages include face-saturated complete cages (FSCC) such as 512 (D-cage), 51262 cage (T-cage), 51263, 4151062, 4151063 and 51264 cages and face-saturated incomplete cages (FSIC) such as [5263]5 and [5264]5 cages. In this study, CO2 hydrate was SI hydrate, composed of D cage and T cage. The 512 cage (D-cage) means that the cage has twelve pentagonal faces and the 512 62 cage (T-cage) means that the cage has ten pentagonal faces and two hexagonal faces. We can see the snapshots of 512, 51262, and 51263 cages in Fig. 2.Each cage face had an adsorption site, which was along the normal vector crossing the face center and was 3 Å away from the center. The CH4 or CO2 molecules were identified as adsorbed, guest or free molecules. The linkages between each two hydrate cages through a cage face were classified into structure I (sI) links, structure II (sII) links, and structure H (sH) links. The linkage between a D-cage and a T-cage was recognized as an sI link because such linkage only existed in the sI hydrate structures, whereas the linkage between two D-cages could be either sII or sH.
We also used a four body order parameter (F4) to analyze the arrangement of H2O molecules. The F4 is defined as follow
 | (4) |
3. Results
3.1. The effect of pressure
To evaluate pressure effect, CO2 hydrates were allowed to grow at 30 MPa, 50 MPa and 100 MPa from the NaCl solution with a fixed initial NaCl concentration of 3.5 wt%. The growth rates of hydrate cages are shown in Fig. 3. The amount of the newly formed D-cages and T-cages were found to grow simultaneously once the simulation started and reached stable after 800 ns.In the initial 800 ns of hydrate growth, the amount of newly formed D- and T-cage increase in generally the same profile when the pressure was 30 and 50 MPa. As the pressure increased up to 100 MPa, the amount of newly formed D- and T-cage were found to grow faster during the initial 300 ns, then followed the same trend as those at 30 and 50 MPa, suggesting that the pressure increase from 30 to 100 MPa had limited promotion effect on the growth of hydrate crystal. Such a result agreed well with previous work, but was contradict with the conclusion that the hydrate growth rate was linearly correlated with gas fugacity difference between hydrate and gas phases which is frequently defined as driving force of hydrate growth.50,51 It should be noted that such a linear relationship between hydrate growth rate and driving force was got from macroscopic measurements where hydrate crystals grew with a continuous increase in amount of crystals in bulk liquid phase. Therefore, pressure increase was assumed to boost the formation of hydrate nuclei rather than the growth of an individual crystal.
In the simulation after 800 ns, the amount of the newly formed T-cages was about 3 times that of D-cages which was consistent with the ratio of T- and D-cage in a typical crystal unit of sI hydrate, suggesting that the hydrate grew as a complete crystal unit which was not influenced by pressure.
3.2. The effect of temperature
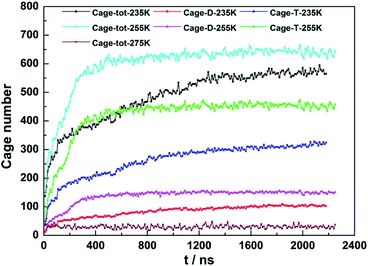
The temperature effect on CO2 hydrate growth were carried out in a system with fixed initial NaCl concentration of 3.5 wt% and pressure at 30 Mpa while the temperature was controlled at 235, 255 and 275 K. The profiles of the newly formed D- and T-cages at different temperature were shown in Fig. 4.As the temperature decreased from 255 to 235 K, the ratio of newly formed T- and D-cages was found to keep around 3.0 throughout each simulation, but the growth patterns of the newly formed cages changed. At 255 K, both the D- and T-cages grew linearly in the first 400 ns and reached stable thereafter. However, the linearly growth lasted only about 150 ns when the temperature decreased down to 235 K, and then the amount of both cages grew slowly and continuously in the next 2000 ns. Although a temperature decrease could gain an increase in driving force at fixed initial pressure, the initial hydrate growth was not found to be faster at lower temperature. In this case, lowering temperature is not beneficial to hydrate crystallization. From another perspective, the water molecules activity that determined largely by temperature was suggested to be more important than the gas diffusivity that affected by pressure in formation of cages on hydrate crystal surface.
3.3. The effect of NaCl concentration
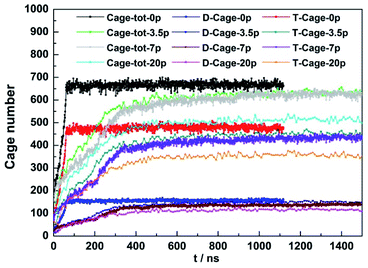
The effect of NaCl concentration on CO2 hydrate growth was measured at 30 MPa, 255 K with a NaCl concentration range from 0 to 20 wt%. The amount of the newly formed D- and T-cages during the simulation at different NaCl concentration was shown in Fig. 5. The amount of hydrate cages went through a linear growth in the initial stage and reached stable thereafter, which was not affected by the salt concentration.At fixed initial thermodynamic conditions, increasing NaCl concentration would impair the stability of CO2 hydrates and was suggested to reduce the CO2 hydrate formation rate.52 As expected, the amount of D-cage and T-cage grown from pure water got the highest linear growth rate at the initial stage and the total amount of the newly formed cages was also higher than the systems containing NaCl. We can see that during the first 400 nanoseconds of growth, with the NaCl concentration increased from 3.5 to 20 wt%, the growth rate of CO2 hydrate decreases slightly, and the total number of cages formed decreases, but such a decrease was not evident.
In the process of the carbon dioxide hydrate growth, the 51262 cage and 512 cage number ratio was slightly above 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
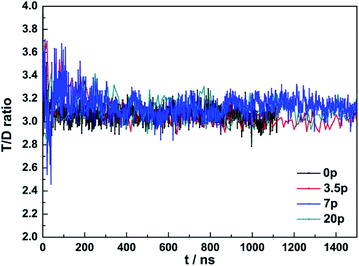
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 when the system reached stable as seen in Fig. 6. However, the T/D cage ratio was much higher at the initial stage, which was around 3.6 in maximum, suggesting that the 51262 cages formed first and faster than the 512 cages. At the same time we analyzed the influence of the NaCl concentration on the T/D cage ratio, and found that its ratio was just reached 3.2 and then stable at about 3 in the pure water system, while added NaCl, the T/D cage ratio could reach 3.6 in maximum. The higher the NaCl concentration, the larger the T/D cage ratio. It was suggested that the NaCl solution would inhibit the D cage's growth. We also observed a carbon dioxide bubbles generated in the process of formation while concentration was set to 7% and 20%.
1 when the system reached stable as seen in Fig. 6. However, the T/D cage ratio was much higher at the initial stage, which was around 3.6 in maximum, suggesting that the 51262 cages formed first and faster than the 512 cages. At the same time we analyzed the influence of the NaCl concentration on the T/D cage ratio, and found that its ratio was just reached 3.2 and then stable at about 3 in the pure water system, while added NaCl, the T/D cage ratio could reach 3.6 in maximum. The higher the NaCl concentration, the larger the T/D cage ratio. It was suggested that the NaCl solution would inhibit the D cage's growth. We also observed a carbon dioxide bubbles generated in the process of formation while concentration was set to 7% and 20%.
Fig. 7 shows the changes of cages in the process of CO2 hydrate formation when the concentration of salt solution is 0 and 3.5 wt%, the formation of the simulation time is 1 microsecond. Furthermore, in the process of the carbon dioxide hydrate formation, we observed that it can form not only 512 and 51262 cages, but also form 51263 cages, which are shown in yellow in Fig. 6. The 51263 cages are not the components of SI, SII and SH hydrates, but can form in the process of gas hydrate formation, which occupied a large mount.48 This means that the 51263 cage is a middle cage type, it can be turned into 51262 or 51264 cage. In the process of simulations, we tracked the salt ions activity, and found that no salt ions getting into the water cages. This is because the salt ions with charges, they will be excluded from the cage while they come close to the cage.
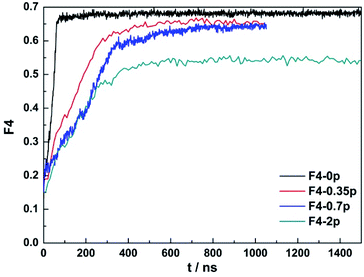
In addition, we analysed the four body order parameter (F4) of CO2 hydrate formation under different concentrations as seen in Fig. 8. The pure CO2 and water solution (the black line) formed carbon dioxide hydrate fast and the F4 value was closer to 0.7, which indicated that carbon dioxide hydrate under pure carbon dioxide aqueous solution had a higher crystallinity. With the increase of concentration of salt solution, the rate of hydrate formation gradually reduced, and the formation of hydrate crystals decreased. This result shown that salt ions inhibited the formation and growth of hydrates, and the sodium chloride was an inhibitor. This was also consistent with the experimental results by Andreas S. Braeuer.53
3.4 The effect of CO2 concentration
The CO2 concentration on CO2 hydrate formation was also taken into consideration in this work. Although CO2 shows much higher solubility than CH4, the nucleation of CO2 hydrate requires a much higher critical concentration. The observed critical concentration for CO2 hydrate nucleation was 0.08 in mole fraction42 while the guest concentration critical concentration for CO2 hydrate nucleation was just 0.04 in mole fraction.54 And they found that if the concentration in the solution under this number, it would nucleate hydrate very hardly.55 So in this paper, in order to analyse how the carbon dioxide concentration affects carbon dioxide hydrate formation. We selected a perfect crystalline mole concentration 0.148 and one concentration can form carbon dioxide hydrate which is 0.1. The F4 parameter of the different mole fraction in Fig. 9. We can see that almost all the carbon dioxide solution formed hydrates when the mole fraction was 0.148, and the F4 parameter value is about to 0.7, but the 0.1 mole fraction solution formed slowly and could not formed completely, and the F4 parameter value is just upon 0.4. This means that the higher the carbon dioxide concentration in water, the easier the carbon dioxide hydrate formed, and the higher the cage crystallinity. | ||
| Fig. 9 The F4 parameter of CO2 hydrate with different CO2 mole fraction in water. The black line of the mole fraction was 0.148 and the red line is 0.1. | ||
The final state of different mole concentration was shown in Fig. 10. The formation of the simulation time of 0.148 mole concentration solution is 1 microsecond while the simulation time of 0.1 mole concentration solution is 1.5 microsecond. The study found that with CO2 hydrate formed, CO2 molecules occupied the T and D cages, the concentration of CO2 solution reduced, and then the growth of hydrate speed decreased. It was also suggested that low concentration of CO2 solution was hard to continue to form hydrate.
4. Conclusions
In this paper, we analyzed the effects of temperature and pressure on the formation of CO2 hydrate. It is found that pressure has little effect on the formation of CO2 hydrate, while temperature has a great effect under the condition of CO2 hydrate can form. The formation rate of CO2 hydrate increased with the decrease of temperature. We compared the different concentrations of salt solution on CO2 hydrate formation, and found that the higher the salt concentration, the slower the CO2 hydrate formation. During the process of the CO2 hydrate formation, it can form 51263 cage and 51263 cage will turn into 51262 or 51264 cage. The 512 cage and 51262 cage number ratio is about 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 in the process of carbon dioxide hydrate formation, this is the ratio of sI hydrate. During the formation of CO2 hydrate, salt ions could not enter the cage or be absorbed on the cage face. This suggests that salt ions inhibit the formation and growth of hydrates. At the same time, we studied the influence of different CO2 mole concentration on CO2 hydrate formation, and found that the higher the CO2 mole fraction in water, the faster the CO2 hydrate formed, and the higher the cage crystallinity. The results provide theoretical support for the micro mechanism of hydrate formation, and provide a theoretical reference for the technology of hydrate storing CO2.
3 in the process of carbon dioxide hydrate formation, this is the ratio of sI hydrate. During the formation of CO2 hydrate, salt ions could not enter the cage or be absorbed on the cage face. This suggests that salt ions inhibit the formation and growth of hydrates. At the same time, we studied the influence of different CO2 mole concentration on CO2 hydrate formation, and found that the higher the CO2 mole fraction in water, the faster the CO2 hydrate formed, and the higher the cage crystallinity. The results provide theoretical support for the micro mechanism of hydrate formation, and provide a theoretical reference for the technology of hydrate storing CO2.
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
We thank the national supercomputing center in Shenzhen for the allocation of computer time. This work is supported by National Natural Science Foundation of China (41603062, 51706230).References
- Z. X. Huo, K. Hester, E. D. Sloan and K. T. Miller, AIChE J., 2003, 49, 1300–1306 CrossRef CAS.
- B. A. Buffett, Annu. Rev. Earth Planet. Sci., 2000, 28, 33 CrossRef.
- E. D. Sloan and C. A. Koh, Clathrate Hydrates of Natural Gases, CRC Press, 3rd edn, 2008 Search PubMed.
- P. Englezos and J. D. Lee, Korean J. Chem. Eng., 2005, 22, 11 Search PubMed.
- C. A. Koh, Chem. Soc. Rev., 2002, 31, 157–167 RSC.
- Z. R. Chong, S. H. B. Yang, P. Babu, P. Linga and X.-S. Li, Appl. Energy, 2016, 162, 1633–1652 CrossRef.
- M. Bui, C. S. Adjiman, A. Bardow, E. J. Anthony, A. Boston, S. Brown, P. S. Fennell, S. Fuss, A. Galindo, L. A. Hackett, J. P. Hallett, H. J. Herzog, G. Jackson, J. Kemper, S. Krevor, G. C. Maitland, M. Matuszewski, I. S. Metcalfe, C. Petit, G. Puxty, J. Reimer, D. M. Reiner, E. S. Rubin, S. A. Scott, N. Shah, B. Smit, J. P. M. Trusler, P. Webley, J. Wilcox and N. Mac Dowell, Energy Environ. Sci., 2018, 11, 1062–1176 RSC.
- J. J. Zheng, Z. R. Chong, M. F. Qureshi and P. Linga, Energy Fuels, 2020, 34, 10529–10546 CrossRef CAS.
- H. P. Veluswamy, A. Kumar, Y. Seo, J. D. Lee and P. Linga, Appl. Energy, 2018, 216, 262–285 CrossRef CAS.
- B. Tohidi, J. H. Yang, M. Salehabadi, R. Anderson and A. Chapoy, Environ. Sci. Technol., 2010, 44, 1509–1514 CrossRef CAS PubMed.
- C. G. Xu, X. S. Li, K. F. Yan, X. K. Ruan, Z. Y. Chen and Z. M. Xia, Chin. J. Chem. Eng., 2019, 27, 1998–2013 CrossRef CAS.
- F. G. Li, Q. Yuan, T. D. Li, Z. Li, C. Y. Sun and G. J. Chen, Chin. J. Chem. Eng., 2019, 27, 2062–2073 CrossRef CAS.
- D. Y. Koh, H. Kang, J. W. Lee, Y. Park, S. J. Kim, J. Lee, J. Y. Lee and H. Lee, Appl. Energy, 2016, 162, 114–130 CrossRef CAS.
- J. M. Schicks, B. Strauch, K. U. Heeschen, E. Spangenberg and M. Luzi-Helbing, J. Geophys. Res.: Solid Earth, 2018, 123, 3608–3620 CrossRef CAS.
- A. Falenty, J. Qin, A. N. Salamatin, L. Yang and W. F. Kuhs, J. Phys. Chem. C, 2016, 120, 27159–27172 CrossRef CAS.
- X. B. Zhou, F. H. Lin and D. Q. Liang, J. Phys. Chem. C, 2016, 120, 25668–25677 CrossRef CAS.
- X. B. Zhou, D. L. Li, S. H. Zhang and D. Q. Liang, Energy, 2017, 140, 136–143 CrossRef CAS.
- J. F. Zhao, L. X. Zhang, X. Q. Chen, Y. Zhang, Y. Liu and Y. C. Song, Energy Explor. Exploit., 2016, 34, 129–139 CrossRef CAS.
- Y. H. Sun, G. B. Zhang, S. L. Li and S. H. Jiang, Chem. Eng. J., 2019, 375 Search PubMed.
- A. N. Salamatin, A. Falenty and W. F. Kuhs, J. Phys. Chem. C, 2017, 121, 17603–17616 CrossRef CAS.
- M. Ota, Y. Abe, M. Watanabe, R. L. Smith and H. Inomata, Fluid Phase Equilib., 2005, 228, 553–559 CrossRef.
- M. Ota, K. Morohashi, Y. Abe, M. Watanabe, R. L. Smith and H. Inomata, Energy Convers. Manage., 2005, 46, 1680–1691 CrossRef CAS.
- D. Y. Koh, H. Kang, D. O. Kim, J. Park, M. Cha and H. Lee, Chemsuschem, 2012, 5, 1443–1448 CrossRef CAS PubMed.
- C. G. Xu, J. Cai, Y. S. Yu, K. F. Yan and X. S. Li, Appl. Energy, 2018, 217, 527–536 CrossRef CAS.
- S. Lee, Y. Lee, J. Lee, H. Lee and Y. Seo, Environ. Sci. Technol., 2013, 47, 13184–13190 CrossRef CAS PubMed.
- S. Lee, S. Park, Y. Lee and Y. Seo, Chem. Eng. J., 2013, 225, 636–640 CrossRef CAS.
- G. Ersland, J. Husebo, A. Graue, B. A. Baldwin, J. Howard and J. Stevens, Chem. Eng. J., 2010, 158, 25–31 CrossRef CAS.
- M. Uddin and D. Coombe, J. Phys. Chem. A, 2014, 118, 1971–1988 CrossRef CAS PubMed.
- P. Guo, Y.-K. Pan, L.-L. Li and B. Tang, Chin. Phys. B, 2017, 26, 073101 CrossRef.
- Y. Liu, J. Zhao and J. Xu, Comput. Theor. Chem., 2012, 991, 165–173 CrossRef CAS.
- N. J. English and G. M. Phelan, J. Chem. Phys., 2009, 131, 074704 CrossRef PubMed.
- F. Jiménez-Ángeles and A. Firoozabadi, J. Phys. Chem. C, 2014, 118, 11310–11318 CrossRef.
- M. R. Walsh, C. A. Koh, E. D. Sloan, A. K. Sum and D. T. Wu, Science, 2009, 326, 1095–1098 CrossRef CAS PubMed.
- L. Y. Ding, C. Y. Geng, Y. H. Zhao and H. Wen, Mol. Simul., 2007, 33, 1005–1016 CrossRef CAS.
- J. X. Liu, Y. J. Yan, H. Y. Liu, J. F. Xu, J. Zhang and G. Chen, Chem. Phys. Lett., 2016, 648 Search PubMed.
- Y. T. Tung, L. J. Chen, Y. P. Chen and S. T. Lin, J. Phys. Chem. B, 2011, 115, 15295–15302 CrossRef CAS PubMed.
- D. S. Bai, X. R. Zhang, G. J. Chen and W. C. Wang, Energy Environ. Sci., 2012, 5, 7033–7041 RSC.
- G. Z. Wu, L. Q. Tian, D. Y. Chen, M. Y. Niu and H. Q. Ji, J. Phys. Chem. C, 2019, 123, 13401–13409 CrossRef CAS.
- S. Sarupria and P. G. Debenedetti, J. Phys. Chem. A, 2011, 115, 6102–6111 CrossRef CAS PubMed.
- Y. Qi, W. Wu, Y. Liu, Y. Xie and X. Chen, Fluid Phase Equilib., 2012, 325, 6–10 CrossRef CAS.
- L. Yi, D. Liang, X. Zhou, D. Li and J. Wang, Mol. Phys., 2014, 112, 3127–3137 CrossRef CAS.
- Z. He, P. Linga and J. Jiang, Phys. Chem. Chem. Phys., 2017, 19, 15657–15661 RSC.
- J. L. F. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505 CrossRef CAS PubMed.
- Z. G. Zhang and Z. H. Duan, J. Chem. Phys., 2005, 122, 214507 CrossRef PubMed.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University PresS, New York, 1987 Search PubMed.
- G. Makov and M. C. Payne, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 4014–4022 CrossRef CAS PubMed.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- G. J. Guo, Y. G. Zhang, C. J. Liu and K. H. Li, Phys. Chem. Chem. Phys., 2011, 13, 12048–12057 RSC.
- P. M. Rodger, T. R. Forester and W. Smith, Fluid Phase Equilib., 1996, 7(116), 326–332 CrossRef.
- Z. Y. Yin, M. Khurana, H. K. Tan and P. Linga, Chem. Eng. J., 2018, 342, 9–29 CrossRef CAS.
- L. Z. Yi, X. B. Zhou, Y. B. He, Z. D. Cai, L. L. Zhao, W. K. Zhang and Y. Y. Shao, J. Phys. Chem. B, 2019, 123, 9180–9186 CrossRef CAS PubMed.
- L. Z. Yi, D. Q. Liang, X. B. Zhou, D. L. Li and J. W. Wang, Mol. Phys., 2014, 112, 3127–3137 CrossRef CAS.
- C. Holzammer, A. Finckenstein, S. Will and A. S. Braeuer, J. Phys. Chem. B, 2016, 120, 2452–2459 CrossRef CAS PubMed.
- G. J. Guo and P. M. Rodger, J. Phys. Chem. B, 2013, 117, 6498–6504 CrossRef CAS PubMed.
- Z. Zhang, P. G. Kusalik and G. J. Guo, Phys. Chem. Chem. Phys., 2018, 20, 24535–24538 RSC.
| This journal is © The Royal Society of Chemistry 2021 |