Open Access Article
Open Access ArticleRemarkable damage in talc caused by electron beam irradiation with a dose of up to 1000 kGy: lattice shrinkage in the Z- and Y-axis and corresponding intrinsic microstructural transformation process speculation
Xiaojun Huanga,
Jiayan Lia,
Xiaoya Sua,
Ke Fanga,
Zishuang Wanga,
Lin Liua,
Honglong Wang *a,
Chenguang Yangb and
Xiaoguang Wanga
*a,
Chenguang Yangb and
Xiaoguang Wanga
aSchool of Textile Science and Engineering, Wuhan Textile University, Yangguang Road No. 1, Jiangxia District, Wuhan 430200, Hubei, China. E-mail: wanghonglong915@163.com
bSchool of Materials Science and Engineering, Wuhan Textile University, Wuhan 430200, Hubei, China
First published on 21st June 2021
Abstract
To reduce the polluted areas caused by the migration of radioactive or toxic matter, a clear understanding of soil matrix stability, especially the lattice, is essential under irradiation conditions like those of β-ray irradiation. In reality, the matrix of soil or clay is silicate, with talc being one of the most simple species with a similar structure to that matter, exhibiting “2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1” stacking and a complete crystal. Therefore, in this work, it was irradiated by an electron beam in air with dose up to 1000 kGy. Then, variations in lattice and the intrinsic microstructural transformation process, especially in terms of defect formation and transformation, were explored. The main results show that irradiation led to talc lattice plane shrinkage and amorphization. Shrinkage and amorphization levels in the Z-axis were more serious than those in the Y-axis. For a 1000 kGy-irradiated sample, the shrinkage level of the (002) lattice plane was close to 2% near 0.2 Å and that of (020) was close to 1.3% near 0.06 Å. Variation in the (002) lattice plane was more obvious than that of (020). The main mechanisms involve the cleavage of tetrahedral Si–O and linkage of tetrahedra and octahedra. Tetrahedral Si–O cleavage was visible, leading to serious amorphization. Nevertheless, lattice plane shrinkage, especially in the Z-axis, was mainly caused by linkage cleavage in this direction. In addition to linkage cleavage, dehydroxylation and H2O volatilization occurred, coupled with H2O radiolysis. Nevertheless, those factors are secondary to lattice variation.
1” stacking and a complete crystal. Therefore, in this work, it was irradiated by an electron beam in air with dose up to 1000 kGy. Then, variations in lattice and the intrinsic microstructural transformation process, especially in terms of defect formation and transformation, were explored. The main results show that irradiation led to talc lattice plane shrinkage and amorphization. Shrinkage and amorphization levels in the Z-axis were more serious than those in the Y-axis. For a 1000 kGy-irradiated sample, the shrinkage level of the (002) lattice plane was close to 2% near 0.2 Å and that of (020) was close to 1.3% near 0.06 Å. Variation in the (002) lattice plane was more obvious than that of (020). The main mechanisms involve the cleavage of tetrahedral Si–O and linkage of tetrahedra and octahedra. Tetrahedral Si–O cleavage was visible, leading to serious amorphization. Nevertheless, lattice plane shrinkage, especially in the Z-axis, was mainly caused by linkage cleavage in this direction. In addition to linkage cleavage, dehydroxylation and H2O volatilization occurred, coupled with H2O radiolysis. Nevertheless, those factors are secondary to lattice variation.
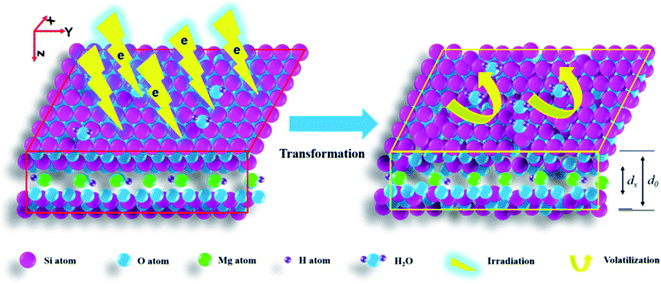
After irradiation, the main occurrence was lattice plane shrinkage and amorphization. Normally, shrinkage of dense material leads to immobilizing radionuclides or toxic matter closely, reducing migration, whereas amorphization leads to easier movement. This means if matter is already wrapped by a lattice it might be difficult to move under electron irradiation. If matter is adsorbed on a surface or occupied lattice sites it might easily move. This understanding is crucial for polluted area control and benefits efficiency elevation of high level radioactive waste (HLRW) disposal projects. For soil or clay proposed as back-fill material they should have a compact density and be replenished at a certain frequency. For a silicate solidified body, trapping in a lattice cavity is necessary. The findings in this work give a new strategy for materials design to promoting retardation capacity, wrapping with a lattice and lattice shrinkage, which is of great significance to environment remediation and waste management.
1. Introduction
Silicate substrate is the most common materials species and family on earth, including clay, soil, sand, rock, minerals, etc., and is crucial to ecosystems and our daily lives in fields such as agriculture, forestry, construction, and metallurgy. It is fundamental matter to human living and disaster response, such as lessening harm induced by toxic matter, fire, flood, and irradiation. Undeniably, atomic energy is one of the greatest achievements in the 20th century, even greatly affecting the world situation at present. In addition to national defense, it is an efficient and economical energy resource, crucial to energy consumption, especially in areas lacking traditional energy resources, such as China, Japan, and France. Its peaceful use brings us huge amounts of power like electricity and heating, with great convenience. Nevertheless, it is also accompanied by much radioactive or toxic matter generation, which is extremely dangerous and radioactive, and can migrate to end up in the environment.1–5Thus, the most important issue is how to efficiently hinder such movement, lessening pollution. In reality, the major matter in the environment is clay as soil. Thus, a deep exploration and understanding of the retardation capacity and structure variation of clay under various conditions is necessary. Except for direct chemical reaction, the most important impact is irradiation, which destroys structure without direct contact, altering structure greatly. A clear understanding of microstructural transformation processes under these harsh irradiation conditions is extremely important. Nevertheless, it is difficult and challenging because of complex composition. Normally, clay has very complex compositions, including oxides, organic matter, gas, silicate, and water, whereas the major components are silicates, which have a similar structure to polysilicate. Polysilicates are a family containing numerous species and stacking models like “2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1” (tetrahedron–octahedron–tetrahedron, TOT) and “1
1” (tetrahedron–octahedron–tetrahedron, TOT) and “1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1” (tetrahedron–octahedron, TO), and major silicates in soil are of a “2
1” (tetrahedron–octahedron, TO), and major silicates in soil are of a “2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1” stacking type. In reality, we cannot explore each component completely. Thus, choosing a simple system to simulate and focus on key factors is an efficient strategy to explore complex processes. In this respect, the chosen species should have clear composition, structure, and appearance and be representative. Taking these factors into consideration, pure and light-colored silicate crystals such as talc are appropriate.
1” stacking type. In reality, we cannot explore each component completely. Thus, choosing a simple system to simulate and focus on key factors is an efficient strategy to explore complex processes. In this respect, the chosen species should have clear composition, structure, and appearance and be representative. Taking these factors into consideration, pure and light-colored silicate crystals such as talc are appropriate.
Talc – Mg3(Si4O10)(OH)2 – is a white-colored, layered silicate crystal with “2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1” stacking. Two SiO4 tetrahedron sheets are linked together by an MgO6 octahedron layer, which displays as a stacking unit without traditional defects (extra elements in tetrahedral or octahedral sites or gap or interlayer, charge separation), shown as an origin to transform to other silicates (e.g. mica). In addition to a simplex structure, it contains small amounts of impurities and H2O, being very pure and appropriate for exploring the retardation capacity and stability variation of the clay matrix upon irradiation derived from radioactive and toxic matter and its migration.
1” stacking. Two SiO4 tetrahedron sheets are linked together by an MgO6 octahedron layer, which displays as a stacking unit without traditional defects (extra elements in tetrahedral or octahedral sites or gap or interlayer, charge separation), shown as an origin to transform to other silicates (e.g. mica). In addition to a simplex structure, it contains small amounts of impurities and H2O, being very pure and appropriate for exploring the retardation capacity and stability variation of the clay matrix upon irradiation derived from radioactive and toxic matter and its migration.
In reality, the surface area of clay or soil particles is primarily occupied by radioactive or toxic matter. According to the law of radioactivity decay, that area might be of very high radioactivity, enduring numerous irradiations and undergoing serious damage in a short time, with the occurrence of preferential radionuclide migration, which is very crucial to macro-property variation.
Normally, radiation involves numerous rays, displaying diverse properties. For instance, heavy ions like He2+, Pb2+, and UO22+ have large charge and mass, have difficulty in penetrating to a great depth, easy to deposit, inducing visible atom displacement and amorphization, and greatly altering the micro-area. After small movement, they might be trapped, and difficult to enlarge the polluted area efficiently without the assistance of extra factors. Light ions like H+ or e− (β-rays), especially β-rays, have high energy and charge with very small mass, penetrating a larger depth, inducing damage in a larger area, showing mild linear energy transfer (LET) effect, even inducing serious damage in impurity, forming complex products. Photons like γ-rays or X-rays have adequate energy with very small mass and charge, displaying strong penetrability, even penetrating concrete to more than 1 meter, showing a low LET effect. For a low LET effect, variation at close range might be weak, slightly altering retention capacity. Naturally, variation at interfaces mainly decides the change in retardation capacity and area extension. In reality, we cannot carry out irradiation experiments for each ray and its combination (α and β or α and γ). Considering it comprehensively, damage induced by light ions, like those involved in β-ray irradiation, seems crucial.
In addition to chemical composition and ray characteristics, crystalline structure is vital to damage level and macro-property variation. Normally, a crystalline region is more stable than an amorphous region, and is extremely crucial for blocking the migration of matter. If elements were trapped by a lattice cavity or unit, they might find it difficult to migrate and the system might be stable, weakening the polluted area extension. If a crystalline region becomes amorphous, nuclides or toxic matter might move easily, unexpectedly. Stabilizing a lattice and a clear understanding of variation in the lattice are thus vital and necessary.
As the dose rate and irradiation level of β-rays in a short time might be very high and electron beam (EB) irradiation is normally used to simulate β-ray irradiation effect and modification,6,7 in this work, pure talc powder was irradiated by an EB from a medium energy electron accelerator in air at a high current in a short time with dose up to 1000 kGy. Then, variations in chemical/crystalline structure and intrinsic microstructure transformation processes were explored, aiming to have a deeper understanding of lattice stability upon direct electron bombardment. The main results show that after irradiation, the lattice planes of talc mainly undergo shrinkage and amorphization and levels in the Z-axis are serious.
2. Experimental section
2.1 Materials
Multi-crystal talc block with an ideal chemical formula of Mg3(Si4O10)(OH)2 was originally bought from the University of Cambridge, UK, similar to that presented in the literature.8–112.2 Sample preparation and irradiation
Prior to irradiation, the talc block was ground to powder with a size of less than 50 μm. Then, aluminum foil with a thickness of 10 μm was chosen and the powder was spread on it with a thickness of less than 0.5 mm. Then, the aluminum foil was folded and irradiated by an EB from a 10 MeV electron accelerator in air with a current of 1.5 mA and dose up to 1000 kGy (Wuhan Aibang High Energy Technology Co. Ltd, Ezhou, China). The main procedure for irradiation was intermittent: 6 kGy per pass, 0.5 h per pass, 3.4 m s−1 of transmission and 6 cm width of irradiation window. After irradiation, samples were stored in air at room temperature prior to characterization.2.3 Characterization
3. Results and discussion
3.1 Lattice stability analysis
Normally, XRD is efficient to explore the variation in a lattice. Fig. 1a shows XRD patterns of talc under EB irradiation with a dose of up to 1000 kGy. All of the patterns are similar and mainly display three intense diffraction peaks at 2θ close to 9.3°, 18.8° and 28.4°, corresponding to the (002), (004) and (006) lattice planes. In addition to these peaks, several peaks with weak intensities appear, which can be assigned to secondary lattice planes (PDF card number 19-0770 in Jade 6.5 base). Excluding them, no extra peaks at interval positions appeared, implying purity and no serious decomposition or phase transformation.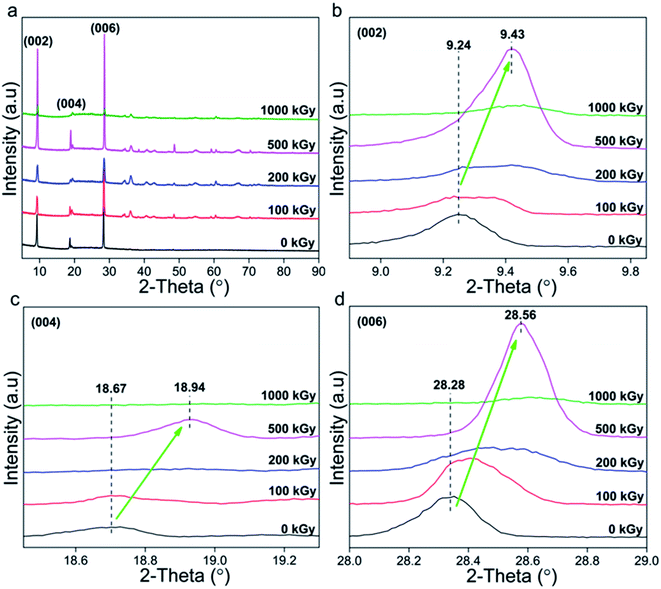 | ||
| Fig. 1 XRD patterns of talc under EB irradiation with a dose of up to 1000 kGy. (a) Complete; (b–d) refined patterns of the (002), (004) and (006) lattice planes. | ||
Naturally, serious decomposition or phase transformation occurs with difficulty, whereas slight damage in partial lattice planes might exist. Fig. 1b–d show the refined patterns of the (002), (004) and (006) lattice planes. For irradiated samples, peaks shifted to higher values by nearly 0.25° (2θ: 9.24 → 9.43, 18.67 → 18.94, 28.28 → 28.56°). According to Bragg's formula (nλ = 2d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), the larger the diffraction angle the smaller the interlayer space d. This means that irradiated samples have a smaller interlayer space d, implying lattice plane shrinkage or compact stacking. Naturally, the (002), (004) and (006) lattice planes are all in the Z-axis, implying shrinkage in this direction.
θ), the larger the diffraction angle the smaller the interlayer space d. This means that irradiated samples have a smaller interlayer space d, implying lattice plane shrinkage or compact stacking. Naturally, the (002), (004) and (006) lattice planes are all in the Z-axis, implying shrinkage in this direction.
To quantitatively describe varied level and range, corresponding interlayer spaces d were calculated (Table 1). Seeing the data, for these three lattice planes, in irradiated samples interlayer spacing d declined by 0.2, 0.07 and 0.03 Å, respectively. To realize varied level more clearly, the ratio dx/d0 was employed as indicated in Table 2, where x, dx, and d0 represent absorbed dose and interlayer spacing of irradiated and pristine samples.
| Dose (kGy) | d(002) (Å) | d(004) (Å) | d(006) (Å) |
|---|---|---|---|
| 0 | 9.565 | 4.7487 | 3.1531 |
| 100 | 9.5206 | 4.7468 | 3.1454 |
| 200 | 9.4473 | 4.7049 | 3.1335 |
| 500 | 9.3923 | 4.6903 | 3.127 |
| 1000 | 9.3686 | 4.6834 | 3.1232 |
| dx/d0 (%) | (002) | (004) | (006) |
|---|---|---|---|
| d100/d0 | 99.54 | 99.96 | 99.76 |
| d200/d0 | 98.77 | 99.08 | 99.38 |
| d500/d0 | 98.19 | 98.77 | 99.17 |
| d1000/d0 | 97.95 | 98.62 | 99.05 |
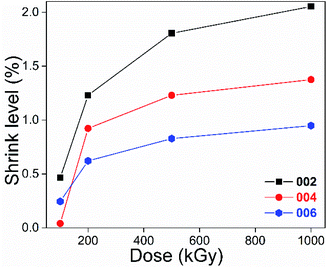
From Table 2, dx/d0 was less than 100% and became smaller as the dose increased. For instance, for the (002) lattice plane, d1000/d0 and d100/d0 were close to 97.9 and 99.5%. A ratio less than 100% indicates lattice plane shrinkage occurred. Its level seems to be enhanced by a dose increase, and can be defined and described as 1 − dx/d0. In this case, for the (002) lattice plane, shrinkage levels of 100-, 200-, 500- and 1000 kGy-irradiated samples can be described as 0.46% (100–99.54), 1.23% (100–98.77), 1.80% (100–98.19) and 2.05% (100–97.95), as shown in Fig. 2. The 1000 kGy-irradiated sample showed more serious shrinkage than the 100 kGy-irradiated sample.
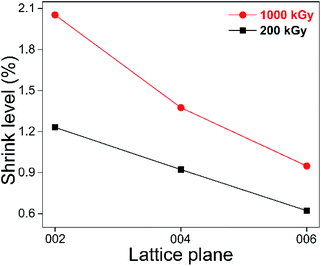
Looking at Fig. 2, excluding the absorbed dose's effect, the shrinkage level of the (002) plane was greater than that of the (004) and (006) lattice planes, showing a dependence on lattice parameters. To make them more visible, the results of the 200 and 1000 kGy-irradiated samples are re-displayed in Fig. 3.
It seems that the shrinkage level of the (002) plane is more than 1.5 and 2 times that of the (004) and (006) lattice planes. For instance, for the 1000 kGy-irradiated sample, that data are close, at 2.05, 1.38 and 0.95%, 2.05 ÷ 0.95 = 2.2. Naturally, (004) can be considered as the (002) lattice plane's second-order diffraction, displaying at half scale. Obvious dependence on lattice parameter means that shrinkage in the Z-axis exhibits an accumulated effect. Taking the 1000 kGy-irradiated sample as an example, the interlayer spacing d of these three lattice planes reduced by 0.2 (9.565 − 9.369 = 0.196), 0.07 (4.749 − 4.683 = 0.066) and 0.03 Å (3.153 − 3.123 = 0.03). 0.2 is larger than 0.07 obviously, but not double the value. According to the Bragg equation (nλ = 2d![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), the larger the lattice parameter the smaller the interlayer spacing d. In this case, the interlayer spacing d of (002) should be double that of the (004) lattice plane. Also, if the variation is almost linear, the decreasing range should exhibit the same trend. As can be seen from Table 1, all of the interlayer spacings d are consistent with this conception. For instance, for the 1000 kGy-irradiated sample, the data of the (002) and (004) lattice planes are close to 9.369 and 4.683 Å (9.369 is double that of 4.683). However, the decreasing range did not show this trend In reality, the (002), (004) and (006) lattice planes can be considered as a repetition of layers in the Z-axis. If the damage is uniform, the variation in range should be proportional, whereas it is not, indicating uneven destruction, partial layer might destroy seriously, expected because of random crash.
θ), the larger the lattice parameter the smaller the interlayer spacing d. In this case, the interlayer spacing d of (002) should be double that of the (004) lattice plane. Also, if the variation is almost linear, the decreasing range should exhibit the same trend. As can be seen from Table 1, all of the interlayer spacings d are consistent with this conception. For instance, for the 1000 kGy-irradiated sample, the data of the (002) and (004) lattice planes are close to 9.369 and 4.683 Å (9.369 is double that of 4.683). However, the decreasing range did not show this trend In reality, the (002), (004) and (006) lattice planes can be considered as a repetition of layers in the Z-axis. If the damage is uniform, the variation in range should be proportional, whereas it is not, indicating uneven destruction, partial layer might destroy seriously, expected because of random crash.
In addition to the Z-axis, the Y- or X-axis lattice planes might also incur damage. To describe the variation clearly, two characteristic Y-axis lattice planes of (020) and (060) were chosen and the results are displayed in Fig. 4a. Looking at the patterns, the peak position of (020) is close to that of (004), whereas the intensities of (020) and (060) are weaker compared to those of the (002) and (006) lattice planes, implying weak diffraction in the Y-axis. In addition to weak intensity, peaks also shifted to higher values, implying lattice plane shrinkage similar to that of the Z-axis. Corresponding interlayer spacings d were also calculated and compared (Tables 3 and 4).
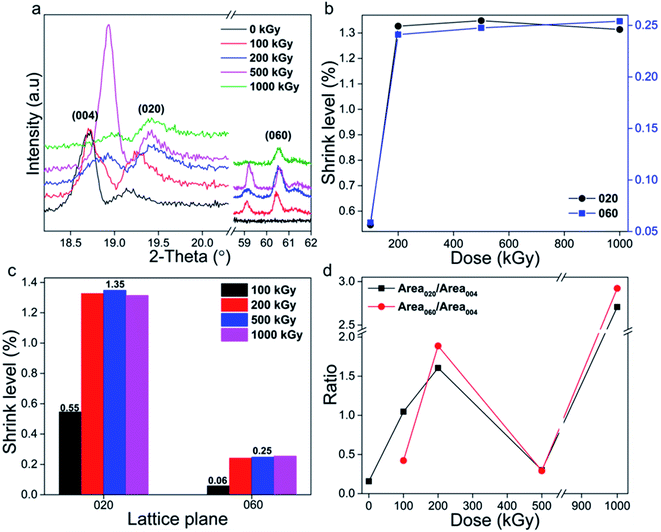 | ||
| Fig. 4 (a) XRD patterns of the (020) and (060) lattice planes. (b and c) Shrinkage level vs. absorbed dose and lattice parameter. (d) Ratio of intensity of the Y- to Z-axis lattice planes. | ||
| Dose (kGy) | d(020) (Å) | d(060) (Å) |
|---|---|---|
| 0 | 4.6359 | 1.5347 |
| 100 | 4.6106 | 1.5338 |
| 200 | 4.5744 | 1.531 |
| 500 | 4.5734 | 1.5309 |
| 1000 | 4.575 | 1.5308 |
| dx/d0 (%) | (020) | (060) |
|---|---|---|
| d100/d0 | 99.45 | 99.94 |
| d200/d0 | 98.67 | 99.75 |
| d500/d0 | 98.65 | 99.75 |
| d1000/d0 | 98.68 | 99.74 |
The shrinkage level was also defined and described as 1 − dx/d0 and the results are indicated in Fig. 4b, showing nonlinear variation. Taking the (020) lattice plane as representative, its shrinkage level increased to 1.3% upon a dose increase to 200 kGy, and then became constant. The (060) lattice plane displays a similar variation trend, with a lower value of 0.25%. The shrinkage level seems to be enhanced visibly at a low dose (≤200 kGy) and is then constant, displaying a threshold, differing with a variation in the Z-axis. This phenomenon is notable. Compared to the Z-axis, the Y-axis lattice plane has a smaller lattice size. For instance, d020 (4.636 Å) is half that of d002 (9.565 Å), implying more compact stacking. Naturally, the atoms in the Y- and X-axis are all in plane while those on the Z-axis are out of plane. Atoms in plane are linked together as a network, very robust and dense. For compact stacking, the variation in the range can be very small. Naturally, the main chemical bonds in plane are Si–O bonds. Thus, the lattice size of the Y-axis lattice plane mainly depends on the length of the –(Si–O–Si)–n or –(O–Si–O)–n bonds in this direction. Commonly, lattice plane shrinkage indicates framework cleavage. As stacking is compact, the free space is very small, and adjacent chemical bonds are linked together with difficulty to cleave completely, generating individual atoms, thus visible collapse occurs with difficulty, displaying weak variation. Naturally, obvious collapse means atoms in the same plane are destroyed synchronously, cannot maintaining primary structure, which is difficult to occur as crash between electron and framework is random. Even when occurring, the shrinkage range can be very small, indicating smaller range compared to Z-axis. Also, the shrinkage limit in Y-axis can be smaller. If the limit is exceeded, the varied level cannot continuously increase. These explanations probably illustrate the observed variation. Normally, damage can be enhanced by dose increase, especially at a low level while being constant at a higher level, as in ultra-high molecular weight polyethylene (UHMWPE) cross-linking.12 That does not mean that the level cannot be further enhanced. Perhaps it might occur at a certain irradiation level, needing clarification.
In addition to the absorbed dose, the variation level also depends on the lattice parameter (Fig. 4c). The shrinkage level and variation range of the (020) plane are more than five and two times those of the (060) lattice plane. Taking the 1000 kGy-irradiated sample as an example, the shrinkage ranges of (020) and (060) lattice planes were close to 0.06 and 0.03 Å, displaying an accumulated effect while uneven. In reality, the lattice parameter of (020) is one third that of (060), implying that it is three times the interlayer spacing d value. Assuming a space packed by (020) lattice planes as a whole, that of (060) is one third and can be considered as a repeat unit. If damage in any repeat unit is close, the range in the whole should be three times. Nevertheless, this is difficult to occur because of random crash. Two times can be recipient. The shrinkage level of (020) was larger than that of (060) lattice plane indicating accumulated effect in adjacent layers.
Considering previous analysis, it seems that after irradiation shrinkage occurred in the lattice planes in the Z- and Y-axes and that the corresponding level in the Z-axis is double that in the Y-axis (2.05 ÷ 1.3 = 1.6). In addition to lattice plane shrinkage, damage might lead to amorphization. For comparison, the (004), (020) and (060) lattice planes were adopted (Fig. 4a) and corresponding diffraction peaks were integrated. Simultaneously, two ratios, Area020/Area004 and Area060/Area004, were employed (Fig. 4d). They seem to have close values and similar variation trends, and almost linearly increased from 0.15 to 2.9 vs. dose increase, except for at 500 kGy. The value for that sample was close to the original. The ratio varying so obviously means that serious amorphization occurred. But, in which direction? The Z- or Y-axis? In reality, lattice planes in the Z-axis of (002) and (006) displayed intense signals while in the Y-axis were weak, implying numerous layers or planes in the Z-axis. Normally, damage easily induces destruction while it rarely induces optimization. In this case, the damage levels in Z- and Y-axis might be diverse. If the amorphization level in the Z-axis is more serious, its diffraction signal might decrease more, increasing the ratio of diffraction intensity of the Y- to Z-axis lattice plane. If the amorphization level in the Y-axis is more serious, the signal of Y-axis lattice might decrease more, decreasing the ratio. If the levels of Z- and Y-axis are close, the signal of the Y-axis lattice plane might decrease relatively more, decreasing the ratio. Looking at the data, the ratio almost linearly increased, except for at a dose of 500 kGy, implying serious and enhanced Z-axis amorphization. In other words, destruction in the Z-axis is more evident.
Naturally, atoms in the Y-axis are all in plane, forming a network that is very robust and compactly stacked, meaning that it is difficult for individual atoms to move a long distance, exhibiting a very low free volume, making it extremely difficult for serious amorphization, lattice shrinkage or expansion to occur. Nevertheless, in the Z-axis, movement is relatively easy and reaction can occur with other species, probably leading to serious amorphization, lattice shrinkage or expansion. This notion has been verified adequately, as exfoliation, intercalation and ion-exchange mainly occurring in this direction.13–26 These descriptions probably explain the observed discrepancy. Normally, discrepancy can be amplified by factor elevation; thus, the ratio seems to increase greatly. The anomaly in the data at 500 kGy might be due to recrystallization due to random damage.
In addition to the Z- and Y-axis, the damage in X-axis should also be discussed. Nevertheless, one is unable to observe a single lattice plane in this direction. As the atoms in X- and Y-axis are all in plane, they might have similar variation trends. A discussion of the Y-axis lattice plane can be representative, and a comparison of lattice plane with atoms in and out plane is significant. Thus, the exploration on the damage in the Z- and Y-axes is complete.
Generally, for talc under EB irradiation with a dose of up to 1000 kGy, the lattice planes in the Z- and Y-axes underwent shrinkage and amorphization, with the corresponding levels seeming to linearly increase vs. the dose and were more serious in the Z-axis. These variations can mainly be ascribed to structural characteristics and irradiation processes. Considering structure, talc is a rigid material. All atoms are linked together by covalent bonds as a macromolecule, stacking compactly and showing very small free volume and being stiff. For this characteristic, force at micro-region is robust and the material is very resistant to lattice destruction. An EB has high energy with relatively low penetrability, and after a short distance, it might deposit. During this process, its energy decays via ionization, excitation and collision. For rigid stacking, the system itself is of high energy, sensitive to disturbance. Under disturbance, partial chemical bonds might cleave forming defects or generating individual atoms, rearranging, leading to lattice plane collapse or amorphization. Besides direct damage, defects or individual atoms might react with other species, forming other structures, altering the crystalline structure. Where might they move and with which species might they react?
According to structure, an individual group is difficult to generate except for H(O)˙ radical as that generation might destroy the geometric structure. Simultaneously, those individuals are normally unstable, and edge atoms might move close to surrounding sites enhancing adjacent chemical bonds. This movement is primary. Besides moving, they might react with other parts forming extra chemical bonds. Which species might form? As main chemical bonds in talc are Si–O–Si/Mg, if no numerous extra matter participated, newly formed chemical bonds might involve these species. Of course, H(O)˙ radical might also react with cleaved parts generating Si/Mg–OH group. In addition to this process, cleaved parts might react with foreign matter. Although a sample is pure, two extra factors cannot be ignored. One is H2O, which normally exists on sample surfaces, edges and in the air.27,28 The other is air mainly containing N2 and O2, normally adsorbed on sample surfaces or edges, probably causing surface defects. Thus, the system seems a little complex. If H2O underwent radiolysis, generating H(O)˙, apart from forming H2 or H2O2 leaving the system, it might react with cleaved parts forming extra Si/Mg–OH altering the crystalline structure. If N2 or O2 participated in reaction, they might form other species like N–O bonds, needing clarification. How might these reactions alter the lattice? Naturally, they all introduce extra groups. To our knowledge, extra groups' introduction mainly leads to lattice expansion.29 Will it lead to apparent expansion? It seems complex. In reality, H atom is extremely small in volume, can be trapped by free space or gaps efficiently, probably not leading to obvious lattice expansion. This phenomenon is common, where H2O or H(O)˙ could penetrate defected glass easily. Conversely, it might form hydrogen bonds strengthening the force within adjacent layers even leading to lattice shrinkage as in muscovite.30 Nevertheless, extra introduction of O or N elements makes the system unstable. For instance, if individual O or N atoms reacted with defects, they might form Si/Mg–(O)–O/N˙, transforming to Si/Mg–(O)–O–Si, and Si/Mg–(O)–N–Si finally. If O2 or N2 reacted with defects directly, they might form Si/Mg–(O)–O–O˙, Si/Mg–(O)–N–N˙, generating Si/Mg–(O)–O–O–Si and Si/Mg–(O)–N–N–Si ultimately. These reactions seem to link the structure compactly. Nevertheless, many are unstable, forming Mg/Si–O–Si, Mg/Si–O˙, and Mg/Si–NOx finally, probably leading to expansion or shrinkage depending on species amount. If they transformed to Mg/Si–O–Si, and Mg/Si–(O)˙ finally, shrinkage might occur. If Mg/Si–NO(x) was abundant, forming other matter, it could alter the lattice unit greatly, differing from the original obviously. Whether its amount was large needs further research.
Naturally, crystallization involves atoms arranged in order while amorphization is the opposite. In reality, talc is a crystal with almost 100% crystallinity. All atoms are arranged in order, at the lowest energy level and entropy, easy to become amorphous under disturbance. According to the second law of thermodynamics, entropy increase is spontaneous. In other words, amorphization is the ultimate consequence. Normally, this process can be accelerated by heating, crashing and chemical reaction. EB irradiation is a procedure involving energy transfer and collision. During this process, some atoms are ionized and excited, moving to other positions, breaking chemical bonds and destroying the lattice. Simultaneously, for mild LET effect, the area surrounding electron movement might be heated displaying a temperature increase, even 100 °C, enhancing atom vibration and accelerating atom migration. Besides direct damage, extra species' reaction intensifies this process. All these factors enhance atom movement. Finally, lattice plane amorphization was observed in irradiated samples.
Apart from variation trend, shrinkage and amorphization levels were enhanced vs. absorbed dose and diverse orientation, with that for Z-axis being more serious than that in the Y-axis. The former is expected, as illustrated earlier, and can be amplified. Dose increase causes more collisions and energy transfer, leading to more ionization and excitation, generating more cleavage, vibration enhancement and chemical reaction, accelerating atom movement and displacement, enhancing lattice damage. The latter can be ascribed to intrinsic structural characteristics. Considering structure, lattice scale in Z-axis is several times that in Y-axis, having abundant free space to accommodate extra species' introduction. Simultaneously, atoms in this direction might and could move a longer distance under disturbance. Thus, if damage occurred, the level would be obvious. In the Y-axis lattice plane, atoms are mainly arranged in tetrahedron sheets and are linked closely in a network, which is difficult to move visibly. For close links, the lattice size is very small, lacking free space, unable to accommodate numerous extra species' introduction, very dense, and probably displaying relatively weak damage level. These descriptions probably explain the differences. Normally, this process can be visualized as a rigid structure. For a rigid structure, in Z-axis as height direction it is fragile having no toughness while containing numerous free spaces which could accumulate extra species' introduction. Nevertheless, with the Y- and X-axes as a base, it is dense, making it very difficult for the introduction of extra parts with enough mechanical strength. Because of numerous free spaces, the wall in the height direction is fragile and easy to destroy. If destruction occurs, consequences can be serious. A small cleavage or extra part introduction might lead to collapse, visible as structure degradation.
After irradiation, lattice plane shrinkage occurred. Can this variation be useful? Apart from collapse, shrinkage mainly leads to denser stacking, probably efficient for waste disposal especially of toxic and radioactive matter like metal ions such as Sr, U, Pb. The smaller the migration ratio of these materials the more efficient the disposal technology or project will be. In this case, if the remediating material was denser, toxic elements might be difficult to migrate; if lattice shrinkage occurred, immobilized toxic elements might be linked closely. All these considerations could reduce migration. For radioactive waste management, toxic materials are normally immobilized or retarded by silicates like concrete or clay, enduring irradiation in service. If toxic elements like U, Pb, and Pu moved to the lattice cavity leading to shrinkage, they might be enwrapped more closely, resulting in a denser structure, enhancing retardation capacity. If this description is correct, it is a crucial finding. A material that can undergo lattice shrinkage will have better retardation capacity, which is a new insight. This strategy might be applied for other waste management. If immobilized matter could react with surrounding elements making it denser, it would probably improve efficiency.
Apart from variation trend, a varied range is vital to stability evaluation. Seeing the data, after 0–1000 kGy irradiation, shrinkage levels in Z- and Y-axis were close to 2 and 1.3%, nearly 0.2 Å for (002) and 0.05 Å for (020). Is this significant?
Naturally, the interlayer spacing d of the (002) lattice plane is close to 9.6 Å, almost the length of the –O–Si–O–Mg–O–Si–O– bond in Z-axis, 5 times the length of the Si/Mg–O bond.31 For EB irradiation, its active species are electrons of high charge and small mass, displaying high energy and mild LET effect, easily inducing chemical bond cleavage, atom displacement and temperature elevation, destroying structure obviously. Besides direct damage, the temperature elevation in the micro-region can be as much as 100 °C, especially under continuous irradiation conditions. To avoid this obvious temperature increase, the sample was irradiated intermittently (irradiation 3–5 s, resting 0.5 h). In this case, atom movement induced by temperature elevation caused by direct energy deposition can be ignored and variation can mainly be attributed to electron interaction. Normally, atoms in a tetrahedron sheet form a network, and are difficult to separate. Even under a certain amount of destruction, the lattice plane could be maintained. In other words, even if some atoms leave lattice sites, the interlayer spacing d can be retained. Atoms in an octahedron layer do not stack so compactly, containing numerous free spaces, probably accommodating introduction of other materials. Simultaneously, some OH groups form hydrogen bonds, strengthening the force at the interface, reducing the interlayer space. It seems that lattice size in Z-axis can be easily adjusted via hydrogen bonding and linkage modification. In other words, if an octahedron sheet exhibited hydrogen bond formation or cleavage or linkage cleavage, the interlayer spacing d in the Z-axis might vary obviously. Normally, chemical bonds are not linked linearly and cleavage is random, so it is difficult to break chemical bonds at the same plane especially in the Z-axis height. Even if this extreme situation occurred, variation in interlayer spacing d can be at the angstrom scale. In this case, the variation range, 0.2 Å, can be considered as obvious. Can size vary more seriously? It seems possible in theory. If that situation occurred, links of tetrahedron and octahedron might cleave completely, forming SiO2, MgO or Mg(OH)x, differing greatly from the original especially in the lattice. For instance, SiO2 is amorphous, having no visible lattice plane, and would not display intense diffraction signals. Characteristic diffraction peaks of MgO are located at other positions like 43°, which are very intense. The most important issue is that it would cause serious fracture, phase separation and gaps, unexpectedly accelerating immobilized matter migration. Considering the patterns, no extra intense peaks at interval positions appeared, implying that no serious decomposition occurred. A notable variation could lead to the enwrapping of toxic matter closely, and a certain level of shrinkage is expected. In real conditions, especially for HLRW disposal, the dose rate in micro-area near toxic or radioactive matter surface is very high. Of course, it might not be that high in an EB irradiation experiment. Accumulated dose can also be a little high, whereas, to polluted area control wasn't. Normally, the concentration of toxic or radioactive matter in a polluted area is small. Thus, a dose of 1000 kGy irradiation can be intermediate for HLRW management but enough for polluted area control. After this level of irradiation, the variation range was close to 0.2 Å. If this strategy was regarded to toxic matter immobilization, it wasn't efficient as dose rate was so high that even after several days it could endure this level irradiation. This means a notable structure should be designed and radiation-resistant elements should be added. If this strategy was considered for polluted area control, it seems stable to irradiation and shrinkage can be favorable. Probably larger shrinkage level can be more efficient.
Amorphization is another factor crucial to toxic matter migration while having distinct effects. If matter was already enwrapped by a lattice, this transformation probably led to crystal shrinkage and more compact stacking and denser structure, enhancing retardation capacity. If matter was adsorbed on crystal surfaces, this transformation also densified the matrix, lessening free volume for matter to get through, reducing the migration ratio. Nevertheless, it might be easier to leave the surface via water washing and dissolving in water. If matter occupied lattice sites, this variation destroyed stacking. For polluted area control, toxic matter adsorbed on or passed through the lattice would crucial when coupling with dissolution in water. Amorphization seems beneficial while a complete decomposition is not expected excluding water effect. Considering patterns, major lattice planes were maintained and amorphization level was not that serious, indicating a certain level of radiation stability of talc.
Generally, for talc under EB irradiation with dose up to 1000 kGy, lattice plane shrinkage mainly occurred and amorphization, with levels in the Z-axis being more serious than those in the Y-axis. Amorphization level seems small and talc exhibits a certain level of radiation stability. The result – lattice shrinkage – might be beneficial for polluted area control. Structure adjustment, like making it easier to collapse, probably enhances retardation capacity.
3.2 Chemical structure damage analysis
Lattice damage is initially caused by chemical structure variation. FT-IR spectroscopy is an efficient method to explore this variation. Fig. 5a shows FT-IR spectra of talc under EB irradiation with a dose of up to 1000 kGy. All spectra are similar and mainly display three characteristic peaks at 3676, 1018 and 670 cm−1 corresponding to Mg3O–H, Si–O stretch and O–H vibrations.9,10 Besides them, several peaks near 536, 465, 451 and 425 cm−1 with low intensities appeared (Fig. 5b), mainly attributed to Si–O–Mg and Mg/Si–O vibrations (Table 5).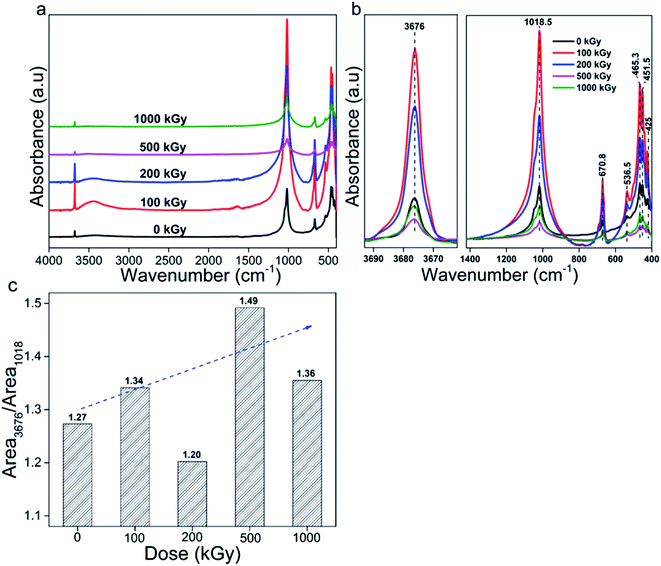 | ||
| Fig. 5 FT-IR spectra of talc under EB irradiation with a dose of up to 1000 kGy: (a) complete; (b) refined. (c) Ratio of MgO–H to Si–O–Si vibration. | ||
| Peak position (cm−1) | Assignments |
|---|---|
| 3676 | Mg3O–H stretching32 |
| 1018 | Si–O–Si stretching32 |
| 670 | O–H deformation,32–36 Si–O vibration,37,38 Si–O–Mg stretching39 |
| 536 | O–H vibration,32 Si–O–Mg stretching,33,34,37 Si–O bending,36 Mg–O stretching40 |
| 465 | Translational motion of O–H,32 Mg–O stretching,33–36 Si–O–Si bending39,41 |
| 451 | Si–O–Mg vibration,34,35 Mg–O vibration37 |
| 425 | Si–O stretching34,39 |
Besides these peaks, for the 100- and 200 kGy-irradiated samples, two peaks near to 3450 and 1640 cm−1 appeared, which were unexpected. Considering the XRD analysis, if N2 participated in the reaction, the NOx group might form. According to the Sadtler Handbook of Infrared Spectra,42,43 nitrite's (–O–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) characteristic stretching bands mainly appear near to 1650–1620 and 1320–1300 cm−1, and nitrate's (O–NO2) characteristic stretching bands mainly appear near to 1640–1610 and 1290–1280 cm−1, and are very strong in intensity. Besides the NOx group, H2O normally exists in samples or KBr particles, which has two characteristic vibrations near to 3450 and 1635 cm−1,8,33,44,45 close to those observed in spectra. Thus, these two extra peaks might be assigned to H2O or the NOx group. If the peak near to 1640 cm−1 is due to the NOx group, an extra peak near to 1300 cm−1 might appear.42,46,47 From the spectra, no extra peak appeared at this position; thus, these extra observed peaks can be assigned to H2O. Can these H2O peaks be ascribed to KBr or the sample itself? Normally, during measurements, the spectrum of KBr was obtained firstly and assigned as background signal. Then, other spectra were obtained from which this signal was subtracted. Naturally, it is difficult to ensure H2O amounts in following measurements were close to the former for humility and mass discrepancy. Finally, the signal of H2O contained in KBr pellet can be observed. For 500- and 1000 kGy-irradiated samples, these two extra peaks were not observed. That is because these two samples were measured a second time on a second day after KBr was further dried at 95 °C for more than 6 h. For the first time, they displayed intense signals. Thus, the peaks near 3450 and 1640 cm−1 can be assigned to H2O adsorbed in KBr and not to the NOx group. Excluding these two peaks, all peaks can be associated with talc, indicating purity and not much N2 participated in reaction.
O) characteristic stretching bands mainly appear near to 1650–1620 and 1320–1300 cm−1, and nitrate's (O–NO2) characteristic stretching bands mainly appear near to 1640–1610 and 1290–1280 cm−1, and are very strong in intensity. Besides the NOx group, H2O normally exists in samples or KBr particles, which has two characteristic vibrations near to 3450 and 1635 cm−1,8,33,44,45 close to those observed in spectra. Thus, these two extra peaks might be assigned to H2O or the NOx group. If the peak near to 1640 cm−1 is due to the NOx group, an extra peak near to 1300 cm−1 might appear.42,46,47 From the spectra, no extra peak appeared at this position; thus, these extra observed peaks can be assigned to H2O. Can these H2O peaks be ascribed to KBr or the sample itself? Normally, during measurements, the spectrum of KBr was obtained firstly and assigned as background signal. Then, other spectra were obtained from which this signal was subtracted. Naturally, it is difficult to ensure H2O amounts in following measurements were close to the former for humility and mass discrepancy. Finally, the signal of H2O contained in KBr pellet can be observed. For 500- and 1000 kGy-irradiated samples, these two extra peaks were not observed. That is because these two samples were measured a second time on a second day after KBr was further dried at 95 °C for more than 6 h. For the first time, they displayed intense signals. Thus, the peaks near 3450 and 1640 cm−1 can be assigned to H2O adsorbed in KBr and not to the NOx group. Excluding these two peaks, all peaks can be associated with talc, indicating purity and not much N2 participated in reaction.
Apart from N2, O2 and H2O might participate in reaction, altering the structure. If O2 participated, it might form peroxide, which is not stable especially during the irradiation process, transforming to Mg/Si–O bond ultimately, probably not altering the chemical bond species obviously. If H2O participated, it probably introduced extra OH, varying the structure efficiently. Thus, variation of OH species is informative. Also, Si–O bond cleavage is normal. To describe these two species' variation clearly, peaks near to 3676 and 1018 cm−1 were integrated as Area3676 and Area1018, representing Mg3O–H and Si–O vibrations, and the ratio Area3676/Area1018 was employed (Fig. 5c).
Seeing the data, the ratio almost linearly increased vs. dose except for 200 kGy. For pristine and 100-, 200-, 500- and 1000 kGy-irradiated samples, the data were near 1.27, 1.34, 1.20, 1.49 (increased by 17%) and 1.36. After irradiation, the ratio increased obviously, which is informative. Normally, there are two processes leading to an increasing ratio. One is extra OH introduction; the other is Si–O cleavage. Which process is predominant? Generally, for H2O, radiolysis and dehydroxylation occurred synchronously. Radiolysis generated H(O)˙ radical probably introducing extra OH; dehydroxylation cleaved M–OH bond decreasing the OH amount. For powder derived from massive rock, H2O existed on surfaces or edges with an amount near 4 wt%.8,33 Naturally, electrons differ obviously from photons like X-rays or γ-rays. For numerous charges and relatively large mass, it is difficult to penetrate deeply, affecting surface area or edge initially, destroying surface H2O. After damage, H2O might form H(O)˙ radical generating H2 or H2O2 that depart the system28,48,49 or reacting with framework forming Si/Mg–OH group. Naturally, the most likely species it encounters is Si-central defect, probably forming numerous Si–OH. If numerous Si–OH were introduced, a peak near 3730 cm−1 might appear.30 Considering the spectra, at higher wavenumber region, only a peak near 3676 cm−1 assigned to the Mg3O–H vibration appeared, implying a small amount of Si–OH formation. Can numerous Mg3O–H groups form? Probably not. This is because for mild LET effect much energy might be deposited in micro-region like surface area initially, probably heating that area, elevating the temperature obviously, causing serious volatilization. As H2O mainly existed at this location and the amount was small, it might be difficult to pass through the tetrahedron layer to react in the octahedron layer forming Mg3O–H, but easily leaving. Thus, extra OH introduction can be ignored. In this condition, a ratio increase indicates Si–O cleavage.
Naturally, Si–O cleavage cannot be ignored as the tetrahedron sheet is the region firstly encountered by electrons. With a dose increase, damage be enhanced leading to more cleavage. If the Mg3O–H amount does not vary, the ratio might increase linearly. Normally, for certain conditions, especially collapse, electrons might penetrate the tetrahedron layer encountering the octahedron layer and edges, cleaving Mg–OH bonds showing up as dehydroxylation. For the 200 kGy-irradiated sample, the ratio declined, implying serious dehydroxylation. If dehydroxylation was serious, that means 500- and 1000 kGy-irradiated samples exhibited very serious Si–O cleavage.
Besides tetrahedron sheet damage, Si–O–Mg bond as link of tetrahedron and octahedron sheets might also cleave, needing discussion. Nevertheless, its vibration is weak and difficult to analyze while speculation can be made via XRD results indirectly. Considering XRD analysis, the shrinkage range in Z-axis was more than three times that in Y-axis. If the link did not cleave, value might be close to network cannot be so large. Obviously decreased range indicates partial link as the Si–O(H)–Mg bond is cleaved. Si–OH–Mg cleavage is the nature of dehydroxylation.
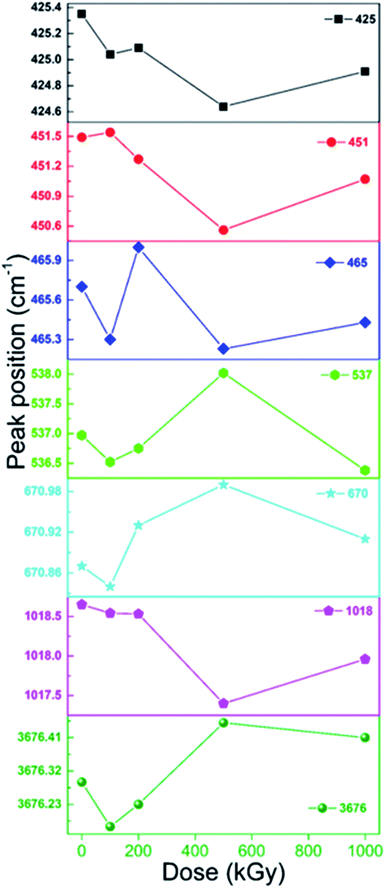
In addition to pattern and ratio, peak position is informative. Fig. 6 shows peak position of bands at 425, 451, 465, 537, 670, 1018 and 3676 cm−1, all shifted slightly. For bands at 425, 451 and 1018 cm−1, they are shifted to lower value by nearly 1 cm−1. While for bands at 670 and 3676 cm−1, they are shifted to higher value by nearly 1 cm−1. For bands at 465 and 537 cm−1, they seem to vary irregularly. Generally, all bands seem to have a spinodal at 500 kGy, which is notable. In reality, bands at 670 and 3676 cm−1 mainly represent Mg3O–H vibration. After irradiation, they shifted to higher wavenumber region, as expected. For numerous charges, electron movement easily induces ionization and Mg atom more easily loses its outer electron cloud compared to O. Under ionization, it might lose part of its outer electron cloud becoming positive, attracting a certain amount of electron cloud from adjacent O, elevating adjacent O electronegativity, strengthening the force within O–H, and thus leading to increase in wavenumber. Ionization of Si atom in Si–OH–Mg structure leads to same variation. Bands at 425, 451 and 1018 cm−1 mainly represent Si–O vibration. After irradiation, they shifted to lower wavenumber region, opposite to the case for O–H, which was unexpected. Naturally, Si–O bonds mainly exist in the tetrahedron sheet and are linked together as a network. Upon irradiation, ionization and excitation occurred synchronously, inducing cleavage, transforming some SiO4 to SiO3 and weakening links in the tetrahedron layer. Rest edged O might move close to adjacent Si in another orientation as another SiO4˙ tetrahedron. In this tetrahedron, as one O atom moves close to central-Si, the O atoms at the other three orientations might move away from center to stable structure, increasing the length of this kind of Si–O bond, leading to a reduction in wavenumber. Bands shifted to lower wavenumber region probably confirmed Si–O cleavage from another aspect. Bands at 465 and 537 cm−1 have complex affiliations as O–H, Si/Mg–O vibrations. For O–H and Mg–O, they might shift to higher wavenumber region; for Si–O, it might shift to lower wavenumber region. Although its variation seems irregular, the band at 537 cm−1 shifted to lower wavenumber region, except for 500 kGy dose, implying serious Si–O cleavage. The band at 465 cm−1 shifted to higher wavenumber region at 200 kGy, probably implying serious link cleavage of tetrahedron and octahedron sheets (Si–O–Mg), conforming results of XRD analysis. Considering the peak positions, the tetrahedra and links of the tetrahedra and octahedra are seriously cleaved.
Generally, after irradiation, peak position of MgO–H shifted to higher wavenumber region, whereas that of Si–O bond shifted to lower wavenumber region, displaying discrepancy, which was a little confusing. Why the discrepant variation trend? A possible reason is intrinsic structure discrepancy. In the MgO–H group, Mg element is more active compared to the central O and easily loses an outer layer electron, transferring partial outer electron cloud. Under irradiation condition, ionization and excitation occurred, losing partial outer electron cloud, lessening its electron transfer compared to pristine structure, and enhancing the force within O–H, leading to an increase in wavenumber. In Si–O structure, such as Si–O–Si/Mg, its interaction within Si–O cannot be as robust as O–H, and adjacent atoms like Si/Mg do not need to transfer as much electron cloud to the central O compared to MgO–H structure. Its interaction is weaker compared to Mg–O in the MgO–H structure. After irradiation, cleavage cannot be ignored, leading to some Si–O bonds being weaker in SiO4˙, partially enhanced in SiO3˙ transferring to SiO4 in air condition. In this case, it is easier to shift to lower wavenumber region. Nevertheless, in the MgO–H group, after Mg–O cleavage, free O–H group might exist. It is very difficult to observe vibration bands of this kind of O–H. If it could occur, its peak position might shift to higher wavenumber region. That is because without transfer of electron cloud within Mg to O the force within O–H might be enhanced, increasing the wavenumber. Simultaneously, the O–H in the MgO–H group is as an edge, whereas Si–O are linked closely by other groups. Additionally, the air atmosphere can also be considered for the Si–O group. If not much air is present, there might be partial shift to higher region, partial to lower region, and a broad band might be observed and not a shift to lower wavenumber. Whereas, air almost has no effects on O–H shift as an edge linkage. With the presence of air, peak position of Si–O bond shifted to lower wavenumber region. It seems variation trend discrepancy can mainly be ascribed to differences within electronegativities of Mg and Si and intrinsic linkage and air condition.
Considering the FT-IR analysis, it is concluded that under EB irradiation with dose up to 1000 kGy, tetrahedron network and linkage of tetrahedron and octahedron were cleaved seriously in conjunction with octahedron dehydroxylation. Cleavage in tetrahedron seems more evident.
3.3 H2O amount analysis
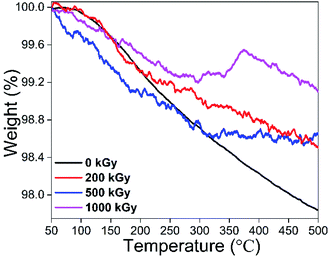
Considering the FT-IR analysis, the 200 kGy-irradiated sample exhibited dehydroxylation; did this also occur for 500- or 1000 kGy-irradiated samples? If it occurred, H2O amount might be higher than or close to that of the pristine sample. Assuming the amount of gas was small, and dehydroxylation, impurity volatilization and matrix decomposition would not happen at temperatures lower than 500 °C, then mass variation in TGA curves at temperatures lower than this can mainly be ascribed to H2O volatilization caused by heating during the measurement period.Fig. 7 shows TGA curves of pristine and 200-, 500- and 1000 kGy-irradiated talc. All of the curves are similar and vary slightly. With a temperature increase to 500 °C, the mass of the pristine and 200-, 500- and 1000 kGy-irradiated samples decreased to 97.8, 98.5, 98.6 and 99.1 wt%, respectively, associated with reductions of 2.2 (100 − 97.8 = 2.2) wt%, 1.5 (100 − 98.5 = 1.5) wt%, 1.4 (100 − 98.6 = 1.4) wt% and 0.9 (100 − 99.1 = 0.9) wt%. Assuming the H2O volatilization was linear with its content being complete, its amount in pristine and 200-, 500- and 1000 kGy-irradiated samples can be 2.2, 1.5, 1.4 and 0.9 wt%.
It seems that the H2O amount declined within irradiated sample, which was confusing. Nevertheless, it can be ascribed to irradiation condition and process. For EB irradiation, its active species are high-energy electrons with high charge and small mass, showing mild LET effect, and difficult to penetrate deeply. After several collisions, energy decayed and the electron itself would be trapped, depositing much energy in its track, heating that area, even elevating the temperature by nearly 100 °C, leading to serious H2O volatilization especially on surfaces, and thus the declining H2O amount. Besides temperature elevation, it might cause H2O radiolysis generating H(O)˙ radical forming H2 or H2O2 that depart the system50,51 or reacting with the framework introducing extra OH. The most likely species might be Si–OH; from FT-IR analysis, SiO–H characteristic stretch near 3730 cm−1 did not appear. Simultaneously, MgO–H species was not introduced adequately. These appearances indicate ignored extra OH introduction. In other words, the reduction in the amount of H2O cannot be ascribed to extra OH introduction.
Besides direct volatilization and radiolysis generating gas leaving the system and reducing the H2O amount, electrons might penetrate the surface, edge and tetrahedron sheet destroying octahedron species like Mg3O–H bond generating H(O)˙, forming H2, H2O2 or H2O leaving the system as dehydroxylation, probably elevating the H2O amount. Normally, volatilization and radiolysis reduce the H2O amount while dehydroxylation increases it. These processes occurred synchronously displaying a complex mechanism for H2O amount variation. Naturally, the ideal O–H amount in talc – Mg3(Si4O10)(OH)2 – is less than 8.9 wt% ((17 × 2)/(24 × 3 + 28 × 4 + 16 × 10 + 17 × 2) = (34/378) ≈ 8.9%). If it all transformed to H2O, the corresponding amount is less than 4.8 wt% ((16 + 2)/(24 × 3 + 28 × 4 + 16 × 10 + 17 × 2) = (18/378) ≈ 4.8%), difficult to occur. If occurring, octahedron and lattice might vary obviously and a new phase such as MgO might form. Considering the XRD analysis, matrix lattices were maintained and interlayer space d varied slightly and no new extra lattice planes appeared, indicating a limited level of dehydroxylation. If the dehydroxylation level was close to 10% and all transformed to H2O, the H2O amount might increase to 0.5 wt%. Naturally, all transformation to H2O is difficult to occur. Even if occurring, it is difficult to offset the decline induced by volatilization or radiolysis. Seeing the data, for 200-, 500- and 1000 kGy-irradiated samples, H2O amount declined by 0.7, 0.8 and 1.3 wt%, larger than 0.5 wt%, implying dehydroxylation was not predominant while volatilization or radiolysis were crucial. Thus, the decline can mainly be ascribed to direct volatilization or radiolysis product volatilization, differing from effects of photons like γ-ray irradiation.10 That is because photons like γ-rays have enough penetrability while exhibiting a low LET effect, meaning it is difficult to deposit energy and elevate temperature hugely in micro-region, causing weak direct H2O or radiolysis product volatilization. The reason for H2O amount reduction can mainly be ascribed to radiolysis reaction with the framework.
Naturally, under EB irradiation, H2O radiolysis and extra OH introduction are common. Nevertheless, the association in this work seems different. That is because the H2O or radiolysis product volatilization on the surface area is very quick, and the temperature elevation caused by direct electron encounter is evident. As the initial H2O amount was small, close to 2.5 wt%, and mainly existed on the surface, it is very easy for it to leave the system completely especially under temperature elevation. If its amount was larger and mainly existed in interlayers, its radiolysis reaction with the framework would be obvious. Nevertheless, these descriptions did not mean that dehydroxylation had not occurred. If this process did not occur, the reduced range might be larger. A moderate level confirmed partial reaction.
Generally, TGA indicates a certain level of dehydroxylation.
3.4 Process and mechanism
In previous sections, the variation in lattice and corresponding microstructure transformation process were explored and speculated. Main results show irradiation led to talc lattice shrinkage and amorphization, and levels in the Z-axis were more serious than those in the Y-axis. The reasons for this can be mainly ascribed to tetrahedral Si–O and the cleavage of link of tetrahedron and octahedron sheets. Tetrahedral Si–O cleavage seems very prominent. Simultaneously, some cleavage of octahedral Mg–OH occurred. The main process can be illustrated in detail as follows.Normally, the tetrahedron sheet is the preferential layer encountered by electrons, being destroyed firstly. Because of a mild LET effect, electrons deposit much energy in their track, breaking the tetrahedron sheet and leading to amorphization. Nevertheless, the tetrahedron sheet is very robust as a network, all atoms are linked together and stacked compactly, being very dense. Small cavities or gaps exist, being difficult to exhibit huge shrinkage level. Even if serious amorphization occurred, the shrinkage level seems small. After penetrating the tetrahedron sheet, electrons move to the octahedron sheet reacting with linkage or OH, causing lattice shrinkage in Z-axis and dehydroxylation. Normally, the octahedron layer stacks loosely compared to the tetrahedron sheet, displaying serious variation in Z-axis. EB irradiation easily triggers H2O radiolysis generating H(O)˙ radical introducing extra OH. Nevertheless, in this work, dehydroxylation was crucial not extra OH introduction, being a little confusing. That is because of the small amount of H2O and its surface distribution. For these characteristics, a slight temperature elevation might decrease the amount obviously and dehydroxylation can be observed. If H2O amount was larger or mainly existed in interlayers, extra OH might be introduced. It seems that lattice shrinkage was mainly caused by cleavage of tetrahedral Si–O and of the linking of tetrahedron and octahedron sheets.
Equations and scheme can display the microstructure transformation process more scientifically. Naturally, tetrahedron mainly contains Si–O–Si, and link of tetrahedron and octahedron is Si–O–Mg bonds; thus, ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Si–O–Si
Si–O–Si![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) and
and ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Si–O–Mg
Si–O–Mg![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) could represent the tetrahedron sheet and tetrahedron and octahedron linkage. Interlayer space d in Z-axis reflects TOT scale probably mainly depending on the length of O–Si–O–Mg–O–Si–O bond in this direction. Thus,
could represent the tetrahedron sheet and tetrahedron and octahedron linkage. Interlayer space d in Z-axis reflects TOT scale probably mainly depending on the length of O–Si–O–Mg–O–Si–O bond in this direction. Thus, ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O–Si–O–Mg–O–Si–O
O–Si–O–Mg–O–Si–O![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) and
and ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Mg–OH could represent TOT unit in the Z-axis and octahedral OH. Under these assumptions, the main process can be illustrated as eqn (1)–(16) and schematically as Fig. 8.
Mg–OH could represent TOT unit in the Z-axis and octahedral OH. Under these assumptions, the main process can be illustrated as eqn (1)–(16) and schematically as Fig. 8.
Eqn (1)–(6) are reactions originally induced by EB irradiation.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Si–O–Si Si–O–Si![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) → → ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Si–O˙ + ˙Si Si–O˙ + ˙Si![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif)
| (1) |
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O–Si–O–Mg–O–Si–O O–Si–O–Mg–O–Si–O![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) → → ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O–Si(O)˙ + ˙(O)–Mg–O–Si–O O–Si(O)˙ + ˙(O)–Mg–O–Si–O![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif)
| (2) |
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Mg–OH → Mg–OH → ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Mg(O)˙ + ˙(O)H Mg(O)˙ + ˙(O)H
| (3) |
| H2O → H˙ + HO˙ | (4) |
| O2 → 2O˙ | (5) |
| H2O(l) → H2O(g)↑ | (6) |
Eqn (7)–(16) are reactions between radiolysis products.
| H˙ + H˙ → H2↑ | (7) |
| H˙ + HO˙ → H2O↑ | (8) |
| HO˙ + HO˙ → H2O2↑ | (9) |
| H2O2 → O˙ + H2O↑ | (10) |
| H2O2 → 2HO˙ | (11) |
| H˙ + O˙ → HO˙ | (12) |
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Si(O)˙ + H(O)˙ → Si(O)˙ + H(O)˙ → ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Si–OH Si–OH
| (13) |
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Si/Mg˙ + O˙ → Si/Mg˙ + O˙ → ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Si/Mg–O˙ Si/Mg–O˙
| (14) |
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Mg(O)˙ + H(O)˙ → Mg(O)˙ + H(O)˙ → ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Mg–OH Mg–OH
| (15) |
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Mg–O˙ + ˙Mg Mg–O˙ + ˙Mg![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) → → ![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) Mg–O–Mg Mg–O–Mg![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif)
| (16) |
Generally, eqn (1) describes tetrahedral Si–O cleavage, leading to amorphization and lattice shrinkage in Y-axis. Eqn (2) describes tetrahedron and octahedron linkage cleavage, leading to lattice shrinkage in Z-axis. Eqn (3) describes dehydroxylation. Eqn (4) and (5) describe H2O and O2 radiolysis. Eqn (6)–(10) describe H2O volatilization and partial gas radiolysis product formation and departure, illustrating H2O amount reduction. Eqn (11) and (12) describe transformation within HO˙. Eqn (13)–(16) describe Si/Mg–OH formation and octahedron deformation, which are secondary.
The previous equations mainly display homolysis products. Some have been confirmed like H(O)˙,28,52 Mg–O˙,53–58 and some have not like H2O(g), Mg–OH and Mg–O–Mg due to difficulty in formation. Firstly, the time for EB irradiation was very short, several seconds, whereas the resting time was long, 0.5 h. Even if temperature increased, it is difficult to observe this elevation in situ.7 Secondly, the H2O amount was small, leaving the surface quickly. Thirdly, the lifetime of normal intermediates was not long, probably not exceeding several hours or days. Fourthly, EB irradiation was performed in a factory, and we cannot characterize it immediately. Naturally, the period of time for 6 kGy irradiation was 0.5 h (irradiation of several seconds, resting for 0.5 h), and a complete 1000 kGy irradiation took more than 4 days. Before characterization, partial intermediates could have transformed to other species, difficult to observe in situ and just suggested via speculation. Even in accurate electron spin resonance experiments, intermediates cannot be assigned completely. Finally, partial intermediates were not verified. Nevertheless, the above equations probably help in understanding the mechanism. Besides homolysis, heterolysis should also be discussed. Normally, heterolysis products are unstable, transforming to electroneutral structures ultimately, similar to homolysis products.59 Thus, a clear description of the homolysis process is representative. Of course, intrinsic transformation process can be explored in more depth with technology development.
Fig. 8 shows a scheme for lattice shrinkage in the Z- and Y-axes of talc under EB irradiation with a dose of up to 1000 kGy. Upon irradiation, tetrahedral Si–O, link of tetrahedron and octahedron sheets and octahedral MgO–H are cleaved, leading to lattice plane shrinkage, amorphization and dehydroxylation.
4. Conclusions
Variations in the lattice and intrinsic microstructure transformation process of talc under EB irradiation with a dose of up to 1000 kGy were explored. The main results show that irradiation led to talc lattice shrinkage and amorphization, and that the levels in the Z-axis were more serious than in the Y-axis. For 1000 kGy-irradiated sample, shrinkage levels of the (002) and (020) lattice planes were close to 2 and 1.3%, nearly 0.2 and 0.06 Å. Main mechanisms involve cleavage of tetrahedral Si–O and of the link of tetrahedron and octahedron sheets. Si–O cleavage was adequate, leading to serious amorphization. Nevertheless, lattice plane shrinkage was mainly caused by linkage cleavage in the Z-axis direction. Simultaneously, dehydroxylation and H2O volatilization occurred associated with H2O radiolysis. Nevertheless, these processes are secondary to lattice variation.After irradiation, lattice plane shrinkage occurred, and the tetrahedron sheet underwent serious amorphization. Normally, shrinkage enwraps matter closely; amorphization leads to easy movement. This means that if matter was already enwrapped by the lattice it might be difficult to move under certain levels of electron irradiation. If material was adsorbed on the surface or occupied lattice sites it might easily move. This understanding is relevant for polluted area control, also benefiting the efficiency of HLRW disposal projects. For soil or clay used as back-fill material it should have compact density and be replenished at certain conditions. For a silicate solidified body it might shrink, trapping in lattice cavity is needed. These findings propose a new strategy to increase the efficiency of HLRW disposal projects. Also, it gives a new strategy for materials design to promote retardation capacity – enwrapping by a lattice and with lattice shrinkage – which is of great significance for environment remediation and waste management.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to Wuhan Aibang High Energy Technology Co. Ltd (Ezhou, China) for EB irradiation. This work was partially supported by Wuhan Textile University Research Seed Funds 2020.References
- M. Debure, C. Tournassat, C. Lerouge, B. Madé, J.-C. Robinet, A. M. Fernandez and S. Grangeon, Sci. Total Environ., 2018, 642, 216–229 CrossRef CAS PubMed.
- M.-L. Feng, D. Sarma, Y.-J. Gao, X.-H. Qi, W.-A. Li, X.-Y. Huang and M. G. Kanatzidis, J. Am. Chem. Soc., 2018, 140, 11133–11140 CrossRef CAS PubMed.
- K. Fujii, K. Ochi, A. Ohbuchi and Y. Koike, J. Environ. Manage., 2018, 217, 157–163 CrossRef CAS PubMed.
- X. Yin, N. Horiuchi, S. Utsunomiya, A. Ochiai, H. Takahashi, Y. Inaba, X. Wang, T. Ohnuki and K. Takeshita, Chem. Eng. J., 2018, 333, 392–401 CrossRef CAS.
- Q. Fan, P. Li and D. Pan, Emerging Natural and Tailored Nanomaterials for Radioactive Waste Treatment and Environmental Remediation – Principles and Methodologies, Interface Science and Technology, 2019, pp. 1–38 Search PubMed.
- M. Zhang, J. Chen, M. Zhang, R. Li, M. Wang, L. Qiu, M. Yuan, X. Feng, Z. Xing, J. Hu and G. Wu, ACS Appl. Mater. Interfaces, 2020, 12, 49258–49264 CrossRef CAS PubMed.
- M. Zhang, J. Chen, S. Zhang, X. Zhou, L. He, M. V. Sheridan, M. Yuan, M. Z. Zhang, L. Chen, X. Dai, F. Ma, J. Wang, J. Hu, G. Wu, X. Kong, R. Zhou, T. E. Albrecht-Schmitt, Z. Chai and S. Wang, J. Am. Chem. Soc., 2020, 142, 9169–9174 CrossRef CAS PubMed.
- M. Zhang, S. A. T. Redfern, E. K. H. Salje, M. A. Carpenter and L. Wang, Am. Mineral., 2010, 95, 1686–1693 CrossRef CAS.
- M. Zhang, Q. Hui, X.-J. Lou, S. A. T. Redfern, E. K. H. Salje and S. C. Tarantino, Am. Mineral., 2006, 91, 816–825 CrossRef CAS.
- H. Wang, Y. Sun, J. Chu, X. Wang, Y. Ji and M. Zhang, J. Radioanal. Nucl. Chem., 2020, 325, 33–42 CrossRef CAS.
- H. Wang, Y. Sun, J. Chu, X. Wang and M. Zhang, Appl. Clay Sci., 2020, 187, 105475 CrossRef CAS.
- H. Wang, L. Xu, R. Li, J. Hu, M. Wang and G. Wu, Radiat. Phys. Chem., 2016, 125, 41–49 CrossRef CAS.
- M. Daab, N. J. Eichstaedt, C. Habel, S. Rosenfeldt, H. Kalo, H. Schießling, S. Förster and J. Breu, Langmuir, 2018, 34, 8215–8222 CrossRef CAS PubMed.
- S. Pérez-Conesa, J. M. Martínez and E. Sánchez Marcos, J. Phys. Chem. C, 2017, 121, 27437–27444 CrossRef.
- K. B. Thapa, K. S. Katti and D. R. Katti, Langmuir, 2020, 36, 11742–11753 CrossRef CAS PubMed.
- M. Munir, M. F. Nazar, M. N. Zafar, M. Zubair, M. Ashfaq, A. Hosseini-Bandegharaei, S. U.-D. Khan and A. Ahmad, ACS Omega, 2020, 5, 16711–16721 CrossRef CAS PubMed.
- G. Montavon, C. Lerouge, K. David, S. Ribet, Y. Hassan-Loni, M. Leferrec, C. Bailly, J.-C. Robinet and B. Grambow, Environ. Sci. Technol., 2020, 54, 12226–12234 CrossRef CAS PubMed.
- Y.-C. Li, S.-J. Wei, N. Xu and Y. He, J. Phys. Chem. C, 2020, 124, 25557–25567 CrossRef CAS.
- M. Sajid, M. Ayoub, Y. Uemura, S. Yusup, B. B. Abdullah, S. Ullah and A. Aqsha, J. Jpn. Inst. Energy, 2020, 99, 16–19 CrossRef CAS.
- M. Sun, K.-Y. Wang, D. Ding, J.-Y. Zhu, Y.-M. Zhao, L. Cheng and C. Wang, Inorg. Chem., 2020, 59, 13822–13826 CrossRef PubMed.
- L. Tian, M. R. Abukhadra, A. S. Mohamed, A. Nadeem, S. F. Ahmad and K. E. Ibrahim, ACS Omega, 2020, 5, 19165–19173 CrossRef CAS PubMed.
- L. Wang, Z. Li, Q. Wu, Z. Huang, L. Yuan, Z. Chai and W. Shi, Environ. Sci.: Nano, 2020, 7, 724–752 RSC.
- Z. Wang, L. Zhang, P. Fang, L. Wang and W. Wang, ACS Omega, 2020, 5, 21805–21814 CrossRef CAS PubMed.
- T. Xia, C. Lei, C. Xu, N. Peng, Y. Li, X.-Y. Yang, Z.-Z. Cheng, M. Gauthier, H.-Z. Gu and T. Zou, Langmuir, 2020, 36, 14268–14275 CrossRef CAS PubMed.
- G. Xie, D. Huang, Y. Xiao, M. Deng and P. Luo, ACS Sustainable Chem. Eng., 2020, 8, 10303–10312 CrossRef CAS.
- H. Zhang, C. S. Hodges, P. K. Mishra, J. Y. Yoon, T. N. Hunter, J. W. Lee and D. Harbottle, ACS Appl. Mater. Interfaces, 2020, 12, 33173–33185 CrossRef CAS PubMed.
- M. Lainé, E. Balan, T. Allard, E. Paineau, P. Jeunesse, M. Mostafavi, J.-L. Robert and S. Le Caër, RSC Adv., 2017, 7, 526–534 RSC.
- M. Lainé, T. Allard, E. Balan, F. Martin, H. J. Von Bardeleben, J.-L. Robert and S. Le Caër, J. Phys. Chem. C, 2016, 120, 2087–2095 CrossRef.
- F. Kishimoto, K. Hisano, T. Wakihara and T. Okubo, Chem. Mater., 2020, 32, 9008–9015 CrossRef CAS.
- H. Wang, Y. Sun, J. Chu, X. Wang and M. Zhang, R. Soc. Open Sci., 2019, 6, 190594 CrossRef CAS PubMed.
- M. E. Abd El-Aziz, K. H. Kamal, K. A. Ali, M. S. Abdel-Aziz and S. Kamel, Int. J. Biol. Macromol., 2018, 118, 2256–2264 CrossRef CAS PubMed.
- K. T. Lu, Y. Zhang, R. D. Aughterson and R. Zheng, Dalton Trans., 2020, 49, 15854–15863 RSC.
- S.-F. Li, S.-C. Yang, S.-L. Zhao, P. Li and J.-H. Zhang, J. Serb. Chem. Soc., 2015, 80, 563–574 CrossRef CAS.
- L. Castillo, O. Lopez, C. López, N. Zaritzky, M. A. García, S. Barbosa and M. Villar, Carbohydr. Polym., 2013, 95, 664–674 CrossRef CAS PubMed.
- L. A. Castillo, S. E. Barbosa, P. Maiza and N. J. Capiati, J. Mater. Sci., 2011, 46, 2578–2586 CrossRef CAS.
- Y. Tan, L. Sha, N. Yu, Z. Yang, J. Qu and Z. Xu, RSC Adv., 2020, 10, 17686–17693 RSC.
- N. T. Huong, N. N. Son, V. H. Phuong, C. T. Dung, P. T. M. Huong and L. T. Son, Adsorpt. Sci. Technol., 2020, 38, 483–501 CrossRef.
- K. Kalantari, M. Bin Ahmad, K. Shameli and R. Khandanlou, Int. J. Nanomed., 2013, 8, 1817–1823 Search PubMed.
- X. Liu, X. Liu and Y. Hu, Clays Clay Miner., 2014, 62, 137–144 CrossRef CAS.
- B. Wang, W. Zhang, L. Li, W. Guo, J. Xing, H. Wang, X. Hu, W. Lyu, R. Chen, J. Song, L. Chen and Z. Hong, Chemosphere, 2020, 256, 127124 CrossRef CAS PubMed.
- A. M. Zayed, M. Fathy, M. Sillanpää and M. S. M. Abdel Wahed, SN Appl. Sci., 2020, 2, 740 CrossRef CAS.
- M. M. Angelini, R. J. Garrard, S. J. Rosen and R. Z. Hinrichs, J. Phys. Chem. A, 2007, 111, 3326–3335 CrossRef CAS PubMed.
- C. Eaborn, The Sadtler Handbook of Infrared Spectra, Bio-Rad Laboratories, Inc., Informatics Division., 1978 Search PubMed.
- D. Ngo, H. Liu, Z. Chen, H. Kaya, T. J. Zimudzi, S. Gin, T. Mahadevan, J. Du and S. H. Kim, npj Mater. Degrad., 2020, 4, 1–14 CrossRef.
- M. Singha and L. Singh, Indian J. Pure Appl. Phys., 2016, 54, 116–122 Search PubMed.
- L. Bosland, F. Funke, N. Girault and G. Langrock, Nucl. Eng. Des., 2008, 238, 3542–3550 CrossRef CAS.
- Y. Liu, C. Han, J. Ma, X. Bao and H. He, Phys. Chem. Chem. Phys., 2015, 17, 19424–19431 RSC.
- C. Fourdrin, H. Aarrachi, C. Latrille, S. Esnouf, F. Bergaya and S. Le Caer, Environ. Sci. Technol., 2013, 47, 9530–9537 CrossRef CAS PubMed.
- R. C. Ewing, Nat. Mater., 2015, 14, 252–257 CrossRef CAS PubMed.
- M. Sassi, E. D. Walter, O. Qafoku, K. M. Rosso and Z. Wang, J. Phys. Chem. C, 2020, 124, 22185–22191 CrossRef CAS.
- W. Zhang, H. Liu, M. M. C. H. van Schie, P.-L. Hagedoorn, M. Alcalde, A. G. Denkova, K. Djanashvili and F. Hollmann, ACS Catal., 2020, 10, 14195–14200 CrossRef CAS PubMed.
- A. Maneewong, B. S. Seong, E. J. Shin, J. S. Kim and V. Kajornrith, J. Korean Phys. Soc., 2016, 68, 83–92 CrossRef CAS.
- T. Allard, J.-P. Muller, J.-C. Dran and M.-T. Ménager, Phys. Chem. Miner., 1994, 21, 85–96 CrossRef CAS.
- D. Gournis, A. E. Mantaka-Marketou, M. A. Karakassides and D. Petridis, Phys. Chem. Miner., 2000, 27, 514–521 CrossRef CAS.
- K. Toriyama, A. Lund and M. Okazaki, Phys. Chem. Chem. Phys., 2000, 2, 4697–4701 RSC.
- G. Calas, T. Allard, E. Balan, G. Morin and S. Sorieul, MRS Online Proc. Libr., 2003, 792, 81–92 Search PubMed.
- S. Sorieul, T. Allard, G. Morin, B. Boizot and G. Calas, Phys. Chem. Miner., 2005, 32, 1–7 CrossRef CAS.
- T. Allard, E. Balan, G. Calas, C. Fourdrin, E. Morichon and S. Sorieul, Nucl. Instrum. Methods Phys. Res., Sect. B, 2012, 277, 112–120 CrossRef CAS.
- H. Yeritsyan, A. Sahakyan, V. Harutyunyan, S. Nikoghosyan, E. Hakhverdyan, N. Grigoryan, A. Hovhannisyan, V. Atoyan, Y. Keheyan and C. Rhodes, Sci. Rep., 2013, 3, 2900 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2021 |