Open Access Article
Open Access ArticleMechanism and kinetic properties for the complete series reactions of chloro(thio)phenols with O(3P) under high temperature conditions†
Zhuochao Tenga,
Xianwei Zhaoa,
Hetong Wanga,
Ying Lia,
Yanan Hana,
Yanhui Sun b and
Fei Xu
b and
Fei Xu *ac
*ac
aEnvironment Research Institute, Shandong University, Qingdao 266237, P. R. China. E-mail: xufei@sdu.edu.cn; Tel: +86-532-58631992
bCollege of Environment and Safety Engineering, Qingdao University of Science & Technology, Qingdao 266042, P. R. China
cShenzhen Research Institute of Shandong University, Shenzhen 518057, P. R. China
First published on 14th May 2021
Abstract
Polychlorinated dibenzo-p-dioxins/dibenzofurans (PCDD/Fs) and polychlorinated dibenzothiophenes/thianthrenes (PCDT/TAs) are two groups of dioxin-like compounds with oxygen and sulfur substitution, respectively. Chlorophenols (CPs) and chlorothiophenols (CTPs) are direct precursors in PCDD/F and PCDT/TA formation. The formation of chlorophenoxy radicals (CPRs) and chlorothiophenoxy radicals (CTPRs) from chlorophenols (CPs) and chlorothiophenols (CTPs) with O(3P) is an important initial step for the formation of PCDD/Fs and PCDT/TAs, respectively. In this paper, the formation of CPRs/CTPRs from the complete series reactions of 19 CP/CTP congeners with O(3P) was studied using the density functional theory (DFT) method. The rate constants of each reaction were calculated using canonical variational transition state (CVT) theory along with a small-curvature tunneling (SCT) contribution over a wide temperature range of 600–1200 K. The effect of the chlorine substitution pattern on the structural parameters, thermochemical properties and rate constants in both CPs and CTPs was discussed. This study shows that the reactions between CPs and O(3P) can be affected by the chlorine substitution at the para-position, and the reactions between CTPs and O(3P) are mostly influenced by both ortho-substitutions. The thiophenoxyl-hydrogen abstraction from CTPs by O(3P) is more likely to occur than the phenoxyl-hydrogen abstraction from CPs by O(3P). Comparison of the reactivity of CP/CTPs with O(3P) with our previous work on CP/CTPs with H and OH shows that the order for phenoxyl-hydrogen abstraction potential is CP + OH > CP + O(3P) > CP + H, and the order for thiophenoxyl-hydrogen abstraction potential is CTP + O(3P) > CTP + H > CTP + OH.
1. Introduction
Polychlorinated dibenzo-p-dioxins (PCDDs) and polychlorinated dibenzofurans (PCDFs) are two series of typical persistent organic pollutants (POPs), which are notorious pollutants with carcinogenic, teratogenic and mutagenic effects and cause serious public concern.1,2 Polychlorinated thianthrenes (PCTAs) and polychlorinated dibenzothiophenes (PCDTs) are two groups of sulfur-substituted structural analogues of PCDDs and PCDFs, respectively. Due to the difference in the number and position of chlorine atoms on the benzene ring, 75 PCDD/PCTA and 135 PCDF/PCDT compounds are formed.3,4 Among them, 2,3,7,8-TeCDD, the “most toxic poison on earth”, is 1000 times as toxic as potassium cyanide (KCN).5 PCTA/DTs, known as dioxin-like compounds, exhibit similar toxicity, persistence, lipophilic and physicochemical properties with PCDD/DFs.6 The toxicity of PCTA/DTs is slightly less than PCDD/DFs, wherein the toxicity equivalent factors (TEF) of 2,3,7,8-TeCTA and 2,3,7,8-TeCDT are 0.01 and 0.001, respectively.7 PCDD/DFs and PCTA/DTs have been detected in various environmental media, such as sediments, waste incineration byproducts, pulp mill wastewater and biological communities.8,9 Oxygen- and sulfur-substituted dioxins are never intentionally synthesized for commercial aim, but are generated from a variety of combustion or thermal processes as unwanted byproducts, such as fly ash and stack gas samples from metal reclamation plant, combustion and heat treatment processes, utilities and industrial boilers using fossil fuels and municipal and hazardous waste incinerators and industrial incinerators.6,10–18 Sinkkonen et al. reported the concentrations of trichlorodibenzothiophene (TriCDT), trichlorinated dibenzo-p-dioxins (TriCDD), tetrachlorodibenzothiophene (TeCDT), tetrachlorinated dibenzo-p-dioxins (TeCDD), pentachlorodibenzothiophene (PeCDT), pentachlorinated dibenzo-p-dioxins (PeCDD) and trichlorothianthrene (TriCTA) in the gas samples from aluminium smelting is 8.944, 7.292, 5.833, 34.027, 1.426, 17.500 and 0.052 ng g−1, respectively.17 Buser reported the concentrations of PCDTs in fly ash was to be up to 55 ng g−1, at or one magnitude below the concentrations of the PCDDs and PCDFs.19 Considering the serious pollution of these toxic substances to the environment, it is of great significance to clarify their formation mechanism in the process of combustion and pyrolysis to reduce their emission in the environment and harm to human beings.Due to the similarity in structure, source, toxicity and concentration of PCTA/DTs and PCDD/DFs in the environment, they have similar formation mechanisms under pyrolysis or combustion conditions.13 Chlorophenols (CPs) and chlorothiophenols (CTPs) are widely recognized to be the main precursors and intermediates for PCDT/F and PCDT/TA formation, respectively.20–22 CPs are widely used as intermediate in herbicide, pesticide, bactericide, drug production and dye production.23 CTPs are mainly from direct application as dyes, pesticides, inks, pharmaceuticals and poly vinyl chloride (PVC).24 CPs are carcinogenic and mutagenic even at trace levels,8,25 which have been included in the priority control list of hazardous substances by the U.S. Toxic Substances Administration and the Disease Registry.26 CTPs have slightly lower toxicity than CPs, which were reported to have strong stimulation to eyes, respiratory mucosa and skin of organisms.27 Under pyrolysis or combustion conditions, CPs and CTPs can readily form chlorophenoxy radicals (CPRs) and chlorotriophenoxy radicals (CTPRs) by abandoning the phenoxyl-H and sulfydryl-H, respectively, via unimolecular reaction, bimolecular reaction or other possible low-energy pathways (including heterogeneous reactions). Unimolecular reactions include the decomposition of CPs/CTPs and the breaking of O–H/S–H bonds. The bimolecular reactions include the abstraction reaction by H, OH, O(3P) or Cl under high temperature.
Under high temperature conditions, PCDD/F and PCTA/DT formation from CPs and CTPs as precursors contains radical–radical coupling and radical–molecule coupling.28–35 Previous studies presented that radical/radical couplings are thermodynamically comparable to radical/molecule recombination for the PCDD/DF and PCTA/DT formation.28–35 Therefore, following the radical/radical routes, a series of theoretical studies on PCTA/DT formation mechanisms from the coupling of 2-CTPRs, 2,4,5-TCTPRs, 2,4-DCTPRs, and 2,4,6-TCPRs were carried out.28,29,36,37 These studies showed that the formation of PCDDs and PCTAs was easier than that of PCDFs and PCDTs, due to the fact that the PCDDs and PCTAs can form via one elementary step less than PCDFs and PCDTs and the potential barrier of the rate-determining step of PCDDs/PCTAs are lower than that of PCDFs/PCDTs.28,29,36,37 However, the existing radical/radical mechanism cannot make a full explanation on the experimental observations that PCDFs rather than PCDDs are favored products in the gas-phase PCDD/DF formation from CPs.38–40 In addition, this conclusion is in stark contrast to the much higher concentration of PCDTs than that of PCTAs under the pyrolysis or combustion environments.38–40 Therefore, the radical/molecule mechanism was reignited, which can give large contribution to the high PCDF-to-PCDD ratio and PCDT-to-PCTA ratio.41,42 In both radical–radical and radical–molecule couplings, the formation of CPRs/CTPRs from CPs/CTPs is the initial and most important step in the PCDD/F and PCTA/DT formations.28–35 Thus, the formation of CPR/CTPRs from CP/CTPs are need to be first studied.
In recent studies conducted from this laboratory, we have performed quantum chemistry to investigate the reaction mechanisms and kinetic properties of the complete series reactions of CPs/CTPs with H and OH radicals.43–45 On the basis of these studies, we complemented and expanded on our previous work in this field to continue to study the formation of CPRs/CTPRs from the complete series reactions of CP/CTP congeners with O(3P) using the direct density functional theory (DFT) method. The rate constants were evaluated by the canonical variational transition-state (CVT) theory with the small curvature tunneling (SCT) contribution at 600–1200 K.46 The effect of the chlorine substitution pattern on the structural parameters, thermochemical properties and rate constants in both CPs and CTPs were examined. The formation potential of C(T)PRs from C(T)Ps with O(3P) are compared with that of C(T)PRs from C(T)Ps with H and OH, respectively. The results, as well as the values in our previous studies in this field, can be input into environmental dioxin prediction and control models as important parameters to predict dioxin formation mechanisms and products, reduce dioxin emissions, health risk and establish dioxin control strategies.
2. Computational method
All the quantum chemistry calculations on the structure optimization, energy calculation and frequency evaluation were carried out using Gaussian 09 program suite47 using density functional theory (DFT) method. The structure optimization of the reactants, transition states and products were performed at the MPWB1K level48 with a standard 6-31+G(d,p) basis set.48 The vibration frequencies were calculated at the same level to determine the nature of the stationary point and calculate the zero-point energy (ZPE) values.48 The complete reactions discussed in this paper were verified using intrinsic reaction coordinate (IRC) calculations and the minimum energy path (MEP) analysis of all transition states.49 Meanwhile, a more flexible basis 6-311+G(3df,2p) is adopted to calculate single-point energy, potential barrier and reaction enthalpies based on the optimized geometries. The potential barriers are the difference between the energy of the transition states and the reactants, and the react heats are the difference between the energy of the products and the reactants, both of which involve the correction for ZPE correction. Transition-states of chloro(thio)phenols and O(3P) treated by one calculation rather than separated chlorophenol and oxygen treated by two separate calculations. Chlorophenols and chlorothiophenols with system charge = 0 and spin multiplicity = 1, chlorophenoxy radicals, chlorothiophenoxy radicals and OH radical with system charge = 1 and spin multiplicity = 2, whereas the system charge = 2 and spin multiplicity = 3 for transition states and O(3P). Generally, the spin multiplicity is the number of system charges plus one.The rate constants of the elementary reaction involved in this paper were calculated in the temperature range of 600–1200 K using the canonical variational transition-state theory (CVT) with the small curvature tunneling contribution (SCT).46 The CVT theory was used to obtain the minimum reaction rate constant at a given temperature (T) by changing the position of the generalized transition state segmentation plane (that is, by changing the reaction coordinates).43 The separation surface in CVT theory can be obtained by
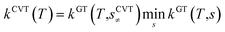 | (1) |
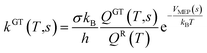 | (2) |
3. Results and discussion
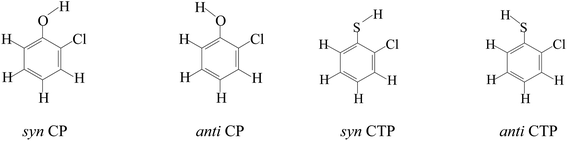
According to different substitution pattern, CPs and CTPs contain 19 congeners respectively, including three monochlorophenols/monochlorothiophenols (2-C(T)P, 3-C(T)P and 4-C(T)P), six dichlorophenols/dichlorothiophenols (2,3-DC(T)P, 2,4-DC(T)P, 2,5-DC(T)P, 2,6-DC(T)P, 3,4-DC(T)P and 3,5-DC(T)P), six trichlorophenols/trichlorothiophenols (2,3,4-TC(T)P, 2,3,5-TC(T)P, 2,3,6-TC(T)P, 2,4,5-TC(T)P, 2,4,6-TC(T)P, 3,4,5-TC(T)P), three tetrachlorophenols/tetrachlorothiophenols (2,3,4,5-TeC(T)P, 2,3,4,6-TeC(T)P and 2,3,5,6-TeC(T)P) and pentachlorophenols/pentachlorothiophenols (PC(T)P). Due to the asymmetry of chlorine substituents, there are syn- and anti-configurations for 2-C(T)P, 3-C(T)P, 2,3-DC(T)P, 2,4-DC(T)P, 2,5-DC(T)P, 3,4-DC(T)P, 2,3,4-TC(T)P, 2,3,5-TC(T)P, 2,3,6-TC(T)P, 2,4,5-TC(T)P, 2,3,4,5-TeC(T)P and 2,3,4,6-TeC(T)P. The hydrogen atom on OH/SH of the syn-configuration faces the closed neighboring Cl, and the hydrogen atom on OH/SH of the anti-configurations face the neighboring H (Fig. 1). In the syn-configurations, weak intramolecular hydrogen bonds are formed, and in the anti-configurations, intramolecular hydrogen bonds exist only in the substituted CPs/CTPs with chlorine substituent at both ortho-positions. The syn-configuration has lower energy than the corresponding anti-configuration, suggesting a stabilization effect of intramolecular hydrogen bonds. Thus, the substituted CPs/CPTs in this paper all adopt syn-configurations.513.1. Conformation analysis
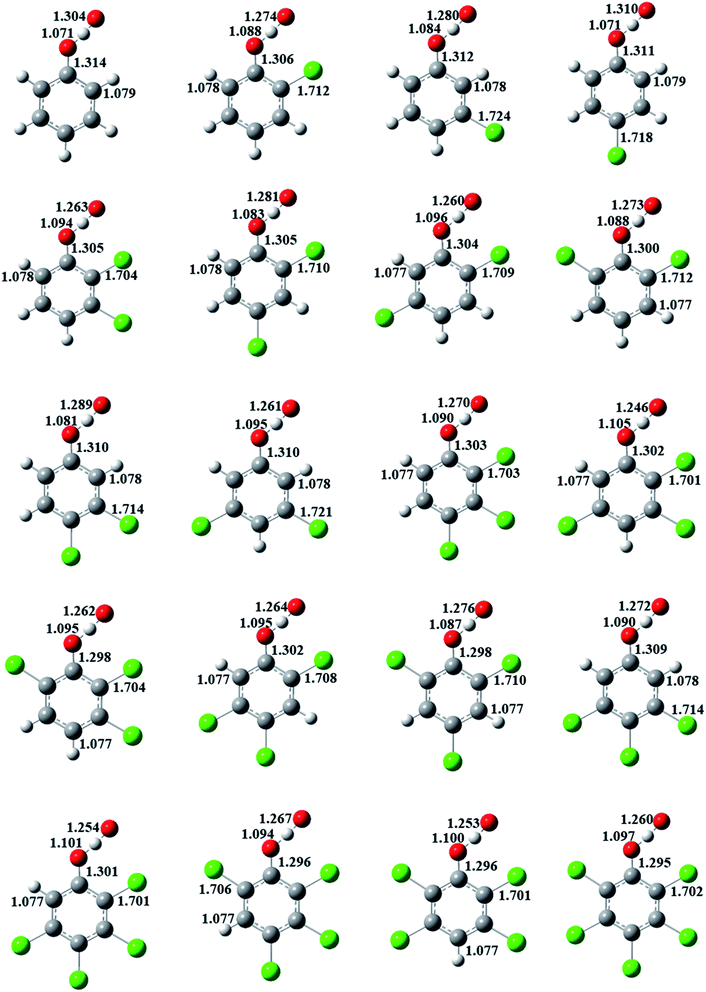
The formation of CPRs/CTPRs from the reactions of CPs/CTPs with O(3P) proceeds via a direct abstraction mechanism. The optimized structures and bond lengths of the transition states for the abstraction reaction from CPs and CTPs with O(3P) at the MPWB1K/6-31+G(d,p) level are depicted in Fig. 2 and 3, respectively. The corresponding CPs/CTPs and CPRs/CTPRs structures parameters provided from previous studies are listed in Fig. S1–S4 of ESI.†43–45 Our previous work has shown that the optimized geometries and the calculated vibrational frequencies of phenol at MPWB1K/6-31+G(d,p) level are in good agreement with the experimental values,51 and the relative error remains within 1.5% for the geometrical parameters and 8.0% for the vibrational frequencies. The S–H bond length (1.333 Å) and C–S bond length (1.761 Å) of thiophenol obtained in our work at MPWB1K/6-31+G(d,p) level are in good agreement with the experimental values of 1.333 Å and 1.773 Å with the discrepancy less than 1.0%.43 That means the theoretical calculation are reliable. When the O(3P) attack CPs/CTPs, the C–O/C–S bond lengths in CPs/CTPs are reduced, and the O–H/S–H bond lengths in CPs/CTPs are elongated. The bond length parameters of C–O/C–S and O–H/S–H bonds in CPs/CTPs and corresponding transition states, the bond length change values and the bond length change ratio of the transition states with respect to CPs/CTPs are presented in Tables S3 and S4 of ESI,† respectively.In Fig. 2, for a given number of chlorine substitutions of CPs, the O–H bonds in para-substituted transition states are shorter than those without chlorine substitution at para-position. For example, the O–H bond lengths of TS(2,3-DCP), TS(2,5-DCP), TS(2,6-DCP) and TS(3,5-DCP) are 1.094, 1.096, 1.088 and 1.095 Å, respectively, which are larger than those of TS(2,4-DCP) and TS(3,4-DCP) (1.083 Å and 1.081 Å). The increase in length of the O–H bond being broken and the elongation of the O–H bond being formed with respect to its equilibrium value in the reactants are the most important aspect of the geometric structure of the transition state. As shown in Fig. S3,† the O–H growth ratios from para-substituted transition states are consistently larger than those from other structures. For example, the O–H bonds in TS(2,3-DCP), TS(2,5-DCP), TS(2,6-DCP) and TS(3,5-DCP) are 14.1%, 14.3%, 13.5% and 14.7% longer than the corresponding equilibrium values of O–H bonds in CPs, and the O–H bonds are elongated by of 12.9% and 13.2% in TS(2,4-DCP) and TS(3,4-DCP).
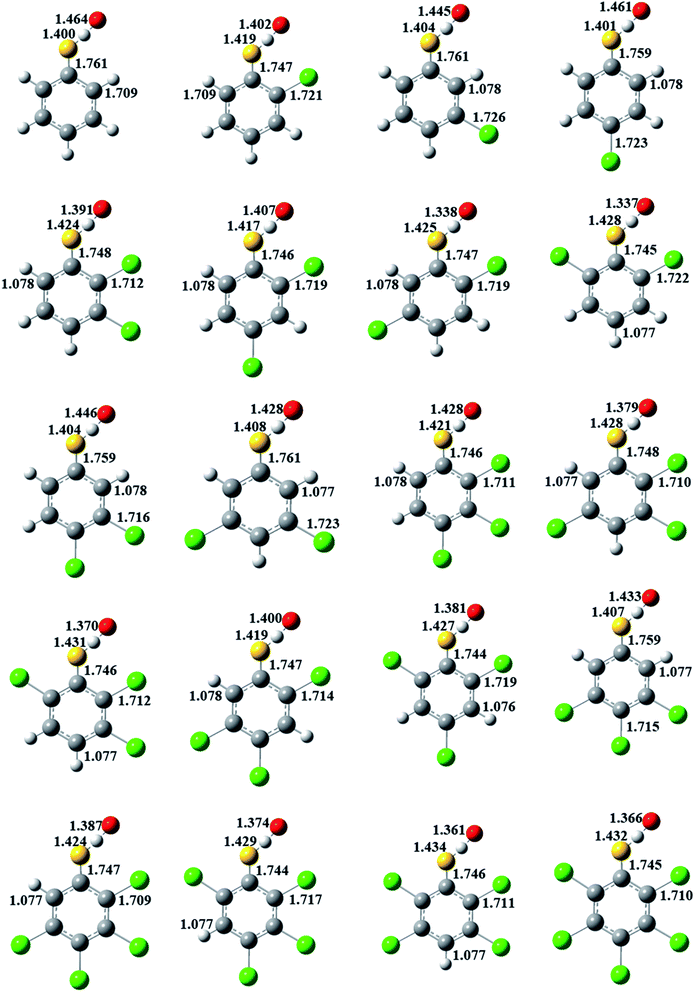
In Fig. 3, for a given number of chlorine substitutions of CPs, the S–H bonds in the transition states with two ortho substitutions are longer than those without ortho-substitution or with one ortho-substitution. For example, the S–H bond length in TS(2,6-DCTP) has relative longer distance (1.428 Å) compared to the values of 1.404–1.425 Å from TS(2,3-DCTP), TS(2.4-DCTP), TS(2,5-DCTP), TS(3,4-DCTP) and TS(3,5-DCTP). The S–H bonds in TS(2,3-DCP), TS(2,4-DCP), TS(2,5-DCP), TS(3,4-DCP), and TS(3,5-DCP) are starched by 5.33–6.98%, and the S–H bond is 7.13% longer than the corresponding equilibrium values of S–H bond in 2,6-CPs.
3.2. Thermomechanical analysis
The potential barriers ΔE‡ (in kcal mol−1), reaction heats ΔH (in kcal mol−1, 0 K) and imaginary frequencies (in cm−1) of the transition states for the thiophenoxyl-hydrogen abstraction from CPs and CTPs by O(3P) at the MPWB1K/6-311+G(3df,2p)//MPWB1K/6-31+G(d,p) level are depicted in Tables 1 and 2, respectively. The formation of CPRs/CTPRs from the reactions of CPs/CTPs with O(3P) is strongly exothermic. The reaction heats for C6H5OH + O(3P) → C6H5O + OH were studied by Cox et al. through experiment.52 The value of −13.38 kcal mol−1 reported by Cox are in agreement with the value of −13.31 kcal mol−1 calculated in this work.52 This can be inferred that calculation accuracy can be expected for the species involved in this study.| ΔE | ΔH | ν | |
|---|---|---|---|
| Phenol | 5.45 | −13.31 | 2272i |
| 2-CP | 7.52 | −11.34 | 2550i |
| 3-CP | 8.20 | −12.26 | 2424i |
| 4-CP | 5.11 | −14.50 | 2273i |
| 2,3-DCP | 8.26 | −10.57 | 2576i |
| 2,4-DCP | 6.97 | −12.70 | 2496i |
| 2,5-DCP | 8.25 | −10.48 | 2613i |
| 2,6-DCP | 7.59 | −12.66 | 2551i |
| 3,4-DCP | 5.95 | −13.50 | 2425i |
| 3,5-DCP | 6.03 | −11.14 | 2513i |
| 2,3,4-TCP | 7.42 | −11.90 | 2569i |
| 2,3,5-TCP | 9.06 | −10.74 | 2691i |
| 2,3,6-TCP | 8.11 | −12.15 | 2645i |
| 2,4,5-TCP | 7.62 | −11.90 | 2652i |
| 2,4,6-TCP | 6.90 | −13.96 | 2599i |
| 3,4,5-TCP | 8.54 | −12.47 | 2500i |
| 2,3,4,5-TeCP | 8.29 | −11.10 | 2712i |
| 2,3,4,6-TeCP | 7.68 | −11.93 | 2669i |
| 2,3,5,6-TeCP | 8.50 | −12.90 | 2710i |
| PCP | 8.00 | −12.88 | 2700i |
| ΔE | ΔH | ν | |
|---|---|---|---|
| Thiophenol | 1.63 | −12.12 | 506i |
| 2-CTP | 2.51 | −12.39 | 531i |
| 3-CTP | 2.28 | −11.90 | 576i |
| 4-CTP | 1.52 | −21.46 | 523i |
| 2,3-DCTP | 2.42 | −13.15 | 1192i |
| 2,4-DCTP | 2.15 | −19.70 | 1046i |
| 2,5-DCTP | 2.47 | −11.03 | 1199i |
| 2,6-DCTP | 3.78 | −13.64 | 1292i |
| 3,4-DCTP | 2.84 | −20.65 | 586i |
| 3,5-DCTP | 2.76 | −11.71 | 651i |
| 2,3,4-TCTP | 4.38 | −19.06 | 1136i |
| 2,3,5-TCTP | 2.66 | −13.06 | 1227i |
| 2,3,6-TCTP | 3.32 | −10.99 | 1320i |
| 2,4,5-TCTP | 2.81 | −18.90 | 1053i |
| 2,4,6-TCTP | 3.62 | −18.08 | 1256i |
| 3,4,5-TCTP | 3.17 | −20.09 | 642i |
| 2,3,4,5-TeCTP | 3.39 | −18.53 | 1155i |
| 2,3,4,6-TeCTP | 3.65 | −17.61 | 1307i |
| 2,3,5,6-TeCTP | 4.28 | −14.44 | 1366i |
| PCTP | 4.63 | −16.94 | 1327i |
From Table 1, the potential barriers are significantly correlated with the position of the chlorine substitution at the phenolic ring, but not with the number of chlorine substituents. For example, for monochlorophenols, the potential barriers of phenoxyl-hydrogen abstraction from 2-CP (7.52 kcal mol−1) and 3-CP (8.20 kcal mol−1) are higher than that from 4-CP (5.11 kcal mol−1). For trichlorophenols, the potential barriers of the phenoxyl-hydrogen abstraction from 2,3,5-TCTP (9.06 kcal mol−1) and 2,3,6-TCTP (8.11 kcal mol−1) are higher than those from 2,3,4-TCTP (7.42 kcal mol−1), 2,4,5-TCTP (7.62 kcal mol−1) and 2,4,6-TCTP (6.90 kcal mol−1), except for 3,4,5-TCTP (8.54 kcal mol−1). Obviously, for a given number of chlorine substitutions, the potential barriers for the phenoxyl-hydrogen abstraction from the para-substituted CPs are consistently higher than those for other structural conformers. The chlorine substitution at the para-position can lower the barrier heights of phenoxyl-hydrogen abstraction from CPs by O(3P). The conclusion is different from the result in our previous study of CPs with H that phenoxyl-hydrogen abstraction from CPs by H are strongly dominated by the chlorine substitution at the ortho-position of CPs, and intramolecular hydrogen bonding appears to stabilize the CTPs and reduce the reactivity of O–H bonds in CPs with the ortho-substitution.44 All the transition states have one and only one imaginary frequency. The values of the imaginary frequencies of transition states from reactions of CPs with O(3P) are shown in Table 1. From Table 1, for a given number of chlorine substitutions, the imaginary frequencies for the para-substituted transition states are smaller than those without para substitution. For trichlorophenols, the imaginary frequencies of the transition states for 2,3,4-TCP, 2,4,5-TCP, 2,4,6-TCP and 3,4,5-TCP are 2569i cm−1, 2652i cm−1, 2599i cm−1 and 2500i cm−1, respectively, whereas the values for 2,3,5-TCP and 2,3,6-TCP are 2691i cm−1 and 2645i cm−1, respectively. The chlorine substitution at the para-position can lower the value of the imaginary frequency, that is, the value change of the imaginary frequency has the same trend with the value of potential barrier.
From the reactions of CTPs with O(3P) in Table 2, for a given number of chlorine substitutions, the potential barriers for the thiophenoxyl-hydrogen abstraction from CTPs with both ortho-substitutions (substitutions at two and six points) by O(3P) consistently are higher than those from CTPs without ortho-substitution or with only one ortho-substitution by O(3P). For example, for dithiochlorophenols, the potential barriers of the thiophenoxyl-hydrogen abstraction from 2,6-DCTP (3.78 kcal mol−1) is higher than those from 2,3-DCTP (2.42 kcal mol−1), 2,4-DCTP (2.15 kcal mol−1), 2,5-DCTP (2.47 kcal mol−1), 3,4-DCTP (2.84 kcal mol−1) and 3,5-DCTP (2.76 kcal mol−1). For tetrathiochlorophenols, the potential barriers of the thiophenoxyl-hydrogen abstraction from 2,3,4,6-TeCTP (3.65 kcal mol−1) and 2,3,5,6-TeCTP (4.28 kcal mol−1) are higher than those from 2,3,4,5-TeCTP (3.39 kcal mol−1). This indicates that the chlorine substitutions at both ortho positions of CTPs increase the strength of the S–H bonds and decrease its reactivity. The imaginary frequency analysis can reconfirm the conclusion above. For example, for tetrathiochlorophenols, the imaginary frequencies of the transition states for 2,3-DCTP, 2,4-DCTP, 2,5-DCTP, 3,4-DCTP and 3,5-DCTP are 1192i cm−1, 1046i cm−1, 1199i cm−1, 586i cm−1 and 861i cm−1, respectively, which is smaller than that for 2,6-DCTP of 1292i cm−1. The CTP transition states from chlorine substitutions at both ortho positions can enhance the imaginary frequencies.
It is necessary to compare the reactions of CPs and O(3P) with the reactions of CTPs by O(3P). For a given CP and CTP, the potential barriers for the phenoxyl-hydrogen abstraction from CP by O(3P) are about 3.04–6.40 kcal mol−1 higher than thiophenoxyl-hydrogen abstraction from corresponding CTP by O(3P). In addition, the thiophenoxyl-hydrogen abstractions by O(3P) are about 0.55–7.62 kcal mol−1 more exothermic than the phenoxyl-hydrogen abstractions by O(3P), except for 3-C(T)P and 2,3,6-C(T)P. This means that CTPRs formation from CTPs with O(3P) is more likely to occur than the CPRs formation from CPs with O(3P).
It is interesting to compare the reaction mechanism of CPs/CTPs and O(3P) with the reactions of CPs/CTPs and H/OH radicals.43–45 The histograms of potential barriers (ΔE) for the phenoxyl-hydrogen abstraction from phenol and CPs and CTPs by O(3P)/H/OH are vividly displayed in Fig. 4 and 5, respectively. For the phenoxyl-hydrogen abstraction from CPs with H/OH/O(3P) in Fig. 4, for a given CP, the potential barriers for the phenoxyl-hydrogen abstraction from CP by O(3P) are about 3.86–6.96 kcal mol−1 lower than those from CP by H, and about 4.12–8.54 kcal mol−1 higher than those from CP by OH.44,45 This indicates that the order for phenoxyl-hydrogen abstraction potential is CP + OH > CP + O(3P) > CP + H.44,45 In Fig. 5, for a given CTP, the potential barrier for the thiophenoxyl-hydrogen abstractions from most CTP by O(3P) are 0.24–1.29 kcal mol−1 lower than those from CP by H radical (except for 3,4-DCTP, 2,3,4-TCTP, 3,4,5-TCTP, 2,3,4,5-TeCTP and PCTP) and 4.49–7.16 kcal mol−1 lower than those from CTPs by OH.43 This means that the order for thiophenoxyl-hydrogen abstraction potential is CTP + O(3P) > CTP + H > CTP + OH.43
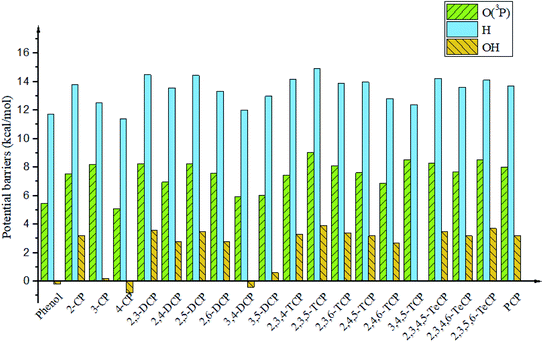 | ||
| Fig. 4 Histograms of potential barriers ΔE‡ (in kcal mol−1, including ZPE correction) for the phenoxyl-hydrogen abstraction from phenol and CPs by O(3P)/H/OH. For comparison, ΔE‡ of CPR formation form CPs with H44 and OH45 are provided by ref. 44 and 45 respectively. | ||
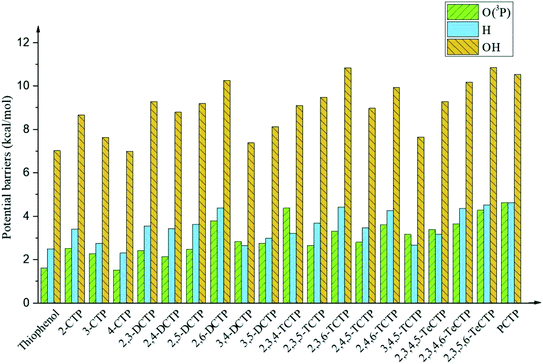 | ||
| Fig. 5 Histograms of potential barriers ΔE‡ (in kcal mol−1, including ZPE correction) for the thiophenoxyl-hydrogen abstraction from thiophenol and CTPs by O(3P)/H/OH. For comparison, ΔE‡ of CTPR formations from CTPs with H43 and OH43 are provided by ref. 43. | ||
3.3. HOMO–LOMO orbitals analysis
Tables S5 and S6† present the HOMO and LOMO energies of reacting species. HOMO–LOMO gap is a critical parameter in measuring molecular chemical stability.53 Generally, small HOMO–LOMO gap means lower stability and high activity. In this study, the HOMO–LOMO energy gap is larger for chlorophenols with chlorine substitution at the para-position than those without para-substitution for a given number of chlorine substitutions, which is consistent with the potential barriers. For example, for dichlorophenols, the HOMO–LOMO energy gap for 2,4-DCP, 3,4-DCP are lower than 2,3-DCP, 2,5-DCP, 2,6-DCP, 3,5-DCP. Similarly, for a given number of chlorine substitution, the energy gap for chlorothiophenols with ortho-substitution are higher than those without ortho-substitution or with only one ortho-substitution. For example, for trichlorothiophenols, 2,3,6-TCTP, 2,4,6-TCTP have higher HOMO–LOMO gap than 2,3,4-TCTP, 2,3,5-TCTP, 2,4,5-TCTP, 3,4,5-TCTP. Generally, the energy gap for CTP is lower than that of CP. That is in good agreement with the potential barriers.3.4. Kinetic calculations
The canonical variational transition state theory (CVT) with small-curvature tunneling (SCT) contribution46 are performed in this study to calculate the rate constants of series reactions between CPs/CTPs with O(3P) under the temperature range of 600–1200 K, as shown in Tables S5 and S6 of ESI.† The temperature range covers the possible formation temperatures of PCDD/Fs and PCDT/TAs. An early modelling studied the rate constants of C6H5OH + O(3P) → C6H5O + OH by Emdee,54 which agrees well with the CVT/SCT value in this paper. For example, at 1000 K, the rate constant is 7.65 × 10−13 by Emdee, which is consistent with the value 2.58 × 10−13 studied by CVT/SCT method. The CVT/SCT rate constants are fitted, and the corresponding Arrhenius formulas are given in Table 3 for the phenoxyl-hydrogen abstraction from CTPs by O(3P) and Table 4 for thiophenoxyl-hydrogen abstraction from CTPs by O(3P), respectively.| Reactions | Arrhenius formulas |
|---|---|
| C6H5OH + O(3P) → C6H5O + OH | k(T) = (8.20 × 10−12)exp(−3266.25/T) |
| 2-CP + O(3P) → 2-CPR + OH | k(T) = (1.08 × 10−11)exp(−5669.24/T) |
| 3-CP + O(3P) → 3-CPR + OH | k(T) = (2.01 × 10−12)exp(−5422.00/T) |
| 4-CP + O(3P) → 4-CPR + OH | k(T) = (3.58 × 10−12)exp(−4113.82/T) |
| 2,3-DCP + O(3P) → 2,3-DCPR + OH | k(T) = (1.47 × 10−12)exp(−5737.14/T) |
| 2,4-DCP + O(3P) → 2,4-DCPR + OH | k(T) = (8.20 × 10−13)exp(−5178.98/T) |
| 2,5-DCP + O(3P) → 2,5-DCPR + OH | k(T) = (7.43 × 10−13)exp(−6000.54/T) |
| 2,6-DCP + O(3P) → 2,6-DCPR + OH | k(T) = (3.97 × 10−12)exp(−5201.50/T) |
| 3,4-DCP + O(3P) → 3,4-DCPR + OH | k(T) = (1.59 × 10−12)exp(−4310.06/T) |
| 3,5-DCP + O(3P) → 3,5-DCPR + OH | k(T) = (4.41 × 10−15)exp(−4572.52/T) |
| 2,3,4-TCP + O(3P) → 2,3,4-TCPR + OH | k(T) = (9.81 × 10−12)exp(−5870.61/T) |
| 2,3,5-TCP + O(3P) → 2,3,5-TCPR + OH | k(T) = (2.04 × 10−13)exp(−6226.97/T) |
| 2,3,6-TCP + O(3P) → 2,3,6-TCPR + OH | k(T) = (1.60 × 10−12)exp(−5673.37/T) |
| 2,4,5-TCP + O(3P) → 2,4,5-TCPR + OH | k(T) = (4.01 × 10−12)exp(−5920.33/T) |
| 2,4,6-TCP + O(3P) → 2,4,6-TCPR + OH | k(T) = (7.12 × 10−12)exp(−5659.22/T) |
| 3,4,5-TCP + O(3P) → 3,4,5-TCPR + OH | k(T) = (1.78 × 10−12)exp(−5527.17/T) |
| 2,3,4,5-TeCP + O(3P) → 2,3,4,5-TeCPR + OH | k(T) = (9.08 × 10−15)exp(−5934.21/T) |
| 2,3,4,6-TeCP + O(3P) → 2,3,4,6-TeCPR + OH | k(T) = (7.46 × 10−13)exp(−5404.86/T) |
| 2,3,5,6-TeCP + O(3P) → 2,3,5,6-TeCPR + OH | k(T) = (1.16 × 10−13)exp(−5324.11/T) |
| PCP + O(3P) → PCPR + OH | k(T) = (1.50 × 10−14)exp(−5733.80/T) |
| Reactions | Arrhenius formulas |
|---|---|
| C6H5OH + O(3P) → C6H5O + OH | k(T) = (2.41 × 10−14)exp(−4858.87/T) |
| 2-CTP + O(3P) → 2-CTPR + OH | k(T) = (3.51 × 10−12)exp(−2809.95/T) |
| 3-CTP + O(3P) → 3-CTPR + OH | k(T) = (7.12 × 10−13)exp(−5178.30/T) |
| 4-CTP + O(3P) → 4-CTPR + OH | k(T) = (1.50 × 10−12)exp(−4887.12/T) |
| 2,3-DCTP + O(3P) → 2,3-DCTPR + OH | k(T) = (1.73 × 10−11)exp(−3132.24/T) |
| 2,4-DCTP + O(3P) → 2,4-DCTPR + OH | k(T) = (6.34 × 10−12)exp(−2778.06/T) |
| 2,5-DCTP + O(3P) → 2,5-DCTPR + OH | k(T) = (3.84 × 10−10)exp(−3574.35/T) |
| 2,6-DCTP + O(3P) → 2,6-DCTPR + OH | k(T) = (1.25 × 10−11)exp(−3897.24/T) |
| 3,4-DCTP + O(3P) → 3,4-DCTPR + OH | k(T) = (1.41 × 10−11)exp(−1010.34/T) |
| 3,5-DCTP + O(3P) → 3,5-DCTPR + OH | k(T) = (6.33 × 10−11)exp(−2724.57/T) |
| 2,3,4-TCTP + O(3P) → 2,3,4-TCTPR + OH | k(T) = (2.85 × 10−12)exp(−3643.04/T) |
| 2,3,5-TCTP + O(3P) → 2,3,5-TCTPR + OH | k(T) = (1.41 × 10−11)exp(−3031.77/T) |
| 2,3,6-TCTP + O(3P) → 2,4,6-TCTPR + OH | k(T) = (1.86 × 10−14)exp(−7705.67/T) |
| 2,4,5-TCTP + O(3P) → 2,4,5-TCTPR + OH | k(T) = (3.36 × 10−14)exp(−2920.48/T) |
| 2,4,6-TCTP + O(3P) → 2,4,6-TCTPR + OH | k(T) = (8.58 × 10−14)exp(−3290.82/T) |
| 3,4,5-TCTP + O(3P) → 3,4,5-TCTPR + OH | k(T) = (3.11 × 10−13)exp(−8033.26/T) |
| 2,3,4,5-TeCTP + O(3P) → 2,3,4,5-TeCTPR + OH | k(T) = (2.08 × 10−12)exp(−2062.79/T) |
| 2,3,4,6-TeCTP + O(3P) → 2,3,4,6-TeCTPR + OH | k(T) = (1.70 × 10−13)exp(−3182.45/T) |
| 2,3,5,6-TeCTP + O(3P) → 2,3,5,6-TeCTPR + OH | k(T) = (8.19 × 10−12)exp(−3662.76/T) |
| PCTP + O(3P) → PCTPR + OH | k(T) = (7.80 × 10−13)exp(−3272.48/T) |
From Table S5 of ESI,† for a given temperature, the CVT/SCT rate constants for the phenoxyl-hydrogen abstraction from the para-substituted CPs by O(3P) are higher than those from other CPs by O(3P). For example, at 600 K, the rate constants for the phenoxyl-hydrogen abstraction from 2,3-TCP, 2,5-TCP and 2,6-TCP are 1.11 × 10−16, 3.62 × 10−17 and 7.27 × 10−16 cm3 per molecule per s, while the rate constants are 1.57 × 10−16 and 1.29 × 10−15 cm3 per molecule per s for 2,4-TCP and 3,4-TCP. This is agreement with the thermodynamic analysis that the chlorine substitution at the para-position of CPs can decrease the O–H bond and increase the reaction activity of CPs with O(3P).
For the reactions of CTPs with O(3P) of Table S6 of ESI,† at a given temperature, the CVT/SCT rate constants of the thiophenoxyl-hydrogen abstraction from CTPs with both ortho-substitutions by O(3P) are lower than those from CTPs without ortho-substitution or with only one ortho-substitution by O(3P). For example, at 1000 K, the rate constant is 7.76 × 10−14 cm3 per molecule per s for the thiophenoxyl-hydrogen abstraction from 2,3,4,6-TeCTP by O(3P), which is higher than the values of 2.64 × 10−13 and 2.99 × 10−13 cm3 per molecule per s for the thiophenoxyl-hydrogen abstraction from 2,3,4,5-TeCTP and 2,3,5,6-TeCTP by O(3P), respectively. This perfectly matches the structural and thermodynamic analysis above that the chlorine substitutions at both ortho positions of CTPs can enhance the potential barrier of CTPs with O(3P). For a given chlorine substitution, the CVT/SCT rate constants for phenoxyl-hydrogen abstraction from CPs by O(3P) are noticeably smaller than those thiophenoxyl-hydrogen abstraction of CTPs by O(3P) over the whole studied temperature range. For example, at 1000 K, the CVT/SCT rate constant of the thiophenoxyl-hydrogen abstraction from 2,3,4-TCP by O(3P) is 2.69 × 10−14 cm3 per molecule per s, whereas the value is 7.29 × 10−14 cm3 per molecule per s for the thiophenoxyl-hydrogen abstraction from 2,3,4-TCTP by O(3P). This is consistent with thermodynamic analysis that thiophenoxyl-hydrogen abstraction from CTPs by O(3P) is more efficient than the phenoxyl-hydrogen abstraction from CPs by O(3P).
4. Conclusion
In this study, we investigated the reaction mechanism of 19 CP/CTP congeners with O(3P) radicals by DFT theory and obtained the structural parameters, thermodynamic calculation and kinetic data. The rate constants of each reaction were calculated using CVT/SCT method over a wide temperature range of 600–1200 K. The effect of the chlorine substitution pattern in reaction of CP/CTPs with O(3P) was discussed. The phenoxyl-hydrogen/thiophenoxyl-hydrogen abstraction of CP/CTP by O(3P) was compare with our previous work of phenoxyl-hydrogen/thiophenoxyl-hydrogen abstraction of CP/CTPs by H/OH radicals. Three main conclusions are listed as follows:(1) The potential barriers of CP/CTPs with O(3P) are significantly correlated with the position of the chlorine substitution at the phenolic ring, but not with the number of chlorine substituents. The chlorine substitution at the para-position of CPs can decrease the O–H bond and increase the reaction activity of CPs with O(3P). The chlorine substitutions at both ortho positions of CTPs increase the strength of the S–H bonds and decrease its reactivity.
(2) The thiophenoxyl-hydrogen abstraction from CTPs by O(3P) is more likely to occur than that phenoxyl-hydrogen abstraction from CPs by O(3P).
(3) The formation potential of C(T)PRs from C(T)Ps with O(3P) are compared with that of C(T)PRs from C(T)Ps with H and OH, respectively. The order for phenoxyl-hydrogen abstraction potential is CP + OH > CP + O(3P) > CP + H, and the order for thiophenoxyl-hydrogen abstraction potential is CTP + O(3P) > CTP + H > CTP + OH.
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This may include administrative and technical support, or donations in kind (e.g., materials used for experiments). This work was supported by the National Natural Science Foundation of China (project Nos. 22076103, 42075106, 201712003, 21976107), the Fundamental Research Funds of Shandong University (No. 2016WLJH51), the China Postdoctoral Science Foundation funded project (No. 2017M612277, 2017T100493) and Shenzhen Science and Technology Research and Development Funds (No. JCYJ20160510165106371). The authors thank Professor Donald G. Truhlar for providing the POLYRATE 9.7 program.References
- H. Hung, P. Blanchard, G. Poole, B. Thibert and C. H. Chiu, Atmos. Environ., 2002, 36, 1041–1050 CrossRef CAS.
- A. T. Serlemitsos, B. A. Warner, S. Castles, S. R. Breon, M. S. Sebastian and T. Hait, in Advances in Cryogenic Engineering: Part A & B, ed. R. W. Fast, Springer US, Boston, MA, 1990, pp. 1431–1437 Search PubMed.
- T. Puzyn, P. Rostkowski, A. Swieczkowski, A. Jedrusiak and J. Falandysz, Chemosphere, 2006, 62, 1817–1828 CrossRef CAS PubMed.
- A. Mostrag, T. Puzyn and M. Haranczyk, Environ. Sci. Pollut. Res. Int., 2010, 17, 470–477 CrossRef CAS PubMed.
- J. L. Domingo, S. Granero and M. Schuhmacher, Chemosphere, 2001, 43, 517–524 CrossRef CAS PubMed.
- S. Sinkkonen, E. Kolehmainen, J. Paasivirta, J. Koistinen, M. Lahtipera and R. Lammi, Chemosphere, 1994, 28, 2049–2066 CrossRef CAS.
- H. T. Wang, C. P. Zuo, S. Y. Zheng, Y. H. Sun, F. Xu and Q. Z. Zhang, Int. J. Mol. Sci., 2019, 20, 1–18 Search PubMed.
- T. Dar, K. Shah, B. Moghtaderi and A. J. Page, J. Mol. Model., 2016, 22, 1–18 CrossRef CAS PubMed.
- C. Li, M. Zheng, B. Zhang, L. Gao, L. Liu, X. Zhou, X. Ma and K. Xiao, Environ. Pollut., 2012, 162, 138–143 CrossRef CAS PubMed.
- B. K. Gullett, A. Touati and C. W. Lee, Environ. Sci. Technol., 2000, 34, 2069–2074 CrossRef CAS.
- G. Skodras, P. Grammelis, P. Samaras, P. Vourliotis, E. Kakaras and G. P. Sakellaropoulos, Fuel, 2002, 81, 547–554 CrossRef CAS.
- R. Addink and E. R. Altwicker, Environ. Sci. Technol., 2004, 38, 5196–5200 CrossRef CAS PubMed.
- H. R. Buser, Chemosphere, 1992, 25, 45–48 CrossRef CAS.
- J. C. Harris and B. E. Bernstein, Child Welfare, 1980, 59, 469–477 CAS.
- S. Sinkkonen, E. Kolehmainen, J. Koistinen and M. Lahtipera, J. Chromatogr., 1993, 641, 309–317 CrossRef CAS.
- S. Sinkkonen, J. Paasivirta, J. Koistinen and J. Tarhanen, Chemosphere, 1991, 23, 583–587 CrossRef CAS.
- S. Sinkkonen, A. Vattulainen, J. P. Aittola, J. Paasivirta, J. Tarhanen and M. Lahtipera, Chemosphere, 1994, 28, 1279–1288 CrossRef CAS.
- A. Yasuhara, T. Katami, T. Okuda, N. Ohno and T. Shibamoto, Environ. Sci. Technol., 2001, 35, 1373–1378 CrossRef CAS PubMed.
- H. R. Buser and C. Rappe, Anal. Chem., 1991, 63, 1210–1217 CrossRef CAS.
- L. Khachatryan, R. Asatryan and B. Dellinger, Chemosphere, 2003, 52, 695–708 CrossRef CAS PubMed.
- R. Parette and W. N. Pearson, Chemosphere, 2014, 111, 157–163 CrossRef CAS PubMed.
- L. Khachatryan, R. Asatryan and B. Dellinger, J. Phys. Chem. A, 2004, 108, 9567–9572 CrossRef CAS.
- D. Abd-El-Haleem, H. Moawad, E. A. Zaki and S. Zaki, Microb. Ecol., 2002, 43, 217–224 CrossRef CAS PubMed.
- R. Navarro, K. Bierbrauer, C. Mijangos, E. Goiti and H. Reinecke, Polym. Degrad. Stab., 2008, 93, 585–591 CrossRef CAS.
- X. Wang, J. Wang, C. Jiao, L. Hao, Q. Wu, C. Wang and Z. Wang, Talanta, 2018, 179, 676–684 CrossRef CAS PubMed.
- M. Honda and K. Kannan, Environ. Pollut., 2018, 232, 487–493 CrossRef CAS PubMed.
- J. Q. Shi, J. Cheng, F. Y. Wang, A. Flamm, Z. Y. Wang, X. Yang and S. X. Gao, Ecotoxicol. Environ. Saf., 2012, 78, 134–141 CrossRef CAS PubMed.
- T. Dar, M. Altarawneh and B. Z. Dlugogorski, Organomet. Chem., 2012, 74, 657–660 Search PubMed.
- T. Dar, M. Altarawneh and B. Z. Dlugogorski, Environ. Sci. Technol., 2013, 47, 11040–11047 CrossRef CAS PubMed.
- C. S. Evans and B. Dellinger, Environ. Sci. Technol., 2005, 39, 122–127 CrossRef CAS PubMed.
- Q. Z. Zhang, S. Q. Li, X. H. Qu, X. L. Shi and W. X. Wang, Environ. Sci. Technol., 2008, 42, 7301–7308 CrossRef CAS PubMed.
- X. H. Qu, H. Wang, Q. Z. Zhang, X. L. Shi, F. Xu and W. X. Wang, Environ. Sci. Technol., 2009, 43, 4068–4075 CrossRef CAS PubMed.
- R. Louw and S. I. Ahonkhai, Chemosphere, 2002, 46, 1273–1278 CrossRef CAS PubMed.
- M. Altarawneh, B. Z. Dlugogorski, E. M. Kennedy and J. C. Mackie, J. Phys. Chem. A, 2007, 111, 2563–2573 CrossRef CAS PubMed.
- C. S. Evans and B. Dellinger, Environ. Sci. Technol., 2003, 37, 1325–1330 CrossRef CAS.
- T. Dar, K. Shah, B. Moghtaderi and A. J. Page, J. Mol. Model., 2016, 22, 1–18 CrossRef CAS PubMed.
- F. Xu, X. L. Shi, Y. F. Li and Q. Z. Zhang, Int. J. Mol. Sci., 2015, 16, 20449–20467 CrossRef CAS PubMed.
- R. Luijk, D. M. Akkerman, P. Slot, K. Olie and F. Kapteijn, Environ. Sci. Technol., 1994, 312–321 CrossRef CAS PubMed.
- N. Ortuno, J. A. Conesa, J. Molto and R. Font, Environ. Sci. Technol., 2014, 48, 7959–7965 CrossRef CAS PubMed.
- S. P. Ryan and E. R. Altwicker, Environ. Sci. Technol., 2004, 38, 1708–1717 CrossRef CAS PubMed.
- W. X. Pan, J. Fu and A. Zhang, Environ. Pollut., 2017, 225, 439–449 CrossRef CAS PubMed.
- C. P. Zuo, H. T. Wang, W. X. Pan, S. Y. Zheng, F. Xu and Q. Z. Zhang, Int. J. Mol. Sci., 2019, 20, 1–23 Search PubMed.
- F. Xu, X. L. Shi, Q. Z. Zhang and W. X. Wang, Int. J. Mol. Sci., 2015, 16, 18714–18731 CrossRef CAS PubMed.
- Q. Z. Zhang, X. H. Qu, H. Wang, F. Xu, X. L. Shi and W. X. Wang, Environ. Sci. Technol., 2009, 43, 4105–4112 CrossRef CAS PubMed.
- F. Xu, H. Wang, Q. Z. Zhang, R. M. Zhang, X. H. Qu and W. X. Wang, Environ. Sci. Technol., 2010, 44, 1399–1404 CrossRef CAS PubMed.
- B. C. Garrett and D. G. Truhlar, J. Phys. Chem., 1979, 83, 1052–1078 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci and G. A. Petersson, Gaussian 09, revision A.02, Gaussian, Inc., Wallingford, CT, USA, 2009 Search PubMed.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2004, 108, 6908–6918 CrossRef CAS.
- R. Gao, F. Xu, S. X. Li, J. Hu, Q. Z. Zhang and W. X. Wang, Chemosphere, 2013, 92, 382–390 CrossRef CAS PubMed.
- J. C. Corchado, Y. Y. Chuang, P. L. Fast, W. P. Hu, Y. P. Liu, G. C. Lynch, K. A. Nguyen, C. F. Jackels, A. Fernandez-Ramos, B. A. Ellingson, B. J. Lynch, J. J. Zheng, V. S. Melissas, J. Villa, I. Rossi, E. L. Coitino, J. Z. Pu, T. V. Albu, R. Steckler, B. C. Garrett, A. D. Isaacson, D. G. Truhlar, Polyrate, version 9.7, University of Minnesota, Minneapolis, 2007 Search PubMed.
- Q. Z. Zhang, W. N. Yu, R. M. Zhang, Q. Zhou, R. Gao and W. X. Wang, Environ. Sci. Technol., 2010, 44, 3395–3403 CrossRef CAS PubMed.
- J. D. Cox, Pure Appl. Chem., 1961, 2, 125–128 CAS.
- K. Fukui, Science, 1982, 218, 747–754 CrossRef CAS PubMed.
- J. L. Emdee, K. Brezinsky and I. Glassman, J. Phys. Chem., 1992, 96, 2151–2161 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: The structure and bond length of chlorophenols, chlorophenoxy radicals, chlorothiophenols and chlorothiophenoxy radicals. The imaginary frequencies, zero-point energies, total energies and bond length change values for the transition states involved in the formation of CPRs/CPRs from CPs/CTPs precursor. Rate constants and cartesian coordinates for the transition states involved in CPRs/CPR formation from CPs/CTPs. See DOI: 10.1039/d1ra02407h |
| This journal is © The Royal Society of Chemistry 2021 |