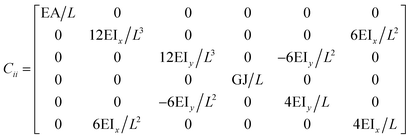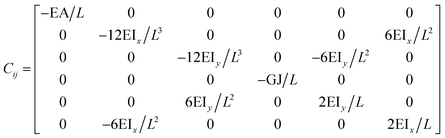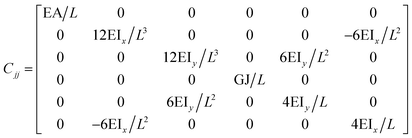Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Multiscale numerical simulation of in-plane mechanical properties of two-dimensional monolayers
Sadegh Imani Yengejeh,
Seyedeh Alieh Kazemi,
William Wen and
Yun Wang *
*
Centre for Catalysis and Clean Energy, School of Environment and Science, Griffith University, Gold Coast Campus, QLD 4222, Australia. E-mail: yun.wang@griffith.edu.au
First published on 7th June 2021
Abstract
Many applications of two dimensional (2D) materials are often achieved through strain engineering, which is directly dependent on their in-plane mechanical characteristics. Therefore, understanding the in-plane mechanical characteristics of the 2D monolayers becomes imperative. Nevertheless, direct experimental measurements of in-plane mechanical properties of 2D monolayers face great difficulties due to the issues related to the availability of high-quality 2D materials and sophisticated facilities. As an alternative, numerical simulation has the potential to theoretically predict such properties. This review presents some recent progress in numerically exploring the in-plane mechanical properties of 2D materials, including first-principles density functional theory, force-field based classical molecular dynamics, and the finite-element method. The relevant case studies are provided to describe the applications of these methods along with their pros and cons. We hope that the multiscale simulation methods discussed in this review will inspire new ideas and boost further advances of the computational study on the in-plane mechanical properties of 2D materials.
1. Introduction
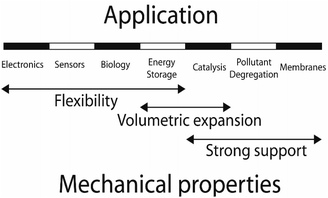
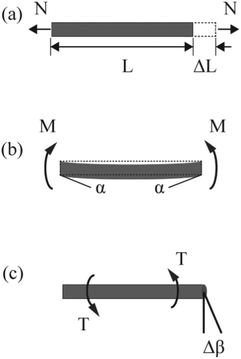
The discovery of graphene through the mechanical exfoliation of bulk graphite opens the field of two-dimensional (2D) materials.1 To date, many 2D materials including hexagonal boron-nitride (h-BN), phosphorene, MXene, layered double hydroxide (LDH), metal–organic frameworks (MOFs), covalent organic frameworks (COFs), and transition metal dichalcogenides (TMDs) have been experimentally and theoretically investigated.2–29 The mechanical properties of 2D materials have become a hot research topic because mechanical properties are physical features when a material is acted upon by external forces during the large-scale practical applications.30 2D materials can be deformed by in-plane stretching or by out-of-plane bending. Therefore, the mechanical characteristics of 2D structures include both in-plane and bending moduli. For 2D monolayers, the in-plane mechanical properties have attracted specific attention since they are directly relevant to the applications through strain engineering, as illustrated in Fig. 1.31–39 As outlined, the 2D materials are promising candidates for stretchable transparent electrodes with high conductance and high flexibility.40 The resistance of the graphene electrode displayed no evident variation up to a bending radius of 2.3 mm corresponding to the uniaxial tensile strain of 6.5%. Meanwhile, the pre-strained substrates could enhance the bending limit up to ∼11%. 2D nanoelectromechanical systems (NEMS) resonators are strongly dependent on their mechanical properties, e.g. Young's modulus, mass density, and resonant frequency.41 The presence of piezoelectricity characteristic coupled with the mechanical flexibility of some 2D materials enables their promising applications in wearable power-generated nano-devices. The associated piezoresistive and piezoelectric effects under mechanical strain in 2D structures extend their applications to a diverse range in nano-industries.42–45 The 2D hybrid organic–inorganic perovskites (HOIPs) solar cells possess power-conversion efficiencies surpassing 25%.46,47 These 2D structures are promising applicants for the next generation of optoelectrical nano-devices, which bandgap can be tuned through strain engineering.48,49 Jiao et al. conducted a systematic study to investigate the structural and mechanical properties of TMDs using DFT calculations. Their theoretical studies revealed that the 2D TcS2 and TcSe2 monolayers exhibit promise as potential candidates for light harvesting.50 Furthermore, the analysis of the band alignment relative to the vacuum level showed that the TcSe2 monolayer is potentially plausible for water splitting. Meanwhile, a 2% compressive strain can also make the TcS2 monolayer suitable for photocatalysts. Considering the importance of strain engineering for 2D materials, many efforts have been devoted to exploring their in-plane mechanical characteristics. Table 1 lists the details of typical in-plane mechanical properties under the different external forces. The in-plane elastic moduli, Young's moduli, shear moduli, and Poisson's ratio are the parameters widely investigated in most studies.| Mechanical property | Description |
|---|---|
| Strength | The amount of the load that a material can tolerate before failure |
| Brittleness | The property of a material when the material fractures under stress without exhibiting much elastic deformation or changes in dimension |
| Stiffness | A material's ability to resist significant elastic deformation while loading |
| Hardness | A material's ability to resist various forms of deformation, indentation, and penetration |
| Toughness | A material's capacity to withstand elastic and plastic deformation without failure |
| Elasticity | A material's capacity to rebound back to their original dimensions after the deformation or being removed from its load |
| Anisotropy | The property difference in terms of the direction or orientation of the material |
| Ductility | A material's capacity to be stretched due to tensile stress |
| Creep | A slow and gradual deformation (or change in dimensions) of materials under a certain applied load in terms of time and temperature |
| Thermal expansion | A change in shape, volume or area caused by changes in temperature |
| Poisson's ratio | Poisson's ratio defines the ratio of transverse strain to the axial strain |
There are different kinds of experimental technologies developed to measure the in-plane mechanical properties of 2D materials. These include (1) nanoindentation of suspended monolayer using atomic force microscopy (AFM); and (2) pressurized blister tests. Lee et al. first used the AFM nanoindentation method to investigate the mechanical characteristics of graphene.51 They reported that the force-displacement properties were interpreted within a framework of nonlinear elastic stress–strain response and yields an elastic stiffness of 340 N m−1. Such quantities reveal graphene as comparatively the strongest and toughest materials ever investigated. Regardless, the experimental measurements require highly sophisticated facilities. Additionally, it is challenging to synthesize large high-quality 2D monolayers for the analysis. As such, numerical simulations to investigate the mechanical characteristics of 2D materials has become attractive, as evidenced by the blue area in Fig. 2.
 | ||
| Fig. 2 A visualized landscape of the recent studies regarding the mechanical characteristics of 2D materials. | ||
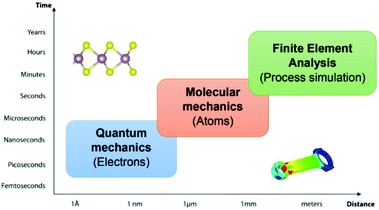
Computational materials science has become a rapidly growing multidisciplinary field. Striving to advance computing capabilities to comprehend, understand, and solve the complex problems of functional materials, including their mechanical properties. The mechanical properties are derivable from the linear stress–strain relationship or quadratic energy-strain relationship. Computational approaches with different size and time scales have been developed to explore the microscopic and macroscopic mechanical behaviours of 2D materials. The methods range from the sub-atomic [e.g. first-principles density functional theory (DFT)], atomistic level [e.g. force field-based classical molecular dynamics (MD)] and macroscopic levels [e.g. finite element analysis (FEA)] for the process simulation and engineering design, as illustrated in Fig. 3. In this review, the principles of the numerical simulation of the in-plane mechanical properties of 2D materials are presented. Some recent cases facilitate further discussion about the pros and cons of different methods.
2. Methodology
2.1 DFT method
The relationship between the in-plane elastic constants and moduli of 2D monolayer materials can be described based on Hooke's law under the in-plane stress condition.
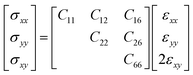 | (1) |
For a first-principles DFT method, the in-plane mechanical properties of 2D materials are calculated through the parabolic dependence of the energy on the elongation.52–57 The energy (Es) can be obtained from the DFT calculations with the different intervals of elongation. Using high-symmetry graphene as an example: the uniaxial strain ε was applied along the x or y direction, which leads to εyy = 0 or εxx = 0, respectively. Under this condition,
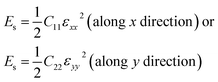 | (2) |
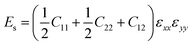 | (3) |
while the equi-biaxial strain is applied. Finally, C66 was calculated by fitting the second-order polynomial.
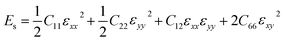 | (4) |
Another method to calculate the in-plane mechanical properties is through the standard approach. In this method, the conventional mechanical properties are first calculated. After that, the multiplication of the conventional stiffness tensors and monolayer thickness will equate to the in-plane stiffness tensors. Here, the thickness of the monolayer needs to be carefully justified. Additionally, the vacuum used to separate the monolayers under the periodic boundary conditions also needs to be thick enough for the converged in-plane stiffness tensors to be retrieved.
The in-plane planar Young's (Y2D) and shear (G2D) moduli, together with Poisson's ratio (ν2D) of 2D monolayer materials, can be derived from the in-plane planar elastic constants as:
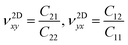 | (5) |
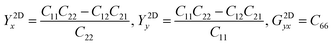 | (6) |
2.2 MD method
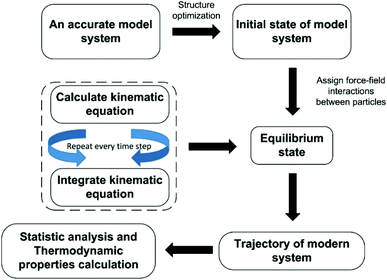
Each atom for MD simulation is subjected to Newton's law of mechanics. The sequential steps to conduct MD simulation can be presented by the flowchart illustrated in Fig. 4.
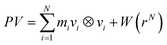 | (7) |
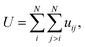 | (8) |
In this equation: N is the total number of atoms, i and j are atomic indices, and uij is the empirical potential. uij is used to describe the interaction energy between atoms. Each energy term uij depends only on a small number (Nk) of atoms located at positions r1,r2,…,rNk, including atoms i and j. These atoms can be either in the supercell or in periodic images. Groups are assumingly chosen so that i is always in the supercell, which is denoted as 0. A periodic image of the group belongs to the periodic cell n. As such, the potential energy can be expressed as a sum of elements of the primary cell in an unambiguous manner:
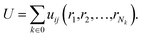 | (9) |
The partial force on a specific atom image can be calculated by deriving this expression with respect to the position rin of the periodic image of atom i in cell n:
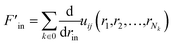 | (10) |
According to the theory of Thompson et al., the virial tensor is:60
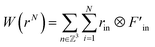 | (11) |
The true mechanical stress tensor is then simply the opposite of the internal pressure tensor:
| σ = −P | (12) |
The stress is proportional to the strain when the strain is small, which obeys the general Hooke's law. The Young's modulus can then be calculated because it is the slope of the strain–stress curve, as illustrated in Fig. 5.61
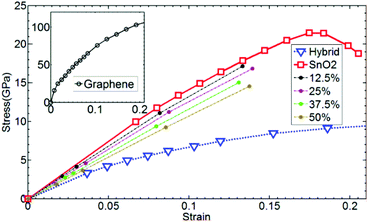 | ||
| Fig. 5 Stress–strain curve of graphene, SnO2, and hybrid structures from the ref. 61. | ||
| Etotal = Evalvance + Enonbond | (13) |
| Evalance = Ebond + Eangle + Etorsion + Einversion | (14) |
| Enonbond = EvdW + Eelectrostatic + EHbond | (15) |
2.3 FE method
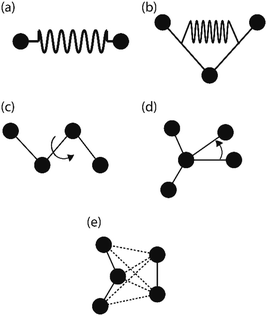
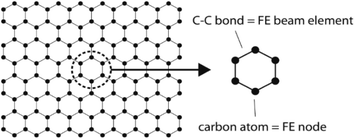
The FE is a numerical method for solving problems, which can be described by partial differential equations or formulated as functional minimization. A domain of interest is represented as an assembly of finite elements. The FEA exhibits two main features. Firstly, the piece-wise approximation of physical fields on finite element provides good precision even with simple approximating functions. Another characterization of the approach is that the locality of the approximation leads to spare equation systems for a discretized problem. Thus, helping to solve problems with a massive number of nodal unknowns.The FE modelling approach was first utilized in 2003, where the theory of classical structural mechanics was extended into the modelling of nanostructures.62 Atoms are bonded together with a corresponding length and angle in a three-dimensional (3D) space. When subjected to loading, materials behave like space frame structures. Thus, the bonds between atoms are considered as connecting load-carrying generalized beam members. Meanwhile, the atoms act as joints of the members, as illustrated in Fig. 7. Structural mechanics analysis is conducted to determine the displacements, strains, and stresses of a structure under given loading conditions. The stiffness matrix approach is one of the elementary instances for solving linear elastic static problems. An additional application is to solve problems that deal with mechanical characteristics such as buckling, plasticity and dynamics. The stiffness matrix C consists of the following submatrices:
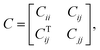 | (16) |
The above elemental stiffness matrices indicate four parameters that are needed including the tensile resistance EA, the torsional stiffness GJ, and the flexural rigidity EIx and EIy. All the while, identifying the length of the element, L. The EA, GJ and EI can be determined based on the energy equivalence since the deformation of a space frame results in the changes of strain energies. Based on the theory of classical structural mechanics, the strain energy of a uniform beam of length L subjected to pure axial force N can be presented as following:
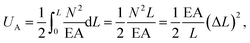 | (17) |
The strain energy of a uniform beam under pure bending moment M is
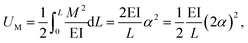 | (18) |
The strain energy of a uniform beam under pure torsion T is
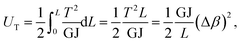 | (19) |
On the other hand, this potential energy between atoms is in the sum of contributions from bond stretch interaction Ur, bond angle bending Uθ, dihedral angle torsion Uϕ, improper (out-of-plane) torsion Uω, and a non-bonded van der Waals interaction.63 For covalent systems, the main contributions to the total steric energy come from the first four terms, which have included four-body potentials. The harmonic approximation is adequate for describing the energy, considering the assumption of small deformation.64 The dihedral angle torsion and the improper torsion are often merged into a single equivalent term for convenience and simplicity's sake, i.e.,
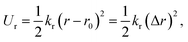 | (20) |
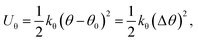 | (21) |
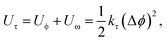 | (22) |
Here, both Ur and UA represent the stretching energy, both Uθ and UM represent the bending energy, and both Uτ and UT represent the torsional energy. It can also be assumed that the rotation angle 2α is equivalent to the total change Δθ of the bond angle, ΔL is equivalent to Δr, and Δβ is equivalent to Δϕ. Hence, by comparing eqn (17)–(22), a direct relationship between the structural mechanics parameters EA, EI and GJ can then be deduced from the molecular mechanics parameters kr, kθ and kτ as following:
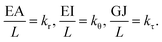 | (23) |
Applying this concept followed by the solution procedure of stiffness matrix method for frame structures, the deformation and related elastic behaviour of 2D materials can be simulated.
3. Applications of numerical simulations
3.1 DFT studies
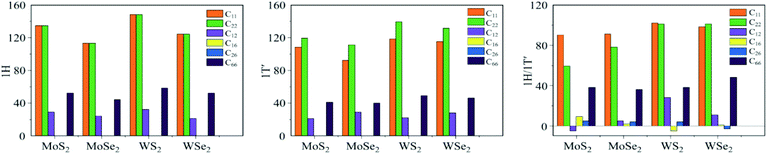 | ||
| Fig. 9 In-plane stiffness tensors Cij of TMDs with different structural phases from the ref. 83. | ||
Luo et al.120 performed a comprehensive DFT-based study to investigate the mechanical properties of the functionalized MXenes. They calculated the elastic constants, free energy, and work function of different MXenes to explore and comprehend the impact of the transition metal and surface functional groups on their characteristics. Apart from some O-termination group exceptions, most of their material models were observed to be dynamically stable. They finally indicated that the Young's moduli for the most investigated MXenes fluctuated from 150 to 400 N m−1 and concluded that the functionalized MXenes usually exhibits stronger structural stability. Kazemi et al. recently conducted a theoretical investigation to study the mechanical properties of 2D titanium carbide MXene-based materials utilizing DFT calculations.121 They discovered that in-plane elastic constants, Young's and shear moduli increase over the thickness of the MXene systems. It further suggests that the improved mechanical properties of the functionalized MXenes. The stronger interaction between the –O terminal group and the Tin+1Cn leads to the stronger mechanical properties of –O functionalized MXenes. Consequently, Ti4C3O2 is the strongest material among all their considered systems. More importantly, all Ti4C3T2 MXenes have the higher in-plane Young's and shear moduli than graphene, which was previously thought to be the strongest known 2D material. Therefore, Ti4C3T2 can be a promising alternative to graphene for applications that need 2D materials with considerably high stiffness and largely resistant to shape change. A similar role for the surface functionalization was also reported by Fu et al.122 Amongst the five functional groups that they considered, (–F, –Cl, –OH, –H, and –O) the oxygen functionalized Ti3C2O2 possesses the largest adsorption energy, the highest in-plane planar elastic modulus, and the greatest enhancement of strength. Those findings pave the avenue for tuning the mechanical properties of MXene-based materials database by engineering their composition.
| Reference | 2D material | XC functional | Investigated properties | Research summary |
|---|---|---|---|---|
| Johari and Shenoy84 | TMDs | GGA-PBE | Mechanical and electrical properties | Performing DFT calculations to evaluate the impact of mechanical strains on the electronic properties of TMDs |
| Jiao et al.50 | TcS2 and TcSe2 | HSE | Structural, mechanical, electronic, and optical properties | DFT calculations were carried out to study the physical properties of monolayer 2D materials and proposing their potential applications in photovoltaics, photocatalysts, and other nanodevices |
| Jiao et al.123 | NaSnP | GGA-PBE | Structural, mechanical, electrical, and optical properties | Investigating the physical properties of monolayer NaSnP and suggesting its promising applications in photovoltaic |
| HSE | ||||
| Lv et al.124 | M2Se3 | GGA-PBE | Mechanical, magnetic, electric, and structural properties | Systematically investigated the physical characteristics of monolayer M2Se3. Exploring superior mechanical flexibility and negative Poisson's ratio in the studied 2D models |
| Lü et al.125 | Phosphorene | GGA-PBE | Young's and shear moduli, Poisson's ratio | Exploring the behaviour of phosphorene and its oxides by investigating their mechanical properties |
| Kazemi et al.121 | MXene | DFT-D3 | In-plane planar Young's and shear moduli | Evaluating the characteristics of 2D titanium carbide applying DFT-D3 calculation to predict their mechanical properties of these 2D materials |
| Imani Yengejeh et al.83 | TMDs | GGA-PBE | Mechanical properties | Investigating the impact of hetero-structure phase on the mechanical properties of TMD monolayers |
For example, Aghdasi et al. performed DFT calculations to study the in-plane Young's modulus of monolayer phosphorene with and without the adsorption of different atoms, including Li, Mg, O, Al, Pt, Pd, and Mo.126 Using the energy-strain method, they found that the in-plane Young's modulus of monolayer phosphorene is anisotropic. Its in-plane Young's modulus along the armchair and zigzag directions are 25.36 and 92.30 N m−1, respectively. They also found that the impacts of different adsorbed atoms on the mechanical properties can either be positive or negative. Additionally, the influence of the atomic adsorption on the in-plane Young's modulus of the armchair phosphorene is more remarkable than the zigzag phosphorene. Observing the adsorbed zigzag phosphorene reached the plastic region at smaller strains.
3.2 MD simulations
MD based simulation can be a promising approach for investigating the physical and mechanical properties of 2D materials using a relatively large size due to the low computational cost.Javvaji et al. used the stress–strain method to investigate the influence of external parameters on the yield properties of graphene.128 They also studied the distribution of the stress–strain plots with varying domain sizes, initial crack lengths and lattice orientations. The yield values were observed to drop significantly for small initial crack lengths less than or equal to 0.1 L. The yield values were also observed to decrease with the increase in domain size, as the larger specimens offer more spaces for dislocations to initiate. Evidence was given for the combined effect of the domain size, lattice orientation and crack length on the yield values of stress and strain. Gamboa et al. conducted a MD simulation to investigate the elastic properties of graphene sheets through implementing the uniaxial tensile tests.129 The values of the Young's modulus and Poisson's ratio obtained in their calculation were 730 GPa and 0.39, respectively. Differing significantly from the former estimations and much closer to experimental values. A proposed explanation was that the effect of atomic relaxation leads to a plausible accuracy. They finally observed an extended linear domain in the stress–strain curves, which is relevant to Young's modulus calculations at finite temperature.
Anastasi et al. conducted an intriguing investigation on the mechanical properties of pristine and nano-porous graphene using MD simulations.130 They studied the fracture behaviour, and the temperature dependence of the 2D material models. Additionally, they investigated the random and uniformly distributed vacancy defects. They discovered that higher temperatures tend to significantly decrease the fracture stress and strain almost linearly with temperature. The elastic modulus was, however, only affected at system temperatures higher than approximately 900 K. Thus, concluding that the fracture stress decreases substantially inversely proportional to the defect density. Their latter attempt was made for potential applications which require non-pristine sheets such as filtration membranes.
Zhao et al. conducted a MD study to evaluate the temperature-dependent mechanical properties of monolayer MoS2.132 Their computational results stated that the mechanical characterizations of the material model vary with temperature. More precisely, the Young's modulus, maximum loading strain, and maximum load stress decrease with the rise in temperature from 4.2 K to 500 K. They also discussed that the tendency of the maximum loading strain with the different temperature is opposite to that of metal materials which are caused by the short-range SW potentials among the TMD atoms. Despite holding the high computational efficiency, the mathematical form of the SW potential may not be suitable for the atomic-thick planar structures, such as graphene and b-BN, as such potentials are less probably to resist the bending motion of these real planar crystals.133–135
Jiang performed a MD simulation to study the misfit strain-induced buckling of the TMDs lateral heterostructures, such as MoS2–WSe2 and MoS2–MoTe2.136 He also utilized the SW potential to describe the interatomic interactions for each TMD and the coupling between different TMDs. Computational results indicated that misfit strain presumably causes buckling of the TMD with larger lattice constants in the lateral heterostructure, due to the atomic-thick nature of TMDs. These results raise many mechanical challenges for the structural stability of the low-dimensional materials.
| Reference | 2D material | Investigated properties | Research summary |
|---|---|---|---|
| Jhon et al.137 | Functionalized MXenes | Tensile mechanical response | Studying the surface termination effect on the mechanical response of the MXenes using MD simulation. Exploring the tensile variations of the MXenes under the impact of surface vacancies |
| Chang et al.138 | Phosphorene | Young's modulus | Examining the mechanical properties of black and blue phosphorene. The results indicate that the temperature has weak impact on the Young's modulus of the structures |
| Vijayaraghavan and Zhang139 | Boron nitride–carbon nanosheet | Mechanical properties | Investigating the tensile characteristics of single layer BN–C nanosheets. It was shown that the BN–C nanosheet with parallel arrangement exhibits slightly improved mechanical resistance than the BN–C nanosheet with series arrangement |
| Hou and Yang58 | Graphene oxides | Tensile properties | Carrying out tensile test to investigate the mechanical properties of graphene oxide sheets |
| Javvaji et al.128 | Graphene | Yield stress and strain | Investigating the combined effect of domain size, crack length, and lattice orientation on the mechanical properties of graphene |
| Anastasi et al.130 | Graphene | Mechanical properties and fracture behaviour | Carrying out uniaxial tensile loading to investigate the mechanical properties of pristine and nanoporous graphene. An increase in system temperature results in a significant reduction in the fracture stress and strain |
| Siriwardane et al.140 | Sulfur-functionalized MXenes | Structural, stability, and ion dynamic properties | Performing computational calculations at 400 K and bond-length analysis to study the physical properties of functionalized MXenes |
| Cellini et al.141 | Diamond boron-nitride | Mechanical properties and pressure induce phase transition | Investigating the mechanical properties and pressure-induced formation of 2D diamond boron nitride. The results show a metastable local rearrangement of the h-BN atoms into diamond crystal clusters when increasing the indentation pressure |
One recent MD simulation example conducted by Yang et al. investigated the temperature-dependent stress–strain relations of monolayer black phosphorus while considering the impact of temperature changes.142 The Young's and shear moduli under uniaxial tension at different temperatures were investigated. The values of the Young's and shear moduli ranged from 24 to 19.2 GPa and 25.4 to 20 GPa, respectively. Observations showed that for a given temperature, the Young's moduli along the zigzag direction are more than four times higher than those along the armchair direction, which matches the DFT conclusion.126 Their predicted strength and moduli were in good agreement with the available experimental data.
3.3 FEM simulations
Due to its significant advantages, the FEM approach has become increasingly popular and a promising alternative for evaluating the macroscopic mechanical properties of low-dimensional materials for a wide range of emerging applications where high conductivity, mechanical strength, high surface area, and high yield strain are required.143,144 FEM's features enable researchers to work on a larger scale of the material models, which consists of numerous atoms in their structural configurations.FEA is also strongly beneficial for conducting the simulations to explore the mechanical properties of defective low-dimensional systems. Recently, Nakanishi et al. investigated the macroscopic mechanical properties of hollow-wall graphene gyroids by performing indentation tests with suitable interpretation by FE simulations.146 They carried out two sets of investigations. Firstly, they used periodic cell calculations to explore the mechanical properties of their systems in terms of the relative density and cell wall characterization of the lattice. Then, the indentation simulations of a continuum with the effective properties of the gyroid were performed. They finally concluded that hollow-wall graphene gyroids combine size-dependent mechanical and electrical properties with a topology of high structural efficiency.
| Reference | 2D material | Approach | Investigated properties | Research summary |
|---|---|---|---|---|
| Khandoker et al.149 | Graphene | FEM | Young's modulus, shear modulus, and Poisson's ratio | Investigating the mechanical properties of graphene using atomistic modeling and continuum approaches on mono- and double-layer graphene. The number of layers affects the Poisson's ratio but not the Young's and shear moduli |
| Damascento et al.150 | Graphene | FEM | Tensile and fracture strength | Conducting an atomistic simulation of FEM to investigate the impact of structural defects on the mechanical properties of graphene |
| Li et al.147 | MoS2 | FEM | Young's modulus | Demonstrating an approach to map the in-plane Young's modulus of single- and double-layer MoS2. The elasticity of both systems cannot be differentiated |
| Zhang et al.151 | Graphene | FEM | Mechanical properties | Modifying the properties of Sn–Cu–Ni solder joint used for solar cells by exploring their mechanical characteristics. Applying FEM to calculate the stress–strain curve |
| Nakanishi et al.146 | Hollow-wall graphene gyroids | FEM | Elastic modulus and yield strength | Evaluating the macroscopic mechanical properties of solid-wall nickel gyroids and hollow-wall graphene gyroids using nano-indentation testing with a suitable interpretation by FE simulation |
| Imani Yengejeh et al.152 | Graphene | FEM | Natural frequency | Performing a numerical investigation to study the mechanical properties of topologically defective and functionalized graphene sheets. Reporting the reduction of natural frequencies of the material models due to the presence of the atomic defects |
3.4. Discussion
Overall, numerical modelling approaches with different size and time scales have been developed for evaluating the in-plane mechanical characteristics of 2D monolayers.The in-plane elastic properties of some of the most studied 2D materials are presented in Table 5.51,83,121,147–149,153–157 Basically, in-plane mechanical properties (such as Young's modulus, shear modulus, hardness, and Poisson's ratio) can be calculated through the linear stress–strain or quadratic energy-strain relationships. DFT methods are independent of any empirical parameters, which provide the highest accuracy and flexibility, as evidenced by the data listed in Table 5. The DFT in-plane Young's modulus and Poisson's ratio of graphene and MoS2 are almost identical to the measured values. There is a considerably large difference in the MXene system. Because materials used for experimental measurements have hybrid terminal groups, this consequently leads to the theory-experiment discrepancy. The simulation quality of MD simulation is greatly affected by the force fields used in the study, as evidenced by Lebedeva et al. on graphene.127 Table 5 lists one of the best MD results, which are also close to the experimental data. These results are caused by the potentials for graphene and TMDs being purposely optimized. Up to date, graphene is the most studied system via the FEA method. However, its calculated in-plane mechanical properties are far from the experiments. For example, the calculated Poisson's ratio of graphene is about four times higher than the DFT and experimental values.
| 2D Material | Method | Procedure | Y2D (N m−1) | G2D (N m−1) | ν2D | Ref. |
|---|---|---|---|---|---|---|
| Graphene | DFT | Energy-strain | 345 | 150 | 0.149 | Wei et al.153 |
| MD | Stress–strain | 320 | 150 | 0.22 | Kalosakas et al.154 | |
| FEA | — | 272–323 | 85–153 | 0.7–0.8 | Khandoker et al.149 | |
| Exp. | AFM | 340 ± 50 | 0.165 | Lee et al.51 | ||
| MoS2 | DFT | Energy-strain | 127.7 | 52 | 0.22 | Imani Yengejeh et al.83 |
| MD | Stress–strain | 149.42 | — | — | Mortazavi et al.155 | |
| FEA | — | 163 | — | — | Li et al.147 | |
| Exp. | AFM | 120 | — | 0.29 | Cooper et al.148 | |
| Ti3C2O2 | DFT | Energy-strain | 366–372 | 145 | 0.258 | Kazemi and Wang121 |
| MD | Stress–strain | 378.3 | — | 0.29 | Plummer et al.156 | |
| FEA | — | — | — | — | — | |
| Exp. | AFM (Ti3C2Tx) | 326 ± 29 | — | — | Li et al.157 |
In addition, the first principles DFT method does not require any pre-set parameters. Its simulations can study chemical reactions involving charge transfer, bond formation and cleavage with high accuracy. Thus, DFT-based simulations provide greater flexibility for calculating the in-plane mechanical properties of 2D materials. As a comparison, only limited force fields are available for most of the 2D materials beyond graphene. The parametrization of the force field either derived from the experimental data or first-principles DFT results is a very time-consuming task. As such, MD-based methods cannot be widely used. The FEA simulation face the same problem because its quality is based on the spring constants, which have the same issues related to the availability and quality.
On the other hand, the force-field-based classical MD methods use empirical interatomic potentials to describe their interaction energies. Thus, significantly reducing the computational time using low cost. Consequently, the MD method can assess the mechanical properties of large 2D materials. Additionally, the impact of temperature on the mechanical properties can also be evaluated. The FEM has the lowest computational cost. Most of the FEM computations can be conducted using desktop computers. Consequently, it can be used to investigate some macroscopic mechanical properties.
To obtain the holistic picture of in-plane mechanical properties of 2D materials, a combination of different computational methods is a plausible approach by taking advantage of each one's strong features. So far, there have been some attempts to combine the computational methods and propose a refined technique to investigate the mechanical properties of the nanostructures. Imani Yengejeh et al. proposed a refined FEA to evaluate the vibrational properties of the defective CNTs and their modifications.158 They implemented the well-established FEA for the perfect material models. For appraising the properties of the defective structure, the accurate DFT structural relaxation was used as FEA cannot consider the rearrangement of the atoms after the introduction of the defect (e.g. vacancy defect). Their obtained results were in good agreement with the experimental findings, which suggested that such a combined multiscale modelling approach is feasible for investigating the mechanical characteristics of the 2D materials.
4. Summary and outlook
Over the past few decades, the family of low-dimensional materials has rapidly grown beyond graphene. Many novel 2D materials including, TMDs, MXene and phosphorene, have become significantly important. The remarkable properties of 2D materials pave a bright future for basic research and large-scale industrial applications. Due to several limitations of the experimental measurements, numerical simulation becomes a promising alternative to evaluate the in-plane mechanical properties of these 2D monolayers.This review described some widely used computational approaches for investigating the in-plane mechanical properties of 2D material. Their features are discussed using some recent study results as examples. DFT-based computation is the most widely used approach to understand the in-plane mechanical properties of 2D materials since their results are reliable. All 2D monolayers can theoretically be investigated using the DFT method after their atomic configurations are correctly built. The DFT results can be used to guide their design and screen for 2D materials at the atomic level to achieve desired mechanical properties. A major disadvantage of the first-principles calculations is that only a few thousand atoms can be simulated. Consequently, seriously limiting the direct comparisons to experimental studies. In experiments, the measurements typically occur on the micrometre length scale. For such larger sizes, classical MD and FEM simulations are desirable. The minuscule computational costs of atomistic simulations using empirical force field potentials and spring constants enable the mechanical properties of some 2D systems to be predicted. Basically, MD simulation is one of the molecular simulation techniques which refer to a set of approaches a conducting computational experiment on molecule models. This simulation method can be classified into two major categories: microscale defined in the range of 0.1–10 nm and mesoscale defined from 10 nm to 100 nm. However, the key ingredient for MD and FEM simulations is an empirical interatomic potential and spring constants, which determines the availability and accuracy of MD and FEM simulations. Since different computational approaches exhibit their advantages and disadvantages, the most appropriate computational technique can be selected in terms of the type of mechanical properties of the 2D material, the required accuracy of the results, and the features of the applied method.
Finally, the development of novel technologies becomes essential to generate a comprehensive understanding of the in-plane mechanical properties of the 2D materials for their applications based on strain engineering. Several promising methods are discussed below:
(1) A combining approach may be an excellent solution to describe a wide range of 2D materials properties as it would enable the incorporation of positive features from each method. For example, the machine learning method has been used to develop the force fields from the DFT results, which can greatly expand the application area of the MD and FEM simulations.159–162
(2) The combination of the experimental measurements and the numerical simulations also holds great potentials. As suggested by the recent study, the experimental measurements can be used to provide accurate spring constants, which can enable the reliable in-plane Young's modules using the low-cost FEA approach.163,164
(3) Machine learning technology can also be used to accelerate the advancement of this area. The DFT-based computational data can be used to build the database. The ensemble learning system can be built using a diverse set of base regressors/classifiers. Construction is done through both traditional learning algorithms (such as support vector machine, decision tree, kernel ridge regression, Gaussian mixture regression) and deep learning algorithms to identify the relationship between the atomic fingerprints and their in-plane mechanical properties.165,166
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was undertaken on the supercomputers in the National Computational Infrastructure (NCI) in Canberra, Australia, which is supported by the Australian Commonwealth Government and the Pawsey Supercomputing Centre in Perth with funding from the Australian Government and the Government of Western Australia.References
- K. S. Novoselov, D. Jiang, F. Schedin, T. Booth, V. Khotkevich, S. Morozov and A. K. Geim, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 10451–10453 CrossRef CAS PubMed.
- Y. Xia, P. Yang, Y. Sun, Y. Wu, B. Mayers, B. Gates, Y. Yin, F. Kim and H. Yan, Adv. Mater., 2003, 15, 353–389 CrossRef CAS.
- B. Anasori, M. R. Lukatskaya and Y. Gogotsi, Nat. Rev. Mater., 2017, 2, 1–17 Search PubMed.
- B. Radisavljevic, A. Radenovic, J. Brivio, V. Giacometti and A. Kis, Nat. Nanotechnol., 2011, 6, 147–150 CrossRef CAS PubMed.
- L. Song, L. Ci, H. Lu, P. B. Sorokin, C. Jin, J. Ni, A. G. Kvashnin, D. G. Kvashnin, J. Lou and B. I. Yakobson, Nano Lett., 2010, 10, 3209–3215 CrossRef CAS PubMed.
- S. Manzeli, D. Ovchinnikov, D. Pasquier, O. V. Yazyev and A. Kis, Nat. Rev. Mater., 2017, 2, 1–15 Search PubMed.
- Q. Wei and X. Peng, Appl. Phys. Lett., 2014, 104, 251915 CrossRef.
- A. Gupta, T. Sakthivel and S. Seal, Prog. Mater. Sci., 2015, 73, 44–126 CrossRef CAS.
- A. J. Howarth, Y. Liu, P. Li, Z. Li, T. C. Wang, J. T. Hupp and O. K. Farha, Nat. Rev. Mater., 2016, 1, 1–15 Search PubMed.
- J. C. Tan and A. K. Cheetham, Chem. Soc. Rev., 2011, 40, 1059–1080 RSC.
- A. Kuc, A. Enyashin and G. Seifert, J. Phys. Chem. B, 2007, 111, 8179–8186 CrossRef CAS PubMed.
- R. C. Andrew, R. E. Mapasha, A. M. Ukpong and N. Chetty, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 125428 CrossRef.
- Y. Sun, Q. Wu and G. Shi, Energy Environ. Sci., 2011, 4, 1113–1132 RSC.
- J. Pang, R. G. Mendes, A. Bachmatiuk, L. Zhao, H. Q. Ta, T. Gemming, H. Liu, Z. Liu and M. H. Rummeli, Chem. Soc. Rev., 2019, 48, 72–133 RSC.
- A. Cao, L. Zhang, Y. Wang, H. Zhao, H. Deng, X. Liu, Z. Lin, X. Su and F. Yue, ACS Sustainable Chem. Eng., 2018, 7, 2492–2499 CrossRef.
- S. Zhao, Y. Wang, J. Dong, C.-T. He, H. Yin, P. An, K. Zhao, X. Zhang, C. Gao and L. Zhang, Nat. Energy, 2016, 1, 1–10 Search PubMed.
- J. Liu, J. Kang and Y. Wang, J. Appl. Phys., 2019, 125, 142906 CrossRef.
- Z. Zhu, H. Yin, C. T. He, M. Al-Mamun, P. Liu, L. Jiang, Y. Zhao, Y. Wang, H. G. Yang and Z. Tang, Adv. Mater., 2018, 30, 1801171 CrossRef PubMed.
- W. Cui, S. Xu, B. Yan, Z. Guo, Q. Xu, B. G. Sumpter, J. Huang, S. Yin, H. Zhao and Y. Wang, Adv. Electron. Mater., 2017, 3, 1700024 CrossRef.
- Y. Wang, X. Liu, J. Liu, M. Al-Mamun, A. Wee-Chung Liew, H. Yin, W. Wen, Y. L. Zhong, P. Liu and H. Zhao, ACS Appl. Energy Mater., 2018, 1, 1688–1694 CrossRef CAS.
- Q. Xiong, Y. Wang, P. F. Liu, L. R. Zheng, G. Wang, H. G. Yang, P. K. Wong, H. Zhang and H. Zhao, Adv. Mater., 2018, 30, 1801450 CrossRef PubMed.
- Y. Qi, Q. Xu, Y. Wang, B. Yan, Y. Ren and Z. Chen, ACS Nano, 2016, 10, 2903–2909 CrossRef CAS PubMed.
- H. Ren, H. Shao, L. Zhang, D. Guo, Q. Jin, R. Yu, L. Wang, Y. Li, Y. Wang and H. Zhao, Adv. Energy Mater., 2015, 5, 1500296 CrossRef.
- J. Sun, S. E. Lowe, L. Zhang, Y. Wang, K. Pang, Y. Wang, Y. Zhong, P. Liu, K. Zhao and Z. Tang, Angew. Chem., Int. Ed., 2018, 57, 16511–16515 CrossRef CAS PubMed.
- P. Zhou, Q. Xu, H. Li, Y. Wang, B. Yan, Y. Zhou, J. Chen, J. Zhang and K. Wang, Angew. Chem., 2015, 127, 15441–15445 CrossRef.
- M. Al-Mamun, H. Zhang, P. Liu, Y. Wang, J. Cao and H. Zhao, RSC Adv., 2014, 4, 21277–21283 RSC.
- V. Ramalingam, P. Varadhan, H. C. Fu, H. Kim, D. Zhang, S. Chen, L. Song, D. Ma, Y. Wang and H. N. Alshareef, Adv. Mater., 2019, 31, 1903841 CrossRef CAS PubMed.
- J. Liu, H. Yin, P. Liu, S. Chen, S. Yin, W. Wang, H. Zhao and Y. Wang, J. Phys. Chem. Lett., 2019, 10, 6955–6961 CrossRef CAS PubMed.
- Z. Zhu, H. Yin, Y. Wang, C. H. Chuang, L. Xing, M. Dong, Y. R. Lu, G. Casillas-Garcia, Y. Zheng and S. Chen, Adv. Mater., 2020, 32, 2004670 CrossRef CAS PubMed.
- B. C. Wyatt, A. Rosenkranz and B. Anasori, Adv. Mater., 2021, 2007973 CrossRef CAS PubMed.
- G. R. Bhimanapati, Z. Lin, V. Meunier, Y. Jung, J. Cha, S. Das, D. Xiao, Y. Son, M. S. Strano and V. R. Cooper, ACS Nano, 2015, 9, 11509–11539 CrossRef CAS PubMed.
- S. Z. Butler, S. M. Hollen, L. Cao, Y. Cui, J. A. Gupta, H. R. Gutiérrez, T. F. Heinz, S. S. Hong, J. Huang and A. F. Ismach, ACS Nano, 2013, 7, 2898–2926 CrossRef CAS PubMed.
- E. Scalise, M. Houssa, G. Pourtois, V. Afanas’ev and A. Stesmans, Nano Res., 2012, 5, 43–48 CrossRef CAS.
- R. Roldán, A. Castellanos-Gomez, E. Cappelluti and F. Guinea, J. Phys.: Condens. Matter, 2015, 27, 313201 CrossRef PubMed.
- S. Yang, C. Wang, H. Sahin, H. Chen, Y. Li, S.-S. Li, A. Suslu, F. M. Peeters, Q. Liu and J. Li, Nano Lett., 2015, 15, 1660–1666 CrossRef CAS PubMed.
- Y. Cai, Q. Ke, G. Zhang, Y. P. Feng, V. B. Shenoy and Y. W. Zhang, Adv. Funct. Mater., 2015, 25, 2230–2236 CrossRef CAS.
- G. H. Ahn, M. Amani, H. Rasool, D.-H. Lien, J. P. Mastandrea, J. W. Ager III, M. Dubey, D. C. Chrzan, A. M. Minor and A. Javey, Nat. Commun., 2017, 8, 1–8 CrossRef CAS PubMed.
- Z. Dai, L. Liu and Z. Zhang, Adv. Mater., 2019, 31, 1805417 CrossRef CAS PubMed.
- Y. Li, K.-A. N. Duerloo and E. J. Reed, Nano Lett., 2014, 14, 4299–4305 CrossRef CAS PubMed.
- K. S. Kim, Y. Zhao, H. Jang, S. Y. Lee, J. M. Kim, K. S. Kim, J.-H. Ahn, P. Kim, J.-Y. Choi and B. H. Hong, Nature, 2009, 457, 706–710 CrossRef CAS PubMed.
- C. Chen and J. Hone, Proc. IEEE, 2013, 101, 1766–1779 CAS.
- W. Wu, L. Wang, Y. Li, F. Zhang, L. Lin, S. Niu, D. Chenet, X. Zhang, Y. Hao and T. F. Heinz, Nature, 2014, 514, 470–474 CrossRef CAS PubMed.
- H. Zhu, Y. Wang, J. Xiao, M. Liu, S. Xiong, Z. J. Wong, Z. Ye, Y. Ye, X. Yin and X. Zhang, Nat. Nanotechnol., 2015, 10, 151 CrossRef CAS PubMed.
- R. Hinchet, U. Khan, C. Falconi and S.-W. Kim, Mater. Today, 2018, 21, 611–630 CrossRef CAS.
- J. Zhang and S. Meguid, Semicond. Sci. Technol., 2017, 32, 043006 CrossRef.
- Best research-cell efficiencies chart, NREL, https://www.nrel.gov/pv/cell-efficiency.html.
- G. Grancini and M. K. Nazeeruddin, Nat. Rev. Mater., 2019, 4, 4–22 CrossRef CAS.
- N.-G. Park, J. Phys. Chem. Lett., 2013, 4, 2423–2429 CrossRef CAS.
- J. Huang, Y. Yuan, Y. Shao and Y. Yan, Nat. Rev. Mater., 2017, 2, 1–19 Search PubMed.
- Y. Jiao, L. Zhou, F. Ma, G. Gao, L. Kou, J. Bell, S. Sanvito and A. Du, ACS Appl. Mater. Interfaces, 2016, 8, 5385–5392 CrossRef CAS PubMed.
- C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385–388 CrossRef CAS PubMed.
- H. Şahin, S. Cahangirov, M. Topsakal, E. Bekaroglu, E. Akturk, R. T. Senger and S. Ciraci, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 155453 CrossRef.
- M. Ashton, J. Paul, S. B. Sinnott and R. G. Hennig, Phys. Rev. Lett., 2017, 118, 106101 CrossRef PubMed.
- B. C. Revard, W. W. Tipton, A. Yesypenko and R. G. Hennig, Phys. Rev. B, 2016, 93, 054117 CrossRef.
- H. L. Zhuang, A. K. Singh and R. G. Hennig, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 165415 CrossRef.
- A. K. Singh, B. C. Revard, R. Ramanathan, M. Ashton, F. Tavazza and R. G. Hennig, Phys. Rev. B, 2017, 95, 155426 CrossRef.
- Y. Ding, Y. Wang, J. Ni, L. Shi, S. Shi and W. Tang, Phys. B, 2011, 406, 2254–2260 CrossRef CAS.
- D. Hou and T. Yang, Phys. Chem. Chem. Phys., 2018, 20, 11053–11066 RSC.
- D. W. Brenner, O. A. Shenderova, J. A. Harrison, S. J. Stuart, B. Ni and S. B. Sinnott, J. Phys.: Condens. Matter, 2002, 14, 783 CrossRef CAS.
- A. P. Thompson, S. J. Plimpton and W. Mattson, J. Chem. Phys., 2009, 131, 154107 CrossRef PubMed.
- L. Miao, J. Wu, J. Jiang and P. Liang, J. Phys. Chem. C, 2013, 117, 23–27 CrossRef CAS.
- C. Li and T.-W. Chou, Int. J. Solids Struct., 2003, 40, 2487–2499 CrossRef.
- A. K. Rappé, C. J. Casewit, K. Colwell, W. A. Goddard III and W. M. Skiff, J. Am. Chem. Soc., 1992, 114, 10024–10035 CrossRef.
- B. R. Gelin, Molecular modeling of polymer structures and properties, Hanser Publishers, 1994 Search PubMed.
- R. Rasuli and M. Ahadian, Nanotechnology, 2010, 21, 185503 CrossRef CAS PubMed.
- M. Asadpour, S. Malakpour, M. Faghihnasiri and B. Taghipour, Solid State Commun., 2015, 212, 46–52 CrossRef CAS.
- F. Scarpa, R. Chowdhury and S. Adhikari, Phys. Lett. A, 2011, 375, 2071–2074 CrossRef CAS.
- Q. Peng, Z. Chen and S. De, Mech. Adv. Mater. Struct., 2015, 22, 717–721 CrossRef CAS.
- M. Mirnezhad, R. Ansari, M. Seifi, H. Rouhi and M. Faghihnasiri, Solid State Commun., 2012, 152, 842–845 CrossRef CAS.
- K. Li, N. Li, N. Yan, T. Wang, Y. Zhang, Q. Song and H. Li, Appl. Surf. Sci., 2020, 515, 146028 CrossRef CAS.
- F. Memarian, A. Fereidoon and M. D. Ganji, Superlattices Microstruct., 2015, 85, 348–356 CrossRef CAS.
- K. N. Kudin, G. E. Scuseria and B. I. Yakobson, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 235406 CrossRef.
- H. Liu, A. T. Neal, Z. Zhu, Z. Luo, X. Xu, D. Tománek and P. D. Ye, ACS Nano, 2014, 8, 4033–4041 CrossRef CAS PubMed.
- X. Qian, J. Liu, L. Fu and J. Li, Science, 2014, 346, 1344–1347 CrossRef CAS PubMed.
- H. L. Zhuang, M. D. Johannes, A. K. Singh and R. G. Hennig, Phys. Rev. B, 2017, 96, 165305 CrossRef.
- Z. Zhu and D. Tománek, Phys. Rev. Lett., 2014, 112, 176802 CrossRef PubMed.
- J. Guan, Z. Zhu and D. Tománek, ACS Nano, 2014, 8, 12763–12768 CrossRef CAS PubMed.
- G. Wang, R. Pandey and S. P. Karna, ACS Appl. Mater. Interfaces, 2015, 7, 11490–11496 CrossRef CAS PubMed.
- E. D. Sandoval, S. Hajinazar and A. N. Kolmogorov, Phys. Rev. B, 2016, 94, 094105 CrossRef.
- Y. Zhao, S. Zeng and J. Ni, Phys. Rev. B, 2016, 93, 014502 CrossRef.
- P. Li and W. Luo, Sci. Rep., 2016, 6, 25423 CrossRef CAS PubMed.
- F. Matusalem, M. Marques, L. K. Teles and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 045436 CrossRef.
- S. I. Yengejeh, W. Wen and Y. Wang, Front. Phys., 2021, 16, 1–7 Search PubMed.
- P. Johari and V. B. Shenoy, ACS Nano, 2012, 6, 5449–5456 CrossRef CAS PubMed.
- D. Chimene, D. L. Alge and A. K. Gaharwar, Adv. Mater., 2015, 27, 7261–7284 CrossRef CAS PubMed.
- D. Sarkar, X. Xie, J. Kang, H. Zhang, W. Liu, J. Navarrete, M. Moskovits and K. Banerjee, Nano Lett., 2015, 15, 2852–2862 CrossRef CAS PubMed.
- V. Sorkin, H. Pan, H. Shi, S. Quek and Y. Zhang, Crit. Rev. Solid State Mater. Sci., 2014, 39, 319–367 CrossRef CAS.
- F. Wang, Z. Wang, L. Yin, R. Cheng, J. Wang, Y. Wen, T. A. Shifa, F. Wang, Y. Zhang and X. Zhan, Chem. Soc. Rev., 2018, 47, 6296–6341 RSC.
- S. Bertolazzi, M. Gobbi, Y. Zhao, C. Backes and P. Samorì, Chem. Soc. Rev., 2018, 47, 6845–6888 RSC.
- S. Bertolazzi, J. Brivio and A. Kis, ACS Nano, 2011, 5, 9703–9709 CrossRef CAS PubMed.
- A. Castellanos-Gomez, M. Poot, G. A. Steele, H. S. Van Der Zant, N. Agraït and G. Rubio-Bollinger, Adv. Mater., 2012, 24, 772–775 CrossRef CAS PubMed.
- S. I. Yengejeh, J. Liu, S. A. Kazemi, W. Wen and Y. Wang, ACS Omega, 2020, 5, 5994 CrossRef PubMed.
- K.-A. N. Duerloo, M. T. Ong and E. J. Reed, J. Phys. Chem. Lett., 2012, 3, 2871–2876 CrossRef CAS.
- J. Luo, X. Tao, J. Zhang, Y. Xia, H. Huang, L. Zhang, Y. Gan, C. Liang and W. Zhang, ACS Nano, 2016, 10, 2491–2499 CrossRef CAS PubMed.
- M. R. Lukatskaya, O. Mashtalir, C. E. Ren, Y. Dall'Agnese, P. Rozier, P. L. Taberna, M. Naguib, P. Simon, M. W. Barsoum and Y. Gogotsi, Science, 2013, 341, 1502–1505 CrossRef CAS PubMed.
- Y. Xie, M. Naguib, V. N. Mochalin, M. W. Barsoum, Y. Gogotsi, X. Yu, K.-W. Nam, X.-Q. Yang, A. I. Kolesnikov and P. R. Kent, J. Am. Chem. Soc., 2014, 136, 6385–6394 CrossRef CAS PubMed.
- Y. Zhong, X. Xia, F. Shi, J. Zhan, J. Tu and H. J. Fan, Adv. Sci., 2016, 3, 1500286 CrossRef PubMed.
- F. Shahzad, M. Alhabeb, C. B. Hatter, B. Anasori, S. M. Hong, C. M. Koo and Y. Gogotsi, Science, 2016, 353, 1137–1140 CrossRef CAS PubMed.
- M. R. Lukatskaya, S. Kota, Z. Lin, M.-Q. Zhao, N. Shpigel, M. D. Levi, J. Halim, P.-L. Taberna, M. W. Barsoum and P. Simon, Nat. Energy, 2017, 2, 17105 CrossRef CAS.
- J. Liu, H. B. Zhang, R. Sun, Y. Liu, Z. Liu, A. Zhou and Z. Z. Yu, Adv. Mater., 2017, 29, 1702367 CrossRef PubMed.
- M.-S. Cao, Y.-Z. Cai, P. He, J.-C. Shu, W.-Q. Cao and J. Yuan, Chem. Eng. J., 2019, 359, 1265–1302 CrossRef CAS.
- R. Sun, H. B. Zhang, J. Liu, X. Xie, R. Yang, Y. Li, S. Hong and Z. Z. Yu, Adv. Funct. Mater., 2017, 27, 1702807 CrossRef.
- W. Feng, H. Luo, Y. Wang, S. Zeng, Y. Tan, L. Deng, X. Zhou, H. Zhang and S. Peng, Sci. Rep., 2019, 9, 1–10 CAS.
- V. M. H. Ng, H. Huang, K. Zhou, P. S. Lee, W. Que, J. Z. Xu and L. B. Kong, J. Mater. Chem. A, 2017, 5, 3039–3068 RSC.
- Z. Ling, C. E. Ren, M.-Q. Zhao, J. Yang, J. M. Giammarco, J. Qiu, M. W. Barsoum and Y. Gogotsi, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 16676–16681 CrossRef CAS PubMed.
- J. Low, L. Zhang, T. Tong, B. Shen and J. Yu, J. Catal., 2018, 361, 255–266 CrossRef CAS.
- J. Peng, X. Chen, W.-J. Ong, X. Zhao and N. Li, Chem, 2019, 5, 18–50 CAS.
- G. Gao, A. P. O'Mullane and A. Du, ACS Catal., 2017, 7, 494–500 CrossRef CAS.
- J. Zhu, E. Ha, G. Zhao, Y. Zhou, D. Huang, G. Yue, L. Hu, N. Sun, Y. Wang and L. Y. S. Lee, Coord. Chem. Rev., 2017, 352, 306–327 CrossRef CAS.
- D. Zhao, Z. Chen, W. Yang, S. Liu, X. Zhang, Y. Yu, W.-C. Cheong, L. Zheng, F. Ren and G. Ying, J. Am. Chem. Soc., 2019, 141, 4086–4093 CrossRef CAS PubMed.
- Z. Li and Y. Wu, Small, 2019, 15, 1804736 CrossRef PubMed.
- Y. Ma, N. Liu, L. Li, X. Hu, Z. Zou, J. Wang, S. Luo and Y. Gao, Nat. Commun., 2017, 8, 1207 CrossRef PubMed.
- S. J. Kim, H.-J. Koh, C. E. Ren, O. Kwon, K. Maleski, S.-Y. Cho, B. Anasori, C.-K. Kim, Y.-K. Choi and J. Kim, ACS Nano, 2018, 12, 986–993 CrossRef CAS PubMed.
- X. Liu, T. Ma, N. Pinna and J. Zhang, Adv. Funct. Mater., 2017, 27, 1702168 CrossRef.
- Y.-Z. Zhang, K. H. Lee, D. H. Anjum, R. Sougrat, Q. Jiang, H. Kim and H. N. Alshareef, Sci. Adv., 2018, 4, eaat0098 CrossRef PubMed.
- K. S. Kumar, N. Choudhary, Y. Jung and J. Thomas, ACS Energy Lett., 2018, 3, 482–495 CrossRef CAS.
- Z. Fu, N. Wang, D. Legut, C. Si, Q. Zhang, S. Du, T. C. Germann, J. S. Francisco and R. Zhang, Chem. Rev., 2019, 119, 11980–12031 CrossRef CAS PubMed.
- A. Lipatov, H. Lu, M. Alhabeb, B. Anasori, A. Gruverman, Y. Gogotsi and A. Sinitskii, Sci. Adv., 2018, 4, eaat0491 CrossRef PubMed.
- A. Lipatov, M. Alhabeb, H. Lu, S. Zhao, M. J. Loes, N. S. Vorobeva, Y. Dall'Agnese, Y. Gao, A. Gruverman and Y. Gogotsi, Adv. Electron. Mater., 2020, 6, 1901382 CrossRef CAS.
- K. Luo, X. H. Zha, Y. Zhou, Q. Huang, S. Zhou and S. Du, Int. J. Quantum Chem., 2020, e26409 CAS.
- S. A. Kazemi and Y. Wang, J. Phys.: Condens. Matter, 2019, 32, 11LT01 CrossRef PubMed.
- Z. Fu, Q. Zhang, D. Legut, C. Si, T. Germann, T. Lookman, S. Du, J. Francisco and R. Zhang, Phys. Rev. B, 2016, 94, 104103 CrossRef.
- Y. Jiao, F. Ma, G. Gao, J. Bell, T. Frauenheim and A. Du, J. Phys. Chem. Lett., 2015, 6, 2682–2687 CrossRef CAS PubMed.
- P. Lv, G. Tang, C. Yang, J. Deng, Y. Liu, X. Wang, X. Wang and J. Hong, 2D Mater., 2018, 5, 045026 CrossRef CAS.
- T.-Y. Lü, H. Feng, Y. Zhang, Y. Lu and J.-C. Zheng, Comput. Mater. Sci., 2017, 139, 341–346 CrossRef.
- P. Aghdasi, R. Ansari, S. Rouhi, S. Yousefi, M. Goli and H. Soleimani, Phys. B, 2021, 600, 412603 CrossRef CAS.
- I. V. Lebedeva, A. S. Minkin, A. M. Popov and A. A. Knizhnik, Phys. E, 2019, 108, 326–338 CrossRef CAS.
- B. Javvaji, P. R. Budarapu, V. Sutrakar, D. R. Mahapatra, M. Paggi, G. Zi and T. Rabczuk, Comput. Mater. Sci., 2016, 125, 319–327 CrossRef CAS.
- A. Gamboa, G. L. Vignoles and J.-M. Leyssale, Carbon, 2015, 89, 176–187 CrossRef CAS.
- A. Agius Anastasi, K. Ritos, G. Cassar and M. K. Borg, Mol. Simul., 2016, 42, 1502–1511 CrossRef CAS.
- P. Ying, J. Zhang and Z. Zhong, J. Appl. Phys., 2019, 126, 215105 CrossRef.
- J. Zhao, J.-W. Jiang and T. Rabczuk, Appl. Phys. Lett., 2013, 103, 231913 CrossRef.
- M. Arroyo and T. Belytschko, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 115415 CrossRef.
- J. W. Jiang, Z. Qi, H. S. Park and T. Rabczuk, Nanotechnology, 2013, 24, 435705 CrossRef PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- J.-W. Jiang, Acta Mech. Solida Sin., 2019, 32, 17–28 CrossRef.
- Y. I. Jhon, Y. T. Byun, J. H. Lee and Y. M. Jhon, Appl. Surf. Sci., 2020, 532, 147380 CrossRef CAS.
- X. Chang, N. Yin and H. Li, Mater. Res. Express, 2019, 6, 115043 CrossRef CAS.
- V. Vijayaraghavan and L. Zhang, Comput. Mater. Sci., 2019, 159, 376–384 CrossRef CAS.
- E. M. Siriwardane, I. Demiroglu, C. Sevik, F. M. Peeters and D. Çakır, J. Phys. Chem. C, 2020, 124, 21293–21304 CrossRef CAS.
- F. Cellini, F. Lavini, E. Chen, A. Bongiorno, F. Popovic, R. L. Hartman, R. Dingreville and E. Riedo, Adv. Sci., 2021, 8, 2002541 CrossRef CAS PubMed.
- Z. Yang, J. Zhao and N. Wei, Appl. Phys. Lett., 2015, 107, 023107 CrossRef.
- L.-B. Luo, C. Xie, X.-H. Wang, Y.-Q. Yu, C.-Y. Wu, H. Hu, K.-Y. Zhou, X.-W. Zhang and J.-S. Jie, Nano Energy, 2014, 9, 112–120 CrossRef CAS.
- X.-Y. Zhang, A. Hu, T. Zhang, W. Lei, X.-J. Xue, Y. Zhou and W. W. Duley, ACS Nano, 2011, 5, 9082–9092 CrossRef CAS PubMed.
- F. Scarpa, S. Adhikari and A. S. Phani, Nanotechnology, 2009, 20, 065709 CrossRef CAS PubMed.
- K. Nakanishi, D. Labonte, T. Cebo, V. P. Veigang-Radulescu, Y. Fan, B. Brennan, A. J. Pollard, S. Hofmann and N. A. Fleck, Acta Mater., 2020, 201, 254–265 CrossRef CAS.
- Y. Li, C. Yu, Y. Gan, P. Jiang, J. Yu, Y. Ou, D.-F. Zou, C. Huang, J. Wang and T. Jia, npj Comput. Mater., 2018, 4, 1–8 CrossRef.
- R. C. Cooper, C. Lee, C. A. Marianetti, X. Wei, J. Hone and J. W. Kysar, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 079901 CrossRef.
- N. Khandoker, S. Islam and Y. Hiung, IOP Conf. Ser.: Mater. Sci. Eng., 2017, 1, 012057 Search PubMed.
- D. Damasceno, R. Rajapakse, E. Mesquita and R. Pavanello, Acta Mech., 2020, 231, 3387–3404 CrossRef.
- L. Zhang, N. Jiang, P. He and S.-J. Zhong, J. Mater. Sci.: Mater. Electron., 2020, 31, 21758–21766 CrossRef CAS.
- S. I. Yengejeh, S. A. Kazemi and A. Öchsner, J. Comput. Theor. Nanosci., 2016, 13, 9232–9238 CrossRef CAS.
- X. Wei, B. Fragneaud, C. A. Marianetti and J. W. Kysar, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 205407 CrossRef.
- G. Kalosakas, N. Lathiotakis, C. Galiotis and K. Papagelis, J. Appl. Phys., 2013, 113, 134307 CrossRef.
- B. Mortazavi, A. Ostadhossein, T. Rabczuk and A. C. Van Duin, Phys. Chem. Chem. Phys., 2016, 18, 23695–23701 RSC.
- G. Plummer, B. Anasori, Y. Gogotsi and G. J. Tucker, Comput. Mater. Sci., 2019, 157, 168–174 CrossRef CAS.
- Y. Li, S. Huang, C. Wei, C. Wu and V. N. Mochalin, Nat. Commun., 2019, 10, 49 CrossRef PubMed.
- S. I. Yengejeh, S. A. Kazemi, O. Ivasenko and A. Oechsner, Solid State Commun., 2016, 231, 36–42 CrossRef.
- F. A. Faber, L. Hutchison, B. Huang, J. Gilmer, S. S. Schoenholz, G. E. Dahl, O. Vinyals, S. Kearnes, P. F. Riley and O. A. Von Lilienfeld, J. Chem. Theory Comput., 2017, 13, 5255–5264 CrossRef CAS PubMed.
- Z. W. Ulissi, A. J. Medford, T. Bligaard and J. K. Nørskov, Nat. Commun., 2017, 8, 1–7 CrossRef PubMed.
- G. R. Schleder, A. C. Padilha, C. M. Acosta, M. Costa and A. Fazzio, JPhys Mater., 2019, 2, 032001 CrossRef CAS.
- D. Dragoni, T. D. Daff, G. Csányi and N. Marzari, Phys. Rev. Mater., 2018, 2, 013808 CrossRef.
- C. Wong, M. Annamalai, Z. Wang and M. Palaniapan, J. Micromech. Microeng., 2010, 20, 115029 CrossRef.
- Z. Shokrieh, M. Seifi and M. Shokrieh, Mech. Mater., 2017, 115, 16–21 CrossRef.
- C. A. Salvador, B. F. Zornio and C. R. Miranda, ACS Appl. Mater. Interfaces, 2020, 12, 56850–56861 CrossRef CAS PubMed.
- E. M. Siriwardane, R. P. Joshi, N. Kumar and D. Çakır, ACS Appl. Mater. Interfaces, 2020, 12, 29424–29431 CAS.
| This journal is © The Royal Society of Chemistry 2021 |