Open Access Article
Open Access ArticleFast 3D-lithium-ion diffusion and high electronic conductivity of Li2MnSiO4 surfaces for rechargeable lithium-ion batteries
Gamachis Sakata Gurmesa ade,
Natei Ermias Benti
ade,
Natei Ermias Benti f,
Mesfin Diro Chaka
f,
Mesfin Diro Chaka g,
Girum Ayalneh Tiruye
g,
Girum Ayalneh Tiruye c,
Qinfang Zhang
c,
Qinfang Zhang d,
Yedilfana Setarge Mekonnen
d,
Yedilfana Setarge Mekonnen *b and
Chernet Amente Geffe*a
*b and
Chernet Amente Geffe*a
aDepartment of Physics, College of Natural and Computational Sciences, Addis Ababa University, P. O. Box 1176, Addis Ababa, Ethiopia. E-mail: chernet.amente@aau.edu.et
bCenter for Environmental Science, College of Natural and Computational Sciences, Addis Ababa University, P. O. Box 1176, Addis Ababa, Ethiopia. E-mail: yedilfana.setarge@aau.edu.et
cMaterials Science Program/Department of Chemistry, College of Natural and Computational Sciences, Addis Ababa University, P. O. Box 1176, Addis Ababa, Ethiopia
dSchool of Materials Science and Engineering, Yancheng Institute of Technology, Yancheng 224051, China. E-mail: qfangzhang@gmail.com
eDepartment of Physics, College of Natural and Computational Sciences, Mettu University, P. O. Box 318, Mettu, Ethiopia
fDepartment of Physics, College of Natural and Computational Science, Wolaita Sodo University, P. O. Box 138, Wolaita Sodo, Ethiopia
gComputational Data Science Program, College of Natural and Computational Sciences, Addis Ababa University, P. O. Box 1176, Addis Ababa, Ethiopia
First published on 5th March 2021
Abstract
High theoretical capacity, high thermal stability, the low cost of production, abundance, and environmental friendliness are among the potential attractiveness of Li2MnSiO4 as a positive electrode (cathode) material for rechargeable lithium-ion batteries. However, the experimental results indicated poor electrochemical performance in its bulk phase due to high intrinsic charge transfer resistance and capacity fading during cycling, which limit its large-scale commercial applications. Herein, we explore the surface stability and various lithium-ion diffusion pathways of Li2MnSiO4 surfaces using the density functional theory (DFT) framework. Results revealed that the stability of selected surfaces is in the following order: (210) > (001) > (010) > (100). Moreover, the Wulff-constructed equilibrium shape revealed that the Li2MnSiO4 (001) surface is the most predominant facet, and thus, preferentially exposed to electrochemical activities. The Hubbard-corrected DFT (DFT + U, with U = 3 eV) results indicated that the bulk insulator with a wide band gap (Eg = 3.42 eV) changed into narrow electronic (Eg = 0.6 eV) when it comes to the Li2MnSiO4 (001) surface. Moreover, the nudged elastic band analysis shows that surface diffusion along the (001) channel was found to be unlimited and fast in all three dimensions with more than 12-order-of-magnitude enhancements compared with the bulk system. These findings suggest that the capacity limitation and poor electrochemical performance that arise from limited electronic and ionic conductivity in the bulk system could be remarkably improved on the surfaces of the Li2MnSiO4 cathode material for rechargeable lithium-ion batteries.
1. Introduction
There is growing interest in the large-scale application of dilithium orthosilicate (Li2MSiO4, M = Fe, Mn, Co, and Ni) cathode materials1–3 for rechargeable lithium-ion batteries (LIB) like that of recent developments in anode materials.4 These are because of their cyclability, thermal stability and polymorphism possibilities over a wide range of temperatures just to mention a few. As a promising cathode material for the next-generation rechargeable LIB, Li2MSiO4 cathode materials are extensively investigated via both experimental and computational approaches. The designed LIBs from such cathode materials are widely used for portable electronic devices and also for sustainable transportation including electric vehicles (EVs) and plug-in hybrid electric vehicles (PHEVs). They also have significant potential to mitigate the intermittency of renewable energy sources such as solar, wind, and hydroelectric power.5,6Arroyo Dambablo et al.7 computationally studied the effect of the different polyoxyanions composed of (XO4)n−, where X = Ge, Si, As, Sb, and P on Li2MXO4 materials based on the relation between the Li+ deintercalation voltage and their corresponding electronegativity. Their findings indicated the best fit for Li2MnSiO4 materials. However, Li+ deintercalation voltages for Co and Ni silicates were found to be too high for the current electrolyte window. Experimental studies8,9 also confirmed that Li2CoSiO4 and Li2NiSiO4 have low capacities and poor reversibility. Li2MSiO4 (M = Mn and Fe) are also highly preferable LIB cathode materials compared to other polyanion compounds such as LiMPO4 (M = Fe, Mn, and Co), which are limited to only a single Li+ insertion and extraction per formula unit.10,11 Moreover, other layered transition metal oxide cathode materials (for example, Li1/3Mn1/3Co1/3O2) are also toxic and costly.12
Previous studies have demonstrated that the method used to synthesize Li2MnSiO4 and other polyanion cathode materials also significantly influences their crystal structures, and so does their ionic conductivity.1,3,13 One of the strategies to improve the electrochemical performance of lithium-ion batteries with Li2MnSiO4 is the optimization of the particle size and morphology. Particularly, the rate of electrochemical performance increases with the reduction in the particle size of Li2MnSiO4. This is because the porous structure significantly shortens the diffusion time of Li+ in Li2MnSiO4 cathode materials. Therefore, since the orthorhombic structure of Li2MnSiO4 has smaller particle size than that of the monoclinic structure, it will have better Li+ diffusion, resulting in better electrochemical performance.1,3,13–15 Polymorphs of Li2MSiO4 tetrahedral structures are well known to be classified into low- and high-temperature forms, which differ in the distribution of cations within tetrahedral sites of a hexagonal close-packed (HCP)-based arrangement of oxygen. According to the literature, five different structures were observed with Li2FeSiO4,16–19 three as-synthesized (two are orthorhombic, Pmnb and Pmn21; one is monoclinic, P21/n) and two cycled phases (Pmn21 cycled and P21/n cycled). Similarly, multiple phases have been reported for Li2MnSiO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2,13,20,21 with two orthorhombic (Pmn21 and Pmnb) and one monoclinic (P21/n) symmetries; Li2CoSiO4
2,13,20,21 with two orthorhombic (Pmn21 and Pmnb) and one monoclinic (P21/n) symmetries; Li2CoSiO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 22–24 has two orthorhombic (Pnb21 and Pmn21) and one monoclinic (P21/n) symmetries, while Li2NiSiO4
22–24 has two orthorhombic (Pnb21 and Pmn21) and one monoclinic (P21/n) symmetries, while Li2NiSiO4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3,25,26 has one crystal symmetry.
3,25,26 has one crystal symmetry.
The structural, electronic and electrochemical properties of Li2MSiO4 depend on the distributions of M. The density functional theory (DFT) predicted some parameter variations, for instance, cell, volume and voltage intercalations between intermediate phases (Li2MSiO4, LiMSiO4 and MSiO4) based on their crystal symmetry.27 According to their report, Li2MnSiO4 in the orthorhombic symmetry with the Pmn21 space group was found to be the most stable structure. Due to the double reversible redox state of Mn ions (Mn2+/Mn3+ and Mn3+/Mn4+) within the electrochemical stability window of LIB common electrolytes,28–31 its theoretical energy density reaches as high as 333 mA h g−1.32 Li2MnSiO4 also has a higher operating voltage of 4.8 V against Li+/Li electrodes with stability of organic electrolytes.28,30,31 Moreover, the Mn4+ is more accessible than Fe4+ and Co4+.33,34 However, the electrochemical performance of Li2MnSiO4 has many drawbacks such as the very low Li+ diffusion coefficient estimated from 10−14 to 10−16 cm2 s−1 and electronic conductivity from 10−12 to 10−16 S cm−1 at room temperature35,36 limiting its electrochemical performance. Unlike other polyanion cathode materials, for instance, LiMPO4,10 bulk Li2MnSiO4 supports two-dimensional Li+ diffusion in its orthorhombic (Pmn21) symmetry.20,37,38
The development of battery nanoelectrodes plays a vital role in achieving higher ionic and electronic transport. These are possible in one way by maximizing fast lithium diffusion pathways and in another way by narrowing electronic bandgaps unlike their corresponding bulk insulator because of the quantum confinement effect.39–41
Previous studies have demonstrated the development of Li2MnSiO4 cathode materials at nanoscale13,18,22 with improved charge/discharge kinetics. For instance, a nanostructured Li2MnSiO4 material was synthesized42 by an easy and fast urea combustion method, which showed an extraordinarily intrinsic electronic conductivity of 4 ± 10−8 S cm−1. Ultrathin nanosheets of Li2MnSiO4 (M = Mn/Fe)31 were also prepared by a rapid one-pot synthesis method using a mixed solvent of aqueous ethanol, and the results revealed a superior energy density of 340 mA h g−1. Very recently, Ding et al. have reported the (100), (010), (001), and (210) facets as stable surface structures of Li2MnSiO4 using DFT calculations combined with experimental characterizations.43 Interestingly, they also managed to successfully synthesize elongated, hexagonal prism-shaped Li2MnSiO4@C nanoplates with the preferentially exposed (001) and (210) facets. The initial discharge capacity was estimated as high as 326 mA h g−1 that corresponds to 1.98 Li+ stored PFU of Li2MnSiO4, while the charge specific capacity was found to be 367.6 mA h g−1, which is higher than that of bulk Li2MnSiO4 (333 mA h g−1) determined by a galvanostatic charge–discharge method. Although the Li+ diffusion rate (1.0043 × 10−13 cm−2 s−1) for Li2MnSiO4@C nanoplates was calculated, the kinetic pathways, Li+ diffusion dimensionalities and electronic structures of preferentially exposed surfaces were not exhaustively emphasized. If the two-dimensional Li+ diffusion and electronic insulating properties of bulk Li2MnSiO4 enhanced to fast three-dimensional Li+ diffusion and electronic conductive properties, higher electrochemical performances could be achieved in Li2MnSiO4 cathode materials for LIBs. The DFT calculation is also a very powerful technique to predict metal–ion and metal–air batteries at bulk, surface, and interface structures emphasizing on the charge (ionic, electronic, and polaronic) transport mechanisms, thermodynamic stability, and their catalytic effect.15,20,35,44–49
Herein, we employed the DFT + U analysis to investigate the electronic properties, structural stability and lithium-ion diffusion pathways in the bulk and selected surface structures of the Li2MnSiO4 cathode material in the rechargeable lithium-ion batteries. Detail analysis will also be given to rationalize the reason behind the superior surface conduction observed on the Li2MnSiO4 (001) surface unlike the previously reported poor bulk Li2MnSiO4 conductivity.
2. Methodology
A. Bulk crystal structure
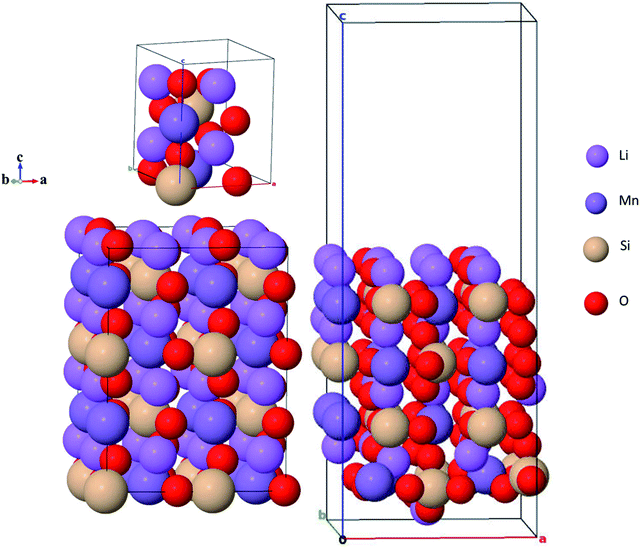
Li2MnSiO4 crystallizes in two main crystal systems: one is the orthorhombic symmetry of the Pmn21 and Pmnb21,27,35,50 space groups at low temperatures and the other is the monoclinic symmetry with the Pn51 and P21/n52 space groups at high temperatures. These various polymorphs of Li2MnSiO4 showed different electrochemical performances due to the variety of Li+ diffusion pathways through their crystal lattices. Among the four polymorphs, the orthorhombic symmetry with the Pmn21 space group is widely studied due to its high thermal stability, although it supports two-dimensional lithium-ion diffusion whereas the monoclinic symmetry is less stable but supports three-dimensional lithium diffusion.37,38 The unit cell of the Pmn21 crystal structure was retrieved from the Material Project open database source (see Fig. 1).53 In the unit cell, the Pmn21 crystal structure has 16 atoms: Li = 4, Mn = 2, Si = 2 and O = 8 atoms. For the present calculations, we construct a 2 × 2 × 2 supercell, comprising 128 atoms: Li = 32, Mn = 16, Si = 16 and O = 64 atoms. Fig. 1(b) shows the supercell of the Li2MnSiO4 crystal structure, while Fig. 1(c) is the corresponding (001) crystal structure to be most emphasized in the subsequent sections. Observing Fig. 1(a) and (b), all the cations are arranged in the tetrahedral complexes of LiO4, MnO4, and SiO4, in which the structure may collapse as hexagonally closely packed oxygen arrays are partially distorted by the Jahn–Teller effect.54B. Surface crystal structures
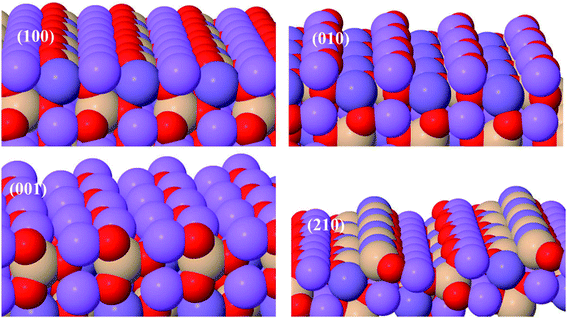
Li2MnSiO4 surface structures were constructed from the bulk supercell with Li–O and Mn–Si–O terminations, especially those experimentally confirmed,43 namely, (210), (001), (010), and (100) surfaces, were emphasized (Fig. 2). The number of atoms in all surfaces are the same (128) with Li = 32, Mn = 16, Si = 16 and O = 64 atoms. All the Li–O terminated Li2MnSiO4 surface structures, namely, (100), (010), and (001) facets are fixed with more than 14 Å vacuum space to get the ground-state energy. The Mn–Si–O terminated Li2MnSiO4 (210) surface structure is the thinnest with 5.506 Å among all the surface structures, which is indicative of the inconvenience as an electrochemically active surface, as it is predominantly covered by the other facets.C. Computational details
Grid-based projector augmented wave method (GPAW) code was implemented to solve electronic-structure problems with the DFT55,56 framework. The exchange correlations were examined with generalized gradient approximations (GGA) by the Perdew–Burke–Ernzerhof (PBE) functional.57 The core electrons were treated by the projected-augmented wave (PAW) method.58 GPAW uses a real space basis set with grid points. The ground-state energies are calculated using grid space fixed at 0.18. With a Monkhorst–Pack grids 2 × 2 × 2 for bulk, 2 × 2 × 1 for the (001) and (210) surfaces, and 2 × 1 × 2 for the (010) surface and 1 × 2 × 2 for the (100) surface. Li2MnSiO4 is found to be antiferromagnetic in agreement with the previous reports,13,27,32 and thus, the magnetic moment for Mn ions is set to be 4. All the structures were relaxed to their ground-state levels by employing spin-polarized calculations until the Hellmann–Feynman forces are less than 0.03 eV A−1. GGA (PBE) often leads to significant deviations from experimental results, in particular the band gap (Eg), due to the incomplete cancellation of the electronic self-interaction energy (SIE) for systems exhibiting a strong localization of the d and/or f-orbital electrons, for instance, Mn(3d) in Li2MnSiO4. Previous studies solved this problem59–61 by employing the appropriate Hubbard correction. For example, U = 3.9 eV was used for Mn(3d), which is not always the case as it also depends on the chemical element incorporated within a particular compound.59–62 With this consideration, Eg was calculated by varying U-values from 1 to 6 eV with an interval of 0.5. U = 3 eV was found to provide the appropriate Eg and used throughout the calculations. Surface free energies of the selected Li2MnSiO4 surface structures were determined using the surface energy equation (eqn (1)):
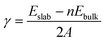 | (1) |
The minimum energy pathway (MEP) and the activation barriers for Li+ diffusion in Li2MnSiO4 were calculated by the climbing-image nudged elastic band (CI-NEB) method.63 A 2 × 2 × 2 supercell was considered throughout the calculations. For each CI-NEB calculation, five intermediate images were constructed to interpolate the initial and final states along the Li+ diffusion path. To calculate the energy barrier (Eb), all images and other ions in the supercell were also allowed to relax to its equilibrium position. From the calculated Eb, the Li+ diffusion rate (r) and Li+ diffusion coefficient (D) were calculated using the Arrhenius equation, D = a2r and r = νe−Eb/kBT,45 where a is the minimum jump length of the Li atom from one site to another along the facile channel, e is the electronic charge, ν is the hopping rate, kB is the Boltzmann constant and T is the temperature. Throughout the present work, ν = 1013 s−1, kB = 8.6173326 × 10−5 eV K−1, and T = 298 K were used.
3. Results and discussion
A. Calculation of surface energies
The structural stability of the selected low index surfaces was identified from the surface free energy calculations by manipulating eqn (1), and the results are summarized in Table 1 and the respective crystal structure facets of Li2MnSiO4 are indicated in Fig. 2. The negative sign indicates that the selected surface structures are stable. Among the facets of Li2MnSiO4, the (210) surface orientation is the most stable surface with a free energy of about −55.6 J m−2.| Orientation | (100) | (010) | (001) | (210) |
|---|---|---|---|---|
| γ (J m−2) | −42.58 | −48.98 | −48.82 | −55.6 |
The results indicate that the identified surfaces are in the low index facet with their relative decreasing order of surface stability as (210) > (010) > (001) > (100), which is in agreement with the recent experiment.43
B. Wulff construction
The Wulff shape for Li2MnSiO4 based on the surface free energies in Table 1 is shown in Fig. 3. The green, red, blue, and yellow colors show that the contribution of 35.64, 24.9, 23.4, and 16.47% of a surface by the (001), (010), (100), and (210) facets is based on the Wulff shape-constructed areal surfaces, respectively. These results indicate that all the Li–O terminated surface structures of Li2MnSiO4 are better than that of Mn–Si–O terminated surface structures, which is the (210) facet.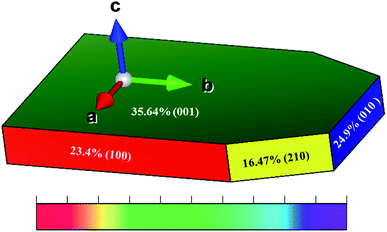 | ||
| Fig. 3 Wulff-constructed equilibrium shape of Li2MnSiO4 based on the calculated relative surface areas and surface free energies. | ||
In contrast to the calculated surface free energy, the Wulff shape illustrates that the areal surface contributions of the (210) and (100) surfaces are relatively minimum with respect to the formation of facets. The majority of the Wulff shape is dominated by the (001) facet, designated by green color in Fig. 3, with intermediate surface stability, hence limiting wide electrochemical kinetics due to the coverage of an electrochemically active surface area of the (210) facet. Therefore, the (001) facet was selected for further analysis because of the higher surface coverage.
C. Bulk and surface electronic structures
Bulk and surface electronic structures were considered to examine the electronic properties and their influence on the overall electrochemical performance of Li2MnSiO4. After relaxations, the total magnetic moments of the bulk and (001) surface structures of anti-ferromagnetic Li2MnSiO4 were calculated to be 80 and 73.54, respectively. The average magnetic moment for the Mn ion in the bulk and (001) surface of Li2MnSiO4 structures were calculated to be 4.43 and 4.17, respectively, slightly decreasing in the surface.The strongly correlated electrons in the case of d-orbital or f-orbitals of transition metal cathode materials need the Hubbard correction (U) due to electron SIE, otherwise underestimate some calculated parameters when compared with the experimental results, for instance, Eg calculated at the DFT (PBE) theory level. Thus, to calculate reasonable Eg values equivalent to experimental results, one needs to add the Hubbard correction, U (eV).59–62 Although it is challenging to fix the specific U-value for a particular d- or f-orbital element, researchers used different U-values without clear-cut reasons especially when the experimental result is not found.
To fix this, we used different U-values from 1 to 6 eV with 0.5 intervals in the GPAW code, as clearly indicated in Table 2. For this work, the calculated Eg values were found to be 3.42 and 0.6 eV for the bulk and (001) surface structures of Li2MnSiO4, respectively. To the best of our knowledge, there is no experimental or calculated Eg value for Li2MnSiO4 using the GPAW code. According to the literature, some reported Eg (eV) values based on the Vienna Ab initio Simulation Package (VASP) code were found for Li2MnSiO4 in the range between 2.21 and 3.44 eV.27,53,64–66 It is obvious that the values of the Hubbard correction used in the VASP code are quite different and higher than the values used in the GPAW code employed in this work. To select the appropriate Eg value for this material, we calculated different Eg values as a function of the Hubbard correction (U-value) about the average Eg reported in previous similar studies, and the results are summarized in Table 2. Accordingly, the U-value of 3 eV is chosen as the appropriate Hubbard correction for both the bulk and surface systems with Eg values of 3.42 and 0.6 eV, respectively.
| U | 0 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Eg | 2.5 | 2.84 | 3 | 3.16 | 3.29 | 3.42 | 3.54 | 3.64 | 3.74 | 3.82 | 3.89 | 3.95 |
| (0) | (0.6) |
Fig. 4 shows the detailed analysis of the electronic projected density of state (PDOS) based on PBE and PBE + U functional for the bulk and (001) surface structures of Li2MnSiO4. Even though Mn(d) and O(p) orbitals are dominant in both cases, as shown in Fig. 4(a) and (c), their contributions are mixed at the PBE functional, i.e. near the Fermi energy level, where the contribution of Mn(d) is more dominant, while O(p) becomes dominating as far away in the higher occupied molecular orbital (HOMO) levels.
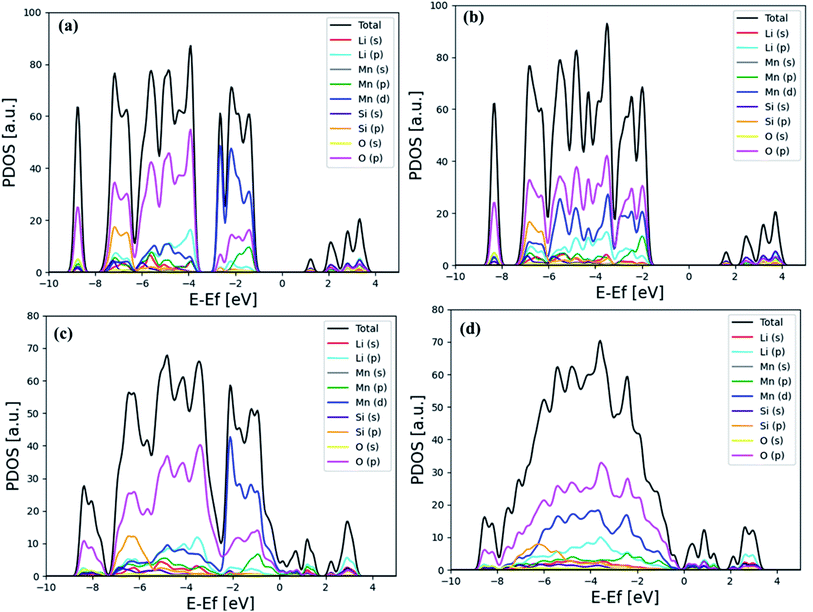 | ||
| Fig. 4 Calculated PDOS indicated for bulk Li2MnSiO4: (a) PBE and (b) PBE + U (at U = 3 eV). Calculated PDOS for the Li2MnSiO4 (001) surface using (c) PBE and (d) PBE + U (at U = 3 eV) functionals. | ||
When the SIE is corrected with the PBE + U functional, the contribution O(p) is more or less uniformly dominant in the lower occupied molecular orbital (LUMO) level. The influence of SIE correction is observed in Fig. 4(b) and (d).
From Fig. 4, it is clearly indicated that O(2p) dominated all the orbitals due to Mn(3d) delocalization, when PBE + U penalty was incorporated in the calculations.
The comparison of dominant spectra PDOS for the bulk and surface is presented in Fig. 5(a) and (b), and it shows that the PDOS of the (001) surface at the Fermi level is more dominant and has exactly metallic properties than the one in the bulk, indicating a higher conductivity as a result of strongly lowering the Eg value of the (001) surface. The calculated Eg value of 0.6 eV in the (001) surface is due to the contribution of other orbitals, as shown in the total density of states (DOS) of Fig. 5(c). Moreover, it should be very clear here that DFT (GGA at PBE) underestimates electronic Eg in the bulk and surface structures of Li2MnSiO4, while DFT + U (PBE + U) calculated Eg in this work is in good agreement with the previous studies.64,65
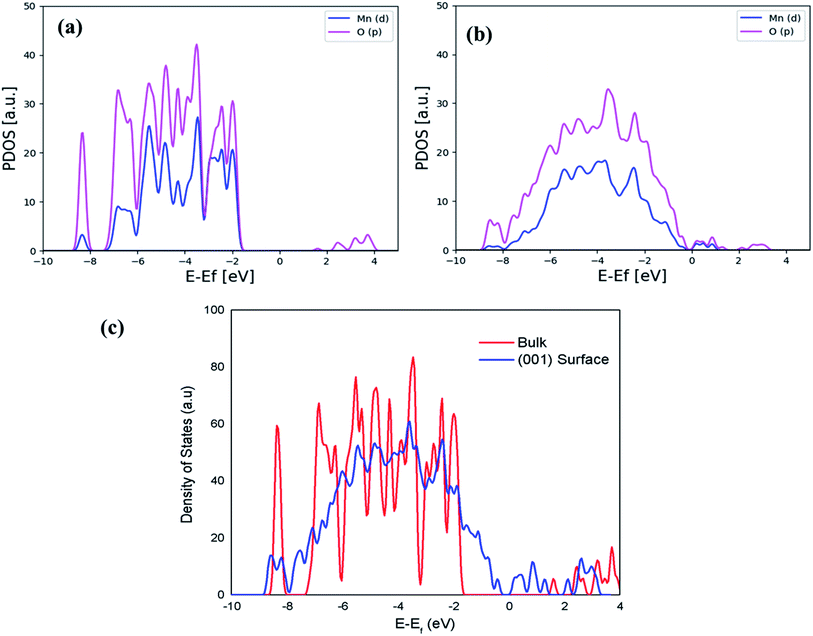 | ||
| Fig. 5 Calculated PDOS for the most dominant spectra for the bulk (a) and (001) surface (b) separately, while (c) presents a comparison of the calculated DOS for the bulk and (001) surface. | ||
D. Bulk and surface diffusion
The ion diffusion paths and dimensionalities within the crystal structures of cathode materials are among the most important fundamental features and also critical for the charge–discharge rate capabilities.15 Fig. 6(a), (b) and Table 3 demonstrate the proposed possible kinetic pathways and calculated parameters including the minimum possible lithium atom (Li) hopping distance (a), energy barriers (Eb), diffusion rate (r) and diffusion coefficient (D). The calculated results indicate that bulk lithium-ion diffusion in Li2MnSiO4 with the orthorhombic symmetry and Pmn21 space group is confined to two-dimensional diffusion along the [100] and [001] directions with an estimated diffusion coefficient from 3.12 × 10−15 to 6.09 × 10−17 cm2 s−1. The corresponding energy barriers are also found to be in the range between Eb = 0.73 and Eb = 0.88 eV, whilst lithium diffusion along the A–G–H pathway (y-axis) is completely limited mainly in the second half hopping. This is because of the tetrahedral units such as MnO4 and SiO4 blocking the Li+ diffusion channels, resulting in a high energy barrier as high as 1.88 eV that corresponds to very slow diffusion coefficient (3.12 × 10−32 cm2 s−1) of Li+ diffusion from the hopping site G to H pathway, as indicated in Fig. 6(a), (b) and Table 3. The calculated results also indicate that the microscopic diffusions following the A–B–C pathway (x-axis) are twice hopping from A to B hopping site (4.4 × 10−15 cm2 s−1) and from B to C hopping site (6.1 × 10−17 cm2 s−1) with their corresponding energy barriers (0.73 and 0.84 eV), respectively. The microscopic diffusions follow the A–G–H pathway from A to G (4.4 × 10−15 cm2 s−1) and G to H (3.1 × 10−34 cm2 s−1) hopping sites with the calculated energy barriers (0.73 and 1.88 eV), respectively.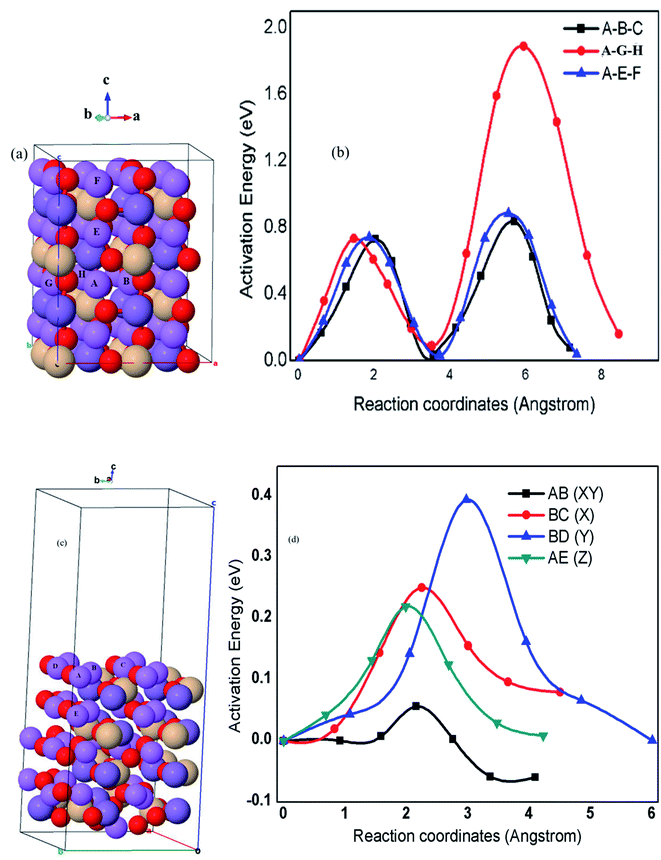 | ||
| Fig. 6 Proposed pathways for Li+ and microscopic Li+ diffusion in bulk (a and b) and (001) surface (c and d) structures of Li2MnSiO4, respectively. | ||
| Pathway | a (Å) | Eb (eV) | r (s−1) | D (cm2 s−1) | |
|---|---|---|---|---|---|
| Bulk | AB | 3.13 | 0.73 | 4.50 × 10−7 | 4.40 × 10−15 |
| BC | 3.13 | 0.84 | 6.0 × 10−9 | 6.10 × 10−17 | |
| AE | 3.19 | 0.74 | 3.50 × 10−7 | 3.10 × 10−15 | |
| EF | 3.18 | 0.88 | 1.00 × 10−9 | 1.30 × 10−17 | |
| AG | 3.13 | 0.73 | 4.51 × 10−7 | 4.40 × 10−15 | |
| GH | 4.41 | 1.88 | 1.60 × 10−19 | 3.10 × 10−34 | |
| (001) surface | AB (XY) | 4.44 | 0.06 | 1.09 × 1012 | 2.14 × 10−3 |
| BC (X) | 3.14 | 0.25 | 5.90 × 108 | 5.83 × 10−7 | |
| BD (Y) | 2.94 | 0.39 | 2.09 × 106 | 1.81 × 10−9 | |
| AE (Z) | 2.99 | 0.22 | 1.90 × 109 | 1.71 × 10−6 | |
Similarly, microscopic diffusion follows the A–E–F pathway (z-axis) from hopping site A to E (3.1 × 10−15 cm2 s−1) and E to F (1.3 × 10−17 cm2 s−1) with calculated energy barriers (0.74 and 0.88 eV), respectively. These results indicate that the microscopic diffusion along the (010) direction from hopping site G to H (1.88 eV) is a rate-limiting step during charge/discharge kinetics, which proves that bulk Li2MnSiO4 with the orthorhombic symmetry and Pmn21 space group is truly confined to two-dimensional Li+ transport pathways, as summarized in Fig. 6 and Table 3.
The calculated Eb in this work is better than the previously reported DFT and atomistic simulation studies,30,36,38 proving that Li2MnSiO4 with the orthorhombic symmetry and Pmn21 space group supports two-dimensional Li+ transport. Despite the calculated high energy barriers (Eb ≈ 0.88 eV) along the (001) and (1000) channels as also reported in other studies, third-dimensional Li+ diffusion, specifically along the (010) channel following AG and GH paths, has not been reported yet. To optimize unlimited and fast Li+ transport paths, all the channels along the 3D direction are of paramount importance that we present by surface designing, particularly, on the Li2MnSiO4 (001) surface.
The Li2MnSiO4 (001) surface was explored to be fast and unlimited Li+ diffusion, and better electronic conductive surface, which is essential to the higher-power capability of rechargeable Li-ion batteries. For detailed analysis, identified Li+ diffusion pathways from bulk to the surface (AE) and on the surface (AB, BC, and BD) were emphasized. The DFT calculations show that surface diffusion along the [100], [010], and [001] directions with a dramatically lowered energy barrier (0.057–0.395 eV) corresponds to a higher estimated diffusion coefficient (2.14 × 10−3 to 1.81 × 10−9 cm2 s−1). Li+ diffusion paths follow similar mechanisms as discussed in the case of bulk diffusion. In Fig. 6(c), (d) and Table 3, the four microscopic Li+ diffusion pathways and estimated energy barriers Eb were identified within the surface and from the surface to bulk (see Fig. 6 and Table 3 for details). The calculated Eb value along the AB (XY), BC (X), BD (Y), and AE (Z) pathways were found to be 0.06, 0.25, 0.40, and 0.22 eV, respectively, attributing to the rapid diffusion coefficient estimated to be 1.90 × 10−3 cm2 s−1 (AB), 9.6 × 10−7 cm2 s−1 (BC), 1.6 × 10−9 cm2 s−1 (BD), and 1.8 × 10−6 cm2 s−1 (AE), respectively, enabling higher charge–discharge rates on the Li2MnSiO4 (001) surface. The surface conductivity of this work is because of the remarkable results of Fig. 4(d), 5(c), 6(c) and Table 3. On the Li2MnSiO4 (001) surface, Li+ diffusion channels were found to be open and Li+ diffuses with very minimum energy costs, inducing surface ionic conductors for this material. With regard to the electron conductivity, the Mn cations with d-orbital and O anions with p-orbital strongly overlapped, indicating the Mn(d) and O(p) hybridizations, which facilitates fast electron transfer, inducing a very narrow bandgap energy (0.6 eV) unlike the bulk insulating property (3.42 eV). The results suggest that Li+ diffusion on the Li2MnSiO4 (001) surface is three dimensional and very fast with a diffusion coefficient estimated to be 12 to 17 orders of magnitude higher than that of bulk Li2MnSiO4. This is also quite different from other polyanion compounds of LIB cathode materials. For instance, LiFePO4 is the well-known material confined to one-dimensional Li+ diffusion along the (010) direction in its bulk and (010) surface structures. However, the (010) surface Li+ diffusion was found to be lower than its bulk diffusion because of the higher energy barrier along this channel, revealing the surface architecture of the Li2MnSiO4 cathode material for high-performance lithium-ion batteries.67
4. Conclusion
Herein, we investigated the Li+ transport paths, electronic structures, and structural stabilities of the Li2MnSiO4 bulk and surfaces using both DFT and DFT + U analysis. The results of surface free energies predicted the following order of stability for low index surface: (210) > (010) > (001) > (100) facet. Based on the calculated free surface energies, an equilibrium shape of the Wulff construction was predicted and the relative percentage of exposure was found to be 35.64% for (001), 24.9% for (010), 23.4% for (100), and 16.47% for (210). Unlike the bulk insulator, electronic analysis results revealed that there are superior (001) surface conductivity pathways in Li2MnSiO4. Moreover, the NEB calculations confirmed unlimited and fast three-dimensional lithium-ion diffusion on the Li2MnSiO4 (001) surface, unlike the corresponding bulk phase due to the large energy barrier. The presence of conductive surface pathways for ion and electron transports along the Li2MnSiO4 surfaces could substantially improve the performance of the Li2MnSiO4-based rechargeable lithium-ion batteries, paving the way for designing and developing high-performance energy storage devices.Data availability
The data that support the findings of this study are available within the article.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by thematic research project (Project no. TR/012/2016 and VPRTT/PY-026/2018/10) funded by Addis Ababa University. Y. S. Mekonnen would like to thank the World Academy of Sciences (TWAS) for supporting this work (Research grants 19-202 RG/CHE/AF/AC_G). G. S. Gurmesa would like to acknowledge Mettu University for sponsorship. Moreover, authors would like to thank Dr Tamiru Teshome for valuable discussions.References
- H. N. Girish and G. Q. Shao, RSC Adv., 2015, 5, 98666 RSC.
- A. R. Armstrong, C. Sirisopanaporn, P. Adamson, J. Billaud, R. Dominko, C. Masquelier and P. G. Bruce, Z. Anorg. Allg. Chem., 2014, 640, 1043 CrossRef CAS.
- P. Vajeeston, F. Bianchini and H. Fjellvåg, Energies, 2019, 12, 224 CrossRef CAS.
- J. Lee, J. Moon, S. A. Han, J. Kim, V. Malgras, Y. U. Heo, H. Kim, S. M. Lee, H. K. Liu, S. X. Dou, Y. Yamauchi, M. S. Park and J. H. Kim, ACS Nano, 2019, 13, 9607 CrossRef CAS PubMed.
- J. R. Croy, A. Abouimrane and Z. Zhang, MRS Bull., 2014, 39, 407 CrossRef CAS.
- M. M. Thackeray, C. Wolverton and E. D. Isaacs, Energy Environ. Sci., 2012, 5, 7854 RSC.
- M. E. Arroyo-de Dompablo, M. Armand, J. M. Tarascon and U. Amador, Electrochem. Commun., 2006, 8, 1292 CrossRef CAS.
- C. Lyness, B. Delobel, A. R. Armstrong and P. G. Bruce, Chem. Commun., 2007, 4890 RSC.
- S. Thayumanasundaram, V. S. Rangasamy, J. W. Seo and J. P. Locquet, Ionics, 2014, 20, 935 CrossRef CAS.
- D. Morgan, A. Van der Ven and G. Ceder, Electrochem. Solid-State Lett., 2004, 7, 2003 CrossRef.
- Y. M. Kang, Y. Il Kim, M. W. Oh, R. Z. Yin, Y. Lee, D. W. Han, H. S. Kwon, J. H. Kim and G. Ramanath, Energy Environ. Sci., 2011, 4, 4978 RSC.
- N. Yabuuchi and T. Ohzuku, J. Power Sources, 2003, 119, 171 CrossRef.
- M. Bini, S. Ferrari, C. Ferrara, M. C. Mozzati, D. Capsoni, A. J. Pell, G. Pintacuda, P. Canton and P. Mustarelli, Sci. Rep., 2013, 3, 1 Search PubMed.
- X. L. Wu, L. Y. Jiang, F. F. Cao, Y. G. Guo and L. J. Wan, Adv. Mater., 2009, 21, 2710 CrossRef CAS.
- M. S. Islam and C. A. J. Fisher, Chem. Soc. Rev., 2014, 43, 185 RSC.
- G. Mali, C. Sirisopanaporn, C. Masquelier, D. Hanzel and R. Dominko, Chem. Mater., 2011, 23, 2735 CrossRef CAS.
- C. Sirisopanaporn, A. Boulineau, D. Hanzel, R. Dominko, B. Budic, A. R. Armstrong, P. G. Bruce and C. Masquelier, Inorg. Chem., 2010, 49, 7446 CrossRef CAS PubMed.
- P. Zhang, C. H. Hu, S. Q. Wu, Z. Z. Zhu and Y. Yang, Phys. Chem. Chem. Phys., 2012, 14, 7346 RSC.
- A. Saracibar, A. Van Der Ven and M. E. Arroyo-De Dompablo, Chem. Mater., 2012, 24, 495 CrossRef CAS.
- M. E. Arroyo-DeDompablo, R. Dominko, J. M. Gallardo-Amores, L. Dupont, G. Mali, H. Ehrenberg, J. Jamnik and E. Morán, Chem. Mater., 2008, 20, 5574 CrossRef CAS.
- R. J. Gummow, N. Sharma, V. K. Peterson and Y. He, J. Solid State Chem., 2012, 188, 32 CrossRef CAS.
- C. Zhang, Z. Chen and J. Li, Chem. Phys. Lett., 2013, 580, 115 CrossRef CAS.
- G. He, G. Popov and L. F. Nazar, Chem. Mater., 2013, 25, 1024 CrossRef CAS.
- A. R. Armstrong, C. Lyness, M. Ménétrier and P. G. Bruce, Chem. Mater., 2010, 22, 1892 CrossRef CAS.
- A. Y. Shenouda and M. M. S. Sanad, Bull. Mater. Sci., 2017, 40, 1055 CrossRef CAS.
- K. M. Bui, V. A. Dinh and T. Ohno, J. Phys.: Conf. Ser., 2013, 454, 012061 CrossRef CAS.
- M. M. Kalantarian, S. Asgari and P. Mustarelli, J. Mater. Chem. A, 2013, 1, 2847 RSC.
- Q. Cheng, W. He, X. Zhang, M. Li and L. Wang, J. Mater. Chem. A, 2017, 5, 10772 RSC.
- T. Muraliganth, K. R. Stroukoff and A. Manthiram, Chem. Mater., 2010, 22, 5754 CrossRef CAS.
- A. Kokalj, R. Dominko, G. Mali, A. Meden, M. Gaberscek and J. Jamnik, Chem. Mater., 2007, 19, 3633 CrossRef CAS.
- S. S. Liu, L. J. Song, B. J. Yu, C. Y. Wang and M. W. Li, Electrochim. Acta, 2016, 188, 145 CrossRef CAS.
- I. Belharouak, A. Abouimrane and K. Amine, J. Phys. Chem. C, 2009, 113, 20733 CrossRef CAS.
- Y. X. Li, Z. L. Gong and Y. Yang, J. Power Sources, 2007, 174, 528 CrossRef CAS.
- Z. Gong and Y. Yang, Energy Environ. Sci., 2011, 4, 3223 RSC.
- R. Dominko, M. Bele, M. Gaberšček, A. Meden, M. Remškar and J. Jamnik, Electrochem. Commun., 2006, 8, 217 CrossRef CAS.
- R. Dominko, J. Power Sources, 2008, 184, 462 CrossRef CAS.
- N. Kuganathan and M. S. Islam, Chem. Mater., 2009, 21, 5196 CrossRef CAS.
- C. A. J. Fisher, N. Kuganathan and M. S. Islam, J. Mater. Chem. A, 2013, 1, 4207 RSC.
- J. Maier, Materials for Sustainable Energy: A Collection of Peer-Reviewed Research and Review Articles from Nature Publishing Group, 2010, vol. 4, p. 160 Search PubMed.
- P. G. Bruce, B. Scrosati and J. M. Tarascon, Angew. Chem., Int. Ed., 2008, 47, 2930 CrossRef CAS PubMed.
- S. Bashir, P. Hanumandla, H. Y. Huang and J. L. Liu, Nanostructured Materials for Next-Generation Energy Storage and Conversion, Fuel Cells, 2018, 4, 517 Search PubMed.
- P. Chaturvedi, A. Sil and Y. Sharma, Solid State Ionics, 2016, 297, 68 CrossRef CAS.
- Z. Ding, Y. Feng, D. Zhang, R. Ji, L. Chen, D. G. Ivey and W. Wei, ACS Appl. Mater. Interfaces, 2018, 10, 6309 CrossRef CAS PubMed.
- Y. S. Meng and M. E. Arroyo-De Dompablo, Energy Environ. Sci., 2009, 2, 589 RSC.
- S. Loftager, J. M. García-Lastra and T. Vegge, J. Phys. Chem. C, 2016, 120, 18355 CrossRef CAS.
- M. D. Radin, J. F. Rodriguez, F. Tian and D. J. Siegel, J. Am. Chem. Soc., 2012, 134, 1093 CrossRef CAS PubMed.
- Y. S. Mekonnen, K. B. Knudsen, J. S. G. Mýrdal, R. Younesi, J. Højberg, J. Hjelm, P. Norby and T. Vegge, J. Chem. Phys., 2014, 140, 1 CrossRef PubMed.
- N. E. Benti, Y. S. Mekonnen, R. Christensen, G. A. Tiruye, J. M. Garcia-Lastra and T. Vegge, J. Chem. Phys., 2020, 152, 1 CrossRef PubMed.
- N. E. Benti, G. A. Tiruye and Y. S. Mekonnen, RSC Adv., 2020, 10, 21387 RSC.
- C. Deng, S. Zhang, B. L. Fu, S. Y. Yang and L. Ma, Mater. Chem. Phys., 2010, 120, 14 CrossRef CAS.
- H. Duncan, A. Kondamreddy, P. H. J. Mercier, Y. Le Page, Y. Abu-Lebdeh, M. Couillard, P. S. Whitfield and I. J. Davidson, Chem. Mater., 2011, 23, 5446 CrossRef CAS.
- V. V. Politaev, A. A. Petrenko, V. B. Nalbandyan, B. S. Medvedev and E. S. Shvetsova, J. Solid State Chem., 2007, 180, 1045 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- P. Babbar, B. Tiwari, B. Purohit, A. Ivanishchev, A. Churikov and A. Dixit, RSC Adv., 2017, 7, 22990 RSC.
- J. Enkovaara, C. Rostgaard, J. J. Mortensen, J. Chen, M. Dułak, L. Ferrighi, J. Gavnholt, C. Glinsvad, V. Haikola, H. A. Hansen, H. H. Kristoffersen, M. Kuisma, A. H. Larsen, L. Lehtovaara, M. Ljungberg, O. Lopez-Acevedo, P. G. Moses, J. Ojanen, T. Olsen, V. Petzold, N. A. Romero, J. Stausholm-Møller, M. Strange, G. A. Tritsaris, M. Vanin, M. Walter, B. Hammer, H. Häkkinen, G. K. H. Madsen, R. M. Nieminen, J. K. Nørskov, M. Puska, T. T. Rantala, J. Schiøtz, K. S. Thygesen and K. W. Jacobsen, J. Phys.: Condens. Matter, 2010, 22(25), 253202 CrossRef CAS PubMed.
- M. Ernzerhof and G. E. Scuseria, Theor. Chem. Acc., 2000, 103, 259 Search PubMed.
- W. Kohn and J. Sham, Phys. Rev. B, 1965, 140, A1133 Search PubMed.
- P. E. Bloechl, Phys. Rev. B, 1994, 50, 17953 CrossRef CAS PubMed.
- L. Wang, T. Maxisch and G. Ceder, Phys. Rev. B, 2006, 73, 1 Search PubMed.
- N. J. Mosey and E. A. Carter, Phys. Rev. B, 2007, 76, 1 CrossRef.
- A. Jain, G. Hautier, C. J. Moore, S. Ping Ong, C. C. Fischer, T. Mueller, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2011, 50, 2295 CrossRef CAS.
- H. Zhao, X. Wu, Y. Li, J. Shen and J. Xu, J. Chin. Ceram. Soc., 2011, 39, 1084–1089 CAS.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978 CrossRef CAS.
- G. Zhong, Y. Li, P. Yan, Z. Liu, M. Xie and H. Lin, J. Phys. Chem. C, 2010, 114, 3693 CrossRef CAS.
- S. Q. Wu, Z. Z. Zhu, Y. Yang and Z. F. Hou, Comput. Mater. Sci., 2009, 44, 1243 CrossRef CAS.
- M. Y. Arsent’ev, P. A. Tikhonov and M. V. Kalinina, Glass Phys. Chem., 2018, 44, 455 CrossRef.
- G. K. P. Dathar, D. Sheppard, K. J. Stevenson and G. Henkelman, Chem. Mater., 2011, 23, 4032 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2021 |