Open Access Article
Open Access ArticleChiroptical characterization tools for asymmetric small molecules – experimental and computational approaches for electronic circular dichroism (ECD) and anisotropy spectroscopy†
Amanda C. Evans *a,
Andrew S. Petit
*a,
Andrew S. Petit *b,
Steven G. Guillenb,
Amanda J. Neukircha,
Søren V. Hoffmann
*b,
Steven G. Guillenb,
Amanda J. Neukircha,
Søren V. Hoffmann c and
Nykola C. Jones
c and
Nykola C. Jones c
c
aBiosciences/Theoretical Divisions, Los Alamos National Laboratory, P.O. Box 1663, Mailstop E529, Los Alamos, NM 87544, USA. E-mail: acevans@lanl.gov
bDept. of Chemistry & Biochemistry, California State University Fullerton, 800 N. State College Blvd., Fullerton, CA 92831, USA. E-mail: apetit@fullerton.edu
cISA, Dept. of Physics and Astronomy, Aarhus University, Ny Munkegade 120, DK-8000, Aarhus C, Denmark
First published on 5th January 2021
Abstract
Synchrotron radiation electronic circular dichroism (SRECD) and anisotropy spectroscopy for both enantiomers of a group of small non-planar chiral molecules are reported here. The experimental SRECD spectra are compared to computational ECD spectra generated using time-dependent density functional theory and a thermal averaging over relevant molecular configurations. The combination of these experimental and computational characterization methodologies for such molecules enables the prediction and understanding of the spectral behavior of other small molecules, in addition to chiroptically characterizing members of the mandelic acid family substructure. Enantiomeric purity of samples can be evaluated in comparison with these spectra and the extent of photolytic enantioinduction can also be predicted using these experimental/calculated SRECD and anisotropy spectra.
Introduction
Chiral centers impart specific structural and functional attributes to molecules that result in unique structural conformations and chiral spectroscopic signatures correlated to distinct physicochemical behaviour and differences in bioactivity/toxicity across biological systems. In particular, the activity of pharmaceutical drug molecules can differ significantly depending upon how “chirally pure” a drug product is.1 Circular dichroism (CD)2 and anisotropy absorption spectra are distinctive spectroscopic chiroptical signatures because they measure how chiral molecules interact with chiral light. CD spectra have historically been3,4 used by the pharmaceutical industry to characterize the chiral purity of drug products, and CD spectra have also been used to characterize large chiral biomolecules such as enzyme proteins and DNA.5We describe here the characterization of small chiral non-planar molecules by measuring their interactions with circularly polarized light (cpl). The studies presented here focus on electronic circular dichroism (ECD) performed in the ultraviolet (UV)-visible range using a synchrotron light source, or synchrotron radiation ECD (SRECD). Previous SRECD studies of small non-planar molecules have focused on amino acids, alcohols, amines, and some carboxylic acids.6–8 This work compares experimental SRECD spectra with computational ECD spectra, with a view towards building an understanding of how molecular conformation results in unique chiroptical signatures and predicting important bands relevant for photolytic enantioinduction. We have focused our studies on a specific family of mandelic acid molecules, as mandelic acid is an important building block for pharmaceutical manufacturing.9–26 The ECD spectrum of mandelic acid has been the subject of previous experimental and computational studies,27,28 but former measurements have never before been reported below 200 nm, and the prior reported spectra do not characterize both enantiomers simultaneously. ECD spectroscopy below 190 nm for characterizing small molecule pharmaceuticals is novel and provides innovative chiroptical characterization of these species into the vacuum ultra-violet (VUV) regions that is not easily accessible using conventional benchtop CD.
ECD spectroscopy measures the differential absorption of right- (rcpl) and left-handed cpl (lcpl) across a range of wavelengths (typically from the near UV into the VUV region) for a given chemical species – either a small molecule or a macromolecule.29 The units of measurement are described in terms of the difference in absorption (ΔA), where A is a dimensionless unit representing the absorption intensity. The graphical illustration of absorption in an ECD spectra is indicated by having an either positive or negative electronic transition band (or “peak”); this is determined by eqn (1).5,29
| ΔA = Alcpl − Arcpl | (1) |
Thus, a positive peak is correlated to a stronger absorption of lcpl and a negative peak is correlated to a stronger absorption of rcpl.
ECD spectroscopy can be obtained for solid, liquid, solution, and gas phase substrates.5,30–32 An ECD spectrum across a set of wavelengths for a given molecule/macromolecule is not purely an intrinsic property of the species being measured. The absorption bands are also dependent specifically upon molecular conformation, in addition to temperature, pH, concentration, phase, and solvent if in solution phase. We have chosen to focus the majority of our studies here on small molecules in solution (water) over a series of dilutions at room temperature – with exceptions made for comparison/solubility purposes.
If both ECD, ΔA, and absorption spectra, A, for a given compound are measured simultaneously, an anisotropy factor g can be determined for the substrate for every wavelength measured
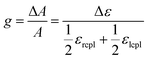 | (2) |
These anisotropy spectra inform choice of wavelength when using cpl to perform chiroptically selective photochemistry.6–8,33–35 The optimal wavelength for chiroptical photochemical induction is driven by the g-factor: the highest g will allow for the enantiomeric enrichment of an initial racemic mixture through the preferential photodegradation of one enantiomer.
Specifically, the enantiomeric enrichment, or excess (ee), which is typically denoted as a percentage (% ee), quantifies the difference in the relative yields of the R- and S-enantiomers after a reaction. Notably, the maximum achievable ee is not exclusively dependent on the differential absorption, ΔA, obtained from ECD spectroscopy but on the anisotropy factor g. The anisotropy factor is directly indicative of the predicted maximal % ee achievable by asymmetric photolysis using cpl to a given extent of reaction, ξ, (0 ≤ ξ ≤ 1)6,8,35 as shown in eqn (3).
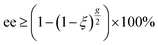 | (3) |
In the context of photochemistry, the extent of reaction reflects the fraction of molecules which undergo reaction after absorbing a photon6–8,30–35 if this irradiation process is considered to be photodegradative. For all anisotropy spectra presented here, a prediction of % ee chiroptically inducible with an extent of reaction of 99.99% is also provided.30–35 Likewise, the maximum % ee may also be estimated6–8,30–35 and these are typically 0.25–0.30% ee higher than the more conservative minimal values estimated based on eqn (3). These values assist in understanding the degree to which an ECD band will affect photodestructive asymmetric induction during photoirradiation studies.
Computational prediction of ECD spectra, as we report here, not only afford complete characterization of a given chiral small molecule, but also can provide insight into which bands are chiroptically relevant for subsequent enantioinductive photoirradiation studies.6–8,30–35 Strong correlation between reliable experimental ECD and computational ECD ensures that computational ECD can be used as predictive tools for choice of wavelength for cpl photoirradiation experiments.
All experimental ECD and anisotropy spectra considered here have been measured using synchrotron radiation as the light source,36 which makes it is possible to accurately measure the CD and absorbance spectra simultaneously, with low signal to noise, which is vital for the generation of anisotropy spectra. Although modern conventional CD instruments are very powerful, they generally experience a rapid drop in intensity below 190 nm, as expected from a lamp-based source. This can be countered to some extent with opening up slits to preserve the light intensity. However, by doing so, spectral artefacts cannot be avoided as opening slits alters spectral resolution and may allow stray light into the system. Such artefacts are not present in a well-tuned SRECD instrument; thus SRECD provides more reliable (and reproducible) spectral data. SRECD has been demonstrated to provide a series of advantages for generating molecularly characteristic spectra, including access to the vacuum UV regions, superior signal-to-noise ratios due to higher photon flux, and the ability to measure lower concentrations of sample.37–40
Experimental
Materials
Enantiomerically pure sample standards of both R- and S-enantiomers of each compound measured were purchased from Sigma Aldrich. All standards (97–99% purity) were of high optical purity (>99% ee). The majority of the sample solutions were freshly prepared in deionized, filtered, and UV-irradiated Milli-Q water at concentrations between 1–50 mg ml−1. Some standards (indicated on the spectral data) were alternatively/additionally prepared in 1,1,1,3,3,3-hexafluoro-propan-2-ol (hexafluoroisopropanol, HFiP, >99%) purchased from Fluorochem.Experimental ECD & anisotropy spectra
SRECD and anisotropy spectra of each enantiomer for each compound were measured on the AU-CD beamline at ASTRID2 at ISA, Department of Physics and Astronomy, Aarhus University.41,42 The extinction coefficient, ε, and the differential extinction coefficient Δε, were measured simultaneously over a range of UV and VUV wavelengths to obtain g(λ) = Δε/ε.6 The photodetector voltage was used to provide absorbance measurements using the method described in Evans, et al.,43 comparing samples between the beamline and a calibrated photospectrometer (Evolution 300, Thermo). Wavelength and rotational strength were checked daily with camphor sulfonic acid (CSA) prior to recording other SRECD spectra.All samples were measured in water or HFiP, as indicated, across a series of dilutions to ensure high spectral quality with low signal-to-noise ratios. All samples were measured at 25 °C using a 100 μm pathlength quartz cell and in some cases also a 20 μm CaF2 cell, a 2 s dwell time per point, and six accumulations. Baselines measured with the appropriate solvent and cell were subtracted from the sample measurements. SRECD spectra were mildly smoothed with a 7-point Savitzky–Golay filter.44
Computational ECD spectra
In order to sample thermal equilibrium for each of the molecules considered in this study, we performed a series of geometry optimizations beginning from a number of different initial molecular configurations obtained by sampling all relevant torsion angles. These geometry optimizations were performed using density functional theory (DFT) with the B3LYP functional, 6-31+G** basis, and SG-1 integration grid. The optimized molecular geometries were verified to be minima by calculating the vibrational frequencies and finding no imaginary frequencies. The free energy of each conformation was then calculated using eqn (4), where Ek is the electronic energy of the kth conformation, Hk is the enthalpy, Sk is the entropy, and T is the temperature.| Gk = Ek + Hk − TSk | (4) |
The enthalpies and entropies were calculated using the standard rigid-rotor/harmonic-oscillator approximations at room temperature. Solvent effects were included using a polarizable continuum model (PCM) parameterized for water or 2-methyl-1-propanol. 2-Methyl-1-propanol was used as computational analogue for HFiP as the two solvents have very similar dielectric constants, 16.77 and 16.70 respectively. All geometry optimizations and vibrational frequency calculations were performed using Q-Chem 5.1.45
At each optimized molecular geometry, the ECD spectrum was calculated using time-dependent density functional theory (TDDFT) with the ωB97XD functional and the 6-311++G** basis.46–48 Solvation effects were included with a PCM model and a (150, 770) integration grid was used. The theoretical line spectrum of each molecular conformation was convoluted with a Gaussian line shape with a full-width at half maximum of 0.1 eV (806.554 cm−1) to approximately account for inhomogeneous broadening. The overall ECD spectrum of the molecule was then obtained by thermally averaging the ECD spectra of the different molecular conformations via:
 | (5) |
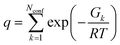 | (6) |
The TDDFT calculations used to generate the ECD spectra were performed using Gaussian 09 and the ECD spectra analysed using GaussView 5.49 The character of the electronic transitions was analysed using natural transition orbitals as implemented in the Q-Chem 5.1 software package.50,51
Only molecular conformations with significant thermal populations (≥0.01) were included in the calculation of 〈CD〉. The ECD spectra of only the R enantiomers were explicitly calculated as the ECD spectra of the R and S enantiomers are identical to within their sign.33,34 The intensities of the calculated ECD spectra have been uniformly scaled to match the experimental intensity range.
An added complexity in the calculations of the ECD spectra of these molecules is the existence of both neutral and anionic forms at equilibrium. Eqn (5) and (6) were separately applied to the neutral and anionic molecular conformations. The resulting 〈CD〉 were then averaged together, with the relative weights of the neutral and anionic forms determined based on the equilibrium concentrations of the acid and conjugate base obtained from the pKa (Table 1) and experimental conditions. As expected for weak acids, the ECD spectra were dominated by the neutral molecules.
Finally, our initial attempts to computationally model the anisotropy spectra were unsuccessful. We attribute this to the fact that g depends inversely on the absorption spectrum and hence is highly sensitive to the tails of the spectral line shapes. We anticipate that a more sophisticated approach towards modeling spectral broadening, for example, one that includes explicit solvent effects, will be required to accurately capture computational anisotropy spectra.
Results and discussion
Experimental and computational spectra
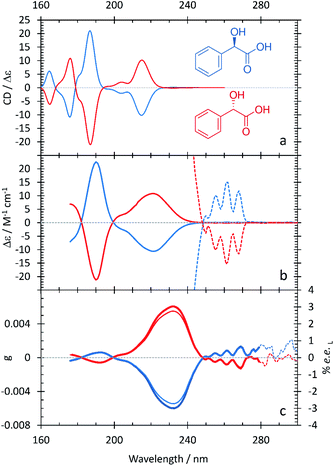
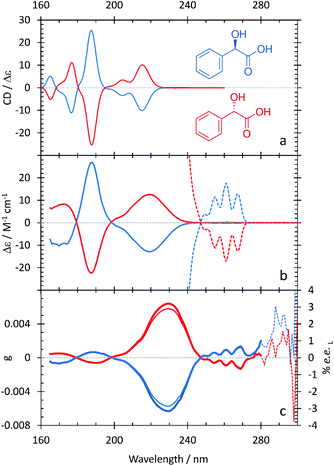
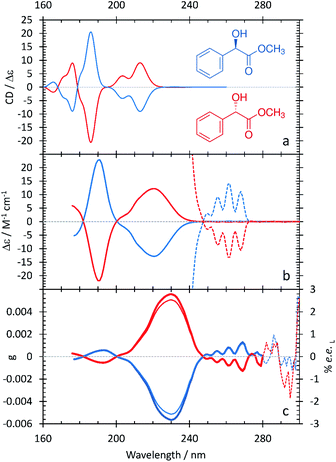
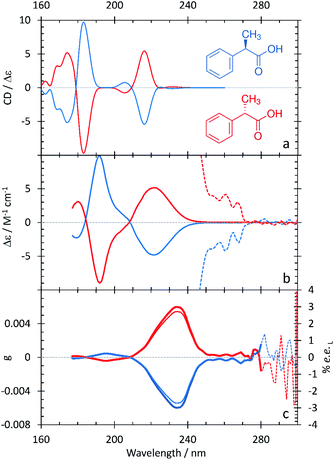
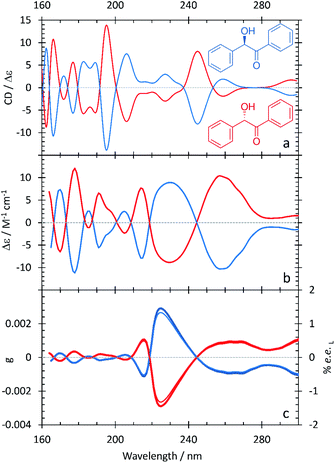
The resulting ECD spectra for each molecule are presented here. In Fig. 1–5, the computational ECD spectra are in the top panel, the experimental ECD spectra in the middle and the anisotropy spectra, g, at the bottom. The experimental CD spectra are amplified at higher wavelengths (>240 nm, shown as dotted lines)52 to highlight a series of low-energy spectral features. Note that mandelic acid was investigated both in water and 2-methyl-1-propanol (computational)/HFiP (experimental).Mandelic acid: experimental and computational spectra
The spectral characteristics of mandelic acid are shown in Fig. 1 and summarized in Table 2. The experimental CD spectrum shows two main electronic bands at 220 and 190 nm, with a weaker overlapping band at 205 nm. Analysis of the natural transition orbitals associated with the electronic transitions shows that the band at 220 nm can be assigned to a n → π* transition primarily involving the carboxylic acid group, whereas the transition at 205 nm is π → π* at the aromatic ring; this analysis is provided in the ESI.† The band at 190 nm is also π → π* and displays some charge-transfer character from the aromatic ring to the carboxylic acid group. At lower transition energies, we find a series of peaks at 255, 260, and 265 nm. As the spacing between these peaks ranges from 754–726 cm−1, we attribute these peaks to a vibrational progression originating from a single π → π* electronic transition at the aromatic ring.10 The anisotropy spectrum for mandelic acid shows one major band at 235 nm, with a minor band at 190 nm. Using eqn (3) and the g values in Fig. 1c, we would predict that a % ee of ≥2.8 could be achieved by irradiating mandelic acid with cpl at 232 nm, which is comparable to previous photoirradiation experiments performed on alanine.6As shown in Table 2 and Fig. 1, the agreement between the experimental and computational ECD spectra of mandelic acid is generally very good, especially in terms of band positions and overall line shapes. Indeed, the TDDFT calculations capture the major band positions to within 0.13 eV. The calculated spectral linewidths are not in exact agreement with experiment because of the ad hoc way in which inhomogeneous broadening was included in the calculated ECD spectra. The largest discrepancies between the experimental and computational ECD spectra occur at low energies. The feature at 232 nm in the computational ECD spectrum, which is attributed to the S0 → S1 transition of mandelic acid, differs from the low-energy features in the experimental SRECD spectrum by 0.57 eV.
| Compound | pKa |
|---|---|
| Mandelic acid | 3.41 |
| Benzoin | 12.60 |
| 2-Phenylpropionic acid | 4.59 |
| Methyl mandelate | 12.19 |
In Fig. 2a, the computational ECD spectrum of mandelic acid in 2-methyl-1-propanol shows good agreement with the experimental spectrum in HFiP (Fig. 2b). Using HFiP as a solvent for mandelic acid, we were able to extend our measurements well into the VUV and observe further absorption bands for this compound. Comparing Tables 2 and 3, mandelic acid shows a very small solvatochromic shift between water and HFiP, with the experimental hypsochromic shifts consistently less than or equal to 3 nm. This is despite the fact that water and HFiP have significantly different dielectric constants, 78.35 for water and 16.70 for HFiP. The solvatochromic shift is too small to be reliably captured by our chosen computational approach.
| Experimental band (nm/eV) | Calculated band (nm/eV) | Assignment |
|---|---|---|
| — | 164.6/7.53 | |
| 175/7.08 | 175.8/7.05 | n → π* with charge-transfer character from carboxylic acid to aromatic ring |
| 190/6.52 | 186.8/6.64 | π → π* aromatic ring with charge-transfer character to –COOH |
| 205/6.05 | 203.8/6.08 | π → π* aromatic ring |
| 220/5.64 | 214.8/5.77 | n → π* carboxylic acid |
| 260/4.77 | 232.0/5.34 | π → π* aromatic ring |
| Experimental band (nm/eV) | Calculated band (nm/eV) | Assignment |
|---|---|---|
| — | 165.0/7.512 | |
| 172/7.21 | 176.6/7.02 | |
| 188/6.59 | 187.4/6.62 | π → π* aromatic ring with charge-transfer character to –COOH |
| 202/6.14 | 204.4/6.07 | π → π* aromatic ring |
| 219/5.66 | 215.2/5.76 | n → π* carboxylic acid |
| 260/4.77 | 232.8/5.33 | π → π* aromatic ring |
Previous experimental work by Verbit and Heffron28 captured the bands at 260 nm and 220 nm but not the three spectral features at lower wavelengths present in Fig. 1. As such, our SRECD spectrum of mandelic acid provides significant new chiroptical information of this molecule. Miyahara and Nakatsuji27 used symmetry adapted cluster-configuration interaction (SAC-CI) theory, along with thermal averaging over molecular conformations, to computationally model the ECD spectrum of mandelic acid. Their approach better captured the low-energy feature at 260 nm than our TDDFT calculations, with this feature calculated to be at 266 nm. However, their calculations predict an incorrect phase for the spectral feature at 200 nm relative to both the calculated and experimental spectra shown in Fig. 1. This research corrects these omissions and advances our understanding of chiroptical behavior of these small molecules by clearly characterizing both enantiomers of mandelic acid and its derivatives down into the vacuum UV (VUV).
Methyl mandelate: experimental and computational spectra
The ECD and anisotropy spectra of methyl mandelate are shown in Fig. 3 and summarized in Table 4. Comparing Fig. 1 and 3, the ECD spectrum of methyl mandelate is very similar to that of mandelic acid, with the same bands present in both spectra. This reflects the fact that the only structural difference from mandelic acid is the replacement of a hydroxyl group with a methoxy group on the α-carbon. The anisotropy spectrum for methyl mandelate shows one major band at 230 nm, with a minor band at 190 nm. The use of eqn (3) leads to a prediction that a % ee of ≥2.6 would be achieved by irradiating methyl mandelate with cpl at 230 nm.| Experimental band (nm/eV) | Calculated band (nm/eV) | Assignment |
|---|---|---|
| — | 165.6/7.49 | |
| 175/7.08 | 176.0/7.04 | |
| 190/6.52 | 186.0/6.67 | π → π* aromatic ring with charge-transfer character to –COOCH3 |
| 206/6.02 | 203.4/6.10 | π → π* aromatic ring |
| 220/5.64 | 213.0/5.82 | n → π* carboxylic methyl ester |
| 262/4.73 | 231.8/5.35 | π → π* aromatic ring |
Fig. 3 shows that the calculated ECD spectrum of methyl mandelate captures the major features in the experimental ECD spectrum. Compared to experiment, the calculated ECD spectrum overestimates the intensity of the band at 186 nm relative to the other bands in the spectrum. Moreover, the relative intensity of the feature at 203.4 nm is too large. As with mandelic acid, the largest discrepancy between theory and experiment occurs with the lowest-energy peak in the spectrum, where the calculations predict a low-intensity feature at 231.8 nm whereas the corresponding peak in experiment occurs at 262 nm, an error of 0.62 eV. For the major bands in the ECD spectrum, the largest error observed in the TDDFT calculations of methyl mandelate is slightly larger than that of mandelic acid at 0.18 eV.
2-Phenylpropionic acid: experimental and computational spectra
The spectral characteristics of 2-phenylpropionic acid in comparison with those of mandelic acid are interesting – replacing the hydroxyl group with an electron-donating methyl group on the α-carbon results in some spectral changes (Fig. 4 and Table 5). The band at 220 nm is broad, as in the ECD spectrum of mandelic acid, but does not contain a clear shoulder at low wavelengths. Instead, the intense feature at 191 nm contains a resolved, overlapping band at 205 nm. The experimental anisotropy spectrum for 2-phenylpropionic acid shows a major band at 235 nm, with a minor band at 195 nm – all bathochromically shifted relative to mandelic acid. Calculations from the g value and eqn (3) suggest that an ee of ≥2.7% would be achieved by irradiating 2-phenylpropionic acid with cpl at 235 nm.| Experimental band (nm/eV) | Calculated band (nm/eV) | Assignment |
|---|---|---|
| — | 162.4/7.63 | |
| — | 168.8/7.34 | |
| 181/6.85 | 174.2/7.12 | |
| 191/6.49 | 183.0/6.77 | π → π* aromatic ring with charge-transfer character to –COOH |
| 205/6.05200 | 205.6/6.034 | π → π* aromatic ring |
| 220/5.64 | 216.2/5.73 | n → π* carboxylic acid |
| 262/4.73 | 231.4/5.36 | Aromatic ring |
The computational ECD spectrum of 2-phenylpropionic acid shown in Fig. 4a successfully captures many of the features present in the experimental spectrum. The band at 216.2 nm is in good agreement with the experimental band at 220 nm, both in terms of position and asymmetric line shape. The features at 183.0 and 205.6 nm, as in the experimental ECD spectrum, share the same sign but are shifted further apart than in experiment due to a 0.28 eV error in the position of the higher-energy portion of the band. Finally, the calculations predict a series of bands below 174.2 nm, the existence of which is suggested in the experimental spectrum by the partially resolved band at 181 nm.
Benzoin: experimental and computational spectra
The SRECD and anisotropy spectra of benzoin shown in Fig. 5 and summarized in Table 6 are much more complex than those observed for the other species considered in this study. In particular, the SRECD spectrum contains multiple bands of high intensity spread throughout the spectrum between 300 and 160 nm. This reflects the fact that benzoin contains two aromatic rings, one of which is conjugated with the π system of the carbonyl. As for mandelic acid, by using HFiP as a solvent we were able to extend our measurements into the VUV and observe further absorption bands for this compound. The anisotropy spectrum for benzoin shows a major band at 222 nm, which is shifted to higher energy than the corresponding feature in the anisotropy spectra of the other compounds. The anisotropy spectrum additionally contains a series of higher-energy bands at 215, 205, 191, 178, and 170 nm and two broad features at longer wavelengths beginning at 245 nm. The anisotropy value at the peak maximum at 225 nm is consistent with an ee of ≥1.3%, a value that is lower than observed with the other molecules considered in this study.| Experimental band (nm/eV) | Calculated band (nm/eV) |
|---|---|
| — | 162.4/7.63 |
| 164/7.56 | 166.2/7.46 |
| 170/7.29 | 171.8/7.22 |
| 178/6.96 | 177.0/7.00 |
| — | 182.8/6.78 |
| 185/6.70 | 189.0/6.56 |
| 191/6.49 | 195.2/6.35 |
| 205/6.05 | 206.2/6.01 |
| 215/5.77 | 227.2/5.46 |
| 232/5.34 | 245.0/5.06 |
| 256/4.84 | 258.8/4.79 |
| 300/4.13 | 296.2/4.19 |
Fig. 5 and Table 6 additionally show that the agreement between the calculated ECD spectrum of benzoin and the experimental SRECD spectrum is much less good than what is observed with the other compounds. This is true for not only the band positions but also their relative intensities and line shapes. We believe that this reflects the challenge inherent in modeling the ECD spectrum of a molecule with many overlapping electronic transitions. Because amplitude in ECD spectra can be positive or negative, overlapping bands can combine in a constructive or deconstructive way. The ability for bands in ECD spectra to deconstructively combine amplifies the effect of errors in electronic transition energies on the overall spectral line shapes. For benzoin, the large number of overlapping bands necessitates a more accurate description of the electronic excited states than the TDDFT/PCM approach that we employed.
Conclusions and outlook
These results have begun to delineate the effects that substitution at the alpha carbon can have on the anisotropic behavior of chiral carboxylic acids and their derivatives. With the exception of benzoin, the differing substituents at the alpha position do not have any significant effect on the position or magnitude of the maximum anisotropy for this group of molecules.From a computational perspective, we have demonstrated the strengths and weaknesses of using TDDFT, in conjunction with a PCM solvation model and a thermal averaging over molecular conformations, to model the ECD spectra of small chiral organic compounds with an aromatic substituent. For mandelic acid, methyl mandelate, and 2-phenylpropionic acid, we demonstrated that our computational approach can provide a reasonable description of the major band positions and line shapes. However, with benzoin, the large number of overlapping electronic transitions led to much larger discrepancies between the computational and experimental ECD spectra. As such, molecules like benzoin likely require more accurate electronic structure approaches, such as ADC(2), in order to reliably capture the ECD spectrum. The calculations could additionally be improved through the inclusion of explicit solvent molecules. As mentioned above, we additionally believe that a thermal averaging over both the chromophore and explicit solvent molecules will be required to reliably model anisotropy spectra.
Examination of the 160–190 nm VUV range is difficult to achieve with the use of classic benchtop CD devices. This research is fundamental and unique in reporting measurements of ECD and anisotropy bands beyond the range 200–400 nm via the use of SRECD, and sets a precedent for chiroptical characterization of other nonplanar chiral small molecules.
Future work will include expanding the library of compounds modelled and measured and developing an approach for utilizing computational chemistry to predict anisotropy factor and hence ee as a function of wavelength, particularly for small bioactive molecules.
Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the through the award of beam time by ISA, Aarhus University, Denmark. The work at Los Alamos National Laboratory (LANL) was supported by the LANL LDRD program. This research used resources provided by the LANL Institutional Computing Program. Los Alamos National Laboratory is operated by Triad National Security, LLC, for the National Nuclear Security Administration of the U.S. Department of Energy (Contract No. 89233218NCA000001). Dr A. C. Evans was also supported by LANL LDRD Reserve funding (#20190602ER). Dr A. S. Petit and Mr S. G. Guillen acknowledge the use of computational resources provided by the Center for Computational and Applied Mathematics at California State University, Fullerton.Notes and references
- N. Vargesson, Birth Defects Res. C. Embryo Today, 2015, 105(2), 140 CrossRef CAS.
- H. E. Smith, Chem. Rev., 1998, 98(4), 1709 CrossRef CAS.
- H. Yao, E. Wynendaele, X. Xu, A. Kosgei and B. De Spiegeleer, J. Pharm. Biomed. Anal., 2018, 147, 50 CrossRef CAS.
- P. Horvath, A. Gergely and B. Noszal, Talenta, 1997, 44, 1479 CrossRef CAS.
- N. Berova, L. Di Bari and G. Pescitelli, Chem. Soc. Rev., 2007, 36, 914 RSC.
- C. Meinert, J. H. Bredehöft, J.-J. Filippi, Y. Baraud, L. Nahon, F. Wein, N. C. Jones, S. V. Hoffmann and U. J. Meierhenrich, Angew. Chem., Int. Ed., 2012, 51(18), 4484 CrossRef CAS.
- J. H. Bredehöft, N. C. Jones, C. Meinert, A. C. Evans, S. V. Hoffmann and U. J. Meierhenrich, Chirality, 2014, 26, 373 CrossRef.
- C. Meinert, N. C. Jones, S. V. Hoffmann and U. J. Meierhenrich, J. Photochem. Photobiol., A, 2016, 331, 130 CrossRef CAS.
- J. Zhou, Q. Liu, G. Fu and Z.-Z. Zhang, J. Zhejiang Univ., Sci., B, 2013, 14(7), 615 CrossRef CAS.
- H. G. Brittain, Mandelic Acid, Anal. Profiles Drug Subst. Excipients, 2002, 29, 179 CAS.
- V. Sladkova, O. Dammer, G. Sedmak, E. Skorepova and B. Kratochvil, Crystals, 2017, 7(1), 13 CrossRef.
- H. Huang and J. Xu, Biochem. Eng. J., 2006, 30, 11 CrossRef CAS.
- H. Lorenz, D. Sapoundjiev and A. Seidel-Morgenstern, J. Chem. Eng. Data, 2002, 47, 1280 CrossRef CAS.
- S. Tulashie, H. Lorenz and A. Seidel-Morgenstern, J. Chem. Eng. Data, 2010, 55, 5196 CrossRef CAS.
- S. Mao, Y. Zhang, S. Rohanl and A. K. Ray, J. Sep. Sci., 2012, 35, 2273 CrossRef CAS.
- Y. He, J. Xu, J. Pan, L. Ouyang and Y. Xu, Bioprocess Biosyst. Eng., 2008, 31, 445 CrossRef CAS.
- E. Takahashi, K. Nakamichi and M. Furui, J. Ferment. Bioeng., 1995, 80, 247 CrossRef CAS.
- S.-W. Zhang, M. T. Harasimowicz, M. M. de Villiers and L. Yu, J. Am. Chem. Soc., 2013, 135(50), 18981 CrossRef CAS.
- M. Terreni, G. Pagani, D. Ubiali, R. F. Lafuente, C. Mateo and J. M. Guisan, Bioorg. Med. Chem. Lett., 2001, 11, 2429 CrossRef CAS.
- K. Tang, J. Yi, K. Huang and G. Zhang, Chirality, 2009, 21, 390 CrossRef CAS.
- J. P. Surivet and J. M. Vatele, Tetrahedron Lett., 1998, 39, 9681 CrossRef CAS.
- J. Mills, K. K. Schmiegel and W. N. Shaw, US Pat.US4391826, Eli Lilly and Company, 1983 Search PubMed.
- L. J. D. Zaneveld, R. A. Anderson, X. H. Diao, D. P. Waller, C. Chany, K. Feathergill, G. Doncel, M. D. Cooper and B. Herold, Fertil. Steril., 2002, 78, 1107 CrossRef.
- H. H. Kope, Y. S. Tsantrizos, J. A. Fortin and K. K. Ogilive, Can. J. Microbiol., 1991, 37, 258 CrossRef CAS.
- C. Mollard, C. Moali, C. Papamicae, C. Damblon, S. Vessilier, G. Amicosante, C. J. Schofield, M. Galleni, J. M. Frere and G. C. K. Roberts, J. Biol. Chem., 2001, 276, 45015 CrossRef CAS.
- J. P. Ley and H. J. Bertram, Tetrahedron, 2001, 57, 1277 CrossRef CAS.
- T. Miyahara and H. Nakatsuji, J. Phys. Chem. A, 2013, 117(51), 14065 CrossRef CAS.
- L. Verbit and P. J. Heffron, Tetrahedron, 1968, 24, 1231 CrossRef CAS.
- N. Berova, P. L. Polavrapu, K. Nakanishi and R. W. Woody, Comprehensive Chiroptical Spectroscopy, John Wiley & Sons, New York, USA, 2012, vol. 1–2 Search PubMed.
- W. Kuhn, J. Phys. Chem. B, 1929, 4, 14 CAS.
- H. Nishino, A. Kosaka, G. A. Hembury, H. Shitomi, H. Onuki and Y. Imoue, Org. Lett., 2001, 3, 921 CrossRef CAS.
- H. Nishino, A. Kosaka, G. A. Hembury, F. Aoki, K. Kiyauchi, H. Shitomi, H. Onuki and Y. Inoue, J. Am. Chem. Soc., 2002, 124, 11618 CrossRef CAS.
- G. Balavoine, A. Moradpour and H. B. Kagan, J. Am. Chem. Soc., 1974, 96, 5152 CrossRef CAS.
- J. J. Flores, W. A. Bonner and G. A. Massey, J. Am. Chem. Soc., 1977, 99, 3622 CrossRef CAS.
- C. Meinert, S. V. Hoffmann, P. Cassam-Chenaï, A. C. Evans, C. Giri, L. Nahon and U. J. Meierhenrich, Angew. Chem., Int. Ed., 2013, 53(1), 210 CrossRef.
- J. C. Sutherland, A. Emrick, L. L. France, D. C. Monteleone and J. Trunk, Biotechniques, 1992, 13(4), 588 CAS.
- B. A. Wallace, Nat. Struct. Biol., 2000, 7(9), 708 CrossRef CAS.
- B. A. Wallace and R. W. Janes, Curr. Opin. Chem. Biol., 2001, 5(5), 567 CrossRef CAS.
- A. J. Miles and B. A. Wallace, Chem. Soc. Rev., 2006, 35(1), 39 RSC.
- A. M. Powl, A. O. O'Reilly, A. J. Miles and B. A. Wallace, Proc. Natl. Acad. Sci. U. S. A., 2009, 74(2), 101 Search PubMed.
- A. J. Miles, S. H. Hoffmann, Y. Tao, R. W. Janes and B. A. Wallace, Spectroscopy, 2007, 21, 245 CrossRef CAS.
- A. J. Miles, R. W. Janes, A. Brown, D. T. Clarke, J. C. Sutherland, Y. Tao and B. A. Wallace, J. Synchrotron Radiat., 2008, 15, 420 CrossRef CAS.
- A. C. Evans, C. Meinert, J. H. Bredehöft, C. Giri, N. C. Jones, S. V. Hoffmann and U. J. Meierhenrich, Top. Curr. Chem., 2013, 341, 271 CrossRef CAS.
- A. Savitzky and M. J. E. Golay, Anal. Chem., 1964, 36(8), 1627 CrossRef CAS.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. B. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuṡ, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C. M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. Distasio, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. D. Hanson-Heine, P. H. P. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T. C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S. P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. Oneill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y. C. Su, A. J. W. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z. Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. L. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J. Da Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C. P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. Van Voorhis, J. M. Herbert, A. I. Krylov, P. M. W. Gill and M. Head-Gordon, Advances in Molecular Quantum Chemistry Contained in the Q-Chem 4 Program Package, Mol. Phys., 2015, 113(2), 184 CrossRef CAS.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10(44), 6615 RSC.
- A. E. Hansen and K. L. Bak, J. Phys. Chem. A, 2000, 104(48), 11362 CrossRef CAS.
- J. Autschbach, T. Ziegler, S. J. A. Van Gisbergen and E. J. Baerends, J. Chem. Phys., 2002, 116(16), 6930 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. SchlegelG. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. MarenichJ. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. ZhengW. LiangM. HadaM. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian, 16, Revision B.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- R. L. Martin, J. Chem. Phys., 2003, 118(11), 4775 CrossRef CAS.
- F. Plasser, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141(2), 024106 CrossRef.
- Data are presented as Δε values, which are in units of M−1 cm−1 and have been calculated from the measured mdeg data, the concentration and pathlength used for measurements.
Footnote |
| † Electronic supplementary information (ESI) available: Natural transitions orbitals for the electronic transitions considered in this study. See DOI: 10.1039/d0ra06832b |
| This journal is © The Royal Society of Chemistry 2021 |