DOI:
10.1039/D1QO00531F
(Review Article)
Org. Chem. Front., 2021,
8, 5165-5181
Emerging computational approaches for the study of regio- and stereoselectivity in organic synthesis
Received
7th April 2021
, Accepted 6th June 2021
First published on 18th June 2021
Abstract
Computational chemistry has become important in organic synthesis as it provides a detailed understanding of molecular structures and properties and detailed reaction mechanisms. Besides mechanistic verifications, computational techniques can be used as complementary tools to predict reagents that make reactions happen based on calculated reaction profiles. Moreover, new catalyst design processes can be accelerated by incorporating these theoretical techniques into the searching protocols. Currently, advanced computer technology enables the fast development of highly accurate computational applications in complex molecular systems at a lower cost. In this review, we highlighted examples of recent applications that demonstrate the advantages, limitations, and solutions of these techniques, especially in multiscale approaches.
Introduction
In the chemical industry, the major interest is the search for highly selective chemical reactions that yield specific valuable products. Therefore, the detailed understanding of selectivity control has been a major task in catalyst development. Computational chemistry is considered as a complementary tool for the understanding of the structures and properties of compounds and for reaction mechanism validations that provide important proof of reaction features. Currently, close collaborations between computational and experimental chemists are growing, which result in improved quality of research, especially the reliable mechanistic studies of chemical reactions with accurate molecular geometry.1–6 The geometry and electronic structure of each stationary point from the reactant to the product along the potential energy surface (PES) can be analyzed, especially the transition state (TS) which has a very short life and cannot be captured in the laboratory. Therefore, various reaction pathways should be determined that enable the comparison of reaction features e.g. energy profiles, reaction intermediates, selectivity, etc. In the case of mechanistic studies, many possible reaction pathways should be covered to achieve a detailed explanation of the reaction profiles. Even computational study alone offers excellent insight into the reaction features with experimental finding helping in the derivation of computational data.7–9 With the fast development of computer technology, computational simulations of reaction mechanisms have become a useful tool to explain and provide theoretical descriptions and predictions. Mechanistic understanding and prediction aid to improve the specific synthesis and also the rational design of new catalysts.10–14
Reaction regio- and stereoselectivity
When an unequal mixture of stereoisomer products is obtained from a chemical reaction, one product is preferred as a result of several factors e.g. steric effects, electronic effects, reaction conditions, etc. In general, the stereoselectivity depends on the difference in the activation energy or reaction energy of each reaction pathway. Thus, a detailed study of the reaction mechanism is necessary for selectivity investigations and modifications. Based on the transition state theory (TST), activation barrier, and PES, the kinetic and thermodynamic control can be practically identified.15–17 It could be influenced by the temperature, reagents, catalyst, and/or solvent used. It is worth noting that enantioselectivity is a result of kinetic control due to each enantiomeric product being isoenergetic (Fig. 1b). However, the real reaction might undergo several pathways, which are competitive. Hence, a complicated reaction model is required to describe the stereoselectivity. Nevertheless, the theoretical calculation of the defined stereo-determining and other important steps could deliver particular mechanistic details.
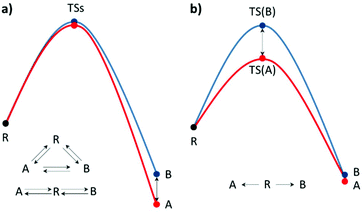 |
| | Fig. 1 Single-step reaction energy profiles of (a) thermodynamic control and (b) kinetic control, where R is the reactant, TS is the transition state and A and B are products A and B, respectively. | |
Thermodynamic control
When a single reactant can be converted into two stereoisomers, A and B, the simplest model is a single step process (Fig. 1). In the case wherein the products A and B are convertible, the product ratio ([A]/[B]) depends on their relative stabilities.18,19 The stereoselectivity can be expressed using the equilibrium equation which is related to the standard-state Gibbs free energy of reaction at certain temperatures:| | 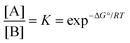 | (1) |
where ΔG° can be calculated using theoretical approaches, accurate thermodynamic data can be provided (within 1–2 kcal mol−1 error). Therefore, the relative stability of the two products can be calculated from the difference in the calculated Gibbs free energies at the appropriate temperature where the thermodynamic calculation for each product conformer is needed.
In a real situation, more than one conformer exists for each diastereomeric product (Fig. 2). Hence, the ratio of the population of products as a function of their free energies can be written as:
| | 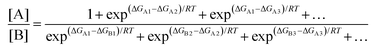 | (2) |
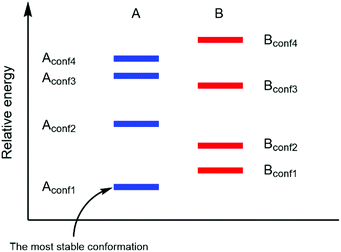 |
| | Fig. 2 Different product stabilities of each conformation of diastereomeric product A and B (adapted with permission from ref. 5). | |
As shown in (2), a fundamental error from computational prediction could occur if only the most stable conformers are taken into account. Hence, several transition state structures should be determined.
Kinetic control
When two competitive pathways lead to different products and one product cannot be converted to the other, in theory, it is assumed that the chemical reaction will follow the minimum energy path (MEP) on the PES. According to the thermodynamics equations, the rate of reaction is related to the Boltzmann distribution equation and activation energy of the reaction. Therefore, the selectivity of the reaction is related to the relative rate of each product formation.20| | 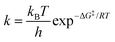 | (3) |
| | 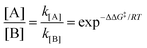 | (4) |
where kB is the Boltzmann constant, h is Plank's constant, and ΔG‡ is the activation free energy. As shown in the equations, the kinetic control focuses on the behavior at the transition state. Therefore, it is unable to explain some cases like bifurcation points where a single transition state could produce two different products.21
As mentioned above, the selectivity of the product has an exponential relationship to both free energy and temperature. It was found that the different energy of transition states or products of 1 kcal mol−1 could yield a product ratio at 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 at 273 K.5 The stereoselectivity is written in terms of enantiomeric excess percentage (%ee) or diastereomeric ratio (dr). In the first case, it indicates the percentage of one enantiomeric product over the other, which is expressed as:
10 at 273 K.5 The stereoselectivity is written in terms of enantiomeric excess percentage (%ee) or diastereomeric ratio (dr). In the first case, it indicates the percentage of one enantiomeric product over the other, which is expressed as:
| | 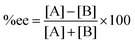 | (5) |
where [A] and [B] are mole fractions of each enantiomeric product. In the theoretical point calculations, the %ee is related to the difference of Gibbs free energy of the diastereomeric transition state of each pathway. Multiple pathways have to be considered. The percentage of existence for the transition states of each diastereomeric formation is expressed as:
| | 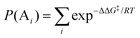 | (6) |
Together with (5) the %ee can be expressed as:
| | 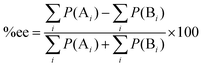 | (7) |
where
P(A
i) and
P(B
i) are percentages of existence for the
ith transition state of the
R and
S forms, respectively.
22
Computational methodologies
Density functional theory (DFT)
Quantum mechanics calculations are extremely useful to investigate at the atomic level. The major advantage of QM calculation is that the bond situations can be calculated. Among them, DFT is the most widely used across many disciplines e.g. physics, chemistry, biology, etc.3,4,6,9,23–26 This method offers acceptable accuracy of electronic properties, energies, and structures with an excellent cost-to-performance ratio. It turns out that micro- and macroscopic properties can be predicted. However, the primary issue of DFT is that its approximate variants in the mathematical equation are still problematic in certain situations. Therefore, the development of new and more accurate functions is actively sought after in computational chemistry research.
Reaction mechanisms and reaction pathways can be studied using QM calculations. The common task of computational simulations is geometry optimization that provides the structure at or near the local minimum of the PES. Moreover, the very short-lived transition state which cannot be isolated through experiment can be optimized at the saddle point on the PES. Information such as molecular interactions and activation energy offers comprehensive insight into the reaction profiles and enables the improvement of the reaction selectivities. Nevertheless, the cost of QM calculations increases rapidly with molecular size. Therefore, pure QM calculation is generally applied to a small molecular system (<200 atoms).
Hybrid methods
To date, computational simulation is known to be an integrated tool to understand the microscopic properties of chemical systems and also solve real world problems. The very fast computational development offers an impressive performance in terms of speed and accuracy of QM calculations. Therefore, reliable geometries, energies, reactivity, and electronic properties of complex molecules have become affordable. However, the pure QM calculation of macromolecules e.g. enzymes still requires high computational resources. Many attempts have been made to facilitate the calculations and this led to the introduction of hybrid methods.27–30 A large molecule is divided into multiple fragments, which can be computed using different levels of theory. In 2013, the Nobel Prize in chemistry was awarded to Karplus, Levitt, and Warshel for the “Development of Multiscale Models for Complex Chemical Systems”.31–34
So far, this hybrid method has been applied to combine the expensive QM and inexpensive classical molecular mechanics (MM) method. Therefore, it is called the QM/MM method. In this approach, the entire system is divided into two regions: QM and MM regions (Fig. 3). The QM region is the part that involves chemical reactions, whereas the MM region is the remaining environment. In general, there are two ways to evaluate the total energy; additive and subtractive schemes.28,35–40 The simple mathematical expressions are:
Additive scheme:
| | | EQM/MM = EQM + EMM + EQM–MM | (8) |
Subtractive scheme:
| | | EQM/MM = EQM,model + EMM,real − EMM,model | (9) |
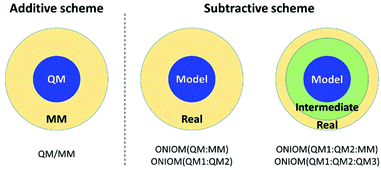 |
| | Fig. 3 Model partition of additive and subtractive schemes. | |
For the additive scheme, the total energy is the sum of the energy of the QM region (EQM), the energy of the MM region (EMM), and the interaction energy between the QM and MM regions (EQM–MM). On the other hand, in the subtractive scheme, the system is defined as layers. The total energy is calculated as the QM energy of the model system (EQM,model) plus the MM energy of the real system (EMM,real) minus the MM energy of the model system (EMM,model). This method is also called ONIOM (our own N-layer integrated molecular orbital and molecular mechanics). The advantages of ONIOM are as follows: (i) it is easy to adapt to combine different QM methods, called ONIOM (QM1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QM2) and (ii) it can be extended to multiple layers (>2 layers) calculations. The energy expression of ONIOM (QM1
QM2) and (ii) it can be extended to multiple layers (>2 layers) calculations. The energy expression of ONIOM (QM1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QM2) is written as:
QM2) is written as:
| | | Eoniom(QM1:QM2) = EQM1,model + EQM2,real − EQM2,model | (10) |
where QM1 is high-level QM and QM2 is low-level QM.
The first developed extended 3-layer ONIOM was demonstrated by Svensson et al. The system is divided into 3 layers which are defined as “model”, “intermediate”, and “real” and are calculated by “high”, “medium”, and “low” levels of theory, respectively.41 The 3-layer ONIOM can be applied as ONIOM (QM1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QM2
QM2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QM3) or ONIOM (QM1
QM3) or ONIOM (QM1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QM2
QM2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MM). The general expression of energy calculation is:
MM). The general expression of energy calculation is:
| | 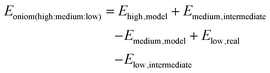 | (11) |
It is noted that the ONIOM approach is implemented in the Gaussian package up to a 3-layer model.
In order to calculate the interaction between QM and MM regions, there are two computational schemes: mechanical embedding (ME) and electronic embedding (EE) schemes.38,42–44 ME is the simplest scheme that treats the QM–MM interaction in a classical way. The electrostatic interactions are calculated using classical determination where the fixed point charges for both QM and MM regions are applied. The polarization of the QM wave function by the MM region point charges is not included in the QM calculations. Therefore, the ME requires the least computational resources. The electrostatic interaction between the QM and MM regions is improved by including the polarization of the QM wave function by the MM environment, via the EE scheme. Compared to the ME scheme, the computational demand is dramatically increased. It is suggested that the total energy of the system is sensitive to the polarization of the wave function. Thus, the energy refinement using ONIOM-EE single point calculation is recommended for optimized ONIOM-ME structures, for medium to large QM region sizes.
Besides macromolecular applications, the ONIOM extends its benefits to the area of physical organic chemistry in which accurate properties can be achieved for extended systems (>100 atoms) where QM1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QM2 or QM
QM2 or QM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MM approaches can be applied. Parts of the molecule that are involved in bond breaking/forming will be calculated using the higher QM method, while the rest is estimated by lower QM methods or classical MM. In this review, we highlighted recent applications of various computational techniques to understand the selectivity of organic synthesis and future application for catalyst and molecular design.
MM approaches can be applied. Parts of the molecule that are involved in bond breaking/forming will be calculated using the higher QM method, while the rest is estimated by lower QM methods or classical MM. In this review, we highlighted recent applications of various computational techniques to understand the selectivity of organic synthesis and future application for catalyst and molecular design.
Case studies
Reaction selectivity studies using DFT calculations
Selective PtCl2-catalyzed intramolecular [3 + 2] cycloadditions.
Kopsane alkaloids are a group of natural products that have a unique heptacyclic structure that are derived from the Kosia plant.45–47 Jia and coworkers recently reported the total synthesis of this molecular structure. It was found that the intramolecular [3 + 2] cycloaddition is a crucial step that provided a stereopure product in mild conditions.48 Moreover, ligand-free PtCl2 was used as a catalyst in dichloroethane solvent. The authors employed computational simulations to model the reaction focusing on the cyclization step. Two enantiomeric formations at the C3 atom, together with two diastereomeric formations at the C6 atom were studied. Therefore, four reaction pathways were investigated (Fig. 4). The B3LYP functional was used for geometry optimization and frequency calculations with the combination of the standard 6-31G(d,p) basis sets for non-metal atoms and SDD effective core potentials basis set for Pt atoms. The solvent effects were taken into account by single-point energy calculations of optimized geometries using a self-consistent reaction field (SCRF) based on a polarized continuum model (PCM) at the same level of theory. The most feasible pathway is when the stereochemistry at the C3 and C7 atoms are both R-isomers. Several important conclusions were drawn; (1) the first ring formation is barrierless for both the P(R,R) and P(R,S) pathways, whereas the activation energy is relatively high (>18 kcal mol−1) for the P(S,S) and P(S,R) pathways as a result of high structural constraint that provided an unfavorable trans-conformation between C4–N5 and C3–C7 bonds (Fig. 4b). (2) The second ring formation step is distinct between the two diastereomeric products. The TS2s of P(R,R) and P(R,S) were 10.92 kcal mol−1 apart in energy, in agreement with the experimental selectivity of a sole product. (3) There are two crucial factors that lowered the activation energy of the second ring formation of the P(R,R) pathway; (i) the higher overlapping of HOMO−1 and LUMO of Int1 and (ii) the conformational constraint of Int1 at C7 atom, in which the olefin side chain points away from the orientation necessary for bond formation in the P(R,S) pathway. (4) According to the overall energy profiles (Fig. 4a), the forward reaction of the P(R,R) pathway is the most feasible. The possibility of the reverse reaction is indicated by relatively low gaps for Int2 to TS2 and Int1 to TS1. However, they are much slower than the forward reaction of the P(R,R) pathway from reactant (RC) to Int1.
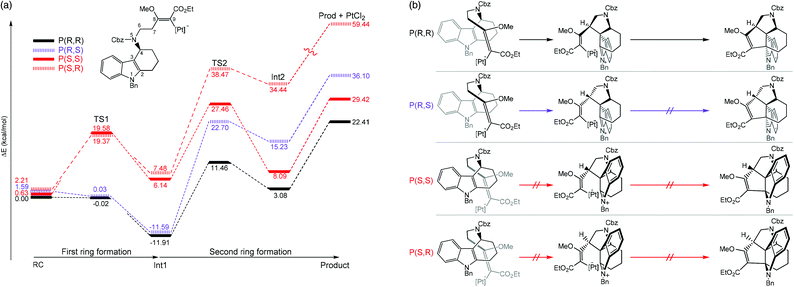 |
| | Fig. 4 (a) Full energy diagrams (in kcal mol−1), as determined at the B3LYP(SCRF)/6-31G(d,p)/SDD//B3LYP/6-31G(d,p)/SDD level. The pathways that lead to different enantiomeric products of C2 and C6 are called P(R,R), P(R,S), P(S,S), and P(S,R). (b) A schematic of species involved in each pathway (adapted with permission from ref. 48). | |
Cu(I) catalysed [2,3]-sigmatropic rearrangements of diazoesters with allylic iodides/sulfides.
Bond reorganization through sigmatropic rearrangement is one of the most important organic reactions which results in a bond shifting from one σ-bond to another.49,50 In 2021, the [2,3]-sigmatropic rearrangements of diazoesters with allylic iodides/sulphides via chiral bisoxazoline-Cu(I) catalysts were studied using DFT calculations to clarify the mechanism of the Cu(I) catalyst on whether the reaction proceeds via metal-bound or free ylide mechanisms (Fig. 5).51 There were four possible pathways derived from experiment. The most favorable pathway, the origin of the regio- and stereoselectivity, as well as the reaction features, were identified to compare between two different substrates. The M06-L/(SDD (for Cu and I atoms) and 6-31G(d)(for other atoms)) levels of theory were employed for geometry optimization and frequency calculations. The energy refinements were carried out using M06-L/(SDD (for Cu and I atoms) 6-311+G(d,p)(for other atoms)) with a solvation model based on density (SMD). The energy decomposition analysis (EDA) into distortion energy (Edist) and interaction energy (Eint) of the key transition states were determined to understand the essential interactions that control the selectivity of the reaction. The M06-L functional was chosen because it offers a good explanation of the non-covalent interactions e.g. hydrogen bonding and long-range interactions. They found that the free iodonium ylide is likely to present as a zwitterion (as C−–I+) that requires the Cu(I) center to stabilize the transformation through [2,3]-sigmatropic rearrangement. It requires an energy of only 7.5 kcal mol−1 at the level of theory used. The by-product from the [1,2]-rearrangement was also investigated. The activation energy of the minor pathway is 1.1 kcal mol−1 higher than the [2,3]-rearrangement. The EDA indicated that the Eint plays a crucial role in regioselectivity, which is consistent with the difference in the electrophilicity of the C1 and C3 atoms. The same approach was applied to the sulfonium ylide system. However, the obtained activation energies were relatively high which could not justify the experimental reactivity (>30 kcal mol−1). An alternative tautomerization followed by ligand exchange to yield the free sulfonium ylide was proposed. This pathway is more acceptable due to reasonable energy profiles. The electronic structure indicated that the double C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S bond is more promising in the free sulfonium ylide system rather than the zwitterion. Therefore, a free ylide mechanism that dictates a free sulfonium ylide leaving the Cu(I) catalyst via ligand exchange is a promising option for sulfonium [2,3]-sigmatropic rearrangement. According to the computational results, the regioselectivity is controlled by the electronic properties of the system and the stereoselectivity is mainly controlled by the substrate–ligand steric interactions.
S bond is more promising in the free sulfonium ylide system rather than the zwitterion. Therefore, a free ylide mechanism that dictates a free sulfonium ylide leaving the Cu(I) catalyst via ligand exchange is a promising option for sulfonium [2,3]-sigmatropic rearrangement. According to the computational results, the regioselectivity is controlled by the electronic properties of the system and the stereoselectivity is mainly controlled by the substrate–ligand steric interactions.
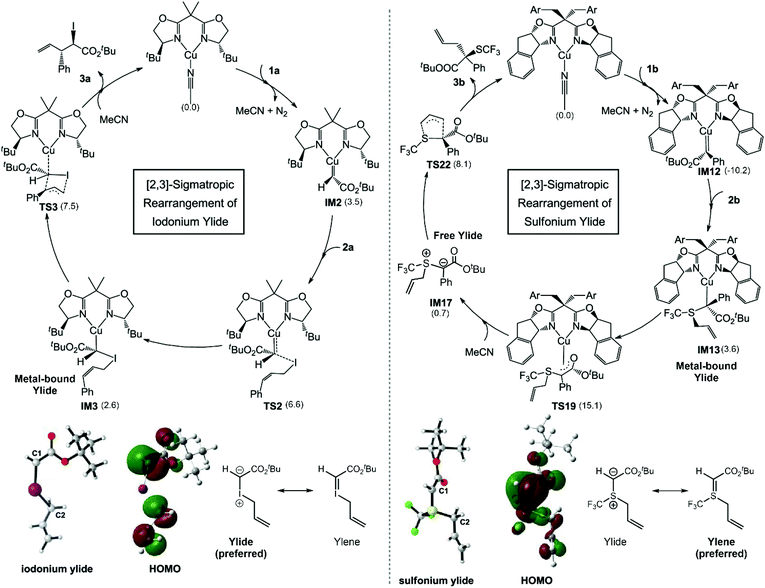 |
| | Fig. 5 The derived catalytic cycle for the [2,3]-sigmatropic rearrangement of iodonium ylide and sulfonium ylide, their HOMOs, and the resonance structure of free ylide molecules. Relative free energies in kcal mol−1 are shown in parentheses (adapted with permission from ref. 51). | |
Catalytic asymmetric homologation of ketones with α-alkyl α-diazo ester using Sc(III) complex.
The one-carbon addition into the alicyclic or cyclic ketone that is triggered by the nucleophilic addition of diazoalkyl carbon to the carbonyl group followed by a 1,2-shift and N2 extrusion.52–54 This chain and ring extension is usually used in natural product synthesis. In this reaction, the well-defined Lewis acid has been used as an asymmetric catalyst for homologation. However, the selectivity and reactivity of the reaction needs to be improved. The low reactivity of acyclic aryl alkyl ketones could be altered using a strong Lewis acid catalyst. Meanwhile, the chemo- and regioselectivity are difficult to control due to the system flexibilities. In addition, the chiral catalyst would assist in stereocontrol. Tan et al. reported that scandium(III)-N-N′-dioxide Lewis acid catalysed the homologation reaction which provided high yield, regio- and enantioselectivity under mild conditions.55 The authors employed the DFT calculations to explain the origin of regio- and enantioselectivity of the Sc(III)-catalyst. The theoretical discussion was based on the M06-L/def2-TZVP//B3LYP-D3/(6-31G(d,p), SDD (for Sc)) level of theory with dichloromethane as implicit solvent using the conductor-like PCM (CPCM) model. It was found that the two binding modes of acetophenone-Sc(III) complexes were nearly degenerate (ΔG = 0.8 kcal mol−1). The new C–C bond was formed as a consequence of the two-step mechanism, where the α-diazo ester attacked at the carbonyl carbon of acetophenone followed by N2 release (Fig. 6). The calculations indicated that the N2 releasing step is the rate-determining step. The computational results are consistent with the experimental finding where the electron-withdrawing group reduces the reactivity of reaction due to the formation of an unstable intermediate. Moreover, steric repulsion between bulky –CO2Me and N2 moieties of the α-diazo ester with the aryl part on the chiral N,N′-dioxide ligand is smaller in the most favorable pathway.
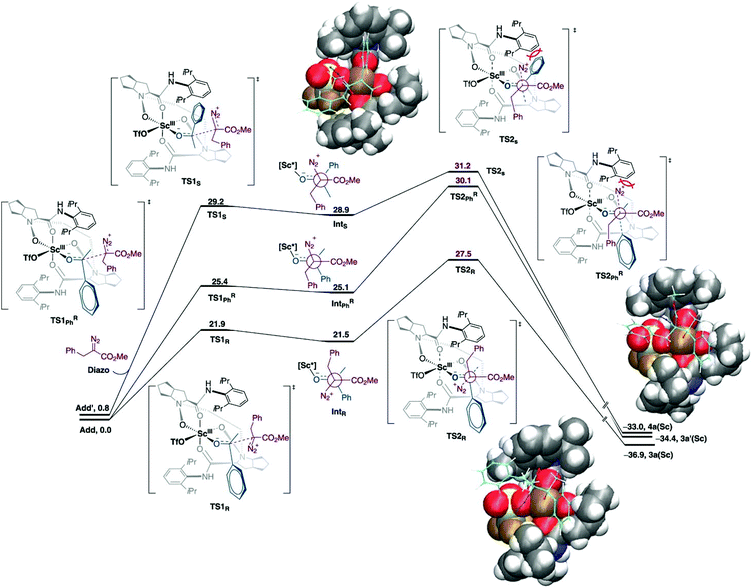 |
| | Fig. 6 Free energy profiles for asymmetric homologation calculated at M06-L/def2-TZVP//B3LYP-D3/(6-31G(d,p), SDD (for Sc)) level of theory. Energies are in kcal mol−1 (reprinted with permission from ref. 55). | |
Selective o-formylation of phenol and its derivatives via the Duff reaction.
The Duff reaction is the o-formylation reaction of phenol and its derivatives with hexamethylenetetramine (HMTA) in acidic media.56–59 It has been widely used due to its inexpensive reagents, moisture tolerance, and compatibility with a wide variety of functional groups. Despite the robustness of the reaction conditions, a detailed mechanism is still elusive. In 2016, Grimblat and coworkers reported the first theoretical study of the selectivity of the Duff reaction.60 It was proposed that the new C–C bond formation proceeded through the reaction between phenols and iminium HMTA+ (protonated HMTA) that provided a β-aminoketone type Mannich base as an intermediate. This intermediate formation is the key regioselective step of reaction followed by hydrolysis to form the final product. The remarkable point of this reaction is that there are two possible regioisomeric products, which could be acquired starting from non-symmetrical phenol derivatives. Initial TS conformational searches were performed using Hyperchem software with the MM+ method. The subsequent geometry optimization and frequency calculations were carried out at the M06-2X/6-311+G(d,p) level of theory with acetic acid as a solvent using the SMD model. The intrinsic reaction coordinate (IRC) calculations were performed for the obtained TSs. 3-Methylphenol (m-cresol) was used as a simplest representative substrate. The TSs that led to different R2, R4, and R6 substituted products were examined. A closer structural inspection found that the hydrogen migration between the phenolic –OH and protonated N of tetramine lowers the TS energy significantly compared to the non-migration TSs, which revealed the importance of H-bonding in transition state stabilization (Fig. 7). Moreover, it is also important in the reactive conjugated cyclohexadienone intermediate formation. The calculated model showed that the total charge of HMTA+ remained unchanged. The C–C distances of TSs were in the range of 1.91–2.24 Å. The calculated selectivity of TSs was 97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (R2/R4/R6). Considering the most stable R2/R6 substituted products, the calculated selectivity of the product was 26
3 (R2/R4/R6). Considering the most stable R2/R6 substituted products, the calculated selectivity of the product was 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 74 (R2/R6) which was in excellent agreement with experimental findings (21
74 (R2/R6) which was in excellent agreement with experimental findings (21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 79). A further seven phenol derivatives were also investigated to understand the steric hindrance and electronic effect of the substituents (Table 1). The calculations suggested that the C–C bond formation of the Duff reaction is an endothermic reaction with energies between 1.50 and 15.05 kcal mol−1. The product ratio prediction using their relative product stabilities agreed well with the reported regioselectivities61–64 and indicated that regioselectivity is under thermodynamic control. Additional studies implied that the R2 substitution was preferred for electron-withdrawing group substituted phenol, meanwhile the R6 substitution occurs when R is an electron-donating group. However, the electronic effect is not the only conclusive feature that controls the selectivity of the reaction.
79). A further seven phenol derivatives were also investigated to understand the steric hindrance and electronic effect of the substituents (Table 1). The calculations suggested that the C–C bond formation of the Duff reaction is an endothermic reaction with energies between 1.50 and 15.05 kcal mol−1. The product ratio prediction using their relative product stabilities agreed well with the reported regioselectivities61–64 and indicated that regioselectivity is under thermodynamic control. Additional studies implied that the R2 substitution was preferred for electron-withdrawing group substituted phenol, meanwhile the R6 substitution occurs when R is an electron-donating group. However, the electronic effect is not the only conclusive feature that controls the selectivity of the reaction.
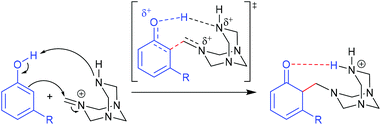 |
| | Fig. 7 The proposed initial step for the Duff reaction (adapted with permission from ref. 60). | |
Table 1 Calculated activation, formation energies, and product ratios of the Duff reaction (adapted with permission from ref. 60)
| Phenol |
Isomer |
ΔG‡ (kcal mol−1) |
Calc. ratio (R2/R6) |
ΔG° (kcal mol−1) |
Calc. ratio (R2/R6) |
Exp. ratio (R2/R6) |
| 1 |
R2 |
21.17 |
97![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
8.97 |
26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 74 74 |
21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 79 79 |
| R6 |
23.91 |
|
8.33 |
|
|
| 2 |
R2 |
17.73 |
95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 5 |
6.03 |
100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
| R6 |
20.03 |
|
13.90 |
|
|
| 3 |
R2 |
24.36 |
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
11.08 |
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
| R6 |
20.22 |
|
1.50 |
|
|
| 4 |
R2 |
17.61 |
95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5 5 |
4.99 |
100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
| R6 |
19.93 |
|
11.68 |
|
|
| 5 |
R2 |
20.84 |
96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 4 |
10.09 |
98![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
89![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11 11 |
| R6 |
23.29 |
|
12.60 |
|
|
| 6 |
R2 |
22.31 |
94![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 6 |
12.38 |
99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0 0 |
| R6 |
24.42 |
|
15.05 |
|
|
| 7 |
R2 |
19.88 |
73![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 27 27 |
9.50 |
5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 95 95 |
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
| R6 |
20.63 |
|
7.71 |
|
|
| 8 |
R2 |
22.64 |
83![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 17 17 |
11.57 |
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
| R6 |
23.87 |
|
7.87 |
|
|
|
Brønsted base activated borylation of propynols.
Organoboranes are organic compounds that consist of the B–C bond. They are key intermediates in many chemical reactions that involve pharmaceutical, bioactive, and material synthesis.65–67 Among them, vinyl boron compounds are used for multi-substituted alkenes synthesis in which transition metals have been exploited as catalysts. Steric effects and functional groups govern the stereo- and regioselectivity of organoborane products. However, the disadvantages of the transition metals catalysts are high cost, multistep operations, inaccessible starting materials, environmental toxicity, and narrow substrate specificity. To overcome these issues, organocatalysts e.g. Lewis bases have been proposed to activate diboron reagents through the acid–base adduct of one boryl group where the nucleophilic borane is generated. In 2018, Kuang and coworkers reported the alternative application of Brønsted-bases to activate diboron reagents with methanol as a co-reagent.68 The nucleophilic boron is enhanced by the formation of methoxydebrate [H-base]+[MeO-B2pin2]−, which is generated by deprotonation of methanol using a Brønsted base. Chen and co-workers elucidated the full reaction mechanism of the Brønsted base mediated borylation of propynols using DFT calculations.69 The geometry optimizations and frequency calculations of all stationary points along the reaction pathways were carried out using the B3LYP functional with a standard 6-31+G(d) basis set. The solvent effects were taken into account using the M11 functional with a 6-311+G(d,p) basis set and a SMD solvation model of the diethyl ether solvent. This reaction consists of two key steps: borylation and reductive dihydroxylation. The overall free energy profile and key structures are shown in Fig. 8. The intermediate 14 was a result of the borylation step through the boryl vinyl anion formation via a five membered ring transition state (5-ts). The direct borylation into C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C was excluded due to the high barrier. The intermediate 14 was observed experimentally. The calculation revealed that the transformation of intermediate 14 to product (Pro) proceeded through reductive dihydroxylation via multiple methoxy exchange between vinyl boron and the methoxyborate reagent. They suggested that the concerted B-methoxy elimination of borane (18-ts) is the rate-determining step for the entire reaction.
C was excluded due to the high barrier. The intermediate 14 was observed experimentally. The calculation revealed that the transformation of intermediate 14 to product (Pro) proceeded through reductive dihydroxylation via multiple methoxy exchange between vinyl boron and the methoxyborate reagent. They suggested that the concerted B-methoxy elimination of borane (18-ts) is the rate-determining step for the entire reaction.
 |
| | Fig. 8 The most favorable pathway of the Brønsted base mediated borylation of propyrols. The relative free energies (ΔG) are calculated at the M11/6-311+G(d)//B3LYP/6-31G(d) in diethyl ether solvent. The values are in kcal mol−1 (revised with permission from ref. 69). | |
Diazo functionalization catalyzed by Ag(I) or Sc(III) complexes.
Diazo compounds are important organic precursors for various chemical syntheses. They are chemically stable due to their resonance structures. In general, the transition metal catalysts are used to activate diazo compounds to form tertiary or quaternary carbons. The metal–carbene complex is considered as a key intermediate in diazo activation, which can undergo migratory insertion to yield a C–C bond. Ag(I) is one of the more widely used catalysts in diazo transformation. Uncoordinated nucleophilic attacks are usually proposed for Ag(I)-catalyzed diazo functionalization as transmetalation is impractical due to the small coordination number of Ag(I), which is 2.70,71 Unlike the Ag(I) complex, the Sc(III) complex, which has a d0 configuration could not generate the Fisher-type metal–carbene complex due to the lack of π-backbonding character. Instead, the Sc(III) complex acts as a Lewis acid that stabilizes the carbene species during the reaction process.72 So, the Sc(III) catalyst might proceed via a similar mechanism to an alkaline-earth metal salt where the free carbene is the key intermediate. In 2020, Liu and co-workers reported the computational study of the Ag(I) and Sc(III) catalyzed diazo alkylation reactions.73 As shown in Fig. 9, they proposed two different chemoselectivities: (i) metal–carbene formation/transformation and (ii) the Lewis acid assisted free carbene intermediate generation reaction. Both pathways were applied for both metal catalysts. All geometry optimizations and frequency calculations were performed using the B3LYP-D3 functional with the standard 6-31+G(d) basis set and LANL08-f for the Ag and Sc atoms. The energy refinements were achieved by the M06 functional with the 6-311+G(d) basis set and LANL08-f basis set for the Ag and Sc atoms in solution phase using the SMD model. The diazo activation to form a zwitterion metal-enolate intermediate (IV) proceeded through either Fisher-carbene formation (II) or a free carbene intermediate (VII). The obtained intermediate IV could transform to either dialkylation (P1) or monoalkylation (P2) products. The Ag(I)-catalyzed reaction preferred the blue pathway (Fig. 9b), where the metal–carbene II is formed during the transformation. The Ag(I)-intermediate IV acted as a nucleophile rather than a Brønsted base. The subsequent annulation and retro-aldol mechanism produced the dialkylation product P1. This is consistent with the experimental finding of Bi and co-workers where P1 is the only product when AgOTf was a catalyst.74 By contrast, the green pathway (Fig. 9b) is more favourable for the Sc(III)-catalyzed reaction. The Sc(III) complex served as a Lewis acid that stabilizes the free-carbene (VII). The Sc(III)-zwitterion enolate intermediate IV likely undergoes 1,4 proton-transfer which yields the monoalkylation (P2) product. The key explanation is that the lack of electron density in Sc(III) is unfavorable for the π-backbonding metal–carbene complex. However, the Ag(I)-carbene complex showed electrophilic character, which makes the metal–carbene formation achievable.
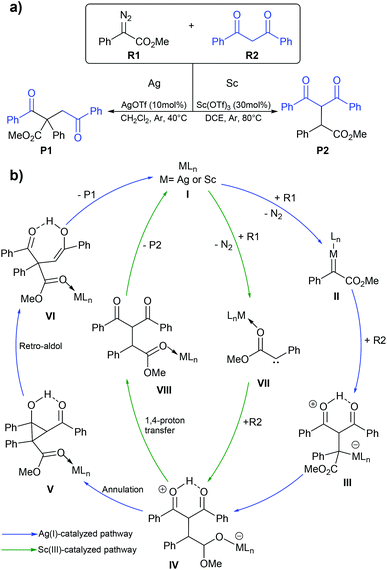 |
| | Fig. 9 (a) The silver(I)- or scandium(III)-catalyzed diazo alkylation reaction and (b) the mechanism for silver(I)- and scandium(III)-catalyzed diazo alkylation. They are shown with blue and green lines, respectively. | |
Reaction selectivity studies using hybrid methods
Nickel-catalyzed asymmetric catalysis.
In recent decades, metal-catalyzed hydrogenations of N-containing molecules have arisen in large-scale productions, especially in the pharmaceutical industry.75–77 To date, noble metal-containing catalysts e.g. Rh, Ir, and Ru have been used in this field. However, these metals are expensive and highly toxic to humans and the environment. Therefore, cheap and effective catalyst replacements have been explored. Xu and coworkers reported that a cheap Ni-binapine catalyst could catalyze the asymmetric transfer hydrogenation of enamide.78 It was found that Ni-(S)-binapine produced a high yield with 97%ee. To explain the selectivity of the Ni-catalyst, the ONIOM (QM1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
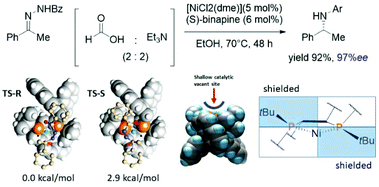
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QM2) approach was applied. The model reaction focused on the hydride insertion step between [(S)-binapine-hydrido nickel(II)]- and s-transoid hydrazine. According to their calculations, the hydrazine chelated to the metal center via the amide group in the early stage of the reaction (Fig. 8). The energy difference between the two diastereomeric transition states was 2.9 kcal mol−1, which is in good agreement with experimental results where the stereoselectivity was 97%ee. Remarkably, the phenyl ring of the benzamide of hydrazine was not involved in stereoinduction due to no significant contact with the Ni-binapine catalyst. Moreover, the replacement of the phenyl ring by the hydrogen atom did not change the energy splitting between the two diastereomeric TSs. The geometry observation of the Ni-binapine catalyst found that the shallow concave site is suitable for the s-transoid hydrazine. The top-left and bottom-right quadrants were shielded by the tert-butyl groups of the binapine ligand. This situation leads to a shape complementary of the catalyst–substrate complex which is often found in enzymatic catalysis (Fig. 10).
QM2) approach was applied. The model reaction focused on the hydride insertion step between [(S)-binapine-hydrido nickel(II)]- and s-transoid hydrazine. According to their calculations, the hydrazine chelated to the metal center via the amide group in the early stage of the reaction (Fig. 8). The energy difference between the two diastereomeric transition states was 2.9 kcal mol−1, which is in good agreement with experimental results where the stereoselectivity was 97%ee. Remarkably, the phenyl ring of the benzamide of hydrazine was not involved in stereoinduction due to no significant contact with the Ni-binapine catalyst. Moreover, the replacement of the phenyl ring by the hydrogen atom did not change the energy splitting between the two diastereomeric TSs. The geometry observation of the Ni-binapine catalyst found that the shallow concave site is suitable for the s-transoid hydrazine. The top-left and bottom-right quadrants were shielded by the tert-butyl groups of the binapine ligand. This situation leads to a shape complementary of the catalyst–substrate complex which is often found in enzymatic catalysis (Fig. 10).
 |
| | Fig. 10 Two diastereomeric transition states of Ni-binapine hydrido complex and structural observation. | |
Yang et al. reported the high stereoselectivity of the Ni-catalyzed reductive amination of ketone with both arylamine and benzhydrazide.79 It was found that the combination of Ni with several bisphosphines showed excellent selectivity. To understand the selectivity of the Ni-catalyst, the Ni-(R)-Ph-BPE catalyst was used as a representative. The hydride insertion into the N-phenylketimine is a key step for the formation of the chiral center. The two-layer ONIOM (QM1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QM2) method was used to investigate that reaction. The geometry optimization and frequency calculations were obtained using the ONIOM (B3LYP/(SDD for Ni, 6-31+G* for H, C, N, O, 6-311+G* for P):M06L/(LANL2DZ for Ni, 6-31G for other atoms). The energy refinements were done using single point calculations of ONIOM (B3LYP/def2-TZVP:M06-L/(SDD for Ni, 6-31+G* for H, C, N, O, 6-311+G* for P)). The effect of i-PrOH (∈ = 18.23) was included using the SCRF model. The partition of QM1
QM2) method was used to investigate that reaction. The geometry optimization and frequency calculations were obtained using the ONIOM (B3LYP/(SDD for Ni, 6-31+G* for H, C, N, O, 6-311+G* for P):M06L/(LANL2DZ for Ni, 6-31G for other atoms). The energy refinements were done using single point calculations of ONIOM (B3LYP/def2-TZVP:M06-L/(SDD for Ni, 6-31+G* for H, C, N, O, 6-311+G* for P)). The effect of i-PrOH (∈ = 18.23) was included using the SCRF model. The partition of QM1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QM2 is shown in Fig. 11c. They found that the two diastereomeric transition states are 2.1 kcal mol−1 apart in energy, which was consistent with the experimental %ee. The structural analysis provided an insight into the major factors that helped in stereoselectivity. As shown in Fig. 9a and b, the phenyl rings of the chiral phospholane ligand located at the top-right and bottom-left quadrants restricted the binding pocket around the Ni-center. The E-ketimine substrate fits perfectly in the binding pocket, while the other substrate was distorted and destabilized the minor product formation due to steric hindrance, which forced the N-phenyl ring to rotate (Fig. 11b). Therefore, the large N-aryl rings in aniline tend to improve the stereoselectivity of the reaction as shown in the experimental results.
QM2 is shown in Fig. 11c. They found that the two diastereomeric transition states are 2.1 kcal mol−1 apart in energy, which was consistent with the experimental %ee. The structural analysis provided an insight into the major factors that helped in stereoselectivity. As shown in Fig. 9a and b, the phenyl rings of the chiral phospholane ligand located at the top-right and bottom-left quadrants restricted the binding pocket around the Ni-center. The E-ketimine substrate fits perfectly in the binding pocket, while the other substrate was distorted and destabilized the minor product formation due to steric hindrance, which forced the N-phenyl ring to rotate (Fig. 11b). Therefore, the large N-aryl rings in aniline tend to improve the stereoselectivity of the reaction as shown in the experimental results.
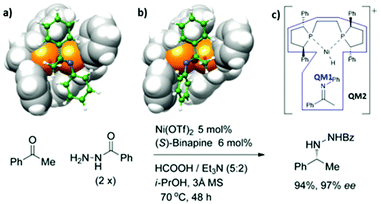 |
| | Fig. 11 Transition-state structures (a) TS-S and (b) TS-R for hydride insertion of cationic [(R)-Ph-BPE](hydrido)nickel(II) into a π-bound N-phenylketimine and (c) QM1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QM2 partition (adapted with permission from ref. 79). QM2 partition (adapted with permission from ref. 79). | |
Y/Yb heterobimetallic catalysed asymmetric ring-opening of donor–acceptor cyclopropanes with primary arylamines.
The chiral phosphoric acids and their derivatives have been used in modern organocatalysis as their structure and electronic properties are easy to modify. The major advantages of organocatalysts are that they are of low toxicity, environmentally friendly, low-cost, and active under mild conditions compared to organometallic catalysts. In 2021, Luo and coworkers introduced a new type of chiral bimetallic catalyst. It consisted of metals coordinated with chiral phosphoric ligands, offering new perspectives in asymmetric catalysis.80 In general, metal ions are often used as a Lewis acid agent. The addition of an organic chiral ligand reduces the acidity of the metal Lewis acid significantly. However, the combination of phosphoric acids (or their derivatives) with metals enhanced the acidity and flexibility of the chiral Brønsted acid catalysts.81–85 This bimetallic catalyst was applied to the asymmetric ring-opening reactions of donor–acceptor cyclopropanes with arylamines. In general, the cyclopropane ring-opening reaction requires extreme conditions that could make it difficult to control the stereoselectivity of the product. Hence, the bimetallic catalyst could yield a better stereoselectivity control under mild conditions. The new reaction mechanism where the bimetallic catalyst possibly triggers a dual functional activity which enhances the activity as well as the selectivity of the reaction. The authors found that the Y(III)/Yb(III) bimetallic catalyst produced high yield and selectivity under controlled conditions.80 To understand the selectivity and reactivity of this catalyst, the two-layer ONIOM (B3LYP/(6-31G(d) (for non-metals), SDD (for metals)):UFF) was exploited for geometry optimization and single point calculations with m-xylene as implicit solvent using the SMD model. The initial geometry is based on the X-ray crystallographic data. The proposed oxidation states of both metals are Y(III) and Yb(III), respectively. The multiple substrate binding conformations were investigated. The most stable conformation is the ®-substrate-Yb(III) complex where it was 3–6 kcal mol−1 lower than other conformations ((S)-substrate-Yb(III), (R)-substrate-Y(III), and (S)-substrate-Y(III) complexes) (Fig. 12). The reaction is likely to proceed via the SN2 mechanism followed by proton transfer through the transition state that leads to the (S)-intermediate and (S)-product (TSYbS). It was 2.0 kcal mol−1 lower than the transition state that leads to the (R)-product (TSYbR). The optimized transition state geometry observation indicated that the TSYbS is more favorable due to the lower geometric distortion. The calculated %ee was 95% which is close to the experimental value of 90%. In addition, the SN2 reaction was identified as the rate- and enantio-determining step.
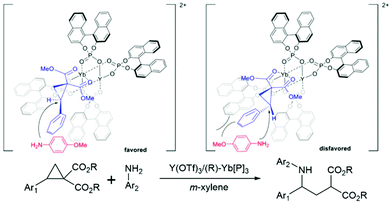 |
| | Fig. 12 Proposed transition states of Y/Yb bimetallic catalysed asymmetric ring-opening of donor–acceptor cyclopropanes with primary arylamines (reprinted with permission from ref. 80). | |
Reaction selectivity studies using multi-level calculations
Chiral Pt(II) phosphinite complex catalyzed asymmetric allylation.
The development of the chiral asymmetric transition metal catalyst for allylation is a challenging task, especially for the enantioselective C–C and C–X (X = heteroatom).86 Transition metals with chiral bisphosphine complexes are widely used as catalysts to deliver products with high selectivity. Computational calculation offers a better insight into the evaluation of enantioselective reaction pathways.87,88 In general, QM methods have been used because of their significant accuracy in thermodynamic calculation which is necessary for reliable %ee prediction. However, the major limitation of the QM method is that the computational cost increased dramatically with the system size. Currently, the ONIOM method allows the combination of high- and low-accuracy methods which can handle a larger number of atoms in the system and offer accurate thermodynamic data. To study the accurate stereo control, the description of diastereomeric transition states that leads to different diastereomeric products is an important step. The energy difference calculated between each TS indicates the competition between each product formation. Moreover, the origin of the energy difference can be determined in term of Edist and Eint energy using (12)where the Eint is the interaction between fragments and Edist is the energy required to distort the fragments into TS geometry.
A combination of MM, QM/MM, and DFT calculations were used to investigate the asymmetric allylation of aldehydes with chiral Pt(II) phosphinite (Fig. 13).88 The initial TS geometry was screened using the MM method with an energy cutoff of 20 kcal mol−1, resulting in 142 conformers remaining out of the original 192 conformers. All of them were subjected to QM/MM calculations, which yielded 50 initial guess structures for TS optimization using the QM/MM method. Finally, there were only 11 structures that were selected from the QM/MM optimized geometries for pure QM calculations. The analysis of the final 11 structures showed that the lowest energy transition state leads to the R-product and contributes the most to the product formation percentage. Based on the Boltzmann distribution calculation, the sum of the overall contribution of the R-product was 73%, which is in excellent agreement with the experimental result of 73%ee. In addition, the relative energy of the transition state structure that exceeded 4 kcal mol−1 compared to the lowest structure did not contribute to the competitiveness of product formation.
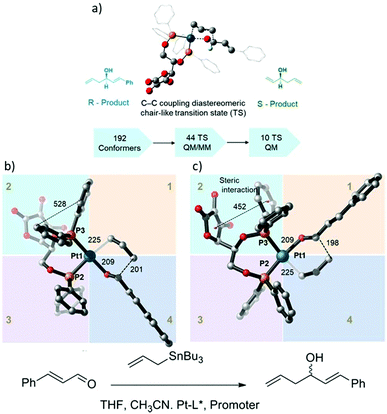 |
| | Fig. 13 (a) Catalytic assumption and calculations workflow, (b) the optimized geometry of the R transition state, and (c) optimized geometry of the S-transition state. All distances are in pm (reprinted with permission from ref. 88). | |
Computational organocatalyst design for asymmetric Friedel–Crafts alkylation of indole.
In organic chemistry, the enantiomeric pure synthesis is one of the most active research fields that aims to obtain target molecules with fewer or no by-products. Moreover, mild conditions and an environmentally friendly catalyst is an area of interest. In this field, organocatalysis is a recent strategy that offers optically active compounds via metal-free reactions under mild conditions.89–92 However, organocatalysts are often substrate specific and require the modification of the steric and electronic properties of the catalyst accordingly to improve the selectivity. So far, catalyst optimization is typically achieved through experimental trial and error, which usually requires extensive time and resources. Therefore, the incorporation of QM calculations would improve the efficiency of catalyst optimization through the quantitative structure–activity relationship (QSAR) model. Computational studies of stereocontrolling transition states and their reactant complexes offer a new rational catalyst design. The theoretical design is finally validated by experimental observations.
Gerosa and co-workers utilized a computational screening method called ONIOM-derived in silico screening (Fig. 14) in organocatalysis for the Friedel–Crafts reaction between (E)-cinnamaldehyde and an indole electrophile.93 The functionalization of indole consists of electrophilic attack at the nucleophilic atom, which involved facial selection. The ONIOM (QM1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QM2) approach was applied to reduce the computational demand of the screening method. The screening workflow is shown in Fig. 14a. Initially, 16 different TS structures were generated. The partition between the high and low layers is shown in Fig. 14b. Full optimization and frequency calculations were performed by ONIOM(B3LYP/6-31G*:AM1). The optimized geometries were subjected to energy refinements using the B3LYP/6-311+G** level with the PCM model using methanol as an implicit solvent to obtain accurate energy profiles. They found that the average difference in energy between the (E) and (Z) configuration formations was 1.1 kcal mol−1 with (E) preferred. It is consistent with the experimental findings. The EDA to determine ΔEiminium, ΔEindole, and ΔEint was also performed. The first two terms were calculated according to the difference between the two diastereomeric TS geometries, while the last term is the interaction energy between the two fragments (catalyst and substrate). The EDA indicated that the iminium and indole are more stable in Re-face formation, which exhibited less distortion in the Re-face attack. The computational prediction demonstrated that the steric interactions of the substituent (R) and CH–π interactions play a crucial role in selectivity (Fig. 14b), with the highest enantiomeric ratio reported to be 92
QM2) approach was applied to reduce the computational demand of the screening method. The screening workflow is shown in Fig. 14a. Initially, 16 different TS structures were generated. The partition between the high and low layers is shown in Fig. 14b. Full optimization and frequency calculations were performed by ONIOM(B3LYP/6-31G*:AM1). The optimized geometries were subjected to energy refinements using the B3LYP/6-311+G** level with the PCM model using methanol as an implicit solvent to obtain accurate energy profiles. They found that the average difference in energy between the (E) and (Z) configuration formations was 1.1 kcal mol−1 with (E) preferred. It is consistent with the experimental findings. The EDA to determine ΔEiminium, ΔEindole, and ΔEint was also performed. The first two terms were calculated according to the difference between the two diastereomeric TS geometries, while the last term is the interaction energy between the two fragments (catalyst and substrate). The EDA indicated that the iminium and indole are more stable in Re-face formation, which exhibited less distortion in the Re-face attack. The computational prediction demonstrated that the steric interactions of the substituent (R) and CH–π interactions play a crucial role in selectivity (Fig. 14b), with the highest enantiomeric ratio reported to be 92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 (Fig. 14c). Thus, this strategy could significantly accelerate and improve the efficiency of rational catalyst design.
8 (Fig. 14c). Thus, this strategy could significantly accelerate and improve the efficiency of rational catalyst design.
 |
| | Fig. 14 (a) Catalytic assumption and calculations workflow, (b) the key interactions of Si and Re transition state attack and system partition. The fully-colored image is the high layer and the greyed-out image is the low layer. (c) Predicted enantioselectivity vs. catalyst number (reprint with permission from ref. 93). | |
Pd-Catalyzed regioselective ring opening borylation of 2-arylaziridines.
Aziridine is a three-membered azaheterocycle, which is a versatile building block in organic synthesis, especially as a precursor for the ring opening reaction of N-containing natural products.94 Transition metal complexes have been used as reactive catalysts for C–N bond cleavage in an SN2 fashion to form azametallabutanes.94–96 The regioselective ring opening C–B cross-coupling reaction of 2-arylaziridines via a Pd(P(t-Bu)2Me/bpy) catalyst was shown to give β-amino-alkylboronates. This reaction is useful in natural product synthesis and amino-functionalization. The C–N bond cleavage of the 3-position proceeded through the formal SN2 type borylative C(sp3)–N bond cleavage of a neutral compound. External bases are not required in this reaction. However, the experimental results showed that the reaction could not function without water. The experimental mechanistic study was performed using the deuterated aziridine as a substrate. It was found that the stereochemistry of the 3-position is completely inverted which proved the SN2 reaction manner that was also supported by computational calculations. The Pd(P(t-Bu)2Me)2 and Pd(P(t-Bu)2Me)2(H2O) were used as catalysts and 2-phenyl-N-tosyl-aziridine as the substrate for this model reaction. The B3LYP-D3/(SDD (for Pd), 6-31G(d) (for other atoms)) in an implicit solvent model of toluene (∈ = 2.3714) was exploited for optimization and frequency calculations. The IRC calculations were performed at the same level of theory to confirm the connectivity between the TS and its local minima. The final energies of each stationary point were calculated as a single point calculation at B3LYP-D3/(SDD (for Pd), cc-pVTZ (for other atoms)). The initial TS screening was sampled using the multi-component artificial force induced reaction (MC-AFIR) method where the energy and their derivatives were obtained using the ONIOM (B3LYP-D3:PM6-D3) method. The SDD (for Pd) and 3-21G(d) (for other atoms) basis sets were used for the screening. The detailed EDA of selected TSs into deformation energy (ΔEdef) and ΔEint was evaluated. The system is divided into two fragments; the substrate and catalyst. The difference in energy between the low-lying TSs leading to desired and undesired product is 3.5 kcal mol−1. The major contribution of this difference came from the ΔEint between them indicating that the interaction between substrate and catalyst is more stable in desired product formation due to lower steric repulsion. The calculated regioselectivity of the aziridine ring-opening step is 89![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11, which was qualitatively in agreement with the experimental result of 99
11, which was qualitatively in agreement with the experimental result of 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Then, proton transfer to an anionic amine was observed. According to the calculations, water molecules could act as a proton source and an internal base in the form of Pd-OH, elevating the four-membered transmetallation between B2(pin)2 and Pd. The supported calculations showed that three water molecules are sufficient to form the hydrogen-bonding network for the proton transfer, which yielded the Pd-OH species. The B(pin)–B(pin) could not coordinate into the inner sphere of the metal center due to steric repulsion between the bulky alkyl group of the ligand and B(pin)–B(pin). However, one of the ligands can be replaced by B(pin) followed by B–B bond cleavage with a barrier of 10.8 kcal mol−1. Ligand exchange between B(pin)-OH and P(t-Bu)2Me ligand occurred. Finally, the reductive elimination process required only 0.1 kcal mol−1. The calculations also revealed that the product dissociation to recover catalyst is facile. The proposed overall catalytic cycle of borylation is shown in Fig. 15. Their experimental and theoretical results provided valuable insight into a new catalyst design involving the ring-opening C–E bond forming cross coupling of aziridine.
1. Then, proton transfer to an anionic amine was observed. According to the calculations, water molecules could act as a proton source and an internal base in the form of Pd-OH, elevating the four-membered transmetallation between B2(pin)2 and Pd. The supported calculations showed that three water molecules are sufficient to form the hydrogen-bonding network for the proton transfer, which yielded the Pd-OH species. The B(pin)–B(pin) could not coordinate into the inner sphere of the metal center due to steric repulsion between the bulky alkyl group of the ligand and B(pin)–B(pin). However, one of the ligands can be replaced by B(pin) followed by B–B bond cleavage with a barrier of 10.8 kcal mol−1. Ligand exchange between B(pin)-OH and P(t-Bu)2Me ligand occurred. Finally, the reductive elimination process required only 0.1 kcal mol−1. The calculations also revealed that the product dissociation to recover catalyst is facile. The proposed overall catalytic cycle of borylation is shown in Fig. 15. Their experimental and theoretical results provided valuable insight into a new catalyst design involving the ring-opening C–E bond forming cross coupling of aziridine.
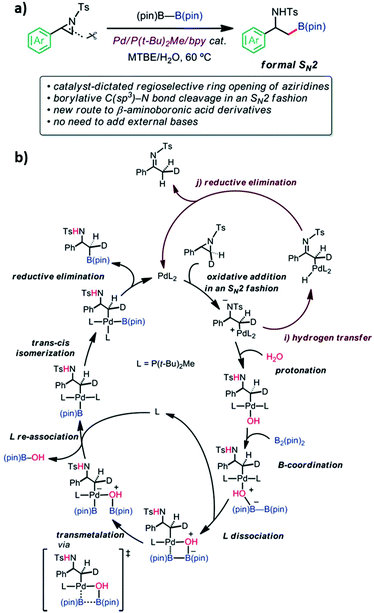 |
| | Fig. 15 (a) Reaction features and (b) the derived catalytic cycle of borylation (reprinted with permission from ref. 94). | |
Outlook and perspective
As shown in this review, the close collaboration between theoretical and experimental chemists has played a crucial role in mechanistic studies. The computational approaches provide quantitative predictions, verification, and proof of reaction selectivity, reaction mechanism, and properties. However, the accuracy of the calculations depends on many factors like reaction models and the choice of method and functional that offers the highest efficiency to implement in routine work. The information acquired may help in understanding and designing new catalysts for specific reactions.
Author contributions
Pratanphorn Nakliang: conceptualization, investigation, writing original draft, writing review, and editing.
Sanghee Yoon: review and editing.
Sun Choi: conceptualization, investigation, and review.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the Mid-career Researcher Program (NRF-2020R1A2C2101636), Medical Research Center (MRC) grant (NRF-2018R1A5A2025286), Brain Pool Program (NRF-2020H1D3A1A02080803), and Bio & Medical Technology Development Program (NRF-2019M3E5D4065251) funded by the Ministry of Science and ICT (MSIT) and the Ministry of Health and Welfare (MOHW) through the National Research Foundation of Korea (NRF). We also thank the Korea Institute of Science and Technology Information (KISTI) Supercomputing Center for providing computing resources (KSC-2020-INO-0010) and the Ewha Womans University Research Grant of 2021, and Peng Cheng Scholar (to S.C.). We also thank Dr Raudah Lazim for discussion and proofreading.
References
-
M. J. Comstock and S. L. Suib, in Selectivity in Catalysis, American Chemical Society, 1993, vol. 517, ch. 1, pp. 1–19 Search PubMed.
- S. M. Bachrach, Challenges in computational organic chemistry, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 482–487 Search PubMed.
- A. Armstrong, R. A. Boto, P. Dingwall, J. Contreras-García, M. J. Harvey, N. J. Mason and H. S. Rzepa, The Houk–List transition states for organocatalytic mechanisms revisited, Chem. Sci., 2014, 5, 2057–2071 Search PubMed.
- G. J. Cheng, X. Zhang, L. W. Chung, L. Xu and Y. D. Wu, Computational organic chemistry: bridging theory and experiment in establishing the mechanisms of chemical reactions, J. Am. Chem. Soc., 2015, 137, 1706–1725 Search PubMed.
- Q. Peng, F. Duarte and R. S. Paton, Computing organic stereoselectivity - from concepts to quantitative calculations and predictions, Chem. Soc. Rev., 2016, 45, 6093–6107 Search PubMed.
- K. N. Houk and F. Liu, Holy Grails for Computational Organic Chemistry and Biochemistry, Acc. Chem. Res., 2017, 50, 539–543 Search PubMed.
- K. N. Houk, M. N. Paddon-Row, N. G. Rondan, Y. D. Wu, F. K. Brown, D. C. Spellmeyer, J. T. Metz, Y. Li and R. J. Loncharich, Theory and modeling of stereoselective organic reactions, Science, 1986, 231, 1108 Search PubMed.
- M. Torrent, M. Solà and G. Frenking, Theoretical Studies of Some Transition-Metal-Mediated Reactions of Industrial and Synthetic Importance, Chem. Rev., 2000, 100, 439–494 Search PubMed.
- S. J. Klippenstein, V. S. Pande and D. G. Truhlar, Chemical Kinetics and Mechanisms of Complex Systems: A Perspective on Recent Theoretical Advances, J. Am. Chem. Soc., 2014, 136, 528–546 Search PubMed.
- K. N. Houk and P. H. Y. Cheong, Computational prediction of small-molecule catalysts, Nature, 2008, 455, 309–313 Search PubMed.
-
L. C. Grabow, in Computational Catalysis, The Royal Society of Chemistry, 2014, pp. 1–58, 10.1039/9781849734905-00001.
- K. Rohmann, M. Hölscher and W. Leitner, Can Contemporary Density Functional Theory Predict Energy Spans in Molecular Catalysis Accurately Enough To Be Applicable for in Silico Catalyst Design? A Computational/Experimental Case Study for the Ruthenium-Catalyzed Hydrogenation of Olefins, J. Am. Chem. Soc., 2016, 138, 433–443 Search PubMed.
- S. E. Wheeler, T. J. Seguin, Y. Guan and A. C. Doney, Noncovalent Interactions in Organocatalysis and the Prospect of Computational Catalyst Design, Acc. Chem. Res., 2016, 49, 1061–1069 Search PubMed.
- D. J. Durand and N. Fey, Computational Ligand Descriptors for Catalyst Design, Chem. Rev., 2019, 119, 6561–6594 Search PubMed.
- K. J. Laidler and M. C. King, Development of transition-state theory, J. Phys. Chem., 1983, 87, 2657–2664 Search PubMed.
- D. G. Truhlar, B. C. Garrett and S. J. Klippenstein, Current Status of Transition-State Theory, J. Phys. Chem., 1996, 100, 12771–12800 Search PubMed.
-
E. G. Lewars, in Computational Chemistry: Introduction to the Theory and Applications of Molecular and Quantum Mechanics, ed. E. G. Lewars, Springer International Publishing, Cham, 2016, pp. 9–49, DOI:10.1007/978-3-319-30916-3_2.
- K.-C. Lin, Understanding product optimization: Kinetic versus thermodynamic control, J. Chem. Educ., 1988, 65, 857 Search PubMed.
- S. R. Marsden, L. Mestrom, D. G. G. McMillan and U. Hanefeld, Thermodynamically and Kinetically Controlled Reactions in Biocatalysis – from Concepts to Perspectives, ChemCatChem, 2020, 12, 426–437 Search PubMed.
- J. I. Seeman, The Curtin-Hammett principle and the Winstein-Holness equation: new definition and recent extensions to classical concepts, J. Chem. Educ., 1986, 63, 42 Search PubMed.
- S. R. Hare and D. J. Tantillo, Dynamic behavior of rearranging carbocations - implications for terpene biosynthesis, Beilstein J. Org. Chem., 2016, 12, 377–390 Search PubMed.
- W. M. C. Sameera and F. Maseras, Transition metal catalysis by density functional theory and density functional theory/molecular mechanics, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 375–385 Search PubMed.
-
R. G. Parr, Dordrecht, in Density Functional Thoery of Atoms and Molecules, 1980 Search PubMed.
- Q. N. N. Nguyen and D. J. Tantillo, The Many Roles of Quantum Chemical Predictions in Synthetic Organic Chemistry, Chem. - Asian J., 2014, 9, 674–680 Search PubMed.
-
W. Koch and M. C. Holthausen, A Chemist's Guide to Density Functional Theory, Wiley-VCH, Weinheim, Germany, 2nd edn, 2001 Search PubMed.
- K. N. Houk, Foreword: Applied computational chemistry, Chem. Soc. Rev., 2014, 43, 4905–4905 Search PubMed.
- M. M. Ignjatovic, O. Caldararu, G. Dong, C. Munoz-Gutierrez, F. Adasme-Carreno and U. Ryde, Binding-affinity predictions of HSP90 in the D3R Grand Challenge 2015 with docking, MM/GBSA, QM/MM, and free-energy simulations, J. Comput.-Aided Mol. Des., 2016, 30, 707–730 Search PubMed.
- L. W. Chung, W. M. C. Sameera, R. Ramozzi, A. J. Page, M. Hatanaka, G. P. Petrova, T. V. Harris, X. Li, Z. F. Ke, F. Y. Liu, H. B. Li, L. N. Ding and K. Morokuma, The ONIOM Method and Its Applications, Chem. Rev., 2015, 115, 5678–5796 Search PubMed.
- T. Vreven, K. S. Byun, I. Komaromi, S. Dapprich, J. A. Montgomery, K. Morokuma and M. J. Frisch, Combining Quantum Mechanics Methods with Molecular Mechanics Methods in ONIOM, J. Chem. Theory Comput., 2006, 2, 815–826 Search PubMed.
- A. E. Cho, V. Guallar, B. J. Berne and R. Friesner, Importance of accurate charges in molecular docking: Quantum mechanical/molecular mechanical (QM/MM) approach, J. Comput. Chem., 2005, 26, 915–931 Search PubMed.
- The Nobel Prize in Chemistry 2013, https://www.nobelprize.org/prizes/chemistry/2013/summary/, (accessed 10 Feb 2020).
- A. Warshel, Multiscale Modeling of Biological Functions: From Enzymes to Molecular Machines (Nobel Lecture), Angew. Chem., Int. Ed., 2014, 53, 10020–10031 Search PubMed.
- M. Levitt, Birth and Future of Multiscale Modeling for Macromolecular Systems (Nobel Lecture), Angew. Chem., Int. Ed., 2014, 53, 10006–10018 Search PubMed.
- M. Karplus, Development of Multiscale Models for Complex Chemical Systems: From H+H2 to Biomolecules (Nobel Lecture), Angew. Chem., Int. Ed., 2014, 53, 9992–10005 Search PubMed.
- H. M. Senn and W. Thiel, QM/MM Methods for Biomolecular Systems, Angew. Chem., Int. Ed., 2009, 48, 1198–1229 Search PubMed.
- R. Lonsdale, J. N. Harvey and A. J. Mulholland, A practical guide to modelling enzyme-catalysed reactions, Chem. Soc. Rev., 2012, 41, 3025–3038 Search PubMed.
- F. H. Wallrapp and V. Guallar, Mixed quantum mechanics and molecular mechanics methods: Looking inside proteins, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 315–322 Search PubMed.
- T. Vreven, K. S. Byun, I. Komáromi, S. Dapprich, J. A. Montgomery, K. Morokuma and M. J. Frisch, Combining Quantum Mechanics Methods with Molecular Mechanics Methods in ONIOM, J. Chem. Theory Comput., 2006, 2, 815–826 Search PubMed.
- L. W. Chung, H. Hirao, X. Li and K. Morokuma, The ONIOM method: its foundation and applications to metalloenzymes and photobiology, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 327–350 Search PubMed.
- L. Cao and U. Ryde, On the Difference Between Additive and Subtractive QM/MM Calculations, Front. Chem., 2018, 6, 89 Search PubMed.
- M. Svensson, S. Humbel, R. D. J. Froese, T. Matsubara, S. Sieber and K. Morokuma, ONIOM: A Multilayered Integrated MO+MM Method for Geometry Optimizations and Single Point Energy Predictions. A Test for Diels−Alder Reactions and Pt(P(t-Bu)3)2+H2 Oxidative Addition, J. Phys. Chem., 1996, 100, 19357–19363 Search PubMed.
- D. Bakowies and W. Thiel, Hybrid Models for Combined Quantum Mechanical and Molecular Mechanical Approaches, J. Phys. Chem., 1996, 100, 10580–10594 Search PubMed.
- S. Dapprich, I. Komáromi, K. S. Byun, K. Morokuma and M. J. Frisch, A new ONIOM implementation in Gaussian98. Part I. The calculation of energies, gradients, vibrational frequencies and electric field derivatives, J. Mol. Struct.: THEOCHEM, 1999, 461–462, 1–21 Search PubMed.
- T. Vreven and K. Morokuma, Investigation of the S0–>S1 excitation in bacteriorhodopsin with the ONIOM(MO:MM) hybrid method, Theor. Chem. Acc., 2003, 109, 125–132 Search PubMed.
- A. Bhattacharya, A. Chatterjee and P. K. Bose, On an Alkaloid of Kopsia Fruticosa. I, J. Am. Chem. Soc., 1949, 71, 3370–3372 Search PubMed.
- W. D. Crow and M. Michael, The Alkaloids of Kopsia longiflora Merrill. I. Isolation of the Alkaloids, Aust. J. Chem., 1955, 8, 129–135 Search PubMed.
- T. Gallagher and P. Magnus, Synthesis of (±)-kopsanone and (±)-10,22-dioxokopsane, hetacyclic indole alkaloids, J. Am. Chem. Soc., 1983, 105, 2086–2087 Search PubMed.
- X. L. Jia, H. H. Lei, F. P. Han, T. Zhang, Y. Chen, Z. S. Xu, P. Nakliang, S. Choi, Y. Guo and T. Ye, Asymmetric Total Syntheses of Kopsane Alkaloids via a PtCl2-Catalyzed Intramolecular [3+2] Cycloaddition, Angew. Chem., 2020, 59, 12832–12836 Search PubMed.
- M. P. Doyle and D. C. Forbes, Recent Advances in Asymmetric Catalytic Metal Carbene Transformations, Chem. Rev., 1998, 98, 911–936 Search PubMed.
- A.-H. Li, L.-X. Dai and V. K. Aggarwal, Asymmetric Ylide Reactions: Epoxidation, Cyclopropanation, Aziridination, Olefination, and Rearrangement, Chem. Rev., 1997, 97, 2341–2372 Search PubMed.
- Z. Y. Liu, X. J. Jin and Y. F. Dang, Mechanistic Studies of Copper(I)-Catalyzed Stereoselective [2,3]-Sigmatropic Rearrangements of Diazoesters with Allylic Iodides/Sulfides, ACS Catal., 2021, 11, 691–702 Search PubMed.
- N. R. Candeias, R. Paterna and P. M. P. Gois, Homologation Reaction of Ketones with Diazo Compounds, Chem. Rev., 2016, 116, 2937–2981 Search PubMed.
- Z. Zhang and J. Wang, Recent studies on the reactions of α-diazocarbonyl compounds, Tetrahedron, 2008, 64, 6577–6605 Search PubMed.
- T. Ye and M. A. McKervey, Organic Synthesis with .alpha.-Diazo Carbonyl Compounds, Chem. Rev., 1994, 94, 1091–1160 Search PubMed.
- F. Tan, M. P. Pu, J. He, J. Z. Li, J. Yang, S. X. Dong, X. H. Liu, Y. D. Wu and X. M. Feng, Catalytic Asymmetric Homologation of Ketones with alpha-Alkyl alpha-Diazo Esters, J. Am. Chem. Soc., 2021, 143, 2394–2402 Search PubMed.
- R. F. Affeldt, A. C. de Amorim Borges, D. Russowsky and F. S. Rodembusch, Synthesis and fluorescence properties of benzoxazole-1,4-dihydropyridine dyads achieved by a multicomponent reaction, New J. Chem., 2014, 38, 4607–4614 Search PubMed.
- G. Marzaro, A. Chilin, G. Pastorini and A. Guiotto, A Novel Convenient Synthesis of Benzoquinazolines, Org. Lett., 2006, 8, 255–256 Search PubMed.
- D. A. Horton, G. T. Bourne, J. Coughlan, S. M. Kaiser, C. M. Jacobs, A. Jones, A. Rühmann, J. Y. Turner and M. L. Smythe, Cyclic tetrapeptides via the ring contraction strategy: chemical techniques useful for their identification, Org. Biomol. Chem., 2008, 6, 1386–1395 Search PubMed.
- X. Chen, J. Wang, S. Sun, J. Fan, S. Wu, J. Liu, S. Ma, L. Zhang and X. Peng, Efficient enhancement of DNA cleavage activity by introducing guanidinium groups into diiron(III) complex, Bioorg. Med. Chem. Lett., 2008, 18, 109–113 Search PubMed.
- N. Grimblat, A. M. Sarotti, T. S. Kaufman and S. O. Simonetti, A theoretical study of the Duff reaction: insights into its selectivity, Org. Biomol. Chem., 2016, 14, 10496–10501 Search PubMed.
- N. Ueberschaar, Z. Xu, K. Scherlach, M. Metsä-Ketelä, T. Bretschneider, H.-M. Dahse, H. Görls and C. Hertweck, Synthetic Remodeling of the Chartreusin Pathway to Tune Antiproliferative and Antibacterial Activities, J. Am. Chem. Soc., 2013, 135, 17408–17416 Search PubMed.
- W. Guo, B. Wu, X. Zhou, P. Chen, X. Wang, Y.-G. Zhou, Y. Liu and C. Li, Formal Asymmetric Catalytic Thiolation with a Bifunctional Catalyst at a Water–Oil Interface: Synthesis of Benzyl Thiols, Angew. Chem., Int. Ed., 2015, 54, 4522–4526 Search PubMed.
- Y. Chen, M. Cheng, F.-Q. Liu, P. Xia, K. Qian, D. Yu, Y. Xia, Z.-Y. Yang, C.-H. Chen, S. L. Morris-Natschke and K.-H. Lee, Anti-AIDS agents 86. Synthesis and anti-HIV evaluation of 2′,3′-seco-3′-nor DCP and DCK analogues, Eur. J. Med. Chem., 2011, 46, 4924–4936 Search PubMed.
- T. Seki, T. Nakao, T. Masuda, K. Hasumi, K. Gotanda, T. Ishimori, S. Honma, N. Minami, K. Shibata and K. Yasuda, Studies on Agents with Vasodilator and β-Blocking Activities. IV, Chem. Pharm. Bull., 1996, 44, 2061–2069 Search PubMed.
- E. C. Neeve, S. J. Geier, I. A. I. Mkhalid, S. A. Westcott and T. B. Marder, Diboron(4) Compounds: From Structural Curiosity to Synthetic Workhorse, Chem. Rev., 2016, 116, 9091–9161 Search PubMed.
- M. Wang and Z. Shi, Methodologies and Strategies for Selective Borylation of C–Het and C–C Bonds, Chem. Rev., 2020, 120, 7348–7398 Search PubMed.
- I. A. I. Mkhalid, J. H. Barnard, T. B. Marder, J. M. Murphy and J. F. Hartwig, C−H Activation for the Construction of C−B Bonds, Chem. Rev., 2010, 110, 890–931 Search PubMed.
- Z. J. Kuang, H. H. Chen, J. X. Yan, K. Yang, Y. Lan and Q. L. Song, Base-Catalyzed Borylation/B-O Elimination of Propynols and B2pin2 Delivering Tetrasubstituted Alkenylboronates, Org. Lett., 2018, 20, 5153–5157 Search PubMed.
- H. H. Chen, T. Zhang, C. H. Shan, S. Liu, Q. L. Song, R. P. Bai and Y. Lan, Mechanism of Bronsted-Base-Mediated Borylation of Propynols: A DFT Study, Org. Lett., 2019, 21, 4924–4928 Search PubMed.
- Z. Li and H. X. Gao, Theoretical study on the mechanism of Ag-catalyzed synthesis of 3-alkylideneoxindoles from N-aryl-alpha-diazoamides: a Lewis acid or Ag-carbene pathway?, Org. Biomol. Chem., 2012, 10, 6294–6298 Search PubMed.
- J. Zhang, C. H. Shan, T. Zhang, J. S. Song, T. Liu and Y. Lan, Computational advances aiding mechanistic understanding of silver-catalyzed carbene/nitrene/silylene transfer reactions, Coord. Chem. Rev., 2019, 382, 69–84 Search PubMed.
- S. Kobayashi, Scandium Triflate in Organic Synthesis, Eur. J. Org. Chem., 1999, 15–27 Search PubMed.
- F. R. Liu, L. Zhu, T. Zhang, K. B. Zhong, Q. Xiong, B. M. Shen, S. H. Liu, Y. Lan and R. P. Bai, Nucleophilicity versus Bronsted Basicity Controlled Chemoselectivity: Mechanistic Insight into Silver- or Scandium-Catalyzed Diazo Functionalization, ACS Catal., 2020, 10, 1256–1263 Search PubMed.
- Z. Liu, P. Sivaguru, G. Zanoni, E. A. Anderson and X. Bi, Catalyst-Dependent Chemoselective Formal Insertion of Diazo Compounds into C−C or C−H Bonds of 1,3-Dicarbonyl Compounds, Angew. Chem., Int. Ed., 2018, 57, 8927–8931 Search PubMed.
- H. Shimizu, I. Nagasaki, K. Matsumura, N. Sayo and T. Saito, Developments in Asymmetric Hydrogenation from an Industrial Perspective, Acc. Chem. Res., 2007, 40, 1385–1393 Search PubMed.
- T. C. Nugent and M. El-Shazly, Chiral Amine Synthesis – Recent Developments and Trends for Enamide Reduction, Reductive Amination, and Imine Reduction, Adv. Synth. Catal., 2010, 352, 753–819 Search PubMed.
- M. Breuer, K. Ditrich, T. Habicher, B. Hauer, M. Keßeler, R. Stürmer and T. Zelinski, Industrial Methods for the Production of Optically Active Intermediates, Angew. Chem., Int. Ed., 2004, 43, 788–824 Search PubMed.
- H. Y. Xu, P. Yang, P. Chuanprasit, H. Hirao and J. R. Zhou, Nickel-Catalyzed Asymmetric Transfer Hydrogenation of Hydrazones and Other Ketimines, Angew. Chem., Int. Ed., 2015, 54, 5112–5116 Search PubMed.
- P. Yang, L. H. Lim, P. Chuanprasit, H. Hirao and J. Zhou, Nickel-Catalyzed Enantioselective Reductive Amination of Ketones with Both Arylamines and Benzhydrazide, Angew. Chem., Int. Ed., 2016, 55, 12083–12087 Search PubMed.
- W. W. Luo, Z. C. Sun, E. H. N. Fernando, V. N. Nesterov, T. R. Cundari and H. Wang, Asymmetric Ring-Opening of Donor-Acceptor Cyclopropanes with Primary Arylamines Catalyzed by a Chiral Heterobimetallic Catalyst, ACS Catal., 2019, 9, 8285–8293 Search PubMed.
- A. Parra, S. Reboredo, A. M. Martín-Castro and J. Alemán, Metallic organophosphates as catalysts in asymmetric synthesis: a return journey, Org. Biomol. Chem., 2012, 10, 5001–5020 Search PubMed.
- M. Rueping, R. M. Koenigs and I. Atodiresei, Unifying Metal and Brønsted Acid Catalysis—Concepts, Mechanisms, and Classifications, Chem. – Eur. J., 2010, 16, 9350–9365 Search PubMed.
- T. Akiyama, J. Itoh, K. Yokota and K. Fuchibe, Enantioselective Mannich-Type Reaction Catalyzed by a Chiral Brønsted Acid, Angew. Chem., Int. Ed., 2004, 43, 1566–1568 Search PubMed.
- M. Terada, Binaphthol-derived phosphoric acid as a versatile catalyst for enantioselective carbon–carbon bond forming reactions, Chem. Commun., 2008, 4097–4112 Search PubMed.
- T. Akiyama, Stronger Brønsted Acids, Chem. Rev., 2007, 107, 5744–5758 Search PubMed.
- J. Fu, X. Huo, B. Li and W. Zhang, Cooperative bimetallic catalysis in asymmetric allylic substitution, Org. Biomol. Chem., 2017, 15, 9747–9759 Search PubMed.
- D. J. Tantillo, Faster, Catalyst! React! React! Exploiting Computational Chemistry for Catalyst Development and Design, Acc. Chem. Res., 2016, 49, 1079–1079 Search PubMed.
- S. Dinda, Computational Study of Enantioselectivity in the Asymmetric Allylation of Aldehydes with Chiral Pt(II) Phosphinite Complexes, J. Org. Chem., 2018, 83, 13911–13921 Search PubMed.
- P. H.-Y. Cheong, C. Y. Legault, J. M. Um, N. Çelebi-Ölçüm and K. N. Houk, Quantum Mechanical Investigations of Organocatalysis: Mechanisms, Reactivities, and Selectivities, Chem. Rev., 2011, 111, 5042–5137 Search PubMed.
- A. Erkkilä, I. Majander and P. M. Pihko, Iminium Catalysis, Chem. Rev., 2007, 107, 5416–5470 Search PubMed.
- D. W. C. MacMillan, The advent and development of organocatalysis, Nature, 2008, 455, 304–308 Search PubMed.
- P. I. Dalko, Asymmetric Organocatalysis: A New Stream in Organic Synthesis, Enantiosel. Organocatal., 2007, 1–17, DOI:10.1002/9783527610945.ch1.
- G. G. Gerosa, M. O. Marcarino, R. A. Spanevello, A. G. Suarez and A. M. Sarotti, Re-Engineering Organocatalysts for Asymmetric Friedel-Crafts Alkylation of Indoles through Computational Studies, J. Org. Chem., 2020, 85, 9969–9978 Search PubMed.
- Y. Takeda, W. M. C. Sameera and S. Minakata, Palladium-Catalyzed Regioselective and Stereospecific Ring-Opening Cross-Coupling of Aziridines: Experimental and Computational Studies, Acc. Chem. Res., 2020, 53, 1686–1702 Search PubMed.
- A. Dauth and J. A. Love, Synthesis and reactivity of 2-azametallacyclobutanes, Dalton
Trans., 2012, 41, 7782–7791 Search PubMed.
- B. L. Lin, C. R. Clough and G. L. Hillhouse, Interactions of Aziridines with Nickel Complexes: Oxidative-Addition and Reductive-Elimination Reactions that Break and Make C−N Bonds, J. Am. Chem. Soc., 2002, 124, 2890–2891 Search PubMed.
|
| This journal is © the Partner Organisations 2021 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Sanghee
Yoon
a and
Sun
Choi
a,
Sanghee
Yoon
a and
Sun
Choi
 *ab
*ab

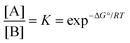
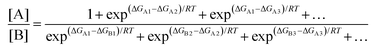

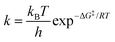
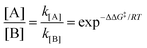
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 at 273 K.5 The stereoselectivity is written in terms of enantiomeric excess percentage (%ee) or diastereomeric ratio (dr). In the first case, it indicates the percentage of one enantiomeric product over the other, which is expressed as:
10 at 273 K.5 The stereoselectivity is written in terms of enantiomeric excess percentage (%ee) or diastereomeric ratio (dr). In the first case, it indicates the percentage of one enantiomeric product over the other, which is expressed as: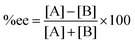
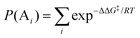
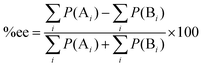
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QM2) and (ii) it can be extended to multiple layers (>2 layers) calculations. The energy expression of ONIOM (QM1
QM2) and (ii) it can be extended to multiple layers (>2 layers) calculations. The energy expression of ONIOM (QM1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QM2) is written as:
QM2) is written as:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QM2
QM2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QM3) or ONIOM (QM1
QM3) or ONIOM (QM1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QM2
QM2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MM). The general expression of energy calculation is:
MM). The general expression of energy calculation is: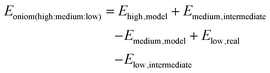
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QM2 or QM
QM2 or QM![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MM approaches can be applied. Parts of the molecule that are involved in bond breaking/forming will be calculated using the higher QM method, while the rest is estimated by lower QM methods or classical MM. In this review, we highlighted recent applications of various computational techniques to understand the selectivity of organic synthesis and future application for catalyst and molecular design.
MM approaches can be applied. Parts of the molecule that are involved in bond breaking/forming will be calculated using the higher QM method, while the rest is estimated by lower QM methods or classical MM. In this review, we highlighted recent applications of various computational techniques to understand the selectivity of organic synthesis and future application for catalyst and molecular design.
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) S bond is more promising in the free sulfonium ylide system rather than the zwitterion. Therefore, a free ylide mechanism that dictates a free sulfonium ylide leaving the Cu(I) catalyst via ligand exchange is a promising option for sulfonium [2,3]-sigmatropic rearrangement. According to the computational results, the regioselectivity is controlled by the electronic properties of the system and the stereoselectivity is mainly controlled by the substrate–ligand steric interactions.
S bond is more promising in the free sulfonium ylide system rather than the zwitterion. Therefore, a free ylide mechanism that dictates a free sulfonium ylide leaving the Cu(I) catalyst via ligand exchange is a promising option for sulfonium [2,3]-sigmatropic rearrangement. According to the computational results, the regioselectivity is controlled by the electronic properties of the system and the stereoselectivity is mainly controlled by the substrate–ligand steric interactions.


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0
0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (R2/R4/R6). Considering the most stable R2/R6 substituted products, the calculated selectivity of the product was 26
3 (R2/R4/R6). Considering the most stable R2/R6 substituted products, the calculated selectivity of the product was 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 74 (R2/R6) which was in excellent agreement with experimental findings (21
74 (R2/R6) which was in excellent agreement with experimental findings (21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 79). A further seven phenol derivatives were also investigated to understand the steric hindrance and electronic effect of the substituents (Table 1). The calculations suggested that the C–C bond formation of the Duff reaction is an endothermic reaction with energies between 1.50 and 15.05 kcal mol−1. The product ratio prediction using their relative product stabilities agreed well with the reported regioselectivities61–64 and indicated that regioselectivity is under thermodynamic control. Additional studies implied that the R2 substitution was preferred for electron-withdrawing group substituted phenol, meanwhile the R6 substitution occurs when R is an electron-donating group. However, the electronic effect is not the only conclusive feature that controls the selectivity of the reaction.
79). A further seven phenol derivatives were also investigated to understand the steric hindrance and electronic effect of the substituents (Table 1). The calculations suggested that the C–C bond formation of the Duff reaction is an endothermic reaction with energies between 1.50 and 15.05 kcal mol−1. The product ratio prediction using their relative product stabilities agreed well with the reported regioselectivities61–64 and indicated that regioselectivity is under thermodynamic control. Additional studies implied that the R2 substitution was preferred for electron-withdrawing group substituted phenol, meanwhile the R6 substitution occurs when R is an electron-donating group. However, the electronic effect is not the only conclusive feature that controls the selectivity of the reaction.

![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C was excluded due to the high barrier. The intermediate 14 was observed experimentally. The calculation revealed that the transformation of intermediate 14 to product (Pro) proceeded through reductive dihydroxylation via multiple methoxy exchange between vinyl boron and the methoxyborate reagent. They suggested that the concerted B-methoxy elimination of borane (18-ts) is the rate-determining step for the entire reaction.
C was excluded due to the high barrier. The intermediate 14 was observed experimentally. The calculation revealed that the transformation of intermediate 14 to product (Pro) proceeded through reductive dihydroxylation via multiple methoxy exchange between vinyl boron and the methoxyborate reagent. They suggested that the concerted B-methoxy elimination of borane (18-ts) is the rate-determining step for the entire reaction.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QM2) approach was applied. The model reaction focused on the hydride insertion step between [(S)-binapine-hydrido nickel(II)]- and s-transoid hydrazine. According to their calculations, the hydrazine chelated to the metal center via the amide group in the early stage of the reaction (Fig. 8). The energy difference between the two diastereomeric transition states was 2.9 kcal mol−1, which is in good agreement with experimental results where the stereoselectivity was 97%ee. Remarkably, the phenyl ring of the benzamide of hydrazine was not involved in stereoinduction due to no significant contact with the Ni-binapine catalyst. Moreover, the replacement of the phenyl ring by the hydrogen atom did not change the energy splitting between the two diastereomeric TSs. The geometry observation of the Ni-binapine catalyst found that the shallow concave site is suitable for the s-transoid hydrazine. The top-left and bottom-right quadrants were shielded by the tert-butyl groups of the binapine ligand. This situation leads to a shape complementary of the catalyst–substrate complex which is often found in enzymatic catalysis (Fig. 10).
QM2) approach was applied. The model reaction focused on the hydride insertion step between [(S)-binapine-hydrido nickel(II)]- and s-transoid hydrazine. According to their calculations, the hydrazine chelated to the metal center via the amide group in the early stage of the reaction (Fig. 8). The energy difference between the two diastereomeric transition states was 2.9 kcal mol−1, which is in good agreement with experimental results where the stereoselectivity was 97%ee. Remarkably, the phenyl ring of the benzamide of hydrazine was not involved in stereoinduction due to no significant contact with the Ni-binapine catalyst. Moreover, the replacement of the phenyl ring by the hydrogen atom did not change the energy splitting between the two diastereomeric TSs. The geometry observation of the Ni-binapine catalyst found that the shallow concave site is suitable for the s-transoid hydrazine. The top-left and bottom-right quadrants were shielded by the tert-butyl groups of the binapine ligand. This situation leads to a shape complementary of the catalyst–substrate complex which is often found in enzymatic catalysis (Fig. 10).

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QM2) method was used to investigate that reaction. The geometry optimization and frequency calculations were obtained using the ONIOM (B3LYP/(SDD for Ni, 6-31+G* for H, C, N, O, 6-311+G* for P):M06L/(LANL2DZ for Ni, 6-31G for other atoms). The energy refinements were done using single point calculations of ONIOM (B3LYP/def2-TZVP:M06-L/(SDD for Ni, 6-31+G* for H, C, N, O, 6-311+G* for P)). The effect of i-PrOH (∈ = 18.23) was included using the SCRF model. The partition of QM1
QM2) method was used to investigate that reaction. The geometry optimization and frequency calculations were obtained using the ONIOM (B3LYP/(SDD for Ni, 6-31+G* for H, C, N, O, 6-311+G* for P):M06L/(LANL2DZ for Ni, 6-31G for other atoms). The energy refinements were done using single point calculations of ONIOM (B3LYP/def2-TZVP:M06-L/(SDD for Ni, 6-31+G* for H, C, N, O, 6-311+G* for P)). The effect of i-PrOH (∈ = 18.23) was included using the SCRF model. The partition of QM1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QM2 is shown in Fig. 11c. They found that the two diastereomeric transition states are 2.1 kcal mol−1 apart in energy, which was consistent with the experimental %ee. The structural analysis provided an insight into the major factors that helped in stereoselectivity. As shown in Fig. 9a and b, the phenyl rings of the chiral phospholane ligand located at the top-right and bottom-left quadrants restricted the binding pocket around the Ni-center. The E-ketimine substrate fits perfectly in the binding pocket, while the other substrate was distorted and destabilized the minor product formation due to steric hindrance, which forced the N-phenyl ring to rotate (Fig. 11b). Therefore, the large N-aryl rings in aniline tend to improve the stereoselectivity of the reaction as shown in the experimental results.
QM2 is shown in Fig. 11c. They found that the two diastereomeric transition states are 2.1 kcal mol−1 apart in energy, which was consistent with the experimental %ee. The structural analysis provided an insight into the major factors that helped in stereoselectivity. As shown in Fig. 9a and b, the phenyl rings of the chiral phospholane ligand located at the top-right and bottom-left quadrants restricted the binding pocket around the Ni-center. The E-ketimine substrate fits perfectly in the binding pocket, while the other substrate was distorted and destabilized the minor product formation due to steric hindrance, which forced the N-phenyl ring to rotate (Fig. 11b). Therefore, the large N-aryl rings in aniline tend to improve the stereoselectivity of the reaction as shown in the experimental results.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QM2 partition (adapted with permission from ref. 79).
QM2 partition (adapted with permission from ref. 79).

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) QM2) approach was applied to reduce the computational demand of the screening method. The screening workflow is shown in Fig. 14a. Initially, 16 different TS structures were generated. The partition between the high and low layers is shown in Fig. 14b. Full optimization and frequency calculations were performed by ONIOM(B3LYP/6-31G*:AM1). The optimized geometries were subjected to energy refinements using the B3LYP/6-311+G** level with the PCM model using methanol as an implicit solvent to obtain accurate energy profiles. They found that the average difference in energy between the (E) and (Z) configuration formations was 1.1 kcal mol−1 with (E) preferred. It is consistent with the experimental findings. The EDA to determine ΔEiminium, ΔEindole, and ΔEint was also performed. The first two terms were calculated according to the difference between the two diastereomeric TS geometries, while the last term is the interaction energy between the two fragments (catalyst and substrate). The EDA indicated that the iminium and indole are more stable in Re-face formation, which exhibited less distortion in the Re-face attack. The computational prediction demonstrated that the steric interactions of the substituent (R) and CH–π interactions play a crucial role in selectivity (Fig. 14b), with the highest enantiomeric ratio reported to be 92
QM2) approach was applied to reduce the computational demand of the screening method. The screening workflow is shown in Fig. 14a. Initially, 16 different TS structures were generated. The partition between the high and low layers is shown in Fig. 14b. Full optimization and frequency calculations were performed by ONIOM(B3LYP/6-31G*:AM1). The optimized geometries were subjected to energy refinements using the B3LYP/6-311+G** level with the PCM model using methanol as an implicit solvent to obtain accurate energy profiles. They found that the average difference in energy between the (E) and (Z) configuration formations was 1.1 kcal mol−1 with (E) preferred. It is consistent with the experimental findings. The EDA to determine ΔEiminium, ΔEindole, and ΔEint was also performed. The first two terms were calculated according to the difference between the two diastereomeric TS geometries, while the last term is the interaction energy between the two fragments (catalyst and substrate). The EDA indicated that the iminium and indole are more stable in Re-face formation, which exhibited less distortion in the Re-face attack. The computational prediction demonstrated that the steric interactions of the substituent (R) and CH–π interactions play a crucial role in selectivity (Fig. 14b), with the highest enantiomeric ratio reported to be 92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 (Fig. 14c). Thus, this strategy could significantly accelerate and improve the efficiency of rational catalyst design.
8 (Fig. 14c). Thus, this strategy could significantly accelerate and improve the efficiency of rational catalyst design.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 11, which was qualitatively in agreement with the experimental result of 99
11, which was qualitatively in agreement with the experimental result of 99![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Then, proton transfer to an anionic amine was observed. According to the calculations, water molecules could act as a proton source and an internal base in the form of Pd-OH, elevating the four-membered transmetallation between B2(pin)2 and Pd. The supported calculations showed that three water molecules are sufficient to form the hydrogen-bonding network for the proton transfer, which yielded the Pd-OH species. The B(pin)–B(pin) could not coordinate into the inner sphere of the metal center due to steric repulsion between the bulky alkyl group of the ligand and B(pin)–B(pin). However, one of the ligands can be replaced by B(pin) followed by B–B bond cleavage with a barrier of 10.8 kcal mol−1. Ligand exchange between B(pin)-OH and P(t-Bu)2Me ligand occurred. Finally, the reductive elimination process required only 0.1 kcal mol−1. The calculations also revealed that the product dissociation to recover catalyst is facile. The proposed overall catalytic cycle of borylation is shown in Fig. 15. Their experimental and theoretical results provided valuable insight into a new catalyst design involving the ring-opening C–E bond forming cross coupling of aziridine.
1. Then, proton transfer to an anionic amine was observed. According to the calculations, water molecules could act as a proton source and an internal base in the form of Pd-OH, elevating the four-membered transmetallation between B2(pin)2 and Pd. The supported calculations showed that three water molecules are sufficient to form the hydrogen-bonding network for the proton transfer, which yielded the Pd-OH species. The B(pin)–B(pin) could not coordinate into the inner sphere of the metal center due to steric repulsion between the bulky alkyl group of the ligand and B(pin)–B(pin). However, one of the ligands can be replaced by B(pin) followed by B–B bond cleavage with a barrier of 10.8 kcal mol−1. Ligand exchange between B(pin)-OH and P(t-Bu)2Me ligand occurred. Finally, the reductive elimination process required only 0.1 kcal mol−1. The calculations also revealed that the product dissociation to recover catalyst is facile. The proposed overall catalytic cycle of borylation is shown in Fig. 15. Their experimental and theoretical results provided valuable insight into a new catalyst design involving the ring-opening C–E bond forming cross coupling of aziridine.




