Ionic conductivity and dielectric properties of bulk SPP-PEG hydrogels as Na+ ion-based SPE materials for energy storage applications†
Abstract
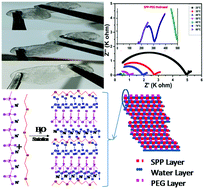
In this work, a green SPP-PEG hydrogel material, containing Na+ ions, was synthesized by a green chemistry method using sodium polyphosphate and polyethylene glycol in water. This hydrogel has an amorphous morphology and a sandwiched matrix with a floating layer, which allows ions to move easily inside the matrix. Flexibility and sticky nature are the key properties that enable forming a good interface on the electrode surface. The hydrogel tends to change to the plasma phase above 70 °C. A Na+ ion–based hydrogel electrolyte shows a stability window of 2.75 volts with >96% ionic nature of conductivity in the order of 10−4 S cm−1 with a diffusivity constant in the order of 10−9 m2 s−1 and mobility in the order of 10−7 m2 V−1 s−1 at room temperature. The hydrogel matrix shows cage-type hopping with a value of power exponent >1 at lower temperatures, and the activation energy of ionic movement was observed to be quite low, i.e. 0.488 eV. Dielectric properties of the hydrogel show a high amount of capacitance with negligible electrode contribution. Regarding temperature dependence, this study confirms that conductivity and matrix relaxation are independent of time and temperature.
- This article is part of the themed collection: 2021 Materials Chemistry Frontiers HOT articles


 Please wait while we load your content...
Please wait while we load your content...