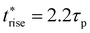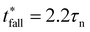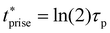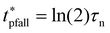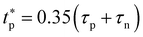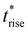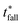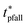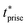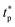Stencil mask defined doctor blade printing of organic single crystal arrays for high-performance organic field-effect transistors†
Yue
Xi
a,
Tao
Wang
b,
Qi
Mu
b,
Congcong
Huang
a,
Shuming
Duan
*a,
Xiaochen
Ren
 *a and
Wenping
Hu
*a and
Wenping
Hu
 *a
*a
aTianjin Key Laboratory of Molecular Optoelectronic Sciences, Department of Chemistry, School of Science, Tianjin University & Collaborative Innovation Center of Chemical Science and Engineering (Tianjin), Tianjin, 300072, China. E-mail: duanshm@tju.edu.cn; renxiaochen@tju.edu.cn; huwp@tju.edu.cn
bSchool of Microelectronics, Tianjin University, Tianjin, 300072, China
First published on 23rd February 2021
Abstract
Organic field-effect transistors (OFETs) are one of the promising candidates for next generation electronics due to their solution processability and good performance superior to amorphous Si devices. Patterning the organic layer is necessary in practical applications to prevent cross talk between different devices. Here, we reported a novel solution processed, high-resolution patterning method named as stencil mask defined doctor blade printing to fabricate regularly patterned organic single crystal arrays. The size of one pattern is around 30 μm, which is smaller than the droplet diameter of conventional inkjet printing. The OFETs based on organic single crystal patterns exhibit extremely low off-state current and high on/off current ratio close to 1010 as well as good device uniformity. The low off-state current demonstrates the potential of the OFET array for low-power or high-performance optical sensing applications. In addition, the short channel OFET array exhibits good frequency response operating at 20 kHz. This work provides an effective patterning strategy to realize solution processed large-area, high-resolution organic single crystal arrays.
1. Introduction
Organic field-effect transistors (OFETs) are the basic building blocks to construct organic integrated circuits.1–3 They are promising candidates for next-generation electronic applications4,5 because of their mechanical flexibility,6 high-performance comparable to oxide semiconductors,7 and solution processability.8 The solubility of organic semiconductors (OSCs), including small molecular weight materials and conjugated polymers, enable cost-effective manufacturing of OSCs by various printing methods to realize high-throughput and continuous fabrication.9,10 To optimize device performance, organic single crystal semiconductors are preferred because of their grain boundary free nature to miniaturize the defect density,11 ensuring excellent and uniform electronic characteristics.12,13 Moreover, to reach a higher level of integration, OFETs are always in an array form with high spatial resolution.14 These applications require the precise patterning of OSC thin films.15,16 Well-patterned OSCs can avoid unwanted leakage current, lower the off-state current and reduce crosstalk between neighboring devices.17,18 Single crystal OSC arrays would be ideal for high-performance organic integrated circuits with excellent uniformity and reproducibility.19–22 However, challenges remain to fabricate organic single crystal arrays with high-resolution by printing methods.23–25Unlike inorganic semiconductors, conventional photolithography processes may not be applicable for OSCs, because the organic semiconductor would be damaged by processing chemicals or high temperature.17,26 Inkjet printing is a promising technology to fabricate large-scale organic electronic device arrays due to its drop-on-demand characteristic and moderate resolution.27–29 Organic patterns are formed by jetting the droplets, so the minimum resolution of one pattern is equal to the diameter of the droplet, typically ranging from 30 to 100 μm.10,30 Further reducing the droplet size may require complex technologies such as electrohydrodynamic jet (E-jet) printing.31 Moreover, the uncontrolled nucleation of organic materials during solidification of droplets results in polycrystalline or amorphous organic thin films.9,32,33 Other than printing, several approaches have been applied to pattern organic semiconductors.34,35 Wang and co-workers employed photolithography-patterned Au electrodes to alter the surface properties of the substrate, and thus to selectively grow TES-ADT single crystals in an array form.36 Self-assembled monolayers and pre-patterned stamps were also employed to direct the nucleation of molecules and subsequent growth of organic crystals. Park et al. prepared highly aligned and patterned transistor arrays with a high density by a differential surface energy and solution shearing method.37 Hasegawa and co-workers obtained a large single crystal array of organic semiconductor C8-BTBT by combining inkjet printing with the solvent–antisolvent crystallization approach.38 However, unlike the low-cost printing process, these methods still require direct photolithography to define the wetting/dewetting region for patterning the organic solution.17,34,35 In addition, multiple grain boundaries are presented in organic thin films, which may increase the device-to-device variation.39–41
In this work, we demonstrated a method to realize solution processed organic single crystal arrays with spatial resolution down to 30 μm, which is smaller than the average droplet size of conventional inkjet printing. A large-area continuous organic single crystalline thin film is first fabricated by using solution shearing, and then covered by a patterned aqueous resist deposited by stencil mask defined doctor blade printing. The aqueous resist defines the pattern of organic single crystals and was finally removed by water rinsing. The patterned single crystal OSC array effectively reduced the parasitic current of the OFET device, resulting in an on/off current ratio close to 1010 on a SiO2 dielectric and 108 within 3 V gate bias on an AlOx dielectric, respectively. The OFET array based on highly oriented OSCs shows good device uniformity. This method demonstrates the potential of printed organic transistors for high-performance, high-resolution organic integrated circuit applications.
2. Results and discussion
Stencil mask defined doctor blade printing
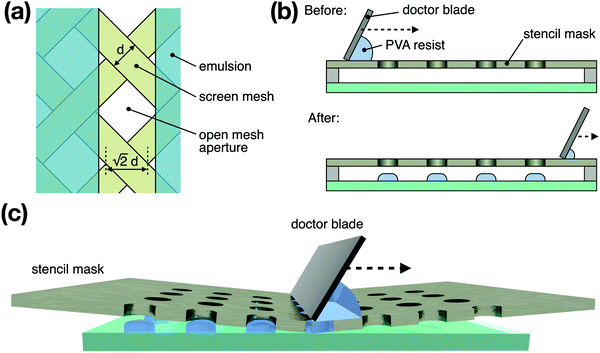
Previously, we demonstrated a new strategy to fabricate organic single crystal array all by solution methods.42 The solution shearing of C8-BTBT/PS blend ink provides a centimeter-scale continuous highly crystalline organic thin film. Because the solution shearing method provides a strong directional convective flow in organic ink, by which the fastest crystal growth axis of the material is easy to align with the coating direction. The insulating polymer in the blended ink also helps to improve the crystallinity of the organic thin film. Then the PVA resist is screen printed on top of the organic layer to form the patterns by performing wet or dry etching. The resulting organic patterns are highly crystalline and share very similar crystal orientation and quality because they originated from the same crystalline thin film. The patterning resolution of the organic layer is determined by the screen mask used for screen printing. In particular, the open mesh aperture of the emulsion coated on the screen mesh defines the printing resolution of screen printing, which is formed by a lithography method.43 The minimum size of opening of the emulsion should be larger than the square root of two times the wire diameter of the screen mesh, as shown in Fig. 1a, otherwise the screen mesh would completely block the open mesh aperture of the emulsion. Therefore, the screen-printing resolution is limited by the wire diameter of the screen mesh. A routinely achievable resolution of screen printed PVA resists ranges from 80 to 100 μm.To overcome the limitations of the screen mesh, we apply a new printing method by replacing the screen mask with a meshless stencil mask made by a molybdenum thin film, named as stencil mask defined doctor blade printing to enhance the printing resolution. The deposition of the PVA resist is realized by pressing the PVA solution through a patterned molybdenum stencil with a doctor blade as shown in Fig. 1b. Homemade printing equipment is built to maintain a small distance between the stencil mask and substrate. A doctor blade is moved across the mask to progressively fill the open mesh apertures with PVA resist, and the elastic deformation of the stencil mask produces a reverse stroke to cause the mask to touch the substrate momentarily along the line of contact, as depicted in Fig. 1c. The meshless nature of the molybdenum stencil enables high-resolution printing of the resist. In this work, the molybdenum stencil is pre-patterned by acid corrosion with a resolution of 30 μm.
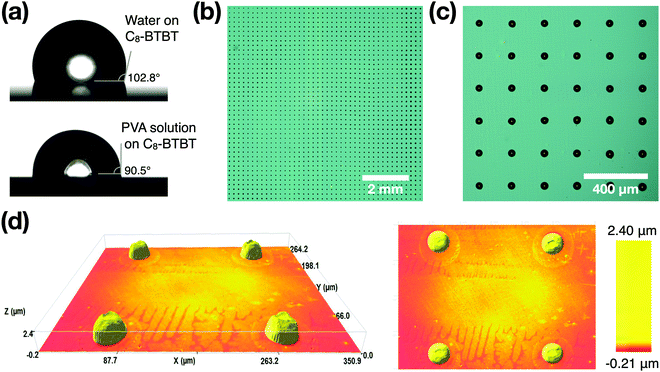
To fabricate a high-resolution organic crystalline array, a large-area highly crystalline C8-BTBT/PS blend thin film is prepared by solution shearing at first (Fig. S1, ESI†). The surface of the C8-BTBT single crystal is hydrophobic with a water contact angle of 102.8°, as shown in Fig. 2a. Although PVA can act as a surfactant in aqueous solution to improve surface wetting, especially at higher concentrations,42 the contact angle of the PVA droplet on the C8-BTBT crystal remains close to 90° (Fig. 2a). In this work, we intentionally use the surface tension of PVA droplets to form a round shaped resist pattern. As a result, the printed 36 wt% PVA aqueous resist has a round shape by using a circular opening stencil mask with a diameter of 30 μm. The overall 1 cm2 printed area and its zoomed-in picture are shown in Fig. 2b and c, respectively. As depicted in Fig. 2b, over 1764 patterns are evenly distributed on 1 cm2 C8-BTBT crystalline thin film. The enlarged Fig. 2c suggests that the average diameter of PVA resist patterns is around 30–40 μm. The statistics of the diameter of the patterns shown in Fig. 2b and c are obtained by applying image processing and plotted in Fig. S2 (ESI†). In Fig. 2b, nearly 85% of the PVA patterns have a diameter ranging from 25 to 35 μm, while the patterns close to the edge slightly deviate from the average size. This is probably due to the higher tension at the edge of the stencil mask during printing and could be improved by increasing the stencil size. The detailed 3D geometry information of the printed PVA resist patterns is measured by Leica DCM8 optical surface measurement equipment and shown in Fig. 2d. The thickness of the resist is around 2 μm with sharp edges, demonstrating the potential for further reducing the pattern size. All the results in Fig. 2b–d indicate high patterning density, high-resolution and good printing quality of stencil mask defined doctor blade printing.
High-resolution OSC single crystal array
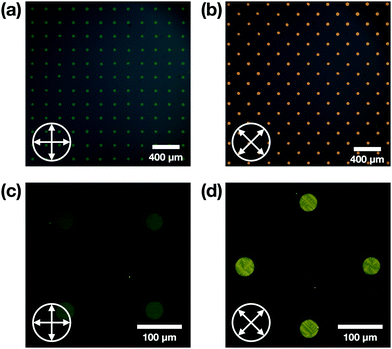
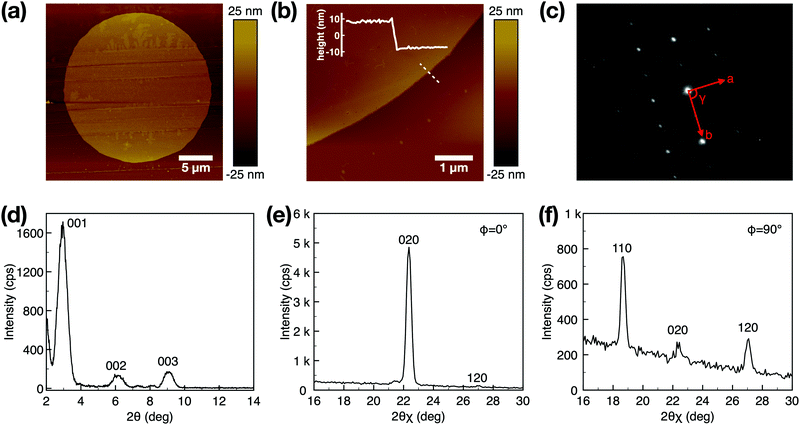
The completion of the OSC single crystal array is fabricated by plasma etching for 40 s followed by water rinsing. To investigate the crystallinity of the as-fabricated C8-BTBT single crystal array, we performed various characterization techniques including polarized optical microscopy (POM), atomic force microscopy (AFM), selected area electron diffraction (SAED), and X-ray diffraction (XRD). The POM images of the OSC array in Fig. 3a and b show that every element in the array has a uniform shape and diameter around 30 μm. When rotating the sample by 45°, all the elements in the array show simultaneous color changing, indicating that they all have the same crystal orientation as well as very similar film thickness and crystal quality. This characteristic is essential for minimizing device-to-device variation of OFETs. Fig. 3c and d show the enlarged POM images of the single crystal array. Within each pattern, there is no grain boundary presented, the color difference in the POM images is due to the thickness variation of the organic crystal. The typical dendritic growth surface morphology is observed for the C8-BTBT material.44 Notice that the 30 μm diameter of the patterns is smaller than one droplet size of conventional inkjet printed OSCs. Moreover, compared to inkjet printing, our method produces a highly aligned, grain boundary free organic crystal array and better patterning uniformity.The atomic force microscopy (AFM) picture in Fig. 4a shows that the smallest diameter of the pattern is smaller than 25 μm. The average root-mean-square roughness of the pattern is 0.68 nm, suggesting that the C8-BTBT has a smooth surface close to the atomic level. As shown in Fig. 4b, the thickness of one C8-BTBT single crystal pattern is 18.6 nm. For a 20 mg mL−1 of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 C8-BTBT/PS blending ratio, the thickness of C8-BTBT is around 8.8 nm, corresponding to three molecular layers.45 The thin thickness and good surface quality are beneficial for reducing the organic bulk resistance at the source/drain contact, resulting in improved charge injection in OFETs. For SAED measurement, as shown in Fig. 4c, the sharp diffraction spots in the SAED pattern indicate a highly crystallized structure of the organic thin film. Lattice constants calculated from the SAED pattern (a = 5.8 Å, b = 7.8 Å, γ = 90.7) agree well with reported C8-BTBT bulk crystal data.
1 C8-BTBT/PS blending ratio, the thickness of C8-BTBT is around 8.8 nm, corresponding to three molecular layers.45 The thin thickness and good surface quality are beneficial for reducing the organic bulk resistance at the source/drain contact, resulting in improved charge injection in OFETs. For SAED measurement, as shown in Fig. 4c, the sharp diffraction spots in the SAED pattern indicate a highly crystallized structure of the organic thin film. Lattice constants calculated from the SAED pattern (a = 5.8 Å, b = 7.8 Å, γ = 90.7) agree well with reported C8-BTBT bulk crystal data.
The crystalline properties and crystal packing are further studied by examining X-ray diffraction (XRD) of the C8-BTBT single crystal array as shown in Fig. 4d. The out-of-plane XRD profile presents a smooth baseline and sharp diffraction peaks indicating the highly ordered and crystalline quality of C8-BTBT. The corresponding secondary diffraction peaks were also observed, manifesting the layer-by-layer growth of organic semiconductor molecules on the substrate. Moreover, these diffraction peaks correspond well to the crystal structure of C8-BTBT reported previously,46 which indicates that the ab-plane is parallel to the substrate. We performed in-plane XRD for organic crystalline thin films before patterning. The results depicted in Fig. 4e and f show one strong Bragg diffraction peak (020) when the incident X-ray beam is parallel to the shearing direction (ϕ = 0°), while the (020) peak decays quickly, and strong (110) and (120) peaks were observed when the sample rotates around the ϕ axis by 90°, indicating that all the patterns in the array are highly crystalline in the in-plane direction and the a-axis of all the C8-BTBT patterns are roughly parallel to the shearing direction.47 The presence of the (120) peak in Fig. 4d suggests that there are a small portion of molecules in the array oriented in a different direction.48
Electrical characteristics of the single crystal OFET array
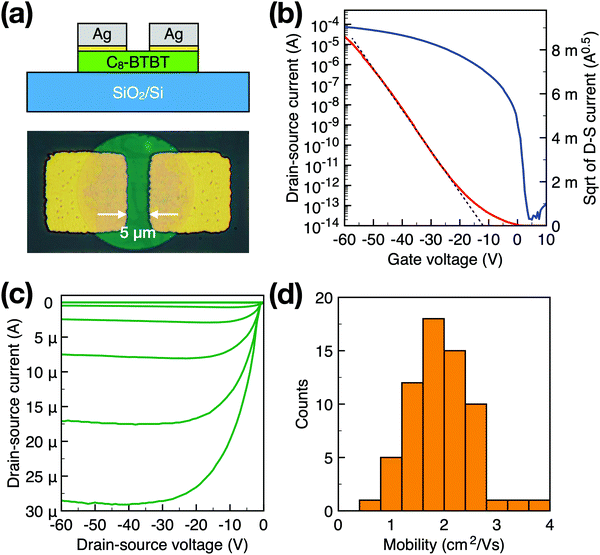
To characterize the electrical properties of the patterned OSC arrays, bottom-gate and top-contact organic field-effect transistors (OFETs) were fabricated on a SiO2/Si substrate finished by thermally evaporated Ag (40 nm) used as source/drain electrodes combined with a 5 nm F4-TCNQ injection layer. As shown by the optical image depicted in Fig. 5a, the fine copper grid was used as a shadow mask, and the channel width and length of the OFET are 20 and 5 μm, respectively. Fig. 5b shows a representative transfer I–V characteristic of a patterned C8-BTBT OFET. The unit-area capacitance (Ci) of the dielectric, which consists of phase separation formed PS and SiO2 is measured to be 10.6 nF cm−2 (Fig. S3, ESI†). In Fig. 5b, the transistor exhibits a standard p-type FET I–V characteristic behavior with a high on/off current ratio close to 1010, which can be attributed to the patterning induced low off-state current. Patterning the OSC eliminates most of the unwanted fringe current from the lateral path, leading to extremely low off-state current. The carrier mobility estimated from the slope of the transfer I–V curve is 2.34 cm2 V−1 s−1, which is lower than the reported value of the same OSC on a SiO2 dielectric.42 The reason for the decreased mobility is probably due to the short channel length of the OFET so that the contact resistance becomes more significant compared to the channel resistance. Therefore, the drain–source voltage (VDS) applied on the channel has been reduced because of the voltage drop on contact resistance, and thus the apparent mobility of the device is decreased. The nonlinearity of the output I–V at a small VDS region proves the existence of contact resistance (Fig. 5c). Because all of the patterns are inherited from the same organic crystalline thin film, the device array exhibits uniform electrical characteristics. As depicted in Fig. 5d and in Fig. S4 (ESI†), the standard deviation of mobility and threshold voltage (Vth) is 0.59 cm2 V−1 s−1 and 1.48 V, respectively.Low voltage single crystal OFET array
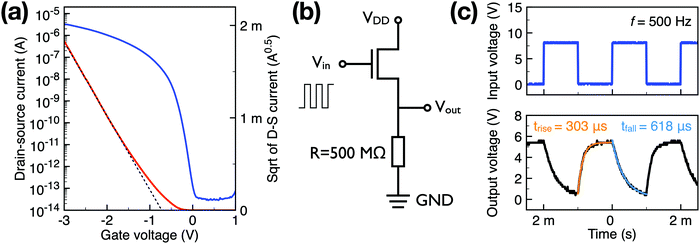
To demonstrate the low-power applications of the high-resolution patterning method, we fabricated a low-voltage OFET array on an anodized AlOx dielectric layer. The representative transfer I–V curve for a patterned C8-BTBT single crystal OFET is shown in Fig. 6a. The saturation mobility and the threshold voltage of the device is 1.53 cm2 V−1 s−1 and −0.74 V, respectively. The Ci of PS/AlOx is measured to be 174 nF cm−2 shown in Fig. S5 (ESI†). Except from a battery range operating voltage benefited from high-k dielectric, the on/off current ratio of the OFET is as large as 108 within −3 V gate bias. The patterned OSC layer effectively reduces the fringe current as well as possible gate leakage current, resulting in a relatively low off-state current in the range of several tens of fA. Therefore, the on/off current ratio of the low-voltage OFET reaches over 108. To confirm this result, we measured eight devices and the averaged on/off ratio is larger than 108 (Fig. S6, ESI†). We summarize the device parameters of recently reported low voltage OFETs as listed in Table 1. It is clear that nearly two orders of magnitude enhancement of the on/off current ratio have been achieved, which is attributed to the patterned OSCs. The extremely low off-state current also largely reduces the static power consumption of OFETs, proving its suitability for low-power applications. Furthermore, the off-state current is directly related to the noise equivalent power of a phototransistor device, and reducing the off-state current could significantly enhance the specific detectivity and dynamic range of the phototransistor, demonstrating the potential of this device for high-performance optical sensing applications.| Semiconductor material | Crystallinity | OFET structure | Saturation VG (V) | On/off ratio | SS (mV dec−1) | Mobility (cm2 V−1 s−1) | Channel length (μm) | W/L | Ref. |
|---|---|---|---|---|---|---|---|---|---|
| C8-DNBDT-NW | Single-crystal | BGTC | −1.5 | 106 | 98 | 6.60 | 100 | 1 | 49 |
| diF-TES-ADT | Crystalline | BGBC | −10 | >104 | — | 0.20 | 50 | 10 | 50 |
| DPPT-TT | Amorphous | TGBC | −10 | >106 | 439 | 0.11 | 65 | 15 | 51 |
| TIPS-pentacene | Amorphous | BGBT | −3 | 104 | 130 | 0.25 | 100 | 200 | 52 |
| TIPS-pentacene | Crystalline | BGTC | −5 | 105 | 550 | 7.00 | 150 | 8 | 53 |
| C9-DNBDT-NW | Single crystal | BGTC | −4 | >1010 | — | 8.60 | 5 | 200 | 54 |
| PIDT-BT | Amorphous | TGBC | −3 | 105 | — | 4.65 | 150 | 150 | 55 |
| TIPS-pentacene | Amorphous | BGBC | −4 | 103 | 500 | 0.20 | 200 | 100 | 56 |
| DPP-DTT | Amorphous | BGTC | −10 | 105 | 590 | 0.30 | 50 | 20 | 57 |
| C10-DNTT | Amorphous | BGBC | −3 | 105 | 110 | 1.8 | 30 | 3 | 58 |
| C8-BTBT | Amorphous | BGTC | −5 | >106 | 87.4 | 3.39 | 200 | 5 | 59 |
| TIPS-pentacene | Crystalline | BGTC | −5 | 105 | 460 | 0.43 | 150 | 10 | 60 |
| C8-BTBT | Single-crystal | BGTC | −3 | 108 | 107 | 1.53 | 5 | 4 | This work |
Dynamic response characteristics of OFETs
The OFETs based on high-resolution OSC patterns benefit high frequency operation. Here, a simple circuit is applied to evaluate the frequency response of the OFET as shown in Fig. 6b. Although high carrier mobility is required for high-speed device applications, the device dimension also plays a critical role in improving the operation frequency,13 because the cut-off frequency of an OFET is determined predominantly by the total resistance and parasitic capacitance of a transistor as shown in eqn (1).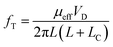 | (1) |
The characteristic rise time trise refers to the time for the output signal to rise from ‘0’ to ‘1’ while the fall time tfall refers to the time for the output signal to fall from ‘1’ to ‘0’. In particular, trise is the time to rise from 10% value of ‘0’ to 90% value of the ‘1’ state. And tfall is the time to fall from 90% value of ‘1’ to 10% value of the ‘0’ state. By fitting the simple exponential functions to the measured output voltage data, the trise and tfall are determined to be 303 μs and 618 μs, respectively. The trise and tfall can also be calculated based on time constant τp and τn, following the formula trise = 2.2τp and tfall = 2.2τn, in which τp and τn are the time constants of the exponential function obtained from data fitting. The maximum signal frequency of the system is defined by fmax = 1/(trise + tfall), which is estimated to be 1.08 kHz in this work. Besides, the propagation delay tp of the system, which reflects how fast the device output reacts to input change, can be calculated by tp = 0.5(tprise + tpfall), where the rise propagation delay tprise and fall propagation delay tpfall are the time for the output signal to increase or fall by 50%, respectively. Ideally, if the input voltage is step changed, it would satisfy the relationship of tprise = ln(2)τp and tpfall = ln(2)τn. The total propagation delay is measured by tp = 0.35(τn + τp), which is 166.99 μs in this work. The above-mentioned characteristic time of the device is summarized in Table 2, where the value obtained from theoretical calculation is marked with a star. Benefited from the high-resolution OSC pattern and short channel length, the OFET can operate above kHz range, while further optimization is necessary by reducing the contact resistance for short channel devices.
3. Conclusions
In summary, we have demonstrated a novel stencil mask defined doctor blade printing method to realize high-resolution OSC single crystal arrays. The application of a stencil mask provides a pattern resolution smaller than one droplet of inkjet printing. All the elements in the array have the same crystal orientation as well as very similar film thickness and crystal quality. The patterned OSC eliminates most of the unwanted fringe current from the lateral path as well as the possible contribution from gate leakage current in OFETs, leading to extremely low off-state current and high on/off current ratio close to 1010 on the SiO2 dielectric and 108 within 3 V gate bias on the AlOx dielectric, respectively. The low off-state current demonstrates the potential of the device array for low-power or high-performance optical sensing applications. Moreover, the short channel OFET array exhibits good frequency response operating at 20 kHz. Our results provide an effective patterning strategy to realize solution processed large-area, high-resolution organic single crystal arrays.4. Experimental
Materials
Chlorobenzene (anhydrous, 99.8%), PS (analytical standard, average molecular weight: ≈2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000), and C8-BTBT (≥99%) were bought from Sigma-Aldrich. PVA-203 (molecular weight: ≈31
000), and C8-BTBT (≥99%) were bought from Sigma-Aldrich. PVA-203 (molecular weight: ≈31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) was purchased from Aladdin. The heavily n-doped Si wafer with thermally grown 300 nm SiO2 was bought from China Electronics Technology Group Corporation. The glass slide was purchased from Biologix Group. All materials were used directly without further purification. The molybdenum stencil was custom made from Beijing Xinxing Bairui Limited, China.
000) was purchased from Aladdin. The heavily n-doped Si wafer with thermally grown 300 nm SiO2 was bought from China Electronics Technology Group Corporation. The glass slide was purchased from Biologix Group. All materials were used directly without further purification. The molybdenum stencil was custom made from Beijing Xinxing Bairui Limited, China.
Stencil mask defined doctor blade printing
An aqueous solution of PVA (36 wt%) was utilized for printing. The 20 μm thick molybdenum stencil mask with a 30 μm diameter circular array opening is placed 1 mm above the substrate. A plastic blade is used to perform printing.Device fabrication
Top contact bottom gate OFETs were fabricated on the SiO2/Si and glass substrate, respectively. The substrates were cleaned by sonicating in deionized water, acetone and isopropanol for 5 mins separately, and then dried by nitrogen flow. For OFETs on a high-k AlOx dielectric, 100 nm Al was thermally evaporated at 40 Å s−1, the sample was then put into sodium citrate/citrate acid solution for anodization. The details of anodization can be found in our previous studies.61 The C8-BTBT and PS in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 blend ratio were dissolved into chlorobenzene with a concentration of 20 mg mL−1. The blended solution was coated on the different substrates by homemade solution-shearing equipment for single crystal growth. The shearing speed was about 0.3 mm s−1, and the substrate is heated to 40 °C. After the printing of the PVA array, the sample was dry etched by oxygen plasma for 40 s, at the power of 20 W. Then the PVA was rinsed by water dipping. The sample was then annealed at 60 °C for 30 mins to remove residual solvent. Finally, 40 nm Ag top electrodes and a 5 nm F4-TCNQ injection layer underneath were deposited by thermal evaporation. A fine 1000 square-hole copper mesh (Xinxing Bairui Limited) for placing the transmission electron microscope (TEM) samples was used as the shadow mask during thermal evaporation. The rib width of the copper mesh is 5 μm. The channel width and length of the OFET is 20 μm and 5 μm, respectively.
1 blend ratio were dissolved into chlorobenzene with a concentration of 20 mg mL−1. The blended solution was coated on the different substrates by homemade solution-shearing equipment for single crystal growth. The shearing speed was about 0.3 mm s−1, and the substrate is heated to 40 °C. After the printing of the PVA array, the sample was dry etched by oxygen plasma for 40 s, at the power of 20 W. Then the PVA was rinsed by water dipping. The sample was then annealed at 60 °C for 30 mins to remove residual solvent. Finally, 40 nm Ag top electrodes and a 5 nm F4-TCNQ injection layer underneath were deposited by thermal evaporation. A fine 1000 square-hole copper mesh (Xinxing Bairui Limited) for placing the transmission electron microscope (TEM) samples was used as the shadow mask during thermal evaporation. The rib width of the copper mesh is 5 μm. The channel width and length of the OFET is 20 μm and 5 μm, respectively.
Characterization
OM and POM images were captured by a Nikon Eclipse Ci-POL polarized microscope. 3D morphology pictures were captured by a Leica DCM8 optical surface measurement system. AFM images were obtained with Intelligent-mode using a Bruker Dimension Icon in air. In-plane and out-of-plane XRD data were obtained by a Rigaku SmartLab X-ray diffractometer with the highest power of 9 kW. The transfer and output I–V curves of the OFETs were measured by a Keithley 4200 SCS semiconductor parameter analyzer equipped with a remote preamplifier. The field-effect mobility of the OFET at the saturation region was measured by IDS = μCiW(VG − Vth)2/2L. For frequency response measurement, RIGOL DG822 is used to generate the input voltage. The Vin and Vout voltage signals were recorded by a Tektronix TDS 1002C oscilloscope.Author contributions
Yue Xi: conceptualization, formal analysis, investigation, methodology, writing – original draft. Tao Wang: methodology, investigation. Qi Mu: investigation, validation. Congcong Huang: investigation. Shuming Duan: methodology, supervision. Xiaochen Ren: methodology, data curation, project administration, writing – review & editing. Wenping Hu: funding acquisition, project administration, resources.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the Ministry of Science and Technology of China (Grants 2018YFA0703200), the National Natural Science Foundation of China (91833306, 51633006, 51703160, 51733004, 51725304, and 52003189), and the China Postdoctoral Science Foundation (2020M680875).Notes and references
- H. Chen, W. Zhang, M. Li, G. He and X. Guo, Interface Engineering in Organic Field-Effect Transistors: Principles, Applications, and Perspectives, Chem. Rev., 2020, 120, 2879–2949 CrossRef CAS PubMed.
- T. Leydecker, Z. M. Wang, F. Torricelli and E. Orgiu, Organic-based inverters: basic concepts, materials, novel architectures and applications, Chem. Soc. Rev., 2020, 49, 7627–7670 RSC.
- K. S. Park, J. Baek, Y. Park, L. Lee, J. Hyon, Y. E. Koo Lee, N. K. Shrestha, Y. Kang and M. M. Sung, Heterogeneous Monolithic Integration of Single-Crystal Organic Materials, Adv. Mater., 2017, 29, 1603285 CrossRef.
- S. Yuvaraja, A. Nawaz, Q. Liu, D. Dubal, S. G. Surya, K. N. Salama and P. Sonar, Organic field-effect transistor-based flexible sensors, Chem. Soc. Rev., 2020, 49, 3423–3460 RSC.
- S. Wang, J. Xu, W. Wang, G. Wang, R. Rastak, F. Molina-Lopez, J. Chung, S. Niu, V. Feig, J. Lopez, T. Lei, S. Kwon, Y. Kim, A. Foudeh, A. Ehrlich, A. Gasperini, Y. Yun, B. Murmann, J. B.-H. Tok and Z. Bao, Skin electronics from scalable fabrication of an intrinsically stretchable transistor array, Nature, 2018, 555, 83–88 CrossRef CAS PubMed.
- Y. Wang, L. Sun, C. Wang, F. Yang, X. Ren, X. Zhang, H. Dong and W. Hu, Organic crystalline materials in flexible electronics, Chem. Soc. Rev., 2019, 48, 1492 RSC.
- H. Sirringhaus, 25th anniversary article: organic field-effect transistors: the path beyond amorphous silicon, Adv. Mater., 2014, 26, 1319–1335 CrossRef CAS PubMed.
- S. G. Higgins, B. V. Muir, J. Wade, J. Chen, B. Striedinger, H. Gold, B. Stadlober, M. Caironi, J. Kim, J. H. G. Steinke and A. J. Campbell, Self-aligned megahertz organic transistors solution-processed on plastic, Adv. Electron. Mater., 2015, 1, 1500024 CrossRef.
- L. Kong, C. Tang, H. J. Peng, J. Q. Huang and Q. Zhang, Advanced energy materials for flexible batteries in energy storage: A review, SmartMat, 2020, 1, e1007 CrossRef.
- K. Fukuda and T. Someya, Recent progress in the development of printed thin-film transistors and circuits with high-resolution printing technology, Adv. Mater., 2016, 29, 1602736 CrossRef PubMed.
- X. Zhang, H. Dong and W. Hu, Organic semiconductor single crystals for electronics and photonics, Adv. Mater., 2018, 30, 1801048 CrossRef PubMed.
- Y. Yao, Y. Chen, H. Wang and P. Samorì, Organic photodetectors based on supramolecular nanostructures, SmartMat, 2020, 1, e1009 CrossRef.
- A. Yamamura, T. Sakon, K. Takahira, T. Wakimoto, M. Sasaki, T. Okamoto, T. Okamoto and J. Takeya, High-Speed Organic Single-Crystal Transistor Responding to Very High Frequency Band, Adv. Funct. Mater., 2020, 30, 1909501 CrossRef CAS.
- P. K. L. Chan, The Motivation for and Challenges to Scaling Down Organic Field-Effect Transistors, Adv. Electron. Mater., 2019, 5, 1900029 CrossRef.
- Y. Liu, J. Feng, B. Zhang, Y. Wu, Y. Chen and L. Jiang, Regular Aligned 1D Single-Crystalline Supramolecular Arrays for Photodetectors, Small, 2018, 14, 1701861 CrossRef PubMed.
- W. Deng, Y. Lv, X. Zhang, X. Fang, B. Lu, Z. Lu and J. Jie, High-resolution patterning of organic semiconductor single crystal arrays for high-integration organic field-effect transistors, Mater. Today, 2020, 40, 82 CrossRef CAS.
- X. Zhang, W. Deng, R. Jia, X. Zhang and J. Jie, Precise Patterning of Organic Semiconductor Crystals for Integrated Device Applications, Small, 2019, 15, 1900332 CrossRef.
- K. Pei, M. Chen, Z. Zhou, H. Li and P. K. L. Chan, Overestimation of carrier mobility in organic thin film transistors due to unaccounted fringe currents, ACS Appl. Electron. Mater., 2019, 1, 379–388 CrossRef CAS.
- S. Kumagai, A. Yamamura, T. Makita, J. Tsurumi, Y. Y. Lim, T. Wakimoto, N. Isahaya, H. Nozawa, K. Sato, M. Mitani, T. Okamoto, S. Watanabe and J. Takeya, Scalable fabrication of organic single-crystalline wafers for reproducible TFT arrays, Sci. Rep., 2019, 9, 1–8 Search PubMed.
- K. Kim, K. Nam, X. Li, D. Y. Lee and S. H. Kim, Programmed Design of Highly Crystalline Organic Semiconductor Patterns with Uniaxial Alignment via Blade Coating for High-Performance Organic Field-Effect Transistors, ACS Appl. Mater. Interfaces, 2019, 11, 42403–42411 CrossRef CAS PubMed.
- X. Zhao, X. Ding, Q. Tang, Y. Tong and Y. Liu, Photolithography-compatible conformal electrodes for high-performance bottom-contact organic single-crystal transistors, J. Mater. Chem. C, 2017, 5, 12699–12706 RSC.
- X. Zhang, J. Mao, W. Deng, X. Xu, L. Huang, X. Zhang, S.-T. Lee and J. Jie, Precise Patterning of Laterally Stacked Organic Microbelt Heterojunction Arrays by Surface-Energy-Controlled Stepwise Crystallization for Ambipolar Organic Field-Effect Transistors, Adv. Mater., 2018, 30, 1800187 CrossRef PubMed.
- K. S. Park, J. Baek, Y. Park, L. Lee, Y. E. K. Lee, Y. Kang and M. M. Sung, Inkjet-Assisted Nanotransfer Printing for Large-Scale Integrated Nanopatterns of Various Single-Crystal Organic Materials, Adv. Mater., 2016, 28, 2874–2880 CrossRef CAS PubMed.
- K. Kim, J. Bae, S. H. Noh, J. Jang, S. H. Kim and C. E. Park, Direct Writing and Aligning of Small-Molecule Organic Semiconductor Crystals via “Dragging Mode” Electrohydrodynamic Jet Printing for Flexible Organic Field-Effect Transistor Arrays, J. Phys. Chem. Lett., 2017, 8, 5492–5500 CrossRef CAS PubMed.
- Y. Zhao, X. Fan, J. Feng, X. Wang, Y. Wu, B. Su and L. Jiang, Regulated Dewetting for Patterning Organic Single Crystals with Pure Crystallographic Orientation toward High Performance Field-Effect Transistors, Adv. Funct. Mater., 2018, 28, 1800470 CrossRef.
- Y. Yao, L. Zhang, T. Leydecker and P. Samorì, Direct Photolithography on Molecular Crystals for High Performance Organic Optoelectronic Devices, J. Am. Chem. Soc., 2018, 140, 6984 CrossRef CAS PubMed.
- S. Chung, K. Cho and T. Lee, Recent progress in inkjet-printed thin-film transistors, Adv. Sci., 2019, 6, 1801445 CrossRef PubMed.
- J. Kwon, Y. Takeda, K. Fukuda, K. Cho, S. Tokito and S. Jung, Three-dimensional, inkjet-printed organic transistors and integrated circuits with 100% yield, high uniformity, and long-term stability, ACS Nano, 2016, 10, 10324–10330 CrossRef CAS PubMed.
- G. Mattana, A. Loi, M. Woytasik, M. Barbaro, V. Noël and B. Piro, Inkjet-Printing: A New Fabrication Technology for Organic Transistors, Adv. Mater. Technol., 2017, 2, 1700063 CrossRef.
- W. Tang, Y. Huang, L. Han, R. Liu, Y. Su, X. Guo and F. Yan, Recent progress in printable organic field effect transistors, J. Mater. Chem. C, 2019, 7, 790–808 RSC.
- J. Zhang, B. Geng, S. Duan, C. Huang, Y. Xi, Q. Mu, H. Chen, X. Ren and W. Hu, High-resolution organic field-effect transistors manufactured by electrohydrodynamic inkjet printing of doped electrodes, J. Mater. Chem. C, 2020, 8, 15219–15223 RSC.
- S. Yang, S. Park, J. Bintinger, Y. Bonnassieux, J. Anthony and I. Kymissis, Employing Pneumatic Nozzle Printing for Controlling the Crystal Growth of Small Molecule Organic Semiconductor for Field-Effect Transistors, Adv. Electron. Mater., 2018, 4, 1700534 CrossRef.
- Y. J. Kwon, Y. D. Park and W. H. Lee, Inkjet-printed organic transistors based on organic semiconductor/insulating polymer blends, Materials, 2016, 9, 650 CrossRef.
- X. Zhang, J. Jie, W. Deng, Q. Shang, J. Wang, H. Wang, X. Chen and X. Zhang, Alignment and Patterning of Ordered Small-Molecule Organic Semiconductor Micro-/Nanocrystals for Device Applications, Adv. Mater., 2016, 28, 2475–2503 CrossRef CAS.
- T. Schmaltz, G. Sforazzini, T. Reichert and H. Frauenrath, Self-assembled monolayers as patterning tool for organic electronic devices, Adv. Mater., 2017, 29, 1605286 CrossRef.
- H. Wang, F. Fontein, J. Li, L. Huang, L. Jiang, H. Fuchs, W. Wang, Y. Wang and L. Chi, Lithographical Fabrication of Organic Single-Crystal Arrays by Area-Selective Growth and Solvent Vapor Annealing, ACS Appl. Mater. Interfaces, 2020, 12, 48854–48860 CrossRef CAS PubMed.
- S. Park, G. Giri, L. Shaw, G. Pitner, J. Ha, J. H. Koo, X. Gu, J. Park, T. H. Lee, J. H. Nam, Y. Hong and Z. Bao, Large-area formation of self-aligned crystalline domains of organic semiconductors on transistor channels using CONNECT, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 5561–5566 CrossRef CAS PubMed.
- H. Minemawari, T. Yamada, H. Matsui, J. Tsutsumi, S. Haas, R. Chiba, R. Kumai and T. Hasegawa, Inkjet printing of single-crystal films, Nature, 2011, 475, 364–367 CrossRef CAS PubMed.
- K. Kim, K. Nam, X. Li, D. Y. Lee and S. H. Kim, Programmed Design of Highly Crystalline Organic Semiconductor Patterns with Uniaxial Alignment via Blade Coating for High-Performance Organic Field-Effect Transistors, ACS Appl. Mater. Interfaces, 2019, 11, 42403–42411 CrossRef CAS PubMed.
- Y. Li, D. Ji, J. Liu, Y. Yao, X. Fu, W. Zhu, C. Xu, H. Dong, J. Li and W. Hu, Quick Fabrication of Large-area Organic Semiconductor Single Crystal Arrays with a Rapid Annealing Self-Solution-Shearing Method, Sci. Rep., 2015, 5, 13195 CrossRef CAS PubMed.
- W. Zhao, J. Jie, Q. Wei, Z. Lu, R. Jia, W. Deng, X. J. Zhang and X. H. Zhang, A Facile Method for the Growth of Organic Semiconductor Single Crystal Arrays on Polymer Dielectric toward Flexible Field-Effect Transistors, Adv. Funct. Mater., 2019, 29, 1902494 CrossRef.
- S. Duan, T. Wang, B. Geng, X. Gao, C. Li, J. Zhang, Y. Xi, X. Zhang, X. Ren and W. Hu, Solution-processed centimeter-scale highly aligned organic crystalline arrays for high-performance organic field-effect transistors, Adv. Mater., 2020, 32, 1908388 CrossRef CAS PubMed.
- W. J. Hyun, E. B. Secor, M. C. Hersam, C. D. Frisbie and L. F. Francis, High-resolution patterning of graphene by screen printing with a silicon stencil for highly flexible printed electronics, Adv. Mater., 2015, 27, 109–115 CrossRef CAS PubMed.
- Q. Ge, J. J. Kwok and Y. Diao, Flow-directed crystallization for printed electronics, Acc. Chem. Res., 2016, 49, 2756–2764 CrossRef PubMed.
- L. Wang, C. Wang, X. Yu, L. Zheng, X. Zhang and W. Hu, Two-dimensional organic single-crystalline p-n junctions for ambipolar field transistors, Sci. China Mater., 2020, 63, 122–127 CrossRef CAS.
- C. Liu, T. Minari, X. Lu, A. Kumatani, K. Takimiya and K. Tsukagoshi, Solution-processable organic single crystals with bandlike transport in field-effect transistors, Adv. Mater., 2011, 23, 523 CrossRef CAS PubMed.
- T. Izawa, E. Miyazaki and K. Takimiya, Molecular Ordering of High-performance soluble molecular semiconductors and re-evaluation of their field-effecttransistor characteristics, Adv. Mater., 2008, 20, 3388–3392 CrossRef CAS.
- Z. Zhou, Z. Zhang, Q. Wu, X. Ji, J. Wang, X. Zeng, S. Feng and P. K. L. Chan, Inch-scale grain boundary free organic crystals developed by nucleation seed-controlled shearing method, ACS Appl. Mater. Interfaces, 2018, 10, 35395–35403 CrossRef CAS PubMed.
- T. Sawada, T. Makita, A. Yamamura, M. Sasaki, Y. Yoshimura, T. Hayakawa, T. Okamoto, S. Watanabe, S. Kumagai and J. Takeya, Low-voltage complementary inverters using solution-processed, high-mobility organic single-crystal transistors fabricated by polymer-blend printing, Appl. Phys. Lett., 2020, 117, 033301 CrossRef CAS.
- S. Sung, W. Lee, M. M. Payne, J. E. Anthony, C.-H. Kim and M.-H. Yoon, Large-area printed low-voltage organic thin film transistors via minimal-solution bar-coating, J. Mater. Chem. C, 2020, 8, 15112 RSC.
- E. Stucchi, A. D. Scaccabarozzi, F. A. Viola and M. Caironi, Ultraflexible all-organic complementary transistors and inverters based on printed polymers, J. Mater. Chem. C, 2020, 8, 15331–15338 RSC.
- S. Lai, G. Casula, P. C. Ricci, P. Cosseddu and A. Bonfiglio, All-organic, low voltage, transparent and compliantorganic field-effect transistor fabricated by means of large-area, cost-effective techniques, Appl. Sci., 2020, 10, 6656 CrossRef CAS.
- V. Raghuwanshi, P. Saxena, S. Rahi, A. K. Mahato, I. Varun and S. P. Tiwari, Solution-processed flexible organic field-effect transistors with biodegradable gelatin as the dielectric layer: an approach toward biodegradable systems, ACS Appl. Electron. Mater., 2020, 2, 3373–3379 CrossRef CAS.
- T. Sawada, A. Yamamura, M. Sasaki, K. Takahira, T. Okamoto, S. Watanabe and J. Takeya, Correlation between the static and dynamic responses of organic single-crystal field-effect transistors, Nat. Commun., 2020, 11, 1–8 Search PubMed.
- Y. Jiang, Z. Liu, Z. Yin and Q. Zheng, Sandwich structured dielectrics for air-stable and flexible low-voltage organic transistors in ultrasensitive pressure sensing, Mater. Chem. Front., 2020, 4, 1459–1470 RSC.
- G. Casula, S. Lai, L. Matino, F. Santoro, A. Bonfiglio and P. Cosseddu, Printed, low-voltage, all-organic transistors and complementary circuits on paper substrate, Adv. Electron. Mater., 2020, 6, 1901027 CrossRef CAS.
- H. Park, S. Yoo, J. C. Won and Y. H. Kim, Room-temperature, printed, low-voltage, flexible organic field-effect transistors using soluble polyimide gate dielectrics, APL Mater., 2020, 8, 011112 CrossRef CAS.
- Q. Mu, Z. Chen, S. Duan, X. Zhang, X. Ren and W. Hu, A low-temperature solution-process high-k dielectric for high-performance flexible organic field-effect transistors, Front. Mater., 2020, 7, 570002 CrossRef.
- J. Choi, J. Kang, C. Lee, K. Jeong and S. G. Im, Heavily crosslinked, high-k ultrathin polymer dielectrics for flexible, low-power organic thin-film transistors (OTFTs), Adv. Electron. Mater., 2020, 6, 2000314 CrossRef CAS.
- V. Raghuwanshi, D. Bharti, A. K. Mahato, A. K. Shringi, I. Varun and S. P. Tiwari, High performance flexible organic field-effect transistors with barium strontium titanate gate dielectric deposited at room temperature, ACS Appl. Electron. Mater., 2020, 2, 529–536 CrossRef CAS.
- X. Ren, K. Pei, B. Peng, Z. Zhang, Z. Wang, X. Wang and P. K. Chan, A low-operating-power and flexible active-matrix organic-transistor temperature-sensor array, Adv. Mater., 2016, 28, 4832–4838 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/d1qm00097g |
| This journal is © the Partner Organisations 2021 |