The block copolymer shuffle in size exclusion chromatography: the intrinsic problem with using elugrams to determine chain extension success

Abstract

Size exclusion chromatography (SEC) based on direct homopolymer calibration is the preferred method for molecular weight determination in macromolecular synthesis. However, using the same method and calibration in block copolymer (BCP) characterization can lead to an apparent molecular weight reduction when in fact the opposite has taken place. This leads to a situation where researchers often have enough difficulties in interpreting their data, creating false conclusions and deeming successful experiments unsuccessful or vice versa. Here, a selection of block copolymers from the literature is discussed for which such an incoherent change in the retention time has been observed. These examples represent four categories of BCPs for which unexpected SEC results can occur. We discuss the importance of a critical evaluation of SEC and the reasons for the deviating behavior and highlight the danger of the common practice to use elugrams to prove or disprove successful chain extensions in synthesis. Next to a critical evaluation of the various cases, we give recommendations for which other detection and characterization methods may enable accurate block copolymer characterization.

---

Introduction

Owing to its accessibility and ease of operation, size exclusion chromatography (SEC), also known as gel permeation chromatography (GPC), has long become the preferred method for polymer molecular weight determination. SEC provides the full molecular weight distribution of a sample, from which molecular weight averages and dispersity (Đ) can be derived. Molecular weight determination by SEC makes use of the proportionality between the hydrodynamic volume V_H of a (co-)polymer chain in a solvent and the product of the intrinsic viscosity [η] and the molecular weight M:¹

V_H ∼ [η]·M (1)

Here, [η] captures to what extent the polymer chain is swollen by the solvent. For practical reasons, eqn (1) is usually written as:

HV = [η]·M, (2)

where the quantity “HV” is a measure for the hydrodynamic volume, given in units of volume per mole, as [η] is typically expressed as an inverse mass concentration (volume per gram). The elution volume of a given polymer sample or, equivalently, its retention time on the SEC column can be accurately correlated to HV as long as the eluent dissolves the polymer well and only negligibly swells or collapses the stationary phase. This correlation forms the basis for what is often referred to as universal calibration, and researchers have grown so used to it that sometimes its applicability is no longer questioned. Since SEC separates strictly based on the hydrodynamic volume, it is an indirect method for determining the molecular weight. Hence, estimates for the latter can only be obtained if the system has been properly calibrated and if the relation between HV and M is known.

Although readily applicable to most homopolymers, molecular weight determination of block copolymers (BCPs) using SEC is generally much less straightforward than typically considered. Besides issues also known to occur for SEC on homopolymers, e.g. associated with aggregation² or chemical dissimilarity with the calibration standard,^3–5 new challenges appear due to the mere fact that the different blocks themselves have different properties and solvation. Consequently, their interaction with both the mobile and stationary phases, as well as their resemblance with the calibration standard, is per definition different. The typical assumption of universal calibration thus does frequently not hold true, despite researchers using this assumption almost without exception in their data interpretation. A step forward is presented by using viscometry, hence allowing for chemically different analytes and standards and by measuring the intrinsic viscosity directly rather than estimating it from calibrations.

The relation between [η] and M is typically expressed via the empiric Mark–Houwink–Sakurada (MHS) equation, which uses the parameters α and K of an unknown analyte for correlation, according to the MHS equation: [η] = KM^α. However, even if the MHS parameters are known precisely (which by itself is a challenge and is usually only true for a selected number of homopolymers), an important prerequisite for its use is that the analyte has similar solvation to the calibration standard. Hence, again related to inhomogeneity in both chain length and composition, the outcome of this exercise should be treated with caution when analyzing a BCP. As mentioned, the direct measurement of the intrinsic viscosity somewhat improves the situation in that MHS parameters must not be known. Employing a viscometer, HV can be directly calibrated using standards, and measurement of the intrinsic viscosity of the analyte sample allows for direct determination of its molecular weight. Yet, the inaccuracy associated with the prerequisite of similar solution behavior of chains remains.

A way out of this dilemma is the use of laser light scattering (LS) in a triple detection SEC system, which allows the measurement of the molecular weight directly without relying on knowledge of HV. Regardless, even when combined with an absolute detection technique, such as multi-angle laser light scattering (MALLS), SEC analysis of BCPs exhibits reliability issues since the eluted composition, and hence the scattering contrast (dn/dc), is time-dependent due to the dispersity in the block length. In principle, dn/dc would need to be known for each exact block composition to yield an exact measurement of the molecular weight, which obviously is not feasible. Concentration determination is hence hampered, which also invalidates light scattering results to a certain degree. Furthermore, LS-based methods usually involve not only high cost, but also require more skilled operators and in-depth analysis since scattering data is less straightforward to analyze properly compared to the simpler RI, UV and viscometry detectors.

It is fair to assume that for routine analysis, most labs do not perform light scattering or do not have access to such detectors in the first place. Hence, in the analysis of block copolymers (and other polymer architectures for that matter), researchers typically make basic assumptions and refrain from even determining molecular weights. A typical recommendation is to plot SEC elugrams rather than molecular weight distributions to avoid any ambiguity with calibrations and generally to avoid the above-described dilemmas. A general assumption thereby is that lower elution volumes are correlated to larger molecular weights. Hence, it is widely accepted that a shift to lower elution volumes presents proof for a successful extension in a block copolymerization and that a lack thereof is synonymous with a failure in reaction. This does not necessarily hold true though, as this still assumes a universal-type calibration/correlation to be valid for the investigated polymers. As we discuss here, this can be a dangerous and misleading assumption.

This mini-review is written in part in a tutorial form and gives a concise and accessible discussion on the challenges, approaches and solutions associated with interpreting molecular weight distributions of BCPs from SEC. We intend to provide practical handles and concepts, rather than presenting a lengthy and exhaustive literature survey to allow practitioners to derive meaningful conclusions. We start our discussion by describing examples of BCPs for which SEC actually works quite well, namely, for BCPs comprising flexible blocks that only interact weakly. After that, we discuss a range of examples of BCPs that seem to behave far less ideally due to the fact that the blocks have quite different chemical or physical properties and hence pose significant challenges on the use of SEC for molecular weight determination or even merely proving block extension.

It is particularly worthwhile reviewing such “inhomogeneous” BCPs since their internally cooperative- or multi-functionality is of strong interest for advanced applications, as smart coatings,^6–9 drug delivery,^10–13 bioimaging,^14–16 optoelectronics^17–20 and energy harvesting and storage.^21–25 We subdivide these non-classical BCPs into four “behavioural categories” and conclude with a brief survey of methods to improve the accuracy of molecular weight estimates. These techniques may either be used in conjunction with SEC or replace it altogether as more viable options. It should be noted that none of the proposed methods represent truly novel concepts, yet SEC is too often used in the literature either as proof or dismissal of success of a reaction, especially in BCP formation without further questioning, and we wish to highlight the problems arising from such conclusions.

Discussion

Classical systems: dual detector approach for BCP molecular weight analysis

The simplest cases are presented by (block-)copolymers of which the monomers form flexible chains and only exhibit weak interactions, i.e. lacking ionic charges, strong dipoles and/or H-bonding capability. In effect, for block-copolymers falling into this category, the covalent link between the different blocks forms the only relevant “hetero-contact”. This enables an interpretation as connected homopolymers²⁶ and therefore allows for molecular weight determination based on a mass fraction-weighted interpolation of the homopolymer SEC calibration curves as typically applied:²⁷

log M_c(V) = ∑w_i(V)·log M_i(V), (3)

where M_c(V) is the molecular weight of the copolymer corresponding to an elution volume V and w_i(V) is the weight fraction of the comonomer i. In this case, the hydrodynamic volume of the block copolymer is trivially related to the hydrodynamic volumes of the separate homopolymers,²⁶i.e. assuming no additional contributions stemming from the interaction between the monomers of the different blocks. This is true for example for BCPs that consist of blocks from the same or similar monomer family.

For any BCP obeying this prerequisite, the molecular weight can be established reasonably well with SEC alone.²⁸ However, even for such straightforward systems, one cannot rely on just a single detection method, i.e. typically UV-vis absorption or refractive index (RI) detection. The reason is that for not perfectly alternating copolymers, not only the molecular weight but also the composition is distributed. In such cases, a dual detection method involving for example both the UV-vis and RI detectors can be used.²⁹ The latter records the copolymer concentration, whereas the former records the composition owing to its high chemical specificity.³⁰ Prior to analyzing the copolymer, solutions of the corresponding homopolymers are eluted through both channels in order to predetermine the detector responses, which are comonomer- and instrument-dependent.^31,32

The eluted masses m_A and m_B (e.g. expressed in grams) of comonomers A and B can then be obtained for each “slice” i of the SEC chromatogram by solving the following system of equations for the measured intensities:³¹

S^UV_i = χ^UV_Am_A,i + χ^UV_Bm_B,i (4)

S^IR_i = χ^IR_Am_A,i + χ^IR_Bm_B,i, (5)

with χ^UV_A,B and χ^RI_A,B being the detector responses. Subsequently, the mole fractions of the comonomers are determined using the known monomer molecular weights, upon which an estimate for the copolymer molecular weight M′ in each slice is obtained from the predetermined number-average molecular weight of the precursor block. Optionally, one may generate a calibration curve by fitting log(M′) versus elution volume. Since the eluted volume is known, the polymer concentrations are easily obtained to finally yield the number- and weight-average molecular weights of the copolymer sample. As an example, Fig. 1 shows this procedure for the BCP poly(styrene)-b-poly(Z-L-lysine) (PS-b-PZL).³¹ We note that there is a wide variety of other detector combinations for this dual detection method^26,33 (for example, infrared (IR)³⁴ and evaporative light scattering detector (ELSD)³⁵) and their applicability depends on the properties of the monomers.

Fig. 1 SEC-UV/RI evaluation method on PS-b-PZL: (A) determination of the chemical composition of copolymer fractions from the UV (dashed) and RI (solid) traces; (B) calculation of the concentration and molar mass of copolymer chains, including generation of a copolymer calibration curve (dotted); and (C) calculation of the copolymer mass distribution. Reproduced from ref. 31 with permission from the American Chemical Society, copyright 2003.

Dual detector SEC has shown to give very reasonable estimates for a range of “classical” BCPs, such as polyisobutylene-b-polystyrene (PIB-co-PS),³² polyacenaphthylene-b-isobutylene-b-acenaphthylene (PAc-b-PIB-b-PAc),³² polystyrene-co-poly(butylene terephthalate) (PS-co-PBD),³⁶ polystyrene-b-poly(methyl methacrylate) (PS-b-PMMA),^30,31 polystyrene-b-polybutadiene (PS-b-PB)³¹ and polystyrene-b-polylysine (PS-b-PZL).³¹ However, as mentioned above, if the hydrodynamic behaviour of the block copolymer differs from the “summed” behaviour of the homopolymers, even dual detector SEC cannot produce reliable results. Early identified examples are cases wherein one or both components carry a bulky side group.³² Besides, a trivial limitation of dual detector SEC is that it does not distinguish between homopolymer contaminants and the copolymer.³²

Examples of “non-classical” block copolymers giving deviant SEC analyses

In case SEC is applied to BCPs for which the combination of the blocks gives a behavior that differs strongly from what one would expect based on the linear combination expressed by eqn (3), observations can be counterintuitive. In these situations, care should be taken when using SEC for molecular weight determination, or, as we shall see, even for just collecting qualitative evidence for chain extension or successful synthesis of a BCP. Since SEC analysis is based on the general assumption that the retention time decreases if the hydrodynamic radius of the polymer becomes larger, counterintuitive results are obtained if during coupling or growth of the second block the polymer coil contracts, collapses or exhibits an increased interaction with the stationary phase. Below, we discuss a number of representative examples (overview in Table 1) of “non-classical” functional BCPs that behave deviant in SEC inasmuch an apparent increase in the retention time is observed with increasing molecular weight.

Table 1 Examples of BCPs exhibiting atypical behavior during SEC

Entry	Polymer^c	Polymer type	M̄ n,SEC	M̄ n	Đ	Ref.
a Determined from ^1H NMR. b Determined by MALDI. c See the main text for abbreviations.
1	OHPV5	Homopolymer	2.3	1.5^a^,^b	1.02	37
2	OHPV5-b-PEG12	Linear BCP	1.9	2.1^a	1.04
3	OHPV5-b-PEG45	Linear BCP	3.7	3.6^a	1.06
4	OHPV5-b-PEG115	Linear BCP	7.7	6.6^a	1.05
5	PF–Br	Homopolymer	6.1	—	1.48	38
6	PF-b-PHFBMA12	Linear BCP	9.5	9.3^a	1.50
7	PF-b-PHFBMA36	Linear BCP	9.6	15.7^a	1.60
8	PF-b-PHFBMA39	Linear BCP	9.1	21.9^a	1.64
9	PF-b-PHFBMA87	Linear BCP	8.7	29.4^a	1.60
10	PNIPAM	Homopolymer	23.0	—	1.3	39
11	PNIPAM-b-PPEGA-b-PNIPAM	ABA-type BCP	14.0	—	1.36
12	PS-b-PNIPAM-b-PPEGA	ABCACBA-type BCP	77.0	—	1.45
13	PEI32	Homopolymer	—	19.3^a	—	40
14	P4VP29-b-PEI32-b-P4VP29	ABA-type BCP	18.7	25.6^a	1.90
15	P4VP35-b-PEI32-b-P4VP35	ABA-type BCP	12.1	27.7^a	2.12
16	P4VP85-b-PEI32-b-P4VP85	ABA-type BCP	10.5	37.8^a	2.17

---

Rod–coil transition. The first set of examples (Table 1, entries 1–4), taken from the work of Winnik et al., represents a range of linear BCPs consisting of a short and stiff oligo(dihexyloxyphenylenevinylene) (OHPV) conjugated, luminescent block and a flexible poly(ethylene glycol) (PEG) block comprising 12, 45 and 115 EG repeat units (Table 1, entries 2–4).³⁷ The GPC traces for these polymers have been reproduced in Fig. 2. Although the retention time consistently decreases with increasing PEG length, an initial increase is observed upon converting the OHPV homopolymer (entry 1) into OHPV-b-(PEG)₁₂. In other words, the (apparent) hydrodynamic volume of the BCP is smaller than that of the precursor. The authors have not explicitly discussed this observation, as it is not the focus of their study. It may however portray a difficulty associated with molecular weight determination of rod–coil BCPs, a trend that is observable consistently with conjugated polymers.

Fig. 2 SEC traces of OHPVx-b-PEGy polymers, corresponding to entries 1–4 in Table 1; (a) RI signal and (b) UV-vis signal recorded at 490 nm. See the main text for the non-abbreviated nomenclature. Reproduced from ref. 37 with permission from the Royal Society of Chemistry, copyright 2014.

The underlying reason for this discrepancy might in part be related to the fact that the molecular weight of the OHPV homopolymer is likely overestimated (∼50% compared to the value from NMR and MALDI) due to its high rigidity. For a given molecular weight, the associated hydrodynamic volume of poly(p-phenylenevinylene) is hence high in comparison with a more flexible polymer used for SEC calibration (i.e. usually polystyrene).⁴¹ This is expressed by the disagreement between the SEC molecular weight average and the estimate obtained by NMR (entry 1). Upon connecting the flexible PEG block, the hydrodynamic properties become more reminiscent of those of the PS calibration standard, leading to an agreement between the SEC and NMR estimates, but perhaps resulting in an apparent reduction in the hydrodynamic volume compared to the OHPV homopolymer. An increase in the retention time due to a higher affinity of the PEG residues with the stationary phase is not likely in view of the apolar column material used in this work³⁷ (crosslinked styrene/divinyl benzene matrix). We note that an increase in the retention time when connecting or growing a flexible block to/from a stiff homopolymer is certainly not always observed^42–44 and speculate that it may depend on the length of the latter and/or whether the stiff block is truly in the rod-like limit.

Low solubility of one block. To show that the situation concerning rod–coil BCPs is everything but straightforward, we proceed with an example for which the decrease in the hydrodynamic volume was only observed after extension of, rather than with, the flexible block. This example concerns the linear semiconducting BCP poly[2,7-(9,9-dihexylfluorene)]-b-poly(2,2,3,3,4,4,4-heptafluorobutyl methacrylate (PF-b-PHFBMA).³⁸ A series with varying PHFBMA block lengths (Table 1, entries 5–9) was synthesized by atom transfer radical polymerization (ATRP) using a 2-bromoisobutyryl-endcapped polyfluorene (PF–Br) as a macroinitiator for polymerization of heptafluorobutyl methacrylate. In contrast to the previous example, the retention time does decrease when converting the PF homopolymer into the BCP (compare Table 1 entries 5 and 6, and the SEC traces in Fig. 3), which is intuitive. However, an unexpected increase in the retention time is observed upon extension of the PHFBMA block length beyond 36 monomeric units (see Table 1 entries 7–9 and Fig. 3). As a result, the SEC estimate for M̄_n follows the opposite trend compared to the value obtained from NMR (see Table 1). The authors do not ascribe the anomaly to the stiff–flexible nature of the BCPs, but rather to the poor solubility of the semifluorinated block in the SEC solvent (THF), resulting in an overall collapse of the BCP at an elevated degree of polymerization.

Fig. 3 SEC traces of polyfluorene homopolymer precursors PF–OH and PF–Br, as well as di-BCPs PF-b-(PHFBMA)_n, corresponding to entries 5–9 in Table 1. See the main text for the non-abbreviated nomenclature. Reproduced from ref. 38 with permission from the Royal Society of Chemistry, copyright 2013.

Interactions between blocks. Similar counterintuitive changes in SEC retention times upon block extension, though likely due to yet another mechanism, have been reported by St Thomas et al. during the characterization of a range of tri- and multiblock copolymers based on the temperature-responsive polymer poly(N-isopropylacrylamide) (PNIPAM) prepared via reversible deactivation radical polymerization (RDRP) techniques (entries 10–12 in Table 1).³⁹ For the ABA-type triblock copolymer PNIPAM-b-poly(poly(ethylene glycol) methyl ether acrylate)-b-PNIPAM (PNIPAM-b-PPEGA-b-PNIPAM), a higher retention time was observed in comparison with the PNIPAM homopolymer (see the red and green traces in Fig. 4), with an associated ∼40% apparent reduction in the molecular weight from M̄_n = 23 000 g mol⁻¹ to 14 000 g mol⁻¹. This work³⁹ does not contain comparative values from, for instance, NMR or mass spectrometry (MS). The authors point out that both PNIPAM and PPEGA are known to be strongly susceptible towards hydrogen bonding (although the latter can only accept and not donate H-bonds). They speculate that mutual H-bonding between the different polymer constituents is responsible for contraction of the coil upon block extension, leading to a concomitant reduction in the hydrodynamic volume and an increase in the retention time.

Fig. 4 SEC traces corresponding to entries 10–12 in Table 1. The red, green and black traces respectively correspond to the PNIPAM homopolymer, tri-BCP PNIPAM-b-PPEGA-b-PNIPAM and hepta-BCP PS-b-PNIPAM-b-PPEGA-b-PS-b-PPEGA-b-PNIPAM-b-PS (not specifically discussed here). See the main text for the non-abbreviated nomenclature. Reproduced from ref. 39 with permission from the Royal Society of Chemistry, copyright 2014.

Interactions between one block and the stationary phase. A third example of a BCP exhibiting an increase in the SEC retention time with increasing block length is the ABA-type tri-BCP with poly(4-vinylpyridine) (P4VP) and poly(ether imide) (PEI) as A and B blocks, respectively, as reported by Liu and coworkers (Table 1, entries 13–16).⁴⁰ These BCPs, based on the engineering plastic PEI, are of interest for mechanically robust and temperature-stable mesoporous polymer membranes. The elugrams obtained using an RI detector (Fig. 5) show that an increase in the P4VP block length from 29 to 85 monomeric units results in an increase in the retention time, which is counterintuitive. Hence, deriving the molecular weight based on a standard PS-calibration results in an apparent decrease in the molecular weight, whereas the opposite trend is observed for the estimates obtained from NMR or absolute measurement based on GPC–MALLS (solid curves in Fig. 5). Furthermore, Fig. 5 shows that besides an increase in the retention time with the P4VP block length, the elugrams become increasingly skewed towards the low molecular weight range.

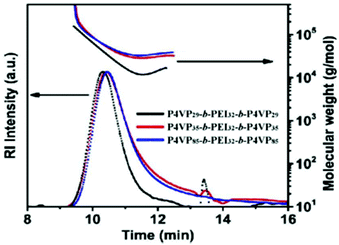Fig. 5 SEC RI elugrams (dotted lines) and the absolute molecular weight (solid curves), determined by GPC–MALLS, of P4VP-b-PEI-b-P4VP tri-BCPs, corresponding to entries 13–16 of Table 1. See the main text for the non-abbreviated nomenclature. Reproduced from ref. 40 with permission from the American Chemical Society, copyright 2020.

Given the fact that PEI and P4VP are flexible polymers, well soluble in the SEC solvent (THF)^45,46 and both incapable of donating hydrogen bonds, the reason for the increase in the retention time must be different from the examples discussed above. Indeed, according to the authors, their data carry the signature of (too) strong attractive interaction between the BCP with the stationary phase of the GPC column. Although the authors do not give a suggestion which block is responsible for the effect, the fact that the observed trend relates to the length of the P4VP block seems to identify the culprit. According to the authors, the observation that the molecular weight fraction determined by GPC–MALLS (solid lines in Fig. 5) shows a “U-shaped” time dependence (see Fig. 5) is characteristic for a strong interaction between the polymer analyte and the GPC stationary phase. Unfortunately, the particular column material used in this work is not mentioned. We finally note that, although the interpretation by the authors is certainly plausible, interpreting results generated using only the RI detector or in combination with MALLS requires some care. The reason is that during elution of the BCP, compositional changes associated with the block length distributions are not accounted for. As mentioned in the introduction, if the refractive index of the solution on which both methods rely strongly varies with time, the shape of the elugrams, as well as the MALLS molecular weight estimates, may be strongly impacted.

Alternative methods for molecular weight determination

The cases discussed above represent a small but, in our view, representative selection of examples from the literature reporting anomalous behavior of functional BCPs during SEC analysis. Although the overview is not exhaustive, it probably covers the most important reasons for which single- or even dual-detection SEC methods may yield counterintuitive results: (i) rod–coil BCPs, (ii) blocks exhibiting a (strong) difference in compatibility with the carrier solvent, (iii) strong mutual interactions between blocks and (iv) strong interaction with the stationary phase of one of the blocks.

Improved SEC analysis. Depending on the type of BCP, column material and solvent, the use of an elevated temperature during SEC may be beneficial. An increase in temperature generally reduces the strength of attractive forces, whether block–block, solvent–block or between the BCP analyte and the stationary phase, and may therefore be amenable for mitigating the challenges associated with categories (ii), (iii) and (iv). However, the boiling point of the SEC solvent or the stability of the column material often limits the accessible temperature range as much as limitations of the used instruments. Most SEC systems in practice will use temperatures below 50 °C for practical reasons. In view of the second example, we note that an elevated temperature is to be avoided if one of the blocks, or the BCP as a whole, exhibits a lower critical solution temperature (LCST). Alternatively, one may use a different solvent⁴⁷ or a solvent mixture⁴⁸ to improve the accommodation of both blocks in the mobile phase. In order to predict an optimal solvent composition for a particular chemical structure, one may employ the Hansen solubility theory.⁴⁹ Besides the composition, the use of additives has also been shown to improve SEC analysis, in particular if the analyte exhibits a strong interaction with the stationary phase (category iv). Depending on the (expected) type of interaction, these may for instance be acidic⁵⁰ or basic species⁵¹ and/or ionic, such as inorganic^52,53 and organic⁵⁴ salts.

Furthermore, we note that the shape and modality of the SEC elugrams could provide information beyond merely proving a successful BCP synthesis. Deconvolution may allow identifying impurities such as homopolymer contamination⁵⁵ and side products, e.g. from branching reactions.⁵⁶ The fact that such impurities can significantly impact the microphase separated morphology of a BCP⁵⁷ emphasizes the importance of an extended evaluation of the modality in SEC elugrams.

If simple remedies such as a change in temperature or mobile phase composition are ineffective or out of scope, an alternative or additional method is required to determine the molecular weight more accurately. Indeed, most of the examples discussed above present estimates obtained with an alternative approach, such as NMR end-group analysis or MS. One should realize though that where most methods only yield a single value, e.g. for the number- or weight-average molecular weight, GPC has the essential advantage of almost solely being capable of mapping a full distribution. Hence, besides focusing on independent alternative approaches, the remainder of this section also presents methods that can be used in conjunction with SEC to obtain more reliable molecular weight estimates and/or compositional mapping of a BCP sample. Although each method has its own advantages, we will critically discuss disadvantages as well and, where appropriate, assess to what extent the method in question circumvents the anomalies discussed in the previous section.

GPC–MALLS. As discussed above in relation to the last example in the previous section, using SEC in conjunction with MALLS (“GPC–MALLS”) allows for absolute determination of the full molecular weight distribution, without the need for a mass calibration procedure. In this method, the fractions eluted from the SEC column are being analyzed real-time by the MALLS detector, where the molecular weight is determined based on direct measurement of the radius of gyration of the polymer.⁵⁸ This method is hence principally suited to address issues associated with categories (i)–(iii). The amount of analyte dissolved in the stock solution needs to be determined accurately to be able to account for the change in the refractive index with the concentration (dn/dc), obtained by online measurement using the RI detector. The method assumes each fraction to be monodisperse. For completeness, when used in the absence of SEC, light scattering yields the weight-average molecular weight (M̄_w). Since the MALLS measurement is independent of the retention time on the GPC column, some of the issues discussed in the previous section are in principle avoided. It should be noted though that for conjugated polymers – as discussed above – MALLS is inherently associated with an error as the incident laser light will cause not only scattering, but potentially also fluorescence. This again can negatively impact the MALLS signals and lead to misinterpretation of data.

Illustratively, Zhao et al. showed that despite exhibiting similar SEC retention times, GPC–MALLS reveals the expected difference in the molecular weight between a poly(oligo(ethylene glycol) monomethyl ether methacrylate) (POEGMA) homopolymer and its equivalent BCP, obtained via a click reaction of the POEGMA block with an azide-functionalized polyfluorene (see Fig. 6).⁵⁹ Although GPC–MALLS is arguably one of the most powerful tools for molecular weight characterization, we emphasize again that it assumes the sample to be compositionally homogeneous, which imparts a risk when analyzing a BCP that is distributed with respect to the block length (as practically all BCPs are),⁶⁰ and of which the refractive index of the individual blocks is significantly different.

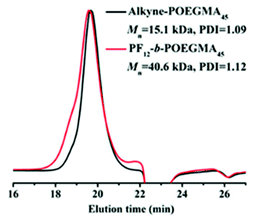Fig. 6 SEC traces of alkyne functionalized poly(oligo(ethylene glycol) monomethyl ether methacrylate (POEGMA) and the BCP polyfluorene-b-POEGMA. Reproduced from ref. 59 with permission from the American Chemical Society, copyright 2018.

SEC–HPLC. A sophisticated and certainly not commonly applied alternative to dual detection SEC for mapping inhomogeneity in both chain length and composition is the combination of SEC with high-performance liquid chromatography (HPLC).^26,61 In this so-called “two-dimensional” chromatography system, SEC discriminates by size and HPLC by polarity under critical solution conditions (that is where the HPLC only discerns for polarity differences, but not for the molecular weight). In other words, in this method, deliberate use is made of the fact that different blocks have a different interaction with the stationary phase of the HPLC column. In this respect, the calibration of the latter is based on the elution volumes of the separate homopolymers. SEC–HPLC also allows for discrimination based on polymer topology, i.e. separation of branched versus linear architectures, as well as discrimination between BCP products and homopolymer contaminants.

As an example, Fig. 7 shows the result of a SEC–HPLC analysis of a very inhomogeneous sample based on polystyrene-b-polybutadiene (PS-b-PBD), containing both linear and branched structures, as well as a distribution in the PBD block length. SEC–HPLC identified up to 16 different species in this particular sample.⁶¹ Again, as the full analysis is based on an additional parameter or material property (polarity in this case), SEC retention time anomalies can be accounted for, depending on their underlying reason. In view of the challenges discussed above, the example given in Fig. 7 represents a system that is of relatively “low risk”: the “classical” BCP PS-b-PBD comprises two flexible apolar blocks, both incapable of exhibiting strong interactions. Nevertheless, even in case a BCP analyte would exhibit non-straightforward behavior in SEC, the combination with HPLC certainly seems very useful to confirm a successful block extension, coupling of grafting.

Fig. 7 SEC–HPLC 2D chromatography contour map (relative eluted concentration) of a complex mixture of PS-b-PBD, containing both linear and branched structures. The horizontal and vertical axes respectively represent the SEC detected molar mass and the PBD content obtained from HPLC. Reproduced from ref. 26 with permission from the author, copyright 2017.

¹H-NMR end group analysis. A popular and readily accessible method for determining the polymer molecular weight average is end group analysis by means of ¹H-NMR spectroscopy. The quotient of the integrals of backbone-related protons with those from end groups, together with the monomer molecular weight, gives an estimate for the number average molecular weight (M̄_n). As shown above, in the examples discussed, this direct method for which no calibration is required is also applicable to block-copolymers and in principle applies to all categories mentioned above. A disadvantage compared to SEC, though, is that end group analysis does not yield the full molecular weight distribution. Furthermore, upon block extension, the proton relaxation times increase. As a result, the integration limits become ill-defined due to signal broadening, which increases the uncertainty in the molecular weight estimate. Importantly, end group analysis does per definition not discriminate between a BCP and the equivalent mixture of the separate blocks.

Diffusion-ordered spectroscopy. To prove the actual presence of the BCP by means of NMR, end group analysis is often extended with diffusion-ordered spectroscopy (DOSY).⁶² This technique discriminates between various species in a mixture based on their self-diffusion rates in solution by applying the usual radiofrequency pulses, though in the presence of a gradient in the magnetic field. The latter provides for spatial information that allows for correlating signals in the NMR spectrum to the diffusivity measured for a specific component. Hence, in the case of a BCP, signals corresponding to different blocks but correlating to the same diffusivity prove that the blocks are indeed connected.^63–66 A decrease in the diffusion coefficient in comparison with the homopolymers or macroinitiator allows for a qualitative evaluation of an increase in the molecular weight. Loo et al. exploited DOSY analysis for mapping the actual molecular weight distribution.⁶⁷ Similar to SEC, they propose to use a calibration procedure based on low dispersity polymer standards with known molecular mass to allow for the conversion of diffusivities obtained for an analyte (see Fig. 8). Since the self-diffusivity depends on whether or not – and if so, to what extent – the overlap concentration is exceeded, we note that if a BCP collapses upon block extension, as discussed above, the DOSY method may yield similar inconsistencies as observed for SEC, in particular when applied to BCPs falling into categories (ii) and (iii).

Fig. 8 (a) Calibration curve of P3HT polymers. (b) Comparison of the absolute molecular weight (solid lines) and distributions derived from DOSY (dotted lines). Reproduced from ref. 67 with permission from the American Chemical Society, copyright 2018.

Elemental analysis and mass spectrometry. For completeness, elemental analysis (EA)^4,68 and MS^37,69,70 can also be used as methods for determining BCP molecular weights and applicable to all four categories mentioned above. EA is analogous to NMR end group analysis in the sense that it (i) requires no calibration, (ii) provides the number-average molecular weight and (iii) is incapable of distinguishing between a BCP and the equivalent mixture of homopolymers. The prerequisites are that the elemental distribution across the copolymer is block-specific and that the molecular weight of the precursor block or macroinitiator is known in advance. In contrast to EA and NMR end-group analysis, MS is well capable of discriminating a BCP from homopolymer contaminants. In fact, MS is perhaps an “ideal” method for molecular weight determination, in the sense that it is principally capable of producing a molecular weight distribution without requiring calibration or even dissolving the polymer in some cases. An important prerequisite, however, is that fragmentation of the molecular ions before detection is suppressed. Hence, only soft ionization methods, such as matrix-assisted laser desorption- or electrospray ionization (MALDI or ESI), come into question. Even so, quantitative interpretation of the MS spectrum is ambiguous since large components are not as easily ionized and detected as small ones. The obtained overall distributions in mass spectrometry are usually misleading, and MS can hence only serve as an additional method to SEC, rather than be useful in stand-alone molecular weight determination.⁷¹ Additionally, copolymers typically show very complex mass spectra that are difficult to assign, even if in recent years automatic peak picking methods have improved significantly. If the molecular weight becomes significantly higher than 10 kg mol⁻¹, MS becomes, however, largely unsuitable.^72,73

Conclusions

This paper highlights cases from recent literature studies concerning functional, “non-classical” BCPs that give inconsistent results when analyzed with size exclusion chromatography (SEC). Although SEC works relatively well for nonpolar, flexible BCPs, in particular when using dual detector approaches, the method has regularly shown to produce deviant results when the blocks have significantly different physical or chemical properties. This is noteworthy, since such inhomogeneous BCPs are relevant to a range of modern applications, either because of new functions arising from cooperativity between the blocks, or the combination of multiple functionalities within the same polymer. It is easy to misinterpret the BCP size-exclusion data for such systems, and it is important to stay alert for the various effects that can occur in such systems. The common denominator for the examples in this review is an increase in the SEC retention time upon block extension, which produces erroneous estimates when relying on standard calibration. We identify a minimum of four scenarios that lead to this counterintuitive behavior: (i) rod–coil BCPs, (ii) the carrier solvent being a poor solvent for one of the blocks, (iii) strong mutual interactions between different blocks and (iv) strong interaction between the stationary phase and one of the blocks. In such cases, extending or replacing SEC analysis with/by another detection technique is advisable, even for obtaining mere proof for block coupling or extension. We provide a brief but practical overview of alternative methods, but also discuss to what extent they actually circumvent the challenges identified above.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank the German Academic Exchange Service (DAAD) and Universities Australia for the financial support in the framework of Project 57446038 “High-Precision Synthesis and Self-Assembly of Semiconducting Block Copolymers”. Open Access funding provided by the Max Planck Society.

Notes and references

1. Z. Grubisic, P. Rempp and H. Benoit, Rubber Chem. Technol., 1969, 42, 636–640.
2. W. Liu, X. Liao, Y. Li, Q. Zhao, M. Xie and R. Sun, Chem. Commun., 2015, 51, 15320–15323.
3. H. C. Hsieh, C. C. Hung, K. Watanabe, J. Y. Chen, Y. C. Chiu, T. Isono, Y. C. Chiang, R. R. Reghu, T. Satoh and W. C. Chen, Polym. Chem., 2018, 9, 3820–3831.
4. L. Y. Shi, Z. Shen and X. H. Fan, Macromolecules, 2011, 44, 2900–2907.
5. Z. Yi, Y. Zhang, Y. Chen and F. Xi, Macromol. Rapid Commun., 2008, 29, 757–762.
6. C. Ong, Y. Shi, J. Chang, F. Alduraiei, Z. Ahmed and P. Wang, Ind. Eng. Chem. Res., 2019, 58, 4838–4843.
7. J. J. Li, Y. N. Zhou and Z. H. Luo, Ind. Eng. Chem. Res., 2014, 53, 18112–18120.
8. L. Wu, L. Wang, Z. Guo, J. Luo, H. Xue and J. Gao, ACS Appl. Mater. Interfaces, 2019, 11, 34338–34347.
9. K. Chen, J. Jia, Y. Zhao, K. Lv and C. Wang, Mater. Des., 2017, 135, 69–76.
10. Y. L. Lo, M. F. Tsai, Y. Soorni, C. Hsu, Z. X. Liao and L. F. Wang, Biomacromolecules, 2020, 21, 3342–3352.
11. H. Cabral, K. Miyata, K. Osada and K. Kataoka, Chem. Rev., 2018, 118, 6844–6892.
12. M. Finnegan, G. Mallon, A. Leach and E. Themistou, Polym. Chem., 2019, 10, 5814–5820.
13. K. Ramesh, A. K. Mishra, J. K. Kim, Y. T. Jeong, Y.-S. Gal and K. T. Lim, Materials, 2020, 13, 3713.
14. N. Zaquen, L. Lutsen, D. Vanderzande and T. Junkers, Polym. Chem., 2016, 7, 1355–1367.
15. I. Chandrasiri, D. G. Abebe, M. Loku Yaddehige, J. S. D. Williams, M. F. Zia, A. Dorris, A. Barker, B. L. Simms, A. Parker, B. P. Vinjamuri, N. Le, J. N. Gayton, M. B. Chougule, N. I. Hammer, A. Flynt, J. H. Delcamp and D. L. Watkins, ACS Appl. Bio Mater., 2020, 3, 5664–5677.
16. C. Ma, T. Han, M. Kang, E. Liarou, A. M. Wemyss, S. Efstathiou, B. Z. Tang and D. Haddleton, ACS Macro Lett., 2020, 9, 769–775.
17. L. C. Hsu, S. Kobayashi, T. Isono, Y. C. Chiang, B. J. Ree, T. Satoh and W. C. Chen, Macromolecules, 2020, 53, 7496–7510.
18. F. Ge, Z. Liu, F. Tian, Y. Du, L. Liu, X. Wang, H. Lu, Z. Wu, G. Zhang and L. Qiu, Polym. Chem., 2018, 9, 4517–4522.
19. J. Zhang, K. Kremer, J. J. Michels and K. C. Daoulas, Macromolecules, 2020, 53, 523–538.
20. Z. A. Page, B. Narupai, C. W. Pester, R. Bou Zerdan, A. Sokolov, D. S. Laitar, S. Mukhopadhyay, S. Sprague, A. J. McGrath, J. W. Kramer, P. Trefonas and C. J. Hawker, ACS Cent. Sci., 2017, 3, 654–661.
21. K. M. Meek and Y. A. Elabd, J. Mater. Chem. A, 2015, 3, 24187–24194.
22. A. Pelz, T. S. Dörr, P. Zhang, P. W. De Oliveira, M. Winter, H. D. Wiemhöfer and T. Kraus, Chem. Mater., 2019, 31, 277–285.
23. M. Wang, J. Sun, X. Cai, Y. Huang and F. Li, Org. Electron., 2021, 88, 106020.
24. H. Idriss, A. Gapin, W. Khelifi, S. Blanc, I. Karamé, S. Chambon, L. Hirsch, A. Bousquet and C. Lartigau-Dagron, Macromolecules, 2020, 53, 9043–9053.
25. L. Y. Su, H. H. Huang, Y. C. Lin, G. L. Chen, W. C. Chen, W. Chen, L. Wang and C. C. Chueh, Adv. Funct. Mater., 2020, 2005753, 1–11.
26. P. Kilz, Two-dimensional Chromatography of Copolymers, in Practical Copolymer GPC/SEC and Related Analysis Using Techniques, ed. P. Kilz and D. Held, LCGC, 2017 (accessed at http://www.pss-polymer.com on 2020-05-19).
27. P. Kilz and H. Pasch, in Encyclopedia of Analytical Chemistry, John Wiley & Sons, Ltd, Chichester, UK, 2006, pp. 7495–7543.
28. J. M. Sebastian and R. A. Register, J. Appl. Polym. Sci., 2001, 82, 2056–2069.
29. A. Revillon, J. Liq. Chromatogr., 1980, 3, 1137–1150.
30. V. V. Nesterov, V. D. Krasikov, Y. V. Chubarova and B. G. Belen'kii, Polym. Sci. U.S.S.R., 1982, 24, 1512–1517.
31. H. Schlaad and P. Kilz, Anal. Chem., 2003, 75, 1548–1551.
32. Z. Fodor, A. Fodor and J. P. Kennedy, Polym. Bull., 1992, 29, 689–696.
33. B. Trathnigg and X. Yan, Chromatographia, 1992, 33, 467–472.
34. J. V. Dawkins and M. Hemming, J. Appl. Polym. Sci., 1975, 19, 3107–3118.
35. M. I. Malik, G. W. Harding, M. E. Grabowsky and H. Pasch, J. Chromatogr. A, 2012, 1244, 77–87.
36. J. R. Runyon, D. E. Barnes, J. F. Rudd and L. H. Tung, J. Appl. Polym. Sci., 1969, 13, 2359–2369.
37. C. Feng, M. Jose Gonzalez-Alvarez, Y. Song, I. Li, G. Zhao, G. Molev, G. Guerin, G. Walker, G. D. Scholes, I. Manners and M. A. Winnik, Soft Matter, 2014, 10, 8875–8887.
38. J. J. Wang, Y. N. Zhou, P. Wang and Z. H. Luo, RSC Adv., 2013, 3, 5045–5055.
39. C. St Thomas, H. Maldonado-Textle, J. N. Cabello-Romero, J. MacOssay, X. Zhang, N. Esturau-Escofet and R. Guerrero-Santos, Polym. Chem., 2014, 5, 3089–3097.
40. Z. Xu, T. Liu, K. Cao, D. Guo, J. M. Serrano and G. Liu, ACS Appl. Polym. Mater., 2020, 2, 1398–1405.
41. H. L. Ricks, U. H. Choudry, A. R. Marshall and U. H. F. Bunz, Macromolecules, 2003, 36, 1424–1425.
42. S. Barrau, T. Heiser, F. Richard, C. Brochon, C. Ngov, K. Van De Wetering, G. Hadziioannou, D. V. Anokhin and D. A. Ivanov, Macromolecules, 2008, 41, 2701–2710.
43. J. T. Wang, S. Takashima, H. C. Wu, Y. C. Chiu, Y. Chen, T. Isono, T. Kakuchi, T. Satoh and W. C. Chen, Adv. Funct. Mater., 2016, 26, 2695–2705.
44. Y. Cui, Z. Wang, X. Huang, G. Lu, I. Manners, M. A. Winnik and C. Feng, Macromolecules, 2020, 53, 1831–1841.
45. J. V. Facinelli, S. L. Gardner, L. Dong, C. L. Sensenich, R. M. Davis and J. S. Riffle, Macromolecules, 1996, 29, 7342–7350.
46. S. C. Tsai, Y. C. Lin, E. L. Lin, Y. W. Chiang and S. W. Kuo, Polym. Chem., 2016, 7, 2395–2409.
47. T. Swift, R. Hoskins, R. Telford, R. Plenderleith, D. Pownall and S. Rimmer, J. Chromatogr. A, 2017, 1508, 16–23.
48. S. Mori, J. Chromatogr. A, 1988, 452, 137–143.
49. C. M. Hansen, Hansen Solubility Parameters A User's Handbook, CRC Press, 2nd edn, 2007.
50. J. C. J. F. Tacx, N. L. J. Meijerink and K. Suen, Polymer, 1996, 37, 4307–4310.
51. M. I. Malik, T. Mahboob and S. Ahmed, Anal. Bioanal. Chem., 2014, 406, 6311–6317.
52. C. L. Maikawa, A. Sevit, B. Lin, R. J. Wallstrom, J. L. Mann, A. C. Yu, R. M. Waymouth and E. A. Appel, J. Polym. Sci., Part A: Polym. Chem., 2019, 57, 1322–1332.
53. M. L. Dias, C. Azuma and E. B. Mano, Polym. Bull., 1996, 36, 729–735.
54. Z. Dong, J. Mao, D. Wang, M. Yang, W. Wang, S. Bo and X. Ji, Macromol. Chem. Phys., 2014, 215, 111–120.
55. G. Gaucher, M.-H. Dufresne, V. P. Sant, N. Kang, D. Maysinger and J.-C. Leroux, J. Controlled Release, 2005, 109, 169–188.
56. M. Edeleva, Y. W. Marien, P. H. M. Van Steenberge and D. R. D′hooge, Polym. Chem., 2021 10.1039/D1PY00151E , Advance Article.
57. A. Vora, R. J. Wojtecki, K. Schmidt, A. Chunder, J. Y. Cheng, A. Nelson and D. P. Sanders, Polym. Chem., 2016, 7, 940–950.
58. B. H. Zimm, J. Chem. Phys., 1948, 16, 1093–1099.
59. X. Zhao, K. Deng, F. Liu, X. Zhang, H. Yang, J. Peng, Z. Liu, L. Ma, B. Wang and H. Wei, ACS Biomater. Sci. Eng., 2018, 4, 566–575.
60. G. Gody, P. B. Zetterlund, S. Perrier and S. Harrisson, Nat. Commun., 2016, 7, 10514.
61. P. Kilz, H. Much and G. Schulz, Adv. Chem. Ser., 1995, 247, 223–242.
62. P. Groves, Polym. Chem., 2017, 8, 6700–6708.
63. A. L. Buckinx, K. Verstraete, E. Baeten, R. F. Tabor, A. Sokolova, N. Zaquen and T. Junkers, Angew. Chem., Int. Ed., 2019, 58, 13799–13802.
64. M. Badoux, S. Drechsler, S. Pal and A. F. M. Kilbinger, Macromolecules, 2017, 50, 9307–9314.
65. S. Huber and S. Mecking, Macromolecules, 2019, 52, 5917–5924.
66. J. H. Vrijsen, I. A. Thomlinson, M. E. Levere, C. L. Lyall, M. G. Davidson, U. Hintermair and T. Junkers, Polym. Chem., 2020, 11, 3546–3550.
67. K. Gu, J. Onorato, S. S. Xiao, C. K. Luscombe and Y. L. Loo, Chem. Mater., 2018, 30, 570–576.
68. K. Nakabayashi, T. Takahashi, R. Sugawara, C. T. Lo and H. Mori, React. Funct. Polym., 2018, 131, 350–360.
69. S. Daripa, K. Khawas, A. Sharma, A. Kumar, B. Pal, S. Das, S. Jit and B. K. Kuila, ACS Appl. Polym. Mater., 2020, 2, 1283–1293.
70. D. Marsitzky, M. Klapper and K. Müllen, Macromolecules, 1999, 32, 8685–8688.
71. T. Gruendling, S. Weidner, J. Falkenhagen and C. Barner-Kowollik, Polym. Chem., 2010, 1, 599–617.
72. L. Charles, Mass Spectrom. Rev., 2014, 33, 523–543.
73. A. H. Ribeiro, J. Haven, A.-L. Buckinx, M. Beuchel, K. Philipps, T. Junkers and J. J. Michels, Polym. Chem., 2021, 12, 216–225.

---