Open Access Article
Open Access ArticleMechanical conductance tunability of a porphyrin–cyclophane single-molecule junction†
Werner M.
Schosser‡
 a,
Chunwei
Hsu‡
a,
Chunwei
Hsu‡
 b,
Patrick
Zwick‡
b,
Patrick
Zwick‡
 c,
Katawoura
Beltako
a,
Diana
Dulić
c,
Katawoura
Beltako
a,
Diana
Dulić
 d,
Marcel
Mayor
d,
Marcel
Mayor
 *cef,
Herre S. J.
van der Zant
*cef,
Herre S. J.
van der Zant
 *b and
Fabian
Pauly
*b and
Fabian
Pauly
 *a
*a
aInstitute of Physics, University of Augsburg, 86135 Augsburg, Germany. E-mail: fabian.pauly@uni-a.de
bKavli Institute of Nanoscience, Delft University of Technology, Lorentzweg 1, Delft 2628 CJ, The Netherlands. E-mail: h.s.j.vanderzant@tudelft.nl
cDepartment of Chemistry, University of Basel, St. Johanns-Ring 19, 4056 Basel, Switzerland. E-mail: marcel.mayor@unibas.ch
dDepartment of Physics, Department of Electrical Engineering, Faculty of Physical and Mathematical Sciences, University of Chile, Avenida Blanco Encalada 2008, Santiago 8330015, Chile
eInstitute for Nanotechnology (INT), Karlsruhe Institute of Technology (KIT), P. O. Box 3640, 76021 Karlsruhe, Germany
fLehn Institute of Functional Materials (LIFM), School of Chemistry, Sun Yat-Sen University (SYSU), 510275 Guangzhou, China
First published on 16th December 2021
Abstract
The possibility to study quantum interference phenomena at ambient conditions is an appealing feature of molecular electronics. By connecting two porphyrins in a cofacial cyclophane, we create an attractive platform for mechanically controlling electric transport through the intramolecular extent of π-orbital overlap of the porphyrins facing each other and through the angle of xanthene bridges with regard to the porphyrin planes. We analyze theoretically the evolution of molecular configurations in the pulling process and the corresponding changes in electric conduction by combining density functional theory (DFT) with Landauer scattering theory of phase-coherent elastic transport. Predicted conductances during the stretching process show order of magnitude variations caused by two robust destructive quantum interference features that span through the whole electronic gap between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO). Mechanically-controlled break junction (MCBJ) experiments at room temperature verify the mechanosensitive response of the molecular junctions. During the continuous stretching of the molecule, they show conductance variations of up to 1.5 orders of magnitude over single breaking events. Uncommon triple- and quadruple-frequency responses are observed in periodic electrode modulation experiments with amplitudes of up to 10 Å. This further confirms the theoretically predicted double transmission dips caused by the spatial and energetic rearrangement of molecular orbitals, with contributions from both through-space and through-bond transport.
1. Introduction
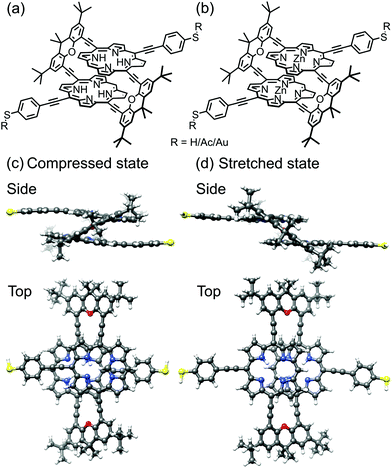
Single-molecule junctions provide an ideal platform to study electronic states in atomically well-defined molecular entities at ambient conditions.1 Particularly, charge transport probes electronic states between molecular attachment points to macroscopic electrodes that are determined by the anchoring groups of a molecule. This renders single-molecule junctions sensitive to geometric and electronic changes, and offers the intriguing possibility to design novel quantum sensors and functional single-molecule electronic components. Electronic states and spin states in single-molecule junctions have been manipulated, e.g. by gate electrodes2–4 or mechanically,5–11 profiting from the precise control of electrode distances in scanning tunneling microscope break junction and MCBJ experiments. Stacked benzene rings offer interesting opportunities for mechanical manipulation of charge transport, and recently they have been explored both theoretically12–17 and experimentally, first in rings held together by van der Waals forces6,9 and thereafter with rings covalently connected by alkyl bridges in paracyclophanes.7,11To explore the potential and limitations of mechanically triggered molecular structures, cyclophanes providing significantly increased π-surfaces have become interesting target structures. Porphyrins are especially promising building blocks for molecular devices.18 Recently the successful synthesis and characterization of mechanically fixed and flexible cofacial porphyrin cyclophanes were demonstrated.19,20 The molecular concept is sketched in Fig. 1: Two porphyrins are expanded by a para-ethynylbenzenethiol subunit to enable their fixation at the electrode surface (blue in Fig. 1). To integrate mechanosensitivity, both porphyrins are interconnected by a pair of rigid xanthene subunits (grey in Fig. 1), which are mounted by acetylenes as revolving joints (light yellow bars in Fig. 1). As a consequence the integrated porphyrin cyclophane (PC) can adapt to distance variations of both electrodes in a sliding motion between both porphyrins. It is, however, worth mentioning that upon pulling and pushing also the distance between both porphyrin planes varies due to the variation of the angle between the interlinking xanthene subunits and the porphyrin planes. By integration of the model compounds PC1 and ZnPC1, displayed in Fig. 2, into a MCBJ experiment, the resulting mechanosensitivity is investigated and benchmarked with simulated expectations. Preliminary results with ZnPC1 in a MCBJ set-up showed sufficient electronic transparency of the structure for the envisioned single-molecule transport experiments, in spite of its dimension.20
 | ||
| Fig. 1 Cartoon representation of the molecular architecture embedded between two gold electrodes for distance modulation experiments. Para-Ethynylbenzenethiol expanded porphyrin decks are sketched in light blue, planar bridging xanthene units in grey, and the revolving acetylene joints in light yellow. The anchoring S-Au bonds, mounting the molecule to the electrodes, are depicted as hooks. While the chemical structure is already indicated, please see Fig. 2 for the exact representations of the studied molecules PC1 and ZnPC1. | ||
Here, we report the in-depth DFT and non-equilibrium Green's functions analysis of the mechanosensitive charge transport through molecular junctions formed by the cofacial porphyrin cyclophanes PC1 and ZnPC1. Particularly, we present MCBJ studies, directly probing the theoretically predicted multiple destructive quantum interference (DQI) features by periodic electrode modulations. Distance-dependent energetic arrangements of the frontier orbitals explain the multiple interference features, which for a stack of two porphyrins are richer than for the previously reported paracyclophane stacks of single benzene rings.7,11 The richness stems from the more extended intramolecular π-systems and the higher mechanical flexibility, enabling larger sliding distances of the two covalently linked molecular porphyrin decks with respect to each other.
2. Results and discussion
In the following we will present results for PC1, see Fig. 1 and 2. Since ZnPC1 shows a similar behavior, it is discussed in the ESI.†2.1. Theoretical
We first describe the mechanical motion of the molecule during the stretching process in detail. Starting from the compressed molecular state, see Fig. 3a, the junction's total energy increases initially to a local maximum at 5.3 Å, see Fig. 4a. Up to this point both porphyrin planes glide over each other in a well-aligned manner, while they slightly separate due to the spatial constraints set by the rigid bridges. The bridges themselves evolve in this displacement interval from a rather flat orientation to a perpendicular angle with respect to the porphyrin planes. At 5.3 Å the total energy decreases abruptly, as the junction releases its tension. This happens through a conformational rearrangement of the molecule, which involves the flipping of a single bridge, see Fig. 3b. The process reduces the distance between the porphyrin planes and at the same time twists them with respect to each other. Due to the attractive van der Waals interactions between the π-systems of the two decks, this intermediate state is energetically favorable. Between 5.3 Å and 6.3 Å the energy rises slightly, while the twist is gradually removed and the porphyrin planes separate. At 6.4 Å the energy of the junction decreases again. This is the result of the flipping of the second bridge, see Fig. 3c. The molecule has now reached a state that resembles the stretched one in Fig. 3d, where the porphyrin planes are aligned in parallel without any twist, as is visible in Fig. 3c at an electrode displacement of d = 6.4 Å. With growing electrode separation the xanthene bridges flatten, the porphyrin planes get closer to each other, while the sliding continuously reduces the intramolecular overlap of the electronic π-systems. In this final elastic phase the total energy rises, until the molecule is fully stretched out, see Fig. 3d, and the contact ruptures at 13 Å. Note that the porphyrins decks are slightly bent before the junction breaks. This differs from the planar configuration in the energy-optimized stretched state of the gas phase, see Fig. 2d, and is due to the mechanical tension exerted by the electrodes. As the inset of Fig. 4a depicts, the junction breaks at an applied force or around 1.3 nN. The mechanical motion of the molecule during the stretching is summarized in a simplified illustration in Fig. 3e.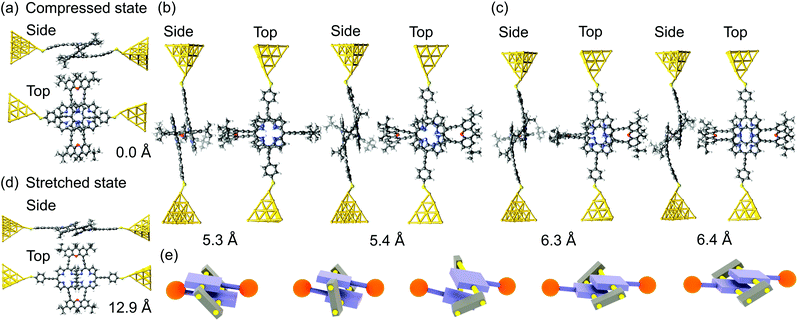 | ||
| Fig. 3 PC1 junction geometries in side and top views during the stretching process (a) in the compressed molecular state at an electrode displacement of d = 0 Å, (b) at the first and (c) at the second bridge flip at d ≈ 5.3 Å and d ≈ 6.3 Å, respectively, and (d) in the stretched state at d = 12.9 Å. In the junctions, hydrogen atoms at the thiol termini are removed as compared to the gas phase geometries in Fig. 2c and d. (e) Sketch of the evolution of the molecular geometry of PC1 with increasing electrode separation. The molecule is connected to gold tip atoms through terminal sulfur atoms on each side. The electrodes are not displayed in this simplified representation. | ||
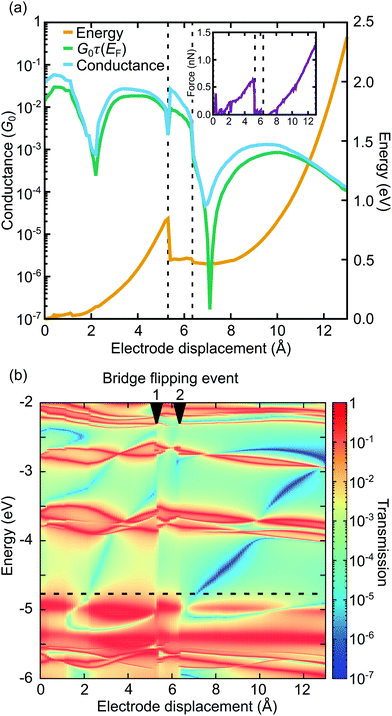 | ||
| Fig. 4 (a) Energy and conductance as a function of electrode displacement. The inset shows the force applied to the junction. The room-temperature conductance at T = 300 K, computed from eqn (2), is compared to the low-temperature approximation G ≈ G0τ(EF). Zero displacement corresponds to the compressed junction state, shown in Fig. 3a. The vertical dashed lines indicate bridge flipping events, see Fig. 3b and c. (b) Transmission as a function of energy and electrode displacement for the single-molecule junction of Fig. 3. Arrows at the top of the plot mark bridge flipping events. The horizontal dashed line shows the Fermi energy EF. Running along it yields the low-temperature approximation of the conductance G ≈ G0τ(EF), shown in panel (a). | ||
The conductance shows a pronounced distance dependence during the stretching process, as evident from Fig. 4a, where conductance is expressed in units of the conductance quantum, G0 = 2e2/h. Especially the two sharp dips at 2.1 Å and 7.3 Å emphasize the large mechanical tunability of the conductance. In the low-temperature approximation G ≈ G0τ(EF) (green curve), it can be tuned by two or four orders of magnitude, respectively, while we observe a substantial increase of dip values, if we take an electronic thermal broadening at T = 300 K into account (light blue curve). (Please see the methods section for further details on how we determine the temperature-dependent conductance from the energy-dependent transmission τ(E).) For a better understanding of electron transport, we study the energy- and distance-dependent transmission of the molecular junction, as displayed in Fig. 4b. The two bridge-flipping processes, discussed above, manifest themselves in the transmission map as sharp vertical discontinuities at 5.3 Å and 6.3 Å, respectively. The dips in the distance-dependent conductance of Fig. 4a (light blue and green curves) are caused by two (light blue and dark blue) valleys in Fig. 4b. They correspond to transmission values below 10−3 and 10−6 inside the electronic gap between HOMO and LUMO states. More precisely, they arise between the almost horizontal red resonance lines at about −5 eV and −3.7 eV, which are related to the molecular frontier orbitals. Since the energy position of the transmission trenches depends on the electrode separation, the conductance can be tuned mechanically. Let us emphasize that since these two transmission valleys cross the entire HOMO–LUMO gap, they are robust features that can be experimentally observed independent of the precise position of the Fermi energy. To complement this study, results for the ZnPC1 derivative are discussed in ESI.1.2.† We find that ZnPC1 shows a similar molecular motion and corresponding DQI features.
The movements of the red resonance lines in Fig. 4b reveal, how molecular orbital energies vary with the stretching distance. In lowest order perturbation theory electronic states of the two porphyrin decks may be viewed as uncoupled, leading to at least twofold degenerate molecular frontier orbitals with distance-independent energies ε(0)α on each deck. The sliding of the π-electron systems of both porphyrin rings then changes the tunnel splitting t(d) between a degenerate pair of frontier orbitals both in magnitude and sign. Such sign changes invert the energetic order of a tunnel-coupled hybridized molecular pair of states of the double decker, since the perturbed energy amounts to εα(d) = ε(0)α ± t(d). Another contribution to energy splittings of the two hypothetically uncoupled porphyrin decks comes from the covalently connected, conjugated xanthene bridges. Due to increased π-orbital overlaps it is largest for flat bridges in compressed and stretched molecular states, while the overlap is diminished for the almost perpendicular bridge orientation in the region of bridge flipping events. Indeed, plots of transmission eigenchannels, see ESI.1.4,† reveal that the bridges contribute to transport at different electrode separations d to a varying extent. This leads to through-bond transport, as compared to the through-space transport from the direct interaction between the π-systems of the two porphyrins.
The DQI features visible in Fig. 4b can be related to orbital symmetries.7,12–14 For off-resonant transport inside the HOMO–LUMO gap, embedding self-energies of the electrodes may be neglected. For this reason, we approximate the Green's function 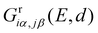 that describes the probability amplitude for propagation of electrons through the molecule at energy E by the zeroth order spectral expression:
that describes the probability amplitude for propagation of electrons through the molecule at energy E by the zeroth order spectral expression:
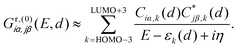 | (1) |
Since each porphyrin deck exhibits two degenerate HOMO and LUMO levels, we have restricted the sum over different orbitals k in eqn (1) to four HOMO and four LUMO states. To explain the transmission behavior and the tunability of DQIs inside the HOMO–LUMO gap, see Fig. 4b, these eight states need to be taken into account due to their energetic vicinity. The molecular orbital symmetry rules presented in ref. 13 and 14 thus need to be extended to multiple levels and be discussed in principle for each distance separately. For instance, we will not specify the orbitals α and β further, but it is important in the following that the orbital characters α and β at i and j remain identical for different k at each d. We find, however, that only the actual HOMO and LUMO states at the respective displacement d need to be studied to argue qualitatively, whether DQI is present or not. We will follow this simplified route in the following, while still presenting the wavefunctions of the gas phase frontier orbital states from gas phase HOMO−3 (GPH−3) to gas phase LUMO+3 (GPL+3) in Fig. 5. Note that the wave functions of all frontier orbitals, displayed in Fig. 5, are of comparable p character at the terminal sulfur atoms i and j, as required for a consistent argumentation.
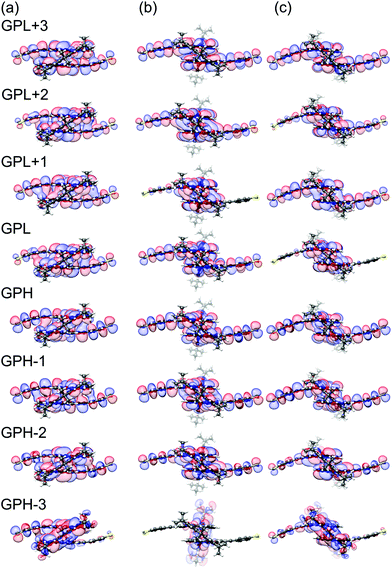 | ||
| Fig. 5 Gas-phase orbitals of PC1 at electrode separations of (a) d = 1.0 Å, (b) d = 6.0 Å and (c) d = 6.4 Å. | ||
Considering only a single HOMO and LUMO state,13 their spectral weights Ciα,HOMOCjβ,HOMO and Ciα,LUMOCjβ,LUMO in eqn (1) at the anchoring atoms i and j need to be of decent size in order to contribute significantly to the Green's function and hence to the transmission at energy E and distance d, which is proportional to 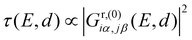 . If the parities of the molecule's HOMO and LUMO are different, i.e. if
. If the parities of the molecule's HOMO and LUMO are different, i.e. if 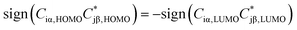 , the terms in eqn (1) will add up and ensure a relatively high transmission value throughout the HOMO–LUMO gap. In contrast, if the parities of the HOMO and LUMO states are the same, the terms cancel each other out at a particular E inside the gap due to the different signs in the denominator and a DQI dip occurs in the transmission.
, the terms in eqn (1) will add up and ensure a relatively high transmission value throughout the HOMO–LUMO gap. In contrast, if the parities of the HOMO and LUMO states are the same, the terms cancel each other out at a particular E inside the gap due to the different signs in the denominator and a DQI dip occurs in the transmission.
Fig. 5 relates the quadruplets of the HOMO and LUMO states of the contacted molecule to those in the gas phase. These orbital wavefunctions were obtained as follows: We removed the gold pyramids from the contacted molecule and replaced them by a hydrogen atom at each contact point. Subsequently, the positions of the added hydrogens were energetically optimized, while keeping all other atoms fixed. Finally, we plotted the frontier orbitals of the resulting molecular geometries.
As mentioned above, for the further analysis we identify the sites i and j with PC1's terminal sulfur atoms. Fig. 5a visualizes the frontier molecular orbitals at an electrode displacement of d = 1.0 Å. GPH and GPL states show decent weight on the terminal sulfur atoms and different parity, which rationalizes the comparatively high transmission values of around 10−3 to 10−2 in the HOMO–LUMO gap at this d as well as the absence of DQI. At d = 1.8 Å however, the previous GPH and GPH−1 wavefunctions exchange roles by rearranging energetically. This results in the same parity for both the new GPH (previous GPH−1) and the GPL. Consequently, DQI emerges, which can be identified as the blue trench in the transmission map of Fig. 4b. Between 4.1 Å and 4.3 Å a complicated level crossing occurs in the GPL quadruplet that causes the GPL+3 to become the new GPL. Since the GPH−1 and GPL+3 in Fig. 5a show different parity, DQI disappears inside the HOMO–LUMO gap. At a displacement of 6.0 Å, see Fig. 5b, GPH and GPL show different parities. This agrees with the absence of DQI in the region from 5.4 Å to 6.3 Å, where the porphyrin planes are twisted with respect to each other, because only one bridge is flipped. Fig. 5c shows the molecular frontier orbitals after both bridges have finally flipped at 6.4 Å. Again, the GPH and GPL have different parity, which corresponds to the absence of DQI until 6.8 Å, where a level crossing is visible for the GPH states. As in the previously discussed HOMO-related level crossing, the GPH−1 that shares the same parity as the GPL becomes the new GPH and causes DQI. This leads to the very pronounced second transmission valley in Fig. 4b. Hence, all the main features of the transmission map can be understood by considering the propagator in eqn (1), i.e., as a result of the electronic structure of PC1. In summary, for a qualitative understanding of the absence or presence of DQI inside the HOMO–LUMO gap, the argumentation with only two levels, namely the GPH and GPL, turns out to be sufficient. However, it requires that the distance-dependent energetic arrangement of GPH and GPL quadruplets is properly tracked.
2.2. Experimental
A two-dimensional (2D) histogram with 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 consecutive fast-breaking traces obtained with PC1 is displayed in Fig. 6a. A reference-free clustering algorithm21 was used to separate traces with molecular features from the direct tunneling ones. The result of the extraction is shown in Fig. 6b. A clear conductance plateau around 2 × 10−6G0 is identified, excellently matching the value of its derivative ZnPC1, as reported previously.20 From this fast-breaking measurement an average length of the breaking trace of 2.3 nm is obtained, lying between the calculated sulfur-to-sulfur lengths of the compressed (2.07 nm) and stretched (2.77 nm) states of the molecule. This finding not only confirms PC1's remarkable single-molecule junction stability in the desired sulfur-connected configuration, which is similar to its Zn derivative, but further suggests that the underlying transport mechanism is influenced negligibly by the presence or absence of Zn atoms in the cyclophane-embedded porphyrins. This conclusion is in agreement with studies on single-porphyrin junctions.22
000 consecutive fast-breaking traces obtained with PC1 is displayed in Fig. 6a. A reference-free clustering algorithm21 was used to separate traces with molecular features from the direct tunneling ones. The result of the extraction is shown in Fig. 6b. A clear conductance plateau around 2 × 10−6G0 is identified, excellently matching the value of its derivative ZnPC1, as reported previously.20 From this fast-breaking measurement an average length of the breaking trace of 2.3 nm is obtained, lying between the calculated sulfur-to-sulfur lengths of the compressed (2.07 nm) and stretched (2.77 nm) states of the molecule. This finding not only confirms PC1's remarkable single-molecule junction stability in the desired sulfur-connected configuration, which is similar to its Zn derivative, but further suggests that the underlying transport mechanism is influenced negligibly by the presence or absence of Zn atoms in the cyclophane-embedded porphyrins. This conclusion is in agreement with studies on single-porphyrin junctions.22
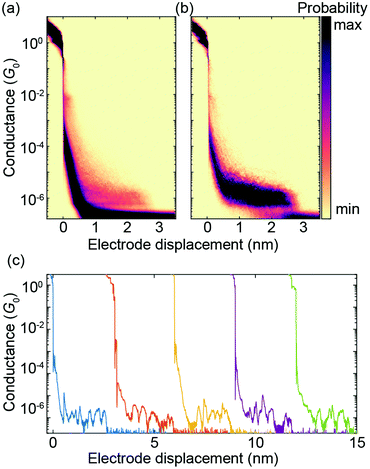 | ||
Fig. 6 Fast-breaking measurement of PC1. (a) 2D conductance-displacement density plot consisting of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 consecutive fast-breaking traces. (b) 2D histogram containing only molecular traces, obtained through a reference-free clustering algorithm.21 (c) Five examples of individual breaking traces, each displaced by hand by 3 nm to ensure good visibility. 000 consecutive fast-breaking traces. (b) 2D histogram containing only molecular traces, obtained through a reference-free clustering algorithm.21 (c) Five examples of individual breaking traces, each displaced by hand by 3 nm to ensure good visibility. | ||
Fig. 6c shows five individual breaking traces of PC1. Multiple oscillations in the conductance up to 1.5 orders of magnitude are visible during the breaking events, demonstrating the largest reported mechanosensitivity in the case of cyclophane-like systems.23 Similar conductance variations in [2.2]paracyclophane single-molecule junctions have been attributed to a stick-slip motion between the anchoring group and the gold electrodes, which enables the molecule to get close to or even cross the DQI-related transmission dip several times in a single breaking event.7 As shown in Fig. 4a, the theoretically predicted breaking trace of a single-molecule junction formed by PC1 features two large conductance oscillations as a result of DQI even without stick-slip motion. It is difficult to distinguish, however, if multiple conductance oscillations arise from crossing several valleys in the transmission-displacement landscape or if they are caused by repeated stick-slip events in a particular breaking trace or both.
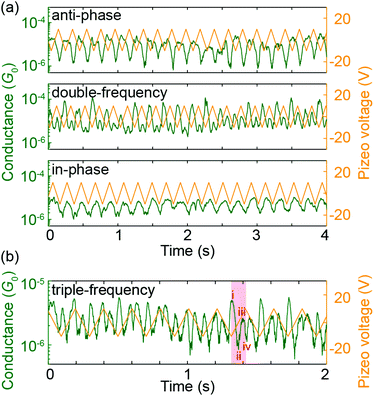
Electrode-displacement modulation measurements were performed to repetitively probe the predicted transmission-displacement landscape of Fig. 4b. Fig. 7a shows anti-phase, double-frequency and in-phase responses, which can be assigned to different starting positions of the modulation measurements in the transmission map. The anti-phase behavior corresponds to a starting position at the left of a DQI dip, where the conductance decreases as the electrodes separate, while the in-phase response results from a starting position at the right of a DQI dip, where the conductance increases as the electrodes move further apart. Finally, the double-frequency case coincides with a starting position so close to a DQI dip that the conductance increases as the electrodes either open or close. These three response behaviors experimentally verify the presence of at least one valley in the energy-displacement transmission map.
In addition to these three responses, we observed higher frequency conductance oscillations. Fig. 7b shows an example of a triple-frequency response (see ESI.2.4† for more examples with both PC1 and ZnPC1). In this case, in one modulation cycle the conductance oscillates up and down three times. Zooming into one single increase of electrode displacement in Fig. 7b, i.e., half of a period (the red shaded area for example), the molecule starts in (i) a high conductance state, (ii) passes a pronounced minimum, (iii) recovers to a high conductance state and (iv) decreases again to take a minimal value. To understand this behavior, we take Fig. 4a as a guide to trace the conductance change. When the molecule is stretched starting from its initial position at d = 0 Å, the computed conductance (i) takes a high value, (ii) drops when approaching the first DQI dip, (iii) increases when leaving the first DQI dip, (iv) decreases again when approaching the second DQI dip. The experimental observations are thus in agreement with the interpretation of the molecule fully crossing one DQI dip and partially entering the second DQI dip. This interpretation is furthermore consistent with the applied modulation amplitude of 5 Å, which does not allow the molecule to fully cross two DQI dips according to the calculations.
To realize a full crossing of two DQI dips, a larger modulation amplitude is required. Excitingly, electrode-displacement modulation experiments with an amplitude of 10 Å were successfully conducted without losing contact to the molecule, while the conductance signal was recorded continuously as a function of time. In rare cases quadruple frequency responses were observed (see bottom panel of Fig. S9b in ESI.2.4† for an exemplary single trace of a 1 nm gap-size modulation using ZnPC1, embracing the full crossing of both DQI dips in the predicted transmission landscape of Fig. 4b). The characteristic is not as clear as the triple-frequency response in Fig. 7b, and the large gap-size manipulation is expected to increase the chance of inducing a slipping motion of the anchoring group on the gold electrodes, which we cannot distinguish.
3. Conclusions
We have presented a combined theoretical and experimental study of charge transport through the porphyrin cyclophane PC1 as well as its derivative ZnPC1. DFT-based calculations predict that during the pulling of the molecular junctions, π-orbitals do not continuously slide over each other. Instead, typically one of the two bridges flips first, followed by the second bridge flip at a later stage. While the π-systems stay parallel, they are slightly twisted with respect to each other between the first and second bridge flipping events. The complex motion of the two conjugated molecular decks leads to two dips in conductance-displacement curves, since there are two such transmission features crossing the entire HOMO–LUMO gap as a function of electrode separation. We further showed that the absence or presence of DQI can be understood by considering the energy and parity of a quadruplet of tunnel-split frontier HOMO and LUMO states of PC1. In contrast to our previous studies of paracyclophanes,7,11 the bridges show some contribution to charge transport. Their overlap with the porphyrin planes is maximized, when they are rather flat in the regions of stretched or compressed states. PC1 and ZnPC1 are thus examples, where both through-bond and through-space charge transport contributions are interlinked.We have experimentally demonstrated a large mechanosensitivity of PC1 at room temperature with conductance variations of up to 1.5 orders of magnitude in fast-breaking measurements. Electrode-displacement modulation experiments show that in addition to the in-phase, anti-phase and double-frequency responses, higher frequency modes are observed. This remarkable experimental detection of higher frequency responses may evidence the presence of the two theoretically predicted robust conductance dips.
For future work, the twisting of molecular decks might be avoided by attaching two bridges at each side of a π-stacked dimer, thus lowering angular freedom and hence stabilizing a more continuous sliding. At the same time the increased rigidity needs to be balanced against the interfacial stiffness, i.e., Au–Au and Au-S bond strengths, to preserve the possibility of mechanical manipulation. Further molecular designs need to be explored in order to better understand the rich variety of mechanosensitive responses and to create novel quantum sensors based on mechanosensitive molecular systems.
4. Methods
4.1. Theoretical
In this paragraph we present the theoretical methods that we use to determine both the geometries of the PC1 molecular junctions during the pulling process and the resulting charge transport properties. Computational parameter settings are specified as well.We compute junction geometries from DFT through energy optimization. To obtain junction structures at different electrode separations, we proceeded as follows: First, the PC1 geometry is optimized in the gas phase in its compressed state, see Fig. 2a. Second, the molecule is placed between two Au20 clusters, forming the extended central cluster of the molecular junction.24 In this step, the geometry is optimized by relaxing both the molecule and the four gold atoms at the top of each pyramid, while the rest of the gold atoms in the metal clusters is kept fixed in a face-centered cubic bulk lattice configuration, see Fig. 3. Third, the stretching process for the junction is started from the compressed molecular state and continued until the point of rupture, when the molecule reaches its stretched state, see Fig. 3. During the process the outermost fixed layers of the gold clusters are separated in steps of 0.1 Å, and the geometry is relaxed in each step in the same way as described before in point two. This yields the junction geometries for a pulling process.
DFT calculations are performed with the quantum chemistry software package TURBOMOLE,25 using the def-SV(P) Gaussian basis set26 for all atoms, the PBE exchange–correlation functional27 and the DFT-D dispersion correction.28 Total energies are converged to an accuracy of better than 10−8 a.u., while geometries are optimized until the change of the maximum norm of the Cartesian gradient is below 10−3 a.u.
We describe electric transport through the single-molecule junctions as phase-coherent and elastic in terms of the Landauer scattering theory.1 The conductance of a single static junction geometry is computed as
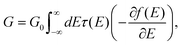 | (2) |
Using the junction geometries and the corresponding electronic structure of DFT, we compute the transmission τ(E) and, from eqn (2), the conductance G for each pulling step. The transport program used for computing the elastic transmission is custom-built and interfaced with TURBOMOLE.24,29 In this step, we employ 32 × 32 k-points for the proper description of the semi-infinite electrodes.
The DFT treatment of quasiparticle energies is frequently improved by applying the DFT+Σ method.30,31 In order to avoid such calculations for every stretching step, we employ this method only for a single representative junction geometry at an electrode displacement of 1.0 Å and correct the Fermi energy in our standard DFT calculations based on this result. In detail, we position EF in the standard DFT calculations in a similar way as in the DFT+Σ calculations. For the junction with the correction applied, the Fermi energy is known to be located at EF,corr = −5.00 eV with respect to vacuum. We then position the Fermi energy EF in the standard DFT calculations in such a way that the ratios of the differences of the HOMO and the LUMO energies, as indicated by the resonances in the corresponding transmission plots, to the respective Fermi energy are the same: (ELUMO,corr − EF,corr)/(EF,corr − EHOMO,corr) = (ELUMO − EF)/(EF − EHOMOs). This yields EF = −4.77 eV.
4.2. Experimental
Electrical transport through single molecules is studied at ambient conditions using the MCBJ technique with electron-beam lithographically defined samples (see ESI.2.1†). Details of the established setup are described in ref. 32 and 33. Two operation modes are used to analyze conductance-displacement relations: fast-breaking and electrode-displacement modulation experiments.In the fast-breaking measurements a constant bias voltage of 100 mV is applied across the junction. The resulting electrical current is monitored continuously. A piezoelectric element pushes the center of a substrate, stretching the evaporated, suspended gold wire. During this process the wire locally thins down to atomic dimensions and eventually ruptures. We calibrate the electrode displacement with the trace length of the 1G0 plateau (corresponding to a single fully open transmission channel of the gold atomic junction).34 Once the nanogap is created, the freshly formed electrodes continuously displace, and an electron tunneling current is measured in the case of an empty gold junction. If molecules are added, conductance traces may feature molecular signatures in terms of plateaus at relatively low conductance values. Reforming the gold wire by lowering the pushing rod allows a statistical analysis by recording numerous consecutive breaking cycles. Thousands of these fast-breaking traces are collected and plotted together in a 2D histogram to investigate conductance-displacement relations statistically.
In the electrode-displacement modulation experiments the gold wires are constricted such that their conductance amounts to 2G0. Due to surface tension, the gold wires break spontaneously and form nanogaps.35 The junctions are then opened to 1 nm, and a displacement modulation with an amplitude of either 5 Å or 10 Å is applied at 5 Hz for 15 s. In the modulation processes the measured conductance as a function of time, referenced to the voltage applied to the piezoelectric element, allows us to differentiate between in-phase, anti-phase, double-frequency and higher order frequency responses. A higher voltage at the piezoelectric element leads to a larger electrode separation.
Author contributions
W. M. S., C. H. and P. Z. contributed equally. W. M. S. and K. B. performed the theoretical DFT and transport calculations, C. H. carried out the MCBJ measurements, and P. Z. synthesized the PC1 and ZnPC1 compounds. P. Z. and D. D. contributed in molecular design, M. M., H. S. J. v. d. Z. and F. P. supervised the study. All authors worked on the manuscript.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This study was supported by the EU and FET open project QuIET (number 767187). C. H. and H. S. J. v. d. Z. acknowledge NWO/OCW (Frontiers of Nanoscience Programme and Vrij Programma-CISS). M. M. receives generous financial support by the Swiss National Science Foundation (SNF grant number 200020-178808) and by the 111 project (90002-18011002). D. D. thanks Fondecyt 1181080, Fondequip EQM140055 and EQM180009 for financing her research.References
- J. C. Cuevas and E. Scheer, Molecular Electronics: An Introduction to Theory and Experiment, World Scientific, Singapore, 2nd edn, 2017 Search PubMed.
- R. Frisenda, G. D. Harzmann, J. A. C. Gil, J. Thijssen, M. Mayor and H. S. J. van der Zant, Nano Lett., 2016, 16, 4733–4737 CrossRef CAS PubMed.
- E. A. Osorio, K. Moth-Poulsen, H. S. J. van der Zant, J. Paaske, P. Hedegård, K. Flensberg, J. Bendix and T. Bjørnholm, Nano Lett., 2010, 10, 105–110 CrossRef CAS PubMed.
- H. Song, Y. Kim, Y. H. Jang, H. Jeong, M. A. Reed and T. Lee, Nature, 2009, 462, 1039–1043 CrossRef CAS PubMed.
- M. Camarasa-Gómez, D. Hernangómez-Pérez, M. S. Inkpen, G. Lovat, E.-D. Fung, X. Roy, L. Venkataraman and F. Evers, Nano Lett., 2020, 20, 6381–6386 CrossRef PubMed.
- R. Frisenda, V. A. E. C. Janssen, F. C. Grozema, H. S. J. van der Zant and N. Renaud, Nat. Chem., 2016, 8, 1099–1104 CrossRef CAS PubMed.
- D. Stefani, K. J. Weiland, M. Skripnik, C. Hsu, M. L. Perrin, M. Mayor, F. Pauly and H. S. J. van der Zant, Nano Lett., 2018, 18, 5981–5988 CrossRef CAS PubMed.
- T. Fu, S. Smith, M. Camarasa-Gómez, X. Yu, J. Xue, C. Nuckolls, F. Evers, L. Venkataraman and S. Wei, Chem. Sci., 2019, 10, 9998–10002 RSC.
- S. Wu, M. T. González, R. Huber, S. Grunder, M. Mayor, C. Schönenberger and M. Calame, Nat. Nanotechnol., 2008, 3, 569–574 CrossRef CAS PubMed.
- T. Brandl, M. El Abbassi, D. Stefani, R. Frisenda, G. D. Harzmann, H. S. J. van der Zant and M. Mayor, Eur. J. Org. Chem., 2019, 5334–5343 CrossRef CAS.
- K. Reznikova, C. Hsu, W. M. Schosser, A. Gallego, K. Beltako, F. Pauly, H. S. J. van der Zant and M. Mayor, J. Am. Chem. Soc., 2021, 143, 13944–13951 CrossRef CAS PubMed.
- K. Yoshizawa, T. Tada and A. Staykov, J. Am. Chem. Soc., 2008, 130, 9406–9413 CrossRef CAS PubMed.
- X. Li, A. Staykov and K. Yoshizawa, Bull. Chem. Soc. Jpn., 2012, 85, 181–188 CrossRef CAS.
- Y. Tsuji and K. Yoshizawa, J. Phys. Chem. C, 2017, 121, 9621–9626 CrossRef CAS.
- G. C. Solomon, J. Vura-Weis, C. Herrmann, M. R. Wasielewski and M. A. Ratner, J. Phys. Chem. B, 2010, 114, 14735–14744 CrossRef CAS PubMed.
- Q. Li and G. C. Solomon, Faraday Discuss., 2014, 174, 21–35 RSC.
- D. Nozaki, A. Lücke and W. G. Schmidt, J. Phys. Chem. Lett., 2017, 8, 727–732 CrossRef CAS PubMed.
- P. Zwick, D. Dulić, H. S. J. van der Zant and M. Mayor, Nanoscale, 2021, 13, 15500–15525 RSC.
- P. Zwick, K. J. Weiland, J. Malinčík, D. Stefani, D. Häussinger, H. S. J. van der Zant, D. Dulić and M. Mayor, J. Org. Chem., 2020, 85, 118–128 CrossRef CAS PubMed.
- P. Zwick, C. Hsu, M. El Abbassi, O. Fuhr, D. Fenske, D. Dulić, H. S. J. van der Zant and M. Mayor, J. Org. Chem., 2020, 85, 15072–15081 CrossRef CAS PubMed.
- D. Cabosart, M. El Abbassi, D. Stefani, R. Frisenda, M. Calame, H. S. J. van der Zant and M. L. Perrin, Appl. Phys. Lett., 2019, 114, 143102 CrossRef.
- M. El Abbassi, P. Zwick, A. Rates, D. Stefani, A. Prescimone, M. Mayor, H. S. J. van der Zant and D. Dulić, Chem. Sci., 2019, 10, 8299–8305 RSC.
- J. Li, P. Shen, S. Zhen, C. Tang, Y. Ye, D. Zhou, W. Hong, Z. Zhao and B. Z. Tang, Nat. Commun., 2021, 12, 167 CrossRef CAS PubMed.
- F. Pauly, J. K. Viljas, U. Huniar, M. Häfner, S. Wohlthat, M. Bürkle, J. C. Cuevas and G. Schön, New J. Phys., 2008, 10, 125019 CrossRef.
- S. G. Balasubramani, G. P. Chen, S. Coriani, M. Diedenhofen, M. S. Frank, Y. J. Franzke, F. Furche, R. Grotjahn, M. E. Harding, C. Hättig, A. Hellweg, B. Helmich-Paris, C. Holzer, U. Huniar, M. Kaupp, A. Marefat Khah, S. Karbalaei Khani, T. Müller, F. Mack, B. D. Nguyen, S. M. Parker, E. Perlt, D. Rappoport, K. Reiter, S. Roy, M. Rückert, G. Schmitz, M. Sierka, E. Tapavicza, D. P. Tew, C. van Wüllen, V. K. Voora, F. Weigend, A. Wodyński and J. M. Yu, J. Chem. Phys., 2020, 152, 184107 CrossRef CAS PubMed.
- A. Schäfer, H. Horn and R. Ahlrichs, J. Chem. Phys., 1992, 97, 2571–2577 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- M. Bürkle, J. K. Viljas, T. J. Hellmuth, E. Scheer, F. Weigend, G. Schön and F. Pauly, Phys. Status Solidi B, 2013, 250, 2468–2480 CrossRef.
- S. Y. Quek, L. Venkataraman, H. J. Choi, S. G. Louie, M. S. Hybertsen and J. B. Neaton, Nano Lett., 2007, 7, 3477–3482 CrossRef CAS PubMed.
- L. A. Zotti, M. Bürkle, F. Pauly, W. Lee, K. Kim, W. Jeong, Y. Asai, P. Reddy and J. C. Cuevas, New J. Phys., 2014, 16, 015004 CrossRef.
- C. A. Martin, D. Ding, H. S. J. van der Zant and J. M. van Ruitenbeek, New J. Phys., 2008, 10, 065008 CrossRef.
- C. A. Martin, R. H. M. Smit, R. van Egmond, H. S. J. van der Zant and J. M. van Ruitenbeek, Rev. Sci. Instrum., 2011, 82, 053907 CrossRef PubMed.
- C. Untiedt, A. I. Yanson, R. Grande, G. Rubio-Bollinger, N. Agraït, S. Vieira and J. M. van Ruitenbeek, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 085418 CrossRef.
- M. Tsutsui, K. Shoji, M. Taniguchi and T. Kawai, Nano Lett., 2008, 8, 345–349 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Details concerning transport calculations and measurements, results especially for ZnPC1 molecular junctions, and summary of chemical synthesis. See DOI: 10.1039/d1nr06484c |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2022 |