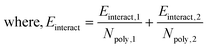Molecular modeling of interfacial layer-by-layer assembly towards functionalized capsule materials†
Andrew W.
Ruttinger
 a and
Paulette
Clancy
a and
Paulette
Clancy
 *b
*b
aRobert Frederick Smith School of Chemical and Biomolecular Engineering, Cornell University, Ithaca, NY 14853, USA
bDepartment of Chemical and Biomolecular Engineering, Johns Hopkins University, Baltimore, MD 21218, USA. E-mail: pclancy3@jhu.edu
First published on 8th November 2021
Abstract
Encapsulated nanomaterials, such as polymer-coated nanoemulsions, have highly tunable properties leading to versatile applications. A current lack of understanding of the fundamentals governing the choice of “capsule” materials (polyelectrolyte + surfactant) and its ensuing performance effectively precludes their widespread use. Computational methods can start to redress this by discovering molecule-scale attributes that significantly control the design of capsule materials tuned to fit desired properties. We use molecular dynamics (MD) to carry out the layer-by-layer (LbL) assembly of six unique polyelectrolyte bilayer systems at a surfactant-mediated interface, modeling early-stage capsule synthesis. Monolayer thickness is related to layer density and polyelectrolyte/surfactant interaction energy through polyelectrolyte molecular weight and radius of gyration, respectively, yielding a simple relationship between absorption kinetics and layer structure. For the second monolayer, faster absorption kinetics are observed for pairings of polyelectrolytes with similarly sized functional groups. Surfactants with a more delocalized charge on the head-group catalyze the build-up of ions at the interface, resulting in faster absorption kinetics and greater confinement of the encapsulated material but leading to thicker, less uniform bilayers. These relationships between capsule building block molecules and nanomaterial capsule properties provide a foundation for property prediction and rational design of optimized multi-functional capsule materials.
1. Introduction
1.1. Nano-encapsulation and applications
The rise of highly functionalized nanomaterials, mainly due to their precise tunability, has spurred development in materials discovery and specialized fabrication techniques.1 In numerous applications, innovation in this area is aided by encapsulation, providing additional functionality while improving the surface area to volume ratio – a key driver for nanomaterial development.2,3Encapsulation can also serve the purpose of material storage, controlled release, protection from an external environment, and improved shelf-life.4 As a result, nano- and micro-encapsulated materials have gained traction in recent years due to their promising applications in, but not limited to, the food industry,5–7 biomedicine,8,9 thermal energy storage,3,10 catalysis,11,12 and photovoltaics.13 As one example, materials capable of storing the latent heat of a phase transition – typically solid-to-liquid – for thermal energy storage, known as “phase change materials”, can be encapsulated to improve their stability and thermal conductivity.3 Despite the versatility of encapsulated nanomaterials, current synthesis techniques often produce materials marred by defects that reduce their quality.1 Efforts focused on the development of controllable encapsulation methods can offer a solution in this regard.
1.2. Layer-by-layer assembly
One popular approach for the encapsulation and coating of functional materials involves layer-by-layer (LbL) assembly.14 This fabrication technique is based on the iterative assembly of oppositely charged molecules to form monolayers – different combinations of polymers and particles, say – with this diversity leading to high tunability of capsule properties.3,14 Charged polymers, called polyelectrolytes, are most commonly used as the capsule materials due to their functional diversity and balance between strength and flexibility.3 Encapsulation of liquids is possible through an adaptation of LbL assembly to a surfactant-mediated interface of an oil/water emulsion, allowing additional control over capsule properties.3 These surfactants feature charged head-groups that facilitate electrostatically driven assembly of the polyelectrolytes. Beyond those already stated, LbL assembly has several advantages over alternative materials fabrication methods: it can be applied to surfaces of any geometry, it is universal and flexible due to its compatibility with other chemistries, and it replicates the chemistry of materials engineering in living organisms.15 While its step-by-step nature requires additional time for fabrication, it allows for precise control over capsule thickness, stability, and composition.3,4,151.3. Current challenges and scope
Despite the documented connection between capsule materials and performance, the literature has called for more research to establish the fundamental factors that lead to specific functional attributes in multi-layered emulsions.3,16 For example, although the primary driver of LbL assembly involves harnessing electrostatic interactions, other interactions, such as hydrogen-bonding, covalent bonding, base-pair interactions, guest–host interactions, and hydrophobic interactions, add complexity to the process.4,17 Polyelectrolyte structure and electrostatic properties have a direct impact on monolayer thickness, porosity, and structure; likewise, surfactants control the surface charge and electrical properties of the first assembled monolayer.16Recent attempts at molecular-level characterization using experimental approaches have aimed to uncover the interactions at play in these systems.18–20 However, these experimental approaches do not provide the microscopic mechanistic detail necessary to demarcate the fundamental interactions that govern LbL assembly. Since capsule properties such as internal structure and surface roughness depend on the depositing surface,21 it becomes critical to understand, and hence tune, early-stage multilayer growth if we are to harness the potential of functionalized capsules. Given the experimental difficulties in acquiring this information, computational approaches have been described in the literature as having an important role to play in property prediction and optimizing the performance of capsules based on the materials used during LbL assembly.14,17 Specifically, molecular dynamics (MD) has been identified as a likely tool for the future design of multilayers.15
Our work builds on the inferences made in previous molecular characterization studies and applies it to a new challenge: uncovering the relationship of the absorption dynamics and nanomaterial capsule structure with the properties of different combinations of building-block molecules during assembly at a liquid–liquid interface. We tackle the challenge of controlled capsule synthesis by carrying out MD simulations of nanomaterial encapsulation through LbL assembly of polyelectrolytes at an oil–water interface. We investigate bilayer LbL assembly for six unique pairs of candidate molecules to understand the structural effect of different choices of surfactant and polyelectrolyte that, together, affect the performance of the resulting capsule. Specifically, our scope targets the effect of functional group structure and the nature of its charge which directly influences LbL assembly. We model absorption kinetics of this LbL assembly to characterize the atomic-level interactions that govern layer growth. Leveraging this insight, we derive correlations between absorption rate, layer thickness, and layer density to provide the first comparison of capsule materials on a molecular scale. We also discuss the relationship between layer orientation, interface coverage, and molecule properties. Our study addresses an acknowledged need in the literature for computational insight into the functional attributes of capsule materials and methods for property prediction.14,15
2. Methods
2.1. Molecular dynamics computations
We used MD to carry out all the preliminary analysis and all the subsequent LbL assembly simulations. We used Sandia's popular MD code, Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS).22 The force field used to represent the molecules was the Optimized Potential for Liquid Simulations (OPLS) due to its validation in similar studies;23–26 this also contains the TIP3P model for water.27 All simulations used a time step of 1 fs and were carried out at 298 K. Bonds and angles were treated as harmonic, and a cut-off of 10 Å was used for the Lennard-Jones interactions. Since LbL assembly is driven by coulombic interactions, we used a long-range coulombic potential coupled to a Particle–Particle Particle–Mesh (PPPM) solver to describe longer-ranged interaction beyond 10 Å.28 Additional computational details and justifications are provided in the ESI.†2.2. System definition
Each system evaluated in this work consists of four components: an oil phase as the encapsulated material, a water phase containing ions wherein LbL assembly occurs, a charged surfactant layer that sits at the water–oil interface, and a depositing polyelectrolyte layer that has the opposite charge of the layer onto which it is being deposited. For the first layer, this is limited to oppositely charged pairs of surfactants and polyelectrolytes. We used PACKMOL to populate our system for all molecules based on satisfying either a specified density or a required number of molecules, except the surfactants which were arranged in a plane across the interface.29 All polyelectrolytes and surfactants are accompanied by a counter-ion (Na+ or Cl−) with opposite charge (Fig. S1†). This counter-ion plays a crucial role in the ion-exchange that drives LbL assembly for capsule synthesis, as we will show in section 3.1.2.3. Polyelectrolytes
Our study evaluated three polyelectrolytes that serve as the capsule materials: sodium poly(styrene sulfonate) (PSS), poly(allylamine) hydrochloride (PAH), and sodium poly(acrylate) (PA) (the sodium salt of poly(acrylic acid) (PAA)). These three choices provided a diversity of charge (positively/negatively charged), functional group (sulfonate, acrylate, and allylamine), and functional group length (6.1, 2.4, and 2.5 Å, respectively). A polyelectrolyte length of 16 repeating units was chosen based on our investigation to define a suitable polyelectrolyte length (described in the ESI†).2.4. Surfactants
We studied the influence of the choice of surfactants on LbL assembly, developing three different interfaces using sodium dodecyl sulfonate (SDSn), sodium dodecyl benzene sulfonate (SDBS), and dodecyl trimethyl ammonium chloride (DTAC). While surfactant structural aspects including alkyl tail length30 and number of alkyl tails31 affect nano-emulsion stability, we focus this work on the structural factors that directly drive multilayer growth. In particular, interactions that arise from the chemical affinities and charge balance between surfactants and polyelectrolytes are known to control the growth mechanism.32,33 Therefore, the three chosen surfactants provide a diversity of charge, charge density, and head group structure – factors critical for LbL assembly. We chose SDSn and SDBS due to their use in previous computational studies.34 DTAC was chosen due to its structural similarity to didodecyldimethylammonium bromide, a common surfactant in capsule synthesis,35,36 and the fact that it features a single dodecyl tail and a chlorine counter-ion, consistent with the counter-ions of the other surfactants/polyelectrolytes chosen for our study.2.5. Solvent and ionic concentration
Hexadecane (C16H34) was selected as the paraffin, due to its use as an encapsulated material in applications such as thermal energy storage.37,38 Its shorter length also made it more computationally accessible. Water was used as the solvent for the polyelectrolyte solution and washing step.Salt concentration also has a significant effect on layer growth behavior, with high salt concentrations resulting in reduced effective polyelectrolyte charge and, consequently, non-linear growth with respect to layer number.32 We used a salt concentration of 0.15 M NaCl as additional ionic concentration in the polyelectrolyte solution. Its role was to facilitate a more linear LbL assembly, and its value fell within the range typically used in the literature.25,39 A salt concentration of 0.15 M NaCl has been demonstrated successfully for PSS/PAH and PAA/PAH pairings, showing its applicability to our studied systems.40
2.6. Computational protocol for layer-by-layer assembly
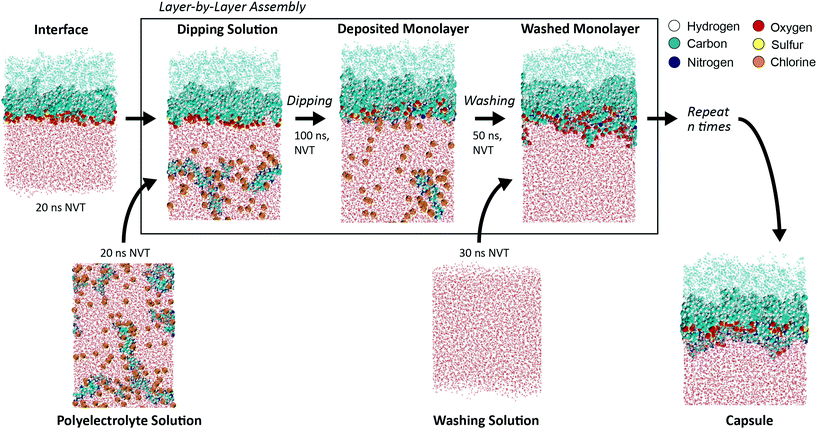
We undertook a series of simulations to verify our chosen computational methods and procedure. The results of these preliminary studies are provided in the ESI.†Our main simulations were designed to model the LbL assembly of a polyelectrolyte bilayer at an oil–water interface stabilized by surfactant emulsifers (Fig. 1). These surfactants were maintained a constant surface area per molecule (SAPM) of 64 Å2/surfactant, which we calculated was the most energetically favorable with respect to SAPM (Table S2, and Fig. S2†). We followed a step-by-step process, involving the iterative deposition of oppositely charged polyelectrolyte layers (“dipping”) and removal of excess polyelectrolyte to prevent aggregation in solution (“washing”).25,26 For each unique system, we performed two dipping and washing cycles, corresponding to the assembly of a polyelectrolyte bilayer. The polyelectrolyte for the first layer has the opposite charge to the surfactant layer, while the polyelectrolyte for the second layer has the opposite charge of the first polyelectrolyte layer.
The long time scales associated with absorption and internal reorganization within deposited polyelectrolyte monolayers makes full-layer relaxation in MD essentially intractable.32,41,42 Instead, we follow the lead of similar kinetic studies that compare the extent of LbL assembly after a set time point,43 in our case 100 ns for the dipping step. This allowed us to make an equitable comparison between the studied systems at a reasonable computational expense. Data on dynamics and kinetics were gathered during this time. The washing step was run for 50 ns, with data on layer structure gathered during the last 40 ns of this simulation. All simulations were run in an isothermal, NVT ensemble. While these interfaces are typically a spherical emulsion in physical experiments, at the length scale of MD, the curvature can be assumed to be negligible and the interface was treated as a planar surface. Further justification on our selected methods and step-by-step dipping and washing procedure are provided in detail in the ESI.†
3. Results and discussion: monolayer assembly
This section provides the first computational description of the (1) absorption kinetics of polyelectrolyte assembly, (2) layer structure, and (3) the relationship between these and the inherent molecular properties of the surfactants and polyelectrolytes. We provide a visual and quantitative depiction of the electrostatic behavior in solution, before modeling the absorption kinetics of different systems. Then, we characterize the resulting monolayer structure, deriving correlations between layer thickness and layer density, and layer thickness and absorption kinetics. Finally, we relate the unique behavior of different systems to structural properties including layer orientation and interface coverage.3.1. Electrostatics as a driving force for LbL assembly
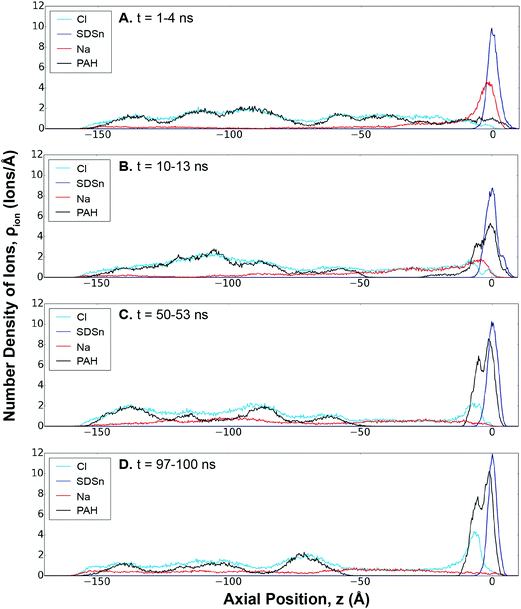
Electrostatic forces are considered to be an important driving force in LbL assembly.44 Initial assembly of a polyelectrolyte layer is considered to be a diffusion-controlled process coupled to the adsorption of the polymer through an electrostatic or steric barrier.32 Using SDSn/PAH as an example, Fig. 2 shows that the polyelectrolyte assembly at the interface is a result of an ion-exchange between PAH and the Na+ counter-ions, in agreement with the literature.43,44 Initially, these Na+ counter-ions are paired in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio with the SDSn. Similarly, PAH and its Cl− counter-ions were paired in solution.
1 ratio with the SDSn. Similarly, PAH and its Cl− counter-ions were paired in solution.
At early stages of the assembly, the mobile Na+ ions begin to diffuse into the solution, leading to a ionic gradient of Na+ (Fig. 2A, red line). This is driven by the entropy gain from the release of the counter-ions from the surfactants and polyelectrolytes into solution.32 In response to this ionic imbalance at the interface, PAH diffuses towards the interface and begins to form charge-pairs with the SDSn. However, since PAH has 16 charges (versus one for an ion), the deposited polyelectrolyte can form more charge-pairs, making it far less mobile than the counter-ions and more strongly bound at the interface. This results in a build-up of polyelectrolytes at the interface, rapidly at first before slowing down as the process continues (Fig. 2, black line). Eventually, the system reaches a more “equilibrated” state, where PAH establishes a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 charge pairing with SDSn at the interface and the Na+ ions are distributed evenly throughout the solution (Fig. 2D).
1 charge pairing with SDSn at the interface and the Na+ ions are distributed evenly throughout the solution (Fig. 2D).
At the boundary between the deposited polyelectrolyte layer and the solution, an increased concentration of Cl− ions balances the PAH charges facing away from the interface. This represents overcharging, which will serve as the source of ions to be exchanged for the LbL assembly of the following layer. Beyond this boundary, the solution near the interface is devoid of PAH, likely due to electrostatic repulsion between the deposited and free polyelectrolyte molecules. In the bulk solution, free PAH molecules are dispersed uniformly amongst dissolved Na+ and Cl− ions. Ion-exchange profiles for the other systems are provided in the ESI (Fig. S11–S13†).
3.2. Interaction energy as a model for absorption kinetics
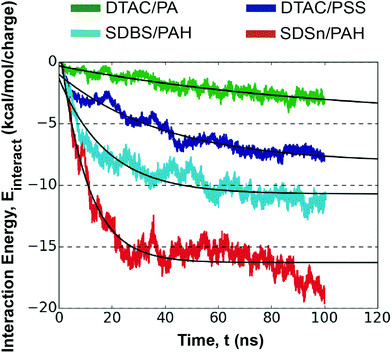
While the mechanism of this ion-exchange is similar, regardless of the choice of surfactants, polyelectrolytes, and ions, the absorption kinetics are dependent on all these factors and can lead to significant differences in behavior and layer structure.44 We quantify the unique absorption kinetics of the LbL assembly for each system using the magnitude of the interaction energy between different species over time (i.e. polyelectrolyte, surfactant, solvent, ions); see Fig. S15.† A larger interaction energy denotes a stronger attraction between the two groups of species. For comparative purposes, each interaction energy is given as an energy per charge in the group of molecules.Importantly, this metric captures the electrostatic interactions between charges, as well as non-electrostatic interactions such as hydrogen-bonding24,44 and hydrophobicity, which are known to facilitate LbL assembly.45 While we do not measure free energy and entropy for direct evaluation of hydrophobicity, the interaction energy between water and polyelectrolyte describes this effect reasonably well.46 Considering the large differences between reported polyelectrolyte/water interaction energies, we can confidently use this energy to compare hydrophobic effects during assembly.
Interaction energies proved capable of characterizing polyelectrolyte assembly well (see Fig. S15†). The interaction energy between the surfactants and their counter-ions provides insight into the entropically driven release of counter-ions into the solution. In all cases, this interaction energy asymptotically approaches zero, signifying that all ions have been exchanged for polyelectrolytes. However, the rate of interaction energy decay varies, and consequently counter-ion release, implicating polyelectrolyte/surfactant attraction. Simultaneously, the magnitude of the polyelectrolyte/surfactant interaction energy increases, asymptotically approaching a value that depends on the combination of molecules in the system. This is expected as deposition occurs, and these polyelectrolyte/surfactant interactions have been shown to play an important role in kinetics, capsule stability, and surface morphology.47,48 This interaction energy is driven by the ability of each unique combination of polyelectrolytes and surfactants to form interacting groups, rooted in the nature of the molecules themselves (Table 1). More details for this calculation are provided in the ESI.†
| System | Interaction energy (kcal per mol per charge) | Number of interacting groups | Absorption time constant, τ (ns) |
|---|---|---|---|
| SDSn/PAH | −18.1 | 104 | 10 |
| SDBS/PAH | −11.4 | 99 | 18 |
| DTAC/PSS | −7.4 | 78 | 40 |
| DTAC/PA | −2.8 | 34 | 103 |
The magnitude of the interaction energy for the four polyelectrolyte/surfactant systems follows the trend: SDSn/PAH > SDBS/PAH > DTAC/PSS > DTAC/PA. From this starting point, we can leverage our fundamental insight to connect polyelectrolyte assembly to well-defined molecular characteristics: first, the surfactant/water interaction energies follow the same trend as the polyelectrolyte/surfactant interaction energies, with SDSn > SDBS > DTAC. While SDBS is a more polar molecule (ESI, Table S2†), its ability to interact with the polar solvent is weaker than SDSn. A likely explanation for this is the ability of SDBS to interact favorably with itself through aromatic stacking, while SDSn tends to repel other surfactants and instead preferentially interacts with other species such as water or ions. Second, the polyelectrolyte/water interaction energy is inversely related to the polyelectrolyte/surfactant interaction energy, with PAH < PSS < PA. A stronger interaction energy with water indicates that the polyelectrolyte is less hydrophobic.46 This suggests that more hydrophobic polyelectrolytes favor monolayer formation, which agrees with experimental observations.45 Finally, the rate of the surfactant/ion interaction energy decay is related to the magnitude of the polyelectrolyte/surfactant interaction energy. This indicates that a higher entropic drive for counter-ion release from a particular surfactant results in a higher affinity between the surfactants and polyelectrolytes, which in turn could facilitate further counter-ion release.
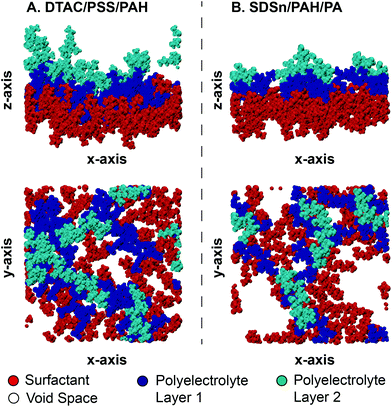
Although diffusion plays an important first step in transporting polyelectrolytes towards the interface for layer assembly, ultimate absorption of the polyelectrolyte is kinetically driven and is governed well by first-order kinetics that originate from an electrostatic barrier.24,32 Electrostatics are encompassed in the polyelectrolyte/surfactant interaction energy, allowing us to model this kinetic absorption. Following a similar approach to that in the literature for estimating absorption kinetics, we fitted an exponential curve to the interaction energy profile between each polyelectrolyte/surfactant pair. This allows us to derive a time constant, τ, that provides a quantitative comparison between rates of polyelectrolyte absorption (Fig. 3).24 Since this energy profile follows a decaying exponential curve, the fitting equation will have the form:
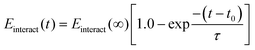 | (1) |
Notably, larger polyelectrolyte/surfactant interaction energies and more interacting groups correlate well with faster absorption kinetics (Table 1). This suggests that polyelectrolyte/surfactant combinations with an affinity for these atomic-scale interactions have more strongly bound polyelectrolyte layers and faster absorption kinetics. SDSn has relatively more electronegative oxygen atoms in its head-group in comparison to the other surfactants, explaining why the oppositely charged polyelectrolytes interact more frequently and more strongly with the head-group. Searching for other surfactants with this type of localized electronegative/electropositive functional group could uncover other surfactants that promote faster polyelectrolyte absorption.
Finally, faster absorption kinetics have been reported for counter-ions with larger ionic radii.43 Ions with a higher hydration ability (Na+ > Cl−) diffuse more slowly, the result of a larger hydrodynamic radius that leads to a more tightly bound hydration shell and, consequently, a weaker interaction between ion and polyelectrolyte.43,44 Our interaction energy profiles reflect this observation, where the polyelectrolyte/ion interaction energy is generally weaker for Na+, leading to a higher polyelectrolyte/solvent interaction energy (Fig. S15†). Despite this, the two fastest systems in our study have Na+ as the counter-ion for the surfactant, as opposed to Cl−. This indicates that the properties of surfactants and polyelectrolytes dominate the observed kinetics, at least at early growth stages in LbL assembly. Then varying the type of counter-ion may be reserved for fine-tuning kinetics. Studies of the ion effect on layer growth have reported a complex interplay of different interactions,44,49 indicating that future computational work should investigate ion effects for enhanced LbL assembly tunability.
3.3. Master equations towards predicting monolayer structure
Structural characteristics of the deposited polyelectrolyte layer, such as layer thickness, layer density, and water content, provide tunable properties for capsule performance, as the chemistry of the encapsulation material directly affects layer composition and stability. Density profiles for each system (see Fig. S17†) reveal idiosyncratic polyelectrolyte layer properties, suggesting that the influences of polyelectrolyte and surfactant are significant. We find our calculated water content values range from 46%–70% (Table S5†). This compares well to a study of LbL assembly in the literature that reports the water content of two different monolayers to be 63%–66%.50 When more polar surfactants, like SDSn and SDBS, are involved, the resulting polyelectolyte layer is thinner than those with the DTAC surfactant (Fig. S17, and Table S5†). However, this trend does not hold for the layer density. Moreover, while water content has been found to have an influence on the resulting layer thickness due to swelling,44,50 there is a lack of agreement between these metrics across our studied systems.To elucidate these relationships, we sought “master” equations that empirically relate monolayer structural properties to LbL assembly dynamics and the inherent molecule characteristics at constant polyelectrolyte, surfactant, and ion concentrations. Such relationships could provide researchers with a quick filter for the design of capsules with targeted properties. Therefore, we quantify the relationships between (1) layer thickness and density and (2) layer thickness and absorption kinetics, using a linear least squares regression to fit our calculated data and derive eqn (2) and (3). The resulting equation constants are independent of surfactant and polyelectrolyte type. Additional research should seek to test the transferability of these equations at varying species concentrations. Since the mechanisms for assembly have been shown to vary with layer,51 these relationships are valid for layer n = 1.
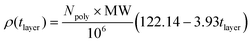 | (2) |
Here, Npoly is the number of deposited polyelectrolytes, MW is the polyelectrolyte molecular weight, and tlayer is the layer thickness.
Physically, this relationship suggests that thinner layers have a higher molecular density, but the final mass density is determined by a scaling factor given in eqn (2). Therefore, although the DTAC/PSS system gives the highest mass density polyelectrolyte layer, its low molecular density results in a thicker layer. While PSS, PA, and PAH each have a degree of polymerization of 16, they have significantly different molecular weights (2949 g mol−1, 1139 g mol−1, and 932 g mol−1, respectively). This explains the difficulties in correlating mass density with layer thickness. Our observations are verified by previous experimental work that has indicated that polyelectrolyte layer thickness increases with increasing molecular weight.52,53
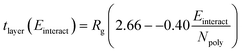 | (3) |
Physically, this correlation suggests that, as the polyelectrolyte/surfactant interaction energy increases, the ratio of the layer thickness to the polyelectrolyte Rg decreases. However, layer thickness is determined by the polyelectrolyte Rg. Preliminary investigation shows that PSS has the highest Rg, meaning it has a higher inherent layer thickness than the other polyelectrolytes, leading to the thickest layer despite having a smaller dimensionless thickness than PA.
3.4. Chemical origins of polyelectrolyte orientation
Although we have defined empirical relationships that provide fast capsule design mechanisms, uncovering the root cause of thickness in the capsule monolayers will be necessary to better direct future work in this area. Previous work in the literature has shown that the average orientation of the deposited polyelectrolytes relative to the surface/interface cross-section is related to the compactness of the monolayer.25To capture this effect, we measure the degree of parallelism of the deposited polyelectrolytes to the interface. Following methods provided in the literature,25 the angle between the interface, which we take as the xy-plane, and the polyelectrolytes can be related through the inertia tensor:
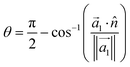 | (4) |
Here, ![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) is the unit vector in the z-direction,
is the unit vector in the z-direction, 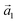 is the major eigenvector of the inertia tensor, and
is the major eigenvector of the inertia tensor, and 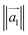 is the magnitude of this eigenvector.
is the magnitude of this eigenvector.
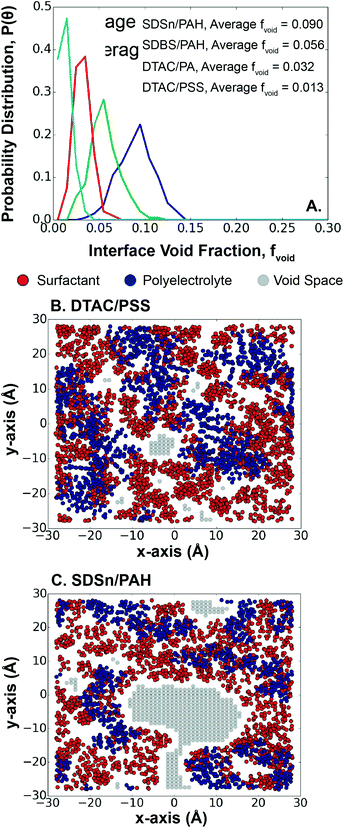
Polyelectrolytes perfectly aligned along the interface exhibit θ = 0. As expected, weaker polyelectrolyte/surfactant interaction energy is correlated to worse alignment with the interface. The DTAC/PA system is the least aligned, with an average θ of 4.37°, while the SDSn/PAH system is the most aligned, with an average θ of 1.84° (Fig. 4). However, the DTAC/PSS system deviates from this trend, being the second most oriented, despite having the second weakest interaction energy. We find that PSS tends to disrupt the surfactant layer, evidenced by an overlap of 13.3 Å between the surfactant and polyelectrolyte layers (Fig. S17†). In comparison, the other systems have an average overlap of 7.6 Å between these layers. This unique ability of PSS, perhaps a result of the aromatic group's ability to exhibit both hydrophobic and hydrophilic interactions,56 leads to a higher than expected orientation.
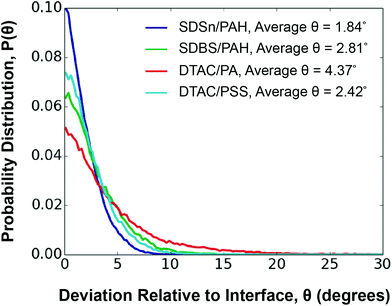 | ||
| Fig. 4 Orientation of layer n = 1 in relation to the interface for each system studied. A legend is provided to identify the different systems. | ||
3.5. Chemical origins of interface coverage
Surface coverage has implications for the encapsulated material, since an exposed interface between the hexadecane and water could lead to hexadecane loss during synthesis. The choice of polyelectrolyte/surfactant system plays a role here, since surface pattern and charge density have been shown experimentally to control multilayer surface coverage and morphology.57 A previous study of LbL assembly qualitatively showed that the first monolayer is relatively evenly distributed across a fixed charged surface.25 However, in the case of LbL assembly at an interface, the charged surface is dynamic, meaning that the positions of the deposited polyelectrolytes are less fixed than on a surface.Measuring the distribution of void space in each system, we find that systems with larger void fractions have higher polyelectrolyte/surfactant interaction energies, except for PSS/DTAC, which has a lower than expected void fraction (Fig. 5A). Again, PSS could play a role here, since the larger size of PSS covers more surface area than the smaller PAH and PA molecules (Fig. 5B). In the case of the other systems, the higher polyelectrolyte/surfactant interaction energy leads to accumulation of the surfactants around the polyelectrolytes, exposing holes in the interface (Fig. 5C). This also results in a wider distribution of void fractions, as the surfactants are more dynamic. In contrast, for systems with weaker interaction energies, the surfactants accumulate less often near the polyelectrolytes and can, instead, fill the holes in the interface. This behavior results in a trade-off between LbL absorption kinetics, layer thickness, and interface control. This trade-off can be mitigated using surfactants with a higher SAPM to better cover the interface, reducing the risk of losing the encapsulated material.
4. Results and discussion: bilayer assembly
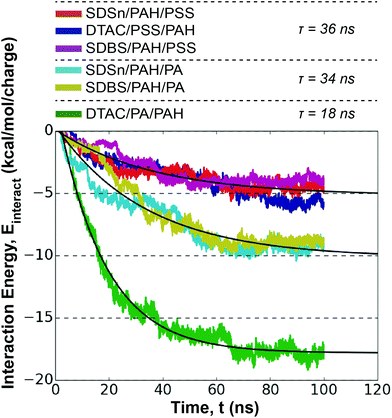
To capture the unique mechanism of LbL assembly for different layers,51 we extend our study of LbL assembly absorption kinetics and capsule structural to a bilayer system. We aim to quantify effects not found in a single monolayer system, like polyelectrolyte/polyelectrolyte interactions and monolayer overlap. The second dipping step for our capsules features the deposition of the oppositely charged polyelectrolytes.4.1. Interaction energy as a model for absorption kinetics
Assembly is again driven by ion-exchange between the Na+/Cl− and the polyelectrolyte, albeit at the polyelectrolyte/polyelectrolyte interface for the second monolayer. Previous studies have demonstrated that the strength of interactions between polyelectrolytes increases diffusivity, affecting layer growth.58 Therefore, the interaction energy between the deposited polyelectrolyte and the depositing polyelectrolyte provides a useful metric for estimating the absorption kinetics (Fig. S20†).Plotting the polyelectrolyte/polyelectrolyte interaction energy shows the emergence of three distinct trajectories (Fig. 6): PAH/PSS pairings < PAH/PA pairings excluding the DTAC/PA/PAH pairing < the DTAC/PA/PAH pairing. We fit eqn (1) to the average value of these groups in order to estimate characteristic absorption time constants, τ.
In general, the surfactant has little effect on the absorption kinetics at the second layer. Unlike the first monolayer deposition, absorption rate does not follow the trend in hydrophobicity of the polyelectrolyte. Instead, the second layer kinetics appear to be driven by the compatibility of the polyelectrolyte pairs. PAH/PA pairs have both faster kinetics and a stronger interaction energy than PAH/PSS pairs. PA and PAH have similar functional group sizes (2.4 and 2.5 Å, respectively) as opposed to PSS and PAH (6.1 and 2.5 Å, respectively), indicating sterics may limit the ability of PSS/PAH to interact electrostatically. Overall, the absorption rates from this dipping step are similar to those from the first monolayer, although the distribution of τ values is narrower.
Compared to PAH/PA pairs with SDSn and SDBS, the absorption rate of DTAC/PA/PAH is nearly twice as fast. Moreover, two more polyelectrolytes are deposited during the 100 ns simulation. Counter-ions play an active role in this step, with each system showing an increase in surfactant/ion interaction energy over the course of the dipping step (Table 2). This increase in interaction energy follows a trend across surfactants (DTAC > SDBS > SDSn) and polyelectrolyte pairs (PAH/PA > PAH/PSS), opposite to the trends observed in polyelectrolyte/surfactant interaction energies during the first monolayer deposition (Table 1). Intuitively, if the polyelectrolyte/surfactant interaction energy is weak and the polyelectrolyte/polyelectrolyte interaction energy is strong, we would expect the first layer to preferentially interact with the incoming polyelectrolyte layer, weakening its interactions with the surfactant. Then, to compensate for this newly available charge at the surfactant layer, a counter-ion would diffuse to the interface. This donation of charge from counter-ions is known as extrinsic charge compensation. As maintaining electroneutrality between polyelectrolyte layers becomes a more prominent driving force, the resulting extrinsic charge compensation from counter-ions reduces the importance of entropy on LbL assembly.32 This has implications on the relative importance of entropic counter-ion release on affinity between the polyelectrolyte layers as LbL assembly progresses.
| System | Poly/poly interaction energy (kcal per mol per charge) | Surfactant/ion interaction energy (kcal per mol per charge) | Extrinsic charge fraction |
|---|---|---|---|
| SDSn/PAH/PA | −9.3 | −1.6 | 0.157 |
| SDSn/PAH/PSS | −4.5 | −0.8 | 0.134 |
| SDBS/PAH/PA | −8.8 | −4.5 | 0.211 |
| SDBS/PAH/PSS | −3.8 | −2.4 | 0.185 |
| DTAC/PA/PAH | −18.1 | −7.5 | 0.278 |
| DTAC/PSS/PAH | −5.7 | −3.8 | 0.248 |
We calculate extrinsic charge (i.e. ions) as the fraction of ions among the total charges within 10 Å of the edge of the first monolayer (Table 2).59 As expected, the extrinsic charge fraction is highest for DTAC/PA/PAH, verifying the uptake of counter-ions to balance the charge at the surfactant layer. The PAH/PA pairs also show an increased presence of ions within this defined layer, compared to PAH/PSS. These results point to the importance of ions to facilitate LbL assembly and the potential trade-off between absorption kinetics for odd and even monolayers. Selection of compatible polyelectrolytes and surfactants can help stabilize this divergence in kinetics to provide a more controllable capsule synthesis.
4.2. Master equations towards predicting bilayer structure
Similar to the first monolayer, the density profiles after the second dipping step reveal the unique structure of each system (Fig. S21 and Table S6†). The deposition of the second monolayer had only a small effect on the first monolayer, manifested in terms of a small increase in thickness (ranging from 0.1–2.9 Å with an average of 1.0 Å), a very small decrease in density (ranging from 0.0–0.04 g cm−3 with an average of 0.01 g cm−3), and a decreased water content (ranging from 3.1–9.1% with an average of 6.0%). This shows that the first monolayer is stable during the second dipping step and the newly deposited polyelectrolytes tend to displace water molecules or build on top of the first monolayer.In all cases, the PA/PAH pairing results in a thinner bilayer than the PSS/PAH pairing, regardless of the order of the polyelectrolytes (Table 3). This is consistent with experimental literature where PSS/PAH bilayers have been reported to be thicker than PA/PAH bilayers at a neutral pH.40,43 This is expected since PSS has a larger Rg than PA. However, the favorable interactions between the PA and PAH polyelectrolytes may also play a role in this behavior. Bilayers with SDSn are noticeably thinner than the other surfactant systems, suggesting that the strong interaction energy between SDSn and polyelectrolyte may have an influence that persists beyond the first monolayer.
| System | Layer overlap (Å) | Total thickness (Å) | Average orientation | Average void fraction |
|---|---|---|---|---|
| SDSn/PAH/PA | 6.43 | 18.12 | 3.32° | 0.115 |
| SDSn/PAH/PSS | 7.55 | 25.72 | 6.73° | 0.059 |
| SDBS/PAH/PA | 6.07 | 21.01 | 7.22° | 0.080 |
| SDBS/PAH/PSS | 7.58 | 30.26 | 6.99° | 0.064 |
| DTAC/PA/PAH | 15.24 | 21.63 | 3.91° | 0.025 |
| DTAC/PSS/PAH | 10.06 | 29.86 | 12.28° | 0.008 |
Experimental evidence shows that higher salt concentration results in thicker monolayers.55,60,61 We observe this phenomenon locally during the second monolayer deposition. Comparing systems with the same polyelectrolyte pairings, with the exception of the DTAC/PSS/PAH system, those with higher extrinsic charge fraction have thicker second monolayers. This uptake of ions, in addition to the first monolayer morphology,21,32,62 appears to play a role in subsequent monolayer structure and thickness. For example, both DTAC systems have a markedly higher layer overlap than the other systems. For the DTAC/PA/PAH system, which exhibits the highest extrinsic charge fraction, overlapping layers make up over 70% of the total bilayer thickness. For SDSn and SDBS systems, the layer overlap for the PA/PAH and PSS/PAH pairings are similar, regardless of surfactant, and increases with overall bilayer thickness.
These results indicate that the surfactant has an influence beyond just direct electrostatic interactions in the first monolayer. At least for polyelectrolyte bilayers formed during LbL assembly, use of SDSn results in thinner bilayers and more uniform monolayers, while DTAC results in thicker bilayers with higher monolayer overlap. Generalizing this trend, we find that surfactants with a more polar and localized head-group charge form more uniform layers and thinner capsules at early stages in LbL assembly. This observation should be investigated further to verify its generality. Once verified, this could be leveraged to help optimize capsule performance.
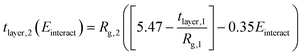 | (5) |
Here, the subscript 1 or 2 denotes the layer number and Einteract represents the interaction energy between the depositing polyelectrolyte and the layer on which it is being deposited. This correlation suggests that both (1) the interactions between all three layers of molecules and (2) the thickness of the first monolayer play a role in the resulting second monolayer thickness. As was the case with eqn (3), this correlation is valid at constant species concentrations. It is important to note that this correlation does not predict layer overlap and, therefore, cannot predict total bilayer thickness. Nevertheless, eqn (3) and (5) together provide a powerful tool for estimating early-stage multilayer growth.
4.3. Chemical origins of polyelectrolyte orientation
Insight into the orientation of the deposited polyelectrolytes shows that the growth of the bilayer tends to lead to a rough surface. This growth behavior has been observed in a similar computational study of polyelectrolyte multi-layers.25 In the case of this second layer, the average misalignment with the interface ranges from 3.3° for SDSn/PAH/PA to 12.3° for DTAC/PSS/PAH (Table 3). This is a significant increase from the small range (1.8° to 4.4°) we observed for the first monolayer, but agrees with experiments that report increasing surface roughness with multilayer thickness.21 We observe that polyelectrolytes tend to deposit on top of the first monolayer, resulting in a build-up of misalignment for subsequent layers. We also find that PA/PAH pairs tend to exhibit more alignment than PSS/PAH pairs, showing an average misalignment of 4.8° compared to 8.7°. Again, this could be a result of better steric compatibility between the PA/PAH pairing than the PSS/PAH pairing. Despite this general trend, exceptions are also observed, suggesting that the relationship between alignment and system extends beyond simple polyelectrolyte/polyelectrolyte pairings.4.4. Chemical origins of interface coverage
Similar to the first monolayer, we find that bilayer systems with PSS tend to have smaller void fractions (Table 3), either due to the size of PSS or the favorability of PAH/PA to bind more closely together. Compared to the first monolayer, four of the six systems decrease in void fraction, showing additional layers tend to improve surface coverage, agreeing with reports in the literature.25,63 However, divergent behavior from two systems indicates the dynamic surface and its interactions with the polyelectrolyte layers play an important role in early-stage capsule formation. We also find that, in general, the void fraction follows the order SDSn > SDBS > DTAC, which is inversely correlated with the extrinsic charge fraction after the second dipping step. Additional ions present in the DTAC systems may spread out the polyelectrolytes, rather than being tightly bound with the polyelectrolytes of the previously deposited layer. This points to the sustained influence of the surfactant for bilayer, and potentially multi-layer, systems.Overall, the result is a trade-off between alignment of the polyelectrolytes and the coverage of the interface. The data in Fig. 7 emphasize this by showing the bilayer and surfactant layer structures for the two most extreme cases – DTAC/PSS/PAH (Fig. 7A) and SDSn/PAH/PA (Fig. 7B). DTAC/PSS/PAH is characterized by high surface roughness and layer overlap, but high interface coverage. Conversely, SDSn/PAH/PA is characterized by layer uniformity, but low interface coverage leading to exposure of the encapsulated material. During the design of capsules via LbL assembly, researchers should aim to find the optimal balance between minimization of lost encapsulated material and more uniform capsules, caused by a smaller void fraction and more aligned layers, respectively.
4.5. Polyelectrolyte multilayer stability
Finally, stability of polyelectrolyte multilayers is an important consideration.20 For one, decreasing interfacial tension helps improve stable emulsion formation.64 Increasing interfacial thickness has been shown to decrease interfacial tension, providing an easy metric to validate our data against.34 With the exception of the DTAC systems, the PAH/PSS pairings exhibit thicker interfaces, suggesting more stable emulsions (Fig. S21†). Encapsulation helps stabilize the emulsion,3 making these considerations important at early-stage layer growth when full encapsulation has not been achieved. Additionally, higher hydrophobicity within the polyelectrolyte layers reduces desorption of polyelectrolyte into the bulk solution, improving capsule stability.20 Following the trend in hydrophobicity of PAH > PSS > PA, the PAH/PSS pairing would offer better stability in this regard. Our computational work supports this observation, showing higher overlap, with the exception of the DTAC systems, and reduced void fraction for these pairings (Table 3). Higher molecular weight polyelectrolytes also offer higher wear stability,65 adding to the favorable properties of the PAH/PSS pairing. The exceptional properties of systems with DTAC warrant further research on LbL assembly with this surfactant.Beyond the scope of our work, factors like alkyl tail length30,66 and number of alkyl tails31 improve emulsion stability. In the case of alkyl tail length, surface tension is reduced by increasing the interface thickness and increasing the hydrophobic interactions near the interface.30 Regarding the number of alkyl tails, additional tails increase surfactant hydrophobicity and reduce contact between the water and oil phases, increasing stability.31 Finally, although we selected the lowest energy SAPM of the surfactants (ESI, Fig. S2†), SAPM can also be tuned to control contact between phases at the interface. Future work should focus on elucidating this indirect molecular-scale relationship between emulsion stability and LbL assembly, complementing our study of the direct relationship that arises from molecule charge-structure characteristics.
5. Conclusions
Recent literature has highlighted the lack of knowledge regarding the interactions that govern LbL assembly, particularly in the area of absorption kinetics, identifying a need for physico-chemical insight.32 Computational studies have uncovered molecular-level insight of LbL assembly, but are limited to single polyelectrolyte pairings on a solid substrate.24–26 Experimental studies have shown the ability to tune multilayers through varying building block molecules, but have limited insight into the molecular mechanisms at play.20,40,54 We bridge the gap here, performing all-atom MD simulations of LbL assembly using different combinations of polyelectrolytes and surfactants to derive quantitative relationships between molecule properties, absorption kinetics, and multilayer structure. Overall, we provide considerable insight into the kinetic and structural characteristics of the system and, beyond that, towards a more optimized synthesis of capsules for applications in nanomaterials.In agreement with the literature, we explicitly show that LbL assembly is entropically driven by the exchange of smaller, mobile counter-ions with larger, less mobile polyelectrolytes.32,43,44 We find that faster absorption kinetics is correlated with higher polyelectrolyte/surfactant interaction energies, a result of higher hydrophobicity in the polyelectrolytes and more polar and charge-localized head groups in surfactants. We observe that the kinetics follow the trend: SDSn > SDBS > DTAC and PAH > PSS > PA. In the second dipping step, we find that, in general, the polyelectrolyte pairings determine the absorption kinetics, regardless of surfactant or polyelectrolyte order. PAH/PA has faster kinetics and a stronger interaction energy, likely due to their steric compatibility as a result of similarly sized functional groups.
This work derived previously unknown correlations independent of surfactant and polyelectrolyte type. We find (1) layer thickness is correlated to number density of a deposited polyelectrolyte through its molecular weight and (2) layer thickness is correlated to polyelectrolyte/surfactant interaction energy through Rg. This second correlation answers a direct call from the literature to relate absorption kinetics and layer structure.32
We find increased polyelectrolyte alignment and reduced interface coverage for systems that show higher polyelectrolyte/surfactant interaction energies, with the exception of PSS. Deviation from this trend may be due to the large size of PSS or because its functional groups disrupt the surfactant layer due to aromatic interactions. Systems with smaller polyelectrolyte/surfactant interaction energies during the first dipping step had an increased extrinsic charge fraction from ions building up near the interface. This tends to lead to higher layer overlap but improved interface coverage. PA/PAH pairings were found to have thinner bilayers, likely due to PA's smaller Rg compared to PSS and the steric favorability of the PA/PAH polyelectrolyte pairing. This trend is in agreement with experimental studies.40,43 These pairings also exhibited higher alignment within the second layer, but reduced interface coverage compared to the PSS/PAH pairing. Again, surfactants like SDSn with more polar and localized-charge head-groups lead to thinner layers and less layer overlap than other surfactants, DTAC in particular.
Finally, our discussion on the relationship of selected molecular properties with absorption kinetics and capsule structure is not exhaustive and its limitations on scope should be noted. Notably, although interaction energies provide an empirical characterization of intermolecular interactions, they are composed of numerous simultaneous factors. This includes, to name a few, hydrogen bonding, charge transfer interactions, coordination interactions, and π–π interactions.32 So, while our derived conclusions show a correlation between the combined effects of these factors and the resulting layer structure, more fundamental relationships could be uncovered by future work to tease out the relative importance of each contributing factor. The effects of degree of polymerization of polyelectrolytes,67 Hofmeister Series compatibility between ions,49 and the surfactant alkyl tail properties discussed earlier add further complexity, offering a rich variety of additional opportunities for further study.
Overall, the thinner and more uniform layers resulting in the SDSn/PAH/PA system are good candidates for encapsulated nanomaterials, but have a risk of loss of the encapsulated material during the early synthesis stages. Future research should aim to mitigate this trade-off, perhaps through optimization of additional system properties such as ionic concentration, solvent, or pH. In-depth investigation of additional surfactants and polyelectrolytes can provide more nuance to the conclusions of this study. Future computational work should investigate growth, structure, and capsule properties (e.g. thermal conductivity for thermal energy storage) of systems with more layers. This work provides a foundation on which future experimental and computational work could build to improve capsule design.
Abbreviations
| LbL | Layer-by-layer |
| MD | Molecular dynamics |
| PSS | Poly(styrene sulfonate) |
| PAH | Poly(allylamine) hydrochloride |
| PA | Sodium poly(acrylate) |
| SDSn | Sodium dodecyl sulfonate |
| SDBS | Sodium dodecyl benzene sulfonate |
| DTAC | Dodecyl trimethyl ammonium chloride |
| R g | Radius of gyration |
| SAPM | Surface area per molecule |
Author contributions
Andrew W. Ruttinger: conceptualization, methodology, software, validation, formal analysis, investigation, writing – original draft, writing – review & editing, visualization; Paulette Clancy: conceptualization, resources, writing – review & editing, supervision, funding acquisition.Conflicts of interest
The authors declare no conflicts of interest, financial or otherwise.Acknowledgements
The authors thank Prof. Jefferson W. Tester for providing expertise and direction throughout the project. We also thank Prof. Joelle Frechette for helpful discussions at the early stages of the project. This work was carried out at the Advanced Research Computing at Hopkins (ARCH) core facility (rockfish.jhu.edu), which is supported by the National Science Foundation (NSF) grant number OAC 1920103. A. W. R. acknowledges the financial support of the NSERC Postgraduate Scholarships-Doctoral (PGS-D) award (CGSD3-502578-2017), the Cornell University Graduate School, and the Whiting School of Engineering at the Johns Hopkins University.References
- N. Baig, I. Kammakakam and W. Falath, Mater. Adv., 2021, 2, 1821–1871 RSC.
- X. Huang and B. Voit, Polym. Chem., 2013, 4, 435–443 RSC.
- E. Shchukina, M. Graham, Z. Zheng and D. Shchukin, Chem. Soc. Rev., 2018, 47, 4156–4175 RSC.
- M. G. Bah, H. M. Bilal and J. Wang, Soft Matter, 2020, 16, 570–590 RSC.
- Y. P. Timilsena, M. A. Haque and B. Adhikari, et al. , Food Nutr. Sci., 2020, 11, 481–508 CAS.
- F. Salaün, Microencapsulation - Processes, Technologies and Industrial Applications, IntechOpen, 2019 Search PubMed.
- C. D. Ferreira and I. L. Nunes, Nanoscale Res. Lett., 2019, 14, 1–13 CrossRef PubMed.
- J. K. Patra, G. Das, L. F. Fraceto, E. V. R. Campos, M. del Pilar Rodriguez-Torres, L. S. Acosta-Torres, L. A. Diaz-Torres, R. Grillo, M. K. Swamy and S. Sharma, et al. , J. Nanobiotechnol., 2018, 16, 1–33 CrossRef PubMed.
- T. Liu, Y. Wang, W. Zhong, B. Li, K. Mequanint, G. Luo and M. Xing, Adv. Healthcare Mater., 2019, 8, 1800939 CrossRef PubMed.
- H. Peng, J. Wang, X. Zhang, J. Ma, T. Shen, S. Li and B. Dong, Appl. Therm. Eng., 2020, 116326 Search PubMed.
- H. O. Otor, J. B. Steiner, C. García-Sancho and A. C. Alba-Rubio, ACS Catal., 2020, 10, 7630–7656 CrossRef CAS.
- C. Gao, F. Lyu and Y. Yin, Chem. Rev., 2021, 121, 834–881 CrossRef CAS PubMed.
- Q. Lu, Z. Yang, X. Meng, Y. Yue, M. A. Ahmad, W. Zhang, S. Zhang, Y. Zhang, Z. Liu and W. Chen, Adv. Funct. Mater., 2021, 31, 2100151 CrossRef CAS.
- J. J. Richardson, J. Cui, M. Bjoörnmalm, J. A. Braunger, H. Ejima and F. Caruso, Chem. Rev., 2016, 116, 14828–14867 CrossRef CAS PubMed.
- S. Zhao, F. Caruso, L. Dahne, G. Decher, B. G. De Geest, J. Fan, N. Feliu, Y. Gogotsi, P. T. Hammond, M. C. Hersam, A. Khademhosseini, N. Kotov, S. Leporatti, Y. Li, F. Lisdat, L. M. Liz-Marzán, S. Moya, P. Mulvaney, A. L. Rogach, S. Roy, D. G. Shchukin, A. G. Skirtach, M. M. Stevens, G. B. Sukhorukov, P. S. Weiss, X. Yue, D. Zhu and W. J. Parak, ACS Nano, 2019, 13, 6151–6169 CrossRef CAS PubMed.
- D. Guzey and D. J. McClements, Adv. Colloid Interface Sci., 2006, 128, 227–248 CrossRef PubMed.
- J. Borges and J. F. Mano, Chem. Rev., 2014, 114, 8883–8942 CrossRef CAS PubMed.
- I. Gammoudi, M. Mathelié-Guinlet, Z. Benabdallah, F. Moroté, H. Kahli, L. Beven, R. Kalfat, A. Othmane, M.-H. Delville and C. Grauby-Heywang, et al. , Thin Solid Films, 2020, 713, 138345 CrossRef CAS.
- D. Reurink, J. Willott, H. Roesink and W. De Vos, ACS Appl. Polym. Mater., 2020, 2, 5278–5289.
- E. Tran, A. N. Mapile and G. L. Richmond, J. Colloid Interface Sci., 2021, 599, 706–716 CrossRef CAS PubMed.
- R. A. Ghostine, R. M. Jisr, A. Lehaf and J. B. Schlenoff, Langmuir, 2013, 29, 11742–11750 CrossRef CAS PubMed.
- S. Plimpton, J. Comp. Physiol., 1995, 117, 1–19 CrossRef CAS.
- B. Qiao, J. J. Cerda and C. Holm, Macromolecules, 2010, 43, 7828–7838 CrossRef CAS.
- B. Qiao, M. Sega and C. Holm, Phys. Chem. Chem. Phys., 2011, 13, 16336–16342 RSC.
- P. A. Sánchez, M. Vögele, J. Smiatek, B. Qiao, M. Sega and C. Holm, Soft Matter, 2019, 15, 9437–9451 RSC.
- P. A. Sánchez, M. Vögele, J. Smiatek, B. Qiao, M. Sega and C. Holm, Molecules, 2020, 25, 1848 CrossRef PubMed.
- W. Jorgenson, D. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef.
- R. Hockney and J. Eastwood, Computer Simulation Using Particles, Adam Hilger, Bristol and New York, NY, USA, 1989, pp. 120–165 Search PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- P. Posocco, A. Perazzo, V. Preziosi, E. Laurini, S. Pricl and S. Guido, RSC Adv., 2016, 6, 4723–4729 RSC.
- S. S. Adkins, X. Chen, Q. P. Nguyen, A. W. Sanders and K. P. Johnston, J. Colloid Interface Sci., 2010, 346, 455–463 CrossRef CAS PubMed.
- E. Guzman, R. G. Rubio and F. Ortega, Adv. Colloid Interface Sci., 2020, 282, 102197 CrossRef CAS PubMed.
- H. Comas-Rojas, C. Enríquez-Victorero, S. J. Roser, K. J. Edler and A. Pérez-Gramatges, Soft Matter, 2013, 9, 4003–4014 RSC.
- J. Xu, Y. Zhang, H. Chen, P. Wang, Z. Xie, Y. Yao, Y. Yan and J. Zhang, J. Mol. Struct., 2013, 1052, 50–56 CrossRef CAS.
- S. Seitz and H. Ajiro, Sol. Energy Mater. Sol. Cells, 2019, 190, 57–64 CrossRef CAS.
- D. Grigoriev, T. Bukreeva, H. Möhwald and D. Shchukin, Langmuir, 2008, 24, 999–1004 CrossRef CAS PubMed.
- H. Bo, E. M. Gustafsson and F. Setterwall, Energy, 1999, 24, 1015–1028 CrossRef CAS.
- K. Pielichowska and K. Pielichowski, Prog. Mater. Sci., 2014, 65, 67–123 CrossRef CAS.
- Q. Yi, G. B. Sukhorokov, J. Ma, X. Yang and Z. Gu, Int. J. Polym. Sci., 2015, 2015, 756237 Search PubMed.
- M. Elzbieciak, M. Kolasinska and P. Warszynski, Colloids Surf., A, 2008, 321, 258–261 CrossRef CAS.
- E. Guzmán, H. Ritacco, F. Ortega and R. G. Rubio, Colloids Surf., A, 2011, 384, 274–281 CrossRef.
- E. Guzmán, H. A. Ritacco, F. Ortega and R. G. Rubio, J. Phys. Chem. C, 2012, 116, 15474–15483 CrossRef.
- O. Mermut and C. J. Barrett, J. Phys. Chem. B, 2003, 107, 2525–2530 CrossRef CAS.
- R. v. Klitzing, Phys. Chem. Chem. Phys., 2006, 8, 5012–5033 RSC.
- N. Kotov, Nanostruct. Mater., 1999, 12, 789–796 CrossRef.
- M. Schauperl, M. Podewitz, B. J. Waldner and K. R. Liedl, J. Chem. Theory Comput., 2016, 12, 4600–4610 CrossRef CAS PubMed.
- J. Kang and L. Dähne, Langmuir, 2011, 27, 4627–4634 CrossRef CAS PubMed.
- M. A. Rahim, W. S. Choi, H.-J. Lee and I. C. Jeon, Langmuir, 2010, 26, 4680–4686 CrossRef CAS PubMed.
- T. López-León, A. B. Jódar-Reyes, D. Bastos-González and J. L. Ortega-Vinuesa, J. Phys. Chem. B, 2003, 107, 5696–5708 CrossRef.
- J. J. Iturri Ramos, S. Stahl, R. P. Richter and S. E. Moya, Macromolecules, 2010, 43, 9063–9070 CrossRef CAS.
- P. A. Patel, J. Jeon, P. T. Mather and A. V. Dobrynin, Langmuir, 2005, 21, 6113–6122 CrossRef CAS PubMed.
- P. Kujawa, P. Moraille, J. Sanchez, A. Badia and F. M. Winnik, J. Am. Chem. Soc., 2005, 127, 9224–9234 CrossRef CAS PubMed.
- W. Yuan, G.-M. Weng, J. Lipton, C. M. Li, P. R. Van Tassel and A. D. Taylor, Adv. Colloid Interface Sci., 2020, 282, 102200 CrossRef CAS PubMed.
- H. Bellanger, K. Casdorff, L. F. Muff, R. Ammann, I. Burgert and B. Michen, J. Colloid Interface Sci., 2017, 500, 133–141 CrossRef CAS PubMed.
- H. Lee, J. Mol. Graphics Modell., 2016, 70, 246–252 CrossRef CAS PubMed.
- S. L. McKay, B. Haptonstall and S. H. Gellman, J. Am. Chem. Soc., 2001, 123, 1244–1245 CrossRef CAS PubMed.
- C. Buron, C. Filiâtre, F. Membrey, C. Bainier, D. Charraut and A. Foissy, Colloids Surf., A, 2007, 305, 105–111 CrossRef CAS.
- A. Salehi, P. S. Desai, J. Li, C. A. Steele and R. G. Larson, Macromolecules, 2015, 48, 400–409 CrossRef CAS.
- H. Riegler and F. Essler, Langmuir, 2002, 18, 6694–6698 CrossRef CAS.
- S. T. Dubas and J. B. Schlenoff, Macromolecules, 1999, 32, 8153–8160 CrossRef CAS.
- K. Tang and N. A. Besseling, Soft Matter, 2016, 12, 1032–1040 RSC.
- M. Lösche, J. Schmitt, G. Decher, W. G. Bouwman and K. Kjaer, Macromolecules, 1998, 31, 8893–8906 CrossRef.
- J.-M. Y. Carrillo and A. V. Dobrynin, Langmuir, 2012, 28, 1531–1538 CrossRef CAS PubMed.
- T. Misono, Interfacial Tension Between Water and Oil, Springer Singapore, Singapore, 2019 Search PubMed.
- X. Dai, Y. Zhang, Y. Guan, S. Yang and J. Xu, Thin Solid Films, 2005, 474, 159–164 CrossRef CAS.
- S. M. Kirby, S. L. Anna and L. M. Walker, Soft Matter, 2018, 14, 112–123 RSC.
- S. Micciulla, S. Dodoo, C. Chevigny, A. Laschewsky and R. von Klitzing, Phys. Chem. Chem. Phys., 2014, 16, 21988–21998 RSC.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed background information; justifications for computational details; detailed description with verification for preliminary investigation, system setup, and main simulations, calculation of interface formation energy versus surface area per surfactant, calculations of the polyelectrolyte radius of gyration and diffusivity, and calculation of the width of surfactant-mediated interfaces; methodology for determining the cutoff for measuring interacting groups; example showing the relaxation of system energy at the beginning of the washing step; ion distribution plots, interaction energy profiles, and density profiles for the first layer; data fitted to derived correlations; interaction energy profiles, polyelectrolyte orientation distributions, and surface void distributions for the second layer. See DOI: 10.1039/d1nr05634d |
| This journal is © The Royal Society of Chemistry 2021 |