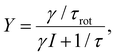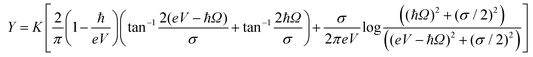One-way rotation of a chemically anchored single molecule-rotor

Abstract

We present the chemical anchoring of a DMBI-P molecule-rotor to the Au(111) surface after a dissociation reaction. At the temperature of 5 K, the anchored rotor shows a sequential unidirectional rotational motion through six defined stations induced by tunneling electrons. A typical voltage pulse of 400 mV applied on a specific location of the molecule causes a unidirectional rotation of 60° with a probability higher than 95%. When the temperature of the substrate increases above 20 K, the anchoring is maintained and the rotation stops being unidirectional and randomly explores the same six stations. Density functional theory simulations confirm the anchoring reaction. Experimentally, the rotation shows a clear threshold at the onset of the C–H stretch manifold, showing that the molecule is first vibrationally excited and later it decays into the rotational degrees of freedom.

---

Introduction

The miniaturization of machines and motors is reaching the limit of a single atom.¹ An important step further is now to understand energy conversion inside a single molecule, with the aim of generating work. A single atom heat engine has been recently experimentally realized,¹ and opto-mechanical intramolecular energy conversion at the single-molecule level was demonstrated by force spectroscopy.² Compared to a single atom, a molecule provides a higher mechanical complexity and more degrees of freedom for constructing a molecular engine. In scanning tunneling microscopy (STM) experiments, the rotation of a single molecule triggered by inelastic tunneling effects has been the focus of research for a long time.^3–11 The production of minute mechanical work was recently demonstrated,¹² opening new routes for the rational design of unidirectional molecule-rotors.^8,9 However, only a few examples of controlled directional rotation of organic molecules around a vertical axis have been demonstrated yet,^6,8–10 and further experimental and theoretical work is needed to understand the relation between inelastic electronic excitation and motion of a single molecule.

Here, we present the sequential unidirectional rotational motion of a chemisorbed single molecule. Its step by step unidirectional rotation is classical, while the inelastic tunneling effect providing the energy for the rotation is quantum in nature.¹³ Our molecule-rotor works on the Au(111) surface at a temperature of 5 K. We use here the term “molecule-rotor” as a sub-class of the broader field of molecular motors encompassing also in-solution and biological molecular machines: a molecule-rotor is a single molecule, which is anchored to a single rotation point on a surface with a strong covalent bond, and is rotating around this rotational axle.

The precursor o-MeO-DMBI-I¹⁴ is designed to undergo iodine dissociation, resulting in a radical form that is an excellent n-type dopant used in organic electronics.^14,15 In a preliminary experimental STM study, the chemisorption of o-MeO-DMBI-I on Au(111) was qualitatively described by the interaction with gold of the radical form obtained after such iodine dissociation.¹¹ However, it is known that an alternative intramolecular reaction can occur with the cleavage of the O–Me bond and the elimination of methyl iodide (MeI), resulting in the formation of 2-(1,3-dimethyl-1H-benzo[d]imidazol-3-ium-2-yl)-phenolate (DMBI-P) (see left two panels of Fig. 1). This reaction was observed for example by photoelectron spectroscopy.¹⁶ To understand which intramolecular reaction causes the experimentally observed chemisorption of the molecule, we performed density functional theory (DFT) calculations of adsorption geometry and bonding energy of o-MeO-DMBI and DMBI-P on Au(111). These calculations indicate that the cleavage of the O–Me bond and the elimination of MeI are necessary to reproduce the recorded STM images and to explain the observed strong anchoring at the O position. Following these results, we performed the combined experimental and theoretical studies presented in this paper to clarify the dissociation reaction responsible for the anchoring on Au(111) and to understand the rotation induced by inelastic tunneling electrons, as well as to investigate the thermal-induced rotation.

Fig. 1 Chemical structure of the precursor and MeI elimination: o-MeO-DMBI-I dissociates to form DMBI-P after a C–O bond cleavage and the formation of volatile methyl iodide (MeI) as the by-product. DMBI-P then chemisorbs on Au(111) by charge back-donation. Right panel: schematic representation of the adsorption geometry of DMBI-P on Au(111).

Results and discussion

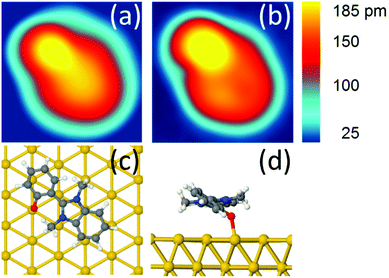
After synthesizing the o-MeO-DMBI-I precursor (see the ESI† for details), we first chemically investigated the dissociation process. Using nuclear magnetic resonance (NMR) thermogravimetric analysis/infrared spectrometry (TGA/IR) and gas chromatography/mass spectrometry (GC/MS) under working conditions similar to those used during the sublimation in ultra-high vacuum (UHV), we experimentally confirmed the MeI elimination. We characterized the cleavage product DMBI-P by ¹H-NMR and demonstrated the scission of the methyl group attached to the oxygen. Investigating the thermal decomposition of o-Me-O-DMBI-I under nitrogen we detected a weight loss of the compound starting at 519 K, consistent with the loss of MeI, and confirmed the MeI formation using GC/MS. All methods prove the thermal decomposition and are consistent with the formation of methyl iodide as a cleavage by-product (see the ESI† for further details).

In light of these results, we conclude that a cleavage reaction takes place during the sublimation of the precursor o-MeO-DMBI-I at 490 K under UHV conditions, resulting in DMBI-P and volatile MeI. As schematically shown in Fig. 1, DMBI-P finally chemisorbs by charge back-donation at the oxygen position on Au(111), in agreement with both DFT and image simulations (Fig. 2). A Bader-charge analysis shows that a total charge transfer of 0.27 electrons from DMBI-P to the substrate takes place. The oxygen atom transfers only 0.08 electrons to the surface, showing that the largest surface effect of the O–Au bond is to redistribute charges between the nearest gold atoms and the oxygen atom in the molecule. Experimentally, the molecule is anchored at the top-site position of the O atom and cannot be moved laterally either by voltage pulses or lateral manipulation. The MeI elimination takes place at temperatures around 490 K in UHV during the sublimation process, making possible the anchoring of DMBI-P on the gold surface via the dealkylated oxygen. MeI is lost in the UHV chamber during the heating of the precursor in the crucible and is not visible in the STM images.

Fig. 2 Single adsorbed DMBI-P molecule-rotor. (a) Experimental STM image of a single DMBI-P molecule on Au(111) (V = 0.2 V; I = 100 pA, dimensions: 1.8 nm × 1.8 nm). The colour scale on the right indicates the apparent height. (b) Simulated constant current STM image calculated from the adsorption geometry in (c) and (d) in good agreement with the experimental image. (c) Top and (d) side views of DMBI-P optimized chemisorption geometry on the Au(111) surface with d(Au–O) = 0.225 nm. The yellow grid depicts the Au (111) surface in a stick-and-ball model. The molecule is adsorbed via the O-atom (red) that coordinates with one of the Au first layer atoms.

After adsorption on Au(111), we observe in the STM images a low coverage of DMBI-P molecules anchored to the surface (Fig. S12†). The molecules show six preferred adsorption orientations on Au(111) each rotated by 60°, corresponding to the high symmetry directions of the hexagonal surface lattice, as already observed in ref. 11. A comparison between an experimental and a simulated STM image of a single DMBI-P is presented in Fig. 2a and b. The good agreement between the two images confirms the adsorption geometry of Fig. 2c and d and the chemical characterization presented above. The anchoring point is given by the oxygen atom of the DMBI-P on the Au(111) surface (Fig. 1).

DMBI-P is composed of 32 atoms, i.e. 3 × 32 = 96 mechanical degrees of freedom on the surface, including the Au–O bond. Calculating the ground state potential energy curve (Fig. S17†) using the ASED+ semi-empirical method,¹⁷ we found small fluctuations in energy (few meV), indicating that the DMBI-P rotor is not a rigid body. Those energy variations are mainly governed by van der Waals interactions between the DMBI-P rotor and the Au(111) surface. Therefore, and in a first approximation, we consider only three main degrees of freedom for describing the mechanics around the Au–O bond: the collective rotation angle Θ, the bond length d(Au–O) and the dihedral angle Φ₁ between the DMBI and the phenyl part of the rotor. Other mechanical degrees of freedom slightly contribute to the rotation mechanics, for example the two DMBI lateral CH₃ fluctuate by 0.1° during a Θ variation by 60° (Fig. S17†).

At a temperature T = 5 K, when we position the STM tip on a specific position of the molecule and apply a voltage pulse V(t) of typically 400 mV, we observe a one-step clockwise rotation Θ of 60° around the Au–O bond (Fig. 3a). The position of the tip is indicated by a black dot. Changing the position of the tip reduces the probability of rotation, without however changing its directionality (see Fig. S14†). A complete rotation can be performed step-by-step by applying a succession of V(t) pulses and keeping the end atom of the tip apex inside the same 0.7 nm × 0.5 nm area (Fig. 3b and c). The area of electron tunneling through the molecule for a one step rotation does not correspond to the centre of rotation (or anchoring point), making a slight reposition of the tip necessary after each voltage pulse (see Fig. 2c).

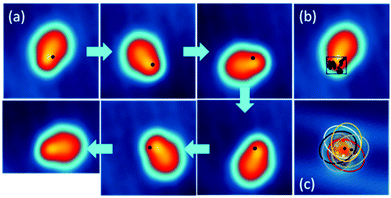Fig. 3 (a) Step by step clockwise rotation of a DMBI-P molecule. The positions of the tip during the voltage pulse are marked with a black dot. Voltage pulses with I = 0.5 nA; V = 0.5 V; t = 10 s are used to induce the rotation. The arrows indicate the sequence of the images and applied voltage pulses. (b) Position of the STM tip during the voltage pulses for the complete rotational cycle. The positions of the tip inducing rotation are marked on the STM image of a DMBI-P molecule and are located inside the area of 0.7 nm × 0.5 nm represented by the black square (STM images: 3.5 nm × 3.5 nm; 0.1 V; 20 pA). (c) Superimposed STM images of the six stable rotation stations highlighted with ellipsoids. The central black star marks the anchoring point of the molecule. The coloured dots indicate the positions where the electrons tunnel through the molecule induces its rotation (marked with the corresponding coloured ellipsoid). Such positions do not correspond to the centre of rotation. Raw data are presented for comparison in Fig. S13.†

The STM images recorded during a complete rotation are in good agreement with the simulated STM images, confirming that DMBI-P adopts the same surface conformation in the six consecutively visited stations. It is important to note that the rotation can be clockwise or anticlockwise depending on the sign of the applied bias voltage pulse and on the molecular chirality on the surface.^11,18 On the other hand, the adsorption position and the Au(111) herringbone reconstruction do not play any relevant role in controlling the rotation.

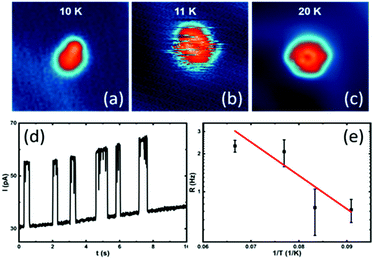
When slowly increasing the substrate temperature T and imaging by STM the same DMBI-P at each T, we first observe at T = 11 K a random flipping between consecutive rotational stations (Fig. 4a and b). When increasing the temperature further, the molecule-rotor randomly jumps over several stable positions. At T = 20 K (Fig. 4c), we observe a nearly hexagonal STM image, indicating that all six stable adsorption positions identified at low temperatures are randomly visited by the DMBI-P rotor during the scanning time (which is 41 s for the entire image). The single stations cannot be resolved anymore. A similar behaviour was reported for other surface-supported molecular rotors albeit at different T due to different potential energy barrier heights for rotation on the surface.¹⁹

Fig. 4 STM images showing the thermal activation of rotation when the temperature T of the surface is gradually increased. The molecule appears stationary at temperature T = 10 K (a), while it starts to rotate at T = 11 K (b), and appears hexagonal in shape at T = 20 K (c) because it is moving faster than the timescale of the STM image (imaging conditions: (a), (b) I = 20 pA, V = 0.2 V; (c) I = 100 pA, V = 0.2 V; dimensions: 5 nm × 5 nm, image recording time: 41 s, corresponding to 0.3 ms per pixel). (d) Example of tunneling current as a function of time at T = 11 K, positioning the tip at a vertical distance of 5.9 Å over the molecule at V = 300 mV showing the rate of thermal rotation. (e) Arrhenius plot for the rotation of individual molecules on Au(111). The rotation rates are determined for 11 K, 12 K, 13 K and 15 K. The data were fitted with R = R₀ exp (–E_ex/k_BT), obtaining E_ex = (5 ± 2) meV and R₀ = (176 ± 50) Hz. Please consider that the exponential pre-factor cannot be interpreted as a frequency for the collective molecular rotation at higher temperatures.

According to the energy equipartition theorem, a single DMBI-P in its |S0〉 electronic ground state at a temperature T cannot accumulate vibrational energy exclusively in a few specific mechanical degrees of freedom like a C–H bond, the Au–O bond or a collective rotational angle. When T increases, the DMBI-P rotor therefore randomly visits in a disordered sequence all the possible Θ energy minima on the |S0〉 PES. This effect is visible in the STM images as a superposition of the different 60° orientations of the molecule-rotor (Fig. 4c).

By positioning the tip on the molecule and fixing it at a vertical distance of 5.9 Å, which is shown to not perturb the rotation at low temperatures, we record the tunneling current versus time during the random rotation (see an example in Fig. 4d), and determine the jumping rate at a specific temperature. As presented in Fig. 4d and at T = 11 K, about 0.7 jumping events occur per second. An Arrhenius plot of the observed random rotation (Fig. 4e) leads to an effective rotation energy barrier height of about 5 meV in the |S0〉 ground state. It is important to note that the exponential fit in Fig. 4e is based on a simplified model of a rigid rotor and that the experimental data are recorded at very low temperatures, making it impossible to extrapolate the behaviour of the rotor at higher temperatures.

This value is in reasonable agreement with the potential energy curve calculated by DFT, which also reproduces the energy minima every 60° (Fig. S15†). Calculated by DFT, the rotation barrier is about 50 meV. However, when corrected by the zero-point motion difference between a 60° global minimum and the transition saddle point on this surface, the energy barrier is about 11 meV in reasonable agreement with the experimental estimation. The rotation barriers of the molecule-rotor for a long rotational sequence of 720° were also calculated using the ASED+ semi-empirical method,^17,20 confirming the energy minima every 60° (Fig. S16†).

We further investigated the unidirectional rotation induced by voltage pulses at low temperatures. We performed more than 20 successful complete rotations with different STM tips and applied more than 600 voltage pulses under similar experimental conditions. In 95% of the cases, we observe a 60° rotation, while only in 4% of the cases the DMBI-P rotor rotates less than 60° to an intermediate position, and in 1% of the cases moves in the opposite direction. The present experiment shows therefore a striking example of unidirectional rotation with identical rotational steps of 60°. The elapsed time before a single rotation step occurs is generally of the order of several seconds. We have determined it by recording the tip height as a function of time during a voltage pulse at a constant current. A jump in the trace indicates a sudden change in the conductance at the position of the tip, caused by a molecular jump (an example is reported in Fig. S18†). To observe a further event, the tip should be slightly moved on the molecule and a voltage pulse applied again (as indicated in the example of Fig. 3), recording a new curve.

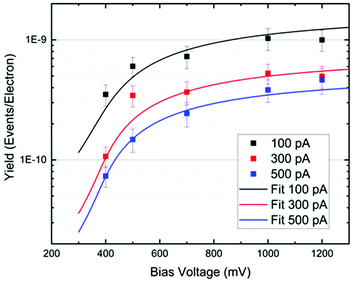
In Fig. 5, we plot the experimental yield Y = R/(I/e) for a single rotation step per electron as a function of the bias voltage. The switching rate R is the inverse of the elapsed time (or the number of switching events per time interval), I is the tunneling current and e the electron charge. Such action spectra^10,21,22 provide information about possible vibrational excitations of the molecule. The fitting of the action spectra by the theory of ref. 21 (see Methods for details) gives for all curves the same threshold of 370 meV, matching the DFT value for the C–H stretch mode of the methyl group at the opposite side of the O–Au bond. Below this mode there is a 170 meV energy gap until the C–H rotation modes are found starting at 198 meV. Therefore, we can conclude that the threshold coincides with the onset of the C–H stretch modes, showing that energy is efficiently funnelled into the molecule via the C–H stretch manifold.

Fig. 5 Yield (rotation probability per electron) versus bias voltage. The different colours indicate different currents. The continuous lines are action spectra fits where the overall factor is scaled to match the experimental values, and a broadening of 0.1 eV is assumed. The threshold of the action spectra fit is at 370 meV, matching the C–H stretch mode of the methyl group.

Furthermore, as one can see from Fig. 5, the rotational yield decreases with the current. This counterintuitive effect can be rationalized by a simple rate equation approach where the stretch mode is populated from the ground state of the molecule by a tunneling electron. This process is linear in the current. The stretch mode can decay populating the frustrated rotational mode as we assumed above. This leads to a yield, Y, given by

where γ is the electron inelastic fraction populating the stretch mode, such that γI is the rate of excitation of the stretch mode, where I is the electronic current. 1/τ is the total decay of the C–H stretch mode and 1/τ_rot is the decay rate of the stretch into the frustrate rotation mode. This simple equation shows that as long as the stretch decay rate is not so large to saturate the evolution of the yield, the yield should decay with the current. A similar result was already described for the excitation of a single step by step rotation of a C₂H₂ molecule.²³ To qualitatively understand it, one can consider that the yield is the reaction rate divided by the current. If the reaction rate is fairly constant, the yield decreases with current.

During a voltage pulse applied to an anchored DMBI-P, electrons are randomly transferred through the molecule, leaving some energy to the ro-vibrational modes of the molecule. While one part of this energy is redistributed to the Au(111) surface, another part goes to the C–H stretch mode, which therefore represents the entry port of the energy needed for a one-step rotation.

The relatively long elapse time needed for rotation (Fig. S18†) can be rationalized considering that, during the electron transfer events, a part of the energy is accumulated in the excited states (see below) after being transferred to the DMBI-P collective rotation angle, providing then the energy needed for a one-step rotation.¹³

As the applied bias voltage is much lower than the tunneling electronic resonances, the excited state involved cannot be completely occupied quantum mechanically. However, due to the basic properties of the tunnel effect through a molecule adsorbed on a surface, the tail of a given electronic state contributes to the tunneling current intensity even if it is far away from the maximum of this resonance. An elementary electron transfer event can be described using a time-dependent quantum mixing between the electronic states |S0+〉 and |S1−〉. In the present case, the |S0+〉 and |S1−〉 resonances are located at −2.5 V and +2.7 V respectively, as experimentally determined and presented in the ESI (Fig. S19†), while the voltage pulses producing a one-step rotation are typically between 0.3 V and 1.2 V. Furthermore, calculations of the frontier mono-electronic states of the adsorbed molecule are in qualitative agreement with the experimental results and show that the bonding of the molecule to the surface is strong enough to stabilize the electronic structure. No molecular electronic states therefore exist near the Fermi energy.

The next step is to discuss the directionality of the observed rotation and to qualitatively describe how the molecule can transform the excitation energy of the C–H stretch mode in a one-way rotation. An intrinsic symmetry breaking in the tunneling junction (including the surface, the molecule and the STM tip apex) is needed to allow a unidirectional rotation. The DMBI-P molecule was selected because it has two different chiralities when adsorbed on Au(111), showing a different sense of rotation with an equivalent voltage pulse.¹¹ The asymmetry of the adsorbed molecule plays a central role, and a corresponding asymmetry should also be present in the electronic states of the corresponding quantum system. However, if we consider only the |S0〉 ground state potential energy surface (PES), the micro-reversibility principle precludes any unidirectional rotation, as discussed above by increasing the surface temperature. Therefore, to explain the directionality the excited state PES, which is explored during the elementary electron transfer events leading to the measured tunneling current, should also play a role. As a consequence, a possible interpretation of a one-step and one-way rotation event is that the vibronic coupling between the C–H stretch and the other nuclear degrees of freedom depends on the mixing of the asymmetric electronic states involved in the elementary electron transfer events. This interpretation is a generalization of the quantum mixing of PES describing the case of molecular motors working in solution, where the unidirectional rotation is explained by a |S1〉 PES landscape with a very peculiar conical intersection.²⁴ For the DMBI-P single molecule case presented here, even a small asymmetry in the |S1〉 PES relative to the |S0〉 PES can lead to a one way step by step rotation. This can be for example a shift in the energy of the |S1〉 PES maxima relative to the |S0〉 PES minima.²⁵ Theoretical calculations are ongoing to characterize the |S1〉 PES energy landscape of DMBI-P.

Qualitatively, to activate this rotation the mechanical strain on the dihedral angle Φ₁ created by the Au–O chemical bond which is keeping the DBMI-P molecule close to the Au(111) surface, should be released. This means that part of the C–H stretch energy is probably transferred to the Au–O bond. Considering that the spring constant for the C–H bond is much larger than that for the Au–O bond (the Au–O bond vibration manifold starts at an energy of about 10 meV, while the C–H stretch manifold starts at about 370 meV), we can conclude that the Au–O bond vibrations are more populated. Therefore, to make the rotation possible, the reaction trajectory on the |S1〉 PES should reach the collective DMBI-P rotation before arriving at the energy needed for the detachment of the molecule.

Methods

The synthesis of the molecular precursor used in this work [2-(2-methoxyphenyl)-1,3-dimethyl-1H-benzo[d]imidazol-3-ium iodide²⁶ (o-MeO-DMBI-I, Fig. 1)] is described in the ESI.† The precursor molecule was sublimated at T = 490 K for 30 seconds under ultra-high vacuum (UHV) conditions on a clean Au(111) surface kept at room temperature.

STM experiments were performed using a custom-built instrument operating at a low temperature of T = 5 K and under ultra-high vacuum (p ≈ 1 × 10–10 mbar) conditions. All shown STM images were recorded in constant-current mode. In our experimental setup, the tip is grounded and the bias voltage is applied to the sample.

DFT calculations were performed with the Vienna ab initio simulation package (VASP) using the PBE approximation to density functional theory. Valence electrons were described using a plane-wave basis with an energy cut-off of 400 eV and projected-augmented-wave potentials. We used the DFT-D3 method with the Becke–Jonson damping method for the description of long-range van der Waals interactions as implemented in VASP. To simulate the surface, we used a Au (111) 8 × 4√3 slab with 4 atomic layers with an inter-slab separation of 20 Å. Structure relaxations were performed until the atomic forces on the molecule and first two layers were smaller than 0.02 eV Å⁻¹. The k-point samplings were 3 × 3 × 1 regular grid of k-points.²⁷ The obtained Au bulk lattice constant under the above conditions is 4.114 Å. The herringbone structure can be neglected because its height is about 0.026 nm, adding a small van der Waals perturbation to the rotation since the length of the binding of the fcc flat part of the surface is slightly smaller than 4 nm.

The fitting of the action spectra of Fig. 5 by the theory of ref. 21 was done using the function:

where K is the overall yield that controls the order of magnitude of the measured Y, the applied bias is V, Ω is the angular frequency of the vibrational mode mediating the reaction and σ is the broadening of the reaction threshold. The fitting curve is then controlled by basically two parameters; Ω that fixes the threshold of a non-zero yield, and σ that controls how fast the yield goes from zero to a measurable value. We find that the threshold is ℏΩ = 370 meV, and that the broadening is σ = 100 meV.

In order to calculate the rotational potential energy surface, we created initial samples of molecules rotated with respect to the oxygen atom. The total energy was converged below 10⁻⁶ eV in both cases.

The nudged elastic band method (NEB method)²⁸ permits us to compute the minimum-energy path between two rotational conformations on the surface. The NEB simulations were realized using 31 images altogether. We split the rotational pathway into two parts: images 1–16 corresponding to 0–60° and images 16–31 corresponding to 60–120°. Firstly, the 1st, 16th and 31st images were separately fully optimized. The 16th image is an intermediate image. Secondly, starting images 2–15 and 17–30 were calculated separately by rigid rotation (each by 4°) of the molecule with respect to the surface, with the pivoting axis perpendicular to the surface at the position of the oxygen atom. Within NEB optimization, the molecule and the first two layers were allowed to relax. STM topographic images have been simulated by the Tersoff and Hamann theory^29,30 using the method described by Bocquet et al.³¹ and implemented in STMpw.³²

Conclusions

In conclusion, we have presented a single molecule, chemically anchored on the Au(111) surface, rotating in one direction step by step at low temperatures when inelastically excited by a tunneling current. The experiments show a clear threshold at the onset of the C–H stretch manifold, showing that the molecule is first vibrationally excited and later decays into the rotational degrees of freedom. The strong chemical bond to the surface stabilizes the electronic structure of the molecular adsorbate with no molecular electronic state around the Fermi energy. This bond maintains the DMBI-P molecule flat and close to the Au(111) surface.

The present work shows a well characterized example of strong molecular anchoring and unidirectional step by step rotation induced by tunneling electrons under controlled conditions, therefore contributing to the understanding of inelastic electronic excitations and motion in a single molecule.

Author contributions

FM and CJ: conceptualization; FE, JM, TK and FM: STM investigation; OA and FL: chemical synthesis and chemical investigation; SS, DAR, VZ, RR, NL and CJ: theory and calculations. All authors contributed to discussion and writing. All authors have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work has received funding from the European Union's Horizon 2020 research and innovation program under the project MEMO, grant agreement no. 766864. Support by the Initiative and Networking Fund of the German Helmholtz Association, Helmholtz International Research School for Nanoelectronic Networks NanoNet (VH-KO-606) is gratefully acknowledged. Computer resources were obtained at the RES computers Finisterrae II in project RES-QCM-2019-1-0024 and Cibeles in project RES-QS-2019-3-0012 and are gratefully acknowledged. F.L. thanks the Fonds der Chemischen Industrie (FCI) for a Liebig Fellowship and C.J. the WPI MANA project for financial support.

Notes and references

1. J. Roßnagel, S. T. Dawkins, K. N. Tolazzi, O. Abah, E. Lutz, F. Schmidt-Kaler and K. Singer, Science, 2016, 352, 325–329.
2. T. Hugel, N. B. Holland, A. Cattani, L. Moroder, M. Seitz and H. E. Gaub, Science, 2002, 296, 1103–1106.
3. B. C. Stipe, M. A. Rezaei and W. Ho, Science, 1998, 279, 1907–1909.
4. H. L. Tierney, C. J. Murphy, A. D. Jewell, A. E. Baber, E. V. Iski, H. Y. Khodaverdian, A. F. McGuire, N. Klebanov and E. C. H. Sykes, Nat. Nanotechnol., 2011, 6, 625.
5. U. G. E. Perera, F. Ample, H. Kersell, Y. Zhang, G. Vives, J. Echeverria, M. Grisolia, G. Rapenne, C. Joachim and S. W. Hla, Nat. Nanotechnol., 2012, 8, 46.
6. G. J. Simpson, V. García-López, A. Daniel Boese, J. M. Tour and L. Grill, Nat. Commun., 2019, 10, 4631.
7. D. Lensen and J. A. A. W. Elemans, Soft Matter, 2012, 8, 9053–9063.
8. J. Ren, M. Freitag, C. Schwermann, A. Bakker, S. Amirjalayer, A. Rühling, H.-Y. Gao, N. L. Doltsinis, F. Glorius and H. Fuchs, Nano Lett., 2020, 20, 5922.
9. S. Stolz, O. Gröning, J. Prinz, H. Brune and R. Widmer, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 14838–14842.
10. T. Jasper-Toennies, M. Gruber, S. Johannsen, T. Frederiksen, A. Garcia-Lekue, T. Jäkel, F. Roehricht, R. Herges and R. Berndt, ACS Nano, 2020, 14, 3907–3916.
11. F. Eisenhut, J. Meyer, J. Krüger, R. Ohmann, G. Cuniberti and F. Moresco, Surf. Sci., 2018, 678, 177–182.
12. R. Ohmann, J. Meyer, A. Nickel, J. Echeverria, M. Grisolia, C. Joachim, F. Moresco and G. Cuniberti, ACS Nano, 2015, 9, 8394–8400.
13. S. Monturet, M. Kepenekian, R. Robles, N. Lorente and C. Joachim, Chem. Phys. Lett., 2013, 567, 1–5.
14. B. D. Naab, S. Guo, S. Olthof, E. G. B. Evans, P. Wei, G. L. Millhauser, A. Kahn, S. Barlow, S. R. Marder and Z. Bao, J. Am. Chem. Soc., 2013, 135, 15018–15025.
15. Z. Bin, L. Duan and Y. Qiu, ACS Appl. Mater. Interfaces, 2015, 7, 6444–6450.
16. M. Schwarze, B. D. Naab, M. L. Tietze, R. Scholz, P. Pahner, F. Bussolotti, S. Kera, D. Kasemann, Z. Bao and K. Leo, ACS Appl. Mater. Interfaces, 2018, 10, 1340–1346.
17. F. Ample and C. Joachim, Surf. Sci., 2006, 600, 3243–3251.
18. P. Mishra, J. P. Hill, S. Vijayaraghavan, W. V. Rossom, S. Yoshizawa, M. Grisolia, J. Echeverria, T. Ono, K. Ariga, T. Nakayama, C. Joachim and T. Uchihashi, Nano Lett., 2015, 15, 4793–4798.
19. J. K. Gimzewski, C. Joachim, R. R. Schlittler, V. Langlais, H. Tang and I. Johannsen, Science, 1998, 281, 531–533.
20. G. Calzaferri, L. Forss and I. Kamber, J. Phys. Chem., 1989, 93, 5366–5371.
21. Y. Kim, K. Motobayashi, T. Frederiksen, H. Ueba and M. Kawai, Prog. Surf. Sci., 2015, 90, 85–143.
22. K. Motobayashi, Y. Kim, H. Ueba and M. Kawai, Phys. Rev. Lett., 2010, 105, 076101.
23. B. C. Stipe, M. A. Rezaei and W. Ho, Phys. Rev. Lett., 1998, 81, 1263–1266.
24. A. Kazaryan, J. C. M. Kistemaker, L. V. Schäfer, W. R. Browne, B. L. Feringa and M. Filatov, J. Phys. Chem. A, 2010, 114, 5058–5067.
25. J. Echeverria, S. Monturet and C. Joachim, Nanoscale, 2014, 6, 2793–2799.
26. P. Wei, T. Menke, B. D. Naab, K. Leo, M. Riede and Z. Bao, J. Am. Chem. Soc., 2012, 134, 3999–4002.
27. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
28. H. Jónsson, G. Mills and K. Jacobsen, in Classical and Quantum Dynamics in Condensed Phase Simulations, ed. B. Berne, G. Ciccotti and K. Jacobsen, World Scientific, Singapore, 1998, ch. 485.
29. J. Tersoff and D. R. Hamann, Phys. Rev. Lett., 1983, 50, 1998–2001.
30. J. Tersoff and D. R. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 1985, 31, 805–813.
31. M.-L. Bocquet, H. Lesnard, S. Monturet and N. Lorente, in Computational Methods in Catalysis and Materials Science, ed. R. A. van Santen and P. Sautet, Wiley-VCH, Weinheim, Germany, 2009, pp. 199–219.
32. N. Lorente and R. Robles, STMpw (Version v1.0b2) doi: DOI:10.5281/zenodo.3581159.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1nr04583k

---