Realization of the Zn³⁺ oxidation state

Abstract

Due to unfilled d-shells, transition metal atoms exhibit multiple oxidation states and rich chemistry. While zinc is often classified as a transition metal, electrons in its filled 3d¹⁰ shell do not participate in chemical reactions; hence, its oxidation state is +2. Using calculations based on density functional theory, we show that the chemistry of zinc can fundamentally change when it is allowed to interact with highly stable super-electrophilic trianions, namely, BeB₁₁(CN)₁₂³⁻ and BeB₂₃(CN)₂₂³⁻, which lie 15.85 eV and 18.49 eV lower in energy than their respective neutral states. The fact that Zn exists in +3 oxidation states while interacting with these moieties is evidenced from its large binding energies of 6.33 and 7.04 eV with BeB₁₁(CN)₁₂³⁻ and BeB₂₃(CN)₂₂³⁻, respectively, and from a comprehensive analysis of its bonding characteristics, charge density distribution, electron localization function, molecular orbitals and energy decomposition, all showing a strong involvement of its 3d electrons in chemical bonding. The replacement of CN with BO is found to increase the zinc binding energy even further.

---

One of the most fundamental quantities that determines the chemistry of an element is its oxidation state, i.e., the number of electrons it loses in a chemical reaction. High oxidation states are often found in high-valence heavy metal elements with relatively soft cores and unfilled outer d orbitals. The highest oxidation states reported to date belong to the +9 state of iridium in IrO₄⁺ (ref. 1) and the +10 state of platinum in PtO₄²⁺ (ref. 2) which are both heavy transition metal elements with unfilled 5d orbitals in their valence configurations. High oxidation states that can tap into the filled d-orbital of a light transition metal element are extremely rare. The known example for a Group 12 element with filled outer d-orbitals to exhibit higher oxidation states than its usual +2 state is Hg. The discovery of a short-lived +3 oxidation state of Hg in 1976, generated through electrochemical reduction,³ led to the search of its +4-oxidation state that is expected to be more stable than the +3-oxidation state because it has the same electronic configuration (5d⁸) as the very stable Au³⁺ cation.⁴ Fifteen years after it was theoretically predicted,^5,6 HgF₄ was synthesized under cryogenic conditions in rare gas matrices in 2007.⁷ However, since Hg is even heavier than Ir and Pt, its high oxidation states are due to relativistic effects.

On the other hand, zinc, a member of the Group 12 elements, is a light transition metal element with a valence configuration of 4s²3d¹⁰. Because its filled 3d¹⁰ shell, being more compact than the 5d¹⁰ shell of Hg, does not participate in chemical bonding, zinc is well-known to have an oxidation state of +2. It will be both interesting and significant to ask if Zn can exhibit the +3-oxidation state and if so under what conditions can this be realized. Note that, for Zn to assume this oxidation state, its 3d electrons must be involved in chemical bonding. This indeed is difficult as the third ionization potential of Zn is the highest among its congeners (39.7, 37.5, and 34.2 eV for Zn, Cd, and Hg, respectively).⁸ In addition, the signature of Zn binding to three monovalent species (X) individually that are more electronegative than itself and the stability of ZnX₃ against dissociation along all possible channels should be apparent. An early study of the interaction of Zn with F atoms by Riedel et al.⁹ using the CCSD(T) level of theory showed that two of the F atoms in ZnF₃ formed partial bonds and they are unstable against dissociation into ZnF₂ + ½F₂. Clearly, Zn in ZnF₃ is not in the +3-oxidation state. Samanta and Jena¹⁰ wondered if the use of more electronegative ligands could enable Zn to assume a +3-oxidation state. Using the density functional theory and the B3LYP exchange–correlation functional, the authors studied the interaction of Zn with three different moieties, namely, F, BO₂, and AuF₆, which have increasing electron affinities of 3.4,¹¹ 4.5 ¹² and 8.4 eV,¹³ respectively. The geometries of the neutral and anionic forms of ZnX₃ (X = F, BO₂, and AuF₆) calculated by these authors are given in Fig. S1 of the ESI.† In agreement with the previous calculations at the CCSD(T) level of theory,⁷ Samanta and Jena found that two of the F atoms in ZnF₃ formed partial bonds, with Zn–F distances being 1.76 Å and 1.93 Å. In Zn(BO₂)₃, two of the BO₂ moieties dimerized and Zn again formed two bonds, one with BO₂ and the other with B₂O₄. However, when an extra electron is attached, both ZnF₃⁻ and Zn(BO₂)₃⁻ assume the C_3v symmetry with Zn forming three bonds. Clearly, Zn behaves as a divalent species in both of these cases. The situation, however, was different for neutral Zn(AuF₆)₃, where the AuF₆ clusters retained their structure, although two of these moieties came slightly closer and the Zn–F bond distances were 2.02 and 2.16 Å (see Fig. S1†). Zn(AuF₆)₃ was found to be stable against dissociation into Zn(AuF₆)₂ + ½Au₂F₁₀ + ½F₂ by +0.26 eV. The authors concluded this to be evidence that Zn is in the +3-oxidation state.

In a subsequent paper, Schlöder et al.¹⁴ questioned this conclusion, arguing that the B3LYP level of theory overestimates the binding energy. This conclusion was reached by first comparing the reaction energies of ZnF₃→ZnF₂ + ½F₂ calculated both at the CCSD(T) and B3LYP level of theories, which are −0.61 eV and −0.19 eV, respectively. The authors argued that a simple extrapolation of the B3LYP performance for ZnF₃ to the larger complex would suggest that the reaction Zn(AuF₆)₃→Zn(AuF₆)₂ + ½Au₂F₁₀ + ½F₂ will be exothermic when calculated at a higher level of theory. As the computation of Zn(AuF₆)₃ at the CCSD(T) level was not possible, Schlöder et al. calculated the reaction energies using the so-called spin component-scaled MP2 (SCS-MP2) method. The reaction energy computed at this level is −3.17 eV compared to +0.28 eV at the B3LYP level. To put this into perspective, it should be pointed out that the reaction energy of ZnF₃→ZnF₂ + ½F₂ at the SCS-MP2 level is −0.98 eV compared to −0.61 eV at the CCSD(T) level. Nevertheless, the discrepancy in the thermodynamic stability of Zn(AuF₆)₃ computed at two levels of theory casts doubt on whether Zn in Zn(AuF₆)₃ is in the +3-oxidation state, although a quantitative assessment of this discrepancy has to wait until calculation at the CCSD(T) level of theory is computationally possible. In addition, whether Zn(AuF₆)₃ would dissociate via a given channel will also depend upon the energy barrier. Thus, both kinetic and thermodynamic calculations are necessary to see if Zn(AuF₆)₃ can be experimentally realized. It is because of these reasons that we opted for a different approach to study if Zn can be in the +3-oxidation state if an appropriate reagent could be found.

Thanks to the recent progress in the study of multiply-charged clusters,^15–18 it is now possible to choose a single cluster that is highly stable as a trianion in the gas phase to interact with Zn. This will avoid the challenges of using three moieties to react with Zn, as depicted above. The choice of the trianions here is guided by focusing on previous studies on the stability of multiply charged anions. The starting point is the well-known dodeca-borate B₁₂H₁₂²⁻ dianion whose second electron is bound by 0.9 eV.¹⁵ Note that the stability of B₁₂H₁₂²⁻ which belongs to the class of closo-boranes was explained by Wade and Mingos^19,20 based on the polyhedral skeletal electron pair theory (PSEPT). According to this Wade–Mingos rule, closo-boranes require (n + 1) pairs of electrons, where n is the number of vertices in the icosahedral skeleton. For B₁₂H₁₂, n = 12; thus, 2(n + 1) = 2(12 + 1) = 26 electrons are needed to satisfy the Wade–Mingos rule. Note that out of the four electrons of a BH pair, two are contributed to cage bonding. Thus, 24 electrons are available and two more are needed. Thus, B₁₂H₁₂²⁻ is amongst the most stable dianions in the gas phase. Zhao et al.¹⁵ showed that replacing H with CN moieties can lead to an even more stable B₁₂(CN)₁₂²⁻. Their calculations, based on density functional theory with the B3LYP functional, yielded its second electron affinity to be 5.3 eV. This prediction has now been verified experimentally¹⁶ and the measured second electron affinity of 5.5 eV agrees well with the theoretical prediction, making B₁₂(CN)₁₂²⁻ the most stable dianion known in the gas phase. Zhao et al.¹⁷ later showed that if one of the B atoms in B₁₂(CN)₁₂²⁻ is replaced by a Be atom, the resulting BeB₁₁(CN)₁₂³⁻ trianion would also be very stable. Indeed, with the calculated third electron affinity of 2.65 eV, BeB₁₁(CN)₁₂³⁻ is one of the most stable trianions thus far. In a subsequent paper,¹⁸ two of the current authors formulated a general scheme for designing ultra-stable clusters in highly charged states by a modular assembly of selective stable anions carrying lesser charges. For instance, a trianion can be built by bringing together a stable monoanion and a stable dianion. Similarly, a tetra-anion (with ‘-4’ additional charges) can be designed by combining either a monoanion and a trianion or two dianions.¹⁶

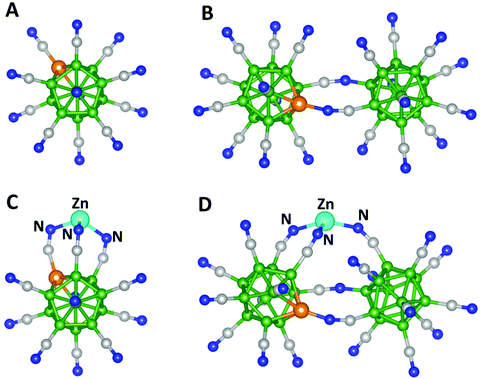
We chose two trianions for our study. The first one is an already established stable trianion, BeB₁₁(CN)₁₂³⁻ (Fig. 1A). The second cluster, BeB₂₃(CN)₂₂³⁻, is formed by combining BeB₁₁(CN)₁₁²⁻ and B₁₂(CN)₁₁⁻ clusters (Fig. S2A of the ESI†). Note that according to the Wade–Mingos rule, B₁₂(CN)₁₁ and BeB₁₁(CN)₁₁ would require one and two electrons to be stable as a monoanion and dianion, respectively. Our calculations showed that the first and second electron affinities of BeB₁₁(CN)₁₁²⁻ are 8.10 and 4.62 eV, respectively, while the calculated first electron affinity of B₁₂(CN)₁₁⁻ is 8.49 eV. We determined the ground state geometries and total energies of BeB₂₃(CN)₂₂ as successive electrons are added and found that it can bind up to three electrons. The optimized geometry of the resulting BeB₂₃(CN)₂₂³⁻ cluster is plotted in Fig. 1B. The first, second and third electron affinities of these clusters are given in Table 1 and the optimized geometries of the neutral, monoanion and dianion BeB₂₃(CN)₂₂ clusters are given in Fig. S2B.† Note that BeB₂₃(CN)₂₂³⁻, with the third electron affinity of 3.25 eV, is even more stable than the previously known BeB₁₁(CN)₁₂³⁻. In addition, the total energy gained by adding the three electrons (EA₁ + EA₂ + EA₃) is 18.49 eV for BeB₂₃(CN)₂₂, while it is 15.85 eV for BeB₁₁(CN)₁₂, making these clusters extraordinary electrophiles. In the following, we present the results of the interaction of Zn with the above two electrophiles.

Fig. 1 Optimized geometries of (A) BeB₁₁(CN)₁₂³⁻, (B) BeB₂₃(CN)₂₂³⁻, (C) neutral ZnBeB₁₁(CN)₁₂ and (D) neutral ZnBeB₂₃(CN)₂₂. Boron atoms are shown in green, carbon in grey, nitrogen in blue, beryllium in orange and zinc in cyan.

Table 1 Calculated electron affinities (EA_i = E[cluster⁻⁽ⁱ⁻¹⁾] − E[cluster⁻ⁱ]; i = 1–3) of the studied clusters, the binding energy (BE) of Zn, and the bond lengths (BL) between Zn and three N atoms. Positive EA_i values suggest that up to i additional electrons can be attached to the cluster without fragmentation or spontaneous electron emission. Both ZnBeB₂₃(CN)₂₂ and ZnBeB₁₁(CN)₁₂ are spin doublets in their ground states

Cluster	EA1	EA2	EA3	BE (eV)	BL (Å)
a Calculated energies using double-hybrid functional with empirical dispersion (B2PLYP + D).^32
BeB23(CN)22	8.86	6.38	3.25	—	—
ZnBeB23(CN)22	8.13	3.33	1.11	7.04	1.94/1.98/1.99
BeB11(CN)12	8.44	4.76	2.65	—	—
ZnBeB11(CN)12	7.23 (7.64^a)	2.22 (2.02^a)	−0.39 (−0.90^a)	6.33 (7.59^a)	1.98/2.01/2.01

---

Geometries of Zn interaction with neutral BeB₁₁(CN)₁₂⁰ and BeB₂₃(CN)₂₂⁰

The optimized geometries of neutral ZnBeB₁₁(CN)₁₂ and ZnBeB₂₃(CN)₂₂ are given in Fig. 1(C) and (D), respectively. The corresponding geometries of their higher energy isomers are given in Fig. S3 of the ESI.† Note that Zn is bound to three N atoms in both clusters, with Zn–N bond lengths of 1.98, 2.01 and 2.01 Å in ZnBeB₁₁(CN)₁₂ and 1.94, 1.98 and 1.99 Å in ZnBeB₂₃(CN)₂₂ (see Table 1). These values are significantly smaller than the Zn–N distances in the known compounds containing four-coordinated Zn, such as Zn(II) quinaldinate complexes, where the distances are in the range of 2.22–2.25 Å.²¹ The binding energies (BE) of the ZnY (Y = BeB₁₁(CN)₁₂, BeB₂₃(CN)₂₂) complexes are calculated as,

BE = −[E(ZnY) − E(Zn) − E(Y)],

where E is the total energy. These are also listed in Table 1. Note that Zn is bound strongly with a binding energy of 7.04 eV in ZnBeB₂₃(CN)₂₂ and 6.33 eV in ZnBeB₁₁(CN)₁₂. To confirm these results, the binding energy is also calculated for the affordable ZnBeB₁₁(CN)₁₂ system using the double-hybrid functional with dispersion (see Methods) and is found to have an even higher value of 7.59 eV (Table 1). The higher binding energy of ZnBeB₂₃(CN)₂₂ than that of ZnBeB₁₁(CN)₁₂ is consistent with the smaller Zn–N bond lengths of ZnBeB₂₃(CN)₂₂ than those of ZnBeB₁₁(CN)₁₂ (Table 1). To put this into perspective, recall that Zn(AuF₆)₃ was stable against dissociation into Zn(AuF₆)₂ + ½Au₂F₁₀ + ½F₂ by only +0.26 eV at the DFT/B3LYP level of theory. In addition, the binding energy of Zn in the ZnO dimer, where Zn has an oxidation state of +2, is 3.91 eV. A natural bond orbital (NBO) charge analysis also shows that the charges on Zn in ZnBeB₂₃(CN)₂₂ and ZnBeB₁₁(CN)₁₂ are significantly more positive (about 1.3 times as shown in Table S1 of the ESI†) than that of Zn in the ZnO dimer. The large binding energies as well as the large positive charge associated with Zn in ZnBeB₂₃(CN)₂₂ and ZnBeB₁₁(CN)₁₂ indicate that the nature of Zn bonding to these highly electrophilic species must be fundamentally different from that of the known compounds with Zn in the +2-oxidation state.

To examine the nature of the bonding of Zn in the clusters, we first study their geometries as successive electrons are added. Note that the added electrons can go to the boron-based clusters to fulfill the Wade–Mingos rule. Consequently, Zn would not have to assume a +3-oxidation state that would otherwise involve its filled 3d¹⁰ shell in chemical bonding. This is indeed what we observed. The ground state geometries of mono-, di-, and trianionic clusters of ZnBeB₁₁(CN)₁₂ and ZnBeB₂₃(CN)₂₂ are given in Fig. S4 of the ESI.† Note that Zn interacts less with N as more electrons are added. In Table 1, we have also listed the energy gain as electrons are successively added to the ZnBeB₁₁(CN)₁₂ and ZnBeB₂₃(CN)₂₂ clusters. Note that ZnBeB₂₃(CN)₂₂ is stable even as a trianion, while ZnBeB₁₁(CN)₁₂ is stable as a dianion. This is again confirmed by using the double-hybrid functional with dispersion (see Methods) as shown in Table 1. Another signature of the weaker binding energy of Zn to the clusters as more electrons are added can also be seen from the corresponding Zn–N bond lengths. For instance, the Zn–N bond lengths increase to 2.14/2.41/2.44 Å in [ZnBeB₂₃(CN)₂₂]²⁻ compared to those of the corresponding neutral clusters (see Table 1). In [ZnBeB₂₃(CN)₂₂]³⁻, Zn only weakly interacts with one N atom with a Zn–N distance of 3.12 Å (Fig. S4 of the ESI†).

Electronic structure and bonding characteristics of Zn interaction with neutral BeB₂₃(CN)₂₂⁰ and BeB₁₁(CN)₁₂⁰ clusters

To further understand the nature of the Zn–N interactions in the above clusters, we studied the charge density distribution and explored the explicit involvement of its 3d electrons by analyzing the partial density of states, projected crystal Hamiltonian population, electron localization function, and energy decomposition. We begin with the charge density difference, which is calculated by subtracting the charge densities of a single Zn atom and the electrophilic cluster from the total charge density of the zinc-bonded cluster. As shown in Fig. 2, in both ZnBeB₁₁(CN)₁₂ and ZnBeB₂₃(CN)₂₂, positive charge densities appear around the middle of the Zn–N bonds and lopsided towards the N atoms. The surrounding areas of Zn and some close areas of N atoms become electron deficient. These suggest that both ionic and covalent types of bonding are prevalent in the interaction between Zn and N.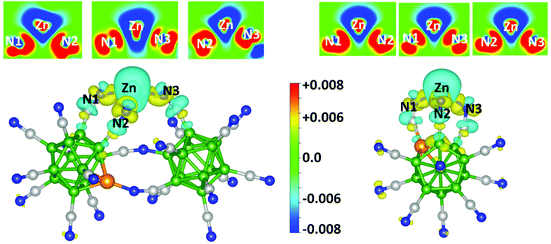

Fig. 2 Calculated charge density differences for ZnBeB₂₃(CN)₂₂ (left) and ZnBeB₁₁(CN)₁₂ (right) in the three N–Zn–N planes (top panel) for the three Zn–N bonds in 2D as well as in 3D.

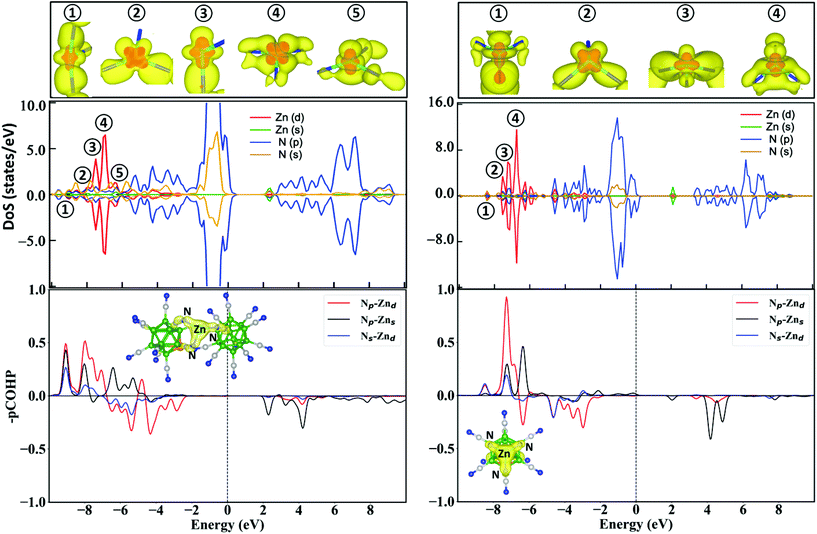
Next, we analyzed the electronic structure of ZnBeB₂₃(CN)₂₂ and ZnBeB₁₁(CN)₁₂ by calculating the partial density of states as well as the bonding, nonbonding, and antibonding interactions between Zn and N atoms and their atomic orbitals. The results shown in Fig. 3 show that Zn(d) electrons explicitly participate in bonding with N(p) and N(s) electrons. The calculated partial densities of states (DoS) reveal the overlaps of the Zn(d) orbitals with the N(p) and N(s) orbitals in the energy range from −8.0 to −2.0 eV for ZnBeB₁₁(CN)₁₂ and −8.5 to −2.5 eV for ZnBeB₂₃(CN)₂₂. The major d peaks appear in the range from −8.1 to −7.0 eV for ZnBeB₂₃(CN)₂₂. These results are consistent with the large bonding peaks between Zn(d) and N(p)/N(s) as seen from the projected crystal Hamiltonian population analysis (–pCOHP in Fig. 3 and Methods). Small d peaks correspond to the anti-bonding orbitals of Zn(d)–N(p) and Zn(d)–N(s) in the range of −7.0 to −2.5 eV. Similarly, for ZnBeB₁₁(CN)₁₂, the major d peaks in the range from −8.0 to −7.0 eV correspond to the bonding orbitals of Zn(d)–N(p) and Zn(d)–N(s), while the antibonding orbitals contribute to the tiny d peaks at higher energies. It is also found that a more advanced meta-GGA SCAN functional (see Methods) will result in very similar DoS and bonding/anti-bonding analysis results, with the Zn(d)–N(p) bonding band shifting to even lower energies, as shown in Fig. S6 of the ESI.†

Fig. 3 Analyses of the electronic structures, partial charge density and bonding/antibonding features of the clusters. The partial densities of states (DoS) are displayed for spin-up (positive) and spin-down (negative) electrons, given that ZnBeB₂₃(CN)₂₂ and ZnBeB₁₁(CN)₁₂ have a multiplicity of 2. The top panels show the partial charge densities of the major d peaks in the DoS, with an isovalue of 0.002 e Bohr⁻³ in yellow and an isovalue of 0.06 e Bohr⁻³ in red. The bottom panels show the crystal Hamiltonian population analysis, where positive (–pCOHP) values correspond to the bonding state and negative values to the antibonding state. The insets in these plots show the partial charge density of all the bonding states for the three Zn–N bonds.

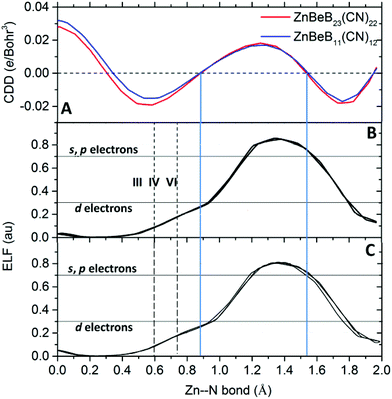
To further characterize the Zn–N bonds in the systems, we computed the electron localization function (ELF). The ELF is a way to classify chemical bonds based on the local quantum mechanical functions of electrons that are related to the Pauli exclusion principle. The ELF can assume values between 0 and 1, with 1 corresponding to perfect localization and 0.5 the localization in an electron gas. Compared to the charge density difference along the Zn–N bond (Fig. 4A), the shared electrons between Zn and N are localized in the range from 0.88 to 1.52 Å from Zn (situated at the origin). Given that the 3d orbital density of Zn corresponds to small ELF values of around 0.3 ²² and the (s,p) orbital densities correspond to large ELF values above 0.7, the localized bonding electrons are contributed by both the d electrons of Zn and the N(s,p) electrons, as shown in Fig. 4B and C for ZnBeB₂₃(CN)₂₂ and ZnBeB₁₁(CN)₁₂, respectively. This is consistent with the results from the previous analysis. Note that the defined ionic radii of six- and four-coordinated Zn(+2) are 0.74 and 0.60 Å, respectively. With the valence now increasing from +2 to +3 and the coordination number reducing down to three, the ionic radius of the three-coordinated +3-oxidation state of Zn is expected to be smaller than 0.6 Å.

Fig. 4 Characterization of the Zn–N bonds in the studied clusters. (A) The linear profiles of the charge density difference (CDD) along the Zn–N bond from Zn (at the origin) to N for the studied clusters. (B) The calculated electron localization function (ELF) along the three Zn–N bonds of ZnBeB₂₃(CN)₂₂. (C) The calculated ELF along the three Zn–N bonds of ZnBeB₁₁(CN)₁₂. The Zn d orbital density has a small ELF value of around 0.3 and the (s,p) orbital densities have a large ELF value above 0.7. The blue solid lines show the range of the localized electrons shared in the bonds. The dashed lines show the ionic radii of six (VI)- and four (IV)-coordinated Zn(+2).

In the above, we have clearly shown that the electrons in the filled 3d shell of Zn participate in the chemical bonding when reacted with the super electrophilic species Y (Y = BeB₁₁(CN)₁₂ and BeB₂₃(CN)₂₂), enabling Zn to exhibit an oxidation state of +3. To show that the colossal stability of Y³⁻ trianions is at the heart of this behavior, we compare the results with a ZnN dimer. Note that the N atom needs three extra electrons to satisfy its octet shell closure just as the Y moiety requires three extra electrons to satisfy the Wade–Mingos rule. In this regard, BeB₁₁(CN)₁₂ and BeB₂₃(CN)₂₂ can be regarded as superatoms mimicking the chemistry of pnictogens. However, in the ZnN dimer, Zn exhibits an oxidation state of +2 as its 3d orbitals overlap negligibly with the N orbitals and do not take part in chemical bonding (Fig. S5 of the ESI†). In addition, the binding energy of the ZnN dimer is 2.31 eV which is about a factor of three smaller than those of ZnBeB₂₃(CN)₂₂ and ZnBeB₁₁(CN)₁₂. The above results are complemented by an energy decomposition analysis (EDA, see Methods) of the Zn–N interaction in ZnBeB₁₁(CN)₁₂. As shown in Table 2, the magnitudes of the electrostatic interaction (ΔE^ele) and electron exchange interaction (ΔE^ex) in ZnBeB₁₁(CN)₁₂ are much greater than those in the ZnN dimer, suggesting a greater extent of charge transfer from Zn to N in the former. The especially large electron repulsion term (ΔE^rep) of the Zn–N interaction in ZnBeB₁₁(CN)₁₂ is due to the participation of the dense Zn 3d electrons in bonding. In addition, the Zn–N interaction in ZnBeB₁₁(CN)₁₂ shows a particularly large polarization term (ΔE^pol), suggesting that the orbitals undergo significant change in their shapes, which is typical in the formation of a covalent bond.³² Therefore, the Zn–N bond in ZnBeB₁₁(CN)₁₂ can be characterized by a dominant covalency due to the Zn(3d) orbitals, yet with a strong ionic interaction component due to the Zn(4s) orbitals. This study, therefore, demonstrates the unusual chemistry the superatoms can promote, which their atomic counterpart cannot.

Table 2 Energy decomposition analysis (EDA)³² of the Zn–N bond in ZnBeB₁₁(CN)₁₂ compared to that in the ZnN dimer. ΔE^ele, ΔE^ex, ΔE^rep, ΔE^pol, ΔE^disp and ΔE are the electrostatic, exchange, repulsion, polarization, dispersion and the total interactions, respectively. All energy terms are given in kcal mol⁻¹ unit. The Zn–N interaction in ZnBeB₁₁(CN)₁₂ shows large electrostatic, exchange and repulsion terms. It also has a particularly large polarization term, suggesting large changes in the orbital shapes when they form the Zn–N bonds in the system. Although we cannot conduct EDA for the larger cluster ZnBeB₂₃(CN)₂₂ due to the limitation of computational power, the Zn–N bond in ZnBeB₂₃(CN)₂₂ is expected to have the similar interaction characters as in ZnBeB₁₁(CN)₁₂, according to our previous analysis on both clusters

Cluster	ΔE^ele	ΔE^ex	ΔE^rep	ΔE^pol	ΔE^disp	ΔE
ZnBeB11(CN)12	−187.92	−160.64	570.27	−336.94	−26.63	−141.86
ZnN dimer	−35.52	−49.30	167.32	−124.09	−11.97	−53.57

---

In conclusion, we have addressed one of the most fundamental concepts in chemistry text books, i.e., filled core orbitals do not participate in chemical reactions. Hence, Zn, with a filled 3d shell, has an oxidation state of +2 and does not exhibit multiple oxidation states as transition metal atoms do, even though it is classified as a transition metal. We show that the core electrons in Zn can indeed take part in chemical bonding if subjected to reactions with super electrophilic agents. BeB₁₁(CN)₁₂ and BeB₂₃(CN)₂₂ are found to be such species as they can accept three additional electrons without fragmentation or spontaneous electron emission and their trianions are more stable than their neutral species by 15.85 eV and 18.49 eV, respectively. These clusters can be viewed as super-pnictogens mimicking the chemistry of Group 15 elements. It is found that such clusters, capable of holding multiple additional electrons while maintaining great stability, can be designed by assembling selected cluster modules.^18,23 It has been shown recently that selected super-/pseudo-halogens with large electron affinities and linear configurations can produce highly charged clusters up to “-4” states.²⁴ For example, linearly configured pseudo-halogens BO⁻ and SCN⁻ can be used as the terminal ligands to replace CN⁻, producing BeB₁₁(BO)₁₂ and BeB₁₁(SCN)₁₂ which are both stable tri-anions in their ground states with EA₃ = 1.30 and 0.59 eV, respectively.^17,18 The calculated binding energy of Zn in a partially substituted species, ZnB₁₁(BO)₃(CN)₉ as shown in Fig. S7 of the ESI† (with three CN⁻ replaced by three BO⁻ terminal ligands), is 6.73 eV which is even greater than that of ZnBeB₁₁(CN)₁₂. The finding in this work opens a new door, where chemical reactions once thought impossible can occur.

Methods

All calculations are carried out using density functional theory (DFT) with the Becke three parameter Lee–Yang–Parr (B3LYP) hybrid functional for exchange and correlation potential.^25,26 The ground state geometries of the neutral and charged clusters are obtained without symmetry constraint using the GAUSSIAN16 package²⁷ and 6-31+G* basis sets. Binding energies and molecular orbitals are obtained from single-point calculations using the above optimized geometries but a larger basis set of 6-311+G(d,p). The adopted functional and basis sets in this paper have been proven to provide reliable results for these relatively large clusters, as demonstrated in the previous work.¹⁷ The charge density analysis, density of states and electron localization function are calculated using the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA)²⁸ implemented in the VASP package.²⁹ The projector augmented wave (PAW) pseudopotential method²⁸ is used. Crystal Orbital Hamilton population (COHP) is the re-partitioning of the band structure energy into a sum of orbital pair contributions that can indicate bonding, nonbonding, and antibonding energy regions.³⁰ The bonding/antibonding analysis between N and Zn is done by using the projected crystal orbital Hamiltonian population (pCOHP) as incorporated in the Lobster package.³¹ pCOHP is a powerful physical quantity to understand the details of bonding, nonbonding, and antibonding interactions between a pair of atoms and their atomic orbitals in a compound.³² The results are further confirmed using the double-hybrid functional with non-local electron correlation effects and empirical dispersion,³³ as well as using the non-empirical strongly constrained and appropriately normed (SCAN) meta-generalized gradient approximation (meta-GGA).³⁴ The energy decomposition analysis based on localized molecular orbitals is carried out using the method in ref. 35 with DFT and the same basis sets.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is partially supported by the U.S. Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering under Award DE-FG02-96ER45579. The resources of the National Energy Research Scientific Computing Center supported by the Office of Science of the U.S. Department of Energy under Contract no. DE-AC02-05CH11231 is also acknowledged.

References

1. G. Wang, M. Zhou, J. T. Goettel, G. J. Schrobilgen, J. Su, J. Li, T. Schloeder and S. Riedel, Identification of an iridium-containing compound with a formal oxidation state of IX, Nature, 2014, 514, 475.
2. S.-X. Hu, et al., On Upper Limits of Oxidation-States in Chemistry, Angew. Chem., Int. Ed., 2018, 57, 3242.
3. R. L. Deming, A. L. Allred, A. R. Dahl, A. W. Herlinger and M. O. Kestner, Tripositive mercury. Low temperature electrochemical oxidation of 1,4,8,11-tetraazacyclotetradecanemercury(II) tetrafluoroborate, J. Am. Chem. Soc., 1976, 98, 4132–4137.
4. C. K. Jørgensen, Conditions for stability of oxidation states derived from photo-electron spectra and inductive quantum chemistry, Z. Anorg. Allg. Chem., 1986, 540, 91–105.
5. M. Kaupp and H. G. von Schnering, Gaseous Mercury(IV) Fluoride, HgF4: An Ab Initio Study, Angew. Chem., Int. Ed. Engl., 1993, 32, 861–863.
6. M. Kaupp, M. Dolg, H. Stoll and H. G. von Schnering, Oxidation State +IV in Group 12 Chemistry. Ab Initio Study of Zinc(IV), Cadmium(IV), and Mercury(IV) Fluorides, Inorg. Chem., 1994, 33, 2322–2331.
7. X. Wang, L. Andrews, S. Riedel and M. Kaupp, Mercury is a transition metal: the first experimental evidence for HgF(4), Angew. Chem., Int. Ed., 2007, 46, 8371–8375.
8. C. E. Moore, Ionization Potentials and Ionization Limits Derived from the Analysis of Optical Spectra, National Standard Reference Data Series 34, National Bureau of Standards, Washington, DC, 1970.
9. S. Riedel, M. Kaupp and P. Pyykkö, Quantum chemical study of trivalent group 12 fluorides, Inorg. Chem., 2008, 47, 3379–3383.
10. D. Samanta and P. Jena, Zn in the +III Oxidation State, J. Am. Chem. Soc., 2012, 134, 8400–8403.
11. C. Blondel, C. Delsart and F. Goldfarb, Electron spectrometry at the μeV level and the electron affinities of Si and F, J. Phys. B: At., Mol. Opt. Phys., 2001, 34, 2757–2757.
12. H.-J. Zhai, L.-M. Wang, S.-D. Li and L.-S. Wang, Vibrationally Resolved Photoelectron Spectroscopy of BO- and BO2-: A Joint Experimental and Theoretical Study, J. Phys. Chem. A, 2007, 111, 1030–1035.
13. P. Koirala, M. Willis, B. Kiran, A. K. Kandalam and P. Jena, Superhalogen Properties of Fluorinated Coinage Metal Clusters, J. Phys. Chem. C, 2010, 114, 16018–16024.
14. T. Schlöder, M. Kaupp and S. Riedel, Can Zinc Really Exist in Its Oxidation State +III?, J. Am. Chem. Soc., 2012, 134, 11977–11979.
15. H. Zhao, J. Zhou and P. Jena, Stability of B12(CN)122−: Implications for Lithium and Magnesium Ion Batteries, Angew. Chem., Int. Ed., 2016, 55, 3704–3708.
16. M. Mayer, et al., Rational design of an argon-binding superelectrophilic anion, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 8167–8172.
17. T. Zhao, J. Zhou, Q. Wang and P. Jena, Colossal Stability of Gas-Phase Trianions: Super-Pnictogens, Angew. Chem., Int. Ed., 2017, 56, 13423–13425.
18. H. Fang and P. Jena, Stable Tetra- and Penta-Anions in the Gas Phase, Angew. Chem., Int. Ed., 2019, 58, 11248–11252.
19. K. Wade, The structural significance of the number of skeletal bonding electron-pairs in carboranes, the higher boranes and borane anions, and various transition-metal carbonyl cluster compounds, J. Chem. Soc., Chem. Commun., 1971, 792–793.
20. D. M. P. Mingos, A General Theory for Cluster and Ring Compounds of the Main Group and Transition Elements, Nat. Phys. Sci., 1972, 236, 99–102.
21. B. Modec, Crystal Chemistry of Zinc Quinaldinate Complexes with Pyridine-Based Ligands, Crystals, 2018, 8, 52.
22. M. Kohout and A. Savin, Influence of core–valence separation of electron localization function, J. Comput. Chem., 1997, 18, 1431–1439.
23. P. Jena and Q. Sun, Super Atomic Clusters: Design Rules and Potential for Building Blocks of Materials, Chem. Rev., 2018, 118, 5755–5870.
24. M. Zhong, H. Fang and P. Jena, Record-high stability and compactness of multiply-charged clusters aided by selected terminal groups, Phys. Chem. Chem. Phys., 2020, 22, 4880.
25. A. D. Becke, Density–functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652.
26. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
27. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford CT, 2016.
28. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
29. G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50.
30. R. Dronskowski and P. E. Bloechl, Crystal orbital Hamilton populations (COHP): energy-resolved visualization of chemical bonding in solids based on density-functional calculations, J. Phys. Chem., 1993, 97, 8617–8624.
31. S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, LOBSTER: A tool to extract chemical bonding from plane-wave based DFT, J. Comput. Chem., 2016, 37, 1030–1035.
32. M. Esser, A. A. Esser, D. M. Proserpio and R. Dronskowski, Bonding analyses of unconventional carbon allotropes, Carbon, 2017, 123, 154–162.
33. T. Schwabe and S. Grimme, Double-hybrid density functionals with long-range dispersion corrections: higher accuracy and extended applicability, Phys. Chem. Chem. Phys., 2007, 9, 3397.
34. J. Sun, et al., Accurate first-principles structures and energies of diversely bonded systems from an efficient density functional, Nat. Chem., 2016, 8, 831.
35. P. Su and H. Li, Energy decomposition analysis of covalent bonds and intermolecular interactions, J. Chem. Phys., 2009, 131, 014102.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d1nr02816b

---