Open Access Article
Open Access ArticleCorrelating in situ RHEED and XRD to study growth dynamics of polytypism in nanowires†
Julian
Jakob
 *ab,
Philipp
Schroth
abc,
Ludwig
Feigl
b,
Mahmoud
Al Humaidi
ac,
Ali
Al Hassan
*ab,
Philipp
Schroth
abc,
Ludwig
Feigl
b,
Mahmoud
Al Humaidi
ac,
Ali
Al Hassan
 bc,
Arman
Davtyan
bc,
Arman
Davtyan
 c,
Daniel
Hauck
c,
Daniel
Hauck
 b,
Ullrich
Pietsch
c and
Tilo
Baumbach
ab
b,
Ullrich
Pietsch
c and
Tilo
Baumbach
ab
aLaboratory for Applications of Synchrotron Radiation, Karlsruhe Institute of Technology, Kaiserstraße 12, D-76131 Karlsruhe, Germany. E-mail: julian.jakob@kit.edu
bInstitute for Photon Science and Synchrotron Radiation, Karlsruhe Institute of Technology, Hermann-von-Helmholtz-Platz 1, D-76344 Eggenstein-Leopoldshafen, Germany
cSolid State Physics, Emmy-Noether Campus, Walter-Flex Straße 3, D-57068 Siegen, Germany
First published on 19th July 2021
Abstract
Design of novel nanowire (NW) based semiconductor devices requires deep understanding and technological control of NW growth. Therefore, quantitative feedback over the structure evolution of the NW ensemble during growth is highly desirable. We analyse and compare the methodical potential of reflection high-energy electron diffraction (RHEED) and X-ray diffraction reciprocal space imaging (XRD) for in situ growth characterization during molecular-beam epitaxy (MBE). Simultaneously recorded in situ RHEED and in situ XRD intensities show strongly differing temporal behaviour and provide evidence of the highly complementary information value of both diffraction techniques. Exploiting the complementarity by a correlative data analysis presently offers the most comprehensive experimental access to the growth dynamics of statistical NW ensembles under standard MBE growth conditions. In particular, the combination of RHEED and XRD allows for translating quantitatively the time-resolved information into a height-resolved information on the crystalline structure without a priori assumptions on the growth model. Furthermore, we demonstrate, how careful analysis of in situ RHEED if supported by ex situ XRD and scanning electron microscopy (SEM), all usually available at conventional MBE laboratories, can also provide highly quantitative feedback on polytypism during growth allowing validation of current vapour–liquid–solid (VLS) growth models.
1. Introduction
In recent years improved control over the growth of self-catalysed III–V nanowires on Si has led to substantial progress, which is mainly driven by the promise of the integration of III–V semiconductors on the cost-effective Si platform.1–8 The integration of these dissimilar material systems is possible due to the small footprint of NWs, facilitating an epitaxial connection. NWs grown in the vapour–liquid–solid (VLS) mode9 by metalorganic vapor-phase epitaxy (MOVPE) or MBE should avoid foreign elements such as Au as catalyst particles, because of the possibility of incorporation in the growing NWs.10 In contrast, the self-catalysed or Ga-assisted growth11,12 in case of GaAs NWs ensures fabrication without any risk of this possible contamination. For the growth of self-catalysed GaAs NWs, progress was achieved in control of NW yield,2,4,6 shape3,4,7 and density,3,6,7 as well as in the crystal structure.1,2,5,8 However, those studies have also shown that these properties cannot be optimized separately via growth parameters. Moreover, an increase in the number density of NWs is accompanied by changing NW diameters3,13 and/or crystal structure.14 The reason is inherent in the VLS growth mode, more precisely in the liquid catalyst particle, which is responsible for the axial growth of the NWs and directly determines the NW morphology,15–20 such as the shape and the crystal structure. Self-catalysed GaAs NWs adopt mainly the cubic zinc blende (ZB), its rotational twin (TZB), and the hexagonal wurtzite (WZ) crystal structure. Their simultaneous occurrence is called polytypism. Good control over the droplet itself enables the realization of dedicated NW morphologies, e.g. tapered NW shape,21 or the fabrication of axial heterostructures formed of different polytypes along the NW growth axis22,23 allowing exploitation of their band structure differences.24,25Powerful techniques allowing in situ characterization during growth can serve as a key to understand and optimize the morphological properties of NWs. Within the available portfolio of in situ techniques, in situ transmission electron microscopy (TEM) during NW growth offers unrivalled spatial resolution down to the atomic scale, together with high temporal resolution, but it is restricted to special equipment not broadly available.20,26–29 The investigations are typically performed with pre-grown NWs26,27 or NWs without epitaxial connection to any substrate,20,28,29 therefore excluding a number of growth effects under standard conditions, e.g. the impact of diffusion processes on the substrate as well as material flux shadowing by the NW ensemble.30
In situ XRD during growth21,31–34 probes the evolution of representative structure properties averaged over a large statistical NW ensemble. By using microfocused beams, even the properties of individual NWs can be in situ examined.35 In both cases, NW growth close to standard growth conditions with epitaxial connection to the substrate can be monitored. However, special growth chambers equipped with X-ray windows are required as well as access to heavy-duty diffractometers at high-flux synchrotron light sources.
In situ RHEED equipment, in contrast to TEM and XRD, is usually already integrated into commercial MBE systems and therefore broadly available. However, although RHEED has gained great importance for quantitative 2D layer growth studies, in case of NW growth, RHEED has mostly been restricted to qualitative conclusions.23,36–41 Only recently, a quantitative evaluation procedure for in situ RHEED studies of NWs has been developed.42 Based on a two beam approximation for dynamical Laue diffraction and taking shadowing effects within the NW ensembles into account, RHEED has been used for a time-resolved height-selective crystal phase analysis during NW growth. Similar to in situ XRD, it allowed representative quantitative information to be gained for large NW ensembles with several thousands NWs, but this required a priori assumptions considering the overall growth dynamics.
In the present article we report a correlative approach to measure RHEED and XRD of NW ensembles, aiming to provide a methodical base for comprehensive studies addressing the dynamics of NW growth under standard MBE conditions. Such studies of large NW ensembles have the potential to complement high-resolution growth studies of single NWs by in situ TEM. By simultaneously measuring in situ XRD and RHEED we prove the consistency of the results from both methods and demonstrate how to exploit their complementary characteristics. We experimentally determine the axial and radial growth rates and the development of the polytype crystal phase fractions as a function of time and, finally, of NW height, without the need of a priori information or any growth model. Since in situ XRD is not broadly available, we also describe the methodical potential of in situ RHEED, if supported by ex situ XRD and SEM. We demonstrated this exemplarily by studying a small sample series allowing us to experimentally validate the predicted relation of Ga droplet contact angles and the crystal phase of GaAs NW segments, recently confirmed for single NWs by an electron microscopy study,20 for the case of large NW ensembles grown by standard MBE.
2. In situ RHEED and XRD by NW ensembles
In this section we compare the main principles of the underlying analysis of the in situ RHEED and XRD intensities from statistical NW ensembles. The time dependent intensity integrated over a RHEED spot or respectively a XRD reciprocal space map of a chosen reciprocal lattice point gh,k,l, corresponding to a certain crystal phase indexed by p, can formally be described by the expression | (1) |
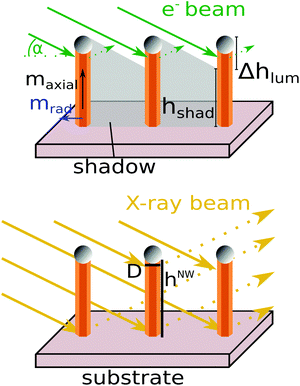
Here, ρNW is the NW number density per unit area, Ag,p represents the scattering power, which is proportional to the magnitude or the square of the magnitude of the structure factor, depending on the validity of the kinematic or dynamic diffraction theory. The NW phase fraction is represented by fp and Ωg takes into account the influence of the NW diameter D and actual shape (the NW cross-section), and its orientation with respect to the incident beam on the NW diffraction and absorption. The illumination efficiency γ(h,t) takes NW ensemble-shadowing effects into account, which, in the case of strong absorption or extinction, have a significant influence on the diffracted intensity.42 All functions within the integral are strongly affected by the growth dynamics and are, therefore, functions of the NW height hNW and growth time t.
For X-ray diffraction, the small ratio of NW diameters (D < 200 nm) compared to extinction and absorption lengths of dynamical X-ray diffraction (both in the range of several μm) justifies the validity of the kinematical diffraction theory. For the same reason, NW shadowing effects on the illumination efficiency are negligible (γ(h,t) ≈ 1) and can therefore be omitted, as illustrated in Fig. 1. Consequently, the integrated intensity of eqn (1) for a phase-sensitive reciprocal lattice point (RLP) can be written as
 | (2) |
It is proportional to the product of the square magnitude of the structure factor, Ag,p ∝ |Fg,p|2 and to the total crystal-phase volume of the illuminated NW ensemble VNWp(t):
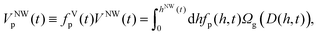 | (3) |
For RHEED, the much shorter electron extinction and absorption lengths compared to X-ray diffraction require the application of dynamical diffraction theory and give rise to self-shadowing phenomena within the individual NWs and ensemble-shadowing between different NWs42 (see also Fig. 1). In eqn (1), the effective scattering cross section Ωg(h,t), which describes the contribution of an infinitesimal horizontal NW slice at height h and time t, to the integrated diffraction intensity of a RLP, takes the self-shadowing into account. It causes attenuation of the forward-transmitted and diffracted-transmitted wave field amplitudes during propagation in the NWs. Therefore, Ωg(D(h,t),Λ), becomes a function of the effective attenuation coefficient Λ, the diameter D and the geometrical shape of the NW cross-section, and of the azimuthal orientation of the NW shape with respect to the electron beam (details in ref. 42).
Further ensemble-shadowing has to be considered, since a growing NW of height hNW(t) casts a growing shadow hshad on a neighbouring NW in its geometrical beam path, in dependence of their mutual positions. By performing averaging over the whole illuminated NW ensemble, we obtain the corresponding mean values, 〈D〉(t), 〈hNW〉(t), and 〈hshad〉(t), respectively.
Depending on the angle of incidence α of the electron beam with respect to the substrate surface, there always remains an illuminated upper part of the NWs beneath the NW apex. This illumination window contains the axial growth front, which therefore is the main contributor to the RHEED diffraction process. However, particularly for randomly positioned NWs the illumination window is not sharp. The ensemble-averaged shadowing is more precisely described by the illumination efficiency function γ(h,t), varying from the NW tip down to the base from maximally complete illumination (γ(h,t) = 1) to maximally complete shadowing (γ(h,t) = 0). Its temporal evolution can be calculated, in some cases, analytically or otherwise numerically, e.g., by use of the Monte Carlo method. Roughly speaking, absorption/extinction mainly changes the mean ‘illumination strength’ of the total diffracting volume of the NW ensemble, and can be considered by introducing effective quantities describing the ensemble averaged illumination height 〈Δhlum〉(t), illumination volume 〈Vlum〉(t), and the mean illuminated NW crystal-phase volume 〈Vlump〉(t),
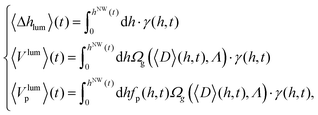 | (4) |
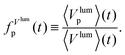 | (5) |
Based on the above considerations, the integrated RHEED diffraction signal of a given phase-sensitive reciprocal lattice point gh,k,l in eqn (1) can be estimated by a formally similar expression as eqn (2),
 | (6) |
From the two eqn (2) and (6) we can easily derive the main similarities and differences of the temporal evolution of the XRD and RHEED signals: the temporal dynamics of the phase-selective XRD and RHEED signals reflect the dynamics of the related effective illuminated crystal-phase volumes, which in case of XRD corresponds to the total NW crystal-phase volume 〈VNWp〉(t), in case of RHEED to 〈Vlump〉(t), respectively,
 | (7) |
In the following we will always abbreviate the rate of change of a physical quantity by the ‘physical quantity rate’. The total intensity rate of the summed up contributions of the different phases-sensitive reflections of XRD and RHEED follows as
 | (8) |
 , whereby for XRD the υNW(t),VNW(t) and for RHEED υlum(t),Vlum(t) must be used.
, whereby for XRD the υNW(t),VNW(t) and for RHEED υlum(t),Vlum(t) must be used.
For XRD, the total sum over the structure factor-calibrated and further parasitic crystallite growth corrected intensities Ĩg,p(t) of the phase-sensitive reflections is always proportional to the whole NW crystal volume,  . Details of the XRD intensity correction for the crystallites can be found in the ESI.† Its time derivative becomes
. Details of the XRD intensity correction for the crystallites can be found in the ESI.† Its time derivative becomes
 | (9) |
 | (10) |
The factor Π depends on the NW shape and is for hexagonal NWs Π = (3/2)√3 and would be for cylindrical NWs Π = π.
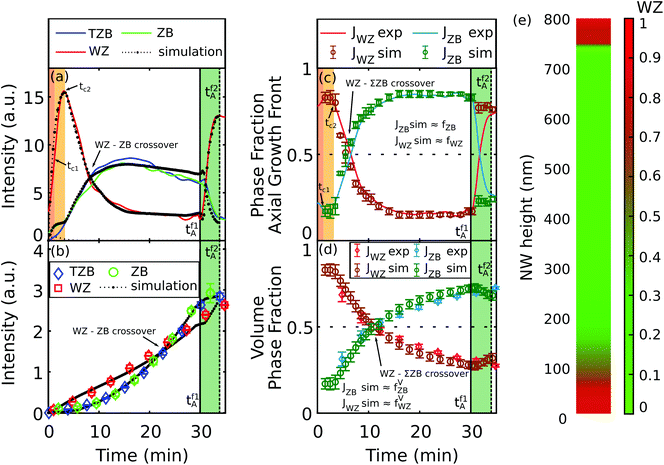
For purely axial growth the total NW volume rate is proportional to the square of the mean initial NW nucleation diameter 〈D0〉 and the axial NW growth rate maxial(t) at a given time. The total intensity increases linearly with the NW height  (and for constant axial growth rate, assumed in Fig. 2(a), also linearly with time). For pure and constant radial facet growth, the total intensity and volume rates are a function of the initial NW diameter after nucleation and the temporal evolution of the radial growth rate
(and for constant axial growth rate, assumed in Fig. 2(a), also linearly with time). For pure and constant radial facet growth, the total intensity and volume rates are a function of the initial NW diameter after nucleation and the temporal evolution of the radial growth rate  . For constant radial growth rates, the total volume and intensity rates will increase linearly with time and, consequently, the volume and intensity themselves develop quadratically with time (Fig. 2(b)). Supposing simultaneous radial and axial growth, but stationary growth conditions (with temporally constant axial and radial growth rates), we obtain the time dependence of the intensity and volume rates given in the third line of eqn (10), where 〈D0〉 should be the mean initial NW base diameter at starting axial growth time (Fig. 2(c)).
. For constant radial growth rates, the total volume and intensity rates will increase linearly with time and, consequently, the volume and intensity themselves develop quadratically with time (Fig. 2(b)). Supposing simultaneous radial and axial growth, but stationary growth conditions (with temporally constant axial and radial growth rates), we obtain the time dependence of the intensity and volume rates given in the third line of eqn (10), where 〈D0〉 should be the mean initial NW base diameter at starting axial growth time (Fig. 2(c)).
Substituting VNW by Vlum, eqn (7) holds formally for XRD and RHEED. However, the total RHEED intensity rate measures the illuminated volume rate  instead υNW. Therefore, eqn (10) cannot be applied to RHEED. But studying carefully the influence of self-shadowing and ensemble-shadowing on the evolution of Vlum one can immediately derive characteristic features of the RHEED intensities:
instead υNW. Therefore, eqn (10) cannot be applied to RHEED. But studying carefully the influence of self-shadowing and ensemble-shadowing on the evolution of Vlum one can immediately derive characteristic features of the RHEED intensities:
In case of purely axial growth, as shown in Fig. 2(d), in the very early growth stage till a first critical time, 0 < t < tc1, the RHEED intensity rate corresponds directly to the axial growth rate maxial(t), and for stationary axial growth the RHEED signal will linearly increase, similar to XRD (highlighted in orange). At this stage, the ensemble-shadowing plays little or no role, and, therefore, the mean illumination height 〈Δhlum〉(t) is equal to hNW(t). Thanks to its high sensitivity to small crystal volumes RHEED shows a much better signal-to-noise ratio (SNR) than XRD. At tc1, when the shadow footprint reaches the first NW neighbours, ensemble-shadowing begins. From this time, the illumination efficiency of the NW ensemble at the NW bottom drops from γ(h = 0,t ≤ tc1) = 1, down to γ(h = 0,t ≥ tc2) = 0, when all shadow footprints reached the NW neighbours at tc2. Consequently, in the time interval tc1 < t < tc2 (highlighted in yellow), the prior linear increase of 〈Δhlum〉(t) and, accordingly of the RHEED signal, diminishes, converging until tc2 to saturation values 〈Δhlum〉 (tc2) and IEDg,p(tc2), and stay constant during further growth t > tc2. In other words, if above t > tc1 the NW volume VNW continues increasing, the shadowed NW volume starts increasing too and consequently the increase of Vlum appears much more moderate and will come to a halt at t ≥ tc2. Accordingly, for the evolution of the illuminated-volume rate during axial growth we find
 | (11) |
Above tc2, the height of the illuminated window of fulfilled condition γ(h,t > tc2) > 0 is stationary in time, but the illuminated window moves upwards during NW growth, at a rate given by the axial growth rate (dγ/dt = maxialdγ/dh). The total RHEED signal saturates and thus becomes completely insensitive to the future evolution of the axial growth rate maxial.
During purely radial growth, the temporal evolution of RHEED behaves as illustrated in Fig. 2(e): for thin wires with D < Λ RHEED is sensitive to mradial. The NW volume increases quadratically, but self-shadowing increases nearly exponentially with growing NW diameter. Both have opposite and therefore competing influences on the dynamics of the RHEED signal. Effectively, for very thin wires, initially the diffraction signal increases, but very quickly flattens out, the signal passes through a maximum and later even decreases to the extent the self-shadowing reduces the illuminated volume Vlum. Finally, sufficiently beyond NW diameters (D ≈ 2Λ), the RHEED signal converges to a stationary intensity value. This means that during radial growth the RHEED signal becomes increasingly insensitive to radial growth rates. For certain azimuthal orientations the RHEED signal may nearly completely disappear, although radial and axial growth may continue (ref. 42). Therefore, a favourable choice of the azimuthal orientation of the NWs in the electron beam is crucial.
For simultaneous radial and axial growth (Fig. 2(f)), the mean initial NW diameter 〈D0〉 and the ratio of radial and axial growth determine the dynamics of RHEED, up to the growth stages when the dynamics of the illuminated volume Vlum and RHEED start to behave completely stationary. However, in contrast to XRD, the RHEED signal can behave stationary even in the presence of ongoing NW growth. Therefore to allow correct interpretation of the RHEED signal and to enable quantitative data evaluation of the whole growth cycle, it is imperative that shadowing effects are taken into account. For growth stages where the influence of axial and radial growth on the RHEED signal is negligible (which does not mean that radial and axial growth itself must be negligible!), the RHEED signal becomes nearly exclusively sensitive to changes of the crystal phase partitioning (the polytypism) within Vlum. For narrow positional NW distributions, the time interval tc1 < t < tc2 decreases. For given positional NW distribution, both the critical times tc1 and tc2 decrease with increasing NW density, and the height of the NW illumination window 〈Δhlum(tc2)〉 shrinks. All those effects are improving the height selectivity of in situ RHEED experiments. But it should be noted that based on the outlined theoretical approach, the RHEED signal, quantitatively evaluated by eqn (6), allows determination the mean height evolution of polytypism also for diluted NW ensembles. All these factors make RHEED an eminently suitable method for quantitative polytypism studies.
For the investigation of polytypism it is useful to determine for both RHEED and XRD the respective intensity ratio Jp(t) of phase-sensitive RLPs with respect to the structure factor corrected sum over all RLPs,
 | (12) |
For XRD it follows from eqn (2) that JXRDp(t) is a direct measure for the phase volume fraction fVp(t), and consequently it is
 | (13) |
Even if the sensitivity of RHEED to any growth rate is more complicated, similarly to XRD the phase sensitive RHEED intensity ratio always directly corresponds to the phase fraction of the illuminated volume  . In the absence of tapering effects one gets
. In the absence of tapering effects one gets
 | (14) |
 | (15) |
Considering a high NW number density resulting in a small illumination height 〈Δhlum〉, the phase sensitive intensity ratio corresponds nearly directly to the mean phase fraction at the NW apex, or alternatively the rate of the phase-sensitive intensity ratio  corresponds nearly directly to the ensemble averaged crystal phase nucleation rate at the axial growth front. Determining the axial growth rate from XRD, we can transform the time dependence of JEDp(t) by eqn (15) into a height dependence of fp(h,tf).
corresponds nearly directly to the ensemble averaged crystal phase nucleation rate at the axial growth front. Determining the axial growth rate from XRD, we can transform the time dependence of JEDp(t) by eqn (15) into a height dependence of fp(h,tf).
At this point we summarize that due to electron shadowing in situ RHEED height-selectively probes rather the upper part of the growing NWs. However in situ XRD always probes the full NW height, including the electron shadowed parts of RHEED, and thus can detect processes inside that shadow not visible for RHEED. Therefore, in situ XRD is characterized by a high sensitivity to the temporal evolution of volume growth rates, which, however, are simultaneously influenced by all, axial and radial (tapering and side-facet) growth rates as a result of both VLS and VS (vapour–solid) growth contribution. In contrast, RHEED exhibits particular, well suited properties in favour of VLS growth characterization, since ensemble-shadowing causes height-selectivity making this diffraction technique sensitive to the crystalline properties of the NW tip below the NW apex, and their temporal evolution. For sufficiently high NW number densities, RHEED analysis becomes highly sensitive to determine transitions in the generation probability of crystal phases at the axial growth front below the droplet. Such sensitivity to the phase purity of large NW ensembles could open a route to gain immediate feedback and good experimental control over the actual impact of the catalyst particles and therefore over the whole VLS growth process.23 Moreover, the comparably large scattering cross section of electrons in solids creates high sensitivity to small volumes, which becomes particularly important for the crystal structure analysis during NW nucleation and early growth stages.
A correlative XRD and RHEED analysis allows differentiation between axial and radial growth contributions and conclusions on the temporal evolution of VS growth of the NW side facets and of the VLS growth at the apex separately, without a priori assumptions about the growth rates and growth models. It thereby also improves the accuracy of the results compared to those of the respective individual methods. Complemented by post growth ex situ SEM, all methods together can generate a comprehensive quantitative experimental picture of the growth dynamics of the NW ensemble under chosen standard MBE growth conditions.
3. Experimental
The growth experiments on self-catalysed GaAs NWs were performed with a MBE growth chamber equipped with a RHEED gun and additional X-ray-transparent Be windows, and designed to be compatible to standard heavy duty diffractometers at high-flux synchrotron beamlines.43 In the first experiment, we measured the evolution of RHEED and XRD intensity patterns simultaneously in situ during NW growth. Here we will compare and combine their results from a methodical point of view, demonstrating both their complementarity and consistency. Applying the methodical results, in a second purely laboratory-based study of in situ RHEED, supported by ex situ XRD and SEM, we demonstrate, how careful correlative analysis can also provide a highly quantitative feedback on temporal polytypism behaviour during growth. In particular, we aim to quantitatively verify the variation of polytype over time as a function of the wetting angle of the gallium droplet at the onset of growth for the case of large NW ensembles grown under standard MBE conditions. It will be compared to the theoretically model predicted in ref. 44 and experimentally shown at a single NW in an environmental TEM in ref. 20.The self-catalysed GaAs NWs were grown with a Ga predepositon step on n-type Si(111) substrates covered with native oxide. For the first simultaneous in situ RHEED and in situ XRD experiment (sample A), we stopped the Ga supply after tf1A = 30 min, but continued measurements till tf2A while the As4 flux was kept constant to consume the liquid Ga droplet at the tip of the NWs.
For the second experiment, we grew a set of five samples (samples B–F) under identical conditions, but interrupted the growth at different, subsequent growth times: sample B where the in situ RHEED signal of WZ emerged (tB = 0.5 min, hNWB = 18 nm), sample C where it reached its maximum (tC = 2.5 min, hNWC = 66 nm), sample D, when it dropped (tD = 5 min, hNWD = 140 nm), sample E where it reached the minimum plateau (tE = 20 min, hNWE = 560 nm), and sample F after it stayed at the minimum plateau till the final growth time and height (tF = 30 min, hNWF = 830 nm). For samples B–F we always stopped both fluxes (Ga and As4) simultaneously and immediately ramped down the substrate temperature (in order to maintain the wetting conditions as best as possible) before characterizing the samples with ex situ XRD and SEM. Combining RHEED, XRD and SEM, the samples series B–F and their respective time series tB–tF allow to conclude on the temporal evolution of NW growth during the early growth stage, but now without the need of a dedicated X-ray compatible growth chamber. Details about the NW growth conditions are in the ESI.†
4. Results and discussion
4.1. Characterization of NW growth
Post-growth SEM analysis for sample A (see Fig. 4(b) in the ESI†) gives evidence for non-tapered NWs with identical final diameter at the bottom and the tip of 〈DNWf,b〉 = 〈DNWf,t〉 = (54 ± 4) nm and a final mean height of 〈hNWA〉 = (800 ± 160) nm. Fig. 3(a) depicts close up images of the three phase sensitive ZB(311), TZB(220) and WZ(10.3) RHEED spots of sample A for four different growth times, demonstrating the large possible temporal variations of RHEED intensity patterns even during stable global growth conditions. Their structure factor calibrated temporal intensity evolution ĨNWp(t) is plotted in Fig. 3(b). Fig. 3(c) shows a typical XRD reciprocal space map (RSM) with the Si(311) Bragg reflection of the substrate and the three phase sensitive GaAs ZB(311), TZB(220) and WZ(10.3) reflections of the NWs. The GaAs Bragg reflections have identical lateral scattering vector components, but are vertically well separated. They are connected by a vertical streak along Qz (parallel to the axial growth direction), arising from the diffuse scattering of stacking faults. Further, in each reflection we observe horizontal facet streaks along Qy originating from the hexagonal cross section of the NWs. They are perpendicular to the growth axis and to two of six facet planes, respectively. The third type of inclined streaks cross the Bragg peaks perpendicular to the reciprocal lattice vectors (along the virtual Debye–Scherrer-rings). These streaks mainly represent a slight orientation distribution of parasitic crystallites (CRY) and NWs, and allow separation of their contributions (as shown in ref. 21). The temporal evolution of the structure factor calibrated XRD integrated intensities ĨNWp(t) is plotted in Fig. 3(e).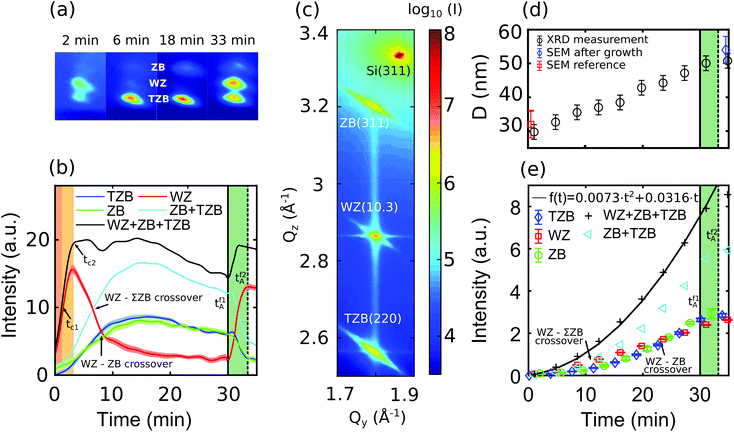 | ||
| Fig. 3 Sample A: (a) RHEED camera frames at different growth times show strong variation of the phase-selective diffraction spot intensities, (b) temporal evolution of structure factor calibrated phase-selective RHEED spot intensities, the sum of the ZB and TZB phases ΣZB and the overall intensity. (c) XRD RSM of the asymmetric truncation rod after growth including the Si(311) reflection of the substrate and the three separated reflections of GaAs ZB(311), TZB(220) and WZ(10.3). (d) Temporal evolution of the mean diameter of the NW ensemble determined by evaluating the size oscillations along Qy originating from the hexagonal cross section of the NWs (see the ESI†). (e) Temporal evolution of phase-sensitive Bragg reflection intensities Ĩp(t). The ΣZB intensity and the overall RHEED intensity evolution are a non-linear function as shown by the polynomial fit. | ||
Following eqn (10), the measured non-linear increase of the total X-ray intensity during the first 30 min gives clear evidence for simultaneous axial and radial growth. Since no tapering has been observed by SEM, the NW diameter averaged over the NW height can be estimated from the size oscillations measured along the facet streaks.21 Their temporal evolution contain information on the NWs radial growth dynamics, which is presented by the results in Fig. 3(d) (details are presented in the ESI†). Additionally, we show the final diameter measured by SEM after growth (in blue) and the initial diameter measured at a reference sample grown under identical growth conditions. From the temporal development of the size oscillations and of the total XRD intensity we determine an initial NW nucleation diameter of D0 ≈ 28 nm. The in situ XRD data give clear evidence for the axial and radial growth rates staying approximately constant during the growth, up to the closure of the Ga-shutter. We determine the axial growth rate of maxial = 26.6 nm min−1 and a (much smaller) radial growth rate of mradial ≈ 0.43 nm min−1.
With only the As shutter left open, the total XRD intensity at t > 30 min continues increasing before coming to an end at about tf2A = 33.5 min. The observed kinks of the XRD intensity curves at tf1A indicate the expiring radial growth. Between (tf1A < t < tf2A) we observe an intensity and volume increase of approximately 10%, which can be related to the continuation of axial growth. Above tf2A = 33.5 min the XRD intensity becomes effectively constant (compare the ESI†), indicating the stop of any NW growth after complete droplet consumption, as proven by SEM. The findings confirm the expectation that the VLS growth can continue under remaining As flux by successively consuming the Ga droplet.
We evaluate the experimental results applying eqn (2), (6) and (12) based on identical morphological parameter sets for the temporal evolution of RHEED and XRD. First we determine the general shape parameters based on which we will evaluate the quantitative evolution of different crystal phases, presented in the following section.
Prior to the intensity simulation we can restrict the input parameter space by the post-growth SEM results of the final state of the NW and CRY sizes, heights and shapes. In particular, we extract ensemble averaged, post-growth base and top diameters of the NWs and CRY, as well as their mean fluctuation, and in addition the number densities of the NW and CRY ensembles (all tabulated in the ESI†). The attenuation length of the 20 keV RHEED electrons in the GaAs NWs is Λ ≈ 12 nm (ref. 42), defining the self-shadowing behaviour of individual NWs. The NW number density of sample A, ρNW = (8.4 ± 2) μm−2, and the low electron incidence angle of α = 1° define the ensemble-shadowing and the related average height selectivity of the RHEED measurements for this sample to approximately 〈Δhlum〉 = 20 nm. For 15 keV X-ray photons with Λ ≈ 20.27 μm,45 the effects are absolutely negligible.
The comparison between the measured and best fitting simulated RHEED and XRD intensity evolution for the respective phase-sensitive reflections curves in Fig. 4(a) and (b) allow quantitative determination of the dynamics of the volume phase fractions of the NWs and the phase fractions at their axial growth front (Fig. 4(c) and (d)). Details of the calculation are summarized in Table 1 in the ESI.†
4.2. Characterization of polytypism
Following section 2, the phase-sensitive XRD reflections allow monitoring the temporal development of the different crystal-phase volumes integrated over the NWs, whereas the RHEED reflections allow detecting the phase changes particularly near the axial growth front.Comparing the phase sensitive XRD intensities in Fig. 3(e), the WZ phase crystal volume develops approximately linearly, whereas the zinc blende related intensities develop initially slower, but later benefit from a non-linear increase, with progressing rates till tf1A = 30 min. The WZ–ZB intensity crossover is at about t = 22 min, the WZ–ΣZB crossover already at about t = 12 min, where ΣZB = ZB + TZB. Considering the temporal evolution of the RHEED intensities in Fig. 3(b) we observe at the beginning of growth (0 min < t < 3 min) a dramatically dominating WZ intensity rate. Immediately afterwards, the WZ intensity rapidly drops (3 min < t < 10 min), later the downturn diminishes and intensity becomes effectively constant between (15 min < t < 30 min = tf1A). The two zinc blende related ZB and TZB intensity curves develop always similar one to another. Compared to WZ, the corresponding ΣZB curve in Fig. 3(b) starts growing with a short delay and a less strong intensity rate. Both, ΣZB and WZ intensity curves intersect at about t ≈ 7 min. Then the zinc blende phases start dominating the intensity distribution, but their intensity rate slows down, passes at t ≈ 15 min its maximum value and decreases afterwards slowly till the end of Ga supply (tf1A = 30 min). At this point, at tf1A, the WZ intensity again begins to strongly increase. Almost simultaneously also all zinc blende related curves show a very short rise before rapidly decreasing. Considering the overall development of the total RHEED intensity, in this time interval it also increases abruptly at tf1A = 30 min till about tf2A = 33.5 min.
From the previous sections we have seen that RHEED has a particularly high sensitivity for phase changes at the axial growth front. As discussed in section 2, the total RHEED intensity develops proportionally to the illuminated volume Vlum. At the very beginning of growth, the illuminated related volume rate υlum(t) is therefore sensitive to the axial growth rate, whereby the phase selective illuminated volume rates υlump(t) are additionally weighted by the illuminated volume phase fractions. The high NW number density of sample A causes efficient ensemble-shadowing. As can be shown by Monte Carlo simulations, in sample A the process of ensemble-shadowing starts already after t > tc1 ≈ 1 min (marked in orange in Fig. 3(b)). Within the short time interval of two more growth minutes (tc1 < t < tc2, marked in yellow) the initially high sensitivity of the illuminated-volume rate υlum(t) of RHEED to the axial growth rate rapidly diminished. At about tc2 ≈ 3 min the illumination height has become stationary (〈Δhlum〉(t > tc2) = Δhlum(tc2)) and, consequently, the total RHEED signal has already completely lost its sensitivity to any further volume increase if generated by axial VLS growth, see eqn (11). The further intensity increase is related to radial growth. Changing ratios of phase-sensitive RHEED signals can be directly attributed to changes of the corresponding phase fractions of that part of growing material, which is located in the now stationary illumination window 〈Δhlum〉(t > tc2) = const below the NW tip. The speed of this relative vertical window-move follows from the axial growth rate maxial(t) (eqn (15)).
The drastic decrease of the WZ phase related RHEED intensity in the time following tc2 can be explained by the concurrence of two effects: (a) a change in the nucleation probability from WZ to ΣZB, as seen by the increase of the overall zinc blende-related phase-volume fraction in the phase sensitive XRD intensities; (b) the particular sensitivity of RHEED to phase changes at the axial growth front, which at this growth stage develop in favor of ΣZB.
In other words, if the change of the ΣZB related phase volume rate observed in the X-ray data arose exclusively from the changing phase generation probability at the axial growth front from WZ-rich towards ΣZB-rich growth, then, for the case of RHEED, the previously grown WZ-rich region (at the NW base) would move with time outside the rising electron illumination window 〈Δhlum〉 into the shadowed region underneath.
Since above tc2 the width of the illumination height window stays constant for a given NW number density (〈Δhlum〉(t > tc2) = const), for hypothetical purely axial growth, any increase of the ΣZB intensity above tc2,A ≈ 3 min would be at the full expense of the WZ signal and lead to the opposite development of the WZ intensity rates as observed between 3 min < t < 9 min. Here it should be noticed that simultaneous negative rates of both WZ and ΣZB RHEED signals are also possible, as has been observed in the middle growth stages (10 min < t < 30 min), but this can only arise either as a result of radial growth, a hypothetical change of the droplet height (influencing ensemble-shadowing, see tf1A = 30 min), or due to variation in the incident electron flux. Concerning the radial growth contributions it can be shown that the competition of positive volume rate and negative influence of self-shadowing damps the increase of RHEED intensity, and above a critical NW diameter of D ≈ 30 nm even leads to negative intensity rates. Contrary to RHEED, radial growth always contributes to positive XRD intensity rates. The measured total X-ray intensity rates confirm rather stationary overall growth conditions between 10 min < t < 30 min, whereby the NW nucleation diameter and radial growth rate obtained from X-ray analysis explain the simultaneous moderate reduction of the overall RHEED signal in this stage. The observed superimposed slight waviness is caused by instabilities of RHEED flux provoked by the less shielded beamline infrastructure and not related to the NW growth (see the ESI† for detailed discussion). Finally, the well fitting simulated RHEED curves in Fig. 4(a), all calculated with identical parameter sets as for the XRD curves in Fig. 4(b), generally confirm our previous findings. In Fig. 4(c) we show the RHEED intensity fractions JEDWZ of WZ and JEDZB of ΣZB and the phase-generation probabilities at the axial growth front fp ≈ JEDp determined from the simulations. The XRD intensity fractions JXRDp and the corresponding volume phase fractions fVp ≈ JXRDp are plotted in Fig. 4(d). By integrating the time dependent (respectively height dependent) VLS phase generation probability determined by RHEED over the whole preceding growth time (respectively NW height hNW(t)), we are able to compare the results from RHEED directly with those of XRD. Except at the very beginning of growth, where the XRD intensities are low and the SNR weak, and where possibly insufficient crystallite correction of the signals shows a higher impact, the XRD simulation and experiment fit very well. In principle, any phase-volume change observed by XRD or RHEED could be caused (a) by phase transformation within the probed NW volume or (b) by a changing phase generation probabilities at the growth fronts. Hypothetical phase transformations and changes at the radial growth front should induce comparable changes in the corresponding intensity fractions of the involved Bragg reflections. XRD intensity fractions probe the affected total crystal volume of the NW ensemble, their growth rates are therefore sensitive to phase transformations in the whole NW and to changes at both the radial and axial growth front. In contrast, due to the large differences of the radial and axial growth rates the RHEED signal is particularly sensitive to the axial phase generation probability and therefore to the VLS growth conditions at the interface of the Ga-droplet and the NW top facet. The agreement between simulation and simultaneously recorded XRD and RHEED intensity profiles confirms the opinion, which is generally widespread but little untried in the literature that volume phase transformations and phase changes during radial growth is highly improbable.
From the methodical point of view it is very interesting that at (tf1A = 30 min) both the RHEED WZ intensity as well as the total RHEED intensity rise abruptly again. This can only be explained by the increase of the mean illuminated height window 〈Δhlum(t)〉 below the NW tip. For stationary VLS conditions, 〈Δhlum(t)〉 must keep constant for t > tc2. But a growing droplet inevitably leads to a reduction, a shrinking droplet to a proportional increase of the electron illumination window 〈Δhlum(t > tf1A)〉 hitting the NWs (and not the droplets). Therefore, the observed increase of the total RHEED intensity between (tf1A = 30 min and tf2A ≈ 33.5 min) gives clear evidence for consumption of the Ga droplet during this time. Moreover it allows estimation of the Ga consumption rate. The Ga droplet under As flux provides the necessary material to maintain for a little while the axial growth. The XRD signal enables characterization of the remaining axial growth rate. At tf2A, when the Ga reservoir of the droplet has been completely consumed, the overall growth comes to a standstill.
It is interesting that the crossover from WZ to ZB at tf1A is relatively sharp, much sharper than the increase of the illumination height fluctuation in the late NW ensemble, caused by the observed fluctuating NW height (compare Table 1 in the ESI†).
This indicates that the WZ-ZB-transition is not related with the actual height but with the NW growth time (the time of the closure of the Ga-shutter). An increasing NW height fluctuation towards the final stage not considered in the evaluation leads to an increased illumination window compared to the simulation. Consequently, even if the time transition is not influenced, the final axial ZB-fraction might be overestimated and the WZ-fraction underestimated. The determined values are to be taken as an upper/lower limit. That is because the longer NWs of the ensemble have larger illumination windows and therefore illuminate for longer time the phases more distant from the growth front. The longer NWs drag the crystal phases of their past longer in the signal.
Thanks to the high time resolution of RHEED, one can directly compare the phase generation rates of the NW ensemble with the experimental phase related intensity fractions of RHEED. If the axial growth rate is given (in our case it is determined by XRD and confirmed by SEM) and no phase-transformation at the radial facets or in the NW volume occurs (as has been confirmed in our case by combining RHEED and XRD), the strong ensemble shadowing allows direct translation the measured temporal evolution of the phase sensitive RHEED intensity fractions by eqn (15) into the final height profile of the corresponding phase fractions (Fig. 4(e)). Until approximately hNWA = 180 nm, the NW stem consists mainly of WZ (shown in red), followed by fast transition to mainly ZB and TZB (shown in green) until the stop of the Ga flux at a NW height of approximately hNWA = 740 nm and a subsequent WZ rich segment until hNWA = 800 nm.
Concluding, we distinguish two regions during growth with a high WZ generation probability and one with ΣZB rich growth. The generation probabilities of the different polytypes in VLS grown NWs are determined by differences of the liquid catalyst's wetting angle at the NW tip.8,15,18,20,23,46,47 Consequently for both regions the wetting angle of the liquid Ga droplet, acting as catalyst particle, may change dramatically.
The impact of the wetting conditions on the catalyst particle and the geometry of the top facet on the crystal phase selection of self-catalyzed GaAs NWs has been described recently by a model introduced by Panciera et al.,20 where four regions could be identified: (i) ZB nucleation with positive tapering at wetting angle β < βmin = 100°, (ii) WZ nucleation without tapering between βmin and βmax = 125°, (iii) ZB nucleation without tapering in a very narrow regime between 125° and 127° and (iv) ZB nucleation with negative tapering, at larger contact angles.
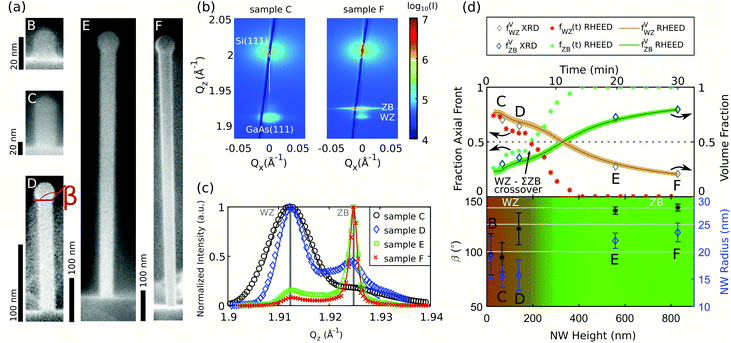
While the explanation of the upper WZ segment is obvious due to the strong droplet variation following the stop of Ga flux and the concomitant consumption of the catalyst on top of the NWs, the explanation of the lower WZ segment needs further investigation. In order to verify the hypothesis of changing wetting angles during the early NW growth stages being responsible for the bottom WZ segment, we study the time series deduced from the samples B–F. Representative SEM images of these samples are depicted in Fig. 5(a), where we can directly observe a trend of the wetting conditions of the liquid droplet to larger angles β over the growth time. Based on the post-growth SEM analysis of samples B–F and the axial growth rate of sample A (confirmed by the measured hNW(tB–tF)), we reconstructed the time-resolved mean polytype distribution from the in situ RHEED experiments combined with the simulations (details of the simulation parameters are listed in Table 1 in the ESI†). To support the results obtained by RHEED, additionally ex situ XRD was measured. In the samples’ XRD reciprocal space maps (two examples are shown in Fig. 5(b) for sample C and F corresponding to tC = 2.5 min, hNWC(tC) = 66 nm and tF = 30 min, hNWF(tF) = 830 nm) we integrated the intensity along Qx and corrected for the background and the crystallite contribution as reported in ref. 34, resulting in the Qz profiles of the NWs GaAs(111) reflection. From these profiles we can determine the volume phase fractions fVp by applying a model based on the stacking sequences of different polytypes created by a Markov chain.34,48 The experimental Qz profiles of each sample, which are corrected for the background and the crystallite contribution, as well as the best fitting results of the Markov simulation model are shown in Fig. 5(c). For the shorter NWs we observe a pronounced signal at the expected WZ position, whereas the longer grown NWs show an opposite trend with the main signal contribution located at the expected ZB position. The resulting volume phase fractions obtained by the Markov model and corresponding to tB–tF are plotted in the upper panel in Fig. 5(d) in dark blue and grey.
The polytype fractions at the axial growth front fp(t) determined by RHEED are depicted in red and light green in the upper panel. By integrating fp(t) along hNW one obtains fVp(t) (in brown and dark green), which is in good agreement with the polytype volume fractions determined by XRD. In the lower panel of Fig. 5(d), we present the mean wetting angle and the mean NW radius of samples B–F. As colour code in the background, the mean height resolved polytype distribution in the NW ensemble is shown.
Growth starts with a high probability of WZ nucleation for the first 200 nm of NW height, the crystal structure stays dominated by WZ. It changes around t = 5 min gradually towards the ZB polytypes. SEM analysis of the samples B–D (tB–tD) shows a constant radius within the fluctuation of the measured NWs. At larger hNW, starting with sample E, negative tapering occurs. The wetting angle β for sample B and C is close to 100° until a NW height of hNWB(tB) = 66 nm, followed by an increase up to a constant value of approximately 140° for the last two samples E and F. At higher β, the crystal structure is ZB with concomitant inverse tapering. These findings are in full agreement with the results presented by Panciera et al.,20 where WZ is expected at wetting angle between 100°–125° and by Dursap et al., where the authors identified also this upper transition angle.23 While Panciera et al. confirmed their model of self-catalysed VLS growth for results obtained during the later stages of nanowire growth in an environmental TEM, our results emphasize its applicability to standard growth conditions in common growth reactors at the onset of NW growth.
5. Conclusions
Studying the reasons for the different temporal evolution of the scattering intensity of in situ XRD and in situ RHEED during growth of statistical NW ensembles allows the targeted use of their complementarity. The former is particularly sensitive to the axial and radial growth rates and the volume fractions of polytypism, the latter to the quantitative nucleation probabilities at the axial growth front. Both are applicable to standard MBE growth conditions.Applying both in situ techniques simultaneously during growth gives a comprehensive quantitative experimental picture of the evolution of growth rates and of polytypism of large NW ensembles. Whereby, thanks to their complementarity, the combined data analysis of both techniques does not require a priori assumptions concerning the particular growth model. It permits the time-dependent evaluation of the growth dynamics and of the evolution of polytypism of the NW ensembles during growth, from which we can also determine the height dependent final state after growth.
Even on its own, in situ RHEED is eminently suitable for quantitative determination of the evolution of the phase fraction of the main polytypes near the axial growth front, if the axial and radial growth dynamics of the ensemble is known. Supported by post-growth ex situ XRD and SEM, the methodical portfolio is sensitive to the phase generation probability defined by the VLS growth, allows access to characterize NW polytypism and to identify and quantify discontinuities of phase purity during the growth process. Assuming the phase fraction of a given height to be known or to be stationary over time, the temporal evolution of the measured phase fractions can be translated into the final height profile of the phase fractions along the NW. The experimental examples quantitatively confirm the relations between the wetting angle and the changes in phase and phase purity expected from the VLS growth model presented in ref. 20, now for the case of large, randomly positioned NW ensembles at the onset of growth.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank B. Krause, A. Weisshardt and S. Stankov for their support at KIT, as well as the INT at KIT for access to the SEM. We acknowledge DESY (Hamburg, Germany), a member of the Helmholtz Association HGF, for the provision of experimental facilities. Parts of this research were carried out at PETRA III and we would like to thank S. Francoual and D. Reuther for assistance in using P09. This work was funded by BMBF project 05K16PSA.References
- P. Krogstrup, R. Popovitz-Biro, E. Johnson, M. H. Madsen, J. Nygård and H. Shtrikman, Nano Lett., 2010, 10, 4475–4482 CrossRef CAS PubMed.
- E. Russo-Averchi, M. Heiss, L. Michelet, P. Krogstrup, J. Nygard, C. Magen, J. R. Morante, E. Uccelli, J. Arbiol and A. Fontcuberta i Morral, Nanoscale, 2012, 4, 1486–1490 RSC.
- F. Matteini, V. G. Dubrovskii, D. Rüffer, G. Tütüncüoğlu, Y. Fontana and A. F. I. Morral, Nanotechnology, 2015, 26, 105603 CrossRef PubMed.
- F. Bastiman, H. Küpers, C. Somaschini and L. Geelhaar, Nanotechnology, 2016, 27, 095601 CrossRef PubMed.
- L. Balaghi, T. Tauchnitz, R. Hübner, L. Bischoff, H. Schneider, M. Helm and E. Dimakis, Nano Lett., 2016, 16, 4032–4039 CrossRef CAS PubMed.
- T. Tauchnitz, T. Nurmamytov, R. Hübner, M. Engler, S. Facsko, H. Schneider, M. Helm and E. Dimakis, Cryst. Growth Des., 2017, 17, 5276–5282 CrossRef CAS.
- H. Küpers, F. Bastiman, E. Luna, C. Somaschini and L. Geelhaar, J. Cryst. Growth, 2017, 459, 43–49 CrossRef.
- M. M. Jansen, P. Perla, M. Kaladzhian, N. von den Driesch, J. Janßen, M. Luysberg, M. I. Lepsa, D. Grützmacher and A. Pawlis, ACS Appl. Nano Mater., 2020, 3, 11037–11047 CrossRef CAS.
- R. S. Wagner and W. C. Ellis, Appl. Phys. Lett., 1964, 4, 89–90 CrossRef CAS.
- M. Bar-Sadan, J. Barthel, H. Shtrikman and L. Houben, Nano Lett., 2012, 12, 2352–2356 CrossRef CAS PubMed.
- A. Fontcuberta i Morral, C. Colombo, G. Abstreiter, J. Arbiol and J. R. Morante, Appl. Phys. Lett., 2008, 92, 063112 CrossRef.
- C. Colombo, D. Spirkoska, M. Frimmer, G. Abstreiter and A. Fontcuberta i Morral, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 155326 CrossRef.
- Y. B. Samsonenko, G. E. Cirlin, A. I. Khrebtov, A. D. Bouravleuv, N. K. Polyakov, V. P. Ulin, V. G. Dubrovskii and P. Werner, Semiconductors, 2011, 45, 431–435 CrossRef CAS.
- P. Schroth, J. Jakob, L. Feigl, S. M. M. Kashani, U. Pietsch and T. Baumbach, MRS Commun., 2018, 8, 871–877 CrossRef CAS.
- P. Krogstrup, S. Curiotto, E. Johnson, M. Aagesen, J. Nygård and D. Chatain, Phys. Rev. Lett., 2011, 106, 125505 CrossRef PubMed.
- D. S. Oliveira, L. H. G. Tizei, D. Ugarte and M. A. Cotta, Nano Lett., 2013, 13, 9–13 CrossRef CAS PubMed.
- V. G. Dubrovskii, G. E. Cirlin, N. V. Sibirev, F. Jabeen, J. C. Harmand and P. Werner, Nano Lett., 2011, 11, 1247–1253 CrossRef CAS PubMed.
- X. Yu, H. Wang, J. Lu, J. Zhao, J. Misuraca, P. Xiong and S. von Molnár, Nano Lett., 2012, 12, 5436–5442 CrossRef CAS PubMed.
- J. Tersoff, Nano Lett., 2015, 15, 6609–6613 CrossRef CAS PubMed.
- F. Panciera, Z. Baraissov, G. Patriarche, V. G. Dubrovskii, F. Glas, L. Travers, U. Mirsaidov and J.-C. Harmand, Nano Lett., 2020, 20, 1669–1675 CrossRef CAS PubMed.
- P. Schroth, J. Jakob, L. Feigl, S. M. Mostafavi Kashani, J. Vogel, J. Strempfer, T. F. Keller, U. Pietsch and T. Baumbach, Nano Lett., 2018, 18, 101–108 CrossRef CAS PubMed.
- T. Rieger, M. I. Lepsa, T. Schäpers and D. Grützmacher, J. Cryst. Growth, 2013, 378, 506–510 CrossRef CAS.
- T. Dursap, M. Vettori, A. Danescu, C. Botella, P. Regreny, G. Patriarche, M. Gendry and J. Penuelas, Nanoscale Adv., 2020, 2, 2127–2134 RSC.
- M. Heiss, S. Conesa-Boj, J. Ren, H.-H. Tseng, A. Gali, A. Rudolph, E. Uccelli, F. Peiró, J. R. Morante, D. Schuh, E. Reiger, E. Kaxiras, J. Arbiol and A. Fontcuberta i Morral, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 045303 CrossRef.
- A. Belabbes, C. Panse, J. Furthmüller and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 075208 CrossRef.
- H. Zheng, J. Wang, J. Y. Huang, J. Wang, Z. Zhang and S. X. Mao, Nano Lett., 2013, 13, 6023–6027 CrossRef CAS PubMed.
- D. Jacobsson, F. Panciera, J. Tersoff, M. C. Reuter, S. Lehmann, S. Hofmann, K. A. Dick and F. M. Ross, Nature, 2016, 531, 317 CrossRef CAS PubMed.
- F. Lenrick, M. Ek, K. Deppert, L. Samuelson and L. Reine Wallenberg, Nano Res., 2014, 7, 1188–1194 CrossRef CAS.
- Z. Zhang, N. Liu, L. Li, J. Su, P.-P. Chen, W. Lu, Y. Gao and J. Zou, Nano Lett., 2018, 18, 6597–6603 CrossRef CAS PubMed.
- P. Schroth, M. Al Humaidi, L. Feigl, J. Jakob, A. Al Hassan, A. Davtyan, H. Küpers, A. Tahraoui, L. Geelhaar, U. Pietsch and T. Baumbach, Nano Lett., 2019, 19, 4263–4271 CrossRef CAS PubMed.
- P. Krogstrup, M. Hannibal Madsen, W. Hu, M. Kozu, Y. Nakata, J. Nygård, M. Takahasi and R. Feidenhans'l, Appl. Phys. Lett., 2012, 100, 093103 CrossRef.
- A. Biermanns, E. Dimakis, A. Davydok, T. Sasaki, L. Geelhaar, M. Takahasi and U. Pietsch, Nano Lett., 2014, 14, 6878–6883 CrossRef CAS PubMed.
- M. Takahasi, M. Kozu, T. Sasaki and W. Hu, Cryst. Growth Des., 2015, 15, 4979–4985 CrossRef CAS.
- P. Schroth, M. Köhl, J.-W. Hornung, E. Dimakis, C. Somaschini, L. Geelhaar, A. Biermanns, S. Bauer, S. Lazarev, U. Pietsch and T. Baumbach, Phys. Rev. Lett., 2015, 114, 055504 CrossRef PubMed.
- S. M. Mostafavi Kashani, D. Kriegner, D. Bahrami, J. Vogel, A. Davtyan, L. Feigl, P. Schroth, J. Jakob, T. Baumbach and U. Pietsch, ACS Appl. Nano Mater., 2019, 2, 689–699 CrossRef CAS.
- S. Breuer, M. Hilse, A. Trampert, L. Geelhaar and H. Riechert, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 075406 CrossRef.
- C. Chéze, L. Geelhaar, A. Trampert and H. Riechert, Appl. Phys. Lett., 2010, 97, 043101 CrossRef.
- D. Rudolph, S. Hertenberger, S. Bolte, W. Paosangthong, D. Spirkoska, M. Döblinger, M. Bichler, J. J. Finley, G. Abstreiter and G. Koblmüller, Nano Lett., 2011, 11, 3848–3854 CrossRef CAS PubMed.
- S. Hertenberger, D. Rudolph, S. Bolte, M. Döblinger, M. Bichler, D. Spirkoska, J. J. Finley, G. Abstreiter and G. Koblmüller, Appl. Phys. Lett., 2011, 98, 123114 CrossRef.
- V. Consonni, M. Hanke, M. Knelangen, L. Geelhaar, A. Trampert and H. Riechert, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 035310 CrossRef.
- J. Jo, Y. Tchoe, G.-C. Yi and M. Kim, Sci. Rep., 2018, 8, 1694 CrossRef PubMed.
- J. Jakob, P. Schroth, L. Feigl, D. Hauck, U. Pietsch and T. Baumbach, Nanoscale, 2020, 12, 5471–5482 RSC.
- T. Slobodskyy, P. Schroth, D. Grigoriev, A. A. Minkevich, D. Z. Hu, D. M. Schaadt and T. Baumbach, Rev. Sci. Instrum., 2012, 83, 105112 CrossRef CAS PubMed.
- V. G. Dubrovskii, Phys. Status Solidi RRL, 2019, 13, 1900301 CrossRef CAS.
- S. A. Stepanov, Advances in Computational Methods for X-Ray and Neutron Optics, 2004, pp. 16–26 Search PubMed.
- V. G. Dubrovskii, Cryst. Growth Des., 2017, 17, 2544–2548 CrossRef CAS.
- W. Kim, V. G. Dubrovskii, J. Vukajlovic-Plestina, G. Tütüncüoglu, L. Francaviglia, L. Güniat, H. Potts, M. Friedl, J.-B. Leran and A. Fontcuberta i Morral, Nano Lett., 2018, 18, 49–57 CrossRef CAS PubMed.
- M. Köhl, P. Schroth and T. Baumbach, J. Synchrotron Radiat., 2016, 23, 487 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/D1NR02320A |
| This journal is © The Royal Society of Chemistry 2021 |