Inverse-designed semiconductor nanocatalysts for targeted CO₂ reduction in water

Abstract

The most commonly used photocatalyst for CO₂ reduction is TiO₂. However, this semiconductor material is far from being ideally suited for this purpose, owing to its inefficient energy harvesting (it absorbs in the UV), low reduction rates (it exhibits short carrier lifetimes), and lack of selectivity with respect to competing reactions (such as the nearly isoenergetic and kinetically more favourable water reduction). In this work we compile a wish-list of properties for the ideal photocatalyst (including high reaction selectivity, availability of multiple redox equivalents at one time, large contact area for CO₂ adsorption with independently tunable band gap, and availability of electrons and holes at different locations on the surface for the two redox reactions to take place), and, using the principles of inverse design, we engineer a semiconductor nanostructure that not only meets all the necessary fundamental criteria to act as a catalyst for CO₂ reduction, but also exhibits all the wish-list properties, as confirmed by our state-of-the-art atomistic semi-empirical pseudopotential modelling. The result is a potentially game-changing material.

---

1. Introduction

The importance of improving air quality in our cities is becoming increasingly clear, not only for obvious environmental reasons and to mitigate the effects of global warming, but also for health concerns as climate change has been shown¹ to directly promote or aggravate respiratory diseases, which, in turn, increase vulnerability to viral infections, such as Covid-19.

Carbon dioxide (CO₂) is the primary greenhouse gas emitted through human activities, accounting for over 80% of all human-related greenhouse gas emissions in 2018 in the US alone, and for over 65% globally,² having increased from about 6.5 billion metric tonnes in 2000 to over 10 in the last decade,³ its main source being the combustion of fossil fuels for transportation and energy.

One of the most promising techniques to decrease environmental CO₂, apart from capture and sequestration, is its photocatalytic reduction. Such process exploits semiconductor materials as catalysts to chemically reduce CO₂, generally in the presence of water. The main products are CH₄, CH₃OH, CO and HCOOH (in order of increasingly negative potential vs. normal hydrogen electrode – NHE). Other products, derived from the C–C coupling reaction, do not exhibit comparable activity and selectivity, because the corresponding reduction reactions are thermodynamically unfavourable^2,3 and consume different numbers of electrons and protons.⁴ The main steps for this reaction to take place are:⁵ (i) light absorption and photogeneration of electron–hole pairs; (ii) carrier migration to the catalyst's surface; (iii) reduction of CO₂ by the electron and oxidation of H₂O (to O₂) by the hole. The efficiency of the CO₂ reduction is therefore determined by the efficiency of the following processes: (i) light harvesting, (ii) charge separation; (iii) surface reaction. Semiconductors are good light absorbers⁶ (i), and, through nanostructuring, their energy bands can be engineered⁷ both to enhance their light harvesting properties⁸ and to correctly match the redox potentials for specific reactions⁵ (iii), e.g., so that their conduction band minimum – CBM – be located above the redox potential for CO₂ reduction, and their valence band maximum – VBM – be below the redox potential for H₂O oxidation.⁵ Furthermore, long carrier lifetimes can be obtained in indirect-band materials,⁶ so that the photogenerated electron and hole do not recombine (ii) before reaching the surface and reacting with CO₂ and H₂O. Alternatively, carrier separation (ii) can easily be achieved in type II heterostructures, by combining two materials with suitably chosen band structures, or at the interface between different crystalline phases of the same material.^9–11 It is therefore not surprising that semiconductors have become increasingly popular catalysts for CO₂ reduction.^5,12,23

Historically TiO₂ has been the material of choice for this reaction due to its low cost, non-toxicity, stability against photoirradiation, and chemical inertness.¹³ However, TiO₂ is far from ideal for this application: for example, as bulk TiO₂ absorbs in the near UV¹⁴ (and at even higher energies when nanostructured), it can convert only a fraction (3–4% at most) of the available solar photons into electron–hole pairs, resulting in poor light harvesting efficiency (i). Furthermore, the carriers’ recombination times in bulk TiO₂, varying from sub-ps¹⁵ to a few tens of ns,¹⁶ are fast compared with typical redox reaction times, leading to reduced charge separation efficiencies (ii). It should therefore not be impossible to find a material that can surpass TiO₂'s photocatalytic efficiency and replace it as catalyst of choice for CO₂ reduction.

This is precisely what we set out to do in this work: to apply inverse-design principles¹⁷ to engineer a semiconductor nanocatalyst with potential for unprecedented efficiency for the following reaction

CO₂ + 8H⁺ + 8e⁻ → CH₄ + 2H₂O (1)

i.e., CO₂ reduction to CH₄. We choose this specific reaction because, having the least negative redox potential, the formation of CH₄ is thermodynamically the most favourable of all most common CO₂ reduction reactions.⁵ However, it is a complex reaction and may involve intermediate steps:⁴ indeed three different pathways are commonly reported in the literature for CO₂ methanation,^18,19 involving dissociation into CO (carbide pathway), synthesis of HCOO (formate pathway), or COOH (carboxyl pathway), depending on the specific catalyst and on the reaction conditions. Nevertheless, there are many examples of nanostructured semiconductor photocatalysts that produce CH₄ as a main (see, e.g., the review by Xie et al.⁵), or even exclusive²⁰ product of CO₂ reduction in water. Furthermore, a study by Yui et al.²¹ has concluded that CO₂ can be reduced to CH₄ at a single site through an 8-electron process, rather than at two separate sites, first through a 2-electron and then through a 6-electron process. Indeed, the different C, H and O affinities of a photocatalyst can heavily affect the adsorption/desorption of reactants/intermediates and the sequence of hydrogenation and deoxygenation, resulting in different product pathways and selectivities.²²

Unfortunately, however, reaction (1) is kinetically less favourable than the competing reduction of water

2H⁺ + 2e⁻ → H₂ (2)

which has a comparable (although slightly higher) redox potential but only requires two electrons, instead of eight. The reduction of CO₂ to CH₃OH has a very similar reduction potential (see maroon dashed line in Fig. 1), but, involving six electrons, is kinetically less favourable than that of water (there are other possible CO₂ reduction reactions, involving C₂₊ products – ethylene, ethanol, propanol, ethane – with intermediate potentials between those of reactions (1) and (2), however, they all involve greater changes in both Gibbs free energy and standard enthalpy,²³ making them thermodynamically less favourable). Therefore (1) thermodynamic selectivity for CO₂ reduction vs. the competing H₂O reduction⁴ (which would, at the same time also ensure selectivity vs. CO₂ to CH₃OH reduction), and (2) availability of eight isoenergetic electrons at one time for the CO₂ → CH₄ reaction, are essential attributes to the ideal catalyst. Indeed, as in all three common methanation pathways mentioned above the redox potential for the initial step is higher than that for water reduction (2),⁵ property (1) would also ensure selectivity for direct CH₄ formation. We note that TiO₂ can provide no such selectivity, as the position of its bulk CBM is higher than the redox potential for water reduction.⁵ Furthermore, the presence of a noble or coinage metal co-catalyst (often used to increase the rate of CH₄ formation) was observed²⁴ to enhance the formation of H₂ more than that of CH₄, leading to an even poorer selectivity of the reacted electrons for CO₂ reduction. It is worth stressing the importance of achieving high selectivity, as the formation of undesired byproducts (a) subtracts precious photogenerated electrons from the main reaction, lowering the yield of the target products, and (b) raises the challenging problem of separating the different products from the resulting mixture.⁴

Fig. 1 Valence (squares) and conduction (circles) band edge energies, calculated with respect to vacuum, as a function of TP size: (a) arm length L, for different values of the diameter D = 1.9 nm (green symbols), 2.1 nm (red symbols) and 2.8 nm (blue symbols); (b) arm diameter D, for L = 3.5 nm (black symbols). The solid lines are a guide to the eye. The dashed lines mark the position of the redox potentials for the reduction of H₂ O to H₂ (−2.997 eV, top brown line), the reduction of CO₂ to CH₃ OH (−3.027 eV, maroon line) and to CH₄ (−3.167 eV, middle brown line), and the oxidation of H₂ O to O₂ (−4.215 eV, bottom brown line), at pH = 7. Their position relative to vacuum was obtained by shifting the values reported in ref. 5 (Fig. 2) using as a reference level our calculated position of the CBM of bulk CdSe (−3.49 eV, also confirmed experimentally⁷).

Size and shape of the catalyst also play a fundamental role in determining its efficiency. In the case of TiO₂ nanoparticles with diameters between 4.5 and 29 nm, for instance, the highest yields were obtained with a size of 14 nm.²⁵ This was interpreted as the result of a competition between two main factors: surface area (determining the availability of surface sites for CO₂ adsorption), and band-gap-dependent light absorption efficiency.²⁵ It would therefore be beneficial to be able to decouple the catalyst's size, or, more specifically, its surface area, from its band gap. Indeed, independently increasing the volume, while keeping a nearly constant band-gap, will also increase absorption through an increase in the absorption cross section. This leads to the next entries in the ‘wish-list’ for our ideal catalyst: (3) a large contact area for CO₂ adsorption and reaction with the electrons and (4) the possibility to tune the band gap independently from it. Also desirable would be (5) the availability of electrons and holes at different locations on the surface for the two redox reactions to take place. Finally, we would like properties (i)–(iii) and (1)–(5) to be exhibited over a wide size window. In other words, it should be possible to produce catalysts with these properties using chemical growth methods with realistic size dispersions.

In what follows we will show that a catalyst exhibiting all requisites to be able to efficiently reduce CO₂ to CH₄, plus the ‘wish-list’ attributes listed above (including the ability to deliver eight electrons in one go), exists and can be synthesized with the present experimental capabilities, making it a potential game-changer of the CO₂ reduction technology.

We start by focussing on property (2), as it is the most crucial requisite enabling the achievement of high reduction efficiencies, and is, nevertheless, not featured by any of the photocatalysts in use today. In order to be able to deliver eight electrons, all at a given potential, a four-fold degenerate ground state is needed. There are two possible strategies to achieve this goal: engineering the material's band structure or its shape. A bulk material with its CBM at the L point in the Brillouin zone would guarantee the required four-fold degeneracy for the ground state. However its absorption efficiency (i) may be low, as its band gap is likely to be indirect. PbSe could be a good candidate, as its VBM is also located at the L point, making it a peculiar direct-band-gap material.²⁶ However, bulk PbSe absorbs in the infra-red (i.e., not where the solar irradiance peaks, (i)) and its band structure does not satisfy (iii), one of the fundamental requirements for CO₂ reduction, as its CBM lies below the redox potential for that reaction. Nanostructuring could solve this problem (but only for very small dot sizes with R ≤ 1 nm (ref. 7)), at the expense, however, of reducing considerably the surface area available for CO₂ adsorption and of losing the four-fold degeneracy of the CBM.²⁷ A better alternative is shape engineering: a nanostructure with four identical regions where the CBM is localised would ensure its four-fold degeneracy. At the same time, such a structure would also enable the simultaneous absorption of eight photons. A tetrapod (TP, see Fig. S1, ESI†),^28,29 is therefore what we will focus on. Unfortunately, however, in a TP made of a single material, due to the band alignment between the zinc blende core and the wurtzite arms, the CBM is always localised in the core, not in the four arms.^28–30 In order to achieve the desired localisation in the arms, the core should be made of a different material having a higher CBM than the arm material. Step (ii) – charge separation and long carrier lifetimes – can be achieved if the core material also has a higher VBM than the arm material, resulting in core-confined holes, and hence in their spatial separation from the electrons. Such a structure would also ensure electrons and holes to be available at different locations on the surface for the two redox reactions to take place (property (5)), and, provided the arms were suitably long, a large contact area to be available for CO₂ adsorption and reaction with the electrons (property (3)), and a large absorption cross section, enabling the simultaneous absorption of eight solar photons. Finally, in TPs, attribute (4) is easily satisfied, as the band gap has been shown,^28,29 to be largely independent of the arm length. Selectivity vs. H₂O reduction (attribute (1)) is also crucial and can be achieved by careful engineering of the core size and arms diameter.

Heterostructured (or core/arms) TPs of different materials (ZnTe/CdSe,³¹ ZnTe/CdS,^31,32 ZnTe/CdTe,³⁴ ZnSe/CdS,³² CdSe/CdS,³³ CdSe/CdTe³⁴) have been synthesized experimentally for over 10 years,³⁵ the seeded growth approach being the most successful method for fabricating more uniform and reproducible structures. Among the different core/arm material pairs, the most popular is CdSe/CdS,³³ where the type I band alignment existing between the CdSe core and the CdS arms³⁶ is exploited to funnel to the core region the electron–hole pairs photogenerated in the arms, endowing these structures with excellent light-harvesting properties that make them ideally suited for applications such as light concentrators, solar cells, and LEDs. According to their bulk band structure, ZnTe/CdTe TPs are also expected to exhibit a type I band alignment,³⁶ however, with both electrons and holes localised in the arms. Unfortunately, as it was discussed above, this kind of band alignment does not suit our purpose as it does not promote charge separation. Furthermore, a high density of structural defects, with alternating regions of wurtzite and sphalerite phases, was recently identified in nanostructures whose arms were made of CdTe by both HRTEM analysis and theoretical modelling.³⁴ Due to the different position of the band edges in zinc blende and wurtzite, the presence of such mixed phases creates local potential wells that could trap the electron, preventing it from reaching the surface and react with CO₂.

ZnTe/CdSe, ZnTe/CdS and ZnSe/CdS have all a type II (or quasi-type II, in the case of ZnSe/CdS) band alignment in the bulk,³⁶ and hence the electron is expected to be confined in the arms and the hole in the core (or throughout the whole structure for ZnSe/CdS). The position of their CBM in the bulk is also above the redox potential for CO₂ reduction, making them good candidates as catalysts for this reaction. Unfortunately, however, it has been recently observed³⁷ that, in mixed cation materials such as these, substantial cation exchange takes place in the core, yielding alloyed structures whose exact composition (hence band alignment) is difficult to predict and control. Moreover, as the location of the CBM in bulk CdS is already above the redox potential for H₂O reduction, TP catalysts with CdS arms can exhibit no selectivity (1) vs. this reaction.

Considering same-cation hetero-nanostructures, CdSe/CdTe TPs have a type II band alignment, but with the electrons confined to the CdSe core. As CdSe can be grown as both seed and arms material and CdTe is also suitable to be grown as seed,³⁴ a possible choice yielding a type II structure with the desired carrier localisation is a CdTe/CdSe³⁸ TP.

Furthermore, as the ability to chemisorb CO₂ plays a crucial role in the efficiency of its photocatalytic reduction to CH₄, and since surface functionalization with organic amines has been proved a successful strategy to enhance such chemisorption in the case of TiO₂,³⁹ the use of CdSe as arm material, for the surface of which a variety of amine groups can routinely be employed as passivants,^7,40 could be an effective choice to further enhance the photocatalytic reduction efficiency in these hetero-nanostructures.

2. Results and discussion

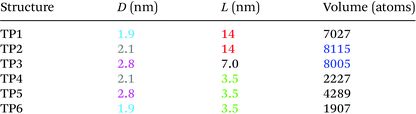
We therefore modelled CdTe/CdSe hetero-nanostructures with different arm diameters D (from 1.9 nm to 2.8 nm) and arm lengths L (from 3.5 nm to 14 nm). For simplicity and ease of notation we will refer to these structures as TPn: TP1 and TP2 have the same arm length L = 14 nm, but different diameters (1.9 nm and 2.1 nm), hence different volumes (TP1 with 7027 atoms and TP2 with 8115 atoms⁴¹); TP3 has shorter (L = 7 nm, i.e., half the length of TP1 and TP2), but thicker (D = 2.8 nm) arms, and a volume (8005 atoms) only slightly smaller than TP2; TP4 has the same arm diameter as TP2 (D = 2.1 nm) but a quarter of its length (L = 3.5 nm), and nearly a quarter of its volume (2227 atoms); TP5 and TP6 have the same diameters as, respectively, TP3 (D = 2.8 nm) and TP1 (D = 1.9 nm), but shorter arms than both (L = 3.5 nm) yielding volumes of 4289 and 1907 atoms, respectively (see Table 1). These nanostructures cover therefore a wide range of aspect ratios L/D, from 1.25 to 7.27. We note that, although initial attempts to grow CdTe/CdSe core/arms TPs yielded structures with short, tapered arms,³⁴ in principle the seeded growth method has the potential to produce CdTe/CdSe with the characteristics modelled in this work, provided suitable mixtures of surfactants are employed. We hope that the present study will spur further research to improve the synthetic processes, leading to the same degree of control that is available with TP made of other materials.³⁴

Table 1 The structures considered in this work (diameter D, length L and number of atoms). Color highlights common features

---

We selected TPs whose CBM was above the redox potential for CO₂ reduction, but, at the same time, lower than the redox potential for the reduction of H₂O to H₂ (see top dashed lines in Fig. 1). This ensures the required selectivity vs. water reduction (property 1), which is expected to be suppressed in these nanostructures by virtue of their band structure alone. In contrast, other semiconductor nanostructures usually require some degree of surface manipulation to enhance their photocatalytic reduction yields of CO₂ in the presence of H₂O. As a consequence, unlike with TiO₂ ²⁴ or other semiconductors, in the case of CdTe/CdSe core/arms TPs the use of both solid–liquid or solid–vapour reaction modes should be possible and should yield similar rates of CH₄ formation, adding further flexibility to the design of the reactor.

The results presented in Fig. 1 also suggest that the TP geometry can be easily engineered for the position of its CBM to lie above (i.e., to be more negative vs. NHE than) the reduction potential of other catalytic reactions for CO₂ reduction (e.g., to CH₃OH, HCHO, CO, and HCOOH, in order of increasingly negative potentials). This will, however, inevitably compromise all selectivity, as water reduction (and CH₄ formation) will be competing with those reactions.

We want to emphasise the importance of accurate band edge engineering in these systems, an example of which is provided by the comparison between the photocatalytic performance of commercial WO₃ microcrystals and nanosheets of the same material: the former, whose CBM is 0.29 eV more positive than the reduction potential of CO₂ to CH₄, could produce no CH₄; the latter, however, whose CBM, owing to increased confinement, is 0.47 eV higher than that of the microcrystals (and just 0.18 eV higher than the CO₂/CH₄ reduction potential) resulted in successful catalysis of CO₂ into CH₄.⁴² Similarly, in the case of Na₂V₆O₁₆ nanoribbons⁴³ successful CO₂ reduction to CH₄ in water was achieved despite their CBM position being just 0.17 eV above the CO₂/CH₄ reduction potential.

Very recently, spherical CdSe nanocrystals (NCs) exhibited remarkable size-tunable selectivity in the photocatalytic reduction of CO₂.⁴⁴ Li and co-workers showed⁴⁴ that, by varying the NC size, the position of the CBM could be tuned to lie between the potential for H₂ evolution and that for CH₃OH generation, resulting in over 70% selectivity towards the latter product. They also found that the observed potentials for both reactions (defined as ‘the potentials at which the electron has just started H₂and CH₃OH production’) were more reducing than the theoretical values. In particular the difference between the observed potential for CO₂ reduction to CH₃OH (∼−0.4 V vs. NHE⁴⁴) and its value at pH 7 (−0.38 V vs. NHE^5,23), attributed by the authors⁴⁴ to kinetic factors including the activation energy and the overpotential, was only ∼0.02 V. Furthermore, they reported the presence of considerable amounts of CH₄ in the reaction products, which were independent of the NC size, as the potential for CO₂ reduction to CH₄ is far below the position of the NCs’ CBM, for all sizes considered in the experiment.⁴⁴ Interestingly, for NC sizes sufficiently large that no CH₃OH was produced, (i.e., when the CBM dropped below the potential for CO₂ reduction to CH₃OH), the selectivity achieved for CH₄ was 79%.⁴⁵ These results suggest that much higher selectivities for CO₂ reduction to CH₄ should be achievable by carefully engineered CdTe/CdSe TPs with suitable arm size and CBM position. Very importantly, they also provide an estimate for the magnitude of the activation energies and overpotentials for such a reaction (∼0.02 V) in these nanostructures.

We verified that the TP's CBM originated from the CdSe arms and the VBM from the CdTe core by decomposing each structure into an isolated CdTe core and an isolated CdSe arm, and run electronic structure calculations on each (see Fig. S2, ESI†).

As a consequence, we found that in all TPs considered: (a) the holes are confined in the core, whereas the electrons are localised in the arms (Fig. 2), as desired; (b) the band gap is smaller than that of both core and arm (but still in the visible region of the spectrum), and can be tuned over a wide range of energies by an appropriate choice of core and arm sizes.

Fig. 2 Valence (bottom) and conduction (top) band edge charge densities (red), calculated for different values of the arm diameter D = 1.9 nm (a), 2.1 nm (b) and 2.8 nm (c), for L = 3.5 nm, and for different values of the arm length L = 3.5 nm (d) and 14 nm (e), for D = 2.1 nm. Cyan dots represent Cd, blue dots represent Se and Te atoms.

However, structures with small diameters (D ≲ 2.1 nm) and short arm lengths (L ≲ 3.5 nm), exhibit two features that would affect their exploitation as efficient photocatalysts: (I) a considerable portion of the CBM charge density is found in the core (Fig. 2); (II) the CBM does not exhibit the expected four-fold degeneracy (Fig. 3 and Fig. S3, ESI†).

Fig. 3 Lowermost four conduction band state charge densities (red), calculated in TPs with D = 2.1 nm and (top) L = 3.5 nm (TP4), and (bottom) L = 14 nm (TP2). Also reported are the corresponding energies, relative to vacuum. Cyan dots represent Cd, blue dots represent Se and Te atoms.

The large overlap between ground state electron and hole wave functions resulting from (I) yields radiative recombination times of the same order of magnitude (i.e., tens on ns), as those observed in CdSe nanocrystals of similar diameters or calculated for CdTe TPs with similar dimensions (Fig. 4); whereas, as a consequence of (II), some of these nanostructures may fail to simultaneously deliver the eight isopotential electrons needed for an efficient CO₂ reduction. It has to be noted that, although the energy separation ΔE_cb1–4 between the first (cb₁ = CBM) and the fourth (cb₄ = CBM + 3) electron state of all of these nanostructures is much smaller than in spherical nanocrystals with similar diameters (about 600 meV in CdSe), where it is much larger than the difference between the redox potentials for CO₂ and H₂O reduction, it may still lead (especially for TPs with thinner arms) to a loss of selectivity (1): i.e., if the energy of the excited electron is above the redox potential for water reduction (top dashed line in Fig. 1), the latter reaction will be more likely to occur than the reduction of CO₂ (if considering the two to eight electron ratio for the two reactions). We also note that, although the large separation ΔE_cb1–4 in spherical structures can be reduced by increasing the nanocrystal's radius, this occurs at the expense of lowering the position of the CBM and decreasing the band gap. In the case of CdSe, for example, the radius increase needed to reduce ΔE_cb1–4 below 100 meV leads to a lowering of the CBM of over 600 meV (which brings it below the redox potential for CO₂ reduction) and to a decrease of the band gap of over 1 eV.⁷

Fig. 4 Radiative recombination lifetimes, calculated at room temperature as a function of volume (red symbols, bottom x axis) and as a function of arm length (black symbols, upper x axis) in TPs with D = 1.9 nm (red squares and black diamonds), 2.1 nm (red squares and black circles) and 2.8 nm (red squares and black triangles). The lifetimes calculated in homogeneous CdTe TPs are also shown (empty red squares) for comparison. The dotted arrows connect symbols relative to the same structure.

Our results suggest that the non-zero amplitude of the electron–hole wave function overlap found in short- and thin-armed TPs, despite the presence of a charge-separating band alignment at the CdTe/CdSe interface, is due to a lack of available volume for the electron to ‘expand’ into. Indeed, the position of the electron charge density moves away from the core region as soon as the arms’ volume increases (Fig. 2). In CdTe/CdSe core/arms TPs, the increase in L also leads to a nearly vanishing ΔE_cb1–4, which decreases from about 17 meV (for L = 3.5 nm) to 0.1 meV (for L = 14 nm), in structures with D = 2.1 nm, ensuring the desired four-fold degeneracy of the CBM. Importantly, as it is the case with uniform-composition TPs,²⁸ within this length window the position of the CBM only varies by a few tens of meV (see Fig. 1), and hence so does the band gap (as the VBM is nearly constant). This has the double benefit of increasing the absorption cross section with volume, whilst maintaining absorption in the visible. Furthermore, from Fig. 1 we can also see that, in this size range, crucially the CBM remains between the redox potentials for H₂O and CO₂ reduction to CH₄ (top brown dashed lines), ensuring excellent selectivity for the latter reaction.

We also find that a simple increase in the arm diameter from 1.9 nm to 2.8 nm, yields an over five-fold increase in radiative lifetime, even for a very short arm (L = 3.5 nm). Most remarkably, however, in structures with D = 2.1 nm, the calculated room temperature radiative lifetime increases by over two orders of magnitude, from 45 ns to 4.6 μs, when increasing L by a factor of 4, from 3.5 nm to 14 nm (filled black circles in Fig. 4). This is in striking contrast with the behaviour of conventional CdTe TPs, where, for similar increases in either D or L, we find no appreciable variation in the calculated radiative recombination time, which remains at around 25 ns (red empty squares in Fig. 4), i.e., comparable to that of spherical nanocrystals, owing to the fact that both CBM and VBM are localized in the core (so that there is little change in their overlap with increasing total volume). Even in CdSe/CdS TPs with an aspect ratio of L/D as large as 10 the observed radiative lifetime is only a factor of 3 longer than in spherical CdSe nanocrystals with similar diameters.³³ As a comparison, the measured recombination time in TiO₂ nanoparticles, CO₂'s reduction catalysts of choice, is sub-nanosecond.⁴⁶

The radiative recombination lifetimes we predict for CdTe/CdSe core/arms TPs with more than 8000 atoms are therefore longer than (or comparable to) the typical redox reaction times (>10^–8 s)⁵ – which are usually too slow to compete with the radiative lifetimes (∼10^–9 s) exhibited by common semiconductor nanocrystals or conventional same-composition TPs. This should allow the charge carriers sufficient time to reach the surface (which is conveniently close, given the small arm diameter, and provides a huge contact area for CO₂ adsorption (3), due to the considerable arm length), and react with CO₂ and H₂O before recombining. Furthermore, the long arms of these nanostructures present many facets with different orientations, providing large amounts of undercoordinated surface metal atoms, which have been shown⁴⁷ to be extremely efficient in transferring electrons to adsorbed reactants, resulting in high catalytic activity and selectivity. Such coordinatively unsaturated Cd atoms also serve as trapping sites for efficient adsorption of CO₂ molecules,⁴⁸ leading to a significant improvement in their photocatalytic reduction.⁴⁹

Long radiative lifetimes are of limited utility in the presence of fast non-radiative recombination pathways. In colloidal nanocrystals, the most efficient of such processes is Auger recombination (AR), where the recombination of an electron–hole pair in the presence of excess electrons and/or holes is accompanied by a (non-radiative) energy transfer to one of the ‘spectator’ particles, which is excited to a higher energy state (see Fig. S4, ESI†). Typical AR lifetimes in CdSe spherical dots with diameters of 2.4 nm are of the order of a few picoseconds,⁵⁰ and decrease with decreasing dot size.

We find that in CdTe/CdSe core/arms TPs the weak electron–hole wave function overlap also leads to strong AR suppression. Our calculated AR times are one to over two orders of magnitude longer than in spherical nanostructures with similar diameters, and increase with arm length, ranging (in TPs with D = 2.1 nm), from about 40 ps (for L = 3.5 nm) to about 800 ps (for L = 14 nm).

We want to stress that this twenty-fold increase with arm length is not due to a simple volume scaling, as the increase in AR times observed in spherical CdSe nanocrystals for a similar volume increase is only of a factor of less than 5.⁵⁰ Interestingly the AR lifetime associated with excess electrons (τ_e) is of the order of ten microseconds, whereas that associated with excess holes (τ_h) is shorter than 1 ns and dominates the total calculated AR time, in the case of a CdTe/CdSe TP with L = 14 nm (for L = 3.5 instead, the two contributions are more similar to each other – of the order of 200 ps for τ_e and 40 ps for τ_h). The origin of such a large disparity is the different contribution from arm and core states to the calculation of the two lifetimes: τ_e involves three arm-delocalised electron and one core-localised hole wave function (the initial state is a hole in the VBM and two electrons in the CBM, the final state is an excited electron), which have little overlap with each other, whereas in the calculation of τ_h three out of four wave functions are relative to core-localised holes (the initial state is an electron in the CBM and two holes in the VBM, the final state is an excited hole), and therefore exhibit a much larger overlap. In contrast, in CdTe TPs, where both CBM and VBM can access the core region, and the charge densities of electrons and holes are distributed more uniformly throughout the nanostructure, we calculate τ_e ≈ τ_h. These results strongly suggest that, owing to their specific band alignment at the heterojunction and the availability of a large volume for the CB wave functions to spread, CdTe/CdSe TPs with long arms favour the accumulation of electrons.

There has been some debate regarding which geometrical feature, arm length⁵¹ or TP volume,⁵² most affects the TP properties. Our results clearly show that both the excitonic structure and the optical properties are determined by the TP volume, more than by the arm length alone. To show this, we will focus on four of our structures: TP1, TP2, TP3, and TP4 (see above). If arm length were the critical structural feature determining the TP properties, we should find similar results for TP1 and TP2 (if it were the diameter, our results should be similar for TP2 and TP4, as they would if the volume were irrelevant). If, however, TP volume were more important, then TP2 and TP3 should exhibit a similar behaviour.

Both excitonic structure and optical properties in semiconductor nanostructures are determined by the electron–hole coupling (quantified by their wave function overlap). A quantitative measure of this overlap is provided by the direct Coulomb matrix elements (J_vc) and by the dipole matrix elements (M_vc), calculated between valence (v) and conduction (c) states. The former represent the electron–hole attraction energy that binds the exciton, and is the main component determining the excitonic red shift, compared to the single-particle picture,⁵³ while the latter determines the nanostructure's optical properties, among which the radiative recombination lifetimes. We calculated that in TP2 J_vc is very small (18 meV) and has the same value for v = VBM, and c = CBM, CBM + 1, CBM + 2, and CBM + 3, (as a comparison, in a spherical CdSe nanocrystal with the same diameter of 2.1 nm we calculate J_VBM,CBM ∼ 400 meV), whereas in TP1 and TP4 J_VBM,CBM (= 39 meV and 105 meV, respectively) is different from J_VBM,CBM+j (= 26 meV, and 82 meV, respectively, for j = 1, 2, 3), evidencing (A) a larger overall electron–hole coupling in TP1 and TP4 than in TP2, and (B) a different degree of overlap between the VBM and the lowermost four CB states in those structures. In contrast, in TP3 J_VBM,CBM and J_VBM,CBM+j are very similar, their difference being of only about 3 meV.

These features have a direct effect on the TPs’ excitonic structure: due to the four-fold degeneracy of its CBM, and to the constant value of the overlap between VBM and CBM + j (for j = 0, 1, 2, 3), TP2 exhibits an almost perfect 32-fold degenerate ground state exciton (obtained from the combination of four CBM and two VBM states and including the spin degeneracy), with the whole fine structure contained within only 6 meV (i.e., the energetic separation between excitons 1 and 32 is only 6 meV. As a comparison, in a spherical CdSe nanocrystal with the same diameter of 2.1 nm we calculate such a separation to be over 600 meV). Despite a similar and nearly perfect four-fold degeneracy of the CBM (the difference between the energetic position of CBM and CBM + 3 is here only 1.5 meV), in TP1 the lowermost 32 excitonic states are instead spread over 39 meV, compared with only 19 meV in TP3, and 80 meV in TP4, reflecting the behaviour found in J_vc in the three structures. We conclude that arm length is important (see TP2 vs. TP4), but volume is even more so (see TP1 vs. TP2).

Turning now our attention to the optical properties, we, again, find that the volume, not the arm length, determines the radiative recombination lifetimes in these hetero-nanostructures (Fig. 4). Indeed, we calculate the longest lifetime (4574 ns) in TP2 (8115 atoms), followed by TP3 (503 ns, 8005 atoms), TP1 (298 ns, 7027 atoms), and TP4 (45.7 ns, 2227 atoms), confirming the strongest electron–hole couplings to occur in TP4 (which has the smallest volume and arm length) and TP1 (which has the same arm length as TP2, but a smaller volume), compared to the other two structures.

3. Conclusions

In conclusion, our electronic structure calculations have shown that CdTe/CdSe core/arms TPs with arms’ diameters of about 2.1 nm (1.9 ≤ D < 2.8) and arms’ lengths ≥14 nm can be extremely efficient light harvesters (i) with large absorption cross sections in the visible part of the spectrum, exhibit charge separation (ii) where electrons and holes are localised in different spatial regions of the hetero-nanostructure (5), leading to long carriers’ lifetimes (compared to both homogeneous TPs and typical redox reaction times), provide short charge migration pathways from the bulk phase to the surface, and a very large surface area rich in coordinatively unsaturated metal atoms promoting reactant adsorption (3) and reaction (iii), which can be increased independently from the band gap (4), exhibit high selectivity for CO₂ reduction vs. the competing H₂O reduction (1), and, finally, are capable to provide eight isoenergetic electrons at one time (2). They therefore present themselves as ideal catalysts for CO₂ reduction to CH₄, exhibiting potential for unprecedented selectivity and for unparalleled efficiency. We stress the word potential here, however, as, despite all of the TPs’ remarkable thermodynamical and dynamical properties listed above, deriving from their electronic structure, optical properties and charge dynamics, it is important to highlight that adsorption/desorption properties of reactants and intermediates also play a fundamental role in determining the product's selectivity and yield. The modelling of such properties is beyond the capability of our approach and the scope of the present work. Nevertheless, the available literature suggests the presence of coordinatively unsaturated metal atoms (such as the Cd atoms abundant on the TP's surface) to facilitate reactant adsorption, leading to high reduction rates. Furthermore, the high selectivity for CH₄ production achieved by large CdSe NCs, and the very low overpotentials and activation energies measured in these systems, provide further support to our claims. We therefore hope these results will stimulate further research, such as detailed catalytic analysis and experimental implementation of TP-based photocatalytic cells, aimed at verifying the effective selectivity and efficiency of these versatile nanostructures for CO₂ reduction to CH₄.

4. Method

The TPs modelled in this work are assumed to have a bulk-like crystal structure. This assumption is supported by both experimental powder diffraction measurements performed on similarly lattice mismatched ZnTe/CdS TPs,³⁴ which evidenced identical crystal structures between the TP arms and wurtzite CdS nanorods elongated along the 0001 direction, and by high-resolution transmission electron microscopy images of CdSe/CdS TPs,³³ which showed defect-free interfaces between (111) planes of zinc blende CdSe cores and (001) planes of wurtzite CdS arms. Accordingly, our TPs are composed of a central zinc blende tetrahedral core with four (111) facets made of CdTe, from which four wurtzite CdSe rod-like arms protrude,^28,33,34 whose surface includes a similar number of Cd and Se atoms (see Fig. S1, ESI†). The unsaturated bonds at the TP surface are passivated by pseudo-hydrogenic, short-range potentials with Gaussian form.⁵⁴ The single-particle energies and wave functions are obtained by solving the Schrödinger equation using the atomistic plane-wave semi-empirical pseudopotential method (SEPM) described in ref. 55, including spin–orbit coupling, and excitonic effects are accounted for, in the calculation of the optical properties (radiative lifetimes and optical spectra), via a configuration interaction scheme⁵³ (where we include up to 9 electron and 15 hole states – for a total of 540 configurations – as we are mostly interested in the properties around the band gap). In the SEPM method,⁵⁵ the single-particle Schrödinger equation, containing SEPM screened atomic potentials fitted to the DFT potentials and to the experimental band structure, is solved non-self-consistently using the folded spectrum method⁵⁶ for a selected set of states near the band gap. This approach allows us to obtain DFT-like accuracy in the calculation of the eigenstates of systems containing tens of thousands of atoms. Indeed SEPM and DFT bulk wave functions exhibit a 99% overlap.⁵⁵ This well-benchmarked and accurate method has been used in the past to successfully predict a wide range of experimental features, including the extinction coefficients as a function of size in CdSe dots,⁵⁷ the size-dependent conduction and valence band edge energies in nanocrystals of different materials,⁷ the exciton dynamics in CdTe⁵⁸ and InSb⁵⁹ colloidal dots, electron transfer rates in Cd chalcogenide nanocrystals,⁶⁰ Auger rates in CdSe nanocrystals,⁶¹ and the electronic states properties of CdSe TPs.³⁰

Auger recombination times are calculated according to established procedures^61,62 with the difference that here a size- and position-dependent dielectric constant ε_in = ε(R),⁵³ was assumed within the TP (and ε_out = 1, was assumed for its environment), instead of a regional screening with ε_in = ε_bulk and ε_out = ε_solvent.⁶² We compared the results of the two approaches in CdSe spherical nanocrystals with similar diameters to the TPs considered here and found that the calculated lifetimes agree for ε_out ≈ 2.5–3.5 (see Fig. S5 ESI†), which includes the dielectric constants of the most commonly used solvents and capping groups.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was undertaken on ARC3, part of the High Performance Computing facilities at the University of Leeds, UK. M. C. gratefully acknowledges financial support from the School of Electronic & Electrical Engineering, University of Leeds.

References

1. J. G. Ayres, et al., Climate Change and Respiratory Disease: European Respiratory Society statement, Eur. Respir. J., 2009, 34, 295–302.
2. https://www.ipcc.ch/report/ar5/wg3/; https://www.epa.gov/ghgemissions/global-greenhouse-gas-emissions-data.
3. T. A. Boden, G. Marland and R. J. Andres, Global, Regional, and National Fossil-Fuel CO₂ Emissions, Carbon Dioxide Information Analysis Center, Oak Ridge National Laboratory, U.S. Department of Energy, Oak Ridge, Tenn., U.S.A, 2017,  DOI:10.3334/CDIAC/00001_V2017.
4. J. Fu, K. Jiang, X. Qiu, J. Yu and M. Liu, Product Selectivity of Photocatalytic CO₂ Reduction Reactions, Mater. Today, 2020, 32, 222.
5. S. Xie, Q. Zhang, G. Liu and Y. Wang, Photocatalytic and Photoelectrocatalytic Reduction of CO₂ Using Heterogeneous Catalysts with Controlled Nanostructures, Chem. Commun., 2016, 52, 35–59.
6. P. Y. Yu and M. Cardona, Fundamentals of Semiconductors - Physics and Materials Properties, Springer-Verlag, Berlin Heidelberg, 4th edn, 2010. ISBN 978-3-642-00709-5.
7. J. Jasieniak, M. Califano and S. E. Watkins, Size-Dependent Valence and Conduction Band-Edge Energies of Semiconductor Nanocrystals, ACS Nano, 2011, 5, 5888–5902.
8. D. V. Talapin, J. Lee, M. V. Kovalenko and E. V. Shevchenko, Prospects of Colloidal Nanocrystals for Electronic and Optoelectronic Applications, Chem. Rev., 2010, 110, 389–458.
9. G. Li, S. Ciston, Z. V. Saponjic, L. Chen, N. M. Dimitrijevic, T. Rajh and K. A. Gray, Synthesizing Mixed-Phase TiO₂ Nanocomposites Using a Hydrothermal Method for Photo-Oxidation and Photoreduction Applications, J. Catal., 2008, 253, 105–110.
10. J. Zhang, Q. Xu, Z. Feng, M. Li and C. Li, Importance of the Relationship Between Surface Phases and Photocatalytic Activity of TiO₂, Angew. Chem., Int. Ed., 2008, 47, 1766–1769.
11. X. Wang, et al., Photocatalytic Overall Water Splitting Promoted by an α-β Phase Junction on Ga₂O₃, Angew. Chem., Int. Ed., 2012, 51, 13089–13092.
12. M. Grätzel, Photoelectrochemical Cells, Nature, 2001, 414, 338–344.
13. M. A. Fox and M. T. Dulay, Heterogeneous Photocatalysis, Chem. Rev., 1993, 93, 341–357.
14. L. Kavan, M. Grätzel, S. E. Gilbert, C. Klemenz and H. J. Scheel, Electrochemical and Photoelectrochemical Investigation of Single-Crystal Anatase, J. Am. Chem. Soc., 1996, 118, 6716–6723.
15. P. Maity, O. F. Mohammed, K. Katsiev and H. Idriss, Study of the Bulk Charge Carrier Dynamics in Anatase and Rutile TiO₂ Single Crystals by Femtosecond Time-Resolved Spectroscopy, J. Phys. Chem. C, 2018, 122, 8925–8932.
16. Y. Yamada and Y. Kanemitsu, Determination of Electron and Hole Lifetimes of Rutile and Anatase TiO₂ Single Crystals, Appl. Phys. Lett., 2012, 101, 133907.
17. https://www.colorado.edu/faculty/zunger-matter-by-design/inverse-design .
18. C. Vogt, M. Monai, G. J. Kramer and B. M. Weckhuysen, The Renaissance of the Sabatier Reaction and its Applications on Earth and in Space, Nat. Catal., 2019, 2, 188–197.
19. S. Kattel, P. Liu and J. G. Chen, Tuning Selectivity of CO₂ Hydrogenation Reactions at the Metal/Oxide Interface, J. Am. Chem. Soc., 2017, 139, 9739–9754.
20. W. Tu, Y. Zhou, Q. Liu, Z. Tian, J. Gao, X. Chen, H. Zhang, J. Liu and Z. Zou, Robust Hollow Spheres Consisting of Alternating Titania Nanosheets and Graphene Nanosheets with High Photocatalytic Activity for CO₂ Conversion into RenewableFuels, Adv. Funct. Mater., 2012, 22, 1215–1221.
21. T. Yui, A. Kan, C. Saitoh, K. Koike, T. Ibusuki and O. Ishitani, Photochemical Reduction of CO₂ Using TiO₂: Effects of Organic Adsorbates on TiO₂ and Deposition of Pd onto TiO₂, ACS Appl. Mater. Interfaces, 2011, 3, 2594–2600.
22. A. Vasileff, C. Xu, Y. Jiao, Y. Zheng and S.-Z. Qiao, Surface and Interface Engineering in Copper-Based Bimetallic Materials for Selective CO₂ Electroreduction, Chem, 2018, 4, 1809–1831.
23. S. Wang, X. Han, Y. Zhang, N. Tian, T. Ma and H. Huang, Inside and Out Semiconductor Engineering for CO₂ Photoreduction: From Recent Advances to New Trends, Small Struct., 2021, 2, 2000061.
24. S. Xie, Y. Wang, Q. Zhang, W. Deng and Y. Wang, MgO- and Pt-Promoted TiO₂ as an Efficient Photocatalyst for the Preferential Reduction of Carbon Dioxide in the Presence of Water, ACS Catal., 2014, 4, 3644–3653.
25. K. Kocí, L. Obalová, L. Matějová, D. Plachá, Z. Lacný, J. Jirkovský and O. Šolcová, Effect of TiO₂ Particle Size on the Photocatalytic Reduction of CO₂, Appl. Catal., B, 2009, 89, 494–502.
26. J. M. An, A. Franceschetti, S. V. Dudiy and A. Zunger, The Peculiar Electronic Structure of PbSe Quantum Dots, Nano Lett., 2006, 6, 2728–2735.
27. According to our calculations,⁷ the energy separation from the CBM of the next two states (CBM + 1 and CBM + 2) is about 10 meV, becoming about 100 meV for CBM + 3.
28. L. Manna, D. J. Milliron, A. Meisel, E. C. Scher and A. P. Alivisatos, Controlled Growth of Tetrapod-Branched Inorganic Nanocrystals, Nat. Mater., 2003, 2, 382–385.
29. L. Manna, E. C. Scher and A. P. Alivisatos, Synthesis of Soluble and Processable Rod-, Arrow-, Teardrop-, and Tetrapod-Shaped CdSe Nanocrystals, J. Am. Chem. Soc., 2000, 122, 12700–12706.
30. J. Li and L.-W. Wang, Shape Effects on Electronic States of Nanocrystals, Nano Lett., 2003, 3, 1357–1363.
31. R. G. Xie, U. Kolb and T. Basché, Design and Synthesis of Colloidal Nanocrystal Heterostructures with Tetrapod Morphology, Small, 2006, 2, 1454–1457.
32. L. Carbone, et al., Synthesis and Micrometer-Scale Assembly of Colloidal CdSe/CdS Nanorods Prepared by a Seeded Growth Approach, Nano Lett., 2007, 7, 2942–2950.
33. D. V. Talapin, J. H. Nelson, E. V. Shevchenko, S. Aloni, B. Sadtler and A. P. Alivisatos, Seeded Growth of Highly Luminescent CdSe/CdS Nanoheterostructures with Rod and Tetrapod Morphologies, Nano Lett., 2007, 7, 2951–2959.
34. A. Fiore, et al., Tetrapod-Shaped Colloidal Nanocrystals of II-VI Semiconductors Prepared by Seeded Growth, J. Am. Chem. Soc., 2009, 131, 2274–2282.
35. N. Mishra, V. G. V. Dutt and M. P. Arciniegas, Recent Progress on Metal Chalcogenide Semiconductor Tetrapod-Shaped Colloidal Nanocrystals and their Applications in Optoelectronics, Chem. Mater., 2019, 31, 9216–9242.
36. Y.-H. Li, et al., Revised Ab Initio Natural Band Offsets of All Group IV, II-VI, and III-V Semiconductors, Appl. Phys. Lett., 2009, 94, 212109.
37. M. J. Enright, et al., Seeded Growth of Nanoscale Semiconductor Tetrapods: Generality and the Role of Cation Exchange, Chem. Mater., 2020, 32, 4774–4784.
38. S. Kim, B. Fisher, H.-J. Eisler and M. Bawendi, Type-II Quantum Dots: CdTe/CdSe(Core/Shell) and CdSe/ZnTe(Core/Shell) Heterostructures, J. Am. Chem. Soc., 2003, 125, 11466–11467.
39. Y. Liao, et al., Efficient CO₂ Capture and Photoreduction by Amine-Functionalized TiO₂, Chem. – Eur. J., 2014, 20, 10220–10222.
40. D. V. Talapin, A. L. Rogach, A. Kornowski, M. Haase and H. Weller, Highly Luminescent Monodisperse CdSe and CdSe/ZnS Nanocrystals Synthesized in a Hexadecylamine-Trioctylphosphine Oxide-Trioctylphosphine Mixture, Nano Lett., 2001, 1, 207–211.
41. We employ atom numbers to unequivocally express the volume, as opposed to using conventional units of nm³, as volume estimates that use the latter are based on an assumed perfect geometrical (i.e., usually cylindrical) shape for the arms, that is never realised at the atomistic level.
42. X. Chen, Y. Zhou, Q. Liu, Z. Li, J. Liu and Z. Zou, Ultrathin, Single-Crystal WO₃ Nanosheets by Two-Dimensional Oriented Attachment Toward Enhanced Photocatalytic Reduction of CO₂ Into Hydrocarbon Fuels Under Visible Light, ACS Appl. Mater. Interfaces, 2012, 4, 3372–3377.
43. S. Feng, X. Chen, Y. Zhou, W. Tu, P. Li, H. Li and Z. Zou, Na₂V₆O₁6xH₂O Nanoribbons: Large-Scale Synthesis and Visible-Light Photocatalytic Activity of CO₂ Into Solar Fuels, Nanoscale, 2014, 6, 1896–1900.
44. A. Li, T. Wang, C. Li, Z. Huang, Z. Luo and J. Gong, Adjusting the Reduction Potential of Electrons by Quantum Confinement for Selective Photoreduction of CO₂ to Methanol, Angew. Chem., Int. Ed., 2019, 58, 3804–3808.
45. We calculate the selectivity S as S_CH4 = 8R_CH4/(2R_CO + 6R_CH3OH + 8R_CH4 + 2R_H2 × 100%, where R represents the productive rate of the observed products (in the specific case: CO, CH₃OH, CH₄ and H₂), and its coefficient is the number of electrons consumed in the multi-electron reaction.⁴.
46. K. Ozawa, et al., Electron-Hole Recombination Time at TiO₂ Single-Crystal Surfaces: Influence of Surface Band Bending, J. Phys. Chem. Lett., 2014, 5, 1953–1957.
47. X. F. Yang, A. Q. Wang, B. T. Qiao, J. Li, J. Y. Liu and T. Zhang, Single-Atom Catalysts: A New Frontier in Heterogeneous Catalysis, Acc. Chem. Res., 2013, 46, 1740.
48. R. García-Muelas and N. López, Statistical Learning Goes Beyond the d-Band Model Providing the Thermochemistry of Adsorbates on Transition Metals, Nat. Commun., 2019, 10, 4687.
49. Y. Zhao, et al., Defect-Rich Ultrathin ZnAl-Layered Double Hydroxide Nanosheets for Efficient Photoreduction of CO₂ to CO with Water, Adv. Mater., 2015, 27, 7824–7831.
50. V. I. Klimov, Optical Nonlinearities and Ultrafast Carrier Dynamics in Semiconductor Nanocrystals, J. Phys. Chem. B, 2000, 104, 6112–6123.
51. N. Mishra, et al., Using Shape to Turn Off Blinking for Two-Colour Multiexciton Emission in CdSe/CdS Tetrapods, Nat. Commun., 2017, 8, 15083.
52. A. A. Lutich, et al., Multiexcitonic Dual Emission in CdSe/CdS Tetrapods and Nanorods, Nano Lett., 2010, 10, 4646–4650.
53. A. Franceschetti, H. Fu, L.-W. Wang and A. Zunger, Many-Body Pseudopotential Theory of Excitons in InP and CdSe Quantum Dots, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 1819–1829.
54. P. A. Graf, K. Kim, W. B. Jones and L.-W. Wang, Surface Passivation Optimization Using DIRECT, J. Comput. Phys., 2007, 224, 824–835.
55. L.-W. Wang and A. Zunger, Local-Density-Derived Semiempirical Pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 17398–17416.
56. L.-W. Wang and A. Zunger, Solving Schrödingers Equation Around a Desired Energy: Application to Silicon Quantum Dots, J. Chem. Phys., 1994, 100, 2394–2397.
57. J. Jasieniak, L. Smith, J. van Embden, P. Mulvaney and M. Califano, Re-Examination of the Size-Dependent Absorption Properties of CdSe Quantum Dots, J. Phys. Chem. C, 2009, 113, 19468–19474.
58. M. Califano, Origins of Photoluminescence Decay Kinetics in CdTe Colloidal Quantum Dots, ACS Nano, 2015, 9, 2960–2967.
59. A. Sills, P. Harrison and M. Califano, Exciton Dynamics in InSb Colloidal Quantum Dots, J. Phys. Chem. Lett., 2016, 7, 31–35.
60. H. Zhu, Y. Yang, K. Hyeon-Deuk, M. Califano, N. Song, Y. Wang, W. Zhang, O. V. Prezhdo and T. Lian, Auger-Assisted Electron Transfer from Photoexcited Semiconductor Quantum Dots, Nano Lett., 2014, 14, 1263–1269.
61. L.-W. Wang, M. Califano, A. Zunger and A. Franceschetti, Pseudopotential Theory of Auger Processes in CdSe Quantum Dots, Phys. Rev. Lett., 2003, 91, 056404.
62. M. Califano, Suppression of Auger Recombination in Nanocrystals via Ligand-Assisted Wave Function Engineering in Reciprocal Space, J. Phys. Chem. Lett., 2018, 9, 2098–2104.

---

Footnote

† Electronic supplementary information (ESI) available: Tetrapod geometry. Band alignments: The CdTe/CdSe tetrapod and its constituent CdTe core and CdSe arms. Energy separation in the conduction band of CdTe/CdSe tetrapods. Auger recombination: Schematics. Auger recombination: Comparison of the lifetimes calculated using two different approaches for the screening. See DOI: 10.1039/D1NR01550H

---