Discovery of intrinsic two-dimensional antiferromagnets from transition-metal borides†
Abstract
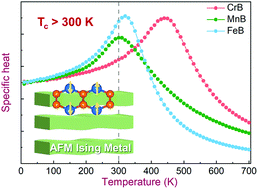
Intrinsic two-dimensional (2D) magnets are promising materials for developing advanced spintronic devices. A few have already been synthesized from the exfoliation of van der Waals magnetic materials. In this work, by using ab initio calculations and Monte Carlo simulation, a series of 2D MBs (M = Cr, Mn or Fe; B = boron) are predicted possessing robust magnetism, sizeable magnetic anisotropy energy, and excellent structural stability. These 2D MBs can be respectively synthesized from non-van der Waals compounds with low separation energies such as Cr2AlB2, Mn2AlB2, and Fe2AlB2. 2D CrB is a ferromagnetic (FM) metal with a weak in-plane magnetic anisotropy energy of 23.6 μeV per atom. Metallic 2D MnB and FeB are Ising antiferromagnets with an out-of-plane magnetic easy axis and robust magnetic anisotropy energies up to 222.7 and 482.2 μeV per atom, respectively. By using Monte Carlo simulation, the critical temperatures of 2D CrB, MnB, and FeB were calculated to be 440 K, 300 K, and 320 K, respectively. Our study found that the super-exchange interaction plays the dominant role in determining the long-range magnetic ordering of 2D MBs. Moreover, most functionalized 2D MBTs (T = O, OH or F) are predicted to have AFM ground states. Alternating transition metals or functional groups can significantly modulate the magnetic ground state and critical temperature of 2D MBTs. This study suggests that the 2D MBs and MBTs are promising metallic 2D magnets for spintronic applications.
- This article is part of the themed collection: Editor’s Choice: Controlling anisotropy in nanomaterials


 Please wait while we load your content...
Please wait while we load your content...