Open Access Article
Open Access ArticleMultiscale simulations of the hydration shells surrounding spherical Fe3O4 nanoparticles and effect on magnetic properties†
Hongsheng
Liu
ab,
Paulo
Siani
b,
Enrico
Bianchetti
b,
Jijun
Zhao
a and
Cristiana
Di Valentin
 *b
*b
aLaboratory of Materials Modification by Laser, Ion and Electron Beams, Dalian University of Technology, Ministry of Education, Dalian 116024, China
bDipartimento di Scienza dei Materiali, Università di Milano-Bicocca, via R. Cozzi 55, I-20125 Milano, Italy. E-mail: cristiana.divalentin@unimib.it
First published on 4th May 2021
Abstract
Iron oxide magnetic nanoparticles (NPs) are excellent systems in catalysis and in nanomedicine, where they are mostly immersed in aqueous media. Even though the NP solvation by water is expected to play an active role, the detailed structural insight at the nanostructure oxide/water interface is still missing. Here, based on our previous efforts to obtain accurate models of dehydrated Fe3O4 NPs and of their magnetic properties and through multiscale molecular dynamics simulations combining the density functional tight binding method and force field, we unravel the atomistic details of the short range (chemical) and long range (physical) interfacial effects when magnetite nanoparticles are immersed in water. The influence of the first hydration shell on the structural, electronic and magnetic properties of Fe3O4 NPs is revealed by high-level hybrid density functional calculations. Hydrated Fe3O4 NPs possess larger magnetic moment than dehydrated ones. This work bridges the large gap between experimental studies on solvated Fe3O4 NPs and theoretical investigations on flat Fe3O4 surfaces covered with water and paves the way for further study of Fe3O4 NPs in biological environments.
1. Introduction
Magnetite (Fe3O4) nanoparticles (NPs) are top-class materials for biomedical applications because of their excellent soft magnetism (high saturation magnetization and low coercive force), good biocompatibility and low cytotoxicity.1,2 They are used as new generation contrast agents for magnetic resonance imaging (MRI) and are ideal materials for targeted drug delivery, magnetic hyperthermia, bioseparation and biosensors.3–7 They are also widely used in catalysis.8 Fe3O4 NPs with variable sizes and different shapes including cubes, octahedra, rhombic dodecahedral, truncated octahedral and spheres have been successfully synthesized.9–16Because Fe3O4 NPs are often prepared from aqueous solutions14,15,17 and because in most of the potential applications mentioned above Fe3O4 NPs are supposed to act in an aqueous environment, the surface/water interface as well as the solvation shells around the NP is expected to play a crucial role.18 However, the detailed atomistic description of the surface water chemistry and of the multilayer dynamical structures is not easy to be achieved, both experimentally and theoretically, and, in addition to that, it may largely depend on the NP shape and exposed facets.
Several studies have been conducted to explore the adsorption of water molecules on flat Fe3O4 surfaces.19–27 For instance, combining X-ray photoelectron spectroscopy (XPS) and density functional theory (DFT) calculations, Kendelewicz and co-workers proposed that, at low water vapor pressure and room temperature, water would not adsorb dissociatively on the Fe3O4(001) surface, except on defect sites and that dissociation can be observed only between water vapor partial pressures of 10−4 and 10−2 Torr.19,21 At high water coverage on the Fe3O4(001) surface, a mixed dissociated and undissociated adsorption mode was suggested by LEED,22 XPS21,25 and high-resolution electron energy loss spectroscopy (HREELS).23 Similarly, on the Fe3O4(111) surface, both dissociated water and undissociated water exist with increasing coverage, according to ultraviolet photoelectron spectroscopy (UPS) and thermal desorption spectroscopy (TDS).24 On the theoretical side, DFT+U, hybrid density functional and density functional tight binding calculations indicate that, on the Fe3O4(001) surface, isolated water molecules would not dissociate, whereas, at high water coverage, a mixed adsorption mode is favored.25–27 Water overlayers on the Fe3O4(001) surface were also investigated by multiscale molecular dynamics simulations.27
However, as mentioned above, the interface between liquid water and Fe3O4 NPs is far different from considering water molecules on flat Fe3O4 surfaces. The detailed structure of the hydration shells for magnetite NPs in water was rarely investigated. By XPS and isosteric heat of adsorption, Tombácz proposed that a high density of hydroxyl groups exists at the surface of Fe3O4 NPs when exposed to water vapor.28 By high-energy X-ray scattering, three distinct interatomic distance peaks (1.48, 1.95 and 2.39 Å) around faceted Fe3O4 NPs in water were found, which are attributed to hydrogen bonds between surface O atoms and H atoms in water, the Fe–O distance between Fe atoms on the surface and O atoms in molecular and dissociated water molecules.29
To our knowledge, the theoretical study of magnetite NPs in water has not yet been performed for the main reason that the accurate simulation of magnetite NPs of realistic size in bulk water with quantum chemical methods is computationally very demanding. Magnetite is a complex magnetic material, which requires high-level quantum mechanical (QM) techniques, beyond standard density functional theory (DFT), for its correct description.26,30 Surrounding magnetite NPs with liquid water is, however, not feasible with DFT methods. Recently, through the development of new Fe–O interaction parameters, we managed to well describe magnetite by the Hubbard corrected self-consistent charge density functional tight-binding (SCC-DFTB+U; from now on, DFTB+U) method, which is a cheap and efficient quantum mechanical simulation method with comparable accuracy to DFT.31 Then, by combining DFTB+U and hybrid DFT methods, we finally succeeded in the quantum mechanical simulation of Fe3O4 NPs of realistic size (about 2.5 nm) and different shapes under vacuum.32
In the present study, we have first investigated the adsorption behavior of one isolated water molecule on the Fe3O4 NP surface by putting one water molecule in contact with the bare roundish Fe3O4 NPs from our previous work.32 Then, we have adsorbed a water monolayer on a roundish NP and performed a global minimum structure search by a high temperature annealing process simulated by DFTB+U dynamics. At the end, by means of a multiscale approach, we surrounded the water-saturated NP with several water multilayers with the aim of simulating bulk water. The theoretical simulations are discussed in comparison with documented experimental data by high-energy X-ray scattering.29
The extent of water dissociation on the surface of Fe3O4 NPs is obtained by performing DFTB+U dynamic simulations, whereas the influence of the first hydration shell on the structural, electronic and magnetic properties of Fe3O4 NPs is studied at the hybrid DFT level of theory. On top of that, by performing a quantum mechanics/molecular mechanics (QM/MM) molecular dynamics simulation of Fe3O4 NP in bulk water, we obtain the atomistic insight into the structure of the solvation shells.
Our work fills the gap in theoretical simulations of magnetite NPs in water. It provides a clear picture of the chemistry at the NP surface and of the hydration shell structure around the NP of realistic size (about 1000 atoms) immersed in liquid water (more than 7000 water molecules). Understanding the fundamental properties of these types of interfaces is crucial for the development of nanoparticle-based applications in aqueous media.
2. Computational details
2.1 DFT calculations
Hybrid DFT calculations (HSE0633) were carried out using the CRYSTAL17 package34,35 for investigating the structural, electronic and magnetic properties of the Fe3O4 NP with one water monolayer adsorbed on it. In these calculations, the Kohn–Sham orbitals are expanded in Gaussian-type orbitals (the all-electron basis sets adopted for the elements in our model systems are H|5-11G*, O|8-411G* and Fe|8-6-411G*, according to the previous work on Fe3O4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 30). The convergence criterion of 0.02 eV Å−1 for force was used for geometry optimization and the convergence criterion for total energy was set as 10−6 Hartree for all the calculations.
30). The convergence criterion of 0.02 eV Å−1 for force was used for geometry optimization and the convergence criterion for total energy was set as 10−6 Hartree for all the calculations.
2.2 DFTB calculations
SCC-DFTB, which is a method cheaper and faster than DFT, can well describe Fe3O4 bulk, surface, NPs and the water/Fe3O4 interfaces.27,31,32 The SCC-DFTB method36–38 is an approximated DFT-based method that derives from the second-order expansion of the Kohn–Sham total energy in DFT with respect to the electron density fluctuations. The SCC-DFTB total energy can be defined as: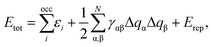 | (1) |
The SCC-DFTB calculations were carried out using the DFTB+ package.39 The “trans3d-0-1” set of parameters40 are used for the Fe–Fe and Fe–H interactions, and the “mio-1-1” set of parameters36 are used for the O–O, H–O and H–H interactions. For the Fe–O interactions, we used the Slater–Koster files fitted by some of us previously,31 which can well describe Fe3O4 bulk, surface, NPs and the water/Fe3O4 interfaces.27,31,32 SCC-DFTB+U41 with an effective U − J value of 3.5 eV was adopted to properly deal with the strong correlation effects among Fe 3d electrons, according to our previous work on magnetite.26,30,32 The convergence criterion of 10−4 a.u. for force was used during geometry optimization and the convergence threshold on the self-consistent charge (SCC) procedure was set to be 10−5 a.u.
SCC-DFTB+U molecular dynamics was performed within the canonical ensemble (NVT) to obtain the global minimum structure of the Fe3O4 NP with one monolayer water adsorption. The time step was set as 1 fs and an Andersen thermostat42 was used to target the desired temperatures. To simulate the temperature annealing processes, the NP with a water monolayer was quickly heated up to 500 K (about 0.5 ps), kept at 500 K for 3.5 ps and then cooled down slowly to 100 K, when no further structural changes were expected. The total simulation time is 24.5 ps. To well describe the hydrogen bonds, a modified hydrogen bonding damping (HBD) function was introduced with a ζ = 4 parameter43 for the SCC-DFTB+U calculations.
2.3 QM/MM calculations
The QM/MM molecular dynamics in this work is carried out through the additive-coupling scheme,44,45 in which the total potential energy for the system is given by| ETOTAL = EQM + EMM + EQM/MM, | (2) |
The coupling between the QM and MM regions consists of an electrostatic term calculated as the Coulomb interaction between the atomic charges of the QM part and the charges of the MM atoms, whereas all the non-Coulomb interactions (van der Waals) between the subsystems have been implemented as a Lennard–Jones (12–6) type potential,
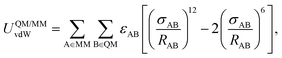 | (3) |
To model the roundish Fe3O4 NP embedded in bulk water, we put the optimized hydrated NP into a water droplet with a diameter of 8 nm by using the PACKMOL program.52 Molecular dynamics was performed within the NVT ensemble with a target temperature of 300 K maintained constant using the Berendsen thermostat. The Newton's equations of motion were integrated in time using the Velocity–Verlet algorithm53 with a time step of 1 fs. The system has been equilibrated for 10 ps and then a production run has been performed for 20 ps.
2.4 MM calculations
The potential energy form for the classical description of the systems is based on the well-established COMPASS force field54 that estimates the vdW forces through a Lennard–Jones (6–9) potential while long-range electrostatics is modeled by a classical Coulomb potential, given by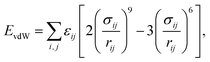 | (4) |
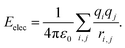 | (5) |
Herein, σij stands for the inter-atomic distance between a pair of atoms at which the potential energy reaches a minimum value, and εij defines the potential well depth of the attractive component. qi and qj represent the partial atomic charges on the classical atoms i and j, separated by an inter-atomic distance rij. For unlike atoms, the sigma and epsilon LJ (6–9) cross-parameters are calculated by the 6th power combining rules55 given by eqn (6) and (7), respectively:
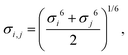 | (6) |
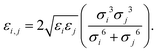 | (7) |
All MM-MD simulations were carried out with the LAMMPS program (version 7 Aug 2019).56 The atomic coordinates of the Fe, O, and H atoms in the partially hydroxylated Fe3O4 NS are frozen at the DFTB-optimized geometry by zeroing the forces on these atoms every MM-MD simulation step. The partially hydrated NP is obtained by removing all the molecular water from the optimized fully hydrated NP. To solvate this system, we made use of the PACKMOL program52 to randomly put water molecules around the Fe3O4 NP within a simulation box of 100 × 100 × 100 Å3. Bonded and non-bonded FF parameters for the COMPASS-based three-site water model and the hydroxyl group are taken from the INTERFACE-FF.57 The LJ (6–9) parameters for the Fe(II), Fe(III), and O(II) atom-types in the Fe3O4 NP are taken from ref. 50. For the Fe–O cross-interaction, we use an optimized set of LJ (6–9) parameters available in ref. 58. The partial-atomic charges on the magnetite atoms are derived from the DFT/HSE06 calculations in line with our previous work.27
To vanish any atomic overlapping and minimize the total energy of the system before the equilibration phase, we carried out a minimization phase with a maximum number of 500![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps and a convergence tolerance of 10−7 for forces through the conjugate gradient algorithm. The equilibration phase was carried out for 10 ns in the isotherm–isobaric (NVT) ensemble until convergence of the bulk-water density at T = 300 K. The production phase explored 50 ns of the phase space in the NVT ensemble at T = 300 K. Electrostatic and LJ (6–9) potentials utilized a cut-off of 10 Å, and the Newton's equations of motion were solved using the Velocity–Verlet integrator53 with a time step of 1.0 fs. The long-range solver particle–particle particle–mesh (PPPM)59 handled the electrostatic interactions with a threshold of 10−6 for forces under Periodic Boundary Conditions (PBC).
000 steps and a convergence tolerance of 10−7 for forces through the conjugate gradient algorithm. The equilibration phase was carried out for 10 ns in the isotherm–isobaric (NVT) ensemble until convergence of the bulk-water density at T = 300 K. The production phase explored 50 ns of the phase space in the NVT ensemble at T = 300 K. Electrostatic and LJ (6–9) potentials utilized a cut-off of 10 Å, and the Newton's equations of motion were solved using the Velocity–Verlet integrator53 with a time step of 1.0 fs. The long-range solver particle–particle particle–mesh (PPPM)59 handled the electrostatic interactions with a threshold of 10−6 for forces under Periodic Boundary Conditions (PBC).
3. Results and discussion
3.1 First hydration shell around the Fe3O4 NP: adsorption of a water monolayer
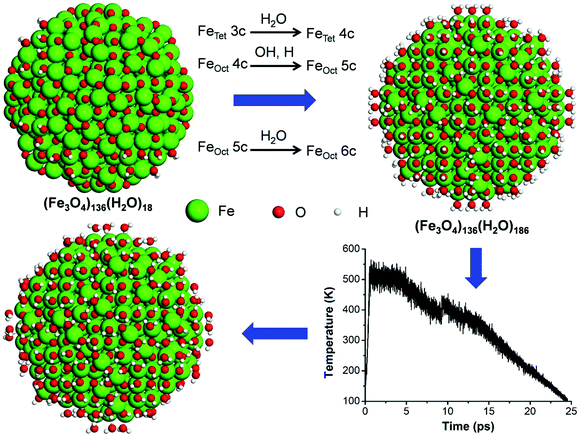
In our previous work, we have obtained the global minimum structure of a roundish Fe3O4 NP under vacuum ((Fe3O4)136(H2O)18) with a diameter of 2.5 nm.32 We expect that water adsorption might affect the curved surface structure. Before putting a whole water monolayer around the Fe3O4 NP, we first investigate the adsorption behavior of a single isolated water molecule on the various undercoordinated Fe sites present on the surface.32 We define two kinds of Fe ions in the NP, FeTet and FeOct, depending on the occupied type of bulk lattice site (tetrahedral and octahedral) and we keep this classification even when they become undercoordinated at the NP surface. Labels, including 3c, 4c, 5c and 6c, are then added to indicate the actual coordination number of the corresponding ions. For example, FeTet-3c and O3c are a three-fold coordinated Fe ion at a tetrahedral site and a three-fold coordinated O ion, respectively.According to previous studies,21–26 both molecular and dissociated (split into OH and H) water are present on flat Fe3O4 surfaces, with the water O atom chemically bound to surface Fe ions. Therefore, both molecular and dissociated adsorption modes are considered at different Fe sites on the NP surface and the resulting binding energy values for a single water molecule adsorbed on various sites are listed in Table 1. On FeTet-3c sites, molecular adsorption is preferred, except for few cases where the H atom from dissociated water adsorbs on a two-fold coordinated surface oxygen atom (O2c). This indicates that O2c is far more reactive than O3c, as one would expect. This agrees with previous results, which show that a single water molecule would not dissociate on FeTet-3c sites of the Fe3O4(111) surface60 because all the O atoms on the surface are three-fold coordinated. In contrast, on FeOct-4c sites, the dissociated mode is always favored with respect to the molecular mode, independent of the O site where H is adsorbed. On FeOct-5c sites, the situation is similar to that on FeTet-3c sites, i.e. molecular adsorption is preferred, except when the dissociated H atom binds to a surface O2c site.
| Adsorption site | Adsorption mode | E b (eV) |
|---|---|---|
| FeTet-3c | Molecular | −1.65 to −1.75 |
| Dissociated (H on O3c) | −0.91 to −1.00 | |
| Dissociated (H on O2c) | −1.32 to −1.74 | |
| FeOct-4c | Molecular | −1.82 to −1.95 |
| Dissociated (H on O3c) | −2.84 to −2.99 | |
| Dissociated (H on O2c) | −3.17 to −3.90 | |
| FeOct-5c | Molecular | −1.50 to −1.86 |
| Dissociated (H on O3c) | −1.11 to −1.24 | |
| Dissociated (H on O2c) | −1.32 to −1.89 | |
On the basis of the results above, we built an initial model of water-saturated Fe3O4 NPs by putting one undissociated water molecule on every FeTet-3c and FeOct-5c sites, one OH and one undissociated water molecule on every FeOct-4c site of the roundish NP cut from bulk Fe3O4 ((Fe3O4)136(H2O)18) from our previous work,32 as shown in Fig. 1. As a consequence, all the Fe ions in the NP become fully coordinated, leading to the molecular chemical formula of (Fe3O4)136(H2O)186. The H atoms from dissociated water are put preferentially on O2c on the NP surface.
We must note that the dissociation behavior depends not only on the adsorption sites but also on the extent of water coverage, as indicated by the studies of water on flat Fe3O4 surfaces.21–26 To obtain the global minimum structure of the water-saturated Fe3O4 NP, we then performed the MD run, with the DFTB+U method, simulating a temperature annealing process up to 500 K, whose temperature profile is shown in Fig. 1. After the annealing, the Fe3O4 NP was further fully optimized at the more accurate hybrid density functional HSE06 level of theory. We observe that, after the annealing, about half of water molecules on FeTet-3c dissociate into OH and H. Some of the H atoms from water dissociation go to O atoms on the NP surface and some of them react with OH on FeOct sites forming molecular water again. The simultaneous dissociation and reforming water processes are due to the complex geomorphology of the NP surface, which cannot be found on flat surfaces. In the end, 43% water molecules on the NP surface are dissociated, indicating the strong ability of the NP surface to provoke this reaction. This agrees well with previous experimental work, in which a high density of hydroxyl groups at the surface of Fe3O4 NPs was found when exposed to water vapor.28
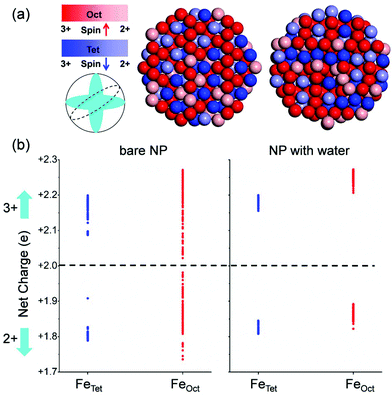
By comparing the simulated extended X-ray absorption fine structure (EXAFS) of Fe3O4 bulk, of the NP under vacuum and of the water-saturated NP (with one adsorbed monolayer), as shown in Fig. S1 in the ESI,† we can conclude that water adsorption improves the degree of crystallinity of the NP due to the saturation of low-coordinated Fe ions on the surface. This agrees with a previous study on ZnS nanoparticles, which shows that the binding of water to the as-formed ZnS nanoparticles significantly reduces distortions of the surface.61 We expect that besides affecting the structure, water adsorption will have consequences also on the electronic and magnetic properties of Fe3O4 NPs. To prove this, we investigated the charge and spin distribution in the magnetite NP covered with a water monolayer using the HSE06 method, as shown in Fig. 2. Interestingly, we find that FeTet2+ ions exist not only on the surface but also inside the NP (Fig. 2a), which is in sharp contrast with the situation for the roundish Fe3O4 NP under vacuum, where FeTet2+ ions only exist on the surface. Detailed analysis of the charges of all the Fe ions in roundish Fe3O4 NP, under vacuum and under water covering, is shown in Fig. 2b. In sharp contrast with the NP under vacuum, the charge grouping in the water-saturated NP is more pronounced, similar to what has been observed in bulk magnetite.30 Therefore, we can state that the effect of water adsorption is to make the NP more crystalline not only from the structural point of view but also from the charge ordering one.
The total magnetic moment (mtot) of the water-saturated Fe3O4 NP is determined by a series of HSE06 full atomic relaxation calculations considering different mtot values. As shown in Fig. S2 in the ESI,† the optimal mtot of the NP after water saturation increases to 656μB from 600μB under vacuum, with high benefit for biomedical applications where NPs with high magnetic moments are more effective. The increment of the mtot can be rationalized by the change in the charge distribution mentioned above. After water saturation, the number of FeTet2+ ions (N(FeTet2+)) increases and the number of FeTet3+ ions (N(FeTet3+)) decreases. In the meantime, the number of FeOct3+ (N(FeOct3+)) increases and the number of FeOct2+ (N(FeOct2+)) decreases in order to maintain the neutrality of the NP. As a consequence, according to the formula for estimating the mtot of Fe3O4 NPs, proposed in our previous work,32i.e. mtot = 5 × (N(FeOct3+) − N(FeTet3+)) + 4 × (N(FeOct2+) − N(FeTet2+)), the mtot increases. Finally, we must note that the main features of the electronic structure of the NP do not change much after water saturation, as indicated by comparison of the density of states shown in Fig. S3 in the ESI.†
3.2 Immersion of the hydrated Fe3O4 NP in bulk water
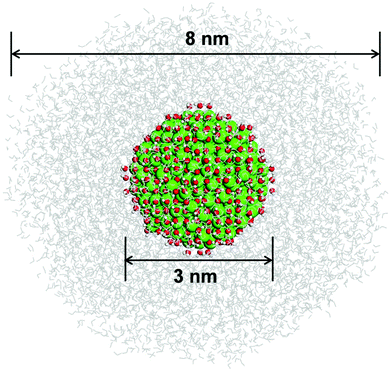
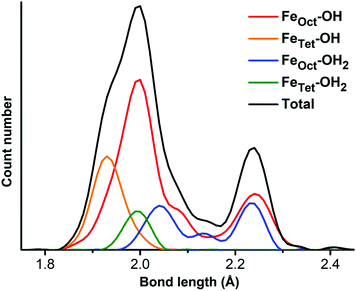
As mentioned in the introduction, to gain a detailed structural insight into the water solvation shells around the roundish Fe3O4 NP, we built a realistic model by immersing the optimized fully hydrated Fe3O4 NP from the previous section into a water droplet with a diameter of 8 nm, as shown in Fig. 3. Then a multiscale QM/MM molecular dynamics simulation has been performed at 300 K for 30 ps, where the hydrated Fe3O4 NP is treated at the DFTB level, whereas the water molecules around are treated at the MM level.First, we focus on the innermost (first) hydration shell, i.e., the direct bonds between surface Fe ions and OH and H2O, which is treated at the DFTB level of theory. The bond length distribution of the Fe–O at the NP/water interface is plotted in Fig. 4. There is a prominent peak centered at 1.99 Å with a shoulder at 1.93 Å, which can well explain the experimentally observed peak at 1.95 Å.29 By projecting the total Fe–O bond length distribution for different Fe ions (FeTet and FeOct) with different O ions (O in OH and H2O), the peak can be rationalized in detail. The peak at 1.99 Å is mainly contributed by bonds between FeOct ions and OH (red line in Fig. 4) and the shoulder at 1.93 Å is due to the bonds between FeTet and OH (orange line). The bond length of FeTet–OH2 is also around 1.99 Å (green line). The bond lengths of FeOct–OH2 are longer than those of FeTet–OH2 and are widely distributed in the range from 1.99 Å to 2.26 Å (blue line). Another peak centered at 2.24 Å (black line) is very close to the experimentally observed peak at 2.39 Å,29 which is contributed by both FeOct–OH and FeOct–OH2 bonds. Note that the FeOct–OH bond length depends on the coordination of the O atom of the OH group. When one OH is bonded to one Fe ion, the bond length is shorter (peak at 1.99 Å), whereas when one OH is bonded with two Fe ions, the bond length is longer (peak at 2.24 Å).
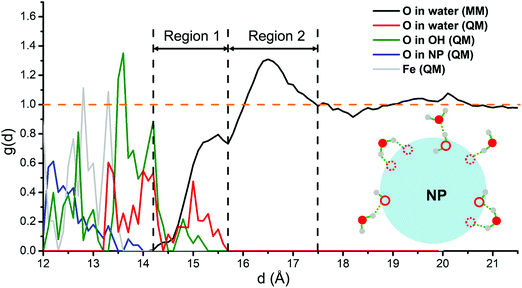
Then, we analyze all the hydration shells. We extract from the QM/MM molecular dynamics runs the radial distribution function (RDF), g(d), of O in water molecules with respect to the NP center. To gain a deeper insight into the Fe3O4 NP/water interface, a decomposed RDF based on the O-type is presented in Fig. 5, i.e., O from molecular water molecules in the MM part (black line), O from molecular water molecules in the QM part (red line) and O from the dissociated OH in the QM part (green line) are shown, respectively. The RDF is normalized by the density of bulk water. In addition, to clearly set the position of the NP surface, the RDFs of the O and Fe atoms in the NP, with meaningless y-values, are also plotted (blue and gray lines, respectively). According to the RDF (blue, gray and green lines), the NP surface atoms are set in a window range of distances between 12 Å and 14 Å, because the NP is not perfectly spherical. Consequently, the water O atoms directly bonded with surface Fe ions present a wide distribution of d values (green and red lines).
The distribution of O in water in the MM part (black line in Fig. 5) presents two clear peaks, one centered at 15.5 Å and the other at 16.5 Å. Through a detailed check of the structures of MM water molecules during the dynamics in the range between 14.2 Å and 15.7 Å (about 2 to 3 Å from the NP surface), we could unravel the nature of the interactions in this region 1, which are schematically shown in Fig. 5. Some of the water molecules in region 1 interact with the surface O of the NP through hydrogen bonds and some of them interact with the innermost hydration shell through hydrogen bonds.
Based on the analysis above, therefore, we can classify the water molecules and OH directly bonded with Fe ions as the first hydration shell, whereas the water molecules in region 1 as the second hydration shell. All the water molecules in region 2 of Fig. 5 do not interact directly with the NP but interact with the second hydration shell through hydrogen bonds and, therefore, can be classified as the third hydration shell. The RDF quickly converges to 1.0 after 17.5 Å, indicating that the water above 5 Å from the NP surface is essentially bulk water. Similarly, previous MM molecular dynamics simulations show that water close to the surfaces of the hematite nanoparticles also forms several ordered layers.62
Note that during the QM/MM molecular dynamics, atoms in the QM part are frozen to their optimized position due to some technical issues. Therefore, the absolute value of the RDF intensity for the O in the QM part (green and red lines) is not precise. However, we believe that atoms in the first hydration shell would not move so much during the dynamics because they are tightly bonded to the NP surface atoms.
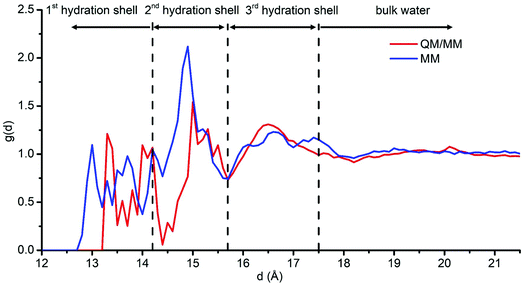
To exclude any effect of freezing water molecules during the QM/MM molecular dynamics, we also performed MM molecular dynamics where all the water molecules are free to move for a longer simulation run (60 ns in total) and in a larger box (10 nm × 10 nm × 10 nm). In this model, the partially hydrated NP, obtained by removing all the molecular water from the optimized hydrated NP, is fully optimized by DFTB+U and then put in a large water box. The RDF for the O atoms in the water molecules based on the last 50 ns of the MM molecular dynamics run is shown in Fig. 6 (blue line). To compare the MM results with those from the QM/MM simulation, we must sum up the black and red lines (not the pink one) in Fig. 5 and display the resulting merged red line in Fig. 6, because the RDF extracted from the MM calculations is only for the O atoms belonging to molecular (undissociated) water molecules, which does not include the contributions of dissociated OH groups fixed on the NP surface. In general, the curves from QM/MM and MM agree quite well one with the other, indicating three hydration shells. However, there is a shift of peaks (about 0.3 Å) in the first hydration shell. This shift is because the optimized force field parameters used in the MM simulation tend to maximize the number of hydrogen bonds established by water molecules with the nanoparticle surface atoms, resulting in a shorter distance between O in water molecules and the center of the NP, as discussed in our previous paper.58 The good agreement between QM/MM and MM data not only confirms the reliability of our results but also suggests that with a chemically stable and fully optimized Fe3O4 NP structure (by hybrid density functional methods) and with reasonable force field parameters58 MM molecular dynamics can be an extremely efficient way to explore Fe3O4 NP/water interfaces and even more complex systems, such as functionalized Fe3O4 NPs in water for biomedical applications.
4. Conclusions
In this work, we presented a multistep investigation of the interaction of roundish Fe3O4 NPs with water, based on hybrid DFT, QM(DFTB)/MM and MM calculations.At the hybrid DFT level of theory, we first investigated single water molecule adsorption modes on various types of uncoordinated Fe sites present on a realistic curved nanoparticle. Then, by decorating all the adsorption sites, we studied a full water monolayer coverage and observed the effect of the first hydration shell on the structural and electronic properties of Fe3O4 NPs: they become more crystalline and the total magnetic moment increases, which has a positive impact on their nanomedical applications. We found out that 43% of water molecules in the first hydration shell dissociate, suggesting a high tendency of roundish Fe3O4 NPs to become hydroxylated.
By a multi-scale approach combining the density functional tight-binding method and classical force field calculations (QM(DFTB)/MM), we investigated the atomistic structure of the hydration shells around the roundish Fe3O4 NP immersed in bulk water. We identified three hydration shells and determined that above 5 Å away from the NP surface water holds essentially its bulk properties. The bond length distribution of the Fe–O at the NP/water interface successfully explains the experimental observations. Interactions between the first and the second hydration shells as well as between the second and the third hydration shells are mainly through H-bonds. Parallel MM calculations lead to very similar results, which suggest that the very cheap MM approach could be used to obtain reliable information on the dynamical behavior of magnetite NPs in aqueous media.
Our work fills the gap in theoretical simulations of magnetite NPs in water and paves the way for further studies of more complex functionalized Fe3O4 NPs in biological environments for nanomedical applications.
Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The project has received funding from the European Research Council (ERC) under the European Union's HORIZON2020 Research and Innovation Programme (ERC Grant Agreement No. 647020).References
- J. M. Perez, L. Josephson, T. O'Loughlin, D. Högemann and R. Weissleder, Nat. Biotechnol., 2002, 20, 816–820 CrossRef CAS PubMed.
- J. Liu, Z. Sun, Y. Deng, Y. Zou, C. Li, X. Guo, L. Xiong, Y. Gao, F. Li and D. Zhao, Angew. Chem., Int. Ed., 2009, 48, 5875–5879 CrossRef CAS PubMed.
- W. Wu, Z. Wu, T. Yu, C. Jiang and W. Kim, Sci. Technol. Adv. Mater., 2015, 16, 023501 CrossRef PubMed.
- Q. A. Pankhurst, N. T. K. Thanh, S. K. Jones and J. Dobson, J. Phys. D: Appl. Phys., 2009, 42, 224001 CrossRef.
- C. Sun, J. S. Lee and M. Zhang, Adv. Drug Delivery Rev., 2008, 60, 1252–1265 CrossRef CAS PubMed.
- S. Laurent, D. Forge, M. Port, A. Roch, C. Robic, L. V. Elst and R. N. Muller, Chem. Rev., 2008, 108, 2064–2110 CrossRef CAS PubMed.
- M. Colombo, S. Carregal-Romero, M. F. Casula, L. Gutiérrez, M. P. Morales, I. B. Böhm, J. T. Heverhagen, D. Prosperi and W. J. Parak, Chem. Soc. Rev., 2012, 41, 4306–4334 RSC.
- M. B. Gawande, P. S. Brancoa and R. S. Varma, Chem. Soc. Rev., 2013, 42, 3371 RSC.
- S. Sun and H. Zeng, J. Am. Chem. Soc., 2002, 124, 8204–8205 CrossRef CAS PubMed.
- Y. Hou, J. Yu and S. Gao, J. Mater. Chem., 2003, 13, 1983–1987 RSC.
- J. Park, K. An, Y. Hwang, J. Park, H. Noh, J. Kim, J. Park, N. Hwang and T. Hyeon, Nat. Mater., 2004, 3, 891–895 CrossRef CAS PubMed.
- M. V. Kovalenko, M. I. Bodnarchuk, R. T. Lechner, G. Hesser, F. Schäffler and W. Heiss, J. Am. Chem. Soc., 2007, 129, 6352–6353 CrossRef CAS PubMed.
- L. Zhao and L. Duan, Eur. J. Inorg. Chem., 2010, 5635–5639 CrossRef CAS.
- X. Li, D. Liu, S. Song, X. Wang, X. Ge and H. Zhang, CrystEngComm, 2011, 13, 6017–6020 RSC.
- L. Zhao, H. Zhang, Y. Xing, S. Song, S. Yu, W. Shi, X. Guo, J. Yang, Y. Lei and F. Cao, Chem. Mater., 2008, 20, 198–204 CrossRef CAS.
- A. G. Roca, M. P. Morales and C. J. Serna, IEEE Trans. Magn., 2006, 42, 3025–3029 Search PubMed.
- X. Cheng, J. Jiang, D. Jiang and Z. Zhao, J. Phys. Chem. C, 2014, 118, 12588–12598 CrossRef CAS.
- A. E. Nel, L. Mädler, D. Velegol, T. Xia, E. M. V. Hoek, P. Somasundaran, F. Klaessig, V. Castranova and M. Thompson, Nat. Mater., 2009, 8, 543–557 CrossRef CAS PubMed.
- T. Kendelewicz, P. Liu, C. S. Doyle, G. E. Brown, E. J. Nelson and S. A. Chambers, Surf. Sci., 2000, 453, 32–46 CrossRef CAS.
- G. S. Parkinson, Z. Novotný, P. Jacobson, M. Schmid and U. Diebold, J. Am. Chem. Soc., 2011, 133, 12650–12655 CrossRef CAS PubMed.
- T. Kendelewicz, S. Kaya, J. T. Newberg, H. Bluhm, N. Mulakaluri, W. Moritz, M. Scheffler, A. Nilsson, R. Pentcheva and G. E. Brown, J. Phys. Chem. C, 2013, 117, 2719–2733 CrossRef CAS.
- N. Mulakaluri, R. Pentcheva, M. Wieland, W. Moritz and M. Scheffler, Phys. Rev. Lett., 2009, 103, 176102 CrossRef PubMed.
- S. Liu, S. Wang, W. Li, J. Guo and Q. Guo, J. Phys. Chem. C, 2013, 117, 14070–14074 CrossRef CAS.
- Y. Joseph, C. Kuhrs, W. Ranke and W. Weiss, Surf. Sci., 1999, 433–435, 114–118 CrossRef CAS.
- M. Meier, J. Hulva, Z. Jakub, J. Pavelec, M. Setvin, R. Bliem, M. Schmid, U. Diebold, C. Franchini and G. S. Parkinson, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E5642–E5650 CrossRef CAS PubMed.
- H. Liu and C. Di Valentin, Nanoscale, 2018, 10, 11021 RSC.
- H. Liu, E. Bianchetti, P. Siani and C. Di Valentin, J. Chem. Phys., 2020, 152, 124711 CrossRef CAS PubMed.
- E. Tombácz, A. Hajdú, E. Illés, K. László, G. Garberoglio and P. Jedlovszky, Langmuir, 2009, 25, 13007–13014 CrossRef PubMed.
- S. L. J. Thomä, S. W. Krauss, M. Eckardt, P. Chater and M. Zobel, Nat. Commun., 2019, 10, 995 CrossRef PubMed.
- H. Liu and C. Di Valentin, J. Phys. Chem. C, 2017, 121, 25736 CrossRef CAS PubMed.
- H. Liu, G. Seifert and C. Di Valentin, J. Chem. Phys., 2019, 150, 094703 CrossRef PubMed.
- H. Liu and C. Di Valentin, Phys. Rev. Lett., 2019, 123, 186101 CrossRef CAS PubMed.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef PubMed.
- R. Dovesi, A. Erba, R. Orlando, C. M. Zicovich-Wilson, B. Civalleri, L. Maschio, M. Rerat, S. Casassa, J. Baima, S. Salustro and B. Kirtman, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1360 Search PubMed.
- R. Dovesi, V. R. Saunders, C. Roetti, R. Orlando, C. M. Zicovich-Wilson, F. Pascale, B. Civalleri, K. Doll, N. M. Harrison, I. J. Bush, P. D'Arco, M. Llunell, M. Causà, Y. Noël, L. Maschio, A. Erba, M. Rerat and S. Casassa, CRYSTAL17 User's Manual, University of Torino, Torino, Italy, 2017 Search PubMed.
- M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260 CrossRef CAS.
- G. Seifert and J. Joswig, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 456 CAS.
- M. Elstner and G. Seifert, Philos. Trans. R. Soc., A, 2014, 372, 20120483 CrossRef PubMed.
- B. Aradi, B. Hourahine and T. Frauenheim, J. Phys. Chem. A, 2007, 111, 5678 CrossRef CAS PubMed.
- G. Zheng, H. A. Witek, P. Bobadova-Parvanova, S. Irle, D. G. Musaev, R. Prabhakar and K. Morokuma, Theory Comput., 2007, 3, 1349 CrossRef PubMed.
- B. Hourahine, S. Sanna, B. Aradi, C. Köhler, Th. Niehaus and T. Frauenheim, J. Phys. Chem. A, 2007, 111, 5671 CrossRef CAS PubMed.
- H. C. Andersen, J. Chem. Phys., 1980, 72, 2384 CrossRef CAS.
- H. Hu, Z. Lu, M. Elstner, J. Hermans and W. Yang, J. Phys. Chem. A, 2007, 111, 5685–5691 CrossRef CAS PubMed.
- H. Lin and D. G. Truhlar, Theor. Chem. Acc., 2007, 117, 185 Search PubMed.
- W. Han, M. Elstner, K. J. Jalkanen, T. Frauenheim and S. Suhai, Int. J. Quantum Chem., 2000, 78, 459–479 CrossRef CAS.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- A. O. Dohn, E. O. Jónsson, G. Levi, J. J. Mortensen, O. Lopez-Acevedo, K. S. Thygesen, K. W. Jacobsen, J. Ulstrup, N. E. Henriksen and K. B. Møller, J. Chem. Theory Comput., 2017, 13, 6010 CrossRef CAS PubMed.
- D. A. Case, R. M. Betz, D. S. Cerutti, T. E. Cheatham, III, T. A. Darden, R. E. Duke, T. J. Giese, H. Gohlke, A. W. Goetz, N. Homeyer, S. Izadi, P. Janowski, J. Kaus, A. Kovalenko, T. S. Lee, S. LeGrand, P. Li, C. Lin, T. Luchko, R. Luo, B. Madej, D. Mermelstein, K. M. Merz, G. Monard, H. Nguyen, H. T. Nguyen, I. Omelyan, A. Onufriev, D. R. Roe, A. Roitberg, C. Sagui, C. L. Simmerling, W. M. Botello-Smith, J. Swails, R. C. Walker, J. Wang, R. M. Wolf, X. Wu, L. Xiao and P. A. Kollman, AMBER 2016, University of California, San Francisco, 2016 Search PubMed.
- F. Paesani, W. Zhang, D. A. Case, T. E. Cheatham and G. A. Voth, J. Chem. Phys., 2006, 125, 184507 CrossRef PubMed.
- L. Zhao, L. Liu and H. Sun, J. Phys. Chem. C, 2007, 111, 10610–10617 CrossRef CAS.
- A. L. Parrill and K. B. Lipkowitz, Reviews in Computational Chemistry, Volume 29, John Wiley & Sons, Inc, Hoboken, NJ, 2016 Search PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157 CrossRef PubMed.
- L. Verlet, Phys. Rev., 1967, 159, 98 CrossRef CAS.
- H. Sun, J. Phys. Chem. B, 1998, 102, 7338–7364 CrossRef CAS.
- M. Waldman and A. T. Hagler, J. Comput. Chem., 1993, 14, 1077–1084 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- H. Heinz, T. J. Lin, R. Kishore Mishra and F. S. Emami, Langmuir, 2013, 29, 1754 CrossRef CAS PubMed.
- P. Siani, E. Bianchetti, H. Liu and C. Di Valentin, J. Chem. Phys., 2021, 154, 034702 CrossRef CAS PubMed.
- R. W. Hockney and J. W. Eastwood, Computer Simulation Using Particles, CRC Press, 1988 Search PubMed.
- P. Dementyev, K. Dostert, F. Ivars-Barcelý, C. P. OÏBrien, F. Mirabella, S. Schauermann, X. Li, J. Paier, J. Sauer and H. Freund, Angew. Chem., Int. Ed., 2015, 54, 13942–13946 CrossRef CAS PubMed.
- H. Zhang, B. Gilbert, F. Huang and J. F. Banfield, Nature, 2003, 424, 1025–1029 CrossRef CAS PubMed.
- D. Spagnoli, B. Gilbert, G. A. Waychunas and J. F. Banfield, Geochim. Cosmochim. Acta, 2009, 73, 4023–4033 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Simulated extended X-ray absorption fine structure spectra for the Fe3O4 bulk and nanoparticle. The relative total energy as a function of the total magnetic moment for the hydrated Fe3O4 NP. Partial density of states on the d orbits of different Fe ions in the Fe3O4 NP. See DOI: 10.1039/d1nr01014j |
| This journal is © The Royal Society of Chemistry 2021 |