Novel two-dimensional tetrahexagonal boron nitride with a sizable band gap and a sign-tunable Poisson's ratio†
Abstract
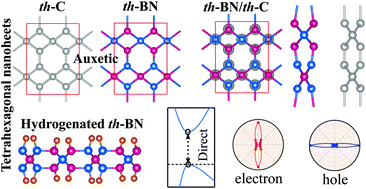
By performing first-principles calculations, a new two-dimensional (2D) boron nitride (th-BN) with perfectly ordered arrangements of tetragonal and hexagonal rings is predicted to be energetically, dynamically, thermally, and mechanically stable. The unique structure endows th-BN with anisotropic mechanical, electronic, and optical properties. Remarkably, th-BN exhibits exceptional mechanical properties such as high in-plane stiffness and sign-tunable Poisson's ratio (PR). The PR of th-BN gradually decreases with the increase of axial strain and even becomes negative at a very small strain (∼2%), which is novel, thereby offering the ability to become non-auxetic, auxetic, and partially auxetic 2D nanomaterials depending on the strain rate and direction. The structure can withstand tensile strain as large as 36%, and shows ultrahigh ideal strength that can even outperform graphene and hexagonal BN. The th-BN is a natural 2D semiconductor with an indirect wide band gap of 4.49 eV. The band gap can be tuned by applying lattice strain and hydrogenation. The full hydrogenated th-BN exhibits an indirect-to-direct band gap transition. The th-BN shows high optical absorption in the ultraviolet region. The optical absorption spectrum is highly direction-dependent and tunable by strain, suitable for high-performance optoelectronic device applications. Furthermore, th-BN can be stacked into two different configurations, and are dynamically stable and exhibit exotic electronic properties. The desirable direct band gap and anisotropic effective mass of the th-C/th-BN heterostructure suggest that th-BN can be a suitable substrate for tetrahexcarbon.
- This article is part of the themed collections: Nanoscale 2022 Lunar New Year Collection and Editor’s Choice: Controlling anisotropy in nanomaterials


 Please wait while we load your content...
Please wait while we load your content...