Open Access Article
Open Access ArticleAtomically resolved interfacial water structures on crystalline hydrophilic and hydrophobic surfaces†
Manuel R.
Uhlig‡
 a,
Simone
Benaglia‡
a,
Simone
Benaglia‡
 a,
Ravindra
Thakkar
b,
Jeffrey
Comer
a,
Ravindra
Thakkar
b,
Jeffrey
Comer
 b and
Ricardo
Garcia
b and
Ricardo
Garcia
 *a
*a
aInstituto de Ciencia de Materiales de Madrid, CSIC, c/Sor Juana Inés de la Cruz 3, 28049 Madrid, Spain. E-mail: r.garcia@csic.es
bNanotechnology Innovation Center of Kansas State, Department of Anatomy and Physiology, Kansas State University, Manhattan, Kansas 66506, USA
First published on 24th February 2021
Abstract
Hydration layers are formed on hydrophilic crystalline surfaces immersed in water. Their existence has also been predicted for hydrophobic surfaces, yet the experimental evidence is controversial. Using 3D-AFM imaging, we probed the interfacial water structure of hydrophobic and hydrophilic surfaces with atomic-scale spatial resolution. We demonstrate that the atomic-scale structure of interfacial water on crystalline surfaces presents two antagonistic arrangements. On mica, a common hydrophilic crystalline surface, the interface is characterized by the formation of 2 to 3 hydration layers separated by approximately 0.3 nm. On hydrophobic surfaces such as graphite or hexagonal boron nitride (h-BN), the interface is characterized by the formation of 2 to 4 layers separated by about 0.5 nm. The latter interlayer distance indicates that water molecules are expelled from the vicinity of the surface and replaced by hydrocarbon molecules. This creates a new 1.5–2 nm thick interface between the hydrophobic surface and the bulk water. Molecular dynamics simulations reproduced the experimental data and confirmed the above interfacial water structures.
Introduction
The interface of an aqueous solution with a solid surface is ubiquitous in chemistry, biology and technology. It participates in many processes from heterogeneous catalysis and electrochemistry to protein folding and cell signaling. Yet the molecular-scale understanding of the interactions between aqueous solutions and solid interfaces remains unsatisfactory.1,2Hydration layers are key components of the structure of interfacial water. Our understanding of hydration layers comes from the surface force apparatus,3,4 X-ray methods,5,6 high-resolution AFM images,7–12 molecular dynamics (MD) and other theoretical methods.1,13–19 The paradigm emerging from those results is that the attractive interaction of the water molecules with the atoms of the crystalline surface leads to an alternation of high and low density water layers.
The spacing between hydration layers measured on hydrophilic surfaces such as mica and calcite surfaces is about 0.3 nm,7 this is, very close to the van der Waals diameter of a water molecule. The same type of layering structure and spacing has been predicted by MD simulations on graphitic and other hydrophobic surfaces.14–16 Yet the experimental evidence is either inconclusive or controversial.20–28 Explanations about the structure and composition of interfacial water on a hydrophobic surface range from the formation of ice-like water24 to the adsorption of air-borne molecules27–29 or the layering of condensed gas molecules.25,26,29–31
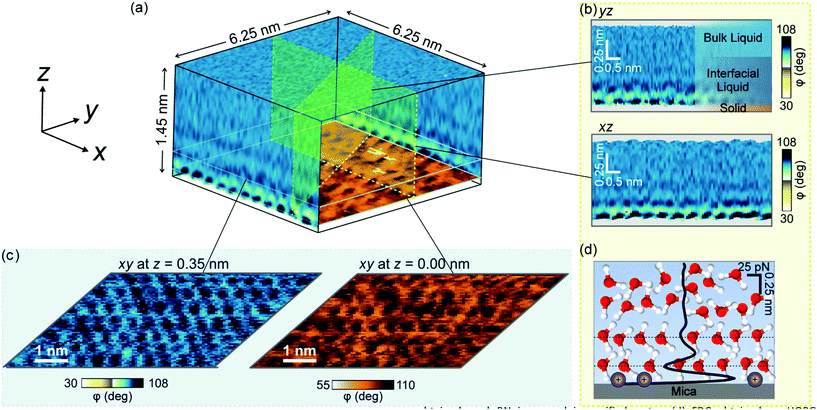
Here we have applied a newly developed AFM mode that provides atomic resolution 3D images of the organization of water on mica, graphite and h-BN to explain the structure of interfacial water on solid surfaces. Fig. 1a shows a volume AFM image of water on mica. Different 2D maps and images of the interface can be extracted from the volume data, such as maps perpendicular to the surface (Fig. 1b) or images parallel to it at different heights (Fig. 1c). The 2D maps perpendicular to the surface show the hydration layers, while the 2D images parallel to the surface reveal the mica lattice, the adsorbed ions or the organization of water molecules in the hydration layers. The data can be processed to obtain the dependence of the force as a function of the distance (FDC) to the surface (Fig. 1d).21,32–34
Results
AFM experiments
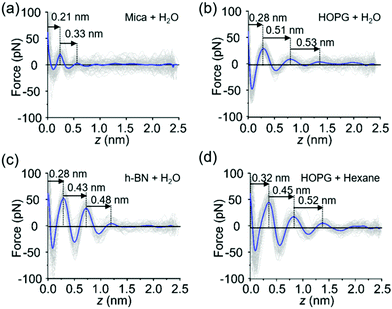
The FDCs measured on mica, graphite and h-BN surfaces immersed in liquid water provide quantitative information on the interfacial water (Fig. 2a–d). The force–distance curves show an oscillatory behaviour that alternates attractive and repulsive regions until the tip establishes mechanical contact with the surface. From then on, the force becomes increasingly repulsive. The peaks observed in the FDC were associated with peaks in the liquid density although they are not located at the same distance from the solid surface.35–37The shape of the FDCs measured on mica (Fig. 2a), graphite (Fig. 2b) and h-BN (Fig. 2c) are quite similar, however, the interlayer separations are different. The spacing between the layers measured on graphite (0.51 nm) and h-BN (0.43 nm) were larger than the interlayer separations measured on mica (0.3 nm). A variety of experimental results obtained on hydrophilic surfaces7 and MD simulations [see below] on both hydrophilic and hydrophobic surfaces13–17 indicates that the layering structure of water has a periodicity of 0.30 ± 0.03 nm. Therefore, the layering observed on graphite and h-BN is incompatible with the presence of water. Interestingly, the interlayer distances observed on graphite agree with the values measured in interfaces formed by organic solvents on a variety of crystalline surfaces.19,38–40 In addition, the values measured on graphite and h-BN immersed in purified water are similar to separations measured on graphite immersed in alkanes (Fig. 2d).
The experiments reported here have been performed with purified water characterized by a resistivity of 18.2 MΩ cm−1. It is known that purified water carries trace amounts of hydrocarbon molecules (1–10 ppb).41 It is likely that these hydrocarbons originate from ambient air.28,42–44 They might be still present in the liquid after the application of stringent purification processes.41 We propose that either airborne or liquid-borne hydrocarbon molecules might accumulate on the graphite (h-BN)–liquid water interface while being absent from the mica–water interface.
Molecular dynamics simulations
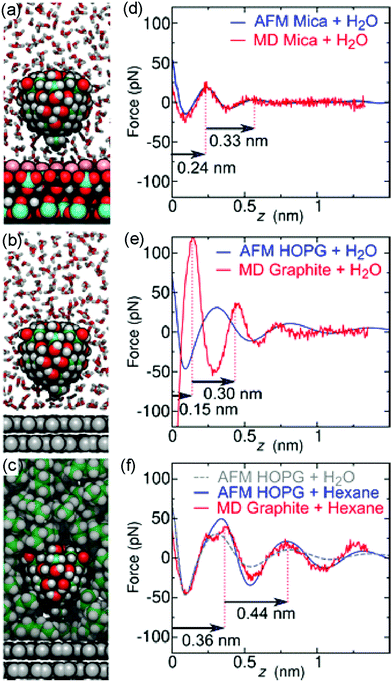
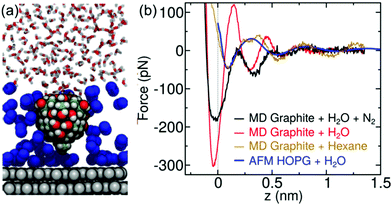
To test the above hypothesis and to understand the free energy factors that drive the formation of interfacial water structures, we performed several sets of MD simulations. First, simulations of mica–solvent and graphite–solvent interfaces predicted that the structure of the solvent overlayers are mostly determined by the chemical nature of the solvent. Notably, as shown in Fig. S7 (ESI),† the distance between the primary and secondary density maxima at mica–water and graphite–water interfaces (0.28 nm) is less than that at mica–hexane and graphite–hexane interfaces (0.44 nm). In fact, the density profiles of all straight-chain alkanes considered (from pentane to decane) show a well-defined characteristic length of 0.44 nm. This value is similar to the distance between maxima in the experimental FDC for graphite immersed in hexane (Fig. 2d). Furthermore, the FDCs for h-BN and graphite surfaces immersed in water (Fig. 2b and c) show similar characteristic lengths, supporting the hypothesis that alkanes or molecules with prominent alkane moieties are present at the interfaces during the experiments.To estimate the forces measured in the experiments, we have constructed a model AFM tip, which is illustrated in Fig. 3a near a mica–water interface, and in Fig. 3b and c near graphite–water and graphite–hexane interfaces. We have calculated the average force on this model tip as a function of distance from the aforementioned interfaces using the adaptive biasing force method.45 Although the tip radius is expected to be several nanometers, the magnitude of the measured forces suggests that contact with the solvation layers or surface is made by some small asperity; hence, our model has a contact area of only a few atoms. Tests with various alternative models showed that the qualitative results depended little on the details of the tip asperity model.
The computational force profile for the mica–water interface agrees remarkably well with the corresponding experimental FDC (Fig. 3d). In particular, the distance between force peaks is well reproduced. Likewise, the computational FDC for the graphite–hexane interface matches well with the experimental FDC for that interface (Fig. 3f). On the other hand, the calculations using a model of a pristine graphite–water interface do not even exhibit qualitative agreement with the graphite–water FDC (Fig. 3e). This disagreement is not surprising given that we hypothesize that a pristine graphite–water interface is a poor model of the interface. Indeed, the simulation system including the graphite–hexane interface (Fig. 3c) appears to be a much better model of the experiment for graphite immersed in water than the system with the pristine graphite–water interface (Fig. 3b). The comparison between experimental and computational FDC requires some considerations about the origin of the z-coordinate (see ESI†).
The hydrocarbons adopt a more ordered structure near the graphite than in bulk.40 As illustrated in Fig. S9a,† hexane molecules at the graphite surface tend to lie flat on the surface and align with each other. Subsequent layers show similar, but weaker, tendencies to align parallel to the surface. To quantify this tendency, we have calculated the orientational order parameter of hexane C–C bonds as function of distance from graphite and mica surfaces (Fig. S9b†). The hexane molecules tend to align parallel to the surface at distances where the hexane density is high and perpendicular to the surface in between, where the density is low. Hence, the diffusion of a hexane molecule from one solvation layer to another requires its reorientation, making diffusion near the surface significantly slower than in bulk hexane (Fig. S9c†).
Time evolution of the interfacial water structure
To understand the origin of the hydrocarbon layers formed at a graphite–water interface we studied the evolution of the interfacial water structure as a function of the time passed from the preparation of the crystalline surface. We prepared two types of surfaces, fresh and exposed. A fresh surface, either from mica, graphite or h-BN, was prepared by cleavage with the resulting surface immediately immersed in purified water (<2 s). An exposed surface was prepared by cleavage with the resulting surface being exposed to ambient air for 30 minutes, then immersed in purified water. The experiments reported in Fig. 2 were performed on exposed surfaces.Fig. 4 shows the interlayer distances measured on fresh and exposed mica and graphite surfaces. On mica, we did not observe any significant differences between the structure of the interfacial water on fresh and exposed surfaces. On the other hand, the interfacial water structure observed on graphite showed a marked difference between fresh and exposed surfaces. On exposed graphite surfaces, the interlayer distances were centered at 0.45 (1st), 0.55 (2nd) and 0.52 nm (3rd). Those values were very close to the values obtained by MD on a graphite surface immersed in an alkane solvent. On fresh surfaces, we observed a decrease of the mean values, in particular for the 1st layer (∼0.35 nm). This value was close to 0.32 nm which characterizes hydration layers. It suggested that water molecules might form hydration layers on graphite whenever hydrocarbons are not adsorbed on the surface. In addition, the difference observed between the mean and median values indicated that the interfacial water structure on a fresh graphite surface was somehow unstable. A low amount of hydrocarbon species adsorbed on graphite is likely to generate a competition between water and hydrocarbon molecules which might lead to a changing interfacial water structure.
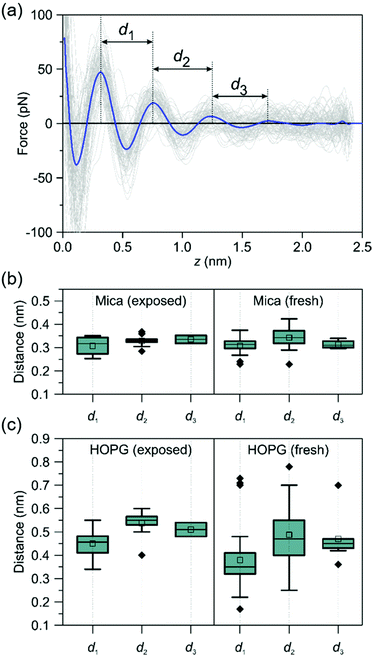 | ||
| Fig. 4 Time-evolution of the interfacial water structures on mica and graphite. (a) Definition of the interlayer distances. FDCs obtained on a HOPG-pentadecane interface. (b) Interlayer distances of purified water on mica (box plots). The interlayer distances do not depend on the time the mica surface was exposed to ambient air. All the values are centered around 0.32 nm. (c) Interlayer distances of purified water on graphite (box plots). On exposed surfaces, the interlayer distances are centered at 0.45 nm (1st), 0.55 (2nd) and 0.52 nm (3rd). A range of values (0.2–0.75 nm) are observed on freshly prepared graphite surfaces. The ESI† includes a table with the actual interlayer distances. | ||
The above data indicates that airborne hydrocarbons are the constituents of the interfacial layers observed on hydrophobic surfaces. The adsorption of hydrocarbons might have two different pathways. They could be directly adsorbed from the air-solid surface interface or from an air–liquid interface.
Comparison with hydrophilic surfaces
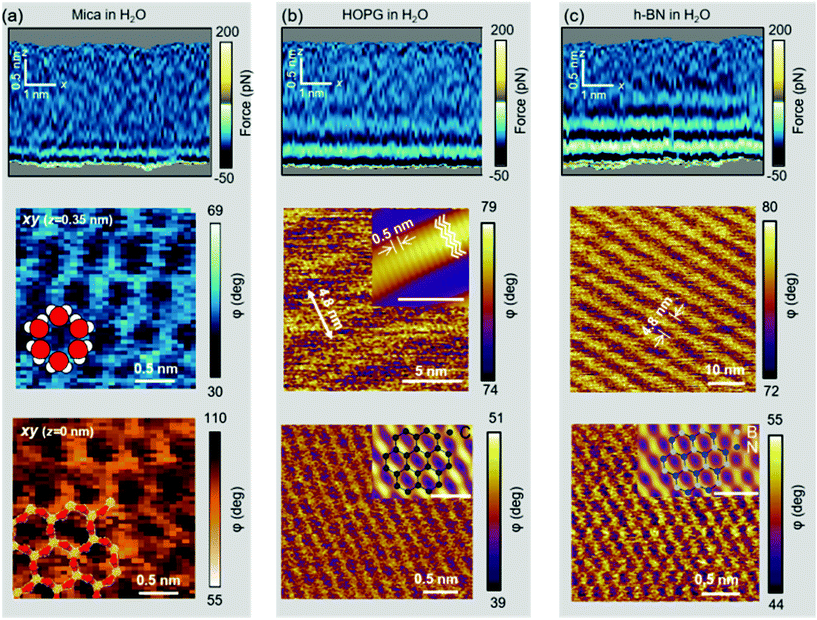
Further evidence of the accumulation of liquid-borne molecules on graphite and h-BN comes from the data extracted from 3D-AFM images. Fig. 5a shows a 2D xz map of the mica–water interface and two xy images taken, respectively, at the mica surface (z = 0.00 nm) and 0.35 nm above the surface. At z = 0.35 nm, the image shows a honeycomb structure formed by water molecules that surround the K+ ions that sit on top of the mica trigonal cavities. Hydrocarbon molecules are not present in this interface.Fig. 5b shows a 2D xz map and two xy images of the graphite–water interface. Three hydrophobic layers are resolved (top panel). The middle panel reveals a ripple structure with a periodicity of 4.8 nm. A finer orthogonal structure with a periodicity of 0.5 nm is also shown. The latter value matches the interlayer distance observed in the 2D xz panel and the periodicity of alkane monolayers formed on graphite and h-BN.46,47 By breaking into this layer we could recover the graphite lattice (bottom panel).48Fig. 5c shows the 2D xz maps and xy images for h-BN immersed in water. The results coincide with those reported for graphite (Fig. 5(b)).
Discussion
The formation of gas layers (N2) was suggested to explain the observed interlayer distances.29,30 Our data do not support that interpretation. To further rule out the gas adsorption model we have performed additional experiments and simulations. Experiments performed by using degassed water did not show any changes in the interlayer distances. A comprehensive MD simulation was performed to study the adsorption of N2 on graphite. Fig. 6 shows simulations of a model tip for graphite–hexane and graphite–N2 + water interfaces. The experimental data obtained on exposed graphite immersed in purified water agrees with the simulation of a graphite-alkane interface. The force predicted for a graphite-N2 gas + water interface agreed neither with the shape nor with the intermaxima distances of the experimental FDCs. Other MD simulations performed on hydrophobic surfaces49 favored the quick formation of gas nanobubbles from an adsorbed layer. This result also contradicted the gas adsorption hypothesis.The structure of the interface is determined by a competition between water and hydrocarbon molecules from the environment. On mica, water experiences strong electrostatic interactions with the surface, overwhelming relatively weak surface–hydrocarbon interactions and resulting in a net repulsive thermodynamic force on hydrocarbon molecules. On hydrophobic surfaces, particularly graphite and h-BN, water molecules are expelled from the interface by hydrocarbons, reducing the overall area of water–hydrophobic contact and resulting in more favorable water–water interaction (Fig. S8†).
Our model of interfacial water on crystalline hydrophobic surfaces challenges the prevalent paradigm in the surface science community.1 It questions the interpretation of some recent experimental data22,24 or the use of hydrophobic nanopores to confine water.50 At the same time, it provides a comprehensive understanding of the interfacial water and support the use of passivating layers to prevent contamination.51 Let's illustrate one of the implications. The dielectric constant ε of water confined between two atomically flat hydrophobic walls was measured down to 1 nm separations.24 A value of ε = 2 was measured for very small separations (1–2 nm), this is, far from the value of bulk water ε = 80. The results were explained by the confinement of the water molecules which inhibits the rotational freedom of the dipole moments.24 However, the existence of a 1–2 nm layer of hydrocarbon molecules provides a different explanation because alkane molecules have already a very low dielectric constant (ε = 2 at T = 295 K).
Conclusions
The prevalent paradigm about hydration layers was derived from experiments performed on hydrophilic surfaces. Assuming a pristine and uncontaminated interface, MD simulations supported their existence on hydrophobic surfaces. However, ambient air and purified water have a trace of hydrocarbon molecules (≤10 ppb in water). These molecules, either by direct adsorption from the air-solid interface or by diffusion from the air–liquid interface, might control the organization of water on hydrophobic surfaces. Until the present work, the presence of trace hydrocarbons was commonly ignored in MD simulations.Atomic resolution volume images reveal a dual interfacial water organization. The structure and composition of the solid–water interface depends on the hydrophilic/hydrophobic character of the surface. On mica, the interfacial water is formed by hydration layers while on graphite and h-BN, the interfacial layer is formed by airborne and waterborne hydrocarbon molecules.
These results illustrate the complexity of real water interfaces where a trace amount of hydrocarbons might dominate the intrinsic properties of the interface. In addition, the data illustrate how advanced high-resolution methods are needed to reach a fundamental understanding of the interactions of real liquid water with surfaces, with implications in molecular biology, energy storage and environmental engineering, among others.
Experimental
Crystalline surfaces
Flakes of hexagonal-boron nitride [h-BN, purchased from HQ Graphene, Netherlands], were mechanically exfoliated with adhesive tape and transferred onto clean Si/SiO2 substrates (275 nm SiO2, thermally oxidized) using a polydimethylsiloxane (PDMS) stamp. For cleaning, the substrates were sequentially ultrasonicated in acetone (99.6%, Acros Organics), ethanol (≥99.8%, Sigma Aldrich), and ultrapure water. After drying the substrates with a flow of nitrogen gas, they were then exposed to oxygen plasma for 15 min (Diener Electronic, Germany).Highly oriented pyrolytic graphite (HOPG, grade ZYB) was purchased from Bruker (USA) and cleaved with adhesive tape before the experiment. Muscovite mica (Grade V-1) was purchased from SPI supplies (USA). The mica was freshly cleaved with adhesive tape and rinsed copiously with ultrapure water before the experiments.
Solvents
Ultrapure water was freshly obtained before the experiments (ELGA Maxima, 18.2 MΩ cm−1). The water's pH value reached a value of 5.6 a few minutes after obtaining it from the machine (Hanna Instruments HI 9024). Some experiments on h-BN and HOPG were performed in n-hexane (>99%, Scharlab), n-octane (>99%, Sigma-Aldrich) and n-pentadecane (>99%, Sigma-Aldrich).AFM imaging
We used a home-made three-dimensional AFM.11,27 The 3D-AFM was implemented on a Cypher VRS platform. Three-dimensional AFM imaging is performed in the amplitude modulation mode52 by exciting the microcantilever at its first eigenmode. At the same time that the cantilever oscillates with respect to its equilibrium position, a sinusoidal signal is applied to the z-piezo to modify the relative z-distance between the sample and the tip. We have used z-piezo displacements with amplitudes between a 1 and 2.5 nm and a period (frequency) of 10 ms (100 Hz). This z-range was chosen because we did not observe features in the liquid structure above ≥1.5 nm. The z-piezo signal is synchronized with the xy-displacements in such a way that for each xy-position on the surface of the material, the tip performs a single and complete z-cycle.The z-data is read out every 10.24 μs and stored in 512 pixels (256 pixels half cycle). Each xy-plane of the 3D map contains 80 × 64 pixels. Hence, the total time to acquire such a 3D-AFM image is 52 s.
Conventional high-resolution AFM imaging was performed on a modified commercial microscope (Cypher VRS, Asylum Research, Oxford Instruments). Before each experiment the AFM holder was cleaned with ethanol and distilled water. After the cleaning procedure, the samples were mounted onto the microscope sample stage. Then, a small droplet of imaging solution was placed on the surface. Immediately after that, the cantilever was immersed into the liquid and the liquid cell was sealed. Within the cell, the temperature was held constant at (28.0 ± 0.1) °C.
Silicon cantilevers with silicon tips were used for 3D-AFM imaging (ArrowUHF AuD and ArrowUHF Al, NanoAndMore, Germany). Cantilevers were cleaned first in a mixture (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 in volume) of isopropanol (99.6%, Acros Organics) and ultrapure water, rinsed with ultrapure water and then placed in a UV-Ozone cleaner (PSD-UV3, Novascan Technologies, USA) for ≈1 h. A contactless method was used to calibrate the microcantilevers.
50 in volume) of isopropanol (99.6%, Acros Organics) and ultrapure water, rinsed with ultrapure water and then placed in a UV-Ozone cleaner (PSD-UV3, Novascan Technologies, USA) for ≈1 h. A contactless method was used to calibrate the microcantilevers.
Molecular dynamics protocols
The molecular dynamics simulations followed protocols validated against experiment in our previous work.53,54 All simulations were performed with NAMD 2.13. Lennard-Jones interactions were calculated with a smooth 1.0–1.2 nm cutoff. For all simulations, the pressure was maintained at 1.01325 bar using the Langevin piston method and the temperature was maintained at 295 K using a Langevin thermostat with a damping parameter of 1 ps−1. All simulations were performed with mass repartitioning of non-water hydrogen atoms (with the mass increased by a factor of 3). The equations of motion were integrated with a 3 fs time step. Electrostatic interactions were calculated using the particle-mesh Ewald method with a grid spacing <0.12 nm. Water molecules were represented by the TIP3P model of the CHARMM force field and kept rigid using the SETTLE method. The lengths of other covalent bonds involving hydrogen were constrained.For organic molecules and graphitic carbon, interatomic interactions were represented using the CHARMM General Force Field (CGenFF), version 4.3. We have previously demonstrated that this force field agrees well with experiment for the thermodynamics of adsorption of small organic molecules on graphitic carbon in aqueous solution53,54 as well as in organic solvents.55 Muscovite mica was represented using CLAYFF. Previous studies56 have validated the combination of CLAYFF with the CHARMM force field framework. Mean forces on the model tip asperity as a function of distance from the surfaces were calculated by the adaptive biasing force method45 as implemented in the Colvars module57 using a 0.005 nm grid. To mimic the fact that the AFM tip is attached to a relatively rigid assembly, a restraint was applied to maintain the orientation of the tip asperity also using the Colvars.
The graphite systems included two rectangular graphene sheets stacked atop one another and aligned perpendicular to the z-axis, with mean dimensions of 2.935 × 2.966 nm2. As in previous work53,54 the atoms of the lower sheet were harmonically restrained to their initial z-position. All calculations of surface interactions were performed relative to the upper sheet, to which no restraints were applied. The muscovite mica surface was created by a 2 × 2 replication of the final structure given by Wang et al.56 to produce a bilayer mica sheet with mean dimensions of 3.583 × 4.140 nm2. The bottom plane of tetrahedral aluminium atoms was harmonically restrained to their initial z-position. Again, all calculations of surface interactions were performed relative to the unrestrained upper layer of mica. Water molecules were added using VMD to create mica–water and graphite–water systems with mean z dimensions of 5.66 and 5.19 nm, respectively. Simulation systems including organic solvents were constructed using the program PackMol to yield systems with z-dimensions of 5.37 nm58. All systems underwent 2000 steps of energy minimization and 150 ps of equilibration before beginning production simulations.
Author contributions
M. R. U. and S. B. performed the experiments. M. R. U., S. B. and R. G. designed and analyzed the experiments. J. C. and R. G. planned the MD simulations. J. C. and R. T. designed, performed and analyzed the MD simulations. R. G. coordinated the activity and wrote the manuscript and SI with contributions from J. C., M. R. U. and S. B. All the authors discussed the results.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge fruitful discussions with F. Biscarini, M. Dong and F. Stellacci. A. Castellanos-Gomez provided some of the h-BN samples. R.G. acknowledges financial support from the European Research Council ERC-AdG-340177, the Ministerio de Ciencia, Innovación y Universidades (PID2019-106801GB-I00; MAT2016-76507-R) and European Commission Marie Sklodowska-Curie grant agreement No. 721874. J.C. acknowledges financial support by the US National Science Foundation under Grant No. CHE-1726332 and DMR-1945589.Notes and references
- O. Björneholm, M. H. Hansen, A. Hodgson, L. M. Liu, D. T. Limmer, A. Michaelides, P. Pedevilla, J. Rossmeisl, H. Shen, G. Tocci, E. Tyrode, M. M. Walz, J. Werner and H. Bluhm, Chem. Rev., 2016, 116, 7698–7726 CrossRef.
- F. Zaera, Chem. Rev., 2012, 112, 2920–2986 CrossRef CAS.
- J. N. Israelachvili and R. M. Pashley, Nature, 1983, 306, 249–250 CrossRef CAS.
- H. W. Cheng and M. Valtiner, Curr. Opin. Colloid Interface Sci., 2020, 47, 126–136 CrossRef CAS.
- H. Zhou, P. Ganesh, V. Presser, M. C. F. Wander, P. Fenter, P. R. C. Kent, D. Jiang, A. A. Chialvo, J. McDonough, K. L. Shuford and Y. Gogotsi, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 035406 CrossRef.
- J. J. Velasco-Velez, C. H. Wu, T. A. Pascal, L. F. Wan, J. Guo, D. Prendergast and M. Salmeron, Science, 2014, 346, 831–834 CrossRef CAS.
- T. Fukuma and R. Garcia, ACS Nano, 2018, 12, 11785–11797 CrossRef CAS.
- T. Fukuma, Y. Ueda, S. Yoshioka and H. Asakawa, Phys. Rev. Lett., 2010, 104, 2–5 CrossRef.
- K. Voïtchovsky, D. Giofrè, J. José Segura, F. Stellacci and M. Ceriotti, Nat. Commun., 2016, 7, 13064 CrossRef.
- S. R. Van Lin, K. K. Grotz, I. Siretanu, N. Schwierz and F. Mugele, Langmuir, 2019, 35, 5737–5745 CrossRef CAS.
- D. Martin-Jimenez, E. Chacon, P. Tarazona and R. Garcia, Nat. Commun., 2016, 7, 12164 CrossRef CAS.
- K. Umeda, L. Zivanovic, K. Kobayashi, J. Ritala, H. Kominami, P. Spijker, A. S. Foster and H. Yamada, Nat. Commun., 2017, 8, 2111 CrossRef.
- K. Miyazawa, J. Tracey, B. Reischl, P. Spijker, A. S. Foster, A. L. Rohl and T. Fukuma, Nanoscale, 2020, 12, 12856–12868 RSC.
- J. G. Vilhena, C. Pimentel, P. Pedraz, F. Luo, P. A. Serena, C. M. Pina, E. Gnecco and R. Pérez, ACS Nano, 2016, 10, 4288–4293 CrossRef CAS.
- B. Luan and R. Zhou, Appl. Phys. Lett., 2016, 108, 131601 CrossRef.
- L. Bai, Z. Zhang and J. Jang, J. Phys. Chem. C, 2019, 123, 21528–21537 CrossRef CAS.
- J. Hernández-Muñoz, E. Chacon and P. Tarazona, J. Chem. Phys., 2019, 151, 034701 CrossRef.
- M. Kanduč, A. Schlaich, E. Schneck and R. R. Netz, Langmuir, 2016, 32, 8767–8782 CrossRef.
- J. Hernández-Muñoz, M. R. Uhlig, S. Benaglia, E. Chacón, P. Tarazona and R. Garcia, J. Phys. Chem. C, 2020, 124, 26296–26303 CrossRef.
- K. Suzuki, N. Oyabu, K. Kobayashi, K. Matsushige and H. Yamada, Appl. Phys. Express, 2011, 4, 2–5 Search PubMed.
- Q. Li, J. Song, F. Besenbacher and M. Dong, Acc. Chem. Res., 2015, 48, 119–127 CrossRef CAS.
- G. Algara-Siller, O. Lehtinen, F. C. Wang, R. R. Nair, U. Kaiser, H. A. Wu, A. K. Geim and I. V. Grigorieva, Nature, 2015, 519, 443–445 CrossRef CAS.
- W. Zhou, K. Yin, C. Wang, Y. Zhang, T. Xu, A. Borisevich, L. Sun, J. C. Idrobo, M. F. Chisholm, S. T. Pantelides, R. F. Klie and A. R. Lupini, Nature, 2015, 528, E1–E2 CrossRef CAS.
- L. Fumagalli, A. Esfandiar, R. Fabregas, S. Hu, P. Ares, A. Janardanan, Q. Yang, B. Radha, T. Taniguchi, K. Watanabe, G. Gomila, K. S. Novoselov and A. K. Geim, Science, 2018, 360, 1339–1342 CrossRef CAS.
- C.-W. Yang, K. Miyazawa, T. Fukuma, K. Miyata and I.-S. Hwang, Phys. Chem. Chem. Phys., 2018, 20, 23522–23527 RSC.
- I. Schlesinger and U. Sivan, J. Am. Chem. Soc., 2018, 140, 10473–10481 CrossRef CAS.
- M. R. Uhlig, D. Martin-Jimenez and R. Garcia, Nat. Commun., 2019, 10, 2606 CrossRef.
- Z. Li, Y. Wang, A. Kozbial, G. Shenoy, F. Zhou, R. McGinley, P. Ireland, B. Morganstein, A. Kunkel, S. P. Surwade, L. Li and H. Liu, Nat. Mater., 2013, 12, 925–931 CrossRef CAS.
- Y.-H. Lu, C.-W. Yang, C.-K. Fang, H.-C. Ko and I.-S. Hwang, Sci. Rep., 2015, 4, 7189 CrossRef.
- I. Schlesinger and U. Sivan, Langmuir, 2017, 33, 2485–2496 CrossRef CAS.
- H. Teshima, Q. Li, Y. Takata and K. Takahashi, Phys. Chem. Chem. Phys., 2020, 22, 13629–13636 RSC.
- E. T. Herruzo, H. Asakawa, T. Fukuma and R. Garcia, Nanoscale, 2013, 5, 2678–2685 RSC.
- D. Martin-Jimenez and R. Garcia, J. Phys. Chem. Lett., 2017, 8, 5707–5711 CrossRef CAS.
- R. Garcia, Chem. Soc. Rev., 2020, 49, 5850–5884 RSC.
- M. Watkins and B. Reischl, J. Chem. Phys., 2013, 138, 154703 CrossRef.
- K. Amano, K. Suzuki, T. Fukuma, O. Takahashi and H. Onishi, J. Chem. Phys., 2013, 139, 224710 CrossRef.
- E. Nakouzi, A. G. Stack, S. Kerisit, B. A. Legg, C. J. Mundy, G. K. Schenter, J. Chun and J. J. De Yoreo, J. Phys. Chem. C, 2020, 125, 1282–1291 CrossRef.
- S. De Beer, P. Wennink, M. Van Der Weide-Grevelink and F. Mugele, Langmuir, 2010, 26, 13245–13250 CrossRef CAS.
- T. Minato, Y. Araki, K. Umeda, T. Yamanaka, K. Okazaki, H. Onishi, T. Abe and Z. Ogumi, J. Chem. Phys., 2017, 147, 124701 CrossRef.
- M.-D. Krass, G. Krämer, U. Dellwo and R. Bennewitz, Tribol. Lett., 2018, 66, 1–10 CrossRef CAS.
- N. Nioradze, R. Chen, N. Kurapati, A. Khvataeva-Domanov, S. Mabic and S. Amemiya, Anal. Chem., 2015, 87, 4836–4843 CrossRef CAS.
- J. M. Hurst, L. Li and H. Liu, Carbon, 2018, 134, 464–469 CrossRef CAS.
- D. Martinez-Martin, R. Longuinhos, J. G. Izquierdo, A. Marele, S. S. Alexandre, M. Jaafar, J. M. Gómez-Rodríguez, L. Bañares, J. M. Soler and J. Gomez-Herrero, Carbon, 2013, 61, 33–39 CrossRef CAS.
- C. Plass-Dülmer, N. Schmidbauer, J. Slemr, F. Slemr and H. D'Souza, J. Geophys. Res., 2006, 111, D04306 CrossRef.
- J. Comer, J. C. Gumbart, J. Hénin, T. Lelièvre, A. Pohorille and C. Chipot, J. Phys. Chem. B, 2015, 119, 1129–1151 CrossRef CAS.
- S. Seibert, S. Klassen, A. Latus, R. Bechstein and A. Kühnle, Langmuir, 2020, 36, 7789–7794 CrossRef CAS.
- J. D. Albar, V. V. Korolkov, M. Baldoni, K. Watanabe, T. Taniguchi, E. Besley and P. H. Beton, J. Phys. Chem. C, 2018, 122, 27575–27581 CrossRef CAS.
- D. S. Wastl, F. Speck, E. Wutscher, M. Ostler, T. Seyller and F. J. Giessibl, ACS Nano, 2013, 7, 10032–10037 CrossRef CAS.
- Q.-Q. Luo and J.-M. Yang, Chin. Phys. B, 2015, 24, 096801 CrossRef.
- E. Breynaert, M. Houlleberghs, S. Radhakrishnan, G. Grübel, F. Taulelle and J. A. Martens, Chem. Soc. Rev., 2020, 49, 2557–2569 RSC.
- C. Su, Z. Yin, Q.-B. Yan, Z. Wang, H. Lin, L. Sun, W. Xu, T. Yamada, X. Ji, N. Zettsu, K. Teshima, J. H. Warner, M. Dincă, J. Hu, M. Dong, G. Su, J. Kong and J. Li, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 20844–20849 CrossRef CAS.
- R. Garcia, Amplitude Modulation Atomic Force Microscopy, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2010 Search PubMed.
- E. R. Azhagiya Singam, Y. Zhang, G. Magnin, I. Miranda-Carvajal, L. Coates, R. Thakkar, H. Poblete and J. Comer, J. Chem. Theory Comput., 2019, 15, 1302–1316 CrossRef CAS.
- J. Comer, R. Chen, H. Poblete, A. Vergara-Jaque and J. E. Riviere, ACS Nano, 2015, 9, 11761–11774 CrossRef CAS.
- J. Calbo, A. López-Moreno, A. de Juan, J. Comer, E. Ortí and E. M. Pérez, Chem. – Eur. J., 2017, 23, 12909–12916 CrossRef CAS.
- J. Wang, A. G. Kalinichev, R. J. Kirkpatrick and R. T. Cygan, J. Phys. Chem. B, 2005, 109, 15893–15905 CrossRef CAS.
- M. Ricci, P. Spijker and K. Voïtchovsky, Nat. Commun., 2014, 5, 4400 CrossRef CAS.
- L. Martinez, R. Andrade, E. G. Birgin and J. M. Martinez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Additional high-resolution AFM images, cantilever calibration protocol, reconstruction of the tip–sample force, details of molecular dynamics simulation. See DOI: 10.1039/d1nr00351h |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2021 |