Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mechanism of magnetization reduction in iron oxide nanoparticles†
Tobias
Köhler
 *abc,
Artem
Feoktystov
a,
Oleg
Petracic
b,
Emmanuel
Kentzinger
*abc,
Artem
Feoktystov
a,
Oleg
Petracic
b,
Emmanuel
Kentzinger
 b,
Tanvi
Bhatnagar-Schöffmann
b,
Tanvi
Bhatnagar-Schöffmann
 bcd,
Mikhail
Feygenson
e,
Nileena
Nandakumaran
bc,
Joachim
Landers
f,
Heiko
Wende
bcd,
Mikhail
Feygenson
e,
Nileena
Nandakumaran
bc,
Joachim
Landers
f,
Heiko
Wende
 f,
Antonio
Cervellino
g,
Ulrich
Rücker
f,
Antonio
Cervellino
g,
Ulrich
Rücker
 b,
András
Kovács
d,
Rafal E.
Dunin-Borkowski
b,
András
Kovács
d,
Rafal E.
Dunin-Borkowski
 d and
Thomas
Brückel
d and
Thomas
Brückel
 bc
bc
aForschungszentrum Jülich GmbH, Jülich Centre for Neutron Science JCNS at Heinz Maier-Leibnitz Zentrum MLZ, 85748 Garching, Germany. E-mail: t.koehler@fz-juelich.de
bForschungszentrum Jülich GmbH, Jülich Centre for Neutron Science JCNS-2 and Peter Grünberg Institute PGI-4, JARA-FIT, 52425 Jülich, Germany
cLehrstuhl für Experimentalphysik IV C, RWTH Aachen University, 52056 Aachen, Germany
dForschungszentrum Jülich GmbH, Ernst Ruska-Centre for Microscopy and Spectroscopy with Electrons and Peter Grünberg Institue, 52425 Jülich, Germany
eJülich Centre for Neutron Science (JCNS-1) and Institute for Complex Systems (ICS-1), Forschungszentrum Jülich GmbH, 52425 Jülich, Germany
fFaculty of Physics and Center for Nanointegration Duisburg-Essen (CENIDE), University of Duisburg-Essen, 47057 Duisburg, Germany
gPaul Scherrer Institut, Swiss Light Source, 5232 Villigen PSI, Switzerland
First published on 30th March 2021
Abstract
Iron oxide nanoparticles are presently considered as main work horses for various applications including targeted drug delivery and magnetic hyperthermia. Several questions remain unsolved regarding the effect of size onto their overall magnetic behavior. One aspect is the reduction of magnetization compared to bulk samples. A detailed understanding of the underlying mechanisms of this reduction could improve the particle performance in applications. Here we use a number of complementary experimental techniques including neutron scattering and synchrotron X-ray diffraction to arrive at a consistent conclusion. We confirm the observation from previous studies of a reduced saturation magnetization and argue that this reduction is mainly associated with the presence of antiphase boundaries, which are observed directly using high-resolution transmission electron microscopy and indirectly via an anisotropic peak broadening in X-ray diffraction patterns. Additionally small-angle neutron scattering with polarized neutrons revealed a small non-magnetic surface layer, that is, however, not sufficient to explain the observed loss in magnetization alone.
1. Introduction
Superparamagnetic iron oxide nanoparticles are attracting considerable interest both from a purely scientific as well as technological point of view. This is driven by several potential and already established applications e.g. in mechanical engineering (seals and adaptive dampers1–3), nanomedicine (contrast agents for magnetic imaging4–10 and cancer treatment by magnetic hyperthermia11–16) and information technology (magnetic data storage and spintronics17,18). Magnetic nanoparticles represent also a fundamentally interesting model case of magnetism in finite size systems. However, understanding the microscopic mechanisms leading to the macroscopic properties of nanoparticles and in particular deviations from model expectations, such as the previously reported reduced magnetization compared to the (theoretical) bulk value remains difficult.19–31Proposed models for the spatial distribution of the magnetization include the presence of a magnetic core–shell structure,24 spin disorder around defects21 and a reduced magnetization in the core due to reversed moments and frustration.22 Small-angle neutron scattering experiments with polarized neutrons on spherical particles with diameters of 9.94 nm revealed a magnetically depleted surface layer of 0.3 nm with canted spins.26 However, it was also stated that the observed reduction in magnetization compared to the bulk values can not be achieved by this surface layer alone, but requires a uniform reduction of the magnetization in the nanoparticle core. Lattice shifts resulting in antiphase boundaries (APBs), i.e. a shift of the iron sublattice while keeping the oxygen lattice unchanged, have been proposed to explain the reduction in magnetization in the particle core.27,29 Mössbauer spectroscopy and magnetometry measurements performed on iron oxide nanoparticles with diameters of 15 nm suggested the lack of a magnetically dead layer.30 Iron oxide nanoparticles with overall size of 7.4 nm were shown to be homogeneously magnetized with no significant spin disorder at the surface.28 Common to all previous works is the limitation to few experimental techniques, allowing conclusions only on specific parts of the problem.
In this study we combine neutron and synchrotron X-ray scattering techniques with magnetometry, transmission electron microscopy (TEM), elemental analysis and Mössbauer spectroscopy to obtain a complete as possible picture of the nanoparticle properties. We find that the nanoparticles possess a macroscopically reduced saturation magnetization, mostly due to the presence of antiphase boundaries as observed with high-resolution TEM (HR-TEM) and X-ray scattering and to a lesser extent due to a small magnetically depleted surface layer and cation vacancies.
2. Experimental
2.1. Materials
Commercially available iron oxide nanoparticles with nominal core diameters of 15 nm with oleic acid coating dispersed in toluene were purchased from Ocean NanoTech (San Diego, USA). These particles were synthesized in organic solvent at high temperature.322.2. Transmission electron microscopy
Transmission electron microscopy (TEM) and high-resolution TEM (HR-TEM) was carried out using a FEI Tecnai G2 F20 field emission transmission electron microscope in bright field mode, operated at 200 kV at the Ernst Ruska-Centre (ER-C), Forschungszentrum Jülich GmbH.33 The sample was prepared by drop coating a carbon layer supported by a Cu-grid. The contrast between the organic shell of the nanoparticles and the amorphous carbon substrate is relatively small, thus only the crystalline core of the particles is visible in the micrographs. Image simulations to verify the contrast were performed with the QSTEM software package.342.3. Mössbauer spectroscopy
Mössbauer spectra were recorded at 4.3 K in transmission geometry and constant acceleration mode using a 57Co(Rh) source in a liquid helium bath cryostat. The particle dispersion was dried and the powder was mixed with chemically inert boron nitride to obtain a homogeneous sample of sufficient volume.2.4. X-ray scattering
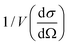 ) was obtained via the reference material FEP 1400 Å. Data analysis was performed with Jscatter.40 The wavelength spread for GALAXI is Δλ/λ ≈ 3 × 10−3 (Ga Kα1 and Ga Kα2 not resolved) but is deemed small enough to not be considered in the fitting.41 For the experiment borosilicate glass capillaries from Hilgenberg GmbH with wall thickness of 0.05 mm and internal diameter of 2.0 mm (ref. 42) were filled with nanoparticle dispersions (0.02 and 0.002 vol% of particles).
) was obtained via the reference material FEP 1400 Å. Data analysis was performed with Jscatter.40 The wavelength spread for GALAXI is Δλ/λ ≈ 3 × 10−3 (Ga Kα1 and Ga Kα2 not resolved) but is deemed small enough to not be considered in the fitting.41 For the experiment borosilicate glass capillaries from Hilgenberg GmbH with wall thickness of 0.05 mm and internal diameter of 2.0 mm (ref. 42) were filled with nanoparticle dispersions (0.02 and 0.002 vol% of particles).
2.5. Small-angle neutron scattering
Small-angle neutron scattering with polarized neutrons (SANSPOL) was performed on KWS-1 operated by the Jülich Centre for Neutron Science at Heinz Maier-Leibnitz Zentrum (Garching, Germany).43,44 Neutrons with a wavelength of 4.9 Å and polarization, P ≈ 90.5%, were detected at two detector distances (2 m and 8 m) with initial beam polarization opposite to the magnetic field, spin down, and parallel to it, spin up (flipper efficiency ε = 0.998). A diluted solution of spherical nanoparticles 0.38 vol.% was measured at 5 contrast conditions. Contrast variation experiments allow to probe directly the nuclear core–shell structure of the nanoparticles and utilization of polarized neutrons allows the magnetic structure to be precisely determined from a simultaneous fit of the multiple datasets of magnetic-nuclear interference. Discrepancies, if present between the magnetic and nuclear core size, will allow conclusions on the presence and thickness of a magnetically dead or depleted layer at the particle surface. Different contrasts were achieved by mixing hydrogenated and deuterated toluene (h-toluene and d-toluene). The final solvent composition constituted 0, 25, 35, 50 and 80 vol.% of d-toluene and the resulting scattering length densities (SLDs) with contrasts (difference in SLD between the nanoparticle core and solvent (ΔSLDcore) and the organic shell and solvent (ΔSLDshell)) are listed in Table 1. Quartz cuvettes (Hellma GmbH, Germany) of 1 mm thickness were filled with 300 μl of the samples and put in sample position where a horizontal magnetic field of 0.5 T was applied orthogonally to the incident neutron beam.| Deuteration (vol%) | SLDsolvent (10−6 Å−2) | ΔSLDcore (10−6 Å−2) | ΔSLDshell (10−6 Å−2) |
|---|---|---|---|
| SLDC7H8 = 0.939 × 10−6 Å−2, SLDC7D8 = 5.664 × 10−6 Å−2, SLDshell = 0.078 × 10−6 Å−2, SLDcorea = 6.656 × 10−6 Å−2. aAssuming γ-Fe2O3 | |||
| 0.0 | 0.939 | 5.717 | 0.861 |
| 24.8(1) | 2.111 | 4.545 | 2.033 |
| 34.7(1) | 2.579 | 4.077 | 2.501 |
| 49.6(1) | 3.283 | 3.373 | 3.205 |
| 79.8(1) | 4.710 | 1.946 | 4.632 |
The data were corrected for the solvent background and empty cell scattering and normalized to absolute intensities by measuring secondary standard samples and the empty beam. For each polarization state 10°-sectors in detector plane parallel and perpendicular to the applied field direction were integrated with the aim of obtaining the purely nuclear scattering contribution and the magnetic-nuclear interference term, respectively. Data reduction and fitting was carried out with qtiKWS and qtiSAS.45
2.6. Magnetometry
Magnetometry was performed using a superconducting quantum interference device (SQUID) magnetometer (MPMS XL, Quantum Design). The nanoparticle dispersion was diluted in paraffin to 0.1 vol.% of the original concentration such that interparticle interactions become negligible. Pieces of the solid nanoparticle–paraffin mixtures were extracted using ceramic tools to avoid contamination with ferromagnetic materials. Zero-field cooled (ZFC) curves were measured by first cooling the sample in zero magnetic field to 10 K, then applying a magnetic field and subsequently recording the magnetization while heating to room temperature. This is followed by a field-cooled (FC) measurement being recorded upon cooling to 10 K with the same magnetic field applied. To confirm the absence of interparticle interactions aged zero field cooled (aZFC) measurements, that would be able to detect a collective superspin glass state, were performed by stopping the zero field cooling process at 120 K for 104 s and then proceeding in the same way as for the regular ZFC curves. Magnetization vs. field curves were obtained by sweeping over a field range of −1 to 1 T for constant temperatures (300 and 10 K). The low temperature curves were recorded after various cooling fields of 0, 0.1 and 1 T. AC-susceptometry was performed using the AC-option of a Quantum Design MPMS-5S SQUID magnetometer with frequencies in the range of 0.1–1500 Hz at temperatures between 5 K and 300 K.2.7. Inductively coupled plasma optical emission spectroscopy (ICP-OES)
ICP-OES was carried out at the central Institute for Engineering, Electronics and Analytics (ZEA-3), Forschungszentrum Jülich GmbH. Samples used for magnetometry measurements were extracted from the sample holder, microwave digested in HNO3 and H2O2 and then analyzed. Co, Fe, Ni, Gd, Cr and Al were considered for determination of the total weight present in the sample. Details are presented in ESI Table S2.†3. Results and discussion
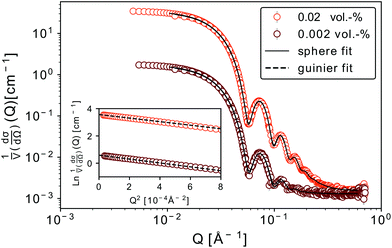
We discuss firstly the SAXS measurements, that provide the particle size and size distribution, being essential for the evaluation and interpretation of the subsequent part.SAXS scattering curves (Fig. 1) measured from two samples with different particle concentrations (0.02 and 0.002 vol%) were simultaneously fit to a model of polydisperse spheres with lognormal size distribution
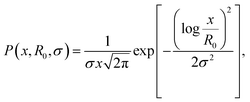 | (1) |
For both concentrations of nanoparticles no interparticle effects were detected. A Guinier approximation of the low-Q region in both cases shows no deviation from the linear behaviour in a ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) I vs. Q2 plot (see inset in Fig. 1), thus confirming that particles are non-interacting and similar in size.46 From a linear fit the radius of gyration, Rg, of the nanoparticles can be extracted without assuming any model. Rg was found to be 6.3 nm, which according to
I vs. Q2 plot (see inset in Fig. 1), thus confirming that particles are non-interacting and similar in size.46 From a linear fit the radius of gyration, Rg, of the nanoparticles can be extracted without assuming any model. Rg was found to be 6.3 nm, which according to 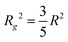 , corresponds to a spherical particle radius of 7.9 nm in agreement with the particle size determined from the solid sphere fit. We have to emphasize that in the X-ray scattering, because of a vanishing contrast between surfactant shell and solvent, the signal originates mainly from iron oxide cores and contribution from the organic coating can be neglected.47
, corresponds to a spherical particle radius of 7.9 nm in agreement with the particle size determined from the solid sphere fit. We have to emphasize that in the X-ray scattering, because of a vanishing contrast between surfactant shell and solvent, the signal originates mainly from iron oxide cores and contribution from the organic coating can be neglected.47
Magnetization curves, M(H) and M(T), normalized to the amount of iron present in the sample as determined by ICP-OES (ESI Table S1†), are displayed in Fig. 2. The maximum of the ZFC curve (Fig. 2(a)) lies at 172 K. For perfectly monodisperse nanoparticles with equal magnetic anisotropy energies this temperature marks the transition from a blocked to an unblocked state, i.e. the blocking temperature TB. For deviations from this ideal case the mean blocking temperature is found at slightly lower values.48,49 AC-susceptibility measurements on our samples (ESI Fig. S7†) suggest a mean blocking temperature of 160 K. Together with the particle volume V, the measurement time τm (taken as ca. 30 s) and the elementary spin flip time τ0, which is typically on the order of 10−9 s for superparamagnetic systems in ZFC/FC measurements, the magnetic anisotropy energy constant K can be determined according to50
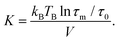 | (2) |
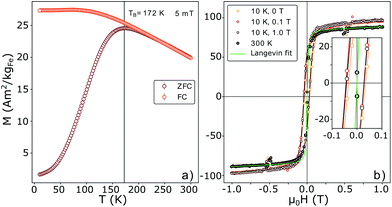 | ||
| Fig. 2 (a) M(T) ZFC and FC curves measured at 5 mT. The maximum of the ZFC curve and the splitting are in very close proximity, pointing to a small size distribution of the particles. The blocking temperature taken at the maximum of the ZFC curve yields 172 K. (b) M(H) curves measured at room-temperature (RT) and 10 K (with cooling fields of 0.0, 0.1 and 1.0 T). The saturation magnetization Msat was normalized to the iron weight in the sample as determined via ICP-OES. A very small shift of the field cooled curves is visible. The green line corresponds to a Langevin fit (eqn (5)). | ||
This results in a magnetic anisotropy energy of 27 kJ m−3, which is comparable to previously reported values for similar particles51,52 and significantly larger than the maghemite magnetocrystalline anisotropy of K = 4.7 kJ m−3 obtained from measurements on single crystal films and powders.53 The close proximity of the splitting of the curves to the maximum of the ZFC curve points to a narrow particle size distribution50 which is consistent with the results obtained from SAXS experiments. The constant, i.e. not decreasing part of the FC curve for temperatures smaller than the ZFC peak temperature indicates the absence of a significant interparticle interaction50 and the absence of an additional paramagnetic signal from impurity atoms or clusters dispersed between the particles.54
A very small exchange bias field of μ0HE = 8mT in the 0.1 T field cooled M(H) curve was detected (inset in Fig. 2b). Exchange bias in iron oxide systems has previously been attributed to a ferro(ferri)magnetic/antiferromagnetic interface, e.g. the presence of wüstite (FeO) in maghemite/magnetite (γ-Fe2O3/Fe3O4) particles.55,56 On the other hand, it has been reported that antiphase boundaries produce exchange bias in thin films57 and according to Wetterskog et al.27 might also occur in nanoparticles. Such lattice translations modify the FeOct.–O–FeOct. bond angles across the APB from 90° to 180° (Fig. 3(e)). In agreement with the Goodenough–Kanamori rules58,59 the superexchange interaction between iron cations at the APB was found to be antiferromagnetic via magneto-resistance measurements on Fe3O4 thin films.60 On the basis of Monte-Carlo simulations it was proposed that APBs are responsible for the drastic reduction of saturation magnetization (Msat) in iron oxide nanoparticles.29 Thus, checking for the existence of such defects in the studied samples is an important step towards answering the central question of the origin of the reduced Msat.
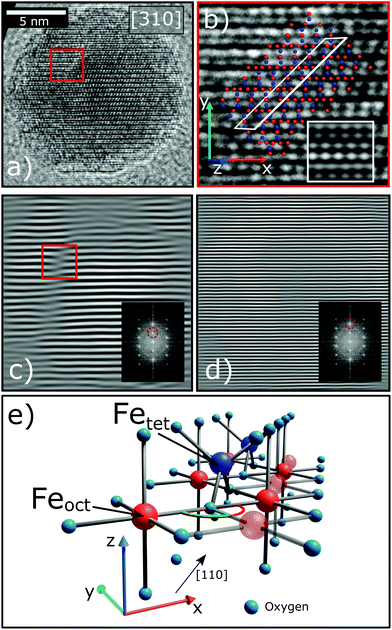
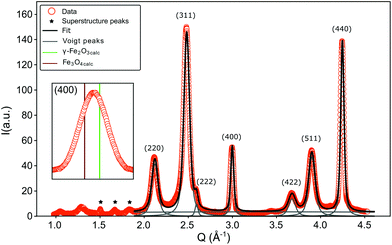
During the synthesis of monodisperse iron oxide nanoparticles via thermal decomposition of an iron-oleate complex61 the particles pass through a stability field of the wüstite (FeO) phase that gets first oxidized to magnetite (Fe3O4) and then to maghemite (γ-Fe2O3). In this process it is common to introduce lattice shifts and antiphase boundaries (APBs).27 The presence of APBs in the samples of this study is directly confirmed by HR-TEM (Fig. 3). They can be more easily identified by masking the Bragg peak of the lattice planes that will be affected by this translation, in this case the220 reflection (Fig. 3(c)). The lattice shift is not affecting the oxygen sublattice (illustrated by masking the 440 peak in Fig. 3(d)) and does not change the net Fe coordination, leading to a very low formation energy.62 HR-TEM, while being very precise, can only provide statistically limited information on the particle structure. To confirm that APBs occur significantly often in the particles, larger ensembles have to be studied, which is provided by X-ray diffraction. This method probes the average crystal structure of the nanoparticles over a large sample volume and the presence of APBs can be deduced from selective peak broadening (Fig. 4).
A coherent structure size can be estimated from the FWHM of the strongest peaks using the Scherrer equation
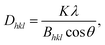 | (3) |
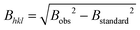 66 with the NIST standard 660a LaB6.
66 with the NIST standard 660a LaB6.
The FWHM for the peaks (220), (311) and (511) are approximately doubled compared to the ones obtained from (222), (440) and (400) (Table 2). A similar result was reported by Wetterskog et al.27 based on peak width analysis of 220, 440 and 400 peaks in iron oxide nanoparticles. This indicates that the structurally coherent domain size is reduced in the direction perpendicular to the (220), (311) and (511) lattice planes. The orientation of the planes corresponding to the (220) peak is the same as that of the shifting plane associated with the APB. The lattice planes (311) and (511) are not completely parallel to this translation, however they are only slightly tilted with respect to the (110) plane. The (440) peak is not influenced by this antiphase boundary lattice shift, in spite of being parallel to the shifting plane, because the corresponding plane distance is smaller than the region of the unit cell affected by the translation. This can be illustrated by Fourier transforming a micrograph of a nanoparticle and masking the respective Bragg peaks before performing the inverse Fourier transform as shown in Fig. 3(c) and (d). The effect of an APB is only visible in the image with the (220) peak masked. The approximate doubling of the FWHM for planes parallel to the APB leads to an approximate halving of the coherent crystallite, which is to be expected considering that the observed XRD pattern represents an average over many particles and particle orientations. If APBs develop with different distances to the particle surface, the average distance will be approximately half the particle diameter. The fact that we clearly observe such doubling of the respective FWHM indicates that a large portion of particles contains APBs.
| hkl | Q (Å−1) | FWHM (°) | D hkl (Å) |
|---|---|---|---|
| K = 0.94, λ = 0.4329 Å. | |||
| 220 | 2.126(1) | 0.33(1) | 71(1) |
| 311 | 2.487(1) | 0.30(1) | 78(1) |
| 222 | 2.598(1) | 0.15(1) | 152(1) |
| 400 | 3.007(1) | 0.16(1) | 149(1) |
| 422 | 3.683(1) | 0.37(1) | 63(1) |
| 511 | 3.907(1) | 0.34(1) | 69(1) |
| 440 | 4.253(1) | 0.18(1) | 135(1) |
As previously mentioned the exchange bias effect visible in inset in Fig. 2(b) could also be attributed to a ferro(ferri)magnetic/antiferromagnetic interface, e.g. the presence of wüstite (FeO) in maghemite/magnetite (γ-Fe2O3/Fe3O4) particles.55,56 The Néel temperature of wüstite (FeO) is 198 K (ref. 67) and is thus obscured by the superparamagnetic transition. For magnetite (Fe3O4) a shoulder or a kink in the ZFC curve of a M(T) measurement would be expected near the Verwey transition temperature TV = 120 K.68 However, in the experimental ZFC curve no feature around the Verwey temperature was observed. According to Goya et al.69 such transition can be suppressed for sufficiently small particles (diameter <50 nm). An exact knowledge about the particle composition is of great importance for a proper assessment of the origin of the exchange bias and can be obtained from the analysis of the pair distribution function, derived from the X-ray total scattering spectrum. It has to be taken into account that three superstructure peaks appear at 1.51, 1.68 and 1.85 Å−1 (marked with asterisks in Fig. 4), which are related to a vacancy ordering mainly on the octahedral sites and a resulting reduction of the symmetry from a cubic to a tetragonal structure.70–72
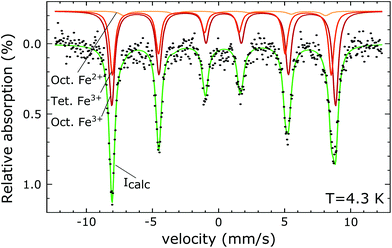
The PDF represents a probability of atoms to be separated by the distance r (Fig. 5) and provides insight into the particle composition and the local crystal structure. It is obtained by a Fourier transformation of the total scattering structure function, S(Q), which is the background corrected and normalized synchrotron powder scattering data I(Q).73 For the refinement a crystal structure model for maghemite with the space group P43212 with a tetragonal/pseudocubic unit cell as proposed in the literature72,74,75 was used as a starting point. As stated above, this choice is supported by the presence of the superstructure peaks in the diffraction pattern (Fig. 4). A thorough discussion of this space group choice is presented in the ESI (ESI Fig. S1, S2 and Table S1†). Refinement parameters are the lattice constants a = b and c, the atomic positions, a scale factor, a factor accounting for temperature effects affecting the low r region (δ) and site occupancy factors (SOFs) of the iron positions. The fit results are shown in Table 3. The X-ray scattering spectrum clearly shows a mixed phase composition of the nanoparticles (inset in Fig. 4). The dominant phase is maghemite (γ-Fe2O3) with a smaller contribution of magnetite (Fe3O4). Wüstite (FeO) should produce a strong peak at around Q = 2.91 Å−1, which is not present in the observed pattern. The lattice parameters obtained from the PDF analysis can be used to quantify this phase composition. The average lattice parameter of 8.358 Å corresponds to roughly 18(10)% Fe3O4. The error of this estimate is quite large due to large deviations of the bulk γ-Fe2O3 lattice parameters in the literature.76 We like to note that in order to exclude a possible influence of the instrument calibration on these measured values bulk reference samples of Fe3O4 and FeO and a nanopowder with a mix of Fe3O4 and γ-Fe2O3 (50 to 100 nm in size) have been measured. An independent estimation of the particle phase composition can be obtained using Mössbauer spectroscopy (Fig. 6). The Mössbauer spectrum consists of three sextet subspectra, assigned to B-site Fe3+ (dark red), A-site Fe3+ (red) and B-site Fe2+ (orange). Due to the limited thermal energy at 4.3 K, no signs of beginning superparamagnetic relaxation are visible, wherefore the subspectra could be reproduced via symmetric sextets. Due to the lower magnetic moment of Fe2+ as compared to Fe3+, the Fe2+ subspectrum exhibits a smaller sextet splitting, as well as a higher isomer shift due to different electronic charge densities close to the iron nucleus.77,78 To obtain higher precision in the estimation of the Fe2+ fraction, hyperfine parameters of the three sextet components were compared to those of larger particles obtained from the identical synthesis route, exhibiting higher contents of Fe3O4. Fe2+ is only present in the Fe3O4 structure and can therefore be used to estimate the phase composition, yielding a Fe3O4 contribution of roughly 15% with the rest being γ-Fe2O3, in agreement to lattice constants of the particles discussed above. A FeO (wüstite) contribution is not apparent in the spectrum, thus also ruling out FeO as the cause for the visible exchange bias in Fig. 2(b) and further supporting the presence of APBs as stated earlier.
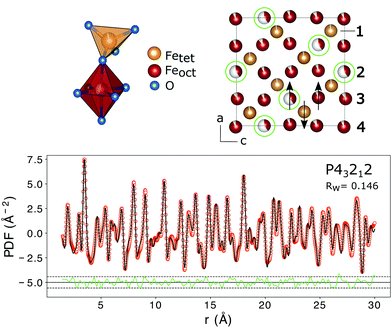 | ||
| Fig. 5 The top left shows the structural units with the iron atoms either octahedrally or tetrahedrally coordinated. Vacancy ordering on the iron positions is indicated with green circles in the top right figure. The numbers correspond to the nomenclature of the iron positions used in Table 3. The arrows show the atomic spin vectors expected for the bulk material leading to a ferrimagnetic structure. In the lower figure the PDF fit of interatomic distances r from 1.5 to 16 Å using a tetragonal/pseudo-cubic crystal structure with space group symmetry P43212 is shown. Interatomic distances smaller than the first coordination sphere were not included in the fit. The dashed lines represent 2 standard deviations of the difference curve. The structural parameters obtained from the fit are listed in Table 3. | ||
| Position | x/a | y/b | z/c | U iso | SOF |
|---|---|---|---|---|---|
| a = b = 8.358(2) Å, c = 8.358(2) Å. δ = 1.66(1) Å−1, particle size = 106(5) Å, Qmax = 18 Å−1, rpoly = 1.3 Å, Rw = 0.146. | |||||
| Fe1(tet.) | 0.7469(5) | 0.9985(5) | 0.1201(5) | 0.0068(5) | 0.98(2) |
| Fe2(oct.) | 0.3672(5) | 0.6328(5) | 0.75 | 0.0073(5) | 0.39(2) |
| Fe3(oct.) | 0.1205(5) | 0.8795(5) | 0.25 | 0.0069(5) | 0.93(2) |
| Fe4(oct.) | 0.3685(5) | 0.8683(5) | 0.9866(5) | 0.0067(5) | 0.92(2) |
| O1 | 0.1414(5) | 0.3833(5) | 0.5077(5) | 0.0119(5) | 1 |
| O2 | 0.3794(5) | 0.1314(5) | 0.0013(5) | 0.0119(5) | 1 |
| O3 | 0.1299(5) | 0.8676(5) | 0.0232(5) | 0.0119(5) | 1 |
| O4 | 0.3749(5) | 0.6293(5) | 0.9933(5) | 0.0119(5) | 1 |
In addition to the particle composition, the PDF allows also the investigation of the local crystal structure as presented in the following. The refined crystal lattice features slightly distorted coordination polyhedra and the refinement of SOFs reveals partial vacancy ordering with the majority of vacancies on octahedral Fe2 lattice sites (Fig. 5). The preference of vacancies for octahedral lattice sites could be a result of the oxidation of Fe3O4 to γ-Fe2O3. Assuming an in situ oxidation of Fe2+-ions to Fe3+ through the migration of electrons a charge imbalance will form locally which drives the Fe3+-ion outwards, leaving a vacancy behind. Since Fe2+ is situated only on octahedral lattice sites in the Fe3O4 structure due to its larger ionic radius, the vacancies will be mainly formed on octahedral sites.79 The vacancy ordering is not complete, as a reduced occupancy is also found on the tetrahedral iron position Fe1 and on the other octahedral iron sites (Table 3). In total, the amount of iron atoms in the unit cell corresponds to an occupation of 85(2)%, which is slightly lower than the theoretical value of 88.9% for maghemite (γ-Fe2O3).71 This leads to a theoretic reduction of the saturation magnetization by 9%, assuming perfect parallel and antiparallel alignment of atomic moments with an applied field on octahedral and tetrahedral positions and magnetic moments of 4.19 and 4.03μB, respectively.71 This is, however, neglecting the influence of vacancies on the local environment and thus the exchange interactions. The average iron–oxygen distances for the vacancy rich Fe2 position (2.119 Å) are larger than for the other two octahedral positions (1.981 Å for Fe3 and 2.064 Å for Fe4), which shows the influence of the vacancies on the local environment. The super-exchange interactions present between the iron atoms are highly dependent on the bond lengths and angles.58 In the refined crystal structure the Fe–O–Fe bond-angles between tetrahedral and octahedral iron are in the range of 114 to 130° giving rise to the antiferromagnetic coupling of both sublattices. The moments of octahedrally coordinated iron atoms couple ferromagnetically with an average Fe–O–Fe bond angle of 90°. However in the vicinity of a vacancy position (Fe2) some bond angles between adjacent iron atoms are altered to 102°. This would probably weaken the ferromagnetic alignment and lead to a reduction of the macroscopic magnetization. On the other hand it was previously shown that vacancy ordering, as observed in the samples of this study, increases the magnetization of iron oxide nanoparticles compared to particles with disordered vacancies,80 even up to bulk values for particles with a high degree of vacancy ordering and otherwise defect free crystal structures.81 Additionally, with the small-box approach used in PDFGUI, i.e. the assumption of periodic boundary conditions, it is not possible to model large range variations in the particle composition or vacancy concentrations. It might be that the increased number of vacancies is linked to structural disorder at the particle surface. Atomistic simulations that might determine the influence of vacancies on the saturation magnetization more precisely are very complex and beyond the scope of this work. However, we can still conclude that the partial vacancy disorder contributes to the observed reduction in magnetization, but alone is not sufficient to explain it in full.
The M(H) curves in Fig. 2(b) were fitted with the Langevin function under consideration of the particle size distribution50,82 as determined from SAXS
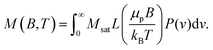 | (4) |
Here, μp is the particle magnetic moment, which is related to the saturation magnetization via Msat = μp/Vtρ, where Vt is the total particle volume and ρ the particle density. P(v) is the particle size distribution, as given in eqn (1). B is the magnetic induction, kB and T are the Boltzmann constant and the temperature, respectively. L(x) is the Langevin function according to
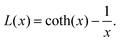 | (5) |
At 300 K the saturation magnetization constituted 83(1) A m2 kgFe−1 (using the amount of iron of 1.363(17) g as obtained by ICP-OES (ESI Table S1†)). Assuming either pure Fe3O4 or γ-Fe2O3 this yields 61(1) A m2 kgFe3O4−1 and 59(1) A m2 kgγ−Fe2O3−1, respectively. Considering the particle composition a value of 60(1) A m2 kgFerrite−1 is obtained. The values for the saturation magnetization are significantly lower than the room temperature bulk values for Fe3O4 (86 A m2 kg−1 (ref. 83)) and γ-Fe2O3 (75 A m2 kg−1 (ref. 84)) suggesting a decrease in saturation magnetization of about 23%. By referring to room temperature data the temperature dependence of the saturation magnetization is implicitly taken into account. Comparison to bulk values is justified through the observation of nearly bulk saturation magnetization values in iron oxide nanoparticles in previous studies.29,83,85
In order to study the magnetic structure of the nanoparticles a series of SANS experiments with polarized neutrons was performed where the scattering intensities for the two neutron spin states are given by
I− (Q, α) = FN2 + (FM2 − 2PFNFM)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2 sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α, α, | (6) |
I+ (Q, α) = FN2 + (FM2 + 2PεFNFM)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin2 sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α, α, | (7) |
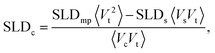 | (8) |
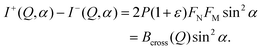 | (9) |
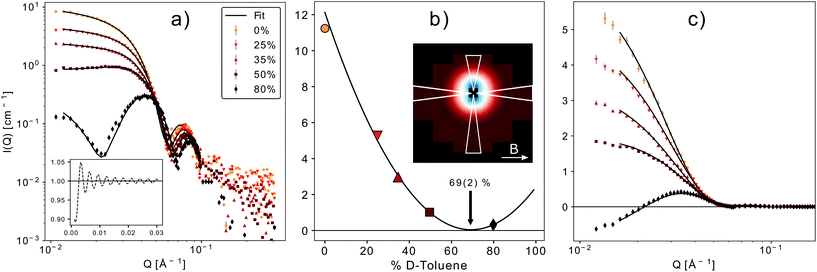 | ||
| Fig. 7 (a) SANSPOL with 5 different contrasts. The black line represents the best fit of a core–shell model with a sticky hard sphere structure factor (inset on the lower left). (b) Contrast matching. The minimum of the parabolic fit corresponds to the match point resulting in a core SLD of 6.8(2) × 10−6 Å−2. The inset shows the 2D-detector image for 50% d-toluene in the up-channel. The white triangles mark the integration sectors. (c) Fit of the magnetic-nuclear interference terms for the 5 contrasts, according to eqn (9). The only fit parameters are the magnetic scattering length density (SLDm) and thickness of a magnetically dead shell. | ||
A simultaneous fit of all five interference terms was performed. For FN the core–shell model was used with all parameters fixed from the analysis of scattering intensity in sectors parallel to the applied magnetic field. In case of FM a core–shell model with magnetic SLDs was used. The only fit parameters were a non-magnetic shell thickness, tmag, and the magnetic scattering length density, SLDm. The shell thickness evaluated to 0.3(1) nm giving a SLDm for the magnetic core of 9.4(2)×10−7 Å−2 (a detailed description of the fitting procedure is presented in the ESI†). The magnetic scattering length density SLDm is related to the magnetic particle moment according to μp = SLDmVeffμB/C, where μB is the Bohr magneton and C is a constant given by C = 1/2gnr0 = 2.7 × 10−5 Å, with gn the neutron gyromagnetic factor, r0 the classical electron radius. Veff is the effective magnetic particle volume.26 Together with Msat = μp/Vtρ the saturation magnetization Msat in A m2 kg−1 is related to SLDm in Å−2via
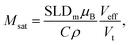 | (10) |
From SLDm a saturation magnetization of 58(4) A m2 kgFerrite−1 is calculated, which is in very good agreement to Msat at 300 K from the SQUID-magnetometry measurements that constituted 59(1) A m2 kgFerrite−1 (Fig. 2b).
In the work of Disch et al.26 spherical particles with diameter of 9.94 nm and FWHM of a lognormal size distribution of 0.055 were used. The authors concluded based on SANSPOL, VSM, SAXS and TEM data that a small magnetically depleted surface layer of 0.3(1) nm is present, but the main factor leading to the observed reduction of the magnetization compared to bulk values must be effects in the nanoparticle core in line with our findings. In the work of Herlitschke et al.28 no magnetic core–shell structure was reported for spherical particles with diameter of 7.4 nm and σ of a lognormal size distribution of 0.057 and the reduction of the magnetization was entirely ascribed to random orientations of atomic moments homogeneously distributed in the particle. A recent study by Zákutná et al.91 on cobalt ferrite nanoparticles with mean diameter of 14.1 nm and lognormal size distribution of σ = 0.031 revealed a magnetically disordered surface region of 0.7 nm thickness. Since the particles used there were composed of cobalt ferrite the results are only partially comparable to pure ferrite nanoparticles. In the work of Krycka et al.24 nanoparticles with diameter of 9.0 nm were investigated by SANS with polarization analysis. Here a magnetic surface layer of 1.0(2) nm with magnetization direction orthogonal to the core was proposed. Measurements were done on self assembled particles with considerable interparticle interactions that might influence this result and make comparisons to our samples difficult. Sharifi Dehsari et al.30 investigated particles ranging in diameter from 6.3 to 16.2 nm and found that particles consist of both magnetite and maghemite phases with possibly magnetic domains for particles larger than 14 nm and concluded from fittings to M(H) curves that no magnetic dead layer is present in all particle sizes. These inconsistent results with regards to a non-magnetic surface layer reflect the difficulties in assessing the particle surface with experimental methods and the data analysis. However, most authors agree that intraparticle effects play a major role in the reduction of saturation magnetization regardless of the presence of a surface layer.
A non-magnetic surface layer of 0.3 nm thickness could account for a magnetization reduction of max. 10%. Considering that the magnetization is 23% lower in the particles of this study compared to bulk reference values a surface layer alone is not sufficient to explain the reduction. The observed increased amount of vacancies in the crystal structure might also reduce the magnetization, however, as mentioned above, the observed ordering of the vacancies counterbalances this effect. Additionally, vacancies might preferably form on the particle surface and lead to the small non-magnetic surface layer that was observed with neutron scattering. The obtained data point to the fact that the observed magnetization reduction stems mainly from the core of the nanoparticles, i.e. due to the presence of antiphase boundaries.
Finally, the Langevin fit to the 300 K M(H) data yields a magnetic particle moment of μp = 63303μB, consistent with the μp obtained from SANS (μp = 63102μB). However, a closer examination of the fit curve shows a deviation from the data for field values between −0.2 and 0.2 T (Fig. 8), which would be better described by a smaller particle moment. In order to achieve the same saturation magnetization such a small particle moment would require a reduced effective magnetic particle radius of 6.8 nm, much smaller than the magnetic radius of 7.5 nm we observed in SANS. More likely are either a distribution of magnetic moments30 or a field dependence of the particle magnetic moment, originating from a field dependence of the magnetic particle volume. The magnetically depleted surface layer could increase for decreasing fields, as was observed for cobalt ferrite nanoparticles.91 In addition the region of canted spins in the vicinity of the APB also increases for decreasing fields, as observed in iron oxide thin films.92 Both effects will reduce the magnetic volume of the particle, and lead to a smaller magnetic moment for smaller fields.
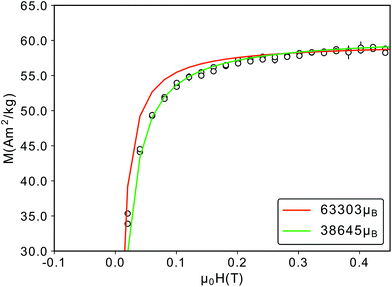 | ||
| Fig. 8 Close-up of the M(H)-RT data depicted in Fig. 2(b). The red curve corresponds to a magnetic particle moment of 63303μB, a better fit is achieved with a smaller particle moment (green). | ||
In summary we were able to assess the structural, chemical and magnetic properties of the iron oxide nanoparticles used in this study. Our findings are compiled in the following:
• Reduced room-temperature saturation magnetization of 60(1) A m2 kgFerrite−1 compared to the bulk materials
• Core size of 7.8(1) nm and σ = 0.095(1) of a lognormal size distribution and organic ligand shell thickness of 1.4(1) nm
• Particles are composed of ca. 15% Fe3O4 and 85% γ-Fe2O3, with no considerable contribution of FeO or other phases
• A magnetically dead surface layer of 0.3(1) nm was found
• Slightly increased number of vacancies, with partial order, thereby reducing the crystal symmetry to a tetragonal space group
• Antiphase boundaries are found directly and indirectly by HR-TEM and X-ray total scattering.
4. Conclusions
In conclusion, to resolve the open question about the underlying mechanism leading to the reduction of magnetization in iron oxide nanoparticles we addressed aspects such as particle size, size distribution, composition, structural and magnetic properties. Our results suggest that the observed reduced magnetization is a consequence of primarily the presence of antiphase boundaries in the nanoparticle core. We presented a consistent and precise analysis of the particle surface and the internal structural defects. For potential improvements of the particle performance in magnetic applications we propose to focus on the elimination of intraparticle effects.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the Paul Scherrer Institut, Villigen, Switzerland for provision of synchrotron radiation beamtime at beamline MS-X04SA of the SLS. AK and RDB acknowledge the financial support to European Union's Horizon 2020 research and innovation programme (Grant No. 856538) and to the Deutsche Forschungsgemeinschaft (Pr. 405553726 - TRR 270). This work is based upon experiments performed at the KWS-1 instrument operated by JCNS at the Heinz Maier-Leibnitz Zentrum (MLZ), Garching, Germany.References
- R. Bailey, J. Magn. Magn. Mater., 1983, 39, 178–182 CrossRef.
- K. Raj, B. Moskowitz and R. Casciari, J. Magn. Magn. Mater., 1995, 149, 174–180 CrossRef CAS.
- Y.-P. Sun, Supercritical Fluid Technology in Materials Science and Engineering: Syntheses: Properties, and Applications, Crc Press, 2002 Search PubMed.
- L. Josephson, C.-H. Tung, A. Moore and R. Weissleder, Bioconjugate Chem., 1999, 10, 186–191 CrossRef CAS PubMed.
- R. C. Semelka and T. K. Helmberger, Radiology, 2001, 218, 27–38 CrossRef CAS PubMed.
- C. Corot, P. Robert, J.-M. Idée and M. Port, Adv. Drug Delivery Rev., 2006, 58, 1471–1504 CrossRef CAS PubMed.
- Y.-W. Jun, J.-H. Lee and J. Cheon, Angew. Chem., Int. Ed., 2008, 47, 5122–5135 CrossRef CAS PubMed.
- S. Laurent, D. Forge, M. Port, A. Roch, C. Robic, L. Vander Elst and R. N. Muller, Chem. Rev., 2008, 108, 2064–2110 CrossRef CAS PubMed.
- C. Sun, J. S. Lee and M. Zhang, Adv. Drug Delivery Rev., 2008, 60, 1252–1265 CrossRef CAS PubMed.
- X. Ma, A. Gong, B. Chen, J. Zheng, T. Chen, Z. Shen and A. Wu, Colloids Surf., B, 2015, 126, 44–49 CrossRef CAS PubMed.
- R. Hergt, S. Dutz, R. Müller and M. Zeisberger, J. Phys.: Condens. Matter, 2006, 18, S2919 CrossRef CAS.
- M. Gonzales-Weimuller, M. Zeisberger and K. M. Krishnan, J. Magn. Magn. Mater., 2009, 321, 1947–1950 CrossRef CAS PubMed.
- K. M. Krishnan, IEEE Trans. Magn., 2010, 46, 2523–2558 CAS.
- C. S. Kumar and F. Mohammad, Adv. Drug Delivery Rev., 2011, 63, 789–808 CrossRef CAS PubMed.
- S. Laurent, S. Dutz, U. O. Häfeli and M. Mahmoudi, Adv. Colloid Interface Sci., 2011, 166, 8–23 CrossRef CAS PubMed.
- A. E. Deatsch and B. A. Evans, J. Magn. Magn. Mater., 2014, 354, 163–172 CrossRef CAS.
- R. L. White, R. Newt and R. F. W. Pease, IEEE Trans. Magn., 1997, 33, 990–995 CrossRef CAS.
- C. Jiang, S. M. Ng, C. W. Leung and P. W. T. Pong, J. Mater. Chem. C, 2017, 5, 252–263 RSC.
- E. Tronc, Adv. Chem. Phys., 1997, 283, 283–449 Search PubMed.
- S. Majetich and Y. Jin, Science, 1999, 284, 470–473 CrossRef CAS PubMed.
- A. Roca, D. Niznansky, J. Poltierova-Vejpravova, B. Bittova, M. Gonzalez-Fernandez, C. Serna and M. Morales, J. Appl. Phys., 2009, 105, 114309 CrossRef.
- T. J. Daou, J.-M. Greneche, S.-J. Lee, S. Lee, C. Lefevre, S. Bégin-Colin and G. Pourroy, J. Phys. Chem. C, 2010, 114, 8794–8799 CrossRef CAS.
- O. Petracic, Superlattices Microstruct., 2010, 47, 569–578 CrossRef CAS.
- K. L. Krycka, R. A. Booth, C. R. Hogg, Y. Ijiri, J. A. Borchers, W. Chen, S. Watson, M. Laver, T. R. Gentile, L. R. Dedon, S. Harris, J. J. Rhyne and S. A. Majetich, Phys. Rev. Lett., 2010, 104, 207203 CrossRef CAS PubMed.
- F. Kronast, N. Friedenberger, K. Ollefs, S. Gliga, L. Tati-Bismaths, R. Thies, A. Ney, R. Weber, C. Hassel, F. M. Römer, A. V. Trunova, C. Wirtz, R. Hertel, H. A. Dürr and M. Farle, Nano Lett., 2011, 11, 1710–1715 CrossRef CAS PubMed.
- S. Disch, E. Wetterskog, R. P. Hermann, A. Wiedenmann, U. Vainio, G. Salazar-Alvarez, L. Bergström and T. Brückel, New J. Phys., 2012, 14, 013025 CrossRef.
- E. Wetterskog, C.-W. Tai, J. Grins, L. Bergström and G. Salazar-Alvarez, ACS Nano, 2013, 7, 7132–7144 CrossRef CAS PubMed.
- M. Herlitschke, S. Disch, I. Sergueev, K. Schlage, E. Wetterskog, L. Bergström and R. P. Hermann, J. Phys.: Conf. Ser., 2016, 711, 012002 CrossRef.
- Z. Nedelkoski, D. Kepaptsoglou, L. Lari, T. Wen, R. A. Booth, S. D. Oberdick, P. L. Galindo, Q. M. Ramasse, R. F. L. Evans, S. Majetich and V. K. Lazarov, Sci. Rep., 2017, 7, 45997 CrossRef CAS PubMed.
- H. Sharifi Dehsari, V. Ksenofontov, A. Möller, G. Jakob and K. Asadi, J. Phys. Chem. C, 2018, 122, 28292–28301 CrossRef.
- Z. Nemati, J. Alonso, I. Rodrigo, R. Das, E. Garaio, J. Á. García, I. Orue, M.-H. Phan and H. Srikanth, J. Phys. Chem. C, 2018, 122, 2367–2381 CrossRef CAS.
- Ocean NanoTech LLC, Technical Specification of Iron Oxide Nanocrystals with Oleic Acid Coating, https://www.oceannanotech.com/media/wysiwyg/TSS/SOR_TSS.pdf, (accessed March 2021) Search PubMed.
- Ernst Ruska-Centre for Microscopy and Spectroscopy with Electrons, J. Large-Scale Res. Facil., 2016, 2, A77 CrossRef.
- K. Koch, QSTEM: Quantitative TEM/STEM Simulations, 2018 Search PubMed.
- P. R. Willmott, D. Meister, S. J. Leake, M. Lange, A. Bergamaschi, M. Böge, M. Calvi, C. Cancellieri, N. Casati, A. Cervellino, Q. Chen, C. David, U. Flechsig, F. Gozzo, B. Henrich, S. Jäggi-Spielmann, B. Jakob, I. Kalichava, P. Karvinen, J. Krempasky, A. Lüdeke, R. Lüscher, S. Maag, C. Quitmann, M. L. Reinle-Schmitt, T. Schmidt, B. Schmitt, A. Streun, I. Vartiainen, M. Vitins, X. Wang and R. Wullschleger, J. Synchrotron Radiat., 2013, 20, 667–682 CrossRef CAS PubMed.
- P. Juhás, T. Davis, C. L. Farrow and S. J. L. Billinge, J. Appl. Crystallogr., 2013, 46, 560–566 CrossRef.
- C. L. Farrow, P. Juhas, J. W. Liu, D. Bryndin, E. S. Božin, J. Bloch, T. Proffen and S. J. L. Billinge, J. Phys.: Condens. Matter, 2007, 19, 335219 CrossRef CAS PubMed.
- Jülich Centre for Neutron Science, GALAXI: Gallium anode low-angle x-ray instrument, J. Large-Scale Res. Facil., 2016, 2, A61, DOI:10.17815/jlsrf-2-109.
- A. Hammersley, J. Appl. Crystallogr., 2016, 49, 646–652 CrossRef CAS.
- R. Biehl, Jscatter, A Program For Evaluation And Analysis Of Experimental Data, 2018 Search PubMed.
- J. S. Pedersen, D. Posselt and K. Mortensen, J. Appl. Crystallogr., 1990, 23, 321–333 CrossRef.
- Hilgenberg GmbH, Technical data sheet 0500, version 1-09/2003 Search PubMed.
- Heinz Maier-Leibnitz Zentrum, et al., J. Large-Scale Res. Facil., 2015, 1, A28 CrossRef.
- A. V. Feoktystov, H. Frielinghaus, Z. Di, S. Jaksch, V. Pipich, M.-S. Appavou, E. Babcock, R. Hanslik, R. Engels, G. Kemmerling, H. Kleines, A. Ioffe, D. Richter and T. Brückel, J. Appl. Crystallogr., 2015, 48, 61–70 CrossRef CAS.
- V. Pipich, QtiKWS: user-friendly program for reduction, visualization, analysis and fit of SA(N)S data, 2012 Search PubMed.
- A. Guinier, G. Fournet and K. L. Yudowitch, Small-angle scattering of X-rays, Wiley, New York, 1955 Search PubMed.
- K. Butter, A. Hoell, A. Wiedenmann, A. V. Petukhov and G.-J. Vroege, J. Appl. Crystallogr., 2004, 37, 847–856 CrossRef CAS.
- M. F. Hansen and S. Mørup, J. Magn. Magn. Mater., 1999, 203, 214–216 CrossRef CAS.
- D. Peddis, C. Cannas, A. Musinu and G. Piccaluga, J. Phys. Chem. C, 2008, 112, 5141–5147 CrossRef CAS.
- S. Bedanta, O. Petracic and W. Kleemann, Handbook of magnetic materials, Elsevier, 2015, vol. 23, pp. 1–83 Search PubMed.
- J. Landers, S. Salamon, H. Remmer, F. Ludwig and H. Wende, ACS Appl. Mater. Interfaces, 2018, 11, 3160–3168 CrossRef PubMed.
- K. Pisane, S. Singh and M. Seehra, Appl. Phys. Lett., 2017, 110, 222409 CrossRef.
- J. K. Vassiliou, V. Mehrotra, M. W. Russell, E. P. Giannelis, R. McMichael, R. Shull and R. F. Ziolo, J. Appl. Phys., 1993, 73, 5109–5116 CrossRef CAS.
- O. Petracic, X. Chen, S. Bedanta, W. Kleemann, S. Sahoo, S. Cardoso and P. Freitas, J. Magn. Magn. Mater., 2006, 300, 192–197 CrossRef CAS.
- M.-H. Phan, J. Alonso, H. Khurshid, P. Lampen-Kelley, S. Chandra, K. Stojak Repa, Z. Nemati, R. Das, Ó. Iglesias and H. Srikanth, Nanomaterials, 2016, 6, 221 CrossRef PubMed.
- H. Khurshid, W. Li, S. Chandra, M.-H. Phan, G. C. Hadjipanayis, P. Mukherjee and H. Srikanth, Nanoscale, 2013, 5, 7942–7952 RSC.
- S. K. Arora, R. Sofin, A. Nolan and I. V. Shvets, J. Magn. Magn. Mater., 2005, 286, 463–467 CrossRef CAS.
- J. B. Goodenough, Phys. Rev., 1955, 100, 564–573 CrossRef CAS.
- J. Kanamori, J. Phys. Chem. Solids, 1959, 10, 87–98 CrossRef CAS.
- W. Eerenstein, T. Palstra and T. Hibma, Thin Solid Films, 2001, 400, 90–94 CrossRef CAS.
- J. Park, K. An, Y. Hwang, J.-G. Park, H.-J. Noh, J.-Y. Kim, J.-H. Park, N.-M. Hwang and T. Hyeon, Nat. Mater., 2004, 3, 891–895 CrossRef CAS PubMed.
- K. P. McKenna, F. Hofer, D. Gilks, V. K. Lazarov, C. Chen, Z. Wang and Y. Ikuhara, Nat. Commun., 2014, 5, 5740 CrossRef CAS PubMed.
- P. Scherrer, Kolloidchemie Ein Lehrbuch, Springer, Berlin, Heidelberg, 1912, pp. 387–409 Search PubMed.
- U. Holzwarth and N. Gibson, Nat. Nanotechnol., 2011, 6, 534–534 CrossRef CAS PubMed.
- A. Monshi, M. R. Foroughi and M. R. Monshi, World J. Nano Sci. Eng., 2012, 2, 154–160 CrossRef.
- B. D. Cullity and S. Stock, Elements of X-ray Diffraction, Prentice-Hall, 3rd edn, 2001 Search PubMed.
- G. Kugel, B. Hennion and C. Carabatos, Phys. Rev. B: Condens. Matter Mater. Phys., 1978, 18, 1317 CrossRef CAS.
- N. Guigue-Millot, N. Keller and P. Perriat, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 012402 CrossRef.
- G. Goya, T. Berquo, F. Fonseca and M. Morales, J. Appl. Phys., 2003, 94, 3520–3528 CrossRef CAS.
- M. Coduri, P. Masala, L. D. Bianco, F. Spizzo, D. Ceresoli, C. Castellano, S. Cappelli, C. Oliva, S. Checchia, M. Allieta, D.-V. Szabo, S. Schlabach, M. Hagelstein, C. Ferrero and M. Scavini, Nanomaterials, 2020, 10, 867 CrossRef CAS PubMed.
- R. Grau-Crespo, A. Y. Al-Baitai, I. Saadoune and N. H. de Leeuw, J. Phys.: Condens. Matter, 2010, 22, 255401 CrossRef PubMed.
- J.-E. Jørgensen, L. Mosegaard, L. E. Thomsen, T. R. Jensen and J. C. Hanson, J. Solid State Chem., 2007, 180, 180–185 CrossRef.
- T. Proffen, S. J. L. Billinge, T. Egami and D. Louca, Z. Kristallogr. - Cryst. Mater., 2003, 218, 1203 Search PubMed.
- K. Kelm and W. Mader, Z. Naturforsch., B: J. Chem. Sci., 2006, 61, 665–671 CrossRef CAS.
- C. Greaves, J. Solid State Chem., 1983, 49, 325–333 CrossRef CAS.
- A. Cervellino, R. Frison, G. Cernuto, A. Guagliardi and N. Masciocchi, J. Appl. Crystallogr., 2014, 47, 1755–1761 CrossRef CAS.
- A. G. Roca, J. F. Marco, M. D. P. Morales and C. J. Serna, J. Phys. Chem. C, 2007, 111, 18577–18584 CrossRef CAS.
- J. Landers, F. Stromberg, M. Darbandi, C. Schöppner, W. Keune and H. Wende, J. Phys.: Condens. Matter, 2014, 27, 026002 CrossRef PubMed.
- P. Sidhu, R. Gilkes and A. Posner, J. Inorg. Nucl. Chem., 1977, 39, 1953–1958 CrossRef CAS.
- M. Morales, C. Serna, F. Bødker and S. Mørup, J. Phys.: Condens. Matter, 1997, 9, 5461 CrossRef CAS.
- D. Li, W. Y. Teoh, C. Selomulya, R. C. Woodward, P. Munroe and R. Amal, J. Mater. Chem., 2007, 17, 4876–4884 RSC.
- F. Wiekhorst, E. Shevchenko, H. Weller and J. Kötzler, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 224416 CrossRef.
- S. J. Kemp, R. M. Ferguson, A. P. Khandhar and K. M. Krishnan, RSC Adv., 2016, 6, 77452–77464 RSC.
- P. Tartaj, T. González-Carreño and C. J. Serna, J. Phys. Chem. B, 2003, 107, 20–24 CrossRef CAS.
- P. Guardia, B. Batlle-Brugal, A. Roca, O. Iglesias, M. Morales, C. Serna, A. Labarta and X. Batlle, J. Magn. Magn. Mater., 2007, 316, e756–e759 CrossRef CAS.
- A. Wiedenmann, J. Appl. Crystallogr., 2000, 33, 428–432 CrossRef CAS.
- A. Michels, J. Phys.: Condens. Matter, 2014, 26, 383201 CrossRef PubMed.
- S. Mühlbauer, D. Honecker, É. A. Périgo, F. Bergner, S. Disch, A. Heinemann, S. Erokhin, D. Berkov, C. Leighton, M. R. Eskildsen and A. Michels, Rev. Mod. Phys., 2019, 91, 015004 CrossRef.
- M. Avdeev, D. Bica, L. Vekas, V. Aksenov, A. Feoktystov, O. Marinica, L. Rosta, V. Garamus and R. Willumeit, J. Colloid Interface Sci., 2009, 334, 37–41 CrossRef CAS PubMed.
- M. V. Avdeev, J. Appl. Crystallogr., 2007, 40, 56–70 CrossRef CAS.
- D. Zákutná, D. Niznansky, L. Barnsley, A. Feoktystov, D. Honecker and S. Disch, Phys. Rev. X, 2020, 10, 031019 Search PubMed.
- S. Arora, R. Sofin and I. Shvets, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 134404 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/D0NR08615K |
| This journal is © The Royal Society of Chemistry 2021 |