Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Formation and growth mechanism for niobium oxide nanoparticles: atomistic insight from in situ X-ray total scattering†
Olivia
Aalling-Frederiksen
 ,
Mikkel
Juelsholt
,
Mikkel
Juelsholt
 ,
Andy S.
Anker
,
Andy S.
Anker
 and
Kirsten M. Ø.
Jensen
and
Kirsten M. Ø.
Jensen
 *
*
Department of Chemistry and Nano-Science Center, University of Copenhagen, 2100 Copenhagen Ø, Denmark. E-mail: kirsten@chem.ku.dk
First published on 15th March 2021
Abstract
Understanding the mechanisms for nanoparticle nucleation and growth is crucial for the development of tailormade nanomaterials. Here, we use X-ray total scattering and Pair Distribution Function analysis to follow the formation and growth of niobium oxide nanoparticles. We study the solvothermal synthesis from niobium chloride in benzyl alcohol, and through investigations of the influence of reaction temperature, a formation pathway can be suggested. Upon dissolution of niobium chloride in benzyl alcohol, octahedral [NbCl6−xOx] complexes form through exchange of chloride ligands. Heating of the solution results in polymerization, where larger clusters built from multiple edge-sharing [NbCl6−xOx] octahedra assemble. This leads to the formation of a nucleation cluster with the ReO3 type structure, which grows to form nanoparticles of the Wadsley–Roth type H-Nb2O5 structure, which in the bulk phase usually only forms at high temperature. Upon further growth, structural defects appear, and the presence of shear-planes in the structure appears highly dependent on nanoparticle size.
Introduction
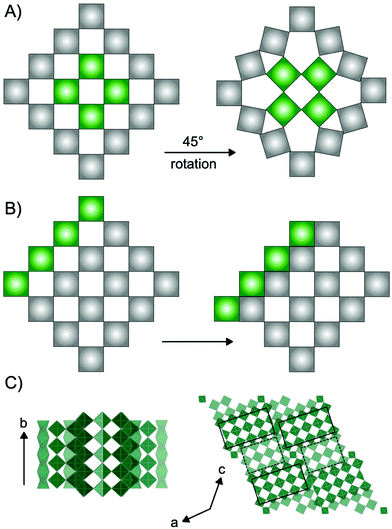
Niobium oxides have in recent years received significant interest due to their versatile electrochemical properties. For example, niobium and niobium-based oxide materials have been shown to be outstanding cathode materials for high-power batteries due to high Li-diffusion rates through their crystal structures.1–7 Additionally, studies have shown that niobium oxides show excellent potential as catalyst materials for production of e.g. fuels and chemicals from biomass sources.8–10 Niobium oxides have furthermore been extensively studied for their electrochromic properties e.g. photodetection11 and in recent years, the potential of amorphous and nanostructured Nb2O5 for electrochromic windows has been investigated.12–14The versatility of applications of niobium-based oxides arises from their rich structural chemistry.9,15 The building block of niobium pentoxide Nb2O5 is the [NbO6] octahedra which occur in the oxide structures as corner-sharing or edge-sharing, i.e. sharing one or two oxygen atoms, respectively. The many opportunities in the arrangement of these octahedra allow for the structural diversity, and a range of Nb2O5 polymorphs as well as non-stoichiometric phases exist. Many of these are based on the ReO3 structure, which is a cubic crystal structure in space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, built from only corner-sharing [ReO6] octahedra. Extended defects in the ReO3 structure can lead to a range of phases with distinct structural differences. Such extended defects are commonly seen in early transition metal oxides such as niobium oxides, as well as vanadium oxides,16 molybdenum oxides17 and tungsten oxides.18 As illustrated in Fig. 1, they appear in different ways: as tetragonal tungsten bronzes (TTB-type defects),19 as Magnéli phases18 and as block-type structured Wadsley–Roth phases.20 The TTB-type structure (Fig. 1A) is found in e.g. mixed niobium oxides (Nb2WO8) and tungsten oxides (W32O82), as well as in the T-Nb2O5, and the related TT-Nb2O5 structure. The structure originates from cubic ReO3, however, a 45° rotation of four octahedra in the ab-plane leads to pentagonal columns in the structure.19 The transformation from the parent to the TTB-type structure furthermore results in a distortion of the octahedra, and the interstitial site formed in the pentagonal columns can be either partially or fully occupied by metal atoms.21 Magnéli phases (Fig. 1B) also originate from the ReO3-type structure but contain slabs of edge-sharing octahedra in two directions parallel to one of the unit cell axes. This leads to ReO3 domains which are infinite in two directions, but finite in the third. The formation of such shear planes has been explained by supersaturation of oxygen vacancies resulting in a collapse of the lattice.22 Magnéli phases are observed in particular in molybdenum-, vanadium- and titanium oxides. In niobium oxides, however, Wadsley–Roth block-type structures are more commonly seen. The block-type structures (illustrated in H-Nb2O5 in Fig. 1C) have finite blocks of the ReO3 structure in a two-direction perpendicular plane, separated by shear planes along (100) and (001). Many Nb2O5 phases and nonstoichiometric niobium oxide phases (e.g. H-Nb2O5, M-Nb2O5, N-Nb2O5, Nb12O29 and Nb22O54) have this block-type structure. The block size, meaning the number of corner-sharing octahedra within a block, differ between the phases, and various sizes of blocks can be present in one phase.20 An effect of crystallographic shear planes in the block structure of ReO3 is that metal atoms in tetrahedral coordination often appears in the intersection between blocks, as is observed in the H-Nb2O5 in Fig. 1C. The monoclinic H-Nb2O5 structure is reported to be the most thermodynamically stable of the niobium pentoxides15 and it is usually formed at high temperature (>900 °C). It contains blocks of two different sizes, (3 × 4) octahedra and (3 × 5) octahedra separated by crystallographic shear planes.15,23
m, built from only corner-sharing [ReO6] octahedra. Extended defects in the ReO3 structure can lead to a range of phases with distinct structural differences. Such extended defects are commonly seen in early transition metal oxides such as niobium oxides, as well as vanadium oxides,16 molybdenum oxides17 and tungsten oxides.18 As illustrated in Fig. 1, they appear in different ways: as tetragonal tungsten bronzes (TTB-type defects),19 as Magnéli phases18 and as block-type structured Wadsley–Roth phases.20 The TTB-type structure (Fig. 1A) is found in e.g. mixed niobium oxides (Nb2WO8) and tungsten oxides (W32O82), as well as in the T-Nb2O5, and the related TT-Nb2O5 structure. The structure originates from cubic ReO3, however, a 45° rotation of four octahedra in the ab-plane leads to pentagonal columns in the structure.19 The transformation from the parent to the TTB-type structure furthermore results in a distortion of the octahedra, and the interstitial site formed in the pentagonal columns can be either partially or fully occupied by metal atoms.21 Magnéli phases (Fig. 1B) also originate from the ReO3-type structure but contain slabs of edge-sharing octahedra in two directions parallel to one of the unit cell axes. This leads to ReO3 domains which are infinite in two directions, but finite in the third. The formation of such shear planes has been explained by supersaturation of oxygen vacancies resulting in a collapse of the lattice.22 Magnéli phases are observed in particular in molybdenum-, vanadium- and titanium oxides. In niobium oxides, however, Wadsley–Roth block-type structures are more commonly seen. The block-type structures (illustrated in H-Nb2O5 in Fig. 1C) have finite blocks of the ReO3 structure in a two-direction perpendicular plane, separated by shear planes along (100) and (001). Many Nb2O5 phases and nonstoichiometric niobium oxide phases (e.g. H-Nb2O5, M-Nb2O5, N-Nb2O5, Nb12O29 and Nb22O54) have this block-type structure. The block size, meaning the number of corner-sharing octahedra within a block, differ between the phases, and various sizes of blocks can be present in one phase.20 An effect of crystallographic shear planes in the block structure of ReO3 is that metal atoms in tetrahedral coordination often appears in the intersection between blocks, as is observed in the H-Nb2O5 in Fig. 1C. The monoclinic H-Nb2O5 structure is reported to be the most thermodynamically stable of the niobium pentoxides15 and it is usually formed at high temperature (>900 °C). It contains blocks of two different sizes, (3 × 4) octahedra and (3 × 5) octahedra separated by crystallographic shear planes.15,23
In Table S1† we give an overview of the most important reported niobium oxides and their crystal structure. We note here that the nomenclature of the different Nb2O5 phases can easily lead to a lot of confusion. Where H-Nb2O5, M-Nb2O5, T/TT-Nb2O5 are named from the temperature at which they are obtained (German: Hoch, Medium, Tief), B-Nb2O5, N-Nb2O5 and P-Nb2O5 have their names from crystallite shapes (German: Blätter, Nadeln, Prismen).15,24 While niobium oxides have been studied for decades, the complex defect chemistry furthermore means that the structures of many of these phases are still debated, and much uncertainty exists on the number of niobium oxide polymorphs and their crystal structures.
The large structural diversity in niobium oxides, along with the strong structure–property relation, means that structure control during synthesis is crucial in material preparation, and much work has been devoted to the synthesis of niobium oxide nanomaterials. While heat treatment of NbO2 in solid state reactions is the simplest way to obtain different modifications of bulk, crystalline Nb2O5,3,24 hydro- and solvothermal synthesis have in general proven to be efficient methods for nanomaterial preparation.25,26 Several studies have demonstrated the synthesis of niobium based oxide nanosheets,1,27 nanorods7,28 and nanospheres8 through hydro- and solvothermal synthesis. Other approaches, such as colloidal synthesis methods14 and electrospinning4 have been reported. However, very little is known on the atomic-scale reaction mechanisms that take place during material synthesis, which hinders rational design of synthesis methods for a given niobium oxide structure.
In situ X-ray total scattering studies is an effective way of following chemical reactions as they take place, revealing important information on the formation mechanism of e.g. various metal oxides.29–35 The use of Pair Distribution Function (PDF) analysis of total scattering data means that structural information can be obtained for matter with and without long-range order, making it possible to follow the structural rearrangements that take place in a synthesis all the way from ionic or molecular clusters in solution to the final material.36,37 Here, we study the solvothermal synthesis of Nb2O5 nanoparticles from NbCl5 in benzyl alcohol, first described by Buha et al.38 This non-aqueous sol–gel route, applying a metal chloride precursor in benzyl alcohol, can be used for synthesis of a range of different oxide materials, also for compounds that are otherwise difficult to prepare, such as niobium oxides.39,40 The solvothermal synthesis approach is furthermore simple and industrially relevant, as it can easily be scaled up. Benzyl alcohol has proven an efficient solvent for control of particle size, phase and crystallinity40 and acts as oxygen supplier, capping agent and solvation medium.41 Deshmukh et al.39 have suggested a reaction scheme for the reaction between metal halides and benzyl alcohol, where a metal hydroxide species first form as an intermediate structure through hydrolysis. However, further details on the possible hydroxide species are unknown, as the reaction rapidly takes place even at room temperature.39 For the niobium oxide synthesis in particular, the mechanisms leading to a specific atomic structure is unknown. From our in situ data, we can suggest a formation mechanism for niobium oxide nanoparticles, where single [NbO6] octahedral building blocks first assemble to form a nucleation cluster of a ReO3 type network. This structure further grows to form the final structure: a Wadsley–Roth block-structure phase. Formation of [NbO6] octahedra takes place through exchange of chloride ligands, and assembly of the octahedra happens as soon as the chloride ligands have been exchanged. We furthermore show how synthesis temperature and applied pressure influence the final structure and induce the formation of shear planes and block structures in the material. Such knowledge gives a new approach to structure control of niobium oxides by synthesis design.
Experimental methods
Niobium oxide synthesis was carried out using a solution of NbCl5 (99%, Sigma Aldrich) in benzyl alcohol (Assay (GC, area%): ≥99.0% (a/a), Sigma Aldrich).38 The synthesis was done in our custom-made reaction cell for in situ X-ray studies of solvothermal synthesis, which is similar in design to that previously described by Becker et al.42 The precursor suspension was injected into a fused silica tube with 0.7 mm inner diameter and 0.09 mm wall thickness. A HPLC pump was used to pressurize the tube and a hot air blower was used to reach the desired temperature within the tube. Four different conditions were studied, 160 °C, 200 °C and 300 °C at 100 bar pressure, and 100 °C at ambient pressure. A high concentration of NbCl5 in benzyl alcohol is necessary to obtain enough scattering signal for PDF analysis, and the precursor was prepared to yield 0.6 M NbCl5. However, the exact concentration in the reaction cell is associated with some uncertainty due to the lack of complete solubility of the NbCl5 in benzyl alcohol.The in situ X-ray total scattering experiments were performed at P02.1 PETRA III, DESY, Germany with a wavelength of λ = 0.2072 Å. The RA-PDF43 geometry was applied using a large 2D detector, measuring 40 by 40 cm and a 216.9 mm sample to detector distance. The time resolution of the collected data was 5 s. The collected 2D data were integrated using Fit2D,44 and the total scattering data were Fourier Transformed to obtain PDFs using PDFgetX3.45 The following parameters were used for the data reduction: Qmin = 0.6 Å−1, Qmax = 14.5 Å−1, Qmaxinst = 22.4 Å−1 and rpoly = 0.9 Å. Before the Fourier transformation, the background scattering signal from the fused silica capillary and the pure solvent at the appropriate temperature and pressure was subtracted. The background subtraction is described in detail in the ESI, Fig. S2.†
The PDFs obtained from crystalline nanoparticles were modelled using PDFgui,46 where real-space Rietveld refinements were performed. Cluster structures with no long-range order were modelled using Diffpy-CMI47 with the DebyePDFCalculator. The modelling is described in detail below and in the ESI.†
Niobium oxide NPs were also synthesized for ex situ characterization. Here, a 3 mm borosilicate NMR tube was filled with the 0.6 M NbCl5 solution, sealed with a septa and lowered into a 100 °C hot oil bath. After 13 minutes of heating, the substance was transferred into a borosilicate glass capillary with an outer diameter of 0.8 mm for X-ray total scattering data collection. Total scattering data were collected at room temperature using a Panalytical Empyrean Series 2 diffractometer with an Ag-source (X-ray wavelength of 0.56 Å), and a GaliPIX detector. An identical measurement was performed with a borosilicate glass capillary with pure benzyl alcohol and used in the background subtraction. The as-prepared suspension was furthermore washed with ethanol, and a dilute suspension was prepared and drop casted on a lacey carbon grid and transmission electron microscopy (TEM) images were collected on a Tecnai T20 G2 200 kV TEM. The images were further processed with the FIJI software.48
Small Angle X-ray Scattering (SAXS) data were collected from the as-prepared suspension. The sample was loaded into a quartz capillary with outer diameter of 1.0 mm, and SAXS data were measured using a SAXSLab instrument (JJ-XRay) with a Rigaku 100 XL+ micro focus sealed X-ray tube and a Dectris 2D 300 K Pilatus detector with X-ray wavelength of 1.54 Å. Data from benzyl alcohol and an empty quartz capillary were measured as backgrounds. The data were integrated using the programme Saxsgui and simulated SAXS formfactor models were calculated with Diffpy-CMI, which uses SasView49 functions.
Results and discussion
Formation of Wadsley–Roth structured Nb2O5
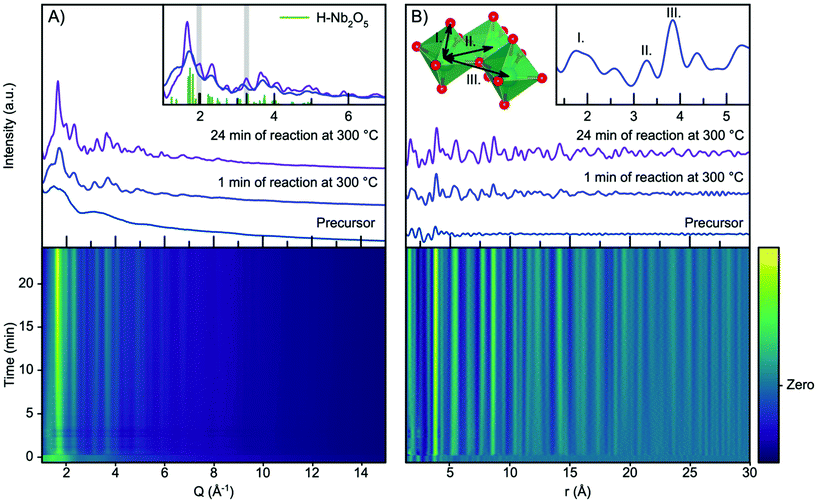
Fig. 2A shows the time resolved scattering data obtained during niobium oxide synthesis at 300 °C. The data are shown as a contour plot, along with three selected scattering patterns from different stages of the reaction (precursor, 1 minute of reaction and 24 minutes of reaction). The synthesis is initiated by applying heating at t = 0 minutes, and the temperature reaches 90% of the setpoint temperature after the first 10 seconds. A rapid change in the scattering pattern is observed as the heat is turned on, and a nanocrystalline phase forms almost instantly as seen from the emergence of broad Bragg peaks. As the reaction progresses, the peaks become more pronounced and sharper as seen when comparing the data obtained at 1 minute and 24 minutes into the reaction.The observed scattering patterns are compared with calculated Bragg peak intensities of H-Nb2O5 in Fig. 2A, inset. A comparison with diffraction patterns calculated from other niobium oxides is shown in Fig. S4.† None of the known niobium oxide crystal structures fully describe the observed scattering patterns, although H-Nb2O5 accounts for the main features in the pattern, especially for the particles formed at the beginning of the reaction. Other features at Q-values 2.0 Å−1 and 3.3 Å−1, highlighted in Fig. 2A inset, evolve during the reaction. We have previously observed that the presence of extended defects in nanomaterials is highly size-dependent,50 and it is likely that the particle growth during this reaction induces defects in the structure. However, the large Bragg peak broadening from nanoparticle size makes a conventional crystallographic analysis of these effects difficult, and we therefore turn our investigation to the Pair Distribution Function (PDF) of the total scattering data.
The time resolved PDFs obtained from the total scattering data are shown in Fig. 2B. As expected from the Q-space data, it is evident from the PDFs that the nanocrystalline phase form immediately as the reaction is initiated as the PDF oscillations extend to higher r, whereas the PDF collected for the precursor shows limited structural coherence. We discuss the structure of the precursor, as well as the nucleation mechanism, in a section below, and first investigate the PDF describing the structure of the nanoparticles forming.
Fig. S5† shows a comparison between the experimental PDF obtained after 1 minute and PDFs calculated from known niobium oxide crystal structures. As expected, the plot shows that many of the structures are very similar locally as they share a structural motif of corner-sharing and edge-sharing [NbO6] octahedra. As shown in the inset in Fig. 2B, the PDF peaks at 3.3 Å and 3.8 Å arise from Nb–Nb pairs in edge- and corner-sharing geometry,51 respectively, while the broad peak at 1.8 Å arises from Nb–O distances within the octahedra.52 By considering the intensity ratio between the edge- and corner-sharing peaks, it is clear that the product from the synthesis is closer in structure to the Wadsley–Roth structures than the TTB-structured T-Nb2O5, which does not give a good description of our data. This is surprising, as the product from a very similar synthesis was found by Buha et al.38 to take the TT-Nb2O5 structure. The TT-phase is expected to be similar in structure to the T-phase, although its structure has never really been resolved.53 We expect the deviation from earlier studies observed here to be an effect of the experimental conditions, e.g. the higher heating rate in the current experiment compared with a conventional solvothermal synthesis using autoclaves, the difference in pressure within the reaction vessels, and the reaction container material. The formation of the H-Nb2O5 phase at the low reaction temperature used here is notable, as this phase usually forms at much higher temperature, (>900 °C), at least in the case of bulk materials.15
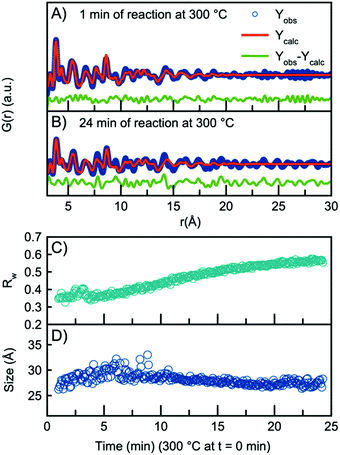
As the H-Nb2O5 has been reported as the most thermodynamically stable of the Wadsley–Roth structured Nb2O5 polymorphs,15 we use this structure as a starting model for further structural analysis. A fit to the data obtained after 1 minute at 300 °C using the H-Nb2O5 model is plotted in Fig. 3A, showing good agreement between model and data. A description of the refinement strategy and the refined parameters can be found in Table S2.† Note that the fits shown only include the r-range from 3–30 Å, thus not including the first peak originating from the first Nb–O distance, which can be seen in Fig. 2B to be highly asymmetric. The evolution of the Nb–O peak will be discussed further below.
The refined crystallite size from the fit in Fig. 3A is 26 Å, however, the fit clearly shows weak features at higher r-values which are not well described by the model. In fact, the refined crystallite size is slightly smaller than a single H-Nb2O5 unit cell in the a/c plane, 35 Å. After 24 minutes of reaction, the misfit at higher r-values becomes much more pronounced as seen in the fit in Fig. 3B. The increased misfit with time is clearly observed in Fig. 3C, where the fit Rw-values are plotted, representing the decreasing quality of the fit when performing sequential refinements. The evolution of the refined crystallite size (sp-diameter, Fig. 3D) in the sequential refinements furthermore indicates that the H-Nb2O5 model cannot describe the long-range order of the PDF as it cuts off the crystallite size at ∼30 Å even though the features in the experimental PDF extend to ∼45 Å (Fig. S6†). Sequential refinements with other Wadsley–Roth niobium oxide phases are shown in Fig. S8,† giving very similar results, and all reported phases give a poor description of the long-range order observed in the PDF obtained at the end of the experiment.
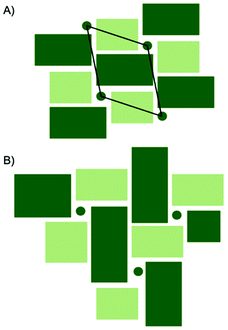
A comparison between the PDFs obtained at 1 minute and 24 minutes in Fig. 2B and S6† show that with time, the peak arising from edge-sharing [NbO6] octahedra becomes more prominent. The H-Nb2O5 structure (Fig. 1C) is built up from ReO3 blocks of (3 × 5) and (3 × 4) corner-sharing octahedra, where edge-sharing occur only between blocks. This is further illustrated in Fig. 4A. The block size in Nb12O29 are (3 × 4) and in Nb22O54 (3 × 4) and (3 × 3) octahedra. The good agreement between data and model in the low r-range when fitting with these three structures, combined with the large misfit at high r-values, indicate that the particles formed in the solvothermal synthesis are indeed built up from ReO3 block structures, but that the block sizes and arrangement may differ from the well-ordered, known and well-characterized bulk structures. HR-TEM analysis has previously shown that disordered regions can be present in niobium oxide nanoparticles. For example, in 1973 IIjima showed the presence of blocks of different sizes assigned as heavily disordered regions in the H-Nb2O5,54 and several studies conducted in the 1970s show similar imperfections in the block structure of Nb2O5.55–57 More recently, Russo et al.8 showed that T-Nb2O5 nanoparticles synthesized through solvothermal synthesis with NbCl5 and acetophenone have regions deviating from the crystalline nature of the material. Fig. 4 shows an illustration of these block defects found in niobium oxide particles compared to the idealized H-Nb2O5 structure. While the idealized H-Nb2O5 in Fig. 4A has two distinctive block sizes illustrated by dark and light green squares, the defect structure shown in Fig. 4B contains various sizes of blocks with no systematic ordering. In a recent study of molybdenum oxide nanoparticles, we saw that nanosizing in a similar way can lead to disordered shear-planes rather than the well-ordered Magneli phases from bulk materials.50
In order to model the long-range order of the particles, we therefore again look towards different Nb2O5 crystal structures. The R-Nb2O5 phase shown in Fig. 5G was first reported by Gruehn in 1966.58 Here, a range of different synthesis methods were shown to result in R-Nb2O5 along with other phases like TT- and a P-Nb2O5 phase, which was reported to be highly similar in structure compared with the R-Nb2O5. The structures and existence of these phases are however associated with much uncertainty, and to the best of our knowledge, the crystal structure of P-Nb2O5 has not been reported. Since the first synthesis of R-Nb2O5 in 1966, the P/R-Nb2O5 phases have rarely occurred in the literature and have mostly been described in computational studies of niobium oxides. For example, Valencia-Balvin et al.59 performed a computational study where they showed that R-Nb2O5 is metastable compared to other structural modifications. Therefore, the existence of these modifications is doubtful and more thorough clarification of the structural chemistry of niobium pentoxide is still needed. However, R-Nb2O5 is the simplest of the niobium pentoxide modifications. Interestingly, its structure is similar to the shear planes forming between block structures in Wadsley–Roth phases as seen in Fig. 1B and C. Fig. 5B shows a fit to the data obtained after 24 minutes of reaction using this R-Nb2O5 structure along with the simple ReO3 structure, while a fit using only the ReO3 structure is shown in Fig. 5A. The refinement values are presented in Tables S7 and 8.† These fits illustrate that many features from the local structure can be described by the ReO3 motifs, while peaks at higher r-values are included by the model from R-Nb2O5. A better result is obtained when combining the R-Nb2O5 structure with H-Nb2O5 as seen in Fig. 5C.
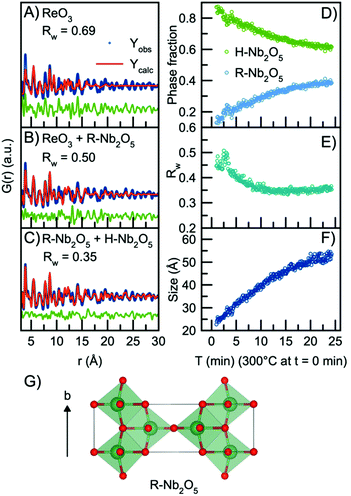 | ||
| Fig. 5 Real-space Rietveld refinement of the PDF collected 24 min into the reaction using the structural model (A) ReO3, (B) ReO3 and R-Nb2O5, (C) R-Nb2O5 and H-Nb2O5. (D) Refined phase fractions of H-Nb2O5 and R-Nb2O5 plotted as a function of time. (E) Fit agreement factor Rw plotted as a function of time. (F) The refined crystallite size (sp-diameter) plotted as a function of time. The crystallite size for the H- and R-phases were constrained to take the same value. (G) The crystal structure of R-Nb2O5 first reported by Gruehn.58 The structure is built from corner-sharing and edge-sharing octahedra. | ||
Compared to the single-phase fit with H-Nb2O5 in Fig. 3B, the agreement factor Rw decreases from 0.55 to 0.35 when including the R-Nb2O5 phase. The model clearly does not fully describe all features of the PDF intensities; however, all main PDF peaks are now included. We do not interpret this as the occurrence of a secondary phase during Nb2O5 synthesis, but rather that the combination of the H- and R-structure accounts for the development of Wadsley–Roth structures with blocks of different sizes, separated by a R-Nb2O5-like interface. In the model, the H-structure thus mainly describes the structure of the blocks, while the R-structure may account for the interface between them. The existing misfit in the PDF when modelling with two different phases likely arises from the heterogeneous nature of the particles, where blocks of different sizes may be present as illustrated in Fig. 4B. This effect is not included in the simple model applied here.
Through sequential refinement with the two-phase model with both H- and R-Nb2O5, we can follow the structural changes after initiation of the reaction. Model details and representative fits from different time points during the reaction is given in the ESI, Fig. S9 and Table S9.†Fig. 5D shows the weight phase fraction of the H- and R-Nb2O5 phase plotted as a function of time. While the phase fraction of H-Nb2O5 decreases, the phase fraction of R-Nb2O5 increases. We interpret this as the formation of disordered block structures, and as the occurrence of increased [NbO6] edge-sharing in the structure.
Fig. 5E illustrates that the Rw values stay between 0.35 and 0.45 for all time points in the reaction, showing that the model gives an adequate description of the data for all reaction stages, unlike the fit with the single H-Nb2O5 phase. The crystallite size for the two phases was constrained to take the same value, and the particle growth is illustrated in Fig. 5F, with the crystallite size growing from ca. 2.5 nm to 5 nm, as expected from the evolution of the PDFs. No significant changes in the refined unit cell parameters for the two structural models are observed in the sequential refinement of the reaction process which indicates a stable refinement, Fig. S10 and 11.† The refinements show an increase in the oxygen atomic displacement parameters, which is an additional indication of increasing disorder in the structure with time and particle growth.
As noted above, we have not included the first Nb–O pair in the refinement, which is the first peak in the PDF. In the contour plot in Fig. 2B (and more clearly in Fig. S7†), we see that with synthesis time, this peak broadens and splits into two, centered at ca. 1.7 Å and 2.1 Å. The splitting is expected to be related to the formation of the defect structure, with different domains and structural motifs present. The shorter Nb–O distance at 1.7 Å agrees with what has previously been reported for the R-Nb2O5 phase.58
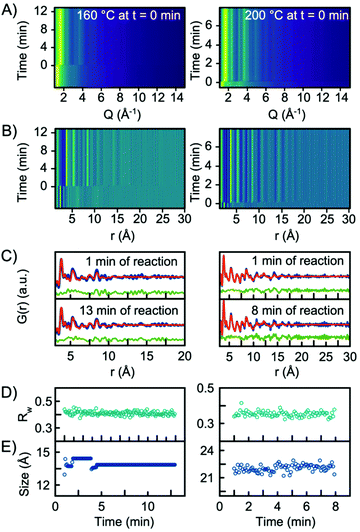
In situ experiments were also carried out at reaction temperatures of 160 °C and 200 °C. Fig. 6A and B show the Q-space data along with the PDFs obtained for the two experiments. When fitting the data with a single-phase H-Nb2O5 structure, the model gives an adequate description of the PDF, and it is not necessary to include the R-Nb2O5 structure in the model, Fig. 6C. In fact, implementing a second phase of R-Nb2O5 in a two-phase refinement of the 160 °C and 200 °C data resulted in a negative refined value of the R-Nb2O5 scale factor. The refinement values using the H-Nb2O5 structural model are shown in Tables S3 and 4.† The refinements showed a crystallite size of ∼1.5 nm and ∼2 nm for the 160 °C and 200 °C experiments respectively, compared to ∼5 nm for 300 °C. As shown in Fig. 6E, we observe no growth of the particles upon heating as was the case for the experiment performed at 300 °C. We furthermore observe no change in the scale factor for the two experiments, as illustrated in Fig. S12 in the ESI.† Combined, the evolution of the scale factors and the growth curves indicate that all precursor material nucleates into the nanocrystalline phase as the heat is turned on. No further material nucleation or particle growth happens when the synthesis temperature is 200 °C or below, within the experimental time investigated here. The fact that the structure of the smaller particles synthesized at 160 °C and 200 °C is well-described by the H-Nb2O5 structure again emphasizes that the defect chemistry of the particles formed in the solvothermal synthesis is highly size-dependent.
Analysis of precursor structure
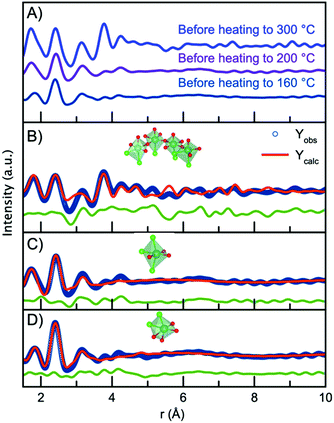
Having established the structure of the end product of the synthesis, we can now consider the structure present before nucleation of the nanocrystalline phase in order to deduce a nucleation mechanism. Fig. 7A shows the PDFs obtained from the precursors for the nanoparticles synthesized at the three different temperatures (300 °C, 200 °C and 160 °C). The data are obtained at room temperature, i.e. before the experiments are initiated. Surprisingly, the three PDFs show different features, which are most likely due to ageing of the precursor solution, as will be discussed below. First, we analyze the precursor PDF obtained from the 300 °C experiment. This PDF shows several sharp peaks, which can be assigned to interatomic distances by considering the chemistry of the NbCl5 precursor. In this structure, Nb5+ is octahedrally coordinated to Cl− with bond distances ranging from 2.2 Å to 2.6 Å,60 agreeing with the sharp peak present at 2.4 Å. However, we also notice a peak at 1.8 Å agreeing with a Nb–O distance. This suggests that upon dissolution of NbCl5 in benzyl alcohol there is both a breakdown of the NbCl5 crystal structure, as well as a substitution of chloride for oxygen, possibly as a hydroxide or alkoxide group. The presence of PDF peaks at higher r-values also illustrates the formation of a structure beyond individual octahedra. To assign these peaks to interatomic distances, we look towards niobium oxychloride structures, such as crystalline Cs2[Nb3O5Cl7] which is a layered-type structure built from [CsCl10] layers and [NbOCl] layers,61 shown in Fig. S13.† By considering the structural motifs in this phase, we can assign the peak at 3.15 Å to Cl/O ligand–ligand distances and the peak at 3.8 Å to Nb–Nb pairs in a corner-sharing geometry. Using the Cs2[Nb3O5Cl7] structure as a starting point, a cluster can be cut from the crystal structure that describes the precursor PDF. This shows that the PDF can be fitted with a polymeric NbxClyOz complex built from corner-sharing octahedra with both oxygen and chloride ligands. The structure and fit to the data are shown in Fig. 7B, with further details given in the ESI.† Some chloride atoms were substituted for oxygen atoms in order to accommodate the Nb–Cl and Nb–O peak ratio. It is here important to note that the structure models shown in Fig. 7 may not be a unique representation of the precursor clusters but contains the main structural motifs present in the precursor solutions. We expect the oxidation state of niobium to be +5 as this is oxidation state of the precursor salt (NbCl5) and the final product (Nb2O5). However, the oxidation state of the precursor has not been determined. It should also be noted that we cannot distinguish between O2−, OH− or alkoxide as ligands in the complex from the X-ray PDF data. The representation given here is therefore a strong simplification of the system.The PDFs obtained for the precursor for the 160 °C and 200 °C experiments show only very local order, and the Nb–Nb peak identified at 3.8 Å is not seen. This shows that the structures present in the precursors for these two experiments are likely isolated [NbCl6−xOx] octahedra. Note again that we cannot from the X-ray PDFs determine whether the oxygen coordinating to niobium is O2−, OH− or an alkoxide. The precursor for the 200 °C experiment shows a higher intensity of the Nb–O peak than that for the 160 °C, suggesting a degree of Cl− ligand substitution. The differences between the PDFs obtained from seemingly similar precursors are likely an effect of ageing of the precursor solution, as ligand exchange and polymerization are likely to take place already at room temperature. Substitution of chloride for oxygen ligands has previously been observed by EXAFS in a similar synthesis during the formation of tungstite in benzyl alcohol by Olliges-Stadler et al.41
The precursor structures in the 160 °C and 200 °C experiments were modelled with single octahedra models. A wavefunction was implemented to account for the exponentially damped sinusoidal oscillation caused by the interaction between niobium in the single octahedra clusters and the solvent, as previously described for nanoparticles and solvent restructuring.62 An illustration of the wavefunction contribution to the model is found in Fig. S14.†
Nucleation mechanism
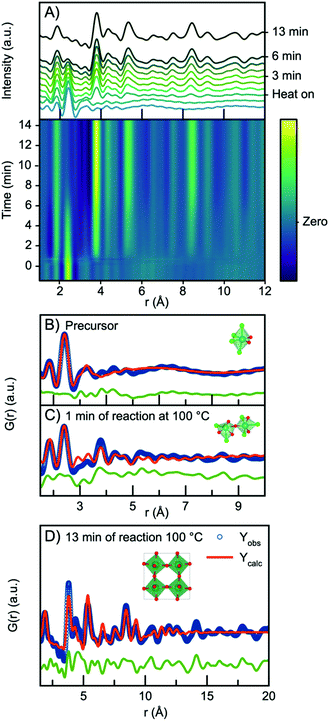
In all three experiments described above, nucleation of the crystalline phase takes place immediately after turning on the heat, and it is therefore not possible to follow the evolution from the NbClxOy precursor structure to the H-Nb2O5 nanoparticles within the time resolution of the experiment. We therefore conducted a similar experiment, but at 100 °C and at ambient pressure, which slowed down the reaction kinetics. The time resolved PDFs are shown in Fig. 8A.Starting from the precursor PDF we can again identify both the Nb–O (1.8 Å) and the Nb–Cl (2.4 Å) distances as before.60 Compared to the precursor PDFs just investigated in Fig. 7, we observe a cluster structure similar to the two observed for the 160 °C and 200 °C experiments with no clear Nb–Nb peak. The PDF can thus be fitted with a single [NbO2Cl4] octahedra as shown in Fig. 8B. However, 1 minute into the synthesis, a clear Nb–Nb peak at 3.8 Å appears, and the PDF can be described by a polymeric cluster (Fig. 8C), similar in structure to that described above for the 300 °C precursor, where ageing and polymerization had taken place. The elevated temperature thus speeds up the polymerization we related to precursor ageing above.
As the reaction proceeds, the intensity of the first Nb–Cl peak slowly decreases, whereas the intensity of the Nb–O peak increases with time, showing that chloride is slowly substituted for oxygen. Almost simultaneously, the intensity of the first corner-sharing Nb–Nb peak increases. This is illustrated in Fig. S15,† showing the intensity of the Nb–O and Nb–Cl peak as a function of time. We can furthermore assign the next Nb–Nb peak at 5.3 Å originating from the 2nd Nb–Nb distance in the ReO3 structure. The intensity of this peak, along with peaks at higher r-values, increase at almost the same rate as the first Nb–Nb peak, and the position shifts towards higher r-values, again illustrated in Fig. S15.† The PDFs thus show that small nanoparticles quickly form as the peaks at higher r-values evolve. The process illustrates that as soon as O/Cl substitution occurs, polymerization to a network of edge-sharing [NbO6] octahedra takes place.
The particles formed at 100 °C show almost exclusively corner-sharing octahedra as we observe no clear PDF peak at 3.3 Å, and when fitting with the simple ReO3 structure (Fig. 8D), the main PDF peaks can all be described, although we once again notice a clear misfit in the high r-region of the refinement. A similar fit (Fig. S16†) can be obtained using HNbO3; a hydroxide which has the same ReO3-type structure. The niobium hydroxide has niobium in oxidation state +5, which is chemically sensible compared to the oxidation state of +6 that the ReO3 structure suggests. The formation of a hydroxide structure agrees with the previously hypothesized formation mechanism for benzyl alcohol syntheses, where hydroxide species are suggested to be intermediate phases in the formation of oxide nanoparticles.39 The lack of a clear PDF peak from edge-sharing octahedra shows that Wadsley–Roth type structures are not suitable models for the particles formed here, and in Fig. S17,† a refinement using the H-Nb2O5 structure shows that this structure does not provide a better fit than the simple ReO3 structure. Implementing a second phase of R-Nb2O5 in a two-phase refinement resulted in a negative refined value of the R-Nb2O5 scale factor. The misfit of the structure above 10 Å of these small particles is thus not related to domain sizes as discussed above.
In order to investigate the nanostructure in the sample further, we conducted an additional experiment under similar conditions, which allowed ex situ investigations of the sample. A PDF from this sample is shown in Fig. S18,† where it agrees well with that seen from the particles formed in the in situ experiment, confirming reproducibility. Fig. S19† shows TEM images obtained from particles synthesized under similar conditions in a separate experiment. The images show a large degree of agglomeration of small particles on the nm scale. SAXS analysis in Fig. S20† also reflects the significant agglomeration, but a signal from small particles of ca. 1.6–2 nm can be identified, agreeing with the size obtained from PDF analysis. These small ReO3-type structures that form under ambient pressure and 100 °C are clearly related to the Wadsley–Roth particles formed at higher temperature and pressure. The ReO3-type network, most likely a hydroxide, can thus be seen as a nucleation cluster in the synthesis, and extended defects in the form of shear planes and Wadsley–Roth block type structures with disordered blocks are induced by temperature.
Conclusions
Using in situ X-ray total scattering, we have gained atomistic insight into the formation pathway of Nb2O5 nanoparticles in the solvothermal synthesis from NbCl5 in benzyl alcohol. From four different in situ total scattering experiments conducted at four different temperatures, we show how the reaction is initialized by substitution of chloride for oxygen which leads to polymerization of [NbO6] octahedra. This results in the formation of small particles, highly similar in structure to ReO3, which can be considered nuclei for the further particle formation. These particles can be described using the HNbO3 niobium hydroxide structure, agreeing with previously proposed mechanisms suggested for benzyl alcohol syntheses. With growth, we observe the formation of Wadsley–Roth structured particles, which we model using the H-Nb2O5-structure. The formation of the H-Nb2O5 particles is surprising, as this phase usually forms only at elevated temperatures around 900 °C. As the particles grow further during the reaction, more edge-sharing in the structure appears, and we cannot fit the data with any of the known niobium oxide structures. However, implementing a simple R-Nb2O5 structure along with the H-Nb2O5 phase, we are able to describe the PDF peaks appearing in the higher r-range. We interpret this as the formation of different structure domains within the particles, and this defect chemistry appears highly dependent on particle size.PDF analysis has thus allowed following the material all the way from NbClxOy precursor complexes, over HNbO3 hydroxide clusters, to the final, nanocrystalline niobium oxide. The type of knowledge of formation mechanisms on the atomic level gained in this study is important for the design of synthesis methods for tailor-made niobium oxide materials. While the complex chemistry of niobium oxide polymorphs means that more work is needed before the synthesis of a given Nb2O5 structure can be rationally designed, the study has provided the first insight that relates particle formation and growth to the atomic structure of Nb2O5, and opens for synthesis control of the defect chemistry in Wadsley–Roth structured phases.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to the Villum Foundation for financial support through a Villum Young Investigator grant (VKR00015416). This work is part of a project that has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme, (Grant agreement No. 804066). We acknowledge the Carlsberg Foundation for financial support through grants CF14-0652 and CF17-0976. Funding from the Danish Ministry of Higher Education and Science through the SMART Lighthouse is gratefully acknowledged. We thank DANSCATT (supported by the Danish Agency for Science and Higher Education) for support. We acknowledge DESY (Hamburg, Germany), a member of the Helmholtz Association HGF, for the provision of experimental facilities. Parts of this research were carried out at P02.1 and we would like to thank Martin Etter for assistance in using the beamline. This work was performed in part at DTU Nanolab, the National Centre for Nano Fabrication and Characterization at the Technical University of Denmark.Notes and references
- M. Liu, C. Yan and Y. Zhang, Sci. Rep., 2015, 5, 1–6 CAS.
- V. Augustyn, J. Come, M. A. Lowe, J. W. Kim, P. L. Taberna, S. H. Tolbert, H. D. Abruna, P. Simon and B. Dunn, Nat. Mater., 2013, 12, 518–522 CrossRef CAS PubMed.
- K. J. Griffith, A. C. Forse, J. M. Griffin and C. P. Grey, J. Am. Chem. Soc., 2016, 138, 8888–8899 CrossRef CAS PubMed.
- A. Le Viet, M. V. Reddy, R. Jose, B. V. R. Chowdari and S. Ramakrishna, J. Phys. Chem. C, 2010, 114, 664–671 CrossRef CAS.
- K. J. Griffith, K. M. Wiaderek, G. Cibin, L. E. Marbella and C. P. Grey, Nature, 2018, 559, 556–563 CrossRef CAS PubMed.
- J. W. Kim, V. Augustyn and B. Dunn, Adv. Energy Mater., 2012, 2, 141–148 CrossRef CAS.
- B. Li, M. Gu, Z. M. Nie, X. L. Wei, C. M. Wang, V. Sprenkle and W. Wang, Nano Lett., 2014, 14, 158–165 CrossRef CAS PubMed.
- K. Skrodczky, M. M. Antunes, X. Y. Han, S. Santangelo, G. Scholz, A. A. Valente, N. Pinna and P. A. Russo, Commun. Chem., 2019, 2, 1–11 CrossRef.
- I. Nowak and M. Ziolek, Chem. Rev., 1999, 99, 3603–3624 CrossRef CAS PubMed.
- A. Fernandez-Arroyo, D. Delgado, M. E. Domine and J. M. Lopez-Nieto, Catal. Sci. Technol., 2017, 7, 5495–5499 RSC.
- X. S. Fang, L. F. Hu, K. F. Huo, B. Gao, L. J. Zhao, M. Y. Liao, P. K. Chu, Y. Bando and D. Golberg, Adv. Funct. Mater., 2011, 21, 3907–3915 CrossRef CAS.
- H. C. Lu, S. Ghosh, N. Katyal, V. S. Lakhanpal, I. R. Gearba-Dolocan, G. Henkelman and D. J. Milliron, ACS Nano, 2020, 14, 10068–10082 CrossRef CAS PubMed.
- A. Llordes, G. Garcia, J. Gazquez and D. J. Milliron, Nature, 2013, 500, 323–326 CrossRef CAS PubMed.
- G. K. Ong, C. A. S. Cabezas, M. N. Dominguez, S. L. Skjærvø, S. Heo and D. J. Milliron, Chem. Mater., 2020, 32, 468–475 CrossRef CAS.
- C. Nico, T. Monteiro and M. P. F. Graca, Prog. Mater. Sci., 2016, 80, 1–37 CrossRef CAS.
- J. M. Allred and R. J. Cava, J. Solid State Chem., 2013, 198, 10–17 CrossRef CAS.
- T. L. Christiansen, E. D. Bojesen, M. Juelsholt, J. Etheridge and K. M. Ø. Jensen, ACS Nano, 2019, 13, 8725–8735 CrossRef CAS PubMed.
- A. Magneli, Acta Crystallogr., 1953, 6, 495–500 CrossRef CAS.
- S. Iijima and J. G. Allpress, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1974, 30, 22–29 CrossRef.
- S. Andersson and A. D. Wadsley, Nature, 1966, 211, 581–583 CrossRef CAS.
- S. Iijima, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1978, 34, 922–931 CrossRef.
- P. L. Gai, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1997, 53, 346–352 CrossRef.
- B. M. Gatehouse and A. D. Wadsley, Acta Crystallogr., 1964, 17, 1545–1554 CrossRef CAS.
- H. Schafer, R. Gruehn and F. Schulte, Angew. Chem., Int. Ed. Engl., 1966, 5, 40–52 CrossRef.
- R. I. Walton, Chem. Soc. Rev., 2002, 31, 230–238 RSC.
- G. Garnweitner and M. Niederberger, J. Am. Ceram. Soc., 2006, 89, 1801–1808 CrossRef CAS.
- R. J. Li, X. Z. Zhu, Q. F. Fu, G. S. Liang, Y. J. Chen, L. J. Luo, M. Y. Dong, Q. Shao, C. F. Lin, R. B. Wei and Z. H. Guo, Chem. Commun., 2019, 55, 2493–2496 RSC.
- K. Okumura, T. Tomiyama, S. Shirakawa, S. Ishida, T. Sanada, M. Arao and M. Niwa, J. Mater. Chem., 2011, 21, 229–235 RSC.
- M. Juelsholt, T. L. Christiansen and K. M. Ø. Jensen, J. Phys. Chem. C, 2019, 123, 5110–5119 CrossRef CAS.
- K. M. Ø. Jensen, M. Christensen, P. Juhas, C. Tyrsted, E. D. Bojesen, N. Lock, S. J. L. Billinge and B. B. Iversen, J. Am. Chem. Soc., 2012, 134, 6785–6792 CrossRef CAS PubMed.
- K. M. Ø. Jensen, H. L. Andersen, C. Tyrsted, E. D. Bøjesen, A. C. Dippel, N. Lock, S. J. L. Billinge, B. B. Iversen and M. Christensen, ACS Nano, 2014, 8, 10704–10714 CrossRef CAS PubMed.
- C. Tyrsted, N. Lock, K. M. Ø. Jensen, M. Christensen, E. D. Bøjesen, H. Emerich, G. Vaughan, S. J. L. Billinge and B. B. Iversen, IUCrJ, 2014, 1, 165–171 CrossRef CAS PubMed.
- K. M. Ø. Jensen, C. Tyrsted, M. Bremholm and B. B. Iversen, ChemSusChem, 2014, 7, 1594–1611 CrossRef CAS PubMed.
- E. D. Bojesen, K. M. Ø. Jensen, C. Tyrsted, A. Mamakhel, H. L. Andersen, H. Reardon, J. Chevalier, A. C. Dippel and B. B. Iversen, Chem. Sci., 2016, 7, 6394–6406 RSC.
- A.-C. Dippel, K. M. Ø. Jensen, C. Tyrsted, M. Bremholm, E. D. Bojesen, D. Saha, S. Birgisson, M. Christensen, S. J. L. Billinge and B. B. Iversen, Acta Crystallogr., Sect. A: Found. Adv., 2016, 72, 645–650 CrossRef CAS PubMed.
- T. L. Christiansen, S. R. Cooper and K. M. Ø. Jensen, Nanoscale Adv., 2020, 2, 2234–2254 RSC.
- S. J. L. Billinge and M. G. Kanatzidis, Chem. Commun., 2004, 749–760 RSC.
- J. Buha, D. Arcon, M. Niederberger and I. Djerdj, Phys. Chem. Chem. Phys., 2010, 12, 15537–15543 RSC.
- R. Deshmukh and M. Niederberger, Chem. – Eur. J., 2017, 23, 8542–8570 CrossRef CAS PubMed.
- M. Niederberger, M. H. Bartl and G. D. Stucky, Chem. Mater., 2002, 14, 4364–4370 CrossRef CAS.
- I. Olliges-Stadler, J. Stotzel, D. Koziej, M. D. Rossell, J. D. Grunwaldt, M. Nachtegaal, R. Frahm and M. Niederberger, Chem. – Eur. J., 2012, 18, 2305–2312 CrossRef CAS PubMed.
- J. Becker, M. Bremholm, C. Tyrsted, B. Pauw, K. M. Ø. Jensen, J. Eltzholt, M. Christensen and B. B. Iversen, J. Appl. Crystallogr., 2010, 43, 729–736 CrossRef CAS.
- P. J. Chupas, X. Y. Qiu, J. C. Hanson, P. L. Lee, C. P. Grey and S. J. L. Billinge, J. Appl. Crystallogr., 2003, 36, 1342–1347 CrossRef CAS.
- A. P. Hammersley, J. Appl. Crystallogr., 2016, 49, 646–652 CrossRef CAS.
- P. Juhas, T. Davis, C. L. Farrow and S. J. L. Billinge, J. Appl. Crystallogr., 2013, 46, 560–566 CrossRef CAS.
- C. L. Farrow, P. Juhas, J. W. Liu, D. Bryndin, E. S. Bozin, J. Bloch, T. Proffen and S. J. L. Billinge, J. Phys.: Condens. Matter, 2007, 19, 1–7 CrossRef PubMed.
- P. Juhas, C. L. Farrow, X. H. Yang, K. R. Knox and S. J. L. Billinge, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 562–568 CrossRef PubMed.
- J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld, B. Schmid, J. Y. Tinevez, D. J. White, V. Hartenstein, K. Eliceiri, P. Tomancak and A. Cardona, Nat. Methods, 2012, 9, 676–682 CrossRef CAS PubMed.
- SasView, https://www.sasview.org, ( 2020) Search PubMed.
- T. L. Christiansen, E. D. Bøjesen, M. Juelsholt, J. Etheridge and K. M. Ø. Jensen, ACS Nano, 2019, 13, 8725–8735 CrossRef CAS PubMed.
- K. Kato, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1976, 32, 764–767 CrossRef.
- F. D. Hardcastle and I. E. Wachs, Solid State Ionics, 1991, 45, 201–213 CrossRef CAS.
- L. K. Frevel and H. W. Rinn, Anal. Chem., 1955, 27, 1329–1330 CrossRef CAS.
- S. Iijima, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1973, 29, 18–24 CrossRef CAS.
- J. S. Anderson, J. M. Browne and J. L. Hutchison, J. Solid State Chem., 1972, 5, 419–431 CrossRef CAS.
- H. Obayashi and J. S. Anderson, J. Solid State Chem., 1976, 19, 331–351 CrossRef CAS.
- J. G. Allpress and R. S. Roth, J. Solid State Chem., 1971, 3, 209–216 CrossRef CAS.
- R. Gruehn, J. Less-Common Met., 1966, 11, 119–126 CrossRef.
- C. Valencia-Balvin, S. Perez-Walton, G. M. Dalpian and J. M. Osorio-Guillen, Comput. Mater. Sci., 2014, 81, 133–140 CrossRef CAS.
- W. Honle and H. G. Vonschnering, Z. Kristallogr., 1990, 191, 139–140 CrossRef.
- D. E. Sands, A. Zalkin and R. E. Elson, Acta Crystallogr., 1959, 12, 21–23 CrossRef CAS.
- M. Zobel, R. B. Neder and S. A. Kimber, Science, 2015, 347, 292–294 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional total scattering data, details on PDF modelling, PDF, SAXS and TEM characterization. See DOI: 10.1039/d0nr08299f |
| This journal is © The Royal Society of Chemistry 2021 |