Open Access Article
Open Access ArticleFemtosecond laser driven precessing magnetic gratings†
Gaolong
Cao‡
ab,
Sheng
Jiang‡
 b,
Johan
Åkerman
*ab and
Jonas
Weissenrieder
b,
Johan
Åkerman
*ab and
Jonas
Weissenrieder
 *a
*a
aMaterials and Nano Physics, Department of Applied Physics, KTH Royal Institute of Technology, Kista, Sweden. E-mail: jonas@kth.se
bDepartment of Physics, University of Gothenburg, Gothenburg, Sweden. E-mail: johan.akerman@physics.gu.se
First published on 18th January 2021
Abstract
Manipulation and detection of spins at the nanoscale is of considerable contemporary interest as it may not only facilitate a description of fundamental physical processes but also plays a critical role in the development of spintronic devices. Here, we describe the application of a novel combination of transient grating excitation with Lorentz ultrafast electron microscopy to control and detect magnetization dynamics with combined nanometer and picosecond resolutions. Excitation of Ni80Fe20 thin film samples results in the formation of transient coherently precessing magnetic gratings. From the time-resolved results, we extract detailed real space information of the magnetic precession, including local magnetization, precession frequency, and relevant decay factors. The Lorentz contrast of the dynamics is sensitive to the alignment of the in-plane components of the applied field. The experimental results are rationalized by a model considering local demagnetization and the phase of the precessing magnetic moments. We envision that this technique can be extended to the study of spin waves and dynamic behavior in ferrimagnetic and antiferromagnetic systems.
Introduction
Laser-induced transient gratings (TG) are formed by spatial and temporal overlap of coincident laser pulses to generate a periodic excitation of a sample through formation of an interference pattern. Resulting dynamic processes may be probed by means of a third pulse, diffracted of the sample, in a technique called transient grating spectroscopy (TGS).1,2 This technique offers opportunities to study the interaction of light and matter under tailored periodic spatial excitation conditions. The spatial excitation period can be tuned from micrometers, using optical wavelengths, to tens of nanometers by means of extreme ultraviolet (EUV) light3,5 or even X-rays.6–9 The technique has been extensively applied to a diverse set of material processes occurring on an ultrafast time scale including the generation of surface acoustic waves,1,3 phonon polariton excitation,10 quasi-particle diffusion,11 molecular diffusion,12 thermal transport,4,13 charge density waves,14 and laser-plasma interactions.15 Considering the fact that spin dynamics are sensitive to inhomogeneous spatiotemporal temperature distributions,16 TGS can be predicted to form a sensitive probe of ultrafast magnetization dynamics. A few pioneering works have studied TG-induced magnetic excitation of surface magnetoelastic waves,16 spin currents17 and writing of strip domains.18 However, TG-induced ultrafast dynamics of magnetic systems have been sparsely investigated at large, although it may be expected to provide rich physics and hold potential applications within e.g. spintronics.19,20 This may be traced to the fact that TGS has been mostly restricted to time-resolved spectroscopy, leaving real space information mostly unknown. Combined temporal and spatial information are important for the understanding of spintronic process as the TG period acts on length scales of relevance to intrinsic magnetic properties, such as the exchange coupling and spin diffusion length scales. Application of electron beam probes, at inherent high spatial resolution, may circumvent the spatial resolution restrictions of optical probes imposed from diffraction limitations. Commercial transmission electron microscopy (TEM), in Lorentz mode, routinely demonstrates nanometer resolution for magnetic structures.21 The recent developments within Lorentz ultrafast TEM (LUEM), through integration of pump-probe into the system,22–24 have demonstrated its ability for studies of ultrafast magnetization dynamics on systems such as skyrmions, vortices, and domain walls.25–29 Direct imaging of magnetization dynamics at combined nanoscale and picosecond resolutions may uncover new details central to the understanding of spintronic processes including ultrafast magnetic switching, formation and perturbation of topological magnetic structures, and spin wave propagation.Motivated by the above, we set out to develop a technique combining TG with LUEM. A fs UV laser pulse and a visible TG were established in a modified TEM. The TG-induced spin dynamics was probed by a photoemitted electron pulse. Specifically, we use an optical TG to excite a ferromagnetic sample, Ni80Fe20, deposited on a Si3N4 membrane. The consequence of the TG excitation is a spatially periodic laser-driven demagnetization that is coupled to a subsequent formation of temperature gradients on the nm scale. The magnetic response of the sample results in a periodic Lorentz image contrast. Time-resolved analysis of oscillations in the local Lorentz contrast, under the influence of an external magnetic field, allows for the determination of the phase and frequency of local precessing magnetic moments, local magnetization, and relevant decay factors of the magnetic grating, which is a collective coherent in-phase precession of magnetization with a spatially periodic modulation of the amplitude. The presented results demonstrate that the technique is capable of investigating spin dynamics at combined ps temporal and nm spatial resolutions. The application of TG-induced magnetic gratings may tentatively be extended to studies of spin waves as the analysis is sensitive to the phase of the precession and may be deployed under external fields. The technique also holds promise for application in other magnetic systems, such as ferri- or antiferromagnets.
Results
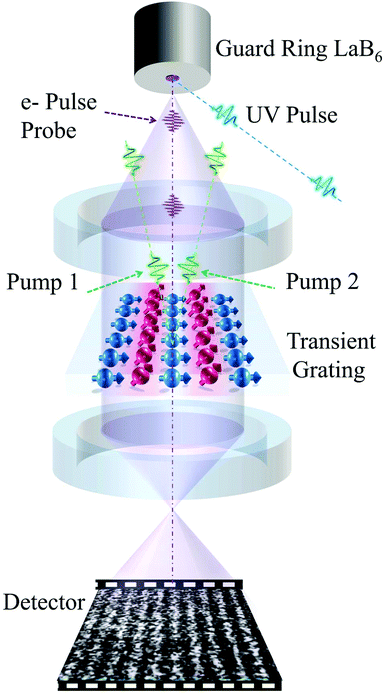
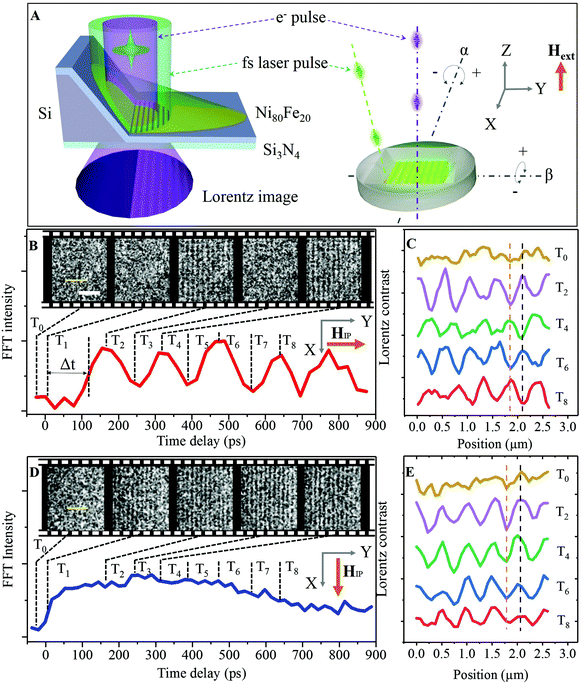
Fig. 1 shows the schematic illustration of the LUEM setup with a transient grating on a magnetic sample. Unlike in conventional LUEM pump-probe schemes, which employ a single spatially homogeneous fs pump laser to initiate dynamics, two fs pump beams (at λ = 515 nm or 1030 nm) are deployed to form the TG on the sample. Two colors of the spins are used to illustrate the regions of constructive and destructive interference on the sample, where red represents high local laser fluence and blue low local laser fluence. The periodic excitation results in formation of coupled thermal and magnetic gratings. A photoemitted electron probe pulse, arriving at an adjustable time delay, detects the local magnetization of the sample. The photoinduced demagnetization of the sample is responsible for the Lorentz contrast and offers a means to study the laser-induced magnetization dynamics.Fig. 2A shows the schematic illustration of the experimental geometry for a ferromagnetic sample placed on a double-tilt holder in the LUEM. The Ni80Fe20 film is deposited on a thin Si3N4 membrane with slanted faces surrounding the sample surface. The pump laser beam is carefully aligned to illuminate both one slanted face and the membrane. The laser pulse reflected from the slanted face interferes with the direct laser pulse at the membrane surface, resulting in an optical grating with a periodic distribution of the laser intensity. An external magnetic field may be applied along the Z direction and the in-plane component of the field can be controlled by applying sample tilt angles α and β. Excitation with this TG then results, through electron–phonon coupling, in a transient thermal grating. The optical excitation process and the following transient thermal grating in turn result in a patterned ultrafast demagnetization of the permalloy sample with the same periodicity as the TG. Inset of Fig. 2B shows the LUEM images in Fresnel mode at an over-focus of 5 mm collected before (−25 ps, T0) and after (+175 ps, T2) excitation with a femtosecond laser pulse at a fluence of 9 mJ cm−2. The Lorentz image collected before excitation, at −25 ps, shows no magnetic contrast, while the image collected +175 ps after excitation exhibits periodic stripes of magnetic contrast. The striped magnetic contrast is formed parallel to the slanted face of the transmission electron microscopy membrane grid. We note that the periodic stripes show no magnetic contrast when the sample is placed in Fresnel mode focus conditions and that the contrast is reversed in under-focus conditions (section S1†). These observations confirm that the periodic structure is indeed a result of magnetic Lorentz contrast. In order to deduce the relationship between the periodic magnetic contrast and the TG (interference pattern), we conducted similar measurements at varying sample tilt angles, α. The periodicity of the magnetic contrast, d, increases with increasing α. The periodicity of the laser interference pattern d in our local experimental geometry can be expressed as (see section S2†):
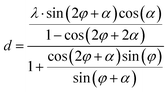 | (1) |
We now turn our attention to the temporal evolution of the photo-induced transient magnetic grating. Fig. 2B shows the temporal trace of the FFT intensity of the periodic magnetic contrast and Lorentz images collected at selected delay times. The results were obtained under an external magnetic field of μ0Hext = 250 mT with the in-plane component HIP oriented along the Y axis (see Fig. 2A) of the sample (sample tilt angles: α = 3° and β = 0°). A gradual increase in the periodic magnetic contrast is observed following laser excitation (after time zero) with a first maximum reached at approximately 175 ps (T2 in Fig. 2B). At longer delays, the FFT intensity oscillates with a decay on the nanosecond time scale. Fig. 2B also presents the representative Lorentz UEM images collected at temporal delays, where the FFT intensity exhibits local maxima and minima. Fig. 2C shows the line profiles extracted from the Lorentz images in Fig. 2B at the position indicated by the dashed yellow line. The line profiles were extracted at a temporal delay before time zero (T0) and at delays corresponding to the first four maxima of the FFT intensity (T2, T4, T6 and T8). A careful inspection of the phase of the line profiles reveals that neighboring (in time) FFT maxima exhibit opposite magnetic contrast at a given spatial position. The contrast reversal can be observed by following the red and black vertical dashed lines in Fig. 2C and implies that the oscillation in the FFT intensity represents a periodic reversal of the Lorentz contrast from the magnetic structure. The line profile before time zero (T0, Fig. 2C) is almost flat. Fig. 2D shows the results from an experiment performed under the same external magnetic field as shown in Fig. 2B but with the HIP rotated 90° to align along the X axis of the sample through tilt angles α = 0° and β = 3°. The periodic magnetic contrast in the LUEM images now becomes visible almost immediately after time zero and reaches a maximum in FFT intensity at approximately 250 ps (T3 in Fig. 2D). After this point, the FFT intensity of the magnetic contrast steadily decreases in intensity. This can also be observed directly in the LUEM inset images shown in Fig. 2D. Analysis of the line profiles extracted from the LUEM images shows that under these conditions no reversal in magnetic Lorentz contrast is observed (vertical dashed lines in Fig. 2E serve as a guide to the eye). Comparing Fig. 2B and D, the inflection point for the leading edge of the FFT intensity of the transient magnetic contrast is shifted by approximately Δt ∼ 100 ps towards shorter delays for HIP aligned along the X axis, as shown in Fig. 2B.
Taken together the results described above indicate that the laser-induced transient magnetic contrast stems from a mechanism including local demagnetization dynamics in response to the formation of a transient thermal grating in the magnetic thin film sample. The periodic demagnetization combined with the applied external field results in a canting of the local metastable magnetization direction and a damped precessing motion of magnetic moments. The full precession period for samples with HIP aligned along the Y axis can be extracted as the temporal separation between two states of equal sign of the magnetic contrast. For the results presented in Fig. 2B, the precession frequency is ∼3.3 GHz, close to the reported frequencies for permalloy under similar experimental conditions.33
Discussion
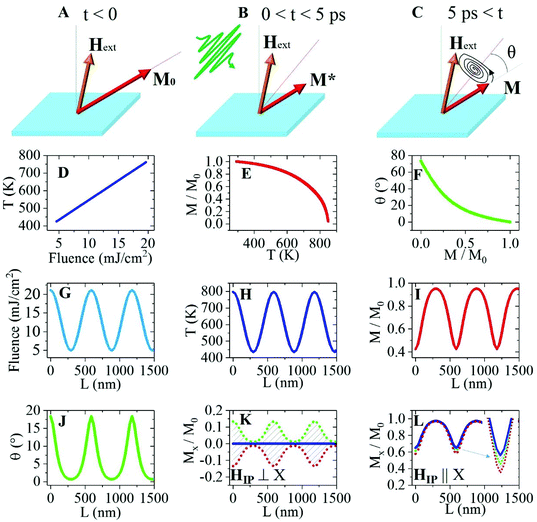
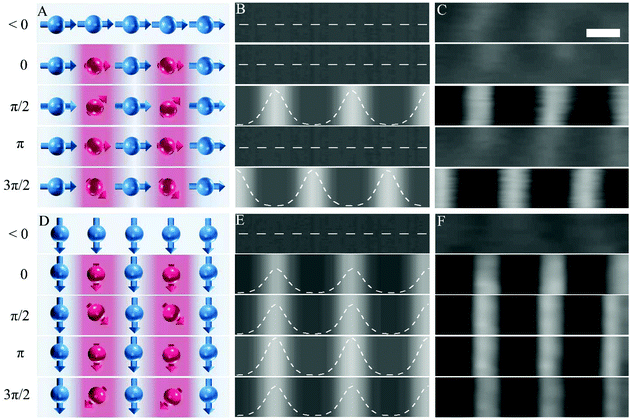
To describe the experimental observations, we propose a model outlined in Fig. 3(A–C). Before the arrival of the fs-laser pump, the magnetic moment M0 (red arrow in Fig. 3A) is aligned along its equilibrium direction under the applied magnetic field Hext (blue arrow in Fig. 3A). Upon the arrival of the laser pulse, the sample experiences rapid demagnetization into a state M*. As a consequence, the metastable equilibrium direction of the magnetization (red dashed line in Fig. 3B) cants by an angle θ towards Hext and a few picoseconds later, the local magnetic moments (M) begin to precess around the metastable magnetization direction (Fig. 3C).34 The three-temperature model35,36 describes how the electronic sub-system is excited during the initial few hundreds of femtoseconds (the duration of the excitation pulse). The relaxation of the electronic subsystem results in an energy transfer to the spin and lattice subsystems. Here, we focus on the lattice temperature whose relevant time scale is comparable to that of the observed magnetic precession: a few picoseconds to hundreds of picoseconds, or even nanoseconds, after photoexcitation. The local temperature of the thin magnetic film is linearly dependent on the local laser fluence, as shown in Fig. 3D. The temperature dependence of the magnetization may be evaluated from Weiss molecular field theory37 as is shown in Fig. 3E. Furthermore, the degree of demagnetization will influence the canting angle of the metastable magnetization direction. The canting angle (θ), which also represents the initial precession angle of the magnetic moments, as a function of demagnetization, is provided in Fig. 3F. Excitation by means of a TG results in a spatially periodic laser fluence distribution across the sample, as shown in Fig. 3G. On a few ps time scale, such excitation will result in a spatially periodic thermal distribution, as shown in Fig. 3H. The local lattice temperature influences the local magnetization with a resulting spatial distribution as shown in Fig. 3I. A change in local magnetization in the presence of a constant applied magnetic field will in turn affect the metastable direction of the magnetization (effective field). From these results, we may estimate the initial local precession angle in Fig. 3J. The rapid change in metastable magnetization direction leads to a Larmor precession of the magnetic moments around the effective field direction as is schematically indicated in Fig. 3C. From the precession of the magnetic moments follows that the projection of the magnetization onto the X direction changes with the phase of the precession. By applying the left-hand rule, for the Lorentz force on electrons, in the relevant experimental geometry we can conclude that only in-plane components of the magnetization will contribute to the Lorentz contrast. This means that only the in-plane magnetic component along the X axis will contribute to the periodic Lorentz contrast in the Y direction of the sample. Calculated in-plane X components of the magnetization (MX), as a function of the spatial coordinate for HIP oriented along the Y-direction, is shown in Fig. 3K. At a temporal delay of a few picoseconds after photoexcitation, the sample is in a state of maximum demagnetization. However, the MX component is near zero since the precession of the magnetic moments has yet to begin (blue solid line in Fig. 3K). At longer delays, the precession will change the amplitude and direction of MX periodically in time within the range indicated by the red and green dotted traces. In contrast, when HIP is oriented along the X direction, the contribution to MX is dominated by the local rapid demagnetization (blue line in Fig. 3L). The variation in MX due to the precession of the magnetic moments is almost negligible, as shown in Fig. 3L and its inset. Note that all spatial periodicities of the aforementioned parameters are the same and determined by the periodicity of the exciting optical grating. Details of the simulations in Fig. 3(D–L) are presented in section S5.†Based on the experimental results from Fig. 2 and the calculations presented in Fig. 3, we are now at the stage to describe the mechanism for the formation of the transient precessing magnetic grating. The illustration in Fig. 4A shows top views of the magnetization configuration at locations of constructive and destructive interference before time zero (<0) and at selected phases/time delays (0, π/2, π, and 3π/2) of the coherent precession. The lengths of the vectors indicate the magnitude of the local magnetic moment. The laser pulse induced spatial variations of MX in the Y direction, across the transient grating, determine the magnetic Lorenz contrast. Before time zero, the magnitude and direction of all magnetic moments are equal and aligned along the Y direction, with no magnetic Lorentz contrast observed in the LUEM micrographs. Following excitation by the TG, the magnetic sample experiences a rapid periodic demagnetization. However, at short temporal delay (within a few picoseconds), all magnetic moments will essentially remain aligned along the Y direction with negligible MX components. A configuration with all local magnetic moments aligned parallel to the magnetization gradient results in no magnetic Lorentz contrast. This is also the situation for precessing moments at phase 0 and π, which refer to the images at contrast minima (T3, T5, and T7 in Fig. 2B). In Fig. 3K, phase 0 and π of the precession correspond to the blue line with zero MX components. MX will increase as the magnetic moments begin to precess around their metastable magnetization direction. Phase π/2 in Fig. 4A shows the precessing magnetic moments at a position for maximum MX. This configuration corresponds to the upper green dotted line in Fig. 3K and a maximum difference in MX (maximum magnetic Lorentz contrast) between the regions of constructive and destructive interference of the TG. The situation is similar for the precessing moments at phase 3π/2, except for the reversal in the direction of MX. The reversal of MX results in an inversion of the magnetic Lorentz image contrast compared to the situation with the precessing spins in phase π/2, in excellent agreement with the experimental results presented in Fig. 2C. Fig. 4B shows the simulated Lorentz images for the magnetization configurations before zero (<0) and in phases 0, π/2, π, and 3π/2, which are referred to the inset images of T0–T5 in Fig. 2B. A description of the simulation can be found in section S6.† A direct comparison of the simulated Lorentz images and the experimental results (FFT filtered) from the same region of the sample can be seen in Fig. 4B and C. The agreement between simulation and experimental results shows that the physical model employed can describe the physics involved. Rotating the direction of HIP by 90° to align parallel to the TG results in strikingly different magnetization dynamics. Fig. 4D shows the top views of the local magnetization configurations at different phases of the precession. The rapid demagnetization at time zero results in a configuration with all local magnetic moments aligned orthogonally to the local magnetization gradient. This configuration fulfills the conditions for magnetic Lorentz contrast and explains why the formation of magnetic contrast is substantially faster compared to the configuration with the magnetic moments aligned parallel to the local magnetic gradient. The Lorentz contrast increases slightly as the magnetic precession proceeds to phase π/2 and π. The increasing contrast may be traced from the change in MX at different phases of the precession as is shown in Fig. 3L. A maximum in Lorentz contrast is expected at phase π. This is in agreement with the experimentally observed maximum in the FFT intensity of the transient magnetic grating at T3 in Fig. 2C. The expected modulation in Lorentz contrast by the precession of the magnetic moments is only about one tenth of the amplitude. This explains why no contrast inversion is observed. Simulated Lorentz images at selected phases of the precession are shown in Fig. 4E and as comparison FFT filtered Lorentz images from the same sample region are presented as shown in Fig. 4F. The process for establishing magnetic Lorentz contrast is distinctly different for the configurations with the magnetic moments aligned parallel and orthogonal to the local magnetic gradient. This explains the temporal shift in inflection points of the initial rising edges in magnetic contrast points, Δt, between Fig. 2B and D. In the configuration with the magnetic moments aligned parallel to the local magnetic gradient, no magnetic contrast is expected immediately after excitation and maximum contrast occurs after a quarter period (π/2) of the precession. This is unlike the situation for a configuration with the magnetic moments aligned orthogonally to the local magnetic gradient where the rapid demagnetization results in an almost immediate Lorentz contrast which is only moderately modulated by the precession of the magnetic moments. Taken together, the presented model describing a precessing transient magnetic grating explains the experimental results for the magnetic Lorentz contrast presented in Fig. 2B–E.
We now focus our attention to the decay factors of the magnetic gratings governing the time dependent decay in magnetic Lorentz contrast. Two decay processes are considered: (1) dissipation of the spatial thermal gratings39 and (2) Gilbert damping of the precession through energy transfer to the phonon subsystem. We begin by simulating the local temperature distribution as a function of time delay, as shown in Fig. 5A and section S4.† Thermal conduction will reduce the temperature difference between regions of constructive (hot) and destructive (cold) optical interference. The temperature difference decreases from approximately 360 K to about 160 K within 1.5 ns. From diminishing thermal gradients a reduction in magnetization gradients and magnetic Lorentz contrast is followed. The second decay process is due to Gilbert damping of the precession angle of the magnetic moments. Gilbert damping drags the precession of the magnetic moments closer to the effective field direction (red dashed line in Fig. 3C). A combination of both these effects is considered for the fit of the experimental LUEM results shown in the upper panel of Fig. 5D. The effective damping for permalloy exhibits a weak temperature dependence under the relevant experimental conditions.40 Therefore, we use the room temperature Gilbert damping parameter (αeff = 0.008) in the simulations.40 The thermal diffusion only (black solid line) and combined thermal and Gilbert damping (red solid line) contribution to the decay in Lorentz image contrast is shown in the upper panel of Fig. 5D. A comparison of the simulated thermal and the combined thermal and Gilbert damping results shows that thermal diffusion dominates the decay in Lorentz image contrast at the current periodicity of the transient grating, but a better fit to the experimental results is found after including the contribution from the Gilbert damping.
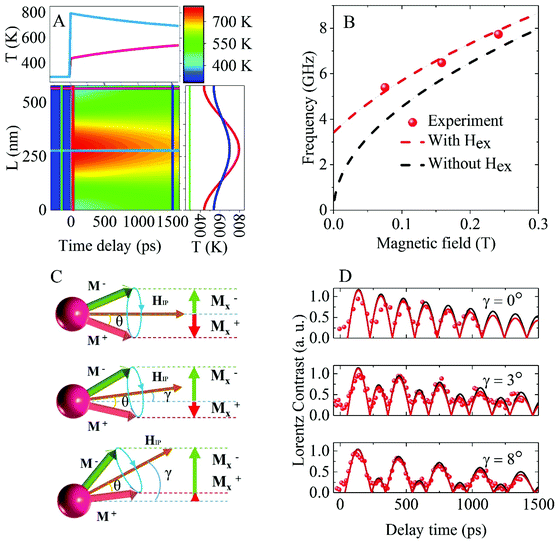 | ||
| Fig. 5 Decay and field dependence (amplitude and in-plane magnetic field direction) of the transient magnetic Lorentz contrast. (A) Simulation of the spatial temperature distribution of the thin film sample across the TG as a function of time delay (in false color). The right panel shows the temperature distribution at −5 ps before (green), and at +5 ps (red) and +1500 ps (blue) after photoexcitation. The top panel shows the temperature evolution for the warmest (blue, constructive interference) and coldest (pink, destructive interference) regions. (B) External magnetic field dependence (μ0Hext) of the FFT intensity of the periodic magnetic contrast. Collected at sample tilt angles α = 15° and β = 0°. The dashed black line shows the calculated FMR frequency using μ0MS = 0.98 T without considering exchange coupling.39 The dashed red line shows the calculated frequency including an effective exchange field μ0Hex = 0.015 T due to the magnetization gradients. (C) Illustration of how a deviation of the in-plane magnetic field component from the Y direction (angle γ) results in asymmetric transient magnetic contrast during the precession. (D) Comparison of experimental and simulated results of the oscillation in Lorentz contrast at indicated angles of γ (see ESI Note 5†). All experimental data are collected at μ0Hext = 0.25 T and sample tilt angles α = 3.0° and β = 0°. The black solid line represents simulated results including thermal diffusion only. The red solid line represents simulated results including both thermal diffusion and Gilbert damping. | ||
The precession frequency of the magnetic moments depends on the external magnetic field.33 The oscillation frequency of the FFT intensity of the periodic magnetic Lorentz contrast represents a direct measure of the precession frequency. Fig. 5B shows the oscillation frequency of the magnetic contrast as a function of the applied magnetic field. The experimental results were extracted at a relatively high tilt angle of the sample (α = 15° and β = 0°) in order to allow for several oscillation periods within a few ns temporal delay. The precession frequency increases with the external field following the expected trend from simulated ferromagnetic resonance (FMR, black dashed line) frequency.38 The discrepancy between the experimental and calculated results may tentatively be attributed to the inhomogeneous demagnetization (shown in Fig. 3I) and the different precession angles (shown in Fig. 3J) in the sample, which may result in a significant exchange coupling. An additional effective field Hex was included in the frequency calculations to accommodate for the contribution from the exchange coupling (see section S5†). The calculated frequency (red dashed line in Fig. 5B) now shows a good agreement with the experimental results.
A deviation of the in-plane magnetic field from the Y direction is expected to influence the transient magnetic Lorentz contrast during the precession. Precession at three different angles of γ (where γ is defined as the angle between HIP and Y) is illustrated in Fig. 5C. In the case of γ = 0 (upper panel), the absolute MX projections and the resulting FFT intensities of the Lorentz contrast will be similar at phase π/2 and 3π/2. Under the conditions 0 < γ < θ, the FFT intensity will be asymmetric during the precession period and the peaks at the π/2 and 3π/2 phase may be discriminated by their relative amplitude as γ and θ determines the relative amplitude of the peaks. Fig. 5D shows the matching experimental results and simulations of the absolute Lorentz image contrast for γ at 0°, 3° and 8° and at an initial precession angle θ = 17°. Under the conditions θ ≤ γ < π/2, the MX projection will not change sign during the precession and no reversal of Lorentz contrast can be detected. Further theoretical studies will be helpful in providing a comprehensive understanding to the damping mechanisms involved at the nanoscale in these transient magnetic gratings.
Conclusions
To summarize, we have demonstrated that the combination of TG and LUEM facilitates imaging of local magnetic dynamics at combined high spatial (nm) and temporal (ps) resolutions. Excitation via a TG induces an ultrafast periodic demagnetization of the sample with a resulting formation of a transient precessing magnetic grating. The transient magnetization dynamics is found to be sensitive to the alignment of the in-plane magnetic field (HIP) with respect to the optical grating. Fields aligned orthogonal to the direction of the optical grating result in strong oscillations of the magnetic Lorentz contrast, while parallel fields show only limited oscillation. The experimental results can be described by a model including the phase of the precessing magnetic moments. From the time-resolved LUEM results, we extract detailed information of the magnetic precession, such as local magnetization, precession frequency and magnetic field dependence, and relevant decay factors of the magnetic gratings.The application of TG-induced magnetic gratings in LUEM may tentatively be extended to the studies of spin waves as it is sensitive to the local phase of the precession and may be deployed under external field, critical in studies of spin wave propagation. Also, excitation by means of TG offers the potential for describing the mechanisms determining magnetization dynamics on its intrinsic time and length scales. The periodicity of the transient magnetic grating can readily be tuned by the laser wavelength or the angle between the two incoming laser beams. A natural extension of the method would be excitation through extreme ultraviolet (EUV) wavelengths, facilitating optical gratings on a few nanometer scale.41,42 The TG facilitates the formation of magnetic domains with tunable nanoscale dimensions, which may allow the study of magnetic dynamics at dimensions comparable to the intrinsic scales of domain walls or other magnetic structures, such as vortices or skyrmions. Furthermore, analysis of local temperatures and thermal diffusion at combined nanometer and picosecond resolutions in materials and devices is challenging.43 As demonstrated in this paper, the transient magnetic contrast in LUEM may serve as a sensitive probe of the transient temperature distribution of magnetic samples and may allow mapping of the local temperature and ultrafast thermal diffusion processes. In other words, the combination of LUEM with TG can be used as an ultrafast nano-thermometer. Finally, we also envision how this technique may be extended to the studies of dynamics in other classes of magnetic materials, such as ferrimagnets or antiferromagnets. As the image contrast presented here originates from the magnetic gradients induced by TG or thermal gratings, it may be feasible to induce sufficient magnetic gradients in systems not necessarily limited in ferromagnets.
Materials and methods
Sample preparation
50 nm thick permalloy (Ni80Fe20) thin films were sputtered on 50 nm thick Si3N4 electron transparent membrane grids for transmission electron microscopy analysis (Ted Pella, USA). The samples were positioned with the slanted side faces facing up, ensuring metallization of both the membrane and side faces. The magnetron sputtering deposition was performed in a high-vacuum chamber with a base pressure of less than 3 × 10−8 Torr [AJA Orion 8]. The argon working pressure was 2.5 mTorr during deposition. All samples were capped with a 3 nm thick Al film to prevent oxidation of the Ni80Fe20.Sample geometry
The sample was placed on the TEM sample holder with the slanted faces of the grid facing towards the direction of the incident electron beam, as indicated in Fig. 2A. The angle of the slanted faces relative to the membrane normal was φ = 35.26°. The thickness of the Si grid frame was 200 μm, the thickness of the Si3N4 membrane was 50 nm, and the membrane window size was 100 μm × 1500 μm. The long edge of the window was carefully positioned parallel to the X axis of the double-tilt TEM holder. The tilt angles α and β are defined as positive for anti-clockwise rotation around the X and Y axis, as shown in Fig. 2A. Fig. 2A illustrates the geometry for the laser illumination of the sample. The laser was carefully aligned to illuminate the intersection between the slanted faces and the membrane surface. The permalloy thin film on the side faces allows them to serve as reflecting mirrors, with approximately 50% reflectivity for 515 nm wavelength at an incident angle of 45°. The interference of the direct and reflected laser beams results in the formation of a TG at the membrane surface.Lorentz mode ultrafast electron microscopy (LUEM)
To avoid saturation of the magnetization of the soft permalloy sample, the ultrafast electron microscope may be operated with the objective lens switched off. Under such operational conditions, the residual magnetic field at the sample position may be kept below 10 Oe and allows for Lorentz mode imaging of the magnetization configuration in the sample. The external magnetic field can be controlled by applying a current to the objective lens. The magnetic field at the sample position was calibrated for relevant objective lens currents by means of a Hall probe TEM holder. The direction of the applied magnetic field is perpendicular to the sample surface at zero sample tilt angle. An in-plane component of the external magnetic field may be realized through the application of α or β tilt angles (see Fig. 2A).The sample was excited by 300 fs laser pulses (λ = 515 nm, f = 35 kHz) focused to a 135 μm diameter Gaussian spot at a typical laser fluence of 9 mJ cm−2. Time-resolved magnetic information was recorded by electron bunches generated through photoemission from a LaB6 guard ring cathode by UV laser pulses (λ = 258 nm) from the same laser source as the excitation pulse. The relative time delay between the pump and probe pulses was tuned by means of a motorized delay stage that allows for varying the optical path length for the pump pulses. Further details of the LUEM setup can be found in ref. 43. The temporal pulse length of the electron bunches was determined by means of photo-induced near field electron microscopy using a Gatan Quantum SE electron energy analyzed. Under the imaging conditions relevant for the present study, the electron pulse length was estimated to be approximately 2 ps. The ultrafast Lorentz micrographs were recorded using a CheeTah1800 (a Medipix3Rx based camera from Amsterdam Scientific Instruments, the Netherlands).
Funding
This work was supported by the Knut and Alice Wallenberg Foundation, the Swedish Research Council (VR), and partially by the Horizon 2020 research and innovation programme (ERC Advanced Grant No. ∼835068 “TOPSPIN”).Author contributions
G. C. and S. J. performed the sample growth and experimental analysis. J. Å and J. W. coordinated the project. All the authors analyzed the results and co-wrote the manuscript. The authors thank Max Yan for fruitful discussions.Data and materials availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Notes and references
- C. Högemann, M. Pauchard and E. Vauthey, Picosecond transient grating spectroscopy: The nature of the diffracted spectrum, Rev. Sci. Instrum., 1996, 67, 3449–3453 CrossRef.
- F. Hofmann, M. P. Short and C. A. Dennett, Transient grating spectroscopy: An ultrarapid, nondestructive materials evaluation technique, MRS Bull., 2019, 44, 392–402 CrossRef.
- A. A. Maznev, et al., Generation of coherent phonons by coherent extreme ultraviolet radiation in a transient grating experiment, Appl. Phys. Lett., 2018, 113, 221905 CrossRef.
- J. A. Johnson, et al., Direct measurement of room-temperature nondiffusive thermal transport over micron distances in a silicon membrane, Phys. Rev. Lett., 2013, 110, 025901 CrossRef.
- F. Bencivenga, et al., Nanoscale transient gratings excited and probed by extreme ultraviolet femtosecond pulses, Sci. Adv., 2019, 5, eaaw5805 CrossRef CAS.
- M. Fuchs, et al., Anomalous nonlinear X-ray Compton scattering, Nat. Phys., 2015, 11, 964–970 Search PubMed.
- T. E. Glover, et al., X-ray and optical wave mixing, Nature, 2012, 488, 603–608 CrossRef CAS.
- F. Bencivenga, et al., Four-wave mixing experiments with extreme ultraviolet transient gratings, Nature, 2015, 520, 205–208 CrossRef CAS.
- R. K. Lam, et al., Soft X-Ray Second Harmonic Generation as an Interfacial Probe, Phys. Rev. Lett., 2018, 120, 023901 CrossRef CAS.
- J. Goldshteyn, A. Bojahr, P. Gaal, D. Schick and M. Bargheer, Selective preparation and detection of phonon polariton wavepackets by stimulated Raman scattering, Phys. Status Solidi B, 2014, 251, 821–828 CrossRef CAS.
- N. Gedik, J. Orenstein, R. Liang, D. A. Bonn and W. N. Hardy, Diffusion of Nonequilibrium Quasi-Particles in a Cuprate Superconductor, Science, 2003, 300, 1411 CrossRef.
- S. Tang, M. Wang and B. D. Olsen, Anomalous Self-Diffusion and Sticky Rouse Dynamics in Associative Protein Hydrogels, J. Am. Chem. Soc., 2015, 137, 3946–3957 CrossRef CAS.
- N. K. Ravichandran, H. Zhang and A. J. Minnich, Spectrally Resolved Specular Reflections of Thermal Phonons from Atomically Rough Surfaces, Phys. Rev. X, 2018, 8, 041004 CAS.
- N. Osada, et al., Photoexcited carrier dynamics of double-layered CdS/CdSe quantum dot sensitized solar cells measured by heterodyne transient grating and transient absorption methods, Phys. Chem. Chem. Phys., 2014, 16, 5774–5778 RSC.
- A. Leblanc, et al., Plasma holograms for ultrahigh-intensity optics, Nat. Phys., 2017, 13, 440–443 Search PubMed.
- J. Janušonis, et al., Transient Grating Spectroscopy in Magnetic Thin Films: Simultaneous Detection of Elastic and Magnetic Dynamics, Sci. Rep., 2016, 6, 29143 Search PubMed.
- X.-G. Wang, L. Chotorlishvili and J. Berakdar, Strain and Thermally Induced Magnetic Dynamics and Spin Current in Magnetic Insulators Subject to Transient Optical Grating, Front. Mater., 2017, 4, 19 Search PubMed.
- C. S. Davies, et al., Towards massively parallelized all-optical magnetic recording, J. Appl. Phys., 2018, 123, 213904 CrossRef.
- A. Kirilyuk, A. V. Kimel and T. Rasing, Ultrafast optical manipulation of magnetic order, Rev. Mod. Phys., 2010, 82, 2731–2784 CrossRef.
- M. van Kampen, et al., All-optical probe of coherent spin waves, Phys. Rev. Lett., 2002, 88, 227201 CrossRef CAS.
- X. Yu, Y. Onose and N. Kanazawa, et al., Real-space observation of a two-dimensional skyrmion crystal, Nature, 2010, 465, 901–904 CrossRef CAS.
- H. S. Park, J. S. Baskin and A. H. Zewail, 4D Lorentz electron microscopy imaging: Magnetic domain wall nucleation, reversal, and wave velocity, Nano Lett., 2010, 10, 3796–3803 CrossRef CAS.
- A. Arbouet, G. M. Caruso and F. Houdellier, Ultrafast Transmission Electron Microscopy: Historical Development, Instrumentation, and Applications, Adv. Imaging Electron Phys., 2018, 207, 1–72 Search PubMed.
- S. A. Aseyev, E. A. Ryabov, B. N. Mironov and A. A. Ischenko, The development of ultrafast electron microscopy, Crystals, 2020, 10, 3390 CrossRef.
- K. B. Schliep, P. Quarterman, W. Jian-Ping and D. J. Flannigan, Picosecond Fresnel transmission electron microscopy, Appl. Phys. Lett., 2017, 110, 222404 CrossRef.
- G. Berruto, et al., Laser-Induced Skyrmion Writing and Erasing in an Ultrafast Cryo-Lorentz Transmission Electron Microscope, Phys. Rev. Lett., 2018, 120, 117201 CrossRef CAS.
- N. Rubiano da Silva, et al., Nanoscale Mapping of Ultrafast Magnetization Dynamics with Femtosecond Lorentz Microscopy, Phys. Rev. X, 2018, 8, 031052 CAS.
- M. Zhang, et al., High Spatiotemporal Resolution of Magnetic Dynamics in Mn-Ni-Ga via Four-Dimensional Lorentz Microscopy, Phys. Rev. Appl., 2019, 12, 034037 CrossRef CAS.
- M. Möller, J. H. Gaida, S. Schäfer and C. Ropers, Few-nm tracking of current-driven magnetic vortex orbits using ultrafast Lorentz microscopy, Commun. Phys., 2020, 3, 1038 Search PubMed.
- M. Stärk, et al., Controlling the magnetic structure of Co/Pd thin films by direct laser interference patterning, Nanotechnology, 2015, 26, 20 CrossRef.
- J. Janušonis, et al., Ultrafast magnetoelastic probing of surface acoustic transients, Phys. Rev. B, 2016, 94, 024415 CrossRef.
- C. S. Davies, et al., Towards massively parallelized all-optical magnetic recording, J. Appl. Phys., 2018, 123, 213904 CrossRef.
- C. Kittel, On the Gyromagnetic Ratio and Spectroscopic Splitting Factor of Ferromagnetic Substances, Phys. Rev., 1949, 76, 743 CrossRef CAS.
- A. A. Rzhevsky, B. B. Krichevtsov, D. E. Bürgler and C. M. Schneider, Magnetization dynamics induced by ultrashort optical pulses in Fe/Cr thin films, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 224434 CrossRef.
- L. Perfetti, et al., Ultrafast electron relaxation in superconducting Bi2Sr2CaCu2O8+δ by time-resolved photoelectron spectroscopy, Phys. Rev. Lett., 2007, 99, 197001 CrossRef CAS.
- J. Walowski, et al., Energy Equilibration Processes of Electrons, Magnons, and Phonons at the Femtosecond Time Scale, Phys. Rev. Lett., 2008, 101, 237401 CrossRef CAS.
- C. Kittel, et al., Introduction to Solid State Physics, John Wiley & Sons, 8th edn, 2004. ISBN 978-0-471-41526-8 Search PubMed.
- S. Jiang, et al., Reduced spin torque nano-oscillator linewidth using He+ irradiation, Appl. Phys. Lett., 2020, 116, 072403 CrossRef CAS.
- J. Janušonis, et al., Transient Grating Spectroscopy in Magnetic Thin Films: Simultaneous Detection of Elastic and Magnetic Dynamics, Sci. Rep., 2016, 6, 29143 CrossRef.
- M. Shigemi, et al., Gilbert Damping for Various Ni80Fe20 Thin Films Investigated Using All-Optical Pump–Probe Detection and Ferromagnetic Resonance, Appl. Phys. Express, 2008, 1, 121301 CrossRef.
- F. Bencivenga, et al., Four-wave mixing experiments with extreme ultraviolet transient gratings, Nature, 2015, 520, 205 CrossRef CAS.
- F. Bencivenga, et al., Nanoscale transient gratings excited and probed by extreme ultraviolet femtosecond pulses, Sci. Adv., 2019, 5, 5805 CrossRef.
- J. Shaozheng, et al., Influence of cathode geometry on electron dynamics in an ultrafast electron microscope, Struct. Dyn., 2017, 4, 054303 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Materials and methods; sections S1–S6. See DOI: 10.1039/d0nr07962f |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2021 |