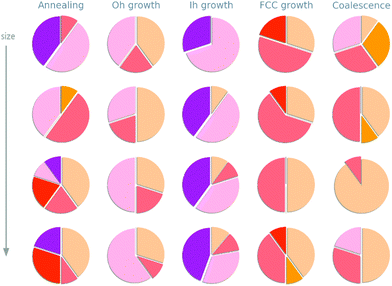Open Access Article
Open Access ArticleBorn to be different: the formation process of Cu nanoparticles tunes the size trend of the activity for CO2 to CH4 conversion†
Elena
Gazzarrini
a,
Kevin
Rossi
 ab and
Francesca
Baletto
ab and
Francesca
Baletto
 *a
*a
aPhysics Department, King's College London, WC2R 2LS, London, UK. E-mail: francesca.baletto@kcl.ac.uk
bLaboratory of Nanochemistry for Energy, Institute of Chemistry, Ecole Polytechnique Fédérale de Lausanne, Lausanne, 1015 CH, Switzerland
First published on 12th February 2021
Abstract
We investigate the impact of the formation process of Cu nanoparticles on the distribution of adsorption sites and hence on their activity. Using molecular dynamics, we model formation pathways characteristic of physical synthesis routes as the annealing of a liquid droplet, the growth proceeding via the addition of single atoms, and the coalescence of individual nanoparticles. Each formation process leads to different and characteristic size-dependent distributions of their adsorption sites, catalogued and monitored on-the-fly by means of a suitable geometrical descriptor. Annealed or coalesced nanoparticles present a rather homogeneous distribution in the kind and relative abundance of non-equivalent adsorption sites. Atom-by-atom grown nanoparticles, instead, exhibit a more marked occurrence of adsorption sites corresponding to adatoms and small islands on (111) and (100) facets. Regardless of the formation process, highly coordinated sites are more likely in larger nanoparticles, while the abundance of low-coordination sites depends on the formation process and on the nanoparticle size. Furthermore, we show how each characteristic distribution of adsorption sites reflects in different size trends for the Cu-nanoparticle activity, taking as an example the electro-reduction of CO2 into CH4. To this end, we employ a multi-scale method and observe that the faceted but highly defected structures obtained during the atom-by-atom growth become more and more active with increasing size, with a mild dependence on the original seed. In contrast, the activity of Cu-nanoparticles obtained by annealing decreases with their size, while coalesced nanoparticles’ activity shows a non-monotonic behaviour.
1 Introduction
To reach the net-zero CO2 emission by 2050, the development of new devices to capture and convert CO2 efficiently is required. As CO2 is thermodynamically stable and kinetically inert,1,2 its efficient conversion requires the use of catalysts at the electrodes capable of selectively reducing CO2 to valuable (e.g. methane (CH4), oxygenated and/or C2 products) hydrocarbon products at low overpotentials. Out of the polycrystalline metals, copper (Cu) is the only heterogeneous catalyst that has the potential to produce valuable hydrocarbons, aldehydes and alcohols from the electrochemical CO2 reduction reaction (CO2RR).1 Even if copper has already been largely used as a catalyst to reduce CO2,1–19 it is still a challenge to get optimal efficiency and selectivity.20 Size-dependent selectivity for ethylene in Cu nanocubes exposing mostly (100) facets has been recently reported.21 At the same time, high selectivity for methane in Cu nanowires,22 spheres,23 and octahedra, mostly exposing (111) facets,24 has been also observed. Alloying Cu and other metals also may increase nanoparticle and nanocrystal activities and selectivity.25,26 The key to the ultimate design of better Cu nanocatalysts requires a systematic understanding of CO2 reduction on the variety of adsorption sites peculiar of individual nanoparticles and how structural instability and rearrangements affect their activity.To propose robust design rules for nanocatalysts, e.g. size and shape trends of their activity, effect of chemical composition and ordering, and avoiding a costly and ineffective trial-and-error procedure, two factors should be simultaneously taken into account: (i) the variety of adsorption sites per isomer,27–32 which influences both activity and selectivity and (ii) the coexistence of different geometries, eventually related to their formation process.33–35
In this work, we find that the size distribution of adsorption sites depends strongly on the formation process, ultimately affecting the size trend of the mass activity of Cu-NPs. Furthermore, because such distribution of adsorption sites is characteristic of the selected formation process, our work opens a way of tuning the catalytic activity by choosing a certain formation protocol. We model the formation of individual Cu NPs as it is supposed to occur inside inter-gas aggregation sources.36–40 Specifically, after the formation of a critical size droplet, it can solidify (annealing), continue to grow via the subsequent deposition of atom (atom-by-atom growth), or from the merging of two previously formed seeds (coalescence). These mechanisms are pictorially reproduced in the left panel of Fig. 1.41–44
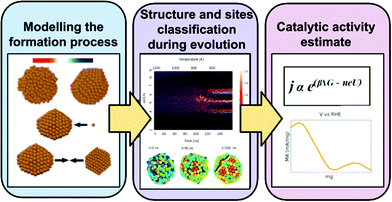 | ||
| Fig. 1 Graphical representation of the multiscale numerical strategy adopted here. The modelling of the formation processes (annealing, growth, and coalescence) is by means of molecular dynamics (MD) starting from a plethora of Cu-NPs of different shapes and sizes. We perform an accurate structural analysis of each trajectory and per each time-step, the NP is classified into geometrical families and the type and the occurrence of each adsorption site is monitored following the time evolution of the atop generalised number. We then estimate the CH4 mass activity for each Cu-NP during their formation process by the multiscale model of ref. 45. | ||
We observe that annealing and coalescence lead to a rather homogeneous distribution of the type and occurrence of adsorption sites as classified accordingly to their generalised coordination number. Atom-by-atom growth, instead, results in characteristic distributions with peaks corresponding to the formation of adatoms and small islands on (111) and (100) facets. In particular, the occurrence of low coordinated atoms peaks at different NP sizes, depending on the formation process. Low coordinated atoms are more abundant in small frozen Cu NPs, coalesced ones of intermediate size (300–600 atoms), and larger atom-by-atom grown Cu-NPs (600–1000 atoms). For the case of highly coordinated sites (i.e. the surface atoms presenting a coordination equal to or greater than the one on the (111) facet), their occurrence increases with the size of the Cu-NPs, regardless of the formation process.
To calculate the mass activity of Cu NPs for CO2 conversion to CH4, we adopt our recent NanoCHE scheme,45 a multiscale method to estimate the catalytic activity of NPs as a function of their structure and structural evolution. By exploiting a scaling relationship previously proposed in the literature,14 we unveil non-trivial size trends of the NP activity depending on the formation process. Using a volcano-plot relationship between coordination and activity which peaks at extremely low coordinated sites, we observe that, at small sizes (below 300 atoms), NPs obtained from annealing are the most active in converting CO2 to CH4. At intermediate sizes (300–600 atoms), coalesced Cu-NPs are instead more favourable. Their size-dependent activity also shows a non-monotonic trend for the sizes and sampling time here considered. At larger sizes (600–1000 atoms) instead atom-by-atom grown NPs appear more active. We further note that, while the activity on atom-by-atom grown NPs positively correlates with size, we also find that the latter trend is oscillatory in nature.
2 Methodology
The workflow of our multi-scale approach is visually represented in Fig. 1 and is based on the following steps.2.1 Modelling the formation process
We consider Cu-NPs of different sizes and shapes between 110 and 976 atoms, i.e. with a diameter of 1–3 nm. We label each structure as a function of the number of atoms it is made up of, e.g. the nomenclature Cu147 labels a Cu NP of 147 atoms. NP initial geometries are: liquid droplets, FCC polyhedra as Octahedra (Oh) or their regular truncation (To), Marks-Decahedra (MDh), Icosahedra (Ih) and defected Icosahedra (dIh), as detailed in section I of the ESI.† Far from exhaustive of all available isomers in the considered size range, the ensemble of morphology under scrutiny provides, in our opinion, a sufficient structural variety to test the effectiveness of our approach. In fact, there is a strong experimental and theoretical evidence which backs up this choice. Icosahedra and decahedra, geometries with 5-fold twinning planes, and FCC-polyhedra are often observed in experiments. Furthermore, theoretically Ih, MDh, and FCC-polyhedra are the most favourable morphology for sizes between 1 and 3 nm both for “magic” and “non-magic” sizes,46–49 in good agreement with experiments.39,48,50,51Among the many formation processes enabling the making of metallic nanocatalysts, we consider the annealing of a liquid droplet, the atom-by-atom growth from a small seed, and the coalescence of two Cu-NPs. We simulate these formation processes by means of molecular dynamics and model the interatomic interactions with a Rosato–Guillope–Legrand potential with parameters for Cu taken from the literature.52 The latter parametrization was fit to reproduce the bulk modulus, elastic constant, and cohesive energy and was found to quantitatively reproduce size-crossovers among structural motifs in Cu and other transition metal nanoparticles.46 We employ a velocity-Verlet algorithm53 to integrate Newton's equation of motion with a time step of 5 fs. The latter timestep is possibly larger than the one usually employed in ab initio molecular dynamics runs, but it is commonly used in simulations employing semi-empirical potentials. Indeed, the stability and robustness of dynamics with second-moment tight-binding formulations was verified also for four-times larger timesteps.54 We apply an Andersen thermostat to control the temperature with a frequency of 5 × 1011 Hz.
During annealing simulation, the structural evolution of a liquid droplet of 147, 250, 561, 585, 891, or 976 atoms is probed over various concatenated canonical NVT runs, where the temperature is lowered from 1200 K to 400 K at a rate of 5 K ns−1. In the atom-by-atom growth simulation, we consider three starting seeds of similar size (Cu146 (Oh), Cu147 (Ih) and Cu201 (To)) and assume that the Cu NPs are grown by the addition of single atoms, deposited every 4 ns with a temperature of 600 K.55 To study coalescence, we investigate the evolution of two nanoparticles moving against each other with a kinetic energy corresponding to a temperature of 600 K. We analyse the first 100 ns of their evolution. For each size and formation process, we perform 10 independent runs, and we average results over them. Section II of the ESI† contains further details on the simulation methods to model different formation processes.
2.2 Monitoring the adsorption sites distribution on-the-fly
We employ Common Neighbor Analysis (CNA) to classify the morphology of the NP into geometrical families – namely FCC, icosahedra (Ih) and decahedra (Dh) – as well as to probe defect formation – i.e. re-entrances and elongated concavities – and the formation of twin planes, grain boundaries, and five-fold axes (see ESI† section III for more details).We use the atop generalized coordination number (aGCN) to enumerate the number and kind of all adsorption sites in the nanoparticle. The aGCN of an adsorption site i is defined as:27,28
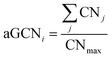 | (1) |
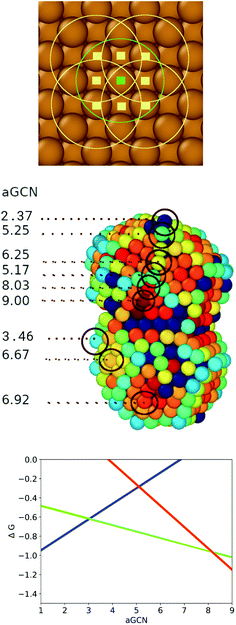 | ||
Fig. 2 Upper panel: Visual example of how the GCN for an atom (labelled with a green square) on a (100) surface is evaluated. We identify the atoms (pale yellow square) in its first neighbour shell (green circle), and calculate their coordination number, by counting the atoms in their first nearest neighbours (yellow circle). We finally evaluate the GCN of the atom labelled in green following eqn (1). Middle panel: A Cu nanoparticle where surface atoms are coloured according to their aGCN, following the colour gradient 2  9. The aGCN is also spelt out for example sites. Any atom with more than 11 nearest-neighbour, are coloured in dark/black blue and they are not able to act as anchor for CO-adsorption. Lower panel: the volcano relationship of eqn (4), which correlates the site aGCN to the CO2 → CH4 reaction free energy, adapted from ref. 14.The rate limiting step for sites with coordination lower than 3.1 is H2O desorption (blue line), for sites with aGCN between 3.1 and 8.4 CO protonation to form CHO (green line), and for sites above 8.4 the formation of COOH from CO2 (red line). 9. The aGCN is also spelt out for example sites. Any atom with more than 11 nearest-neighbour, are coloured in dark/black blue and they are not able to act as anchor for CO-adsorption. Lower panel: the volcano relationship of eqn (4), which correlates the site aGCN to the CO2 → CH4 reaction free energy, adapted from ref. 14.The rate limiting step for sites with coordination lower than 3.1 is H2O desorption (blue line), for sites with aGCN between 3.1 and 8.4 CO protonation to form CHO (green line), and for sites above 8.4 the formation of COOH from CO2 (red line). | ||
As depicted in the middle panel of Fig. 2, sites corresponding to vertexes and single adatoms have an aGCN less than 4, while atoms lying at the edges of any facet show an aGCN between 4 and 5. Sites on the (111) and (100) surface respectively show a generalized coordination of 7.5 and 6.67. The aGCN further discriminate atoms still belonging to a facet but closer to the edge, with a value between 5 and 6.5. Atoms at convex sites in correspondence of steps, kinks, and re-entrances instead show a coordination larger than 7.5. Atoms that are not at the surface have an aGCN approaching the bulk limit of 12. It is worth noting that while we focus only on atop adsorption sites, as CO likely adsorbs in that way, we note that our framework could also be adapted to account for bridge and hollow adsorption too.
2.3 Estimate of the NPs’ mass activity
To monitor the activity of Cu-NPs during their formation process and to derive a size behaviour of the mass activity, we employ the NanoCHE model.45 The latter is a multiscale model built upon the computational hydrogen electrode model, pioneered by Nørskov and co-workers,56 which enables to simulate a linear sweep voltammetry experiment for systems characterised by a variety of non-equivalent and competing adsorption sites.Within the NanoCHE framework, for a temperature T and a certain applied voltage U*, the mass activity  of a nanoparticle is calculated from the current density it produces, J, its mass, MNP, and its area, Asurf:45
of a nanoparticle is calculated from the current density it produces, J, its mass, MNP, and its area, Asurf:45
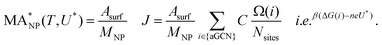 | (2) |
In equation 2, MNP is estimated from the number of atoms, N, in the NP, times their atomic mass, i.e. 63.546 a.u. for Cu. Asurf is instead calculated as a function of the aGCN,45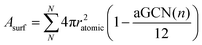 , where the sum is over all atoms N in the NP, and ratomic is the atomic radius of Cu, 0.128 nm. aGCN is the list of all the atop generalized coordination number that a NP shows, and it is constantly updated during the evolution of the NP.
, where the sum is over all atoms N in the NP, and ratomic is the atomic radius of Cu, 0.128 nm. aGCN is the list of all the atop generalized coordination number that a NP shows, and it is constantly updated during the evolution of the NP. 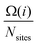 counts the number of adsorption sites with aGCN = i over the total number of surface sites. The constant C is fitted to reproduce experimental activities. As discussed in detail in sect. IV of the ESI,†C is found to be equal to −3.01 × 1014 mA cm−2. β is the short-hand notation for the Maxwell–Boltzmann factor,
counts the number of adsorption sites with aGCN = i over the total number of surface sites. The constant C is fitted to reproduce experimental activities. As discussed in detail in sect. IV of the ESI,†C is found to be equal to −3.01 × 1014 mA cm−2. β is the short-hand notation for the Maxwell–Boltzmann factor, 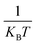 . To scrutinise on equal footing structures sampled within different ensembles, T is kept at 300 K, the temperature at which catalytic activities are usually probed experimentally.57,58 We note that while Cu-NPs may be formed at higher temperatures, they do not undergo major structural rearrangements if rapidly annealed to room temperature,59 hence justifying the choice of probing all NP activities at room temperature. Finally, ΔG is the reaction free energy of the rate limiting step of the chemical reaction under study, calculated as a function of the atop generalised coordination number of the site where the reaction occurs. While the NanoCHE was first developed to predict the activity of Pt nanoparticles over oxygen reduction, we show here that it could be extended easily to other electrochemical reactions. From this point of view, the NanoCHE model appears as a quite general approach to estimate the activity of metallic nanoparticles. In this view, we critically assess further improvements.
. To scrutinise on equal footing structures sampled within different ensembles, T is kept at 300 K, the temperature at which catalytic activities are usually probed experimentally.57,58 We note that while Cu-NPs may be formed at higher temperatures, they do not undergo major structural rearrangements if rapidly annealed to room temperature,59 hence justifying the choice of probing all NP activities at room temperature. Finally, ΔG is the reaction free energy of the rate limiting step of the chemical reaction under study, calculated as a function of the atop generalised coordination number of the site where the reaction occurs. While the NanoCHE was first developed to predict the activity of Pt nanoparticles over oxygen reduction, we show here that it could be extended easily to other electrochemical reactions. From this point of view, the NanoCHE model appears as a quite general approach to estimate the activity of metallic nanoparticles. In this view, we critically assess further improvements.
Under the assumption of Brønsted–Evans–Polanyi relationships holding for the process of interest,60 the difference in binding energies between the two adsorbates determining the rate limiting step conversion dictates the activity of the site at which the reaction occurs. Although the pathway from CO2 to CH4 on Cu sometimes shows bifurcations (i.e. CHO can attach via C or O),61 the reaction steps established by Peterson et al.13,62 were employed to calculate the reaction free energy:
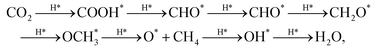 | (3) |
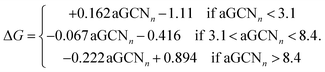 | (4) |
For completeness, in Fig. 2 middle and lower panels, we report the volcano shaped structure–activity relationships and show adsorption sites with different generalized coordination to exemplify their coordination environments. We note that such relationships are extracted from GGA DFT calculations employing a revised Perdew–Burke–Ernzerhof functional and no dispersion correction. The choice of functional may affect the trends observed in numerical investigations.63
3. Results and discussion
3.1 Formation process and NP structure
Depending on the formation process, a variety of geometries are observed in the size range between 1 and 3 nm. These are visually resumed in Fig. 3 where, for each formation process, we report the proportion of trajectories which result in the formation of an icosahedron, a decahedron, a fcc structure, or their defected counterparts.In agreement with previous study, we observe a structural crossover with size.46–49 At small ones, the Ih archtype and its defected counterpart are more likely to be osberved. They represent the majority of all structures but for the case of growths started from a truncated octahedron. Increasing the size of the nanoparticle, FCC like structures and defected decahedra are more probable, until they become the most likely to be observed. Such structural crossover sizes appear formation process dependent.
We remark, however, that this analysis offers only a qualitative indication of the true distributions of morphology resulting in each of the formation processes under consideration. It is likely that a larger number of independent runs are needed to obtain finely converged statistics. Nevertheless, our multi-scale model to calculate the activity of Cu-nanoparticles assumes an explicit dependence on the distribution of non-equivalent adsorption sites only. The statistics to converge the latter converge for a lesser number of runs, vide infra.
The heterogeneity in morphology distributions stems from kinetic factors and from the intrinsic complexity of the potential and free energy landscape of metallic NPs. Pathways connecting different isomers may appear either as shallow, resulting in fast and fluxional rearrangements among different geometries, or characterized by high energetic barriers, determining kinetic trapping in one isomer, and the appearance of surface defects.59 Section V of the ESI† reports a detailed discussion on the energetic landscapes of the systems under investigation. Our study on the formation process of 1–3 nm Cu nanoparticles confirms that:
• The nucleation into a morphology or another is the most likely cause for the morphological heterogeneity during the annealing.64
• The interplay between initial seed geometry and kinetic effects determines the formation of either icosahedral-like or asymmetric-FCC geometries.65
• Nanoparticles from the coalescence are likely to assume non-spherical geometries.66
3.2 Shape and Non-equivalent site distribution evolution during each formation process
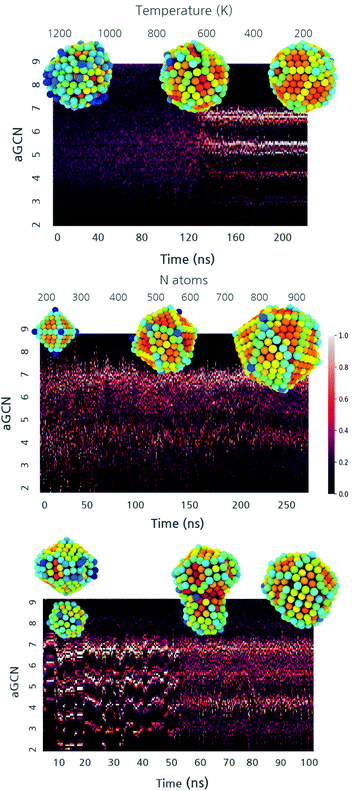
The heterogeneity in the shapes sampled during annealing, growth, and coalescence parallels the one in the non-equivalent adsorption site distributions (Fig. 4). At the beginning, the aGCN distribution is widely spread for liquid droplets and it narrows down to specific signatures when the NP solidifies. Such a transition in the aGCN distribution emerges at the phase transition temperature. Another general consideration about the differences between solid and liquid nanoparticles pertains the average coordination number observed in the two phases. Nanodroplets are by definition more disordered and this reflects in a lesser coordination of atoms at their surface. We indeed observe a decrease in the surface area during the annealing process, dropping from values between 1.2–5.4 × 10–15 cm2 to 1–3.8 × 10–15 cm2, respectively. Together with Fig. 4 top panel, the interested reader is referred to the ESI Fig. S5† upper panel for other examples corroborating this observation.When analyzing the evolution of the aGCN distributions during a growth process as a function of time (and thus size), we note that the single addition of an adatom on a rather close-shell geometry results in the formation of low coordinated sites. For reference, we report in Fig. 4 middle panel (see also ESI S5† middle panel) the time evolution of the aGCN distribution of surface sites during the growth from an Oh. For the case of the growth from an Ih seed, the latter proceeds in a layer-by-layer fashion and the icosahedral center is always preserved during this process. In contrast, Oh (and the To) evolve either: (1) in structures with many (111), (100) and (211) facets and a strong anisotropy, or (2) undergo kinetic rearrangements towards more favourable morphology (i.e. dIh for the case of the Oh or dDh for the To). These solid–solid transitions are exemplified in Fig. S5† middle left panel.
When looking at the aGCN distribution evolution during coalescence, exemplified in Fig. 4 lower panel (and S5† lower panel), we note three stages. Before the collision, the system is made up of two ordered individual nanoparticles; hence, the aGCN occurrence for the whole system is, simply, the sum of the two. During the collision, the distribution of aGCN changes considerably, indicating a highly defected and disordered atomic arrangement. Conversely, the Cu-NPs cannot be described neither as icosahedral, decahedral, or FCC cuts. This is also related to the rather pronounced anisotropy they exhibit. The aGCN list and occurrence are very disordered and spread out, but still reminiscent of the initially preferred aGCN values, around 5 and 6.5, which corresponds to the sites in the initial structures which are not affected by the collision. We further highlight how the neck generated by the first moment of the collision is always highly coordinated. After the collision, atomic rearrangements at the surface succeed one another. This may also result in collective rearrangements (e.g. time = 0.01 ns). Depending on the size of the system, the chosen observation time-scale either enables (small sizes) or forbids (large sizes) a complete rearrangement towards a defected but lesser anisotropic morphology.
Previously, it has been shown by numerical calculations59,67 and experiments39,40,50,68–70 that kinetic trapping in high-energy isomers take place even if the latter are quite unfavourable w.r.t. the global minimum at the same size. We further verified that the NEAS distribution of each metastable isomer is stable within the 102–103 ns timescale (see ESI section VI†). As a final note, we remark that we have analysed NEAS distributions in Cu-nanoshapes obtained from three out-of-the-equilibrium formation routes representative of, e.g., inert-gas aggregation sources. Nevertheless, the proposed framework is transferable to estimate the NEAS distributions and hence the mass activity of any NP structure. Nanoparticle shapes can be predicted via global minimum search algorithms, e.g. basin hopping71,72 or genetic optimization.73 Similarly, the probability to remain in a certain structural basin can be evaluated by accounting for energetic and entropic contributions.74,75
3.3 Formation process, NP size, and resulting non-equivalent site distributions
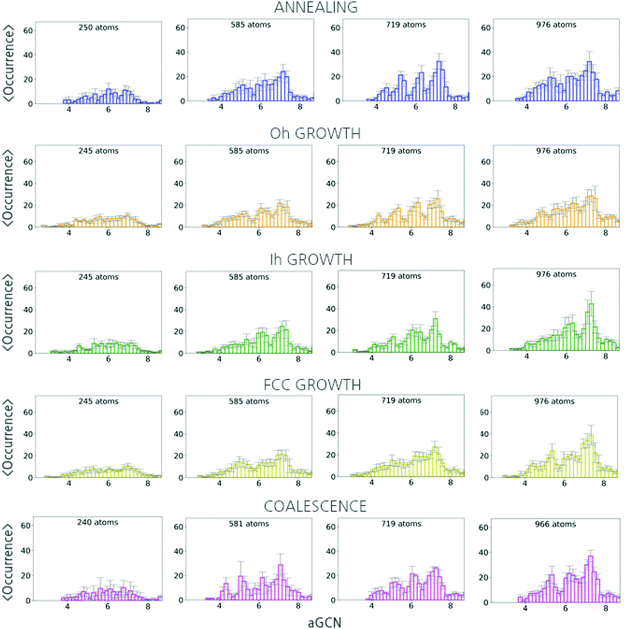
In Fig. 5, we report the aGCN distributions for size-selected geometries sampled during the three formation processes under consideration.For the case of annealing (top panel), the number and type of non-equivalent adsorption sites change drastically with the nanoparticle size. The aGCN distribution of solidify Cu250 nanoparticles show peaks at around 5.5 and 7, suggesting an abundance of small (111)-like facets. Cu585 solid structures display aGCN zeniths at around 5.5, 6.5 and 7.5, which correspond to a more ordered and faceted geometry delimited by (211), (100) and (111) facets. Finally, the aGCN distributions for Cu719 and Cu976 show a high occurrence of aGCN-sites between 8 and 9. This corresponds to a higher probability of finding the surface decorated by re-entrances, islands, and steps. The occurrence of sites of this nature, in turn, appears to correlate with the NP size. Vice versa the relative abundance of low-coordinated sites is marked for small Cu-NPs (below 300 atoms) and anti-correlates with size.
For the case of atom-by-atom grown NPs, (three central panels) although the genome distribution is more uniform for smaller structures, it evolves towards specific signatures as the size grows. Notwithstanding the structural diversity of the initial seed and final products, the aGCN distributions appear rather similar for the three sets of four independent trajectories considered. Regardless of the initial seed and final morphology, we in fact observe peaks in the aGCN occurrence at values of around 7.5, corresponding to (111) facets, the most energetically favourable surface for FCC metals, and particularly so for the case of Cu. The number of sites corresponding to atoms at steps and re-entrances (generalized coordination above 7.5) is instead small. The occurrence of sites along (100) surfaces (aGCN = 6.67) and corresponding to vertex and adatoms (coordination less than 5) is also noticeable as a feature in the aGCN distributions. The formation of anisotropic shapes results in a lesser number of low-coordinated sites during the course of the growth.
Looking at the aGCN distributions of coalesced nanoparticles, Fig. 5 lower panel, we observe that they are homogeneously distributed for Cu-NPs of small sizes. Features of the original individual NPs are instead partly preserved in systems larger than 300 atoms. At the same time, in the neck region, several steps and defects are formed leading to a large variety of atop generalised coordination values, namely above 7.5 or below 4.
3.4 Formation process, NP size, and NP activity
The heterogeneity of the type and occurrence of the adsorption sites of Cu NPs, which is related to their formation processes, leads to different size trends of the NP catalytic properties. Under the assumption that the structure–property relationship expressed in eqn (4) contains all the needed ingredients in determining the activity of a NP, we are equipped to predict the catalytic activity of Cu-NPs obtained through diverse formation processes in the conversion of CO2 into CH4.As a rule of thumb, because under-coordinated atoms are the most active according to the structure–property relationships in eqn (4), we expect that defects enhance the catalytic activity towards methane conversion. Using eqn (2), we calculate the current density and mass activity of Cu NP catalysts driving the conversion of CO2 into CH4 at an applied potential close to V vs. RHE = −1.1 V. We then report on the size-dependence of the current density for CO2 conversion to CH4 as a function of the formation process through which the Cu-NPs are synthesized. These estimates are reported in Fig. 6. The MA prediction statistics are converged to a satisfactory degree according to a bootstrapping analysis (ESI, section VII†).
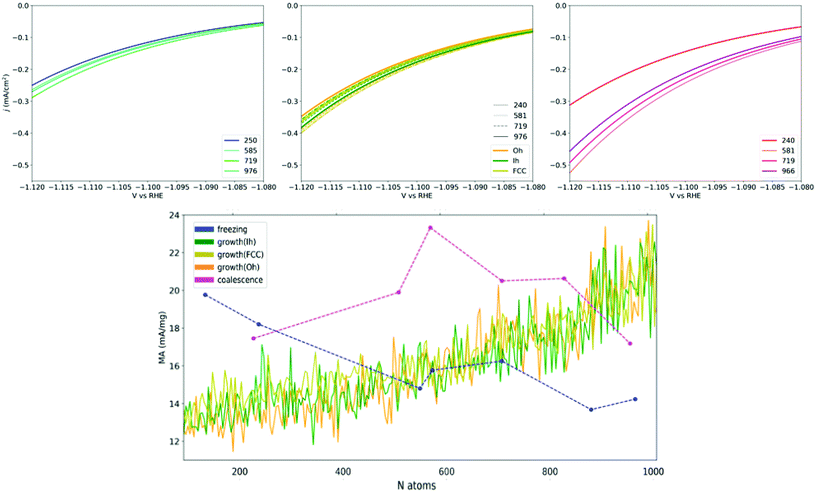 | ||
| Fig. 6 Upper row shows the current densities for CO2 → CH4 conversion around U = −1.1 V vs. RHE for Cu-NPs of different sizes. Left panel represents Cu-NPs from the annealing of a liquid droplet (top-left, blue), the middle panel from the atom-by-atom growth (top-centre, orange is for Oh seed, dark-green for Ih and olive for FCC initial seeds, respectively). Right panel reports coalesced Cu-NPs (top-right, pink). The bottom row shows the mass activity for CH4 conversion at U = −1.1 V vs. RHE plotted versus the size of Cu-NPs sampled over the three formation processes (blue annealing; green-orange growth; magenta coalescence). Dashed lines for annealing and coalescence are a guide to the eye. Growth lines look continuous as data are available at each size. These data points are filtered via a Gaussian Kernel for readability. The non-filtered data show oscillations within ±5 mA mg−1, due to the instantaneous appearance/disappearance of surface defects with aGCN values close to the structural relationship's maximum (Fig. 2). | ||
In agreement with the aGCN distributions reported in Fig. 5, respectively for annealing, atom-by-atom growth and coalescence, we observe that the activity trend depends strongly on the formation-process and nanoparticle size. While the calculated current densities and MA* range between 0.1 and 1 mA cm−2 and 10–24 mA mg−1 respectively, we observe that: (i) Annealed Cu-NPs exhibit a decreasing mass activity with size, their MA moves from 19.9 mA mg−1 in NPs of 147 atoms down to 14.2 mA mg−1 in NPs of 976 atoms. Indeed the current densities, regardless of size, span only between 0.1 and 0.2 mA cm−2. (ii) Atom-by-atom grown NPs find, on average, an enhancement of their MA activity from 12 to 23 mA mg−1, although strong oscillations occur, mainly due to local surface rearrangements, and depending on the initial core. The current density magnitude positively correlates with nanoparticle size. (iii) Coalesced NPs show a rather smooth but non-monotonic size-behaviour with their MA lying in the 16.9–23.4 mA mg−1 range. Their current densities at −1.1 V vs. RHE extend between −0.1 and −0.3, with the largest observed for the case of NPs of the largest sizes. Between 200 and 800 atoms, the NPs with the largest mass activity are obtained from the coalescence of smaller NPs of 1-2 nm in diameter, with a gain of about 6 mA mg−1 NP with respect to NPs formed following a different process. On the other end, Cu-NPs grown atom-by-atom become the most active at larger sizes, above 800 atoms.
In comparison with experimental data (beyond the ones used to fit the constant in eqn (2)), we observe that the magnitude of current densities, 0.1–1 mA cm−2, finds a good agreement with the one for CO2 conversion to CH4 reported in the literature for Cu catalysts, e.g., Cu foils and pristine surfaces.1
Besides such quantitative agreement, other comparisons are not trivial because of the complex multi-product outcome in the reduction of CO2. We note that the hydrogen evolution reaction (HER) is known to compete with CO2 reduction, with an increased activity for the latter observed only in catalysts of larger sizes than the ones here considered for the case of spherical nanoparticles.23 Also, it is has been reported that (100) facets are less active than (111) for CH41,76 at U* vs. RHE = 1.1 V, which is the applied potential we use in eqn (2). We note that towards accounting in eqn (2) for the transformation of CO2 into molecules other than CH4, one can introduce one or multiple terms simulating the competition between different products. This may then enable to recover the above experimental observations.
By the same token in the literature, it is reported that an increased tendency to form either CH4 or C2 products is due to the presence of active sites at steps close to facets (steps at (111) facets for methane, steps at (100) for C2 products). These adsorption sites show a lower coordination than one of the atoms on (111) surfaces.1,76–79 Employing a volcano relationship between coordination and activity, which peaks at low aGCN, values may in turn also help in the design of Cu catalysts active for CO2 conversion into C2 products.
As final consideration, let us stress that the workflow in Fig. 1 is fully general and that corrections and modifications to the structure–property relationship in eqn (4) can be made, although this is out of the aim of this work. In turn, other, more accurate and complex, functions of structural/electronic descriptors accounting for, e.g., multiple elements in the catalyst, and also found, e.g., by means of statistical learning models beyond linear ones, may improve and generalize the framework here discussed. Also, the reaction free energy estimator can encode a potential-dependent term, so to predict consistently CO2RR activity over a range of applied potentials.80
4 Conclusions
We systematically analyse Cu nanoparticles’ structural properties grown following different routes representative of inert gas aggregation sources. We demonstrate how the chosen formation method could impact, and potentially tailor, the activity of Cu-NPs for the conversion of CO2 into methane. We show that the formation process leads to different shape distributions, even in the same size range. Each characteristic shape distribution influences the kind and abundance of non-equivalent adsorption sites, distinguished and catalogued according to their atop generalised coordination number. We observe that the occurrence of highly coordinated sites mainly correlates with the nanoparticle's size. Cu-NPs are likely to be delimited by (111) facets, especially during the atom-by-atom growth, as expected by surface energy considerations. On the other hand, the abundance of low-coordinated sites depends strongly on the NP's formation route. Employing an extended version of the nanoCHE model – a multi-scale approach bridging structural features to activity – we observe and explain non-trivial size-trends during the CO2 into CH4 reaction. Our work proposes the manufacturing process of Cu-NPs as a feasible tool to tailor the non-equivalent adsorption site distribution and hence the activity of copper nanoparticles. Nonetheless, we are aware that a better quantitative prediction requires experimentally validated structure–property relationships. The latter will account for bias-dependent barriers and multiple products from the electrochemical reduction of CO2. We hope to stimulate the community's interest in providing a full structural characterisation of Cu-NPs before and after CO2 conversion of differently grown samples.Data availability
The LoDiS package to run MD simulation is available at: https://github.com/kcl-tscm/LoDiS. The Python3 code used to estimate the mass activity for CO2 into CH4 is available at: https://github.com/kcl-tscm/CO2RR_Cu_NPs. Example snapshots sampled during the trajectories discussed in this report are also available at the same page.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Raffaella Buonsanti for fruitful discussions. The authors further thank Alejandro Santana-Bonilla, Matteo Tiberi, Robert Jones, Laia Delgado, Raphael Pinto-Miles, and Armand Auquier for their suggestions in developing the computational tools within the LoDiS software project, supported by the IAA-EPSRC grant EP/R511559/1. F. B. thanks the EPSRC – “Towards an Understanding of Catalysis on Nanoalloys” Critical Mass Grant (EP/J010812/1) as does KR (ER/M506357/1). All the authors are grateful to the Royal Society, grant RG 120207, and the IT support offered by the NMS Faculty at King's College London.References
- C. Hahn, T. Hatsukade, Y.-G. Kim, A. Vailionis, J. Baricuatro, D. Higgins, S. Nitopi, M. Soriaga and T. Jaramillo, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 5918–5923 CrossRef CAS PubMed.
- X. Kang, Q. Zhu, X. Sun, J. Hu, J. Zhang, Z. Liu and B. Han, Chem. Sci., 2016, 7, 266–273 RSC.
- S. Min, X. Yang, A.-Y. Lu, C. Tseng, M. Hedhili, L. Li and K. Huang, Nano Energy, 2016, 27, 121–129 CrossRef CAS.
- D. Raciti, K. J. Livi and C. Wang, Nano Lett., 2015, 15, 6829–6835 CrossRef CAS PubMed.
- S. Nitopi, E. Bertheussen, S. Scott, X. Liu, A. Engstfeld, S. Horch, B. Seger, I. Stephens, K. Chan, C. Hahn, J. Nørskov, T. Jaramillo and I. Chorkendorff, Chem. Rev., 2019, 119, 7610–7672 CrossRef CAS PubMed.
- K. Manthiram, B. Beberwyck and A. Alivisatos, J. Am. Chem. Soc., 2014, 136, 13319–13325 CrossRef CAS PubMed.
- S. Roberts, K. Kuhl and A. Nilsson, Angew. Chem., Int. Ed., 2015, 54, 5268–5271 CrossRef.
- D. Ren, Y. Deng, A. Handoko, C. Chen, S. Malkhandi and B. Yeo, ACS Catal., 2015, 5, 2814–2821 CrossRef CAS.
- K. Kuhl, E. Cave, D. Abram and T. Jaramillo, Energy Environ. Sci., 2012, 5, 7050–7059 RSC.
- H. Mistry, A. S. Varela Gasque, C. Bonifacio, I. Zegkinoglou, I. Sinev, Y.-W. Choi, K. Kisslinger, E. Stach, J. Yang, P. Strasser and B. Roldan Cuenya, Nat. Commun., 2016, 7, 12123 CrossRef PubMed.
- C. Li and M. Kanan, J. Am. Chem. Soc., 2012, 134, 7231–7234 CrossRef CAS PubMed.
- J. Vickers, D. Alfonso and D. Kauffman, Energy Technol., 2017, 5, 775–795 CrossRef CAS.
- A. Peterson, F. Abild-Pedersen, F. Studt, J. Rossmeisl and J. Nørskov, Energy Environ. Sci., 2010, 3, 1311–1315 RSC.
- Z. Zhao, Z. Chen, X. Zhang and G. Lu, J. Phys. Chem. C, 2016, 120, 28125–28130 CrossRef CAS.
- W. Durand, A. Peterson, F. Studt, F. Abild-Pedersen and J. Nørskov, Surf. Sci., 2011, 605, 1354–1359 CrossRef CAS.
- X. Zhang, L. Jin-Xun, B. Zijlstra, I. Filot, Z.-Y. Zhou, S. Sun and E. Hensen, Nano Energy, 2017, 43, 200–209 CrossRef.
- W. Tang, A. Peterson, A. S. Varela Gasque, Z. Jovanov, L. Bech, W. Durand, S. Dahl, J. Nørskov and I. Chorkendorff, Phys. Chem. Chem. Phys., 2011, 14, 76–81 RSC.
- Y. Hori, R. Takahashi, Y. Yoshinami and A. Murata, J. Phys. Chem. B, 1997, 101, 7075–7081 CrossRef CAS.
- Y. Hori, A. Murata and R. Takahashi, J. Chem. Soc., Faraday Trans. 1, 1989, 85, 2309–2326 RSC.
- J. Qiao, Y. Liu, F. Hong and J. Zhang, Chem. Soc. Rev., 2014, 43, 631–675 RSC.
- R. M. Arán Ais, D. Gao and B. Roldan Cuenya, Acc. Chem. Res., 2018, 51, 2906–2917 CrossRef PubMed.
- D. Gao, R. M. Arán Ais, H. S. Jeon and B. Roldan Cuenya, Nat. Catal., 2019, 2, 198–210 CrossRef CAS.
- R. Reske, H. Mistry, F. Behafarid, B. RoldanCuenya and P. Strasser, J. Am. Chem. Soc., 2014, 136, 6978–6986 CrossRef CAS PubMed.
- Y. Kang, C. Chen, J. Snyder, N. Marković, P. Yang and V. Stamenkovic, Science, 2014, 343, 1339–1343 CrossRef PubMed.
- X. Liu, J. Xiao, H. Peng, X. Hong, K. Chan and J. K. Nørskov, Nat. Commun., 2017, 8, 15438 CrossRef CAS PubMed.
- C. Cui, L. Gan, M. Heggen, S. Rudi and P. Strasser, Nat. Mater., 2013, 12, 765–711 CrossRef CAS PubMed.
- F. Calle-Vallejo, J. M. García-Lastra, P. Sautet and D. Loffreda, Angew. Chem., Int. Ed., 2014, 8316–8319 CrossRef CAS PubMed.
- F. Calle-Vallejo, J. Tymoczko, V. Čolić, H. Vu, M. Pohl, K. Morgenstern, D. Loffreda, P. Sautet, W. Schuhmann and A. Bandarenka, Science, 2015, 350, 185–189 CrossRef CAS PubMed.
- K. Rossi, G. Asara and F. Baletto, ChemPhysChem, 2019, 20, 3037–3044 CrossRef CAS PubMed.
- K. Rossi, G. Asara and F. Baletto, Phys. Chem. Chem. Phys., 2019, 21, 4888–4898 RSC.
- K. Reuter, C. Plaisance, H. Oberhofer and M. Andersen, J. Chem. Phys., 2017, 146, 040901 CrossRef PubMed.
- K. Kalz, M. Kraehnert, R. Dvoyashkin, R. Dittmeyer, R. Glaser, U. Krewer, K. Reuter and J. A. Grunwaldt, ChemCatChem, 2017, 9, 17–29 CrossRef CAS PubMed.
- D. Foster, R. Ferrando and R. Palmer, Nat. Commun., 2018, 9, 1323 CrossRef CAS PubMed.
- H. Zhai and A. Alexandrova, ACS Catal., 2017, 7, 1905–1911 CrossRef CAS.
- Z. B. Zhang and Z. A. Alexandrova, Acc. Chem. Res., 2020, 53, 447–458 CrossRef CAS PubMed.
- H. Haberland, M. Karrais and M. Mall, Z. Phys. D: At., Mol. Clusters, 1991, 040901 Search PubMed.
- K. Wegner, P. Piseri, H. V. Tafreshi and P. Milani, Cluster beam deposition: A tool for nanoscale science and technology, J. Phys. D: Appl. Phys., 2006, 39(22), 439–459 CrossRef.
- H. Haberland, Gas-Phase Synthesis of Nanoparticles, 2017 Search PubMed.
- A. A. Turkin, M. V. Dutka, Y. T. Pei, D. I. Vainshtein and J. T. M. De Hosson, J. Appl. Phys., 2012, 111, 124326 CrossRef.
- D. Pearmain, S. J. Park, A. Abdela, R. E. Palmer and Z. Y. Li, Nanoscale, Wiley-VCH Verlag GmbH & Co. KGaA, 2017, ch. 1, Print ISBN:9783527340606, Online ISBN:9783527698417, DOI:10.1002/9783527698417.
- M. Dutka, A. A. Turkin, D. I. Vainchtein and J. T. M. De Hossona, J. Vac. Sci. Technol., A, 2015, 3, 031509 CrossRef.
- M. Vaidulych, J. Hanus, J. Kousal, S. Kadlec, A. Marek, I. Khalakhan, A. Shelemin, P. Solar, A. Choukourov, O. Kylian and H. Biederman, Plasma Processes Polym., 2019, 6, 1900133 CrossRef.
- L. Martinez, K. Lauwaet, G. Santoro, J. Sobrado, R. J. Pelaez, V. J. Herrero, I. Tanarro, J. Ellis, G. J. Cernicharo, C. Joblin, Y. Huttel and J. Martin-Gago, Sci Rep., 2018, 8(1), 7250 CrossRef CAS PubMed.
- M. Gracia-Pinilla, E. Martinez, G. Silva-Vidaurri and E. Perez-Tijerina, Nanoscale Res. Lett., 2010, 5, 180 CrossRef CAS.
- K. Rossi, G. G. Asara and F. Baletto, ACS Catal., 2020, 10, 3911–3920 CrossRef CAS.
- F. Baletto, R. Ferrando, A. Fortunelli, F. Montalenti and C. Mottet, J. Chem. Phys., 2002, 116(9), 3856–3863 CrossRef CAS.
- A. L. Garden, A. Pedersen and H. Jónsson, Nanoscale, 2018, 10, 5124–5132 RSC.
- S. G. Lambie, G. R. Weal, C. E. Blackmore, R. E. Palmer and A. L. Garden, Nanoscale Adv., 2019, 1, 2416–2425 RSC.
- J. M. Rahm and P. Erhart, Nano Lett., 2017, 17(9), 5775–5781 CrossRef CAS PubMed.
- D. Nelli, A. Krishnadas, R. Ferrando and C. Minnai, J. Phys. Chem. C, 2020, 124(26), 14338–14349 CrossRef CAS.
- L. D. Marks and L. Peng, Nanoparticle shape, thermodynamics and kinetics, J. Phys.: Condens. Matter, 2016, 28(5), 053001 CrossRef CAS PubMed.
- https://github.com/orgs/kcltscm/teams/lodis, 2019.
- D. Frenkel, B. Smit, J. Tobochnik, S. McKay and W. Christian, Comput. Phys., 1997, 11, 351 CrossRef.
- O. A. Villarreal, Marcos A. Oviedo and E. P. M. Leiva, J. Chem. Theory Comput., 2012, 8, 1744–1749 CrossRef PubMed.
- F. Baletto and R. Ferrando, Rev. Mod. Phys., 2005, 77, 371–423 CrossRef CAS.
- J. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. Kitchin, T. Bligaard and H. Jonsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- D. Esrafilzadeh, A. Zavabeti, A. R. Jalili, P. Atkin, J. Choi, B. Carey, R. Brkljača, A. O'Mullane, M. Dickey, D. Officer, D. MacFarlane, T. Daeneke and K. Kalantar-zadeh, Nat. Commun., 2019, 10, 865 CrossRef PubMed.
- E. García-Suárez and A. Riisager, in Sustainable Catalysis: Energy-Efficient Reactions and Applications, Introduction to Room-Temperature Catalysis, 2018 Search PubMed.
- K. Rossi, L. Pavan, Y. Soon and F. Baletto, Eur. Phys. J. B, 2018, 91, 1–8 CrossRef CAS.
- M. Evans and M. Polyani, Trans. Faraday Soc., 1937, 33, 448–452 RSC.
- F. Calle-Vallejo and M. T. M. Koper, ACS Catal., 2017, 7, 7346–7351 CrossRef CAS.
- A. Peterson and J. Nørskov, J. Phys. Chem. Lett., 2012, 3, 251–258 CrossRef CAS.
- J. Davis, F. Baletto and R. Johnston, J. Phys. Chem. C, 2015, 119, 9703–9709 CrossRef CAS PubMed.
- K. Rossi, L. Bartok-Partay, G. Csanyi and F. Baletto, Sci. Rep., 2018, 8, 1–9 Search PubMed.
- F. Baletto, C. Mottet and R. Ferrando, Phys. Rev. Lett., 2000, 84, 5544 CrossRef CAS PubMed.
- D. Nelli, M. Cerbelaud, R. Ferrando and C. Minnai, Nanoscale Adv., 2021, 3, 836–846 RSC.
- K. A. Fichthorn and T. Yan, J. Phys. Chem. C, 2021 DOI:10.1021/acs.jpcc.0c10159.
- Z. W. Wang and R. E. Palmer, Phys. Rev. Lett., 2012, 108, 245502 CrossRef CAS PubMed.
- E. Ringe, R. P. Van Duyne and L. D. Marks, J. Phys. Chem. C, 2013, 117(31), 15859–15870 CrossRef CAS.
- L. Martinez, M. Díaz, E. Román, M. Ruano, D. P. Llamosa and Y. Huttel, Langmuir, 2012, 28(30), 11241–11249 CrossRef CAS PubMed.
- T. V. Bogdan, D. J. Wales and F. Calvo, J. Chem. Phys., 2006, 124(4), 044102 CrossRef PubMed.
- G. G. Rondina and J. L. Da Silva, J. Chem. Inf. Model., 2013, 53(9), 2282–2298 CrossRef CAS PubMed.
- S. Heiles and R. L. Johnston, Int. J. Quantum Chem., 2013, 113(18), 2091–2109 CrossRef CAS.
- F. Calvo, J. P. K. Doye and D. J. Wales, Chem. Phys. Lett., 2002, 366(1–2), 176–183 CrossRef CAS.
- E. Panizon and R. Ferrando, Phys. Rev. B, 2015, 92(20), 205417 CrossRef.
- A. Loiudice, P. Lobaccaro, E. Kamali, T. Thao, B. Huang, J. Ager and R. Buonsanti, Angew. Chem., Int. Ed., 2016, 128, 5789–5792 CrossRef.
- O. Piqué, F. Vines, F. Illas and F. Calle-Vallejo, ACS Catal., 2020, 10(18), 10488–10494 CrossRef.
- C. Choi, S. Kwon, T. Cheng, M. Xu, P. Tieu, C. Lee, J. Cai, H. M. Lee, X. Pan, X. Duan, I. Goddard, A. William and Y. Huang, Nat. Catal., 2020, 3(10), 804–812 CrossRef CAS.
- K. Jiang, Y. Huang, G. Zeng, F. T. Toma, W. A. Goddard III and A. T. Bell, ACS Energy Lett., 2020, 5, 1206–1214 CrossRef CAS.
- A. J. Garza, A. T. Bell and M. Head-Gordon, ACS Catal., 2018, 8, 1490–1499 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Initial configuration geometries, molecular dynamics simulation set-ups, geometric characterization routines, nanoCHE details for calculating NP activity, considerations on the potential energies of NPs sampled during different formation processes. See DOI: 10.1039/D0NR07889A |
| This journal is © The Royal Society of Chemistry 2021 |