Extended curly arrow rules to rationalise and predict structural effects on quantum interference in molecular junctions

Abstract

The ability to easily and reliably predict quantum interference (QI) behaviour would facilitate the design of functional molecular wires with potential applications in switches, transistors and thermoelectric devices. A variety of predictive methods exist, but with the exception of computationally-expensive DFT-based charge transport simulations, these often fail to account for the experimentally observed behaviour of molecules that differ significantly in structure from alternant polycyclic aromatic hydrocarbons. By considering a range of prior studies we have developed an extension to predictive “curly arrow rules”. We show that, in most cases, these extended curly arrow rules (ECARs) can rationalise the type of QI exhibited by conjugated molecular wires containing heteroatoms, cross-conjugation and/or non-alternant structures. ECARs provide a straightforward “pen-and-paper” method to predict whether a molecular wire will display constructive, destructive or “shifted destructive” QI, i.e. whether or not its transmission function would be expected to show an antiresonance, and if this antiresonance would occur close to the Fermi energy or be shifted elsewhere.

---

Introduction

Quantum interference (QI) is a fascinating phenomenon that is responsible for many of the most promising properties of molecular wires and can result in their behaviour differing significantly from that expected of a macroscale system.^1–4 In a conventional circuit, the combined conductance of two parallel conductors is the sum of their individual conductances. At the molecular scale, interactions between different conductance pathways are subject to quantum effects because propagating electrons behave as waves. Depending on the phase difference between electron pathways, wavefunctions can interfere constructively or destructively, respectively giving higher or lower conductance than would be expected classically.^3,5–8 An archetypal manifestation of QI can be seen when comparing the conductance of otherwise identical molecular wires incorporating para- or meta-substituted benzene rings: para-isomers are consistently more conductive than their meta-analogues.^9–11 Considered simply,^1,12 in the para case, two equivalent pathways exist through the π-system, there is no phase difference and constructive QI (CQI) occurs. In the meta case a longer and a shorter pathway coexist through the π-system, electrons from each pathway have a phase difference and destructive QI (DQI) occurs.

QI can significantly affect the conductance of molecular wires with more elaborate structural features, so it is important to consider QI effects when designing conductive molecules. QI effects are fundamental to some proposed applications of molecular electronics, such as single-molecule transistors,¹³ switches,^14,15 and thermoelectric devices.^16–18 Many qualitative and quantitative methods to predict and explain QI behaviour have been developed. These include curly arrow rules (CARs),^19,20 graphical and topological rules,^21–26 orbital symmetry rules,^27,28 magic ratio rules (MRRs),^3,29–31 QI maps⁸ and charge transport simulations using molecular orbitals based on Hückel (tight-binding) theory and/or density functional theory (DFT).^{1,23,24,32–34}

Short of full DFT-based charge transport simulations, it can be difficult to apply predictive methods to systems that are not based on a bipartite hydrocarbon lattice, such as species containing five-membered rings³² or non-alternant hydrocarbons.³⁵ Heteroatoms can also afford a predictive challenge. Their effect on QI has been investigated in a range of experimental and theoretical studies.^{3,5,10,29,36–42} A general conclusion is that heteroatom substitution has little or no effect on CQI^39–42 but can greatly influence DQI.^10,36,38

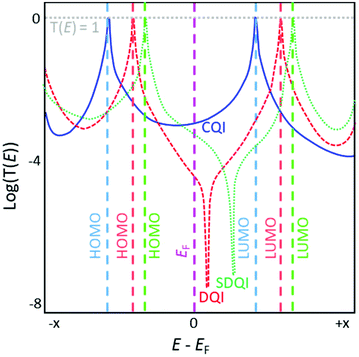
Charge-transport simulations of molecular conductance rely on the calculation of the transmission function of a molecular junction.¹ Transmission functions can also be determined experimentally.⁴³ A calculated transmission function is visualised by plotting the transmission coefficient T(E) of an electron (i.e. the probability of an electron passing across the junction, through the molecule) as a function of the energy of the electron relative to the Fermi energy (E_F) of the system (Fig. 1). The conductance of a molecular junction at a given energy is proportional to T(E). Limitations remain; as stated in a recent review, “While our qualitative understanding of electron transport in molecular junctions has reached a high level (⋯), the quantitative agreement between experiments and theory is often still not firm. (⋯) many unknowns hamper a proper comparison”.³⁴ A prominent problem is that the DFT-derived E_F is not necessarily accurate and may require correction.¹

Fig. 1 Sketch illustrating typical transmission functions of conjugated molecules exhibiting CQI (blue solid curve), DQI (red dashed curve) and SDQI (green dotted curve) on an arbitrary energy scale. Molecular orbital energies for each molecule are indicated using dashed lines in a matching colour, with the Fermi energy (E_F) shown in pink.

In a typical transmission function for a molecular junction, resonances associated with the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) of the molecule appear below and above E_F, respectively, usually in the form of Lorentzian peaks where T(E) = 1 at the maxima. In the low bias regime, the energy of the system usually lies within the HOMO–LUMO gap, close to E_F. The molecular orbital closest in energy to E_F dominates the conductance properties of the junction (e.g. in Fig. 1 the LUMO dominates for the blue curve and the HOMO for the red and green curves); this is often related to the nature of the terminal group that anchors the wire to the electrodes.⁴⁴ DQI features manifest as antiresonances in the transmission function of a molecular junction; these are typically sharp dips where T(E) approaches 0, although sufficiently high σ-conductance can mask these dips.^45,46 Antiresonances often occur close to the energy of the system (i.e. near E_F, e.g. red curve in Fig. 1) meaning the conductance of the junction is necessarily low in the low bias regime due to DQI. Antiresonances are not seen for molecules that exhibit CQI (e.g. blue curve in Fig. 1).

Compared to equivalent hydrocarbons, the inclusion of heteroatoms in molecules (as pendant substituents or within the hydrocarbon lattice) can shift DQI features in the transmission function away from E_F (or beyond the HOMO–LUMO gap), resulting in increased molecular conductance around E_F (i.e. in the low-bias regime) relative to the unsubstituted system (e.g. green curve vs. red curve in Fig. 1).^24,47 We will refer to this phenomenon as shifted destructive quantum interference (SDQI) to distinguish it from ‘conventional’ DQI around E_F. SDQI has been proposed as a design tool for the creation of molecular transistors and rectifiers.⁴⁸ More recently, SDQI has been identified as a potential means of controlling the Seebeck coefficient (S) of molecular wires for thermoelectric applications, for which high S is desirable.⁴⁷S is related to the slope of the transmission function. Molecules that show CQI usually have relatively flat, featureless transmission functions around E_F, and hence they have low S in the low-bias regime (blue curve, Fig. 1). If a DQI feature occurs close to E_F, much higher values of S are possible, but molecular conductance is low and S is expected to be highly sensitive to experimental conditions (red curve, Fig. 1).⁴⁷ The shift of the DQI feature in the case of SDQI could allow for a balance between high conductance and high (relative to CQI molecules), reproducible S (green curve, Fig. 1). A straightforward means to identify molecules for which SDQI is expected is therefore highly desirable, as it would facilitate design strategies for materials for molecular thermoelectrics.¹⁷

“Curly arrows”, which represent the movement of electrons, are absolutely fundamental to the study of organic chemistry.^49,50 They are used to illustrate bond breaking and bond formation, to predict the regiochemistry of reactions and to explain concepts such as conjugation and aromaticity. While curly arrows may appear somewhat abstract to non-chemists, ab initio simulations of the movement of electrons during chemical reactions were recently shown to agree well with curly arrow notation.⁵¹ CARs provide chemists with an intuitive means of interpreting many observed QI effects. While this use of curly arrows is widely accepted in the literature, surprisingly few works set out how curly arrows work in this context.^19,20,52,53 In the interdisciplinary field of molecular electronics this can lead to a ‘language barrier’ between chemists, for whom curly arrows are instinctive, and physicists, who may ignore the simplicity of curly arrows and prefer to interpret QI phenomena in more mathematical terms, such as graphical rules or MRRs. This is despite the predictions of CARs and graphical rules typically agreeing for alternant hydrocarbons (see below). MRRs are best suited to analysis of CQI.⁵⁴ They can impressively predict the ratio of conductances for different connectivities through a molecular core,^18,30 and have been applied to bipartite lattices containing heteroatoms²⁹ and non-alternant hydrocarbons.³¹ However, MRRs require increasing levels of matrix manipulation as the molecular core gets larger and, to our knowledge, have not been applied to systems containing 5-membered heterocycles or cross-conjugation. Charge transport calculations are perhaps the most robust method for predicting QI behaviour, but these are computationally-expensive, particularly when DFT is used to define molecular orbitals. Simpler “pen-and-paper” approaches, such as CARs or graphical rules, remain desirable as an initial screening method for molecular designs.

In this article we present a simple extension to CARs that accounts for heteroatoms, cross-conjugation and non-bipartite structures and can predict CQI, DQI or SDQI. The extension is based on a holistic overview of previous studies of QI behaviour. We will begin by summarising CARs as previously presented and illustrating their broad agreement with many graphical methods for alternant hydrocarbons. Using two examples of heteroatom-containing molecular wire structures from the literature (anthraquinone isomers and substituted, meta-connected oligo(arylene-ethynylenes)), it will be shown that predictions made by CARs can be incorrect for molecules that are more complex than alternant hydrocarbons. Our extended curly arrow rules (ECARs) will then be presented in the context of rationalising the reported behaviour of these species. After establishing ECARs, they will be shown to rationalise observations from a broad selection of previous studies. Some limitations of ECARs will then be discussed and compared to the limitations of other predictive methods. This analysis provides the means to use ECARs as a facile predictive method for QI behaviour in molecular wires.

Results and discussion

Curly arrow rules (CARs)

CARs in molecular electronics are a manifestation of the observation that pathways consisting of alternating single and double (or triple) bonds result in higher conductance than those that do not.^42,55 Hosoya alluded to the use of curly arrows as a means of predicting QI behaviour in 2015.⁵² A more detailed description was presented by Stuyver et al. later that year,¹⁹ with some elaboration in a subsequent publication.²⁰ Stuyver et al. define their CARs as follows:²⁰

“For an alternant hydrocarbon, if the displacement of electrons from one contact to the other cannot be drawn with the help of curly arrows, then [DQI] will take place around the Fermi level”.

These authors also show that for such systems only a single resonance form needs to be considered by demonstrating that if a suitable pathway exists for one resonance structure, a pathway can also be drawn for all other resonance structures.²⁰ Conversely, if a suitable pathway cannot be drawn for a given resonance structure, it cannot be drawn for any other. Further examples of CARs, including application to some non-alternant systems, were presented in a review by Su et al.⁵³

For reasons that will become clear when discussing our extension to CARs, we present a slightly different interpretation of Stuyver et al.'s rule that achieves the same result for alternant hydrocarbons. Rather than displacing electrons between contacts (i.e. the anchoring groups of the molecules), we will instead replace one contact with an electron donating substituent “D” and the second with an electron accepting substituent “A”. If, through curly arrow pushing, a lone pair from D can be delocalised through a conjugated wire to A, such that D gains a positive charge and A gains a negative charge (affording a quinoidal structure through the wire), CQI is expected. In contrast, DQI is expected if the negative charge can be delocalised only onto the backbone of the wire (and not onto substituent A). This D and A approach is conceptually similar to donor-bridge-acceptor (D-B-A) molecules which have been used extensively in studies of photoinduced and thermally induced charge transfer.^56,57Fig. 2 illustrates this modified approach using some of the examples previously described by Stuyver et al.¹⁹

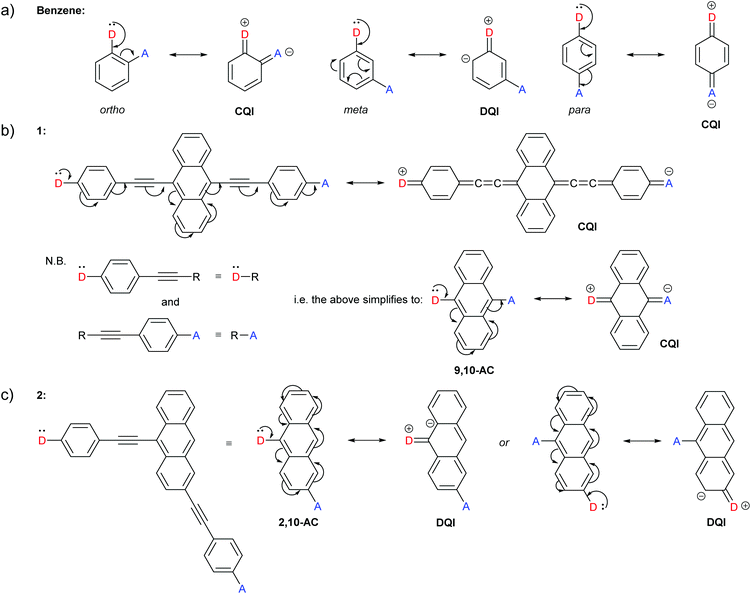Fig. 2 Examples of our interpretation of CARs applied to structures previously presented by Stuyver et al.:¹⁹ (a) Expected QI behaviour for isomeric benzene-based molecular wires; (b) and (c) expected QI behaviour for isomeric anthracene molecular wires 1 and 2 with respective molecular cores 9,10-AC and 2,10-AC. (b) also shows that para-conjugated anchoring units can be treated as large anchoring groups, and (c) shows that the choice of which contact is replaced by D, and which by A, is arbitrary.

The occurrence of DQI through meta-connected benzene, and CQI for ortho- or para-substituted isomers is rationalised with CARs in Fig. 2a. Fig. 2b shows the application of CARs to a 9,10-disubstituted anthracene (AC) centred molecular wire (1), for which CQI is predicted. Fig. 2b also illustrates that only the core hydrocarbon, 9,10-AC, need be considered in cases where CQI would be expected for the remaining structure. As the phenylene–ethynylene units to which the anchor groups of 1 are attached are para-substituted, they can simply be treated as large anchoring units and replaced by D or A with no change to the curly arrow pathways available through the molecular core. This simplification is often used in studies using MRRs.^29,30 This approach is applied to the 2,10-disubstituted AC derivative 2 in Fig. 2c to give the 2,10-AC core and will be used in most of the examples below. Fig. 2c also shows that the choice of which contact is replaced by D, and which is replaced by A, is arbitrary; neither alternative permits delocalisation of the D lone pair to A, and DQI is expected.

Relation of CARs to graphical rules

Graphical rules for QI can be expressed in several ways. Here, three graphical methods will be related to CARs to highlight the similarities between the approaches despite the different language used. Many rules for alternant hydrocarbons divide the carbon framework of a molecule into two categories, e.g. “starred” and “unstarred” or “a” and “b” atoms, in which starred (a) atoms are bonded only to unstarred (b) atoms and vice versa. DQI is predicted for all connectivities between atoms of the same category.²⁵ This can also be expressed in terms of walks between atomic sites: DQI is expected when there are only even-length walks between anchoring points.²⁵ For alternant hydrocarbons this corresponds to walks between atoms of the same category. Fig. 3a shows anthracene and naphthalene as examples using the starred/unstarred convention (IUPAC nomenclature for different substituent positions is shown for reference). In order to delocalise a D lone pair onto an A group, at least one pathway of alternating double and single bonds, beginning and ending with double bonds, must exist between the contact points, e.g. the 9,10-connectivity (unstarred to starred) shown for 9,10-AC in Fig. 2b. The specific pathway taken can vary with resonance structure. A pathway of this type exists in all cases where one atom from each category is selected. No connectivities between atoms of the same category satisfy this criterion, and therefore CARs agree with the graphical rule and predict DQI for these cases, e.g. the 2,10-connectivity (unstarred to unstarred) shown for 2,10-AC in Fig. 2c.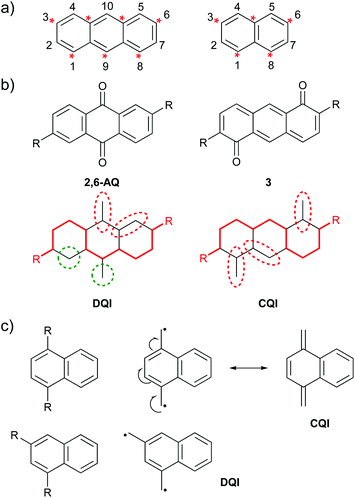

Fig. 3 Examples of graphical rules for predicting QI behaviour: (a) IUPAC substituent numbering and the starred/unstarred convention applied to anthracene (left) and naphthalene (right); (b) above: structures of isomeric species 2,6-AQ and 3 used by Markussen et al. when defining their graphical rule,²¹ below: Markussen diagrams for the above species; (c) diradical stability approach used by Tsuji et al.²⁶ illustrated using isomeric naphthalene derivatives.

Markussen et al. proposed a graphical approach in which a continuous path is drawn between the anchoring points (red line in Fig. 3b).²¹ Any atoms outside this pathway are paired with neighbours where possible (dashed red ovals in Fig. 3b) and if unpaired atoms remain (dashed green circles in Fig. 3b), DQI is predicted. Fig. 3b shows two of the species that were used to explain this rule. For 2,6-connected anthraquinone (2,6-AQ) it is not possible to connect the anchoring sites using a pathway that does not leave unpaired atoms. In contrast, for the isomeric species 3, pathways exist in which all atoms not involved can be paired with a neighbour. The pathway used to connect the anchoring sites in 3 consists of alternating double and single bonds, beginning and ending with double bonds – i.e. CARs would predict CQI as a D lone pair can be delocalised to an A unit. No such pathway exists for 2,6-AQ, for which DQI is predicted, i.e. CARs agree with the graphical rule.

The final graphical approach we will consider is the link between QI and diradical stability proposed by Tsuji et al.²⁶ This method is very similar to CARs. Methylene radicals (CH₂˙) are attached at the two anchoring positions. If the two radicals can be delocalised such that a closed-shell system is formed, CQI is predicted, whereas if they cannot, and the structure must remain a diradical, DQI is predicted. Fig. 3c illustrates this for two connectivities of naphthalene described by Tsuji et al.²⁶ For 1,4-connectivity (top), the resulting diradical can be converted to a closed-shell structure (CQI), whereas for 1,3-connectivity (bottom) it cannot (DQI). Once again, CARs agree with the graphical rule. In the 1,4-connected case, a pathway exists between the anchoring sites consisting of alternating double and single bonds, beginning and ending with double bonds, and CARs would predict CQI, whereas such a pathway does not exist in the isomeric 1,3-connected case and CARs would predict DQI.

The above examples were selected to illustrate that CARs and graphical rules are often manifestations of similar effects, presented using different languages. The extension to CARs we expound below considers the chemical properties of different atoms, which cannot be fully captured using graphical rules alone, and as such will not agree with these graphical rules to the same extent as the examples given above.

Breakdown of CARs

CARs as presented by Stuyver et al.²⁰ hold qualitatively for alternant hydrocarbon frameworks and can be applied to many other molecules. However, the introduction of cross-conjugation and heteroatoms can cause this approach to break down, as illustrated by the following examples.

QI effects in 2,6-disubstituted anthracene (AC) and anthraquinone (AQ) species have been the subject of several experimental studies,^58–60 and behave as would be expected based on CARs. Alqahtani et al. recently studied isomeric 2,6- and 2,7-connected AC and AQ based molecular wires computationally.⁶¹ Their charge transport calculations showed significant differences in the transmission functions depending on the connectivity of the anchoring groups (Fig. 4a). For AC, an alternant hydrocarbon, behaviour is as expected based on CARs, as shown in Fig. 4b. For three different anchoring substituents (one example shown in Fig. 4a), the transmission function of the 2,6-disubstituted isomer (i.e. para-like connectivity), 2,6-AC, shows relatively high conductance in the HOMO–LUMO gap with no DQI feature. In contrast, that of the 2,7-disubstituted isomer (i.e. meta-like connectivity), 2,7-AC, shows lower conductance in the HOMO–LUMO gap with a clear antiresonance feature, typical of DQI. Similar behaviour was observed for analogous 9,10-dihydroxyanthracene species, although in this case the DQI antiresonance was shifted to higher energy than the AC analogue; the authors attributed this to an electrostatic gating effect caused by the oxygen atoms in these substituents.⁶¹

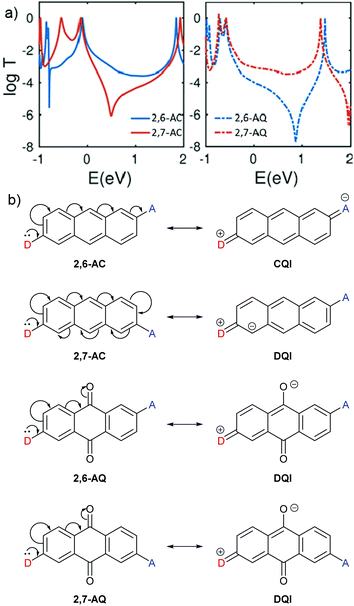Fig. 4 (a) Calculated transmission functions of isomeric ethynyl-anchored anthracene (AC, left) and anthraquinone (AQ, right) molecular wires adapted with permission from Alqahtani et al.,⁶¹ © 2018 Wiley–VCH Verlag GmbH & Co. KGaA, Weinheim; (b) structures of the AC and AQ cores of these wires, and application of CARs to these systems. Note that D and A have each been used to replace an ethynyl anchoring unit as described above (e.g.Fig. 2).

The analogous AQ systems, however, do not follow CARs. A lone pair from a D group at one anchoring point cannot be delocalised to an A group at the other anchoring point for either 2,6-AQ or 2,7-AQ, due to the cross-conjugated nature of AQ (Fig. 4b). In each case, the furthest site from the D group to which its lone pair can be delocalised is the oxygen atom of the carbonyl para to D. In the same way as a D lone pair cannot be delocalised to a meta A group in the case of benzene, charge cannot be delocalised to the carbonyl meta to D in AQ. While the transmission functions of 2,6-AQ show the expected DQI feature for all three anchoring methods, those of 2,7-AQ do not show any DQI within the HOMO–LUMO gap and resemble more closely those of 2,6-AC (for the transmission function in Fig. 4a, the DQI antiresonance appears to be shifted beyond the LUMO to ca. 2 eV). These observations led the authors to conclude that “CARs break down in molecular junctions formed by cross-conjugated anthraquinone”.⁶¹ To our knowledge, these theoretical results are yet to be confirmed in experimental conductance studies.

Jiang et al. reported unusual QI behaviour in a combined experimental and computational study of meta-connected oligo(phenylene-ethynylene) (OPE) molecular wires substituted with methoxy groups at different positions on the central ring.³⁶ Here we will name their structures based on the relationship between the methoxy substituent and the two phenylene–ethynylene units bearing the sulfur-based anchoring groups; either ortho to one and para to the other (o,p-MeO), meta to both (m,m-MeO) or ortho to both (o,o-MeO) (Fig. 5a). As it is an extension of meta-linked benzene, the parent unsubstituted wire, m-OPE3 (3 refers to the number of benzene rings in the oligomer), would be correctly expected, based on CARs, to exhibit DQI and have low conductance (Fig. 5b). The addition of a methoxy substituent to any of the three positions has no effect on the inability to delocalise a lone pair from a D group in one anchoring position to an A group at the other. Therefore, according to CARs the three substituted wires (o,p-MeO, m,m-MeO and o,o-MeO) would each be expected to have similar properties to m-OPE3, i.e. show DQI and conduct poorly. However, charge transport simulations and scanning tunnelling microscopy break junction (STM-BJ) experiments showed that o,p-MeO is substantially more conductive than m-OPE3 or m,m-MeO, which have very similar properties.³⁶ The results for o,o-MeO are insightful; experimentally its conductance is lower than m,m-MeO and m-OPE3, but it can be shown computationally that its conductance can be “switched on” by altering the conformation of the methoxy substituent to a sterically unfavourable position in which an oxygen lone pair can interact with the π-system. This geometry gives conductance comparable to o,p-MeO. The authors rationalise these results in terms of MRRs, and show that for o,p-MeO and “switched on” o,o-MeO, the DQI feature in the transmission function is perturbed away from the centre of the HOMO–LUMO gap and no longer coincides with E_F.

Fig. 5 (a) Structures of methoxy-substituted meta-OPE3 wires studied by Jiang et al.;³⁶ (b) application of CARs to the parent unsubstituted wire m-OPE3.

Similar behaviour has been reported for meta-oligo(arylene ethynylene)s (OAEs) with a central pyridine ring (discussed in more detail below; see Fig. 8). If the pyridine nitrogen is in the m,m position, conductance is similar to the parent m-OPE3, whereas higher conductance is observed for the o,p and o,o isomers.¹⁰ The conformational switching described for the methoxy species in Fig. 5a is not observed for pyridine, where steric effects are not a factor.

Extended curly arrow rules (ECARs): repairing the breakdown

In the above examples, the molecules that do not follow CARs contain oxygen or nitrogen heteroatoms. For the AQ species⁶¹ the heteroatoms are located in electron-withdrawing carbonyl groups, whereas for the methoxy-substituted OPEs³⁶ the ether oxygen atoms are electron donating. In the pyridine series¹⁰ the pyridine nitrogen is electron-withdrawing. The observed trends can be explained by the following extended curly arrow rules (ECARs) for QI around E_F:

Rule 1. Identify the two anchoring units of a molecular wire and replace one with a donor group D and the other with an acceptor group A. If the D lone pair can be delocalised onto A using curly arrows, CQI is expected, if not DQI is expected.

Rule 2. If DQI is expected, identify any electron-withdrawing groups (EWGs) or electron-donating groups (EDGs) present in the molecular wire. If EWGs are present, replace each anchor with D. If a lone pair from each D can be independently delocalised to the same EWG, DQI is expected to be shifted away from E_F (SDQI). If EDGs are present, replace each contact with A. If a lone pair (or negative charge) from the same EDG can be independently delocalised to each A, SDQI is expected. Otherwise, DQI is expected around E_F.

Rule 1 (ECAR-1) is a variation of CARs as presented previously (using D and A groups), and Rule 2 (ECAR-2) is the extension to give ECARs. Fig. 6a shows the application of ECAR-2 to the AQ derivatives discussed above (Fig. 4b).⁶¹ The carbonyl groups are EWGs, therefore each anchoring unit is replaced by D. For 2,6-AQ, the lone pair of each D can be delocalised to an EWG, but as each is delocalised to a different EWG, DQI is still expected. However, for 2,7-AQ, the lone pair of each D can be independently delocalised to the same EWG (but not to the other EWG). This situation meets the ECAR-2 criteria for shifting of DQI (SDQI), as observed in the charge transport calculations.⁶¹Fig. 6b illustrates the region of the AQ π-system into which each D can delocalise electrons using coloured boxes. For 2,6-AQ, for which DQI is predicted computationally, there is a node between the two regions. For 2,7-AQ, for which the DQI antiresonance is shifted away from E_F, the two regions partially overlap at a carbonyl functionality, i.e. the two D groups are cross-conjugated with the same carbonyl. The relationship between cross-conjugation and ECARs is discussed further below. Furthermore, the previously-mentioned shifted antiresonance observed for 2,7-anchored 9,10-dihydroxyanthracene,⁶¹2,7-AC(OH)₂, can be readily interpreted as SDQI using the hydroxyl groups as EDGs. As shown in Fig. 6c, the lone pair of the 9-hydroxy substituent can be delocalised to an A unit in either anchoring position.

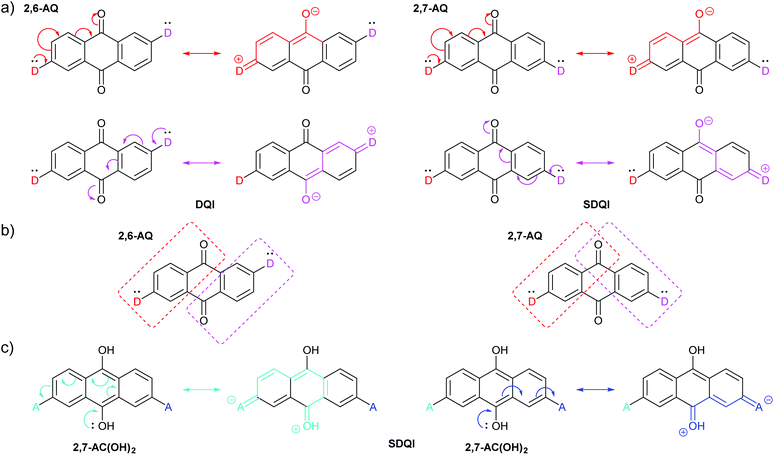Fig. 6 (a) Applying ECAR-2 to isomeric AQ derivatives investigated by Alqahtani et al.;⁶¹ (b) the π-systems conjugated to the two D-groups of 2,6-AQ do not overlap, while those of 2,7-AQ overlap at the carbonyl para- to both D groups; (c) applying ECAR-2 to the 9,10-dihydroxyanthracene derivative 2,7-AC(OH)₂, previously investigated by Alqahtani et al.⁶¹

Fig. 7 shows the application of ECAR-2 to the methoxy-substituted meta-OPE3s discussed above (Fig. 5).³⁶ The methoxy groups are EDGs, so as for dihydroxyanthracene (Fig. 6c), each contact is replaced by A. From this point, rather than showing initial structures repeatedly in figures, the independent curly arrows associated with each A (or D) group will be shown in different colours on the same central structure, with matching coloured arrows indicating the corresponding resultant structures to either side or above and below. Any bonds involved in the curly arrow pathway will also be shown in the matching colour in the resultant structure. ECARs correctly predict SDQI for o,p-MeO and DQI for the m,m-MeO. SDQI is predicted for o,o-MeO, but the curly arrow pathway shown in Fig. 7 requires an oxygen lone pair in the methoxy group to be correctly aligned with the OPE π-system. As this was shown not to be due to sterics,³⁶ this new analysis is consistent with the experimental observation of DQI.

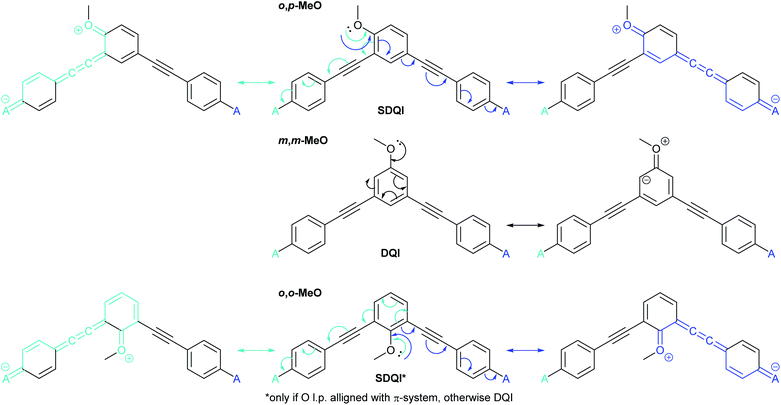Fig. 7 Applying ECAR-2 to methoxy-substituted meta-OPE3 wires studied by Jiang et al.³⁶ Here the anchoring units are shown in full to facilitate comparison with Fig. 5.

Fig. 8 shows the equivalent rationalisation for pyridine-centred OAEs.¹⁰ Here the pyridine nitrogen atom can act as an EWG, so each contact is replaced by D. ECAR-2 predicts SDQI for the more conductive isomers, o,p-Py and o,o-Py, and DQI for the less conductive isomer, m,m-Py (and the parent m-OPE3). This is consistent with their relative experimental and calculated conductances, and their reported transmission functions.¹⁰

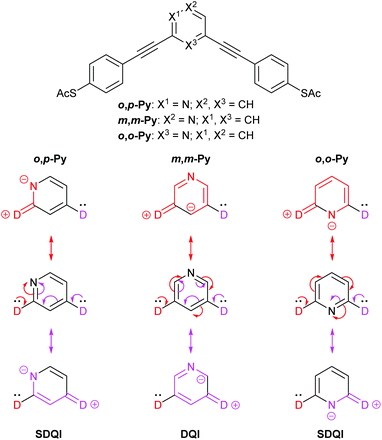Fig. 8 Structures of pyridine-centred OAE3 wires studied by Liu et al.,¹⁰ and application of ECAR-2 to the molecular cores (i.e. the para-conjugated phenylene–ethynylene groups are treated as part of the anchoring units).

For both the methoxy (Fig. 7) and pyridine series (Fig. 8), the positions at which heteroatom substitution causes SDQI correspond to those predicted to have a shifted DQI feature in a computational study by Garner et al.²⁴ Their study also showed that the direction and relative magnitude of DQI shifts for substituted alternant hydrocarbons can be predicted using a graphical method (similar behaviour has also been discussed elsewhere^48,62). For simple functionalised aromatics of this type, this result represents an advantage of the graphical method²⁴ over ECARs, but it will be shown below that ECARs are applicable to a wider variety of chemical structures than the graphical method.

Further examples where ECARs apply

Having established and demonstrated ECARs, the following sections will show their applicability to a range of molecules studied previously. The examples selected are by no means exhaustive but were chosen to account for a variety of structural features that deviate from simple polycyclic aromatic hydrocarbon systems.

Heteroatom effects in polycyclic aromatics

Sangtarash et al. used a tight binding model and DFT-based charge transport calculations to study several polycyclic aromatic hydrocarbons with different connectivities. They were compared to derivatives in which a single C–H site was replaced by nitrogen.⁴⁷ Heteroatom substitution had no effect on connectivities for which CQI was observed. For connectivities where a DQI feature was observed for the parent hydrocarbon, it was also observed for the heteroatom-substituted analogue. However, for some connectivities the DQI feature was shifted away from E_F (i.e. SDQI). For a general system, the sign of the Seebeck coefficient at E_F, and hence the direction in which the antiresonance is shifted, was related to both the connectivity of the system and the nature of the heteroatom (electron donating or withdrawing).⁴⁷ It is significant that for all of the cases where SDQI was observed, it is possible to independently delocalise a lone pair from a D at each anchoring position to the nitrogen heteroatom (cf. the pyridine-containing OAEs in Fig. 8), i.e. ECARs agree with the calculations. Similarly, where the DQI feature does not shift, ECARs predict DQI. As an example, Fig. 9 shows the application of ECARs to three 4-azapyrene (4AP) species studied by Sangtarash et al.⁴⁷ using the nitrogen atom as an EWG for ECAR-2. CQI, DQI and SDQI are predicted in agreement with the calculated transmission functions (Fig. 9, inset). This further confirms the applicability of ECARs to heteroatom-containing analogues of alternant hydrocarbons, and emphasises the importance of accounting for the chemical properties of heteroatoms.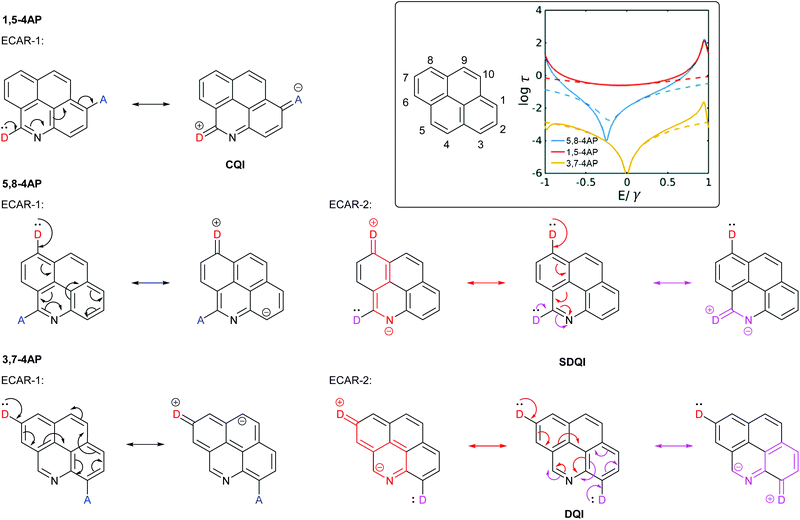

Fig. 9 Application of ECARs to 4-azapyrene (4AP) molecular cores studied by Sangtarash et al.⁴⁷ Inset: IUPAC substituent numbering for pyrene and calculated transmission functions of the 4AP species adapted from Sangtarash et al.⁴⁷ with permission from the PCCP Owner Societies (solid and dashed lines represent different calculation methods).

Five-membered rings

Alanazy et al. compared OAE3 molecular wires with central 9,9-dimethylfluorene or fluorenone groups and 2,7- (para-type) or 3,6- (meta-type) connectivity (Fig. 10a).³⁸ As these, and species from separate studies discussed below, have cores consisting of bridged biphenyls with para- or meta-type connectivity, the molecular cores will be referred to as p-BP-X and m-BP-X, respectively, where X indicates the functionality bridging the biphenyl (BP). For either pyridyl or thiol anchoring groups, the conductance of 2,7-connected p-BP-CMe₂ and p-BP-CO was similar, as would be expected based on ECAR-1, which predicts CQI for any X unit (Fig. 10b). With 3,6-connectivity, conductance was low in the case of m-BP-CMe₂, but close to that of the p-BP-X series for m-BP-CO. CARs, as previously presented, would suggest poor conductance for both m-BP-X cores, and indeed the authors state “no bond-alternation path directly connects the [anchors]”.³⁸ Based on computational studies, they conclude that “unlike a methylene carbon, the carbonyl group provides significant coupling between the two phenyl rings”.³⁸ This is precisely the implication of ECARs, which agree with the experimental observation. The fluorenone carbonyl is an EWG which can independently accept a lone pair from a D group placed in either anchoring position (Fig. 10c) so SDQI is expected for m-BP-CO based on ECAR-2. No EWG or EDG is present when dimethylfluorene is the central aryl unit, so DQI is expected for m-BP-CMe₂. The good agreement between ECARs and the experimental results establishes that ECARs are applicable not only to molecules comprised of six-membered rings but also to those including five-membered rings.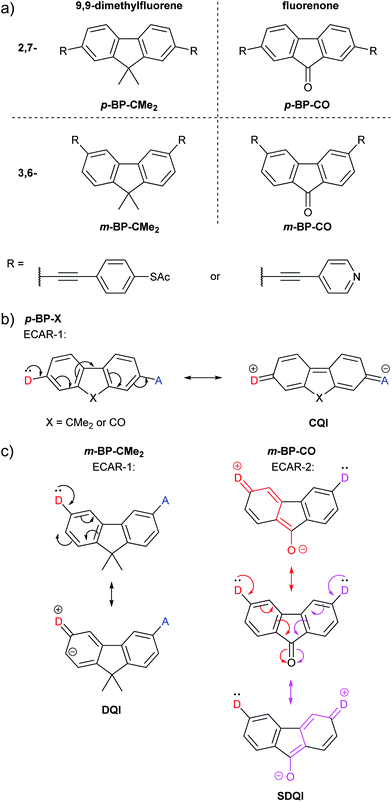

Fig. 10 (a) Structures of 9,9-dimethylfluorene and fluorenone wires studied by Alanazy et al.;³⁸ (b) application of ECAR-1 to the 2,7-connected core systems p-BP-X; (c) application of ECARs to the 3,6-connected core systems m-BP-X.

In another study of species containing five-membered rings, Zhang et al. used benzodithiophene (BDT) derivatives to investigate the effect of different types of cross-conjugation on QI.⁶³ They studied two isomeric BDT wires which we will refer to as trans-BDT and cis-BDT (their thiophene sulfur atoms are, respectively, para or meta to one another relative to the central benzene ring) and the quinone derivative of the trans isomer, trans-BDTQ (Fig. 11). The observed conductance trend, trans-BDT > cis-BDT > trans-BDTQ, led Zhang et al. to conclude that “quinones suppress conductance more than cross-conjugation alone”.⁶³Fig. 11 shows that ECARs rationalise the observed results and are compatible with five-membered heterocycles. ECARs predict CQI for trans-BDT, SDQI for cis-BDT and DQI for trans-BDTQ (D–A delocalisation according to ECAR-1 is not possible for trans-BDTQ; this is not shown). The corresponding behaviour is observed in the transmission functions presented by Zhang et al.;⁶³ no DQI feature is observed for trans-BDT, a highly shifted DQI feature is observed for cis-BDT (close to the HOMO resonance) and a DQI feature is observed close to E_F for trans-BDTQ. Li et al. have reported a “two-pathway” tight-binding approach that can reproduce the shifted DQI feature observed for cis-BDT and its reduced conductance relative to trans-BDT,⁴⁰ but this method has not been extended to quinoidal systems. Note that ECARs would predict SDQI for cis-BDTQ (Fig. 11), which was not included in the study by Zhang et al. This is in contrast to the authors’ conclusion that “quinones are (⋯) a poor testbed for tuning QI effects (⋯) because their strong electron-withdrawing nature places a deep, destructive feature near E_Firrespective of other functional groups”.⁶³ This example further demonstrates the importance of isomerism observed for the BDT species and the AQ wires discussed above (Fig. 6).

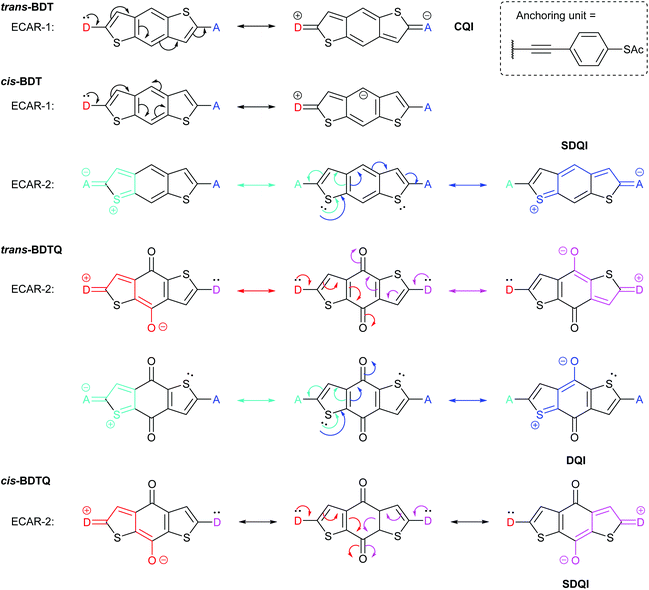Fig. 11 Application of ECARs to the core of BDT and BDTQ systems, some of which were studied by Zhang et al.⁶³ For cis-BDT, ECAR-2 is demonstrated using one of two equivalent sulfur atoms as the EDG.

Zhang et al. reported a QI-based molecular switch using a diketopyrrolopyrrole (DPP) derivative.⁶⁴ The two isomeric wires shown in Fig. 12a were studied: one is alkylated on both nitrogen atoms and the other is alkylated on one nitrogen and one oxygen atom. We will refer to these as N,N-DPP and N,O-DPP, respectively. Both isomers have a conjugated pathway between their anchoring groups (i.e. ECAR-1 would predict CQI, not shown) and their experimental conductances are high and lie within error of one another. The non-alkylated nitrogen of N,O-DPP can be easily and reversibly protonated, affording a substantially reduced (ca. 17 times lower) molecular conductance for protonated N,O-DPP (control experiments with N,N-DPP, which does not have a basic nitrogen atom, show no change within error).⁶⁴ The authors attribute this reduced conductance to the formation of a cross-conjugated resonance structure, associated with DQI, after protonation (Fig. 12b). DFT indicates the cross-conjugated form is dominant⁶⁴ (note the favourable formation of a 6 π e⁻ aromatic pyrrole ring). In the linearly conjugated form, the positive charge remains on the protonated nitrogen and the fully conjugated pathway of the neutral species is still available (CQI). For the favoured cross-conjugated form, ECARs can predict SDQI using the carbonyl group as an EWG (but not the N or O lone pairs as EDGs), as shown in Fig. 12c. SDQI, rather than DQI, agrees well with the calculated transmission function (which shows a relatively shallow dip shifted away from E_F) and the still relatively high experimental conductance versus the parent non-protonated N,O-DPP. Contributions from other fully conjugated resonance structures may also influence conductance behaviour, but once again ECARs are applicable to structures containing heteroatoms and five-membered rings.

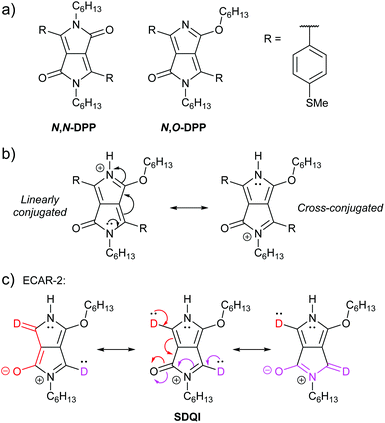Fig. 12 (a) Structures of DPP wires studied by Zhang et al.;⁶⁴ (b) resonance stabilisation of protonated N,O-DPP; (c) application of ECAR-2 to the stable cross-conjugated resonance structure of the protonated N,O-DPP core.

Acyclic pathways

A study of a photo/thermoswitchable wire based on dihydroazulene (DHA) and vinylheptafulvene (VHF) by Huang et al.⁶⁵ provides an opportunity to test the applicability of ECARs to an acyclic cross-conjugated conductance pathway. The studied wire has three key states which can interconvert under appropriate stimulus (Fig. 13a): two isomeric DHA forms with anchoring groups in the 2,6- or 2,7-positions (2,6-DHA and 2,7-DHA, respectively) and an intermediate ring-opened VHF form. The VHF form has four possible isomers based on the geometry of the alkene substituents. These isomers behave equivalently under ECARs analysis, so here only the s-cis E isomer⁶⁵ will be considered (VHF in Fig. 13a). (We note that different deviations from coplanarity may affect the relative properties of these isomers.) Unlike the aromatic cores described previously (and azulene, below), different stable resonance forms do not exist for the DHA and VHF cores due to the sp³ carbons in the 5-membered ring. The ring system also deviates from planarity.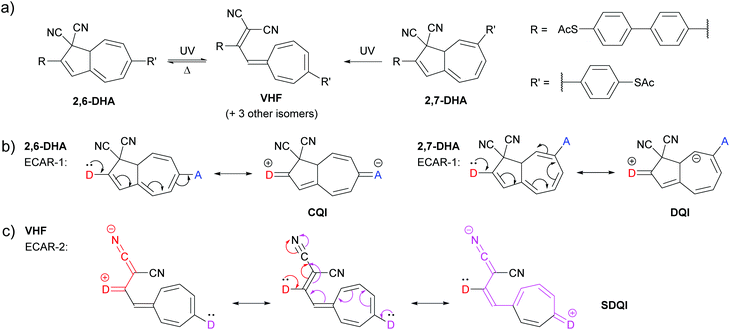

Fig. 13 (a) Structures and switching mechanisms of switchable forms of a molecular DHA/VHF wire studied by Huang et al.;⁶⁵ (b) application of ECAR-1 to the DHA isomers; (c) application of ECAR-2 to the VHF form.

Reversible stimulus-induced switching between 2,6-DHA (high conductance) and VHF (low conductance) was observed using the mechanically controlled break junction (MCBJ) method. Starting from 2,7-DHA (very low conductance) it was possible to switch irreversibly to VHF and then reversibly to 2,6-DHA. The relative conductances of the three states were rationalised using Markussen diagrams²¹ and DFT-based charge transport simulations.⁶⁵ The high conductance of 2,6-DHA was attributed to an absence of DQI (we consider this equivalent to CQI) and the very low conductance of 2,7-DHA to DQI. In relation to the low conductance of VHF the authors discuss a “shifted interference” feature, stating that the “anti-resonance is (⋯) shifted away from the middle of the band gap due to the electron-accepting character of CN”,⁶⁵ This is, in effect, a description of SDQI which is notably attributed to the influence of EWGs.

ECARs agree with the above rationalisation. As shown in Fig. 13b, CQI is predicted for 2,6-DHA using ECAR-1, whereas DQI is predicted for 2,7-DHA. While EWGs are present in 2,7-DHA, an SDQI pathway cannot be generated according to ECAR-2 as the nitrile groups are separated from the conjugated pathway by an sp³ carbon atom. For VHF, ECAR-2 predicts SDQI: D groups in either anchoring position can donate a negative charge to either nitrile group (one example is shown in Fig. 13c).

Non-alternant hydrocarbons

Non-alternant structures can also cause CARs to break down, but ECARs can help to rationalise the observed behaviour. The most prominent example of a non-alternant hydrocarbon that has been the subject of several molecular conductance studies, and considerable debate, is azulene. Xia et al. investigated the conductance of the four azulene molecular wires with thiochroman anchors shown in Fig. 14a.³⁵ Their structures vary in the position of the anchoring groups and will be referred to based on the positions of these substituents; some species also contain methyl substituents for synthetic reasons. The IUPAC substituent numbering for azulene is shown in Fig. 14b. The authors’ expectation, based on graphical rules²¹ was that 1,3-Az and 5,7-Az would exhibit DQI and conduct poorly relative to 2,6-Az and 4,7-Az, for which DQI was not predicted. ECAR-1 would predict the same, as shown in Fig. 14d. However, all four molecules were observed to show respectable molecular conductance, with 1,3-Az and 2,6-Az the most conductive of the series, followed by 4,7-Az, and 5,7-Az the lowest. The authors concluded that the graphical rules did not apply to non-alternant hydrocarbons and stated “Breakdown of Interference Rules of Azulene” in the title of the study.³⁵

Fig. 14 (a) Structures of azulene-based molecular wires studied by Xia et al.;³⁵ (b) IUPAC substituent numbering for azulene and formation of a zwitterionic resonance form; (c) calculated transmission functions of wires with these azulene cores reprinted with permission from Xia et al.³⁵ Copyright 2014 American Chemical Society; (d) application of ECAR-1 to the neutral resonance form of the azulene wires; (e) application of ECAR-1 to selected zwitterionic resonance forms of the azulene wires for which CQI pathways can be drawn.

Schwarz et al. studied analogues of 1,3-Az, 2,6-Az and 4,7-Az with (4-thioacetyl)phenylethynyl anchoring units and different alkyl substituents using an MCBJ at low temperature under different biases.⁶⁶ They found that the 2,6- and 4,7-connectivities were the most conductive and the 1,3-connectivity showed step-like features in its I–V curve. They attributed the difference in conductance behaviour to a difference in conductance channels rather than QI effects. The difference in trends between the two series could relate to anchoring group effects.

Xia et al. observed no DQI feature in the HOMO–LUMO gap of the transmission function for 2,6-Az and 4,7-Az, whereas for 1,3-Az and 5,7-Az a DQI feature was observed in the HOMO–LUMO gap, albeit shifted away from E_F (Fig. 14c).³⁵ A shifted DQI feature is also seen for the 1,3-linked wire studied by Schwarz et al.⁶⁶ This implies that CQI occurs for 2,6-Az and 4,7-Az and SDQI occurs for 1,3-Az and 5,7-Az. We will now try to account for this behaviour using ECARs.

The high dipole moment of azulene^67,68 is indicative that its zwitterionic resonance forms, consisting of a fused cyclopentadienyl anion and a tropylium cation (each stable 6 π e⁻ aromatic species), make a significant contribution to its electronic structure (Fig. 14b). Fig. 14e shows the application of ECAR-1 to the azulene wires reported by Xia et al. in selected zwitterionic resonance forms. Unlike neutral species, in the zwitterionic case the choice of resonance form can make a difference to the behaviour predicted by ECARs, as the mobile charges can be considered to act as either an EDG or an EWG for ECAR-2. Many zwitterionic resonance forms are possible. Here we will consider forms that retain the formal aromaticity of both charged rings and should therefore be most stable (numbered i–viii in Table 1). The positive or negative charge cannot be moved away from its initial ring, or onto the transannular bond, without causing one ring system to lose the favourable 6 π e⁻ configuration. Therefore, to retain aromaticity in both rings requires that the negative charge be located in the 1-, 2- or 3-position, and the positive charge in the 4-, 5-, 6-, 7- or 8-position (note that only the 4-, 6- and 8-positions are possible when the negative charge is in the 2-position). For species other than 4,7-Az, combinations which are equivalent due to symmetry exist. These are noted in Table 1 when both are shown, but they will not be counted separately in the following discussion.

Table 1 ECARs QI predictions for selected zwitterionic resonance forms of azulene wires studied by Xia et al.³⁵ Where two of the shown resonance forms are equivalent by symmetry (excluding any methyl substituents), this is noted for the second incidence

Core resonance form		QI type predicted by ECARs
		1,3-Az	2,6-Az	4,7-Az	5,7-Az
a SDQI is predicted using ECAR-2 when the anchoring units are replaced with A groups. b SDQI is predicted using ECAR-2 when the anchoring units are replaced with D groups.
i		SDQI (A)^a	SDQI (D)^b	SDQI (D)	SDQI (A/D)
ii		SDQI (A)	SDQI (D)	SDQI (D)	SDQI (D)
iii		SDQI (A)	DQI	SDQI (D)	CQI
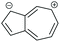
iv		SDQI (A)	CQI	SDQI (D)	SDQI (D)
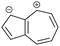
v		SDQI (A)	SDQI (D)	CQI	SDQI (A/D)
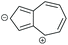
vi		CQI	DQI	DQI	SDQI (A)
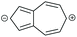
vii		CQI	DQI	DQI	SDQI (A)
viii		≡ vi	≡ vi	CQI	≡ vi

---

For each of the four connectivities, at least one zwitterionic resonance form allows delocalisation of a D lone pair from one anchoring position to an A unit at the other (see examples in Fig. 14e), and hence a pathway exists for which CQI is predicted. For 1,3-Az, ECARs predict CQI for zwitterionic resonance forms vi and vii in which the negative charge is in the 2-position. For 2,6-Az, the negative charge must be in the 1-position and the positive charge in the 7-position (form iv) for a CQI pathway to exist. CQI is predicted for 4,7-Az for resonance forms v and viii, with the positive charge in the 8-position, and for 5,7-Az only for form iii, when the positive charge is in the 6-position and the negative charge is in the 1-position. A range of pathways exist for all structures for which it is possible to independently delocalise either: (i) a D lone pair from each anchoring position to the positive charge (EWG), or (ii) the negative charge (EDG) to A groups in each anchoring position, such that ECAR-2 predicts SDQI (summarised in Table 1). For 1,3-Az and 5,7-Az this is possible for all zwitterionic resonance forms for which CQI is not predicted, so DQI is not predicted in any case. DQI is predicted for two zwitterionic resonance forms of 4,7-Az (vi and vii) and three of 2,6-Az (iii, vi and vii), and SDQI in the remaining cases. For 1,3-Az all SDQI pathways rely on delocalisation of the negative charge to A units. For 2,6-Az and 4,7-Az all SDQI pathways involve delocalisation of D lone pairs to the positive charge. SDQI pathways for 5,7-Az are possible using either the positive or negative charge, in approximately equal proportions.

The experimental results for azulene derivatives can therefore be interpreted as follows based on ECARs and the reported transmission functions.³⁵ The properties of 2,6-Az and 4,7-Az are consistent with CQI. For these species, ECAR-1 predicts CQI for the neutral resonance structures. CQI appears to dominate over SDQI and DQI contributions from the zwitterionic resonance forms. The properties of 1,3-Az and 5,7-Az are consistent with SDQI. ECAR-1 predicts DQI for neutral resonance structures, but ECAR-2 predicts either CQI or SDQI for all of their zwitterionic resonance forms, which appears to be sufficient to result in SDQI overall. The implication is that CQI in the neutral state cannot be inhibited by DQI (and SDQI) in the zwitterionic state, but that DQI in the neutral state can be suppressed by CQI and SDQI in the zwitterionic state to give SDQI overall. Regardless of the resonance form they occur in, the more conductive pathways dominate the properties of the wire (cf. the contribution of σ-channels overcoming DQI features from π-channels in overall transmission functions,⁴⁵ although in this case sharp SDQI resonances are still present).

A significantly larger shift away from E_F in the DQI feature is observed for 1,3-Az than for 5,7-Az.³⁵ The authors offer no explanation for this shift in the transmission functions. The following observations based on ECARs provide some insight. The resonance forms of 1,3-Az for which SDQI is predicted differ only in the tropylium ring, which is not involved in the delocalisation of the negative charge to A groups. The negative charge is localised on two symmetry-equivalent positions, and the EDG-to-A pathways are the same in all cases. For 5,7-Az the SDQI resonance forms are much more varied and involve both EDG-to-A pathways, and D-to-EWG pathways, with the charges involved located at different inequivalent positions. The different charge locations could result in opposite shifts in the DQI feature, as seen computationally for substituted meta-connected benzenes,²⁴ and therefore result in a smaller overall shift of the DQI feature away from E_F for 5,7-Az. Note also that 1,3-Az has more resonance forms for which CQI is predicted than 5,7-Az, which may also pertain to the higher conductance of 1,3-Az.

The key message here is that ECARs can qualitatively rationalise the QI behaviour observed by Xia et al.³⁵ for azulene wires. The high conductance of 1,3-Az, for which SDQI is expected, relative to 4,7-Az, for which CQI is predicted, may relate to thiochroman anchoring group effects,³⁵ which are not accounted for by ECARs. This is supported by the results obtained by Schwarz et al. for similar systems with different anchors ((4-thioacetyl)phenylethynyl) in which 2,6- and 4,7-connectivities were found to be more conductive than 1,3-connectivity.⁶⁶

The effect of protonation on the conductance of 1,3-, 4,7- and 5,7-connected azulenes with 4-(methylthio)phenyl anchoring groups was investigated by Yang et al. using the MCBJ method.⁶⁹ The azulene cores of these wires were the same as those studied by Xia et al.³⁵ (Fig. 14a), and consequently the same behaviour is expected for the neutral species: namely CQI for 4,7-connectivity and SDQI for 1,3- and 5,7-connectivity. The observed conductance trend⁶⁹ was 1,3- > 4,7- > 5,7-, in qualitative agreement with Xia et al.³⁵ Again, the conductance of the 1,3-connected molecule was higher than might be expected based on ECARs (SDQI is predicted for 1,3-connectivity but CQI is predicted for 4,7-connectivity), presumably due to anchoring effects. Protonation using TFA increased the conductance of all three species, with the size of the increase following the trend 5,7- > 1,3- > 4,7-, i.e. larger for the species for which SDQI is predicted than for that for which CQI is predicted. The conductance trend for protonated species is 1,3- > 5,7- > 4,7-. These trends are not easily explained with ECARs, given that protonation of azulene derivatives is expected to occur at the 1- or 3-position (i.e. those where the negative charge is most often located in the zwitterionic resonance forms), even in the presence of bulky substituents.^68,70 Protonation of a 1,3-connected azulene in the 1- or 3-position affords an sp³ carbon in the conductance pathway which means a conjugated pathway does not exist between the anchoring groups. Consequently, conductance would be expected to be low, in contrast to the experimental observation. We conclude, therefore, that the conductance behaviour of the charged azulene systems is controlled by more complex phenomena than connectivity.

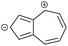
The fulvenes are another family of non-alternant hydrocarbons. Like azulene, fulvenes have zwitterionic resonance forms in which aromaticity is gained, evidenced by the existence of measurable dipole moments.^71,72 The simplest fulvene is 3-methylenecyclopropene (triafulvene), for which a zwitterionic form including an aromatic 3-membered ring with 2 π e⁻ can be drawn (Fig. 15a). Connecting anchoring points to the exocyclic carbon affords a cross-conjugated system which was investigated computationally by Pedersen et al. and showed a significantly shifted DQI feature in its DFT-based transmission function.²³ This can readily be related to the zwitterionic resonance form using ECARs (Fig. 15b). In the neutral state, ECAR-1 predicts DQI as delocalisation of a D lone pair to an A is not possible for this connectivity. In the zwitterionic state, SDQI is predicted by ECAR-2 as the negative charge of the zwitterion can be considered an EDG, and delocalised independently to an A group in either anchoring position (shown for only one equivalent A in Fig. 15b). As for azulene, SDQI in the zwitterionic resonance form appears to be sufficient to overcome DQI in the neutral form and dominate the properties of the molecule.

Fig. 15 (a) Neutral and zwitterionic resonance forms of triafulvene; (b) application of ECARs to a triafulvene system studied by Pedersen et al.²³ in neutral and zwitterionic resonance forms.

A more detailed analysis of QI in fulvene was reported by Tsuji et al., who made predictions by applying their graphical rule based on diradicals and compared these with calculated transmission functions.²⁶ A zwitterionic resonance form containing an aromatic 6 π e⁻ cyclopentadienyl ring can be drawn for fulvene (Fig. 16a). CQI cannot trivially be predicted in the neutral resonance form using ECAR-1 for three of the studied connectivities: 1,3-, 2,3- and exocyclic connectivity (Fig. 16b). In all three cases, when ECAR-2 is applied to the zwitterionic resonance form, SDQI is predicted (Fig. 16b, symmetry-equivalent pathways not shown). Indeed, all three species show DQI features shifted away from the centre of the HOMO–LUMO gap in their transmission spectra.²⁶

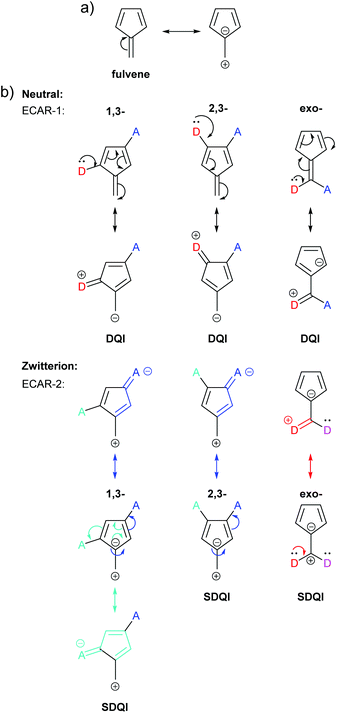Fig. 16 (a) Neutral and zwitterionic resonance forms of fulvene; (b) application of ECARs to three connectivities of fulvene studied by Tsuji et al.²⁶ in neutral and zwitterionic resonance forms.

In summary, we conclude based on azulene, triafulvene and fulvene, that ECARs are applicable to non-alternant hydrocarbons with zwitterionic resonance forms.

Cross-conjugated molecules

The relationship between cross-conjugation and QI has been the subject of considerable discussion.^{21,23,58,63,73,74} ECARs suggest that QI is influenced by not only the presence of cross-conjugation, but also the nature of the functionality that causes it. For example, a carbonyl group should be considered differently to an alkene, as the former is a good EWG and the latter is not. This parallels an effect proposed by Kocherzhenko et al. who calculated that adding charge to a gating moiety in a cross-conjugated position resulted in an increased charge transfer probability in D-B-A systems.⁷⁵

To reinforce the interplay between QI behaviour and the nature of a cross-conjugating group, we will now consider again the cross-conjugated triafulvene connectivity discussed above (Fig. 15). This was compared to an analogous cross-conjugated system based only on ethene (Fig. 17a).²³ As stated above, the DFT-based transmission function for the triafulvene wire shows a DQI feature shifted away from E_F, and ECARs can be used to predict SDQI for the zwitterionic resonance form. The DFT-based transmission function of the ethene analogue has a substantial DQI feature close to E_F (ref. 23) (also observed in similar species⁷³). Ethene contains neither a good EDG or EWG, nor is able to form a stable zwitterionic form (while suitable curly arrows can be drawn, there is no charge stabilisation to favour it): therefore, ECARs would predict DQI for this system. An analogous connectivity through [3]radialene (Fig. 17b) was studied by Tsuji and Yoshizawa.²⁸ Here, as for ethene, there is no functionality that provides a suitable EDG or EWG and a stable zwitterionic form does not exist, so ECARs would predict DQI. Indeed, the calculated transmission function has a DQI feature around E_F.²⁸

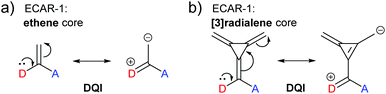Fig. 17 ECARs predict DQI when two anchors are connected to the same alkene carbon of (a) ethene or (b) [3]radialene.

The effect of different cross-conjugating groups has been investigated computationally^58,74 and experimentally⁷⁴ for AQ derivatives and analogues. These include species cross-conjugated with hydrocarbon-based alkene derivatives rather than carbonyls, extended tetrathiafulvalenes and tetracyano-p-quinodimethane (TCNQ) derivatives. However, in all cases the 2,6-connectivity is used, so ECARs predict DQI regardless of the quinoidal substituents (cf. Fig. 6). Substantial variation is observed in both the calculated transmission functions and experimental conductance studies.⁷⁴ Notably, not all species show DQI features in the HOMO–LUMO gap, and some species show a shifted DQI feature, suggestive of SDQI which is not predicted by ECARs. We note that the same value of E_F was used for all species as an approximation. If E_F varies significantly between species, the extent to which the antiresonances appear to be shifted could be over- or underestimated. The QI behaviour may also relate to effects other than connectivity, for example, deviation from planarity in the species other than AQ may play a role. Nevertheless, all of the cross-conjugated species are less conductive than the parent AC, for which ECARs predict CQI.

Heteroatom-substitution is key to QI in cross-conjugated species: prediction of SDQI by ECARs is always reliant on an EWG or EDG with a π-orbital that can be independently conjugated with both anchoring positions. ECARs highlight that the connectivity of cross-conjugated systems is critical, strictly differentiating between cross-conjugated molecules in which anchoring groups can and cannot interact with the same cross-conjugating functionality. Amongst the most obvious manifestations of this effect are the isomeric AQ and BDT species discussed above (Fig. 6 and 11).

Limitations of ECARs

As a simple “pen and paper” method, it is to be expected that ECARs cannot correctly account for QI behaviour in all cases. This section will use literature examples to explore the limitations of ECARs, explain their origins, and compare them with other predictive methods. Lack of orbital alignment between the molecular backbone and EDGs or EWGs, as seen in Fig. 7, is shown to account for anomalies related to molecular geometry.

As ECARs (and other graphical methods) are based on π-conjugation, they fail to accurately account for the behaviour of systems where π-transport is not dominant. This is usually only a concern for very short molecular backbones. For example, Borges et al. showed that 3,3′-bipyridine, for which ECARs would predict DQI, is similarly or more conductive than 4,4′-bipyridine, for which ECARs would predict CQI.⁴⁶ By calculating the contributions of different orbitals to the transmission function, the authors attributed this to high σ-conductance in 3,3′-bipyridine.⁴⁶ Longer analogues of these systems, where σ-contributions are no longer significant, follow the expectations of ECARs.

Yang et al. studied the series of pyridine-anchored molecular wires shown in Fig. 18a in which different 5-membered (hetero)cycles were used as the central ring.⁷⁶ For the symmetrically substituted series (s5-X), where in all cases the lone pair of a D in one anchoring position can be delocalised to an A at the other (Fig. 18b), CQI is expected according to ECAR-1. There was no significant variation in the measured conductance for the different bridging units X = O, NEt, S or CMe₂. The authors noted that this is in contrast to an earlier study of analogues with amine anchors⁷⁷ in which conductance followed the trend X = CMe₂ > O > S; i.e. conductance decreased as aromaticity increased. This difference between the two studies was attributed to the nature of the anchoring groups;⁷⁶ pyridine leads to LUMO-dominated conductance and amine to HOMO-dominated conductance.

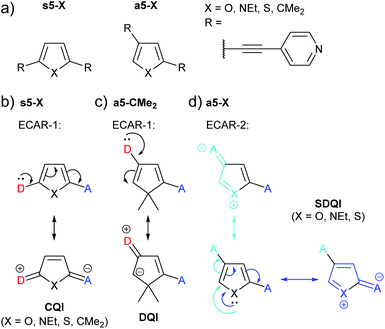Fig. 18 (a) Structures of molecular wires containing 5-membered (hetero)cycles studied by Yang et al.;⁷⁶ (b) application of ECAR-1 to the symmetric series s5-X; (c) application of ECAR-2 to asymmetric, non-aromatic a5-CMe₂; (d) application of ECAR-2 to aromatic species from the asymmetric series a5-X.

For the asymmetrically substituted series (a5-X), a CQI pathway cannot be drawn according to ECAR-1: delocalisation of a lone pair from one anchoring position to the other is not possible (illustrated for a5-CMe₂ in Fig. 18c). However, DQI features were not observed within the HOMO–LUMO gap of the transmission functions of the furan (a5-O) and pyrrole (a5-NEt) species, and a higher conductance (although lower than their symmetrical analogues, s5-X) was observed experimentally for these compounds compared to the cyclopentadiene (a5-CMe₂) and thiophene (a5-S) systems.⁷⁶ The conductance of a5-S was below the sensitivity of the MCBJ equipment used for the experiments. The authors related the higher conductance of the a5-O and a5-NEt compared to a5-S and a5-CMe₂ to the higher electronegativity of the heteroatom in a5-O and a5-NEt, which in effect enhances the asymmetry of these two molecules.⁷⁶ However, the higher conductance of a5-O and a5-NEt compared to a5-CMe₂ can be rationalised by applying ECAR-2. The oxygen and nitrogen atoms in a5-O and a5-NEt can function as EDGs and independently delocalise their lone pair to A groups in either anchoring position (Fig. 18d). This is not possible for a5-CMe₂ as no EDG (or EWG) is present. Sulfur also has a lone pair of electrons, and based on ECAR-2 a5-S would be expected to behave in the same manner as a5-O and a5-NEt, which is not the case experimentally.⁷⁶ This discrepancy can be explained in terms of the increased aromaticity of thiophene in comparison to pyrrole and furan; the trend for aromaticity of thiophene > pyrrole > furan is well known.^78,79 The results suggest that in a5-S, the sulfur lone pair is sufficiently delocalised into the aromatic 6 π e⁻ system that it is not available to act as an EDG. This is notably in contrast to the fused thiophenes in the BDT derivatives discussed above (Fig. 11). A limitation of ECARs is, therefore, that in rare circumstances species that can formally be EDGs (and presumably EWGs) do not act in this way, due to competing subtle electronic effects in the molecules that are not immediately obvious based on chemical intuition. Alternatively, the shift of the DQI feature may be sufficiently small for a5-S that SDQI is indistinguishable from DQI (the DQI resonance of a5-S is closer to the LUMO resonance and E_F than that of a5-CMe₂ ⁷⁶).

We note that incorrectly accounting for the trend observed for a5-X cores is not limited to ECARs. Prior to the publication of the experimental results above,⁷⁶ Borges and Solomon investigated a range of five-membered rings computationally using a four-site model based on Kohn–Sham DFT.³² Their results predict a conductance trend of X = NPh > S > O > CMe₂ for systems with the same cores as a5-X. Li et al. also studied some a5-X cores using their “two-pathway” tight-binding method.⁴⁰ In both cases, as for ECARs, the prediction for a5-S cores does not agree with experiment.

A related study of doubly-benzannulated 5-membered rings by Gantenbein et al.⁸⁰ shows further deviation from the expectations of ECARs. Like the fluorene derivatives discussed above (Fig. 10), the molecular cores (p-BP-X and m-BP-X, Fig. 19a) can be considered as biphenyl derivatives bridged by substituent X. The pyridylethynyl anchoring units were attached such that they were either both para (p-BP-X) or both meta (m-BP-X) with respect to the aryl–aryl C–C bond of the parent biphenyl. As in the above study of 5-membered heterocycles,⁷⁶ X was varied in the series O, NEt, S and CMe₂.

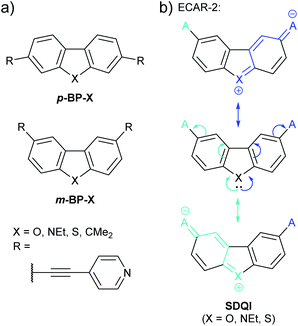Fig. 19 (a) Structures of wires incorporating doubly-benzannulated five-membered rings (i.e.p-BP-X and m-BP-X cores) studied by Gantenbein et al.;⁸⁰ (b) application of ECAR-2 to the m-BP-X core of some of these systems.

As shown previously for p-BP-CMe₂ and p-BP-CO (Fig. 10), for all members of the p-BP-X series it is possible to delocalise a lone pair from a D at one anchoring position to an A at the other, so CQI is expected according to ECAR-1. However, in this case, similarly to the amine-anchored species with s5-X cores discussed previously,⁷⁷ the molecular conductance of the wires varied with bridging substituent X. With the exception of the dimethylfluorene derivative p-BP-CMe₂, conductance decreased with increasing aromaticity, following the trend X = O > NEt > CMe₂ > S. The authors note that the unusual result for p-BP-CMe₂ is in agreement with previous studies from other laboratories in which fluorene derivatives do not follow expected trends.⁸⁰ This variation of conductance with aromaticity cannot be predicted using ECARs, and illustrates the fact that ECARs can only qualitatively predict the expected type of QI, not the magnitude of the expected conductance.

CQI pathways do not exist for the m-BP-X series according to ECAR-1. Similarly to the a5-X series above, ECAR-2 predicts SDQI for the heterocyclic systems m-BP-O, m-BP-NEt and m-BP-S (Fig. 19b), but DQI for the dimethylfluorene core m-BP-CMe₂ (Fig. 10, above). As for the a5-X series (Fig. 18), other effects mean that ECARs are not correct in all cases. The conductance of the m-BP-X series follows the trend X = CMe₂ ≈ NEt > O ≈ S. The unexpectedly high conductance (based on ECARs) of m-BP-CMe₂ could relate to the observed reduction in conductance with aromaticity, or the previously mentioned tendency for fluorene derivatives not to follow expected conductance trends. The low conductance of the dibenzothiophene species m-BP-S can be related to its increased aromaticity, as for thiophene a5-S above (although again the contrast with BDT (Fig. 11) is noteworthy). For a5-O and a5-NEt (Fig. 18a) O and N were considered EDGs able to contribute a lone pair according to ECARs. In the case of the m-BP-X series (Fig. 19a) this appears to remain the case for N, but not for O. The low conductance of m-BP-O was attributed to the high electronegativity of O causing its lone pair to be tightly bound and poorly able to delocalise across the π-system.⁸⁰ If this is the case, O will not be able to act as an EDG as expected by ECARs. This is the converse of the exception observed for (dibenzo)thiophene (a5-S and m-BP-S), in which the lone pair is already significantly delocalised, and represents the same limitation of ECARs: not all species that can behave as EDGs (and presumably EWGs) will act in this way in practice.

Similar deviations from the expectations of ECARs are observed in structurally similar molecular wires with m-BP-X type cores (Fig. 20a). m-BP-X cores directly substituted with thiomethyl anchors with X = SiPh₂, O and NPh were investigated by Klausen et al.⁸¹ Within the measurable range of their STM-BJ study, it was not possible to observe significant conductance features for the wires with m-BP-SiPh₂ or m-BP-O cores, or the parent biphenyl. However, the wire with a m-BP-NPh core showed reasonable conductance for its length, leading the authors to claim that the NPh bridging unit “turned on” the conductance of the core. As above, nitrogen appears to function as an EDG whereas oxygen does not. The authors used molecular orbital calculations to explain the trend in a similar manner to Gantenbein et al.,⁸⁰ stating that “the O lone pair is too small and its energy too low for effective overlap [with the π-system]”.⁸¹ ECARs would predict DQI for a m-BP-SiPh₂ core in the same manner as for m-BP-CMe₂ because SiPh₂ is not expected to accept or donate a lone pair. This result agrees with the absence of an experimental conductance feature,⁸¹ and further supports the above suggestion that the behaviour of fluorene derivatives is anomalous.

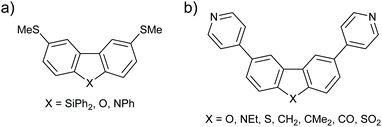Fig. 20 Structures of further molecular wires with m-BP-X cores studied by (a) Klausen et al.;⁸¹ and (b) Grace et al.⁸²

Grace et al. investigated more species with p-BP-X and m-BP-X cores, in this case with directly attached para-pyridyl anchors.⁸² As already seen in many cases above, for p-BP-X cores little variation was observed as the bridging substituent X was varied (ECAR-1 predicts CQI in all cases), whereas the series of m-BP-X cores shown in Fig. 20b gave a broad range of conductances. As for similar species above, ECAR-2 predicts SDQI for the carbazole (m-BP-NEt) and fluorenone (m-BP-CO) cores, which were observed to be the most conductive. For this series, unlike that with ethynyl-linked anchors (Fig. 19), the conductance of the fluorene cores (m-BP-CH₂ and m-BP-CMe₂) is low, suggestive of DQI as would be predicted by ECARs. The conductances of the dibenzofuran (m-BP-O) and dibenzothiophene (m-BP-S) cores are similar to the fluorene systems (m-BP-CH₂ and m-BP-CMe₂). Once again, this suggests that the predicted SDQI (according to ECAR-2) for the m-BP-O and m-BP-S cores does not occur, presumably for the same reasons discussed above (high electronegativity of O and aromaticity of thiophene). Finally, the lowest conductance in this series is observed for the dibenzothiophene-S,S-dioxide (m-BP-SO₂). Although SO₂ is formally a strong EWG, the S=O bonds do not lie in the same plane as the π-system of the wire (cf. the importance of the conformation of the methoxy group in the meta-OPE3 wires in Fig. 7). Therefore, it is logical that the SO₂ unit should not be treated as an EWG for ECAR-2. As the SO₂ unit is unable to act as an EWG for geometric reasons then DQI (rather than SDQI) would be expected. The experimental results indeed suggest DQI occurs for m-BP-SO₂.

Some p-BP-X and m-BP-X cores were also considered in the computational study by Borges and Solomon.³² For m-BP-X cores, their method predicts a conductance trend of X = NH > O > SiH₂ > CH₂, which is not consistent with the experimental observations discussed above.^80–82 For example, dibenzofuran tends to give low conductance and in some cases fluorene derivatives exhibit very high conductance. Li et al.'s “two-pathway” tight-binding approach qualitatively matches the observed tendency of carbazoles (X = NR) with meta-connectivity to have higher conductance than analogous dibenzofurans (X = O) and dibenzothiophenes (X = S), although their calculations indicate that the latter pair are not significantly less conductive than the former.⁴⁰ We note that the nature of any substituent used to satisfy the valency of the nitrogen atom is not stated by Li et al.⁴⁰ If no substituent was added to the nitrogen, the molecular core is not comparable with those studied experimentally. The inconsistencies between these two computational studies^32,40 and experimental results^80–82 are similar to those of ECARs.

Conclusions

An extension to curly arrow rules for predicting quantum interference has been presented. The improved method is based on extensive prior experimental and computational results and accounts for QI behaviour observed in species containing heteroatoms and five-membered rings. It can also be applied to non-alternant species with zwitterionic resonance forms, such as azulene and fulvenes. The extended rules are:

Rule 1. Identify the two anchoring units of a molecular wire and replace one with a donor group D and the other with an acceptor group A. If the D lone pair can be delocalised onto A using curly arrows, CQI is expected, if not DQI is expected.

Rule 2. If DQI is expected, identify any EWGs or EDGs present in the molecular wire. If EWGs are present, replace each anchor with D. If a lone pair from each D can be independently delocalised to the same EWG, SDQI is expected. If EDGs are present, replace each contact with A. If a lone pair (or negative charge) from the same EDG can be independently delocalised to each A, SDQI is expected. Otherwise, DQI is expected around E_F.

Limitations of these rules are observed when they are applied to some previously reported series of compounds. ECARs require that π-transport dominates conductance properties; short molecules where σ-transport is significant may not behave as expected. ECARs alone do not account correctly for QI behaviour when atoms or functional groups that might on first sight be expected to act as EDGs or EWGs do not in fact do so. Often this can be related to poor π-orbital alignment between an EDG or EWG and the molecular backbone, which can be accounted for by considering molecular geometry. In rare cases, disagreement between ECARs and experiment can be attributed to subtle electronic effects that cannot always be reliably predicted by chemical intuition, such as extensive delocalisation or localisation of a lone pair. ECARs are qualitative and limited to predicting the expected type of QI: namely, CQI, DQI or SDQI. They cannot quantitatively predict the magnitude of molecular conductance.

The strength of ECARs is that it is a convenient, qualitative, “pen-and-paper” method to predict QI effects which is widely applicable to molecular wires with diverse structural features. Indeed, ECARs can rationalise observed behaviour in cases where other methods to predict QI fail, without the use of computationally-expensive and time-consuming charge transport simulations. We look forward to testing the applicability of ECARs to new molecular systems and to exploring the potential of ECARs in the design of materials for molecular thermoelectric devices.

Author contributions

L. J. O. initiated the writing of this manuscript and wrote the majority of the text, with input and guidance from M. R. B.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by EPSRC grant EP/P027520/1 and EC H2020 FET Open projects: grant agreement numbers 767187 ‘QuIET’ and 766853 ‘EFINED’.

Notes and references

1. C. J. Lambert, Chem. Soc. Rev., 2015, 44, 875–888.
2. M. Magoga and C. Joachim, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 16011–16021.
3. C. J. Lambert and S.-X. Liu, Chem. – Eur. J., 2018, 24, 4193–4201.
4. J. Liu, X. Huang, F. Wang and W. Hong, Acc. Chem. Res., 2019, 52, 151–160.
5. X. Li, Z. Tan, X. Huang, J. Bai, J. Liu and W. Hong, J. Mater. Chem. C, 2019, 7, 12790–12808.
6. K. Walczak, Cent. Eur. J. Chem., 2004, 2, 524–533.
7. H. Vazquez, R. Skouta, S. Schneebeli, M. Kamenetska, R. Breslow, L. Venkataraman and M. S. Hybertsen, Nat. Nanotechnol., 2012, 7, 663–667.
8. S. Gunasekaran, J. E. Greenwald and L. Venkataraman, Nano Lett., 2020, 20, 2843–2848.
9. G. Yang, H. Wu, J. Wei, J. Zheng, Z. Chen, J. Liu, J. Shi, Y. Yang and W. Hong, Chin. Chem. Lett., 2018, 29, 147–150.
10. X. Liu, S. Sangtarash, D. Reber, D. Zhang, H. Sadeghi, J. Shi, Z.-Y. Xiao, W. Hong, C. J. Lambert and S.-X. Liu, Angew. Chem., Int. Ed., 2017, 56, 173–176.
11. C. R. Arroyo, S. Tarkuc, R. Frisenda, J. S. Seldenthuis, C. H. M. Woerde, R. Eelkema, F. C. Grozema and H. S. J. van der Zant, Angew. Chem., Int. Ed., 2013, 52, 3152–3155.
12. S.-H. Ke, W. Yang and H. U. Baranger, Nano Lett., 2008, 8, 3257–3261.
13. C. A. Stafford, D. M. Cardamone and S. Mazumdar, Nanotechnology, 2007, 18, 424014.
14. R. Baer and D. Neuhauser, J. Am. Chem. Soc., 2002, 124, 4200–4201.
15. M. Baghernejad, X. Zhao, K. B. Ørnsø, M. Füeg, P. Moreno-García, A. V. Rudnev, V. Kaliginedi, S. Vesztergom, C. Huang, W. Hong, P. Broekmann, T. Wandlowski, K. S. Thygesen and M. R. Bryce, J. Am. Chem. Soc., 2014, 136, 17922–17925.
16. R. Miao, H. Xu, M. Skripnik, L. Cui, K. Wang, K. G. L. Pedersen, M. Leijnse, F. Pauly, K. Wärnmark, E. Meyhofer, P. Reddy and H. Linke, Nano Lett., 2018, 18, 5666–5672.
17. L. Rincón-García, C. Evangeli, G. Rubio-Bollinger and N. Agraït, Chem. Soc. Rev., 2016, 45, 4285–4306.
18. X. Wang, T. L. R. Bennett, A. Ismael, L. A. Wilkinson, J. Hamill, A. J. P. White, I. M. Grace, O. V. Kolosov, T. Albrecht, B. J. Robinson, N. J. Long, L. F. Cohen and C. J. Lambert, J. Am. Chem. Soc., 2020, 142, 8555–8560.
19. T. Stuyver, S. Fias, F. De Proft and P. Geerlings, J. Phys. Chem. C, 2015, 119, 26390–26400.
20. T. Stuyver, N. Blotwijk, S. Fias, P. Geerlings and F. De Proft, ChemPhysChem, 2017, 18, 3012–3022.
21. T. Markussen, R. Stadler and K. S. Thygesen, Nano Lett., 2010, 10, 4260–4265.
22. J. Gu, W. Wu, T. Stuyver, D. Danovich, R. Hoffmann, Y. Tsuji and S. Shaik, J. Am. Chem. Soc., 2019, 141, 6030–6047.
23. K. G. L. Pedersen, A. Borges, P. Hedegård, G. C. Solomon and M. Strange, J. Phys. Chem. C, 2015, 119, 26919–26924.
24. M. H. Garner, G. C. Solomon and M. Strange, J. Phys. Chem. C, 2016, 120, 9097–9103.
25. Y. Tsuji, E. Estrada, R. Movassagh and R. Hoffmann, Chem. Rev., 2018, 118, 4887–4911.
26. Y. Tsuji, R. Hoffmann, M. Strange and G. C. Solomon, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, E413–E419.
27. K. Yoshizawa, T. Tada and A. Staykov, J. Am. Chem. Soc., 2008, 130, 9406–9413.
28. Y. Tsuji and K. Yoshizawa, J. Phys. Chem. C, 2017, 121, 9621–9626.
29. S. Sangtarash, H. Sadeghi and C. J. Lambert, Nanoscale, 2016, 8, 13199–13205.
30. Y. Geng, S. Sangtarash, C. Huang, H. Sadeghi, Y. Fu, W. Hong, T. Wandlowski, S. Decurtins, C. J. Lambert and S.-X. Liu, J. Am. Chem. Soc., 2015, 137, 4469–4476.
31. S. Sangtarash, C. Huang, H. Sadeghi, G. Sorohhov, J. Hauser, T. Wandlowski, W. Hong, S. Decurtins, S.-X. Liu and C. J. Lambert, J. Am. Chem. Soc., 2015, 137, 11425–11431.
32. A. Borges and G. C. Solomon, J. Phys. Chem. C, 2017, 121, 8272–8279.
33. K. G. L. Pedersen, M. Strange, M. Leijnse, P. Hedegård, G. C. Solomon and J. Paaske, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 125413.
34. F. Evers, R. Korytár, S. Tewari and J. M. van Ruitenbeek, Rev. Mod. Phys., 2020, 92, 035001.
35. J. Xia, B. Capozzi, S. Wei, M. Strange, A. Batra, J. R. Moreno, R. J. Amir, E. Amir, G. C. Solomon, L. Venkataraman and L. M. Campos, Nano Lett., 2014, 14, 2941–2945.
36. F. Jiang, D. I. Trupp, N. Algethami, H. Zheng, W. He, A. Alqorashi, C. Zhu, C. Tang, R. Li, J. Liu, H. Sadeghi, J. Shi, R. Davidson, M. Korb, A. N. Sobolev, M. Naher, S. Sangtarash, P. J. Low, W. Hong and C. J. Lambert, Angew. Chem., Int. Ed., 2019, 58, 18987–18993.
37. C. M. Guédon, H. Valkenier, T. Markussen, K. S. Thygesen, J. C. Hummelen and S. J. van der Molen, Nat. Nanotechnol., 2012, 7, 305–309.
38. A. Alanazy, E. Leary, T. Kobatake, S. Sangtarash, M. T. González, H.-W. Jiang, G. R. Bollinger, N. Agräit, H. Sadeghi, I. Grace, S. J. Higgins, H. L. Anderson, R. J. Nichols and C. J. Lambert, Nanoscale, 2019, 11, 13720–13724.
39. M. Baghernejad, Y. Yang, O. A. Al-Owaedi, Y. Aeschi, B.-F. Zeng, Z. M. Abd Dawood, X. Li, J. Liu, J. Shi, S. Decurtins, S.-X. Liu, W. Hong and C. J. Lambert, Chem. – Eur. J., 2020, 26, 5264–5269.
40. Y. Li, X. Yu, Y. Zhen, H. Dong and W. Hu, J. Phys. Chem. C, 2019, 123, 15977–15984.
41. D. Miguel, L. Álvarez de Cienfuegos, A. Martín-Lasanta, S. P. Morcillo, L. A. Zotti, E. Leary, M. Bürkle, Y. Asai, R. Jurado, D. J. Cárdenas, G. Rubio-Bollinger, N. Agraït, J. M. Cuerva and M. T. González, J. Am. Chem. Soc., 2015, 137, 13818–13826.
42. H. Liu, W. Ni, J. Zhao, N. Wang, Y. Guo, T. Taketsugu, M. Kiguchi and K. Murakoshi, J. Chem. Phys., 2009, 130, 244501.
43. B. Capozzi, J. Z. Low, J. Xia, Z.-F. Liu, J. B. Neaton, L. M. Campos and L. Venkataraman, Nano Lett., 2016, 16, 3949–3954.
44. S. V. Aradhya and L. Venkataraman, Nat. Nanotechnol., 2013, 8, 399–410.
45. G. C. Solomon, D. Q. Andrews, R. H. Goldsmith, T. Hansen, M. R. Wasielewski, R. P. Van Duyne and M. A. Ratner, J. Am. Chem. Soc., 2008, 130, 17301–17308.
46. A. Borges, E. D. Fung, F. Ng, L. Venkataraman and G. C. Solomon, J. Phys. Chem. Lett., 2016, 7, 4825–4829.
47. S. Sangtarash, H. Sadeghi and C. J. Lambert, Phys. Chem. Chem. Phys., 2018, 20, 9630–9637.
48. D. Q. Andrews, G. C. Solomon, R. P. Van Duyne and M. A. Ratner, J. Am. Chem. Soc., 2008, 130, 17309–17319.
49. W. O. Kermack and R. Robinson, J. Chem. Soc., Trans., 1922, 121, 427–440.
50. J. Clayden, N. Greeves, S. Warren and P. Wothers, Organic Chemistry, Oxford University Press, New York, 2001.
51. Y. Liu, P. Kilby, T. J. Frankcombe and T. W. Schmidt, Nat. Commun., 2018, 9, 1436.
52. H. Hosoya, Curr. Org. Chem., 2015, 19, 293–310.
53. T. A. Su, M. Neupane, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, Nat. Rev. Mater., 2016, 1, 16002.
54. L. Ulčakar, T. Rejec, J. Kokalj, S. Sangtarash, H. Sadeghi, A. Ramšak, J. H. Jefferson and C. J. Lambert, Sci. Rep., 2019, 9, 3478.
55. J. Zhang, W. Sun, H. Liu, Y. He and J. Zhao, Comput. Mater. Sci., 2014, 87, 100–106.
56. C. Schubert, J. T. Margraf, T. Clark and D. M. Guldi, Chem. Soc. Rev., 2015, 44, 988–998.
57. B. Albinsson, M. P. Eng, K. Pettersson and M. U. Winters, Phys. Chem. Chem. Phys., 2007, 9, 5847–5864.
58. H. Valkenier, C. M. Guédon, T. Markussen, K. S. Thygesen, S. J. van der Molen and J. C. Hummelen, Phys. Chem. Chem. Phys., 2014, 16, 653–662.
59. V. Kaliginedi, P. Moreno-García, H. Valkenier, W. Hong, V. M. García-Suárez, P. Buiter, J. L. H. Otten, J. C. Hummelen, C. J. Lambert and T. Wandlowski, J. Am. Chem. Soc., 2012, 134, 5262–5275.
60. D. Fracasso, H. Valkenier, J. C. Hummelen, G. C. Solomon and R. C. Chiechi, J. Am. Chem. Soc., 2011, 133, 9556–9563.
61. J. Alqahtani, H. Sadeghi, S. Sangtarash and C. J. Lambert, Angew. Chem., Int. Ed., 2018, 57, 15065–15069.
62. L. A. Zotti and E. Leary, Phys. Chem. Chem. Phys., 2020, 22, 5638–5646.
63. Y. Zhang, G. Ye, S. Soni, X. Qiu, T. L. Krijger, H. T. Jonkman, M. Carlotti, E. Sauter, M. Zharnikov and R. C. Chiechi, Chem. Sci., 2018, 9, 4414–4423.
64. Y.-P. Zhang, L.-C. Chen, Z.-Q. Zhang, J.-J. Cao, C. Tang, J. Liu, L.-L. Duan, Y. Huo, X. Shao, W. Hong and H.-L. Zhang, J. Am. Chem. Soc., 2018, 140, 6531–6535.
65. C. Huang, M. Jevric, A. Borges, S. T. Olsen, J. M. Hamill, J.-T. Zheng, Y. Yang, A. Rudnev, M. Baghernejad, P. Broekmann, A. U. Petersen, T. Wandlowski, K. V. Mikkelsen, G. C. Solomon, M. B. Nielsen and W. Hong, Nat. Commun., 2017, 8, 15436.
66. F. Schwarz, M. Koch, G. Kastlunger, H. Berke, R. Stadler, K. Venkatesan and E. Lörtscher, Angew. Chem., Int. Ed., 2016, 55, 11781–11786.
67. A. G. Anderson and B. M. Steckler, J. Am. Chem. Soc., 1959, 81, 4941–4946.
68. H. Xin and X. Gao, ChemPlusChem, 2017, 82, 945–956.
69. G. Yang, S. Sangtarash, Z. Liu, X. Li, H. Sadeghi, Z. Tan, R. Li, J. Zheng, X. Dong, J. Liu, Y. Yang, J. Shi, Z. Xiao, G. Zhang, C. Lambert, W. Hong and D. Zhang, Chem. Sci., 2017, 8, 7505–7509.
70. K. K. Laali, Chem. Rev., 1996, 96, 1873–1906.
71. T. D. Norden, S. W. Staley, W. H. Taylor and M. D. Harmony, J. Am. Chem. Soc., 1986, 108, 7912–7918.
72. K. Najafian, P. v. R. Schleyer and T. T. Tidwell, Org. Biomol. Chem., 2003, 1, 3410–3417.
73. D. Q. Andrews, G. C. Solomon, R. H. Goldsmith, T. Hansen, M. R. Wasielewski, R. P. V. Duyne and M. A. Ratner, J. Phys. Chem. C, 2008, 112, 16991–16998.
74. M. Carlotti, S. Soni, X. Qiu, E. Sauter, M. Zharnikov and R. C. Chiechi, Nanoscale Adv., 2019, 1, 2018–2028.
75. A. A. Kocherzhenko, L. D. A. Siebbeles and F. C. Grozema, J. Phys. Chem. Lett., 2011, 2, 1753–1756.
76. Y. Yang, M. Gantenbein, A. Alqorashi, J. Wei, S. Sangtarash, D. Hu, H. Sadeghi, R. Zhang, J. Pi, L. Chen, X. Huang, R. Li, J. Liu, J. Shi, W. Hong, C. J. Lambert and M. R. Bryce, J. Phys. Chem. C, 2018, 122, 14965–14970.
77. W. Chen, H. Li, J. R. Widawsky, C. Appayee, L. Venkataraman and R. Breslow, J. Am. Chem. Soc., 2014, 136, 918–920.
78. A. T. Balaban, D. C. Oniciu and A. R. Katritzky, Chem. Rev., 2004, 104, 2777–2812.
79. K. E. Horner and P. B. Karadakov, J. Org. Chem., 2013, 78, 8037–8043.
80. M. Gantenbein, L. Wang, A. A. Al-jobory, A. K. Ismael, C. J. Lambert, W. Hong and M. R. Bryce, Sci. Rep., 2017, 7, 1794.
81. R. S. Klausen, J. R. Widawsky, T. A. Su, H. Li, Q. Chen, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, Chem. Sci., 2014, 5, 1561–1564.
82. I. M. Grace, G. Olsen, J. Hurtado-Gallego, L. Rincón-García, G. Rubio-Bollinger, M. R. Bryce, N. Agraït and C. J. Lambert, Nanoscale, 2020, 12, 14682–14688.

---