Nanomechanics of self-assembled DNA building blocks

Abstract

DNA has become a powerful platform to design functional nanodevices. DNA nanodevices are often composed of self-assembled DNA building blocks that differ significantly from the structure of native DNA. In this study, we present Flow Force Microscopy as a massively parallel approach to study the nanomechanics of DNA self-assemblies on the single-molecular level. The high-throughput experiments performed in a simple microfluidic channel enable statistically meaningful studies with nanometer scale precision in a time frame of several minutes. A surprisingly high flexibility was observed for a typical construct used in DNA origami, reflected in a persistence length of 10.2 nm, a factor of five smaller than for native DNA. The enhanced flexibility is attributed to the discontinuous backbone of DNA self-assemblies that facilitate base pair opening by thermal fluctuations at the end of hybridized oligomers. We believe that the results will contribute to the fundamental understanding of DNA nanomechanics and help to improve the design of DNA nanodevices with applications in biological analysis and clinical research.

---

Introduction

The assembly of DNA from a linear scaffold into complex structures makes DNA a powerful tool to design nanodevices with nanometer scale precision. The high precision is achieved by non-covalent hybridization of complementary DNA-oligomers to a single-stranded DNA scaffold.¹ Recently, DNA origami was developed to expand the available number of non-repeating structures from a few hundred nucleotides to around fifteen thousand,^1,2 offering the assembly of large 2D or 3D structures triggering drug release and allowing for molecular detection or protein production.^3,4 DNA-assemblies differ from native DNA not only in their three-dimensional structure but also in their two-dimensional shape. The sequence of hybridized oligomers constitutes a discontinuous backbone with repeated nicks in the DNA strand. The effect of repeated nicks, gaps or kinks on the mechanical properties of DNA is subject of current research.^5–9 There is evidence that repeated nicks or gaps enhance the flexibility of DNA constructs compared to native DNA.^5,10 The mechanical response of native DNA under force has been successfully elucidated in single-molecule experiments by means of optical tweezers^11–13 and atomic force microscopy.¹⁴ These techniques allow for a precise measurement of force as a function of elongation and time with sub-nanometer and sub-piconewton resolution. Ultimate precision is obtained by repeated force measurements on the same molecule, unfortunately with a low-throughput. It has been demonstrated that this limitation of conventional single-molecule force spectroscopy can be overcome by high-throughput techniques based on force measurements of many molecules in parallel.^15–19

In this study, we demonstrate Flow Force Microscopy (FlowFM) as a massively parallel approach that combines the advantages of single-molecule force spectroscopy with our recently developed high-throughput assay for simple and fast force measurements.^15,20 A DNA tether, functionalized with the molecules of interest, is attached between the wall of a microfluidic channel and a micrometer-size bead (Fig. 1). Increasing the hydrodynamic flow rate in the microfluidic channel rises Stoke's friction acting on the bead attached to the free end of the molecule and increase the force from sub-pN level to several tens of pN. Linear flow force ramps enable force spectroscopy experiments on hundreds of surface-tethered beads in parallel. Notably, the high-throughput experiments are performed in a simple microfluidic cell mounted on a standard optical microscopy equipped with a CCD camera. The bead displacement is tracked through the optical path with a spatial resolution of below 20 nm (ESI Fig. 2). We first demonstrate the capability of FlowFM to perform massive parallel force-spectroscopy measurements on biologically relevant force scales for the example of digoxigenin and its antibody.

Fig. 1 (A) Sketch of experimental setup for the observation of tethered particle motion in a microfluidic flow channel. (B) Optical microscopy determines the position and movement of thousands of surface-tethered beads in parallel (scalebar: 100 μm). (C) Sketch of the molecular arrangement with and without flow force. Micro-beads are attached to the channel surface via DNA constructs. Upon liquid flow, a force is acting on the beads and the DNA constructs are stretched out in the direction of flow. (D) 2D histogram of 302 force–distance curves recorded in one optical field of view, color scale reflects the number of data points in one bin.

Fig. 2 (A) Rupture-force distribution of the digoxigenin–anti-digoxigenin bond at different force loading rates. (B) The most probable rupture force, obtained from the Gaussian fits to histograms in (A), as a function of loading rate, the error bars represent the standard deviation. The straight line is a weighted fit to the data according to Bell-Evans model; the weighting factor is the inverse square of the standard error of the mean.

We then study the elastic response of a DNA self-assembly to increasing force with a focus on the persistence length. The DNA assembly is composed of a single-stranded DNA backbone (M13mp18 plasmid with 7.2 knt) and hybridized with matching 60 nt-oligomers. We found the persistence length of our single-stranded backbone in good agreement with literature values (see ESI note 3†). We determine the persistence length for 1615 individual molecules and observe an enhanced flexibility compared to literature values for native double stranded DNA. The higher flexibility is explained by the disrupted backbone of the self-assembled DNA construct. The hybridization of complementary oligomers is prone to base-pair opening at their end points due to thermal fluctuations. This base-pair opening around the nicks results in repeated single-stranded gaps along the DNA chain which lower the persistence length as described by Rivetti et al.⁵

Parallelization of single-molecule measurements not only reduces the number of experiments required to record sufficient data for statistically sound conclusions (see ESI note 5†) but also facilitates the study of rare events out of equilibrium. We create a small number of looped DNA constructs in a large population of linear constructs using DNA-duplex formation of an additional 60nt DNA-oligomer with two 30 nt single-stranded regions along the DNA assembly. In Flow Force Microscopy experiments, we were able to determine the force require for mechanical separation of the DNA-duplex and to investigate its dissociation kinetics.

Results

Antibody–antigen interaction

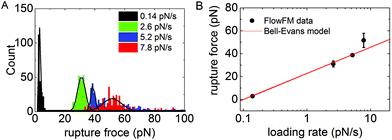
To demonstrate the operation of FlowFM on biologically relevant force scales, we performed dynamic force-spectroscopy experiments on the bond of digoxigenin and its antibody. The digoxigenin–anti-digoxigenin interaction is often used for surface-tethering of DNA molecules^13,16,18 and its bond kinetics were studied in dynamic force-spectroscopy measurements.^18,21 For our experiment, the digoxigenin was covalently attached to an oligomer hybridized onto the 3′-end of our DNA-construct. The DNA-construct was used as a linker between the anti-digoxigenin covered wall of the microfluidic flow chamber and the polystyrene bead. Without applying a fluid flow in the chamber, we observed the Brownian diffusive motion of the tethered beads for 1 minute. The symmetry of the movement is used to discriminate between single and multiple-tethered beads. Single-tethered particles show a symmetric in-plane motion that was quantified using the covariance matrix of xy particle positions (see Method section for details). Increasing the fluid flow in the chamber to 500 μl min⁻¹ increases Stoke's friction acting on the beads. The increasing force leads to a stretching of the DNA molecules similar to force spectroscopy measurements in AFM or optical tweezers, but in a highly parallel manner. Force-spectroscopy measurements were repeated for four different rates of flow increase, i.e. for four different rates of force loading. Unbinding of the digoxigenin–anti-digoxigenin bond was detected as the loss of the bead from the microscopy video. The loading rate at the moment of rupture was determined from the change in fluid height in the reservoir (see ESI Fig. 1 for details†). Unbinding forces for the rupture events of each verified single tether were included in the histogram in Fig. 2A. Each histogram of rupture events was obtained from videos in a single field of view recorded in several seconds or minutes. The statistical distribution of unbinding forces was modeled by a Gaussian distribution. The most probable rupture force was plotted as a function of the force loading rate in Fig. 2B. The rupture force increases logarithmically with loading rate r as predicted by the Bell-Evans model²²where x_β is the length scale of the reaction, k_B is the Boltzmann constant and T is the temperature. The non-forced off-rate k_off = 0.01 s⁻¹ with a standard deviation of 6.5 × 10⁻⁴ s⁻¹ was obtained from the Bell-Evans fit to the data in Fig. 2B and is in good agreement with literature values for similar systems.^18,21

Mechanics of DNA-assemblies

The flexibility of DNA assemblies was investigated by means of FlowFM. Double stranded DNA (dsDNA) is one of the most studied single molecules and exhibits a well-defined stretching signature in AFM or optical tweezers^13,14 force-spectroscopy experiments. The force-extension curve follows the extensible worm-like chain model until the curve exhibits a plateau at constant force. The plateau is referred to as overstretching regime, where the dsDNA undergoes a conformational transition from double stranded to single stranded.²³ The overstretching transition occurs in a defined force range that was used to calibrate the relation between force and fluid flow rate for every FlowFM experiment (ESI Fig. 1†). We recorded 1615 force–distance curves on individual DNA constructs for three different loading rates in near physiological conditions using phosphate-buffered saline with pH 7.4 (Fig. 3). In Fig. 3A, 302 force–distance curves recorded in a single FlowFM measurement with a loading rate of 1.4 pN s⁻¹ are overlaid in a 2D histogram. The typical force-extension signature of DNA is observed with the linear increase in the low-force regime and a steep increase when the distance approaches the contour length of 2.5 μm. A measure for the flexibility of polymers is the persistence length that was determined by modeling each force-extension curve with the worm-like–chain model. To exclude corrections of the WLC model due to elasticity in the enthalpic stretching regime, we included only the data of the low-force regime below 10 pN in the fitting procedure. For statistical evaluation, the values of persistence length are summarized in the histogram in Fig. 3B. A Gaussian distribution indicates an average persistence length of 10.2 nm with a standard deviation of 3.2 nm. The value for the persistence length is significantly smaller than the values reported for dsDNA of 45 nm to 53 nm for near-physiological buffer conditions.^5,13,24,25 No significant effect of loading rate on the persistence length is observed for the studied range of loading rates. A persistence length clearly below the expected value of 50 nm has been already observed by optical tweezers experiments on the same DNA construct.^16,26

Fig. 3 (A) 2D Histogram of 302 curves recorded in one FlowFM experiment for a loading rate of 1.4 pN s⁻¹. The bin size (0.12 pN × 44 nm) is chosen according to the resolution limit of the force scale. The color scale reflects the number of data points. (B) Persistence length as result of fits to the WLC model for 1615 force–distance curves recorded with three different force-loading rates, each colour reflects an independent experiment. We found P* = 10.2 nm as the most probable value with a standard variation of 3.2 nm. (C) Typical force–distance curves recorded with an atomic force microscope on the same DNA construct. The WLC fit (green line) to the low force regime of the black curve reports a persistence length of 11.1 nm. Inset: histogram of persistence length of WLC fit to 23 force–distance curves with a most probable persistence length of 8.7 nm with a standard deviation of 2.1 nm.

In order to validate the FlowFM results with an established method, we performed single-molecule force-spectroscopy experiments of the same DNA construct using the same surface attachment and linkers by means of atomic force microscopy (AFM). The force is applied by a tipless cantilever that pulls the micron bead perpendicular from the surface (scheme in Fig. 3C). In Fig. 3C, a typical AFM force–distance curve is shown that exhibit a non-linear stretching regime. The sudden force-drop reports the bond dissociation of the digoxigenin–anti-digoxigenin complex at the surface. The histogram of persistence length as a fit result of the WLC model to the stretching regime up to 10 pN results in a persistence length of 8.7 nm, in good agreement with our FlowFM results. Please note that obtaining a similar data set as the one represented by the histogram of persistence lengths in Fig. 3B would require the parallel operation of hundreds of AFMs for a comparable duration of experiments. Magnetic tweezers and centrifuge force microscopy can enable similar quantities as FlowFM. The advantage of FlowFM is the simple experimental setup without any moving compartments and the direct observation of the bead position that features a straightforward data analysis.

Shear rupture of DNA oligomer duplexes

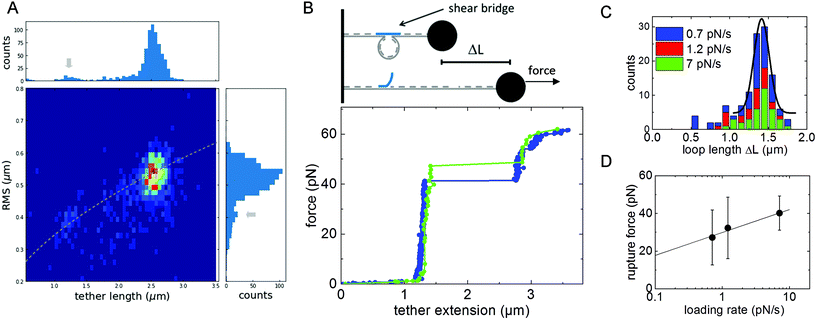
We modified our DNA construct such that it forms a loop similar to DNA nanoswitches introduced in ref. 26. We left two regions on the DNA strain single-stranded, each with a length of 30 nt, and introduced a complementary DNA-oligomer of 60 nt. Upon binding, the complementary oligomer is expected to change the DNA conformation to a looped state by forming a DNA duplex with the two single-stranded regions on the DNA chain (Fig. 4B, inset). In order to verify the successful DNA looping, the change in conformation was analyzed in three steps with increasing precision similar to the proofreading steps developed by the Wong lab in ref. 15. First, we analyzed the Brownian motion of beads attached to the end of the DNA tethers without applied flow. Then, we applied a small force to stretch the DNA and measure the tether length. Third, we applied force-loading ramps in dynamic force spectroscopy experiments to dissociate the DNA-duplex and measure the rupture force.

Fig. 4 (A) Density plot of RMS distance of particle motion without flow force versus tether length for a stretching force of 11 pN. The histograms are projections of the respective values, arrows indicate the second maximum, dotted line reflects RMS² = 2PL. (B) Typical force-extension curves including shear bridge rupture of looped DNA construct using FlowFM for loading rates of 7 pN s⁻¹ and 0.7 pN s⁻¹. (C) Histogram of tether length changes for rupture events in FlowFM measurement with a most probable length change and standard deviation of 1.41 ± 0.09 μm. (D) Mean shear-bridge rupture force as a function of loading rate, error bars reflect standard deviation of mean value. The straight line is a weighted fit to the data according to Bell-Evans model; the weighting factor is the inverse square of the standard error of the mean.

The reduction of the tether length in the looped conformation results in a smaller fluctuation of the tethered beads.²⁷ The fluctuations are quantified as root-mean-square displacement from the center of gyration (x̄,ȳ). For statistical analysis, the RMS displacement values are summarized in a histogram. Two peaks at 0.41 μm and 0.55 μm indicate a heterogenic distribution corresponding to two different tether lengths. As an additional proofreading step, we directly measure the tether length by applying a force of 11 pN to the beads and stretching the DNA tether in the direction of flow. The histogram of tether length also exhibits two peaks at 1.3 μm and 2.5 μm. A 2D histogram of both quantities in Fig. 4A demonstrates the correlation between measured tether length and RMS displacement value following the prediction of RMS²∼ L.^27,28 Due to a lack of models for tethered particle measurements with non-zero bead sizes, no quantitative model can be applied. As a third and most precise validation step of the successful DNA looping, we dissociated the DNA-duplex in dynamic force-loading experiments. DNA duplexes are anticipated to be stable for a duration orders of magnitudes longer than the several minutes of our particle motion experiments.²⁹ To observe the force-induced dissociation of the DNA duplex, we performed dynamic force spectroscopy measurements. The system is driven out of thermodynamic equilibrium and bond dissociation kinetics can be studied.²² In Fig. 4B, two exemplary force-extension curves for the lowest and highest loading rate are shown. The tether length increases with the characteristic of the WLC model, followed by a sudden step increase in length at a force of about 40 pN. For the observation of this signature of a loop-opening, one of the two binding sites of 30 bp length has to be ruptured. The step-like change in tether length is summarized in histograms in Fig. 4C for experiments with three different loading rates. The most probable length change is ΔL = 1.41 μm with a standard deviation of 0.1 μm revealing a contour length of 0.36 nm per base pair for a loop size of 3912 base pairs. In general, relative changes in length as observed for the loop-opening are particularly precise because the elasticity of the attachment to the surface or bead do not contribute to the measured distance. The slight difference to the literature value of 0.34 nm per bp will be discussed in the next section with respect to the flexibility of DNA assemblies. The mean loop-opening rupture force is plotted as a function of loading rate in Fig. 4D. The rupture force increases with loading rate r as described by the Bell-Evans model²² in eqn (1). The Bell-Evans fit reveals an off-rate of k_off = 6 × 10⁻⁴ 1 s⁻¹ with a standard deviation of 1.7 × 10⁻³ 1 s⁻¹ and a reaction distance of x_β = 7.7 Å with a deviation of 4.4 Å. The reaction kinetics of the DNA duplex are discussed with respect to single-bond kinetics in the next section.

Discussion

The experimental results confirm the capability of FlowFM to reveal nanomechanical properties of DNA constructs with high precision. We will now discuss the molecular processes underlying the surprisingly small persistence length and the dependencies on the force loading rate.

We observe a significant smaller persistence length of P = 10.2 nm compared to literature values for dsDNA ranging from 45 nm to 53 nm.^{5,13,19,24,25} The lower persistence length indicates that the molecular arrangement of our DNA construct offers a higher flexibility than known for natural dsDNA. We suggest that the higher flexibility originates from the intrinsic structure of the DNA assemblies. Additional flexibility of the molecular layer used for the attachment of the DNA molecules to the surface or bead can be neglected at the small forces used for analysis. Maximal deformations of attachment layers are in the order of several tens of nm (ref. 30 and 31) and, thus, negligible for the length scale of our DNA construct in the order of μm.

Functional DNA constructs are self-assembled starting from a single-stranded DNA chain and hybridizing complementary oligomers onto the scaffold. The hybridization reaction results in a double-stranded DNA construct that consist of one DNA strand with a continuous backbone and a complementary DNA strand composed of short oligomers resulting in a discontinuous backbone. The discontinuities are also referred to as nicks in literature. Nicks can have important biological functions in DNA-mediated systems.³⁴ The impact of nicks on the elasticity of DNA is still under debate.^6,7,32,33 The overall stability of the double stranded DNA construct is given by stacking interactions between adjacent base pairs.³² Thermal fluctuations lead to base pair opening and thus to single-stranded gaps in between the hybridized oligomers. Single-stranded DNA exhibits a higher flexibility than double-stranded DNA with a persistence length of 1.7 nm for short sequences.^13,35

The entropic stretching regime of natural DNA has been successfully described by the worm-like-chain model with a constant persistence length along the polymer chain.³⁶ Rivetti et al. extended the WLC model for polymers with sections of different flexibility and included the possibility of permanent bends along the DNA chain. They applied their model to calculate the mean-square end-to-end distance of double stranded DNA molecules containing single-stranded regions.⁵ For DNA with a contour length L much larger than the persistence length, the persistence length can be calculated as P = RMS²/2L. For a DNA construct without permanent bends, the Rivetti equation reduces to:

The effective persistence length P_eff predicted for our DNA-assembly was calculated based on the contour lengths l_n of all N + 1 sections along the backbone (see ESI for details†). For hybridized double-stranded sections, we applied a local persistence length of P_n = 50.0 nm, for non-hybridized single-stranded sections we chose P_n = 1.7 nm. The list of single and double stranded sections is given in the ESI.† Base pair opening at the end-points of the hybridized oligomers was included into the model as variation of the length of double – and single-stranded sections along the chain of 60nt-oligomers. For example, with two open base pairs per end point, there is a single-stranded section with a length of 4 nt between the double-stranded section with 56 bp length each.

The effective persistence length as a function of the number of open base pairs at the end-points of hybridized oligomers is shown in Fig. 5. A monotonous decrease with the number of open base pairs is observed. The persistence length of 10.2 nm as obtained in FlowFM experiments is predicted for an average number of 2.4 open base pairs per oligomer end-point (see Fig. 5B). This number corresponds to a fraction of about 8.7% single stranded bases at room temperature and is in good agreement with simulations of DNA hybridization and for experiments on melting DNA duplexes.^37–40 The effect of single-stranded gaps on the flexibility of DNA molecules was observed before in gel migration experiments and with electron microscopy.^7,41 Thermally activated duplex opening along the double stranded sections starting at mismatching base pairs or buldge loops can occurs also for a dsDNA construct without nicks and do not contribute to the reduction of persistence length observed in our study.⁴⁰ In Fig. 5, the persistence length for zero open base pairs does not equal 50 nm as expected for a fully double stranded DNA construct. This small deviation is due to the configuration of our particular DNA construct. We segmented the single stranded DNA-scaffold in 131 sections and identified thirteen regions along our plasmid scaffold that exhibit less secondary structure and can be used for efficient functionalization, for example for shear bridges. The sections around these regions differ in length and can also include short single stranded regions (see ESI Table1 for details†). The unusually small persistence length is thus in full agreement with expectations for a strongly segmented dsDNA with many nicks. Open base pairs at the end points of hybridized oligomers leave small sections of single-stranded DNA which facilitate the reduction of the overall effective persistence length by a factor of five. Thermally activated opening of base pairs also reduces the stability of DNA-duplexes. In the following section we will discuss their influence on the dissociation kinetics of shear bridges which lead to the loop formation.

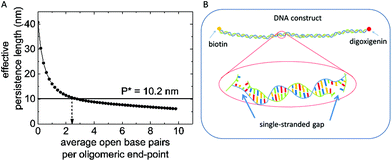Fig. 5 (A) Effective Persistence length as a function of open base pairs per oligomer end-point calculated with eqn (2). (B) Schematic of our self-assembled DNA construct, fluctuational base-pair opening at the end-point of the oligomers lead to single-stranded gaps in between the double stranded section of about 2–6 nucleotides.

In dynamic force-spectroscopy experiments, we observed a rupture force of about 40 pN for the highest loading rate of 7 pN s⁻¹. The rupture force compares well with values reported in ref. 29 for a similar loading rate, where the shearing force was studied for three DNA duplex lengths. In line with our experimental results, the authors observed a logarithmic increase of rupture force with loading rate. This is particularly interesting because the complexation rate for single DNA base pairs is on the order of 500 times per second.⁴² These high rates indicate a complexation which is five orders of magnitudes faster than the typical time scale of our force-spectroscopy experiment of seconds to minutes. Single base pairs are in thermodynamic equilibrium during the measurement. The loading rate dependence of the dissociation force then indicates that unbinding rates are lower for a DNA duplex. The lower dissociation rate suggests a cooperative unbinding of the individual base pairs forming the duplex. In force spectroscopy experiments, the force applied to the ends of the DNA construct loads all base pairs at the same time in a shear conformation. The base pairs at the end of each duplex can open up by thermal activation even without applied load. In case of applied load, the dissociation of one base pair leads to an immediate increase in contour length preventing the rebinding of the base pair. Next, the adjacent base pairs can open up leading to a sequential unzipping of the shearing bridge. At a certain force, all remaining base pairs are suddenly ruptured resulting in an abrupt change of conformation from the looped to the linear conformation for our DNA construct. An estimate for the number of bonds that are zipped open before the bond fully dissociates is provided by the length scale in the Bell-Evans model.²⁹ The length scale x_β reflects the distance between the bound state where the loop is formed and the transition state before the loop opens. From the Bell-Evans fit we obtained a length scale of x_β = 7.7 Å with a standard deviation of 4.4 Å, indicating that about 2–6 base pairs are opened before the bond dissociates, assuming an increase in contour length of 2 Å per base at a stretching force of 40 pN.⁴³ We attribute the higher contour length observed for the DNA loops to a similar effect. In contrast to double-stranded DNA, the contour length for single-stranded DNA increases over a wide range of forces and is about 0.57 nm per base at a force of 40 pN where the rupture occurs. A fraction of 8.7% single-stranded bases lead to an average contour length of 0.36 nm per base for the DNA construct at the moment of rupture, in excellent agreement with the contour length observed for the loop-opening.

Interestingly, no loading rate dependence was observed for the persistence length although the decrease in persistence length was attributed to similar thermal opening of base pairs at the end points of oligomers. The persistence length is determined from the bending of the force-extension curve in the low-force regime below 10 pN. In contrast to the high-force regime in which the bond-rupture of the DNA-duplex is observed, there is no difference in extension between single and double stranded sections in the low-force regime.⁴³ Without increase in extension length, a fast rebinding of open base pairs is possible. As consequence, the opening and rebinding of base pairs at the endpoints of oligomers occurs in equilibrium during the measurements of persistence length and no rate dependence is observed.

Conclusions

In conclusion, we demonstrate FlowFM as a novel technique for high-throughput dynamic force spectroscopy of single DNA constructs. Statistical distributions for the strength of relevant interactions such as antibody–antigen bonds or DNA shear bridges are readily obtained. The self-assembled DNA construct exhibits a persistence length of 10.2 nm, a factor of 5 lower compared to native double-stranded DNA. We attribute the higher flexibility to the segmented nature of self-assemblies used in DNA origami. Thermally induced base-pair openings at the end-points of complementary oligomers lead to single-stranded gaps in between double stranded segments which reduce the effective persistence length of the DNA construct. We believe that the results will contribute to the fundamental understanding of the mechanics of DNA assemblies and help to improve the design of DNA nanodevices. The FlowFM technique can easily be extended to other DNA constructs or polymers and has the potential to become a standard method for rapid nanomechanical testing of macromolecules. Moreover, our massively parallel approach with tethered particles allows to study rare events as demonstrated for a small number of DNA loops in a large population of linear DNA constructs. New techniques for studying rare events such as protein unfolding or antibody binding are an important asset in biological analysis and clinical research.

Materials and methods

DNA-assembly

The DNA-construct with anti-dioxigenin and biotin functionalities was assembled from circular M13mp18 ssDNA (New England Biolabs) similar to ref. 44 and 45 in two main steps. First, the single-stranded plasmid was linearized by enzymatic cleavage using BtscI (New England Biolabs) and a DNA-oligonucleotide complementary to the enzymatic cut site for 60 minutes at 50 °C, followed by a deactivation at 95 °C. 131 complementary oligomers (Intergrated DNA technologies) were designed to complement the single-stranded scaffold resulting in a double stranded DNA-construct with a segmented backbone. The first and last oligomer were functionalized with biotin or digoxigenin to enable attachment to the streptavidin-coated micrometer beads and the anti-digoxigenin functionalized surface of the channel wall. In the second step, the construct was assembled in a temperature ramp from 90 °C to 12 °C with −1 °C min⁻¹ using a 10-fold excess of DNA oligomers compared to the scaffold in presence of NEBuffer 2 (New England Biolabs). To prepare the single-stranded DNA construct, the backbone oligomers were omitted from the hybridization protocol (see ESI Fig. 3 for details†). The DNA constructs were stored at 4 °C and used immediately or stored at −20 °C for later use.

Assembly of looped DNA-construct

To design a looped DNA construct, two oligomers of 30 nt were not included into the hybridization procedure. Instead, a 60 nt oligomere with the sequence CTC AAA TAT CAA ACC CTC AAT CAA TAT CTC CAG AAC GAG TAG TAA ATT GGG CTT GAG ATG was added in 10-fold excess to the single-stranded scaffold to form rare shearing bridges with the DNA scaffold. The first 30 nt of the shear bridge oligomer are complementary to the one single-stranded region, the last 30 nt are complementary to the second single-stranded region. Upon hybridization of the 60 nt oligomer, the DNA construct forms a loop with a length of 3912 nt.

Surface preparation

Clean cover slips were functionalized with DNA probes using the specific binding between anti-digoxigenin and digoxigenin, where digoxigenin is coupled to the DNA construct (see DNA nanoswitch formation). In a three-step process, the cover slips were first coated with nitrocellulose (NC), followed by unspecific adsorption of anti-digoxigenin (anti-dig) which finally couples the dig-functionalized DNA constructs. First, the cleaned cover glass was coated with 1 μL of 0.2% NC solution and stored under low pressure. In the second step, the surface was incubated for 20 min with 0.05 g l⁻¹ anti-digoxigenin (Roche), diluted in 1× PBS, pH 7.4. After antibody attachment, the channel was passivated with 10 mg ml⁻¹ Western Blocking Reagent in PBS ordered from Sigma Aldrich for 1 h whereby the blocking solution was replaced every 15 min. Subsequently, the channel was rinsed thoroughly with 80 μl of 1× PBS, pH 7.4. The DNA constructs were attached to streptavidin-coated Dynabeads MyOne C1 ordered from Thermo Fisher Scientific. The Dynabeads were washed extensively and diluted to a concentration of 1 g mL⁻¹ in PBS before mixing with DNA constructs, incubated for a minimum of 5 min and subsequently introduced into the fluid chamber. After tethering, the chamber was flipped upside down and loose beads were washed out by applying a gentle fluid flow of 2 μl min⁻¹.

Assembly of fluid cell

The fluid cell was constructed by sandwiching a double-sided Kapton tape between a nitrocellulose coated cover slip and a microscopy slide. A 1 mm × 10 mm rectangular channel was cut into the Kapton tape using a CO₂ laser cutter. Two 0.8 mm holes were drilled into the microscopy slide as in- and outlet for solutions. The tubing was connected to the in- and outlet via 10 μl pipette tips gently pushed into the holes.

Flow cell measurement

All Flow cell measurements were performed with a syringe pump (Al-100 World Precision Instruments, Saratosa, USA) equipped with a 1 ml syringe. A CCD camera (DMK 33GX178, ImagingSource, Bremen, Deutschland) was mounted on a standard optical microscope. A 20× magnification was used for recording the movement of surface-tethered beads in one field of view with a sampling rate of 5 fps. Prior to every experiment, the random motion of the beads was recorded for 60 s. The tethered particle motion allows for determination of the center of gyration and the symmetry of the bead motion that was used to single out single-tethered beads. Subsequently, a laminar flow with rates from 0 μl min⁻¹ to 500 μl min⁻¹ was applied. Particularly for high force-loading ramps, the actual flow rate in the channel can vary from the expected flow rate when assuming a linear flow profile. To determine the actual flow rate in the channel, the height of the fluid in the reservoir pipette was tracked with an additional camera for each force loading rate (see ESI† for details on force calibration).

Data analysis

The videos were analyzed using the open source software ImageJ 1.50i (Wayne Rasband, National Institute of Health, USA) and a particle tracker ImageJ Plugin written by Sbalzarini and Koumoutsakos.⁴⁶ The particle tracker provides x and y positions of each individual bead over time. The ImageJ software includes all trajectories into a table that was further analyzed with a custom script written in python. The tether extension was calculated from the bead displacement in the in-plane coordinates x and y with a trigonometric function, see ESI Fig. 2† for details. Single-tethered particles were singled out using the symmetry-test of the tethered particle motion for 60 s without flow. The symmetry factor S relies on the observation that single-tethered particles show a symmetric in-plane motion and is calculated from the eigenvalues of the covariance matrix of particle positions.⁴⁷ Particles with a symmetry factor between 1 and 1.1 are considered as single-tethered and included in further analysis. We calibrated the flow force for each experiment using the overstretching transition from double to single-stranded DNA. The transfer from double-stranded DNA to single-stranded DNA can be observed as a sudden elongation of tether length starting at 60 pN.

DNA looping experiments

To observe rare DNA loops, we first recorded the motion of the tethered beads for 1 minute, well above the proposed observation time for a micrometer-sized beads and several kbp long DNA tether.⁴⁷ The root mean square movement for each single-tethered bead was analyzed with an experimental error of below 20 nm, see ESI Fig. 2† for details. In force spectroscopy experiments on DNA constructs, we studied the forced loop-opening of the DNA duplex that was observed as a sudden change in tether length. A length-change was counted as rupture event when the bead was tracked for a minimum of three data points after a length-change of more than 0.5 μm occurred.

Atomic force spectroscopy experiments

AFM experiments are performed with a JPK Nanowizard 3 Setup on the same surface and beads as described for the FlowFM measurements. Instead of mounting the fluidic cell, the preparation and measurement was carried out on the flat cover slip that was functionalized with NC, digoxigening and DNA as described in the section surface preparation. After adding the micro beads, the surface was washed intensively to remove loose beads before placing the sample in the AFM. Gold-coated tipless MLCT-O01 C cantilevers purchased from Bruker with a nominal spring constant of 0.01 N m⁻¹ were functionalized with BSA-biotin (1 mg ml⁻¹ in PBS) over night. The sensitivity of the force probes was determined from force–distance curves for each cantilever on a hard glass surface. Prior to force-spectroscopy measurements, the biotin-functionalized cantilever was placed above a streptavidin-coated bead and a force–distance curve with a dwell time of 1s was conducted to adhere the bead to the cantilever. Force–distance curves were recorded with a velocity of 1 μm s⁻¹ and a dwell time of 1 s to allow the digoxigenin group attached to the free end of the DNA to find an anti-digoxigenin binding site on the surface. To reduce thermal drift, a waiting time of more than 1 hour was included before starting single-molecule force spectroscopy measurements. The data analysis was carried out in three steps. First, the force probes have been calibrated using the overstretching plateau as described for FlowFM. Second, the pulling distance was converted to tip–surface distance and in the third step, the WLC model was fit to the experimental data in the low-force regime below 10 pN.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Authors acknowledge Joachim Blau for technical support with FlowFM setup; J. B. acknowledges Wesley P. Wong and Darren Yang for contributions to the initial concept, instrumentation, and experimental design, as well as valuable discussions and experimental help with conducting flow measurements on DNA constructs in microfluidic channels.

Notes and references

1. P. W. K. Rothemund, Folding DNA to create nanoscale shapes and patterns, Nature, 2006, 440, 297–302,  DOI:10.1038/nature04586.
2. K. F. Wagenbauer, C. Sigl and H. Dietz, Gigadalton-scale shape-programmable DNA assemblies, Nature, 2017, 552, 78–83,  DOI:10.1038/nature24651.
3. H. Yu, D. T. L. Alexander, U. Aschauer and R. Häner, Synthesis of Responsive Two-Dimensional Polymers via Self-Assembled DNA Networks, Angew. Chem., Int. Ed., 2017, 56, 5040–5044,  DOI:10.1002/anie.201701342.
4. D. Yang, M. J. Campolongo, T. N. Nhi Tran, R. C. H. Ruiz, J. S. Kahn and D. Luo, Novel DNA materials and their applications, Wiley interdisciplinary reviews, Nanomed. Nanobiotechnol., 2010, 2, 648–669,  DOI:10.1002/wnan.111.
5. C. Rivetti, C. Walker and C. Bustamante, Polymer chain statistics and conformational analysis of DNA molecules with bends or sections of different flexibility, J. Mol. Biol., 1998, 280, 41–59,  DOI:10.1006/jmbi.1998.1830.
6. J. B. Hays and B. H. Zimm, Flexibility and stiffness in nicked DNA, J. Mol. Biol., 1970, 48, 297–317,  DOI:10.1016/0022-2836(70)90162-2.
7. J. B. Mills, J. P. Cooper and P. J. Hagerman, Electrophoretic evidence that single-stranded regions of one or more nucleotides dramatically increase the flexibility of DNA, Biochemistry, 1994, 33, 1797–1803,  DOI:10.1021/bi00173a024.
8. T. E. Cloutier and J. Widom, DNA twisting flexibility and the formation of sharply looped protein-DNA complexes, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 3645–3650,  DOI:10.1073/pnas.0409059102.
9. Y. Zhang and D. M. Crothers, High-throughput approach for detection of DNA bending and flexibility based on cyclization, Proc. Natl. Acad. Sci. U. S. A., 2003, 100, 3161–3166,  DOI:10.1073/pnas.0530189100.
10. D. Demurtas, A. Amzallag, E. J. Rawdon, J. H. Maddocks, J. Dubochet and A. Stasiak, Bending modes of DNA directly addressed by cryo-electron microscopy of DNA minicircles, Nucleic Acids Res., 2009, 37, 2882–2893,  DOI:10.1093/nar/gkp137.
11. M. D. Wang, H. Yin, R. Landick, J. Gelles and S. M. Block, Stretching DNA with optical tweezers, Biophys. J., 1997, 72, 1335–1346,  DOI:10.1016/S0006-3495(97)78780-0.
12. T. P. Hoekstra, M. Depken, S.-N. Lin, J. Cabanas-Danés, P. Gross, R. T. Dame, E. J. G. Peterman and G. J. L. Wuite, Switching between Exonucleolysis and Replication by T7 DNA Polymerase Ensures High Fidelity, Biophys. J., 2017, 112, 575–583,  DOI:10.1016/j.bpj.2016.12.044.
13. S. B. Smith, L. Finzi and C. Bustamante, Direct mechanical measurements of the elasticity of single DNA molecules by using magnetic beads, Science, 1992, 258, 1122–1126,  DOI:10.1126/science.1439819.
14. M. Rief, H. Clausen-Schaumann and H. E. Gaub, Sequence-dependent mechanics of single DNA molecules, Nat. Struct. Biol., 1999, 6, 346–349,  DOI:10.1038/7582.
15. W. P. Wong, J. Blass, D. Yang and C. H. Hansen, Children's Medical Center Corporation, WO/2019/100080, 2018.
16. K. Halvorsen and W. P. Wong, Massively parallel single-molecule manipulation using centrifugal force, Biophys. J., 2010, 98, L53–L55,  DOI:10.1016/j.bpj.2010.03.012.
17. I. de Vlaminck, T. Henighan, M. T. J. van Loenhout, I. Pfeiffer, J. Huijts, J. W. J. Kerssemakers, A. J. Katan, A. van Langen-Suurling, E. van der Drift, C. Wyman and C. Dekker, Highly parallel magnetic tweezers by targeted DNA tethering, Nano Lett., 2011, 11, 5489–5493,  DOI:10.1021/nl203299e.
18. G. Sitters, D. Kamsma, G. Thalhammer, M. Ritsch-Marte, E. J. G. Peterman and G. J. L. Wuite, Acoustic force spectroscopy, Nat. Methods, 2015, 12, 47–50,  DOI:10.1038/nmeth.3183.
19. A. M. van Oijen, P. C. Blainey, D. J. Crampton, C. C. Richardson, T. Ellenberger and X. S. Xie, Single-molecule kinetics of lambda exonuclease reveal base dependence and dynamic disorder, Science, 2003, 301, 1235–1238,  DOI:10.1126/science.1084387.
20. Y. Zheng, M. K. L. Han, R. Zhao, J. Blass, J. Zhang, D. W. Zhou, J.-R. Colard-Itté, D. Dattler, M. Hoth, A. J. García, B. Qu, R. Bennewitz, N. Giuseppone and A. del Campo, Optoregulated force application to cellular receptors using molecular motors, bioRxiv, (preprint posted 2020). DOI: DOI:10.1101/2020.03.31.015198.
21. G. Neuert, C. Albrecht, E. Pamir and H. E. Gaub, Dynamic force spectroscopy of the digoxigenin-antibody complex, FEBS Lett., 2006, 580, 505–509,  DOI:10.1016/j.febslet.2005.12.052.
22. F. Flyvbjerg, F. Jülicher, P. Ormos, F. David and H. Flyvbjerg, ed. Physics of bio-molecules and cells. Physique des biomolécules et des cellules. Session LXXV. 2-27 July 2001, Springer, Berlin, 2002, vol. 75.
23. J. van Mameren, P. Gross, G. Farge, P. Hooijman, M. Modesti, M. Falkenberg, G. J. L. Wuite and E. J. G. Peterman, Unraveling the structure of DNA during overstretching by using multicolor, single-molecule fluorescence imaging, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 18231–18236,  DOI:10.1073/pnas.0904322106.
24. A. Brunet, C. Tardin, L. Salomé, P. Rousseau, N. Destainville and M. Manghi, Dependence of DNA Persistence Length on Ionic Strength of Solutions with Monovalent and Divalent Salts, Macromolecules, 2015, 48, 3641–3652,  DOI:10.1021/acs.macromol.5b00735.
25. C. Bustamante, J. F. Marko, E. D. Siggia and S. Smith, Entropic elasticity of lambda-phage DNA, Science, 1994, 265, 1599–1600,  DOI:10.1126/science.8079175.
26. D. Yang, A. Ward, K. Halvorsen and W. P. Wong, Multiplexed single-molecule force spectroscopy using a centrifuge, Nat. Commun., 2016, 7, 11026,  DOI:10.1038/ncomms11026.
27. D. Song, B. Mousley, S. Gambino, E. Helou, J. Loparo and A. C. Price, Tethered particle motion with single DNA molecules, Am. J. Phys., 2015, 83, 418–426,  DOI:10.1119/1.4902187.
28. D. E. Segall, P. C. Nelson and R. Phillips, Volume-exclusion effects in tethered-particle experiments, Phys. Rev. Lett., 2006, 96, 88306,  DOI:10.1103/PhysRevLett.96.088306.
29. T. Strunz, K. Oroszlan, R. Schäfer and H. J. Güntherodt, Dynamic force spectroscopy of single DNA molecules, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 11277–11282,  DOI:10.1073/pnas.96.20.11277.
30. V. V. Naik, M. Crobu, N. V. Venkataraman and N. D. Spencer, Multiple Transmission-Reflection IR Spectroscopy Shows that Surface Hydroxyls Play Only a Minor Role in Alkylsilane Monolayer Formation on Silica, J. Phys. Chem. Lett., 2013, 4, 2745–2751,  DOI:10.1021/jz401440d.
31. J. Blass, M. Albrecht, G. Wenz, R. Guerra, M. Urbakh and R. Bennewitz, Multivalent Adhesion and Friction Dynamics Depend on Attachment Flexibility, J. Phys. Chem. C, 2017, 121, 15888–15896,  DOI:10.1021/acs.jpcc.7b05412.
32. P. Furrer, J. Bednar, A. Z. Stasiak, V. Katritch, D. Michoud, A. Stasiak and J. Dubochet, Opposite effect of counterions on the persistence length of nicked and non-nicked DNA, J. Mol. Biol., 1997, 266, 711–721,  DOI:10.1006/jmbi.1996.0825.
33. M. R. Sawaya, R. Prasad, S. H. Wilson, J. Kraut and H. Pelletier, Crystal structures of human DNA polymerase beta complexed with gapped and nicked DNA, Biochemistry, 1997, 36, 11205–11215,  DOI:10.1021/bi9703812.
34. N. Maizels and L. Davis, Initiation of homologous recombination at DNA nicks, Nucleic Acids Res., 2018, 46, 6962–6973,  DOI:10.1093/nar/gky588.
35. M.-N. Dessinges, B. Maier, Y. Zhang, M. Peliti, D. Bensimon and V. Croquette, Stretching single stranded DNA, a model polyelectrolyte, Phys. Rev. Lett., 2002, 89, 248102,  DOI:10.1103/PhysRevLett.89.248102.
36. J. F. Marko and E. D. Siggia, Stretching DNA, Macromolecules, 1995, 28, 8759–8770,  DOI:10.1021/ma00130a008.
37. Y. Yin and X. S. Zhao, Kinetics and dynamics of DNA hybridization, Acc. Chem. Res., 2011, 44, 1172–1181,  DOI:10.1021/ar200068j.
38. T. E. Ouldridge, P. Sulc, F. Romano, J. P. K. Doye and A. A. Louis, DNA hybridization kinetics, Nucleic Acids Res., 2013, 41, 8886–8895,  DOI:10.1093/nar/gkt687.
39. Y. Li, L. Zhao, Y. Yao and X. Guo, Single-Molecule Nanotechnologies, ACS Appl. Bio Mater., 2019, 3, 68–85,  DOI:10.1021/acsabm.9b00840.
40. C. Trapp, M. Schenkelberger and A. Ott, Stability of double-stranded oligonucleotide DNA with a bulged loop, BMC Biophys., 2011, 4, 20,  DOI:10.1186/2046-1682-4-20.
41. E. Protozanova, P. Yakovchuk and M. D. Frank-Kamenetskii, Stacked-unstacked equilibrium at the nick site of DNA, J. Mol. Biol., 2004, 342, 775–785,  DOI:10.1016/j.jmb.2004.07.075.
42. M. Guéron and J.-L. Leroy, in Nuclear Magnetic Resonance and Nucleic Acids, Elsevier, 1995, pp. 383–413.
43. M. C. Williams, J. R. Wenner, I. Rouzina and V. A. Bloomfield, Entropy and Heat Capacity of DNA Melting from Temperature Dependence of Single Molecule Stretching, Biophys. J., 2001, 80, 1932–1939,  DOI:10.1016/S0006-3495(01)76163-2.
44. C. H. Hansen, D. Yang, M. A. Koussa and W. P. Wong, Nanoswitch-linked immunosorbent assay (NLISA) for fast, sensitive, and specific protein detection, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 10367–10372,  DOI:10.1073/pnas.1708148114.
45. M. A. Koussa, K. Halvorsen, A. Ward and W. P. Wong, DNA nanoswitches, Nat. Methods, 2015, 12, 123–126,  DOI:10.1038/nmeth.3209.
46. I. F. Sbalzarini and P. Koumoutsakos, Feature point tracking and trajectory analysis for video imaging in cell biology, J. Struct. Biol., 2005, 151, 182–195,  DOI:10.1016/j.jsb.2005.06.002.
47. Mathematics of DNA Structure, Function and Interactions, ed. C. J. Benham, S. Harvey, W. K. Olson, D. W. Sumners and D. Swigon, Springer Science+Business Media LLC, New York, NY, 2009, vol. 150.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/d0nr06865a

---