Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thermo-osmosis in hydrophilic nanochannels: mechanism and size effect
Wei Qiang
Chen
,
Majid
Sedighi
 * and
Andrey P.
Jivkov
*
* and
Andrey P.
Jivkov
*
Department of Mechanical, Aerospace and Civil Engineering, School of Engineering, The University of Manchester, Manchester, M13 9PL, UK. E-mail: Majid.Sedighi@manchester.ac.uk; Andrey.Jivkov@manchester.ac.uk
First published on 11th January 2021
Abstract
Understanding thermo-osmosis in nanoscale channels and pores is essential for both theoretical advances of thermally induced mass flow and a wide range of emerging industrial applications. We present a new mechanistic understanding and quantification of thermo-osmosis at nanometric/sub-nanometric length scales and link the outcomes with the non-equilibrium thermodynamics of the phenomenon. The work is focused on thermo-osmosis of water in quartz slit nanochannels, which is analysed by molecular dynamics (MD) simulations of mechano-caloric and thermo-osmotic systems. We investigate the applicability of Onsager reciprocal relation, irreversible thermodynamics, and continuum fluid mechanics at the nanoscale. Further, we analyse the effects of channel size on the thermo-osmosis coefficient, and show, for the first time, that these arise from specific liquid structures dictated by the channel size. The mechanical conditions of the interfacial water under different temperatures are quantified using a continuum approach (pressure tensor distribution) and a discrete approach (body force per molecule) to elucidate the underlying mechanism of thermo-osmosis. The results show that the fluid molecules located in the boundary layers adjacent to the solid surfaces experience a driving force which generates the thermo-osmotic flow. While the findings provide a fundamental understanding of thermo-osmosis, the methods developed provide a route for analysis of the entire class of coupled heat and mass transport phenomena in nanoscale structures.
1 Introduction
Thermo-osmosis is a non-equilibrium heat and mass transfer cross-phenomenon. It is one of the main physical mechanisms of thermally induced particle motion. While the other observed mechanisms, generically referred to as the thermophoresis (also thermal diffusion or the Ludwig–Soret effect), involve thermally induced migration of particle mixtures, e.g., thermally induced flux of aqueous species relative to the fluid, thermo-osmosis describes the migration of a single-component fluid due to thermal gradients. This mechanism is encountered in many areas of biology,1 chemistry,2 energy,3,4 separation and membrane technologies5 and energy geo-structures.6,7 Although its discovery has been reported as early as 1907,8 the need for an in-depth understanding of thermo-osmosis has re-emerged recently due to the important role of thermo-osmosis in a wide range of engineering processes and technologies (e.g. membrane systems, thermo-osmotic energy conversion heat recovery; geo-energy systems). In the fields of energy and environment, the thermo-osmotic response of nanoporous membranes has been used for low-grade waste heat harvesting3,4 and recovery of water from organic wastewater solution.5 Thermo-osmosis has also been reported to be an important process for fuel cell operation.2 In addition, quantifying the role of thermo-osmosis in tight rocks (e.g. shale) and clay soils is essential for underpinning the design and safety assessments of many geotechnical infrastructures such as nuclear waste repositories and ground-source heat or energy foundations.6,7Compared to the theoretical studies of thermophoresis, in particular thermal diffusion,9–13 the microscopic mechanistic understanding of thermo-osmosis is rather incomplete, although its macroscopic thermodynamical description has been widely discussed and used both in modelling multiscale–multiphase couplings problems14,15 and in experimental works.16,17 In fact, there is a debate between two approaches for describing the underlying mechanism for thermo-osmosis, namely the interfacial approach and the energetic approach.18 Further understanding of thermo-osmosis at the nanoscale is of particular interest because the very limited studies of thermo-osmosis at solid–fluid interfaces19–23 do not allow for linking the two approaches and for a complete understanding of the underlying mechanisms.
The parameter controlling thermo-osmosis is the thermo-osmotic coefficient. It describes the magnitude of fluid flux induced by a unit temperature gradient. Experimental and theoretical works have shown that the thermo-osmotic coefficient can be described as a function of the interfacial excess enthalpy distribution of the fluid and its hydrodynamic properties at the interface.24 However, the influence of various factors on the mechanism of thermo-osmosis is still unclear. For example, the excess enthalpy distribution is affected by temperature, pressure, liquid polarity,25 and liquid structure in the boundary layer.19 This makes it difficult to be experimentally measured.21,26 The experimental results from previous studies16,17 also show that the magnitude and the direction of thermo-osmotic flow can vary for different types of chemicals. Furthermore, the existing formulas for the thermo-osmotic coefficient are derived on the basis of a local continuum theory,21e.g. Navier–Stokes equation, where assumptions are made on the fluid properties near the solid surface including the excess enthalpy distribution and fluid viscosity. Such continuum approximations may be sufficient for solid–fluid interfaces at larger length scales. However, for the solid–fluid interfaces at the nanometric/sub-nanometric scales, the validity of the continuum description for the interfacial liquid structure or hydrodynamics is not proven. Understanding thermo-osmosis at such length scales requires a mechanistic approach.
Analysis of thermo-osmosis at solid–fluid interfaces by molecular dynamics (MD) is the natural approach to address the knowledge gap, as it provides direct, comprehensive and detailed information on the microscopic thermodynamic states and hydrodynamic characteristics at the interfaces. Several groups have started utilising the approach. For instance, Ganti et al.21 reported that different schemes of MD simulations to measure the thermo-osmotic coefficient would yield consistent results. Fu et al.20 investigated the effect of interfacial wettability and interfacial hydrodynamic characteristics on the thermo-osmotic coefficient. However, little progress has been made on the understanding and quantification of the relation between the thermo-osmotic response and the interfacial fluid structure.
The aims of this work are to develop a new mechanistic understanding and theoretical description of thermo-osmosis at nanometric/sub-nanometric length scales and to link with the non-equilibrium thermodynamic formulation of the coupled phenomenon. The system selected for investigation is quartz and water. This choice is dictated by two constraints. Firstly, the molecular dynamics limits the spatial dimension of the system that is analysed to nanochannels of several nanometres width. Secondly, the inclusion of charged minerals (e.g., kaolinite) and aqueous solutes will not produce pure thermo-osmotic flow, as surface charges and concentration gradient will create unwanted coupling effects. Quartz is electrically neutral and accounts for approximately 20% of the Earth's exposed crust,27 making it a major constituent of soils, clays, and rocks. It is acknowledged that such systems contain a multitude of minerals, but it is reasonable to consider that nanoscale pores are formed in single minerals. Moreover, understanding water interaction in quartz or other silica phases is of interest to many fields such as geology,28 biology,29 physics30,31 and chemistry.32,33 This specific system is also relevant to membrane science as there are membranes made up quartz and other silica phases such as hydrophilic quartz fibre membranes34 and silica membranes.35 While a number of studies have been dedicated to the interactions of water with quartz and other silica phases, research on temperature effects, such as thermo-osmosis, in quartz–water systems is very limited. This is in contrast with the need to understand such effects, since natural or artificial temperature gradients are ubiquitous in the real quartz–water system, and they may generate substantial, otherwise unaccounted for mass transport. Besides, quartz surfaces can be fully hydroxylated within the water environment, exhibiting strong hydrophilicity.36 Therefore, investigation on the quartz–water interfaces can naturally provide fundamental insights to the studies on fluid properties in the hydrophilic environment.
The aims of the work are achieved by molecular dynamics simulations of thermo-osmosis in quartz slit nanochannels. Microscopic thermo-osmotic coefficients are measured by mechano-caloric and thermo-osmotic systems, introduced in sections 2.2. Results presented in sections 3.1 demonstrates the validity of Onsager reciprocal relation at nanoscale and consistency between the microscopic thermo-osmotic coefficient and the macroscopic thermo-osmotic coefficient based on irreversible thermodynamics. The dependence of the thermo-osmotic coefficient on the channel size is analysed in section 3.2. It is quantified and found to be a consequence of the changing liquid structure in boundary layers adjacent to the solid surfaces. The changing liquid structure alters either the excess enthalpy distribution or the hydrodynamic properties of the interfacial water. The mechanism of thermo-osmosis in quartz nanochannels is revealed in section 3.3 by quantifying the mechanical interactions of the interfacial water under different temperatures using a continuum approach (pressure tensor distribution) and a discrete approach (body force per molecule). It is found that the fluid molecules experience a driving force for thermo-osmotic flow only in the boundary layers adjacent to the solid surfaces. The systems analysed, the analysis methods, and the insights of this work provide a solid foundation for future research in the field of thermophoretic phenomena.
2 Theory and method
In this section, we describe the macroscopic/thermodynamic and the microscopic/mechanistic perspectives to thermo-osmosis in nano-sized systems. We are interested in the coefficients of proportionality between different gradients (pressure and temperature) and fluxes (fluid and heat). In order to distinguish between the two perspectives, we will denote the coefficients of the thermodynamic formulation (macroscopic coefficients) with uppercase letters, and the coefficients of the mechanistic formulation (microscopic coefficients) with lowercase letters. The thermodynamic formulation, introduced in section 2.1, shows the dependence of the macroscopic coefficients on the system size, interfacial hydrodynamics and the excess enthalpy density. Determining excess enthalpy for nano-sized systems requires molecular-level analysis, which leads to the mechanistic formulation by MD models introduced in section 2.2. The MD simulation details are provided in section 2.3, while the calculation of various parameters from these simulations is presented in section 2.4.2.1 Irreversible thermodynamics of thermo-osmosis in nanochannels
Based on irreversible thermodynamics, coupled fluid flow and heat transfer can be described by the following system of equations22,26,37,38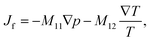 | (1) |
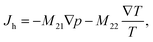 | (2) |
The off-diagonal parameter M12 in eqn (1) is the macroscopic thermo-osmotic coefficient, which controls the fluid flux induced by a temperature gradient. The off-diagonal parameter M21 in eqn (2) is the macroscopic mechano-caloric coefficient, which controls the heat flux induced by a hydraulic pressure gradient. The Onsager reciprocal relation for this coupling states that M12 = M21.39,40
We consider a quartz slit nanochannel and introduce x-axis parallel to and z-axis normal to the quartz surfaces (z = 0 at a surface). Further, we consider coupled fluid flow and heat transfer described by eqn (1) and (2), resulting from a non-zero applied temperature gradient along the x-axis and a zero applied hydraulic pressure gradient. In this situation, the fluid flux is induced by the thermal gradient alone and governed by the thermo-osmotic coefficient.
The changes of temperature, dT, and pressure, dp, are related to the changes of the chemical potential of a single component system, dμ, via the Gibbs–Duhem equation
| Ndμ = −SdT + Vdp, | (3) |
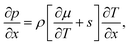 | (4) |
The variation of the chemical potential with temperature in eqn (4) can be simplified under the condition of hydrostatic equilibrium in the bulk fluid,21,41i.e. for z → +∞. In this case p equals the bulk fluid pressure pb, and
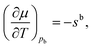 | (5) |
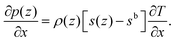 | (6) |
The normal variation of the specific entropy of the interfacial fluid molecules can be described by21
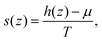 | (7) |
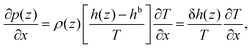 | (8) |
Then we can then solve the linearized (Navier–)Stokes equation as
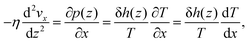 | (9) |
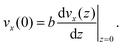 | (10) |
The thermo-osmotic velocity in the bulk fluid is then obtained as20
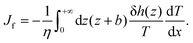 | (11) |
Eqn (8) shows that a temperature gradient applied to the interfacial fluid results in a pressure gradient parallel to the surface, which drives the thermo-osmosis with fluid flux given by eqn (11). Comparing eqn (1) and (11) and recalling the condition of zero applied hydraulic pressure, leads to the following expression for the macroscopic thermo-osmotic coefficient, and via Onsager reciprocal relations the macroscopic mechano-caloric coefficient
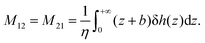 | (12) |
When no-slip (stick) boundary condition is applied,44i.e. when b = 0 (or when the fluid/solid friction coefficient κ → ∞), eqn (12) reduces to
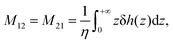 | (13) |
2.2 Molecular dynamics setup for nanochannel simulations
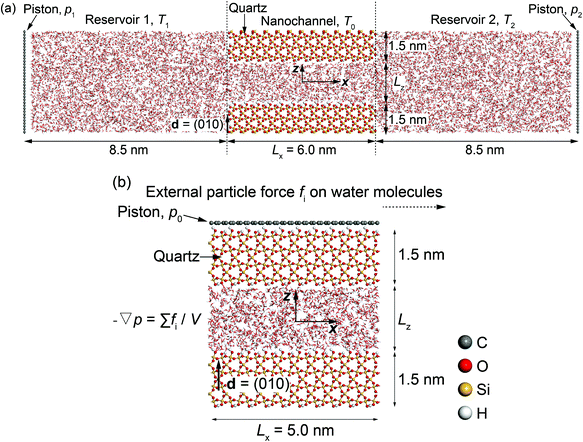
Two molecular dynamics systems are used to calculate the phenomenological coefficients controlling thermo-osmosis in quartz slit nanochannels. These include a thermo-osmotic system, illustrated in Fig. 2(a), which follows a similar carbon nanotube membrane and water system devised by Fu et al.,42 and a mechano-caloric system, illustrated in Fig. 2(b), which is developed based on a similar system by Fu et al.20 primarily for Lennard-Jones liquid and Einstein solids, as well as graphene–water systems. Both systems contain a slit nanochannel of width Lz between two quartz slabs of 1.5 nm thickness each. The size of the simulation domains in y direction is 5.0 nm (Ly = 5.0 nm).In the thermo-osmotic system, Fig. 2(a), the nanochannel is connected to two water reservoirs with pressure applied by two rigid graphene pistons. MD simulations with this system are performed with two sets of boundary conditions. The first set prescribes equal pressure at the pistons, i.e. zero applied pressure gradient, and different temperatures in the two reservoirs, i.e. non-zero applied thermal gradient along the quartz nanochannel. This allows for obtaining the microscopic thermo-osmotic coefficient m12, as well as m22 if required, from calculated fluid and heat fluxes, respectively. The second set of boundary conditions prescribes different pressures at the pistons, i.e. applied non-zero pressure gradient, and equal temperatures in the two reservoirs, i.e. zero applied thermal gradient. This allows for obtaining the microscopic mechano-caloric coefficient m21, as well as m11, from calculated fluid and heat fluxes at the two ends of the nanochannel, respectively. In both sets, periodic boundary conditions are considered in y and z-direction. The MD simulations provide further the excess enthalpy density, required for the calculation of the macroscopic coefficients by eqn (12) or (13). The thermo-osmotic system is adopted only to demonstrate the thermo-osmosis phenomenon and validate the Onsager reciprocity relations, while the majority of the results are obtained with the mechano-caloric system. Details of the use of the thermo-osmotic system are given in Appendix A.
In the mechano-caloric system, Fig. 2(b), a graphene piston, which is composed of a two-dimensional monolayer of sp2-bonded carbon (C) atoms in a hexagonal honeycomb lattice, is set at the top of the upper quartz slab with a pressure of 1 atmosphere in the negative z-direction. In the simulations, we apply periodic boundary conditions in x and y directions. A body force per particle fi is exerted to every water molecule to generate an external pressure gradient ∇p parallel to the x-axis – an approach commonly employed in previous studies.47–49 Notably, this approach is different from the thermo-osmotic system, where the external pressure was applied by two rigid graphene pistons. Previous study50 suggested that these two different approaches should lead to highly consistent outcomes. The generated Poiseuille flow induces an excess heat flux, which allows for independent from the thermo-osmotic system calculation of the microscopic mechano-caloric coefficient m21. The reason for considering the mechano-caloric system is that the simulations with the thermo-osmotic system require a relatively high computational cost. Demonstrating that the two systems lead to the same coefficient and that the Onsager reciprocal relations are fulfilled will allow for subsequent parametric studies with the computationally simpler mechano-caloric system. Importantly, the mechano-caloric system is used for explaining the mechanism of thermo-osmosis in section 3.3.
To observe the structural and dynamical behaviours of this quartz-water system, the simulation domains were segmented into equal bins of size 0.004 nm. The selection of this size of bins is justified in Appendix B. The bins have been used to calculate average temperature, mass density, number density, charge, excess enthalpy, velocity, and pressure profiles.
2.3 Molecular dynamics simulation procedure
All MD simulations have been performed with the LAMMPS51 and visualized with the VMD52 package. The crystal structure of α-quartz (α-SiO2)27,53 is adopted to build the quartz slit nanochannels, and sufficient water molecules are added to fill the nanochannels and reservoirs. The typical surface d = (010)54,55 of bulk α-quartz structure is cleaved as the quartz–water interface. This is illustrated in Fig. 3 together with the distribution of partial charges at the quartz surface sites. Due to the discontinuity of the bulk α-quartz structure at the quartz–water interface, the under-coordinated surface oxygen (O) and silicon (Si) atoms are capped with hydrogen (H) or hydroxyl (OH) groups as in previous studies.30,56,57 Simulations are conducted in the NVT ensemble with a 1.0 fs time step, and the long-range coulombic (electrostatic) interactions are resolved by the particle–particle and particle–mesh (PPPM) method58 and temperature is controlled by a canonical sampling thermostat that uses global velocity rescaling with Hamiltonian dynamics.59 Regarding the force field, ClayFF, parameterized by Cygan et al.60 for describing the interaction of clays with water, is adopted to describe the quartz–water system in our simulations and the flexible single point charge (SPC)61,62 water model is used in this forcefield.60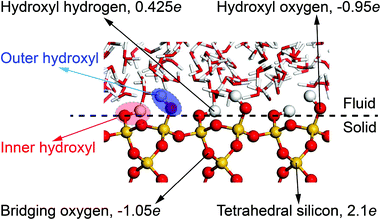 | ||
| Fig. 3 Distribution of partial charges at the quartz–water interface. The position of oxygen in inner hydroxyl groups is taken to define quartz surfaces. | ||
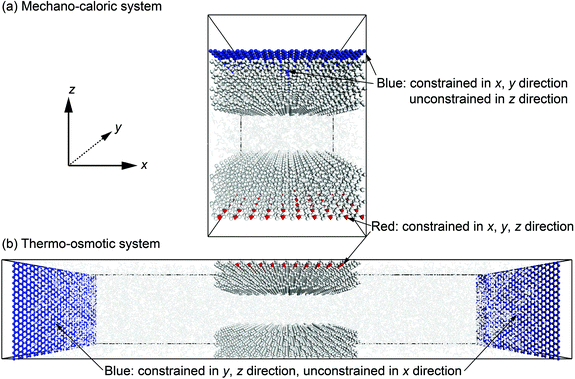
Note that in the ClayFF force field, the bond interactions only define the hydroxyl (–OH) on the quartz surfaces and O–H bonds in water molecules. In our simulations, some silicon (Si) atoms in the upper and lower quartz slabs are fully or partially constrained to achieve the stability of the nanochannels during the simulations. The carbon (C) atoms in the graphene pistons are only allowed to move in one direction to apply constant pressure to the fluid. Fig. 4 illustrates the degrees of freedom of atoms in mechano-caloric system and thermo-osmotic systems. Thermostats are applied to all atoms except for the constrained silicon (Si) atoms.
The graphene pistons are maintained rigidly in order to restrict potential distortions and to exert a constant and uniform normal pressure on the water. A Lennard-Jones 12-6 potential and Lorentz–Berthelot combining rules60,63 are used for the description of the intermolecular interactions between graphene pistons and water molecules. Table 1 lists the adopted potential parameters for graphene pistons, which are similar to those used by Wang et al.64 A cutoff radius of 1.5 nm is used for both Lennard-Jones interactions and coulombic interactions in the system.
| Atoms | Masses (u) | σ (Å) | ε (kJ mol−1) | q(e) | |
|---|---|---|---|---|---|
| Graphene pistons | Carbon | 12.01115 | 3.39848 | 0.29288 | 0.00000 |
2.4 Calculations of fields and coefficients
The pressure tensor of interfacial water is calculated by using the atom-based virial equation.65 The pressure variation of interfacial water along x-direction (or y, z-direction if required) is calculated by21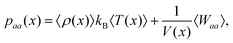 | (14) |
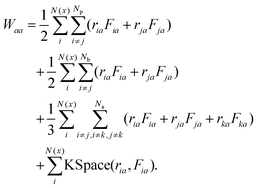 | (15) |
In eqn (15), N(x) is the number of atoms in the bin at position x, Np is the number of neighbours of atom i, Nb is the number of bonds containing atom i, Na is the number of angles containing atom i. r1 and r2 represent the positions of the pairwise interacting two atoms. F1 and F2 stand for the forces acting on the two atoms as the result of the pairwise interaction. The first term on the right-hand side of eqn (15) is a pairwise energy contribution from all Np neighbours. The second term is a bond contribution from all Nb bonds. The third term is an angle contribution from all Na angles. The fourth term is the KSpace contribution which is as the result of the long-range coulombic interactions.
Based on eqn (2), the mechano-caloric system, Fig. 2(b), subjected to pressure gradient is used to calculate the microscopic mechano-caloric coefficient m21 by
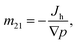 | (16) |
 | (17) |
The local specific enthalpy is found by21
| h(z) = u(z) + pxx(z), | (18) |
| δh(z) = h(z) − hb, | (19) |
| hb = h(z = 0). | (20) |
The fluid velocity profile of the planar Poiseuille flow, which is generated by a pressure gradient ∇p in the nanochannel can be theoretically computed by solving the Stokes equation66
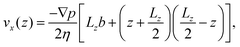 | (21) |
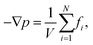 | (22) |
3 Results and discussion
Due to the high computational cost of the thermo-osmotic system, Fig. 2(a), we use mechano-caloric system, Fig. 2(b), in our studies. Therefore, in section 3.1 we first justify the equivalence of the two systems in the sense that they yield equal reciprocal coefficients obeying Onsager relations. Then we use the mechano-caloric system to study the nanochannel size effects on thermo-osmotic coefficient and the mechanism of thermo-osmosis in section 3.2 and section 3.3, respectively.3.1 Equivalence of mechano-caloric and thermo-osmotic systems
Details of calculations with the thermo-osmotic system are given in Appendix A. In summary, it has been found by molecular dynamics simulations that m11 = 2.30 × 10−16 m4 (s N)−1, m12 = (1.19 ± 0.03) × 10−18 m2 s−1, and m21 = (1.21 ± 0.04) × 10−8 m2 s−1, demonstrating that the Onsager reciprocal relation (m12 = m21) is obeyed microscopically. Furthermore, the macroscopic thermo-osmotic (and mechano-caloric) coefficient has been also obtained as M12 = M21 ≈ (1.22 ± 0.02) × 10−8 m2 s−1, demonstrating consistency with the microscopic values.To demonstrate the equivalence of the two systems, the mechano-caloric system shown in Fig. 2(b) with channel width Lz = 2.0 nm is used here to calculate the mechano-caloric coefficient m21. The system is subjected to the following simulation steps. The water and quartz slabs are maintained at 300 K. The system is firstly equilibrated for 1.2 ns. External particle forces fi are then exerted to water molecules in the x-direction to produce a Poiseuille flow across the channel length. A constant acceleration a0 is applied to all oxygen (O) and hydrogen (H) atoms via fi.67 The pressure gradient is calculated by eqn (22). The hydrodynamic resistance may increase as the channel size decreases according to the previous study.43 Therefore, the pressure gradient was tested for different channel widths to ensure that a steady flow was generated. After 0.4 ns, the fluid flow becomes stable, and the numerical velocity profile is recorded every 0.001 ns for 0.8 ns afterwards. The calculations use a similar approach to Appendix A to obtain the heat flux from the excess enthalpy density and velocity profiles. The profiles are not shown here as they will be presented in the next sub-section. The calculated microscopic mechano-caloric coefficient is m21 = (1.2 ± 0.06) × 10−8 m2 s−1, which is very close to the microscopic coefficients obtained with the thermo-osmotic system. This provides further support for the validity of the Onsager reciprocal relations at molecular level, and more importantly allows us to use the computationally simpler mechano-caloric system for studying size effects on the microscopic coefficients controlling thermo-osmosis.
3.2 Nanochannel size effect on the thermo-osmotic coefficient
Previous studies suggest that the channel size can change the liquid structure of the interfacial fluid, causing a potential significant alteration to the transport properties of the channel.31,43 This section will present microscopic evidence for the effects of channel size Lz on thermo-osmotic coefficient. The mechano-caloric system, Fig. 2(b), with several channel sizes (widths) ranging from 0.8 to 3 nm (Lz = 0.8, 1, 1.5, 2, 2.5, 3 nm) is analysed to calculate the corresponding microscopic mechano-caloric coefficients, which are equal to the microscopic thermo-osmotic coefficients by the established validity of the Onsager reciprocal relation at the molecular level.The liquid structure of the interfacial water can be effectively analysed by the spatial arrangement and the solvation (hydration) mode of the interfacial water molecules.30 We follow a previous investigation on silicon–water interfaces68 to study the spatial arrangement of the interfacial water molecules by looking at the mass density and the charge distribution profiles of the interfacial water for different channel sizes.
Firstly, the calculated mass density distribution profiles, ρm(z), are shown in Fig. 5. The results highlight significant mass density fluctuations/variations near the quartz–water interfaces and approximately constant density in the mid-section of the nanochannel. The constant mid-section density is found to be equal to the density of bulk water: 1000 kg m−3. As discussed in previous studies,41,68,69 these variations are related to interactions between the interfacial water molecules and the quartz surfaces. Analogous interfacial fluid density variations at other solid–fluid interfaces have been reported previously.33,41,63,70 These variations indicate that in the vicinity of the quartz–water interface, the interfacial water molecules tend to occupy some fixed layers which are close and parallel to the quartz surfaces.41,68 The peaks (maxima) in the mass density curves show clearly the locations of these layers. The interval of adjacent peaks stems from the strong Lennard-Jones repulsion of oxygen (O) atoms along z-direction in adjacent water layers.68 In contrast, the troughs (minima) of the mass density curves show that the interfacial water molecules have the lowest distribution probability at these interlayer regions.
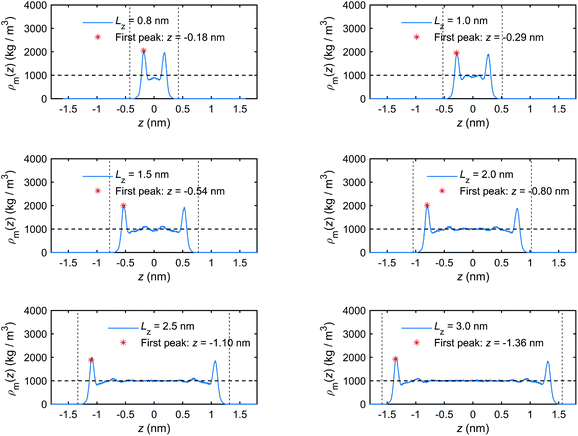 | ||
| Fig. 5 Mass density distribution profiles of the interfacial water obtained for the quartz slit nanochannels with different sizes (MD simulations of the mechano-caloric system). | ||
Fig. 6 presents the charge distribution profiles, Q(z). The results show that the spatial/molecular orientation of the interfacial water molecules is simultaneously under the strong influence in the vicinity of the quartz–water interfaces, as also shown by Markesteijn et al.68 for silicon–water interfaces. The first peak (maximum) in charge distribution profiles shows that larger number of hydrogen (H) atoms instead of oxygen (O) atoms are located in the vicinity of the quartz–water interface because the hydrogen (H) atom carries a charge of +0.41e while the oxygen (O) atom carries a charge of −0.82e in the ClayFF force field.60 Similarly, the first trough (minimum) in Fig. 6 describes a layer consisting mainly of oxygen (O) atoms in place of hydrogen (H) atoms. The position z of the first trough (minimum) in the charge profiles (Fig. 6) is consistent with that of the first peak in the mass density curve (Fig. 5). In addition, the second minimum and maximum indicate a similar trend for the peak and trough in the mass density profile. The charge distribution profiles are approximately zero in the middle of the channel if channel size is large enough (i.e. Lz ≥ 1.5 nm). This shows a random spatial distribution and orientation (disordered configuration) of the interfacial water molecules,68 which behave as bulk (free) water.30
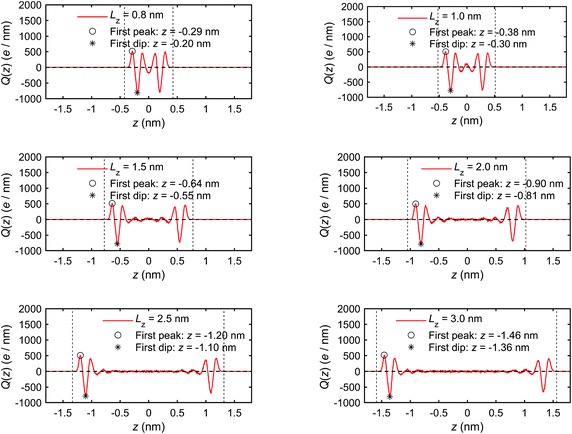 | ||
| Fig. 6 Charge distribution profiles of interfacial water obtained for the quartz slit nanochannel of different sizes (MD simulations of the mechano-caloric system). | ||
The results presented in Fig. 5 and 6 show the formation of a thin region in the vicinity of the quartz–water interface where the liquid structure of the interfacial water is significantly different from the bulk (free) water in terms of distribution and orientation. This layer can be called a boundary or an interaction layer.22 In the boundary layer, the interfacial water molecules form a layer-by-layer, highly ordered liquid structure near the solid surface, which is reflected by the alternating peaks and troughs in the mass density and charge distribution profiles. Contrary to the boundary layer, the bulk liquid in the middle of a sufficiently wide nanochannel is composed of randomly distributed liquid molecules, which is reflected by the absence of large fluctuations (peaks and troughs) in the corresponding distribution profiles for channels wider than 1.5 nm. Therefore, the boundary layer can be estimated to extend to the position where the profile fluctuations become negligible compared to the first peaks and troughs. Based on the results presented in Fig. 5 and 6, the thickness of the boundary layer is estimated to be ∼0.75 nm for all simulated cases. Notably, when the channel width is less than two times the boundary layer thickness, i.e. Lz < 1.5 nm, the boundary layers at the two quartz–water interfaces overlap and the middle of the channel does not contain bulk water.
One potential difference between water behaviour in channels of different widths could arise from differences in water solvation mode. The variation of the solvation mode with channel size was obtained by calculating the spatial distribution function (SDF) of the interfacial water molecules. Details of SDF can be found in Chen at al.30 The SDF provides an alternative method for analysis of the liquid structure, to the frequently-used radial distribution function (RDF),71 specifically suitable for 3-D representations. The SDF describes statistically the relative positions between any central water molecule and neighbouring water molecules. The positions of neighbouring water molecules are determined by the molecular mass centres.30,63 The spatial probability is calculated by averaging over the solvation modes of all water molecules within a searching radius for neighbouring water molecules. Fig. 7 provides a visualisation of SDF with the searching radius r = 0.5 nm.
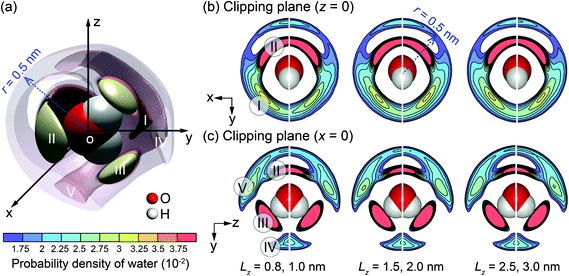 | ||
| Fig. 7 SDF cloud visualization: (a) 3-D plot for the channel with Lz = 3.0 nm; (b) and (c) 2-D plots on clipping planes z = 0 and x = 0 for different channel widths (Lz). | ||
In more detail, Fig. 7(a) shows a 3-D plot of the probable positions, calculated by SDF, of the water molecules surrounding a central water molecule. Three most favourable positions of the adjacent water molecules are depicted as I–III. Molecules in positions II and III belong to the first solvation shell and are most strongly bonded.72 These are less affected by the channel size. Molecules in the position I belong to the second solvation shell.72 The projections on 2-D planes, shown in Fig. 7(b) and (c), indicate that the molecules in the channel with Lz = 1.0 nm have different arrangement from the larger channels. Firstly, molecules in position I are missing, and the characteristics of positions IV and V are different from the other cases. This is an indication that a unique liquid structure is formed for this specific channel width. It is anticipated that a distinctive value of the thermo-osmotic coefficient for the channel width Lz = 1.0 nm will be obtained due to possibly distinct thermodynamic properties and hydrodynamic response of interfacial water. Note that a persistent solvation mode is created for interfacial water molecules when Lz ≥ 1.5 nm, indicating that the effect of channel size on liquid structure diminishes for larger channels.
The excess enthalpy distribution profiles of interfacial water for different channel sizes are calculated by eqn (19) and shown in Fig. 8. The presence and sizes of the boundary layers and the bulk water section can be clearly identified and coincide with those in Fig. 5 and 6. The excess enthalpy profiles vary significantly in the boundary layers and are zero in the bulk water, when present. In smaller channel sizes, e.g. Lz < 1.5 nm, the interference of the overlapping boundary layers results in a complex variation of the excess enthalpy. Interestingly, the first trough is found before the first peak, which differs from some previous studies20,42 reporting excess enthalpy distribution profiles. The difference arises from different substrates used. In our case, there are dangling hydroxyl groups on the quartz surfaces, seen in Fig. 3, which create spaces for some liquid water molecules to penetrate into the quartz.69 The penetrating water molecules are strongly attracted and trapped within these spaces, which can be seen in Fig. 8 for the example of Lz = 2.0 nm, where the vertical dotted lines representing H position are inside the physical quartz boundary. This results in negative potential energy and according to eqn (18) in negative excess enthalpy density, which explains the appearance of trough before the first peak.
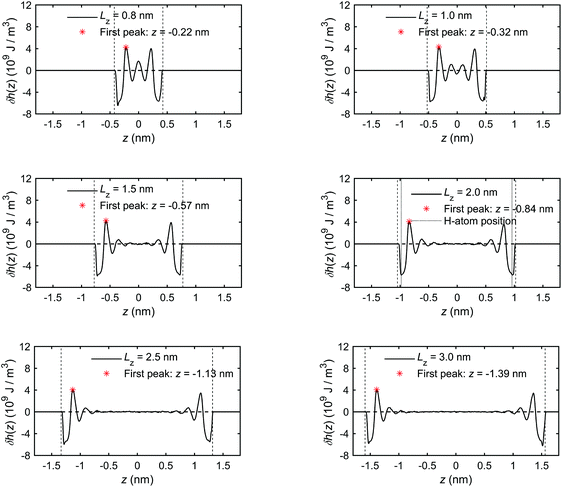 | ||
| Fig. 8 The excess enthalpy distribution profiles of interfacial water obtained for the quartz slit nanochannel of different sizes (MD simulations of the mechano-caloric system). | ||
We note that the positions of the first troughs in mass density profiles are different from those of the first peaks in charge density and excess enthalpy distribution profiles. This can be explained by the following observation. The mass density distribution profiles, ρm(z), shown in Fig. 5, are representing disproportionally the distribution of oxygen (O) atoms because of their greater molar mass compared with hydrogen (H) atoms. Number density distribution profiles, ρ(z), of O and H atoms are presented in Fig. 24 of Appendix C to demonstrate that the peaks of O number density distributions almost coincide with peaks of mass density distributions and coincide with troughs of charge distributions, while the peaks of H number density distributions coincide with peaks of charge distributions. The peaks in excess enthalpy distribution occur between the peaks in O and H number density distributions, approximately coinciding with the peaks in O number density distributions. The troughs (except the first trough) in excess enthalpy distribution coincide with the peaks in H number density distributions. We further provide the pressure tensor distribution profiles in Fig. 25 of Appendix C, which is also found to have the same coincidence.
In addition to the excess enthalpy, the existence of interfacial regions may significantly affect the hydrodynamic properties of the interfacial water.44Fig. 9 shows the velocity profiles of the interfacial water molecules along the x-direction, vx(z), for different channel sizes. It is seen that the velocity distribution profiles vanish at the quartz–water interfaces and have maxima at the middle of the channel. The fitting curves shown in the plots are based on eqn (21) and are used to determine the hydrodynamics parameters η and b. The curves are fitting the simulation results with high correlation, indicating that the induced pressure-driven flow is described well by planar Poiseuille flow, and the continuum hydrodynamics remains valid in nanometric/sub-nanometric channels. The fitting results for b indicate that there is basically no slippage at the quartz–water interfaces (b ≈ 0 nm), due to the large friction coefficient κ between interfacial water and quartz surfaces (κ ≈ 1011 N s m−3 from the fitting results). The fitting results for η show that for Lz ≥ 1.5 nm, η gradually reduces to a constant value (∼0.60 mPa s) which is expected to further converge to the shear viscosity of SPC bulk water at 300 K and 1 atm (∼0.475 mPa s)73 when the channel width continues to increase, while for Lz < 1.5 nm, the overlap and interference of the two boundary layers leads to a higher value and a complex variation with channel size of water viscosity.
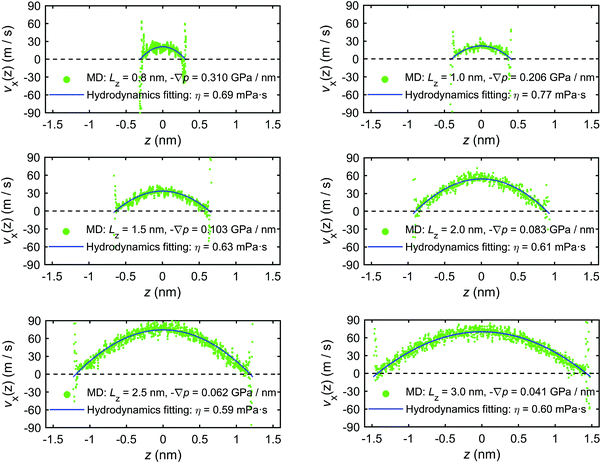 | ||
| Fig. 9 Velocity profiles of interfacial water molecules along x-direction for different channel sizes (MD simulations of the mechano-caloric system). | ||
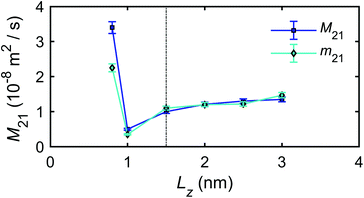
The microscopic mechano-caloric (or thermo-osmotic) coefficient m21 for different channel sizes Lz is calculated by eqn (16). The corresponding macroscopic coefficient M21 is also calculated by eqn (12), using the calculated excess enthalpy density and fitted viscosity and slip length. For each nanochannel size, we performed three independent simulations with different initial configurations of interfacial water molecules, from which we computed the error bars on m21 and M21. Fig. 10 shows the variation of the thermo-osmotic coefficient with channel size Lz.
The results present new findings and observations:
(1) The microscopic thermo-osmotic coefficients measured by MD simulations (m21) and the macroscopic coefficients calculated by thermodynamics (M21) are approximately the same for all channel sizes, with the exception of the smallest.
(2) For channels with Lz ≥ 1.5 nm, m21 is approximately constant, while for Lz ≥ 1.5 nm, m21 varies with the channel size. This is due to the overlap and interference of the boundary layers which affect the excess enthalpy distribution and hydrodynamic properties of interfacial water, causing variations of the thermo-osmotic coefficient.
(3) A unique value for thermo-osmotic coefficient was found for the case of Lz = 1.0 nm, and shown to be associated with the unique liquid structure (i.e. solvation mode) observed in Fig. 7.
(4) The MD simulations with the mechano-caloric system have revealed the dependence of the thermo-osmotic coefficient on the channel size. It has been found that this dependence emerges from the changing liquid structure in boundary layers adjacent to the solid surfaces, which alters either the excess enthalpy distribution or the hydrodynamic properties of the interfacial water. The comparisons between number/mass density, charge, excess enthalpy, and pressure distribution profiles, as well as the coincidence of the corresponding peak/trough values (Fig. 5, 6, 8, 24 and 25) indicate that the excess enthalpy distribution profile is dictated by the layered liquid structure of interfacial water. The velocity distribution profiles and the fitting results of fluid viscosity in Fig. 9 indicate that the dynamic properties of the interfacial fluid are also strongly affected by the interfacial liquid structure. Specifically, with channel size increasing, the fluid viscosity firstly increases and then decreases to a steady value. This is in agreements with the observed variation of the thermo-osmotic coefficient, since according to eqn (12) and (13) the thermo-osmotic coefficient is inversely proportional to the fluid viscosity.
3.3 Mechanism of thermo-osmosis
This section provides a mechanistic demonstration that the thermo-osmotic flow of interfacial water is driven by a pressure gradient induced by a temperature gradient. Though Ganti et al.21,74 have revealed and confirmed the similar mechanisms for conceptual nonpolar Lennard-Jones system, this mechanism has not been found in a more complex and realistic system (e.g., quartz–water interfaces). Therefore, we followed the same method and used a more advanced MD configuration with a dynamically self-adjusted piston to achieve a constant bulk fluid pressure and revisit this mechanism in a realistic quartz–water system.We use the mechano-caloric system, Fig. 2(b), with the channel width Lz = 2.0 nm. This is subjected to zero external pressure gradient ∇p = 0 along the channel (x direction). A series of MD simulations with a range of temperatures from 270 K to 360 K are performed. The corresponding pressure distributions across the channel section are obtained by eqn (14). For each temperature, the simulation system is relaxed/equilibrated first for over 1.6 ns. The gap between the quartz surfaces (channel size) is adjusted dynamically by the graphene piston to ensure the bulk pressure of interfacial water remains at the designated value (Ppiston = 1 atm ≈ 0.0001 GPa). The measurement of pressure is then followed for 1.2 ns.
Fig. 11 presents the number density profiles ρ(z) in the channel obtained for all temperatures studied. In the figure, z = 0 nm represents the middle point of the channel, and z ≈ 1.0 nm represents the quartz surface. It is found that the increasing temperature leads to increasing nanochannel gap due to the thermal expansion of the interfacial water, as the enclosed pressure applied by graphene piston is kept constant at 1 atm.
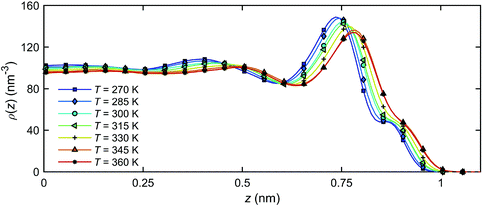 | ||
| Fig. 11 Number density distribution ρ(z) of the interfacial water across the channel width at different temperatures. | ||
Fig. 12 presents the temperature distributions of the interfacial water along z-direction T(z) at different temperatures, indicating that no temperature gradient exists in this direction.
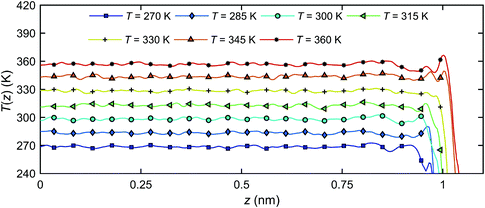 | ||
| Fig. 12 The temperature profiles of interfacial water along z-direction T(z) at different temperatures. | ||
Fig. 13 presents the pressure tensor components of the interfacial water in the channel for the case of T = 300 K (as an example). It can be observed that in the middle of the nanochannel, the pressure components are equal, i.e. pxx = pyy = pzz = pbulk ≈ 0 GPa. However, near the quartz surfaces, the pressure components vary several orders of magnitude from the bulk. The component pxx is approximately equal to pyy over the entire channel section, indicating insignificant anisotropy on the plane parallel to the quartz surfaces. However, pzz deviates considerably from pxx and pyy near the quartz surfaces. The boundary layer discussed in section 3.2 can be identified in Fig. 13 as the region where the influences due to the quartz–water interactions are substantial on the properties of interfacial water.
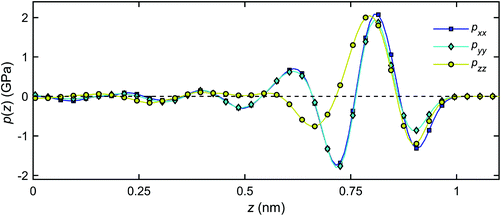 | ||
| Fig. 13 Distribution of the pressure tensor components of the interfacial water across the channel width at T = 300 K. | ||
Fig. 14 shows the distribution of the pressure component pxx across the channel width for all temperatures studied. For all temperatures, pxx in the bulk is within 1% of the designated value of 1 atm, and deviates significantly from this value as the quartz surfaces are approached. The pressure starts oscillating with a wavelength corresponding roughly to the size of a single water molecule (∼0.28 nm)41,63 and its amplitude increases with decreasing temperature. The latter observation may be related to a higher bulk density of fluid at a lower temperature, Fig. 11, and subsequently, a stronger effect of solid on the thermal mobility according to a previous study.41
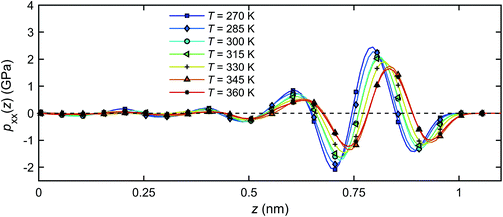 | ||
| Fig. 14 Pressure distributions of the interfacial water across the channel width under different temperatures. | ||
The pressure profiles in Fig. 14 suggest that a temperature gradient will not produce a pressure gradient in the x-direction in the bulk water, since the pressure is nearly independent of temperature away from the quartz surfaces (z = 0). The bulk water is in mechanical equilibrium. In the vicinity of the quartz–water interface, however, a finite pressure gradient along the channel will be generated by changing the temperature, seen by different pressure magnitudes at different temperatures in Fig. 14. Such pressure differential can be seen as the main driving force for the flow in the x-direction.
The pressure gradient can be obtained by eqn (8). Fig. 15 presents the pressure gradient of the interfacial water 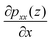 across the channel width under different temperatures when a unit temperature gradient is applied in the x-direction (∇T = 1 K m−1. Under the same temperature gradient ∇T, the magnitude of the pressure gradient will decrease as the water temperature increases.
across the channel width under different temperatures when a unit temperature gradient is applied in the x-direction (∇T = 1 K m−1. Under the same temperature gradient ∇T, the magnitude of the pressure gradient will decrease as the water temperature increases.
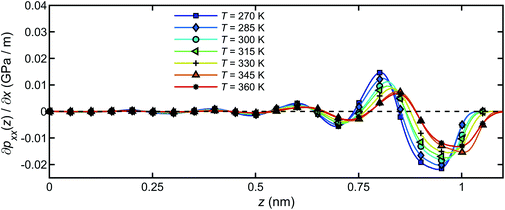 | ||
| Fig. 15 The pressure gradient of the interfacial water across the channel width for a unit temperature gradient under different temperatures. | ||
The considerations above assumed that the interfacial water was a continuum, i.e. thermally induced pressure on a fluid element. The body force on each water molecules can be calculated microscopically. The body force on a fluid element at a distance z from the quartz surface is given by
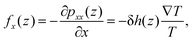 | (23) |
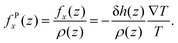 | (24) |
Fig. 16 presents the distribution of particle forces across the channel width under different temperatures when a unit temperature gradient is applied in the x-direction (∇T = 1 K m−1. It is seen that only in the boundary layer, the water molecules will experience a body force to drive the flow along the x-direction. In the bulk region, no particle force will act on the water molecules. In addition, under the same temperature gradient ∇T, the magnitude of the body force will decrease as the water temperature increases, which is in accord with the result in Fig. 14 and 15.
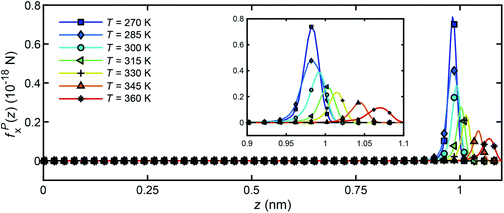 | ||
| Fig. 16 Distribution of particle forces across the channel width for unit temperature gradient under different temperatures. | ||
By investigating the mechanical interactions of the interfacial water under different temperatures using a continuum approach (pressure tensor distribution) and a discrete approach (body force per molecule), we have revealed and confirmed the microscopic mechanism of thermo-osmosis of water in quartz nanochannels. It has been found that only in the boundary layers adjacent to the solid surfaces, the fluid molecules experience a driving force that produces a thermo-osmotic flow.
4. Conclusions
The thermo-osmotic flow of water in quartz slit nanochannels has been investigated by MD simulations. The microscopic thermo-osmotic coefficient has been measured by analysis of mechano-caloric and thermo-osmotic systems. The following conclusions are drawn from the results and discussion of the work:• The validity of Onsager reciprocal relation and the continuum hydrodynamics description of flow at the nanoscale has been confirmed, and the consistency between the microscopic and the macroscopic/thermodynamic thermo-osmotic coefficient has been demonstrated;
• The channel size effect on the thermo-osmotic coefficient has been quantified by analysis of systems with different channel widths, ranging from 0.8 to 3.0 nm. It has been found that the liquid structure of the interfacial water changes with decreasing channel size, due to the overlap and interference of liquid boundary layers adjacent to the solid surfaces. This leads to changes in the excess enthalpy distribution and in the hydrodynamic properties of interfacial water, causing variations of the thermo-osmotic coefficient;
• The pressure tensor distributions of the interfacial water under different temperatures have been quantified. It has been found that the temperature gradient inside the nanochannel induces a pressure gradient parallel to the quartz surface. This pressure gradient is identified as the source of thermo-osmotic motion of the interfacial water. It has been found that, although the bulk water is at mechanical equilibrium under a thermal gradient, such an equilibrium state cannot be achieved in the vicinity of the quartz–water interfaces. Layers of water at these surfaces experience a pressure gradient parallel to the surfaces, which drives the thermo-osmotic flow.
The modelling and simulation approaches used in this work, as well as the insights provided by the results, form a good foundation for further investigation of coupled transport phenomena in nanoscale structures.
Author contributions
The manuscript was written through the contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts of interest to declare.Appendix A. The thermo-osmotic system
For the studied thermo-osmotic system, the water flux is calculated by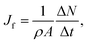 | (25) |
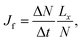 | (26) |
The thermo-osmotic system subjected to temperature gradient is used to calculate the microscopic thermo-osmotic coefficient by
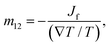 | (27) |
The thermo-osmotic system subjected to pressure gradient is used to calculate the microscopic coefficient m11 by:
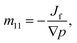 | (28) |
A.1. Determination of m12 using the thermo-osmotic system with a temperature gradient
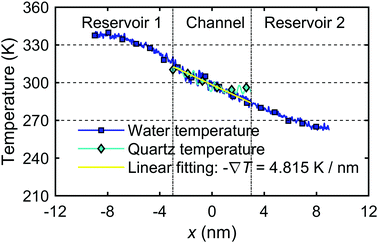
The system shown in Fig. 2(a) of the main text with the channel width Lz = 2.0 nm is subjected to the following simulation steps. The two water reservoirs are kept at the same pressure (p1 = p2 = 1.0 atm) applied by two graphene pistons. The system is first relaxed/equilibrated for 1.2 ns by maintaining both the water and quartz at an initial temperature (T1 = T2 = T0 = 300 K). The temperature gradient in the nanochannel is then applied by increasing the temperature of reservoir 1 to 330 K (T1 = 330 K) and decreasing the temperature of reservoir 2 to 270 K (T2 = 270 K). The system is then stabilized for another 3.0 ns until the temperature profile reached steady-state and a relatively stable flow is achieved under the constant temperature gradient created by the two reservoirs. The calculation of the microscopic thermo-osmotic coefficient, eqn (27), requires the temperature gradient and the water flux.Fig. 17 shows the temperature profile of both water and quartz along the channel from the MD simulation. The results show that a constant temperature gradient ∇T is created along the quartz slit nanochannel. The quartz temperature profile is consistent with the interfacial water temperature profile. Linear regression of the water temperature profile inside the nanochannel gives −∇T = 4.815 K nm−1. Note that the range of water temperature in the system is of ∼260–340 K, previous studies75,76 have indicated that SPC water is held in the stable liquid phase in this temperature range and atmospheric pressure.
The calculation of water flux by eqn (26) requires the water molecule numbers transported through the nanochannel in a time interval. Fig. 18(a) presents the changes of water molecule numbers and temperatures with time in the reservoir 1 (ΔN1), reservoir 2 (ΔN2) and in the channel (ΔN0). It can be observed that the temperature gradient between the two reservoirs drives the water molecules from the hot reservoir to the cold reservoir at a constant rate, demonstrating the establishment of a thermo-osmosis process in the system. The change of water molecule numbers, ΔN, required for eqn (26), is obtained as an average of the changes in the two reservoirs, i.e. ΔN = (|ΔN1| + |ΔN2|)/2, and the water flux is calculated to be Jf = 0.191 m s−1.
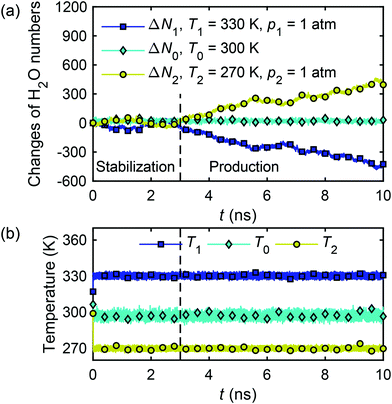 | ||
| Fig. 18 Changes of water molecule numbers (a) and temperatures (b) in two reservoirs and nanochannel with time in the thermo-osmotic system (∇T ≠ 0, ∇p = 0). | ||
The microscopic thermo-osmotic coefficient is calculated by eqn (27) to be m12 = 1.19 × 10−8 m2 s−1. The (nearly) linear flow profile in Fig. 18(a) indicates that the thermo-osmotic coefficient m12 is a constant, and the inequality m12 > 0 represents a flow from the hot reservoir to the cold reservoir.
We extended our simulations to more scenarios of temperature gradients and calculated the corresponding microscopic thermo-osmotic coefficients. The results are shown in Table 2. The results for the thermo-osmotic coefficient can be summarised by m12 = (1.19 ± 0.03) × 10−8 m2 s−1.
| Set 1 | Set 2 | Set 3 | |
|---|---|---|---|
| T 1 (K) | 330 | 320 | 310 |
| T 2 (K) | 270 | 280 | 290 |
| T 0 (K) | 300 | 300 | 300 |
| m 12 (10−8 m2 s−1) | 1.19 | 1.22 | 1.17 |
A.2. Determination of m21 using the thermo-osmotic system with a pressure gradient
The system shown in Fig. 2(a) of the main text with the channel width Lz = 2.0 nm is subjected to the following simulation steps. The temperature in the two reservoirs and the nanochannel is set at T1 = T2 = T0 = 300 K and the pressure on the two graphene pistons is set at p1 = p2 = 1.0 atm ≈ 1.01 × 10−4 GPa. The system is initially relaxed/equilibrated for 1.2 ns, after that the temperature is kept constant everywhere (∇T = 0) and a pressure gradient is generated by increasing p1 = 3001 atm ≈ 0.30 GPa, and maintaining p2 = 1 atm.Fig. 19(a) shows the calculated changes of water molecule numbers in reservoir 1 (ΔN1), reservoir 2 (ΔN2) and in the channel (ΔN0), as well as the pressure acting on the two pistons with time. As in sub-section A.1, the water flux is calculated from the average change of water molecule numbers and eqn (26).
 | ||
| Fig. 19 Changes of water molecule numbers (a) and corresponding pressure (b) acting on two pistons with time in the thermo-osmotic system (∇T = 0, ∇p ≠ 0). | ||
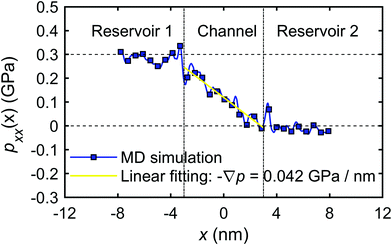
The calculation of the microscopic coefficient m11 by eqn (28) requires the pressure gradient along the nanochannel. The pressure tensor is calculated by eqn (14), and the pressure profile along the x-direction is shown in Fig. 20. The profile indicates a pressure drop induced by the viscous entrance effects.71 Therefore, the generated −∇p = 0.042 GPa nm−1 is lower than the expected theoretical value (0.05 GPa nm−1). Using the calculated water flux and pressure gradient into eqn (28) gives m11 = 2.30 × 10−16 m4 (s N)−1.
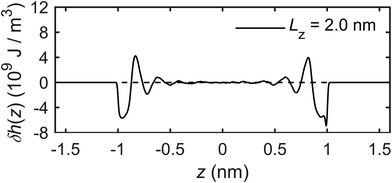
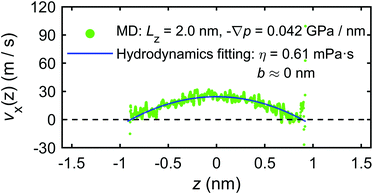
The calculation of the microscopic mechano-caloric coefficient m21 by eqn (16) requires the heat flux in addition to the pressure gradient. This is calculated by eqn (17) using the excess enthalpy density and the velocity profiles. Fig. 21 presents the excess enthalpy density profile over the channel section calculated by eqn (19). Fig. 22 presents the velocity profile of the interfacial water molecules along the x-direction vx(z). The hydrodynamics fitting curve based on eqn (21) is also shown. The fitting yields b ≈ 0 and η ≈ 0.61 mPa s. Using the calculated heat flux and pressure gradient in eqn (16) provides the microscopic mechano-caloric coefficient m21 = 1.22 × 10−8 m2 s−1.
We extended our simulations to more scenarios of pressure gradients and calculated the corresponding microscopic mechano-caloric coefficients. The results are shown in Table 3. They can be summarised by the following expression for the mechano-caloric coefficient m21 = (1.21 ± 0.04) × 10−8 m2 s−1. We note that the calculated microscopic thermo-osmotic coefficient in section A.1. is m12 = (1.19 ± 0.03) × 10−8 m2 s−1, which shows that the Onsager reciprocal relation (m12 = m21) is obeyed microscopically. Furthermore, using the excess enthalpy profile and the calculated slip length and viscosity in eqn (12) the value of the macroscopic thermo-osmotic (and mechano-caloric) coefficient is obtained as M12 = M21 ≈ (1.21 ± 0.02) × 10−8 m2 s−1, which is consistent with the microscopic values.
| Set 1 | Set 2 | Set 3 | |
|---|---|---|---|
| p 1 (atm) | 3001 | 4001 | 5001 |
| p 2 (atm) | 1 | 1 | 1 |
| m 21 (10 −8 m 2 s −1 ) | 1.22 | 1.25 | 1.17 |
| M 21 (10 −8 m 2 s −1 ) | 1.21 | 1.23 | 1.19 |
By conducting the MD simulations of a thermo-osmotic system, we have shown how the thermo-osmosis emerges from the collective behaviour of microscopic constituents, allowing for the calculation of the microscopic coefficients m11, m12, m21. Further, we have shown that the calculated mixed coefficients obey the Onsager reciprocal relation (m12 = m21) and that they can be considered as emergent properties of the system since they are very close to the value based on irreversible thermodynamics (m12 = m21 = M12 = M21).
Appendix B. Effect of bin size on density profiles and their peak/trough values
The choice of bin size will influence the accuracy of the derived first peak value (z0, ρ0): the smaller the bin size, the more accurate profiles and peak values will be obtained, as the error range can be narrowed down by decreasing the bin size. For example, for the position of the peak z0, a bin size of 0.04 nm causes an error range −0.04 nm–0.04 nm. However, a very small bin size can cause significant fluctuations of profiles as there is not enough data in each bin to be averaged for producing smooth profiles. To assess whether the peak value will change as the bin size changes, we take the mass density profiles for the case Lz = 1.0 nm as an example. By varying the bin size, the corresponding profiles and peak values are derived and shown in Fig. 23. When the bin sizes are too large, e.g. 0.040–0.100 nm, the produced profiles are quite rough and the peak values cannot be accurately determined. When the bin size is too small, e.g. 0.002 nm, the lack of enough data in each bin results in fluctuating profiles. With intermediate bin sizes, e.g. 0.004–0.010 nm, the profile fluctuations are avoided with acceptable accuracy of peak values. Therefore, in our study, a bin size of 0.004 nm is adopted.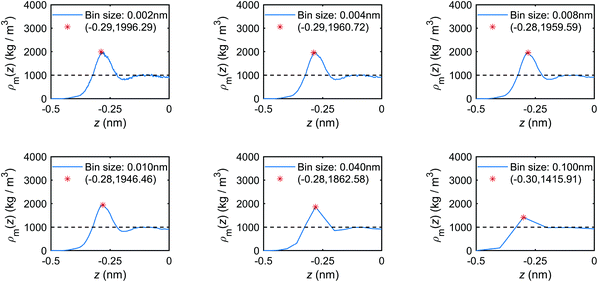 | ||
| Fig. 23 Mass density distribution profiles of the interfacial water obtained with different bin sizes (MD simulations with the mechano-caloric system with channel size 1.0 nm). | ||
Appendix C. Number density and pressure distribution profiles for different channel size
The mass density distribution profiles, ρm(z), presented in Fig. 5 of the paper are disproportionally affected by the distribution of oxygen (O) atoms, because of their greater molar mass (∼16 g mol−1) compared with hydrogen (H) atoms (∼1 g mol−1). We present the number density distribution profiles, ρ(z), of O and H atoms in Fig. 24, with the pressure tensor distribution profiles, ρxx(z), in Fig. 25, and mass density, charge density, excess enthalpy distribution profiles in Fig. 5, 6 and 8, respectively to clarify the coincidence of peak/trough values in different distribution profiles.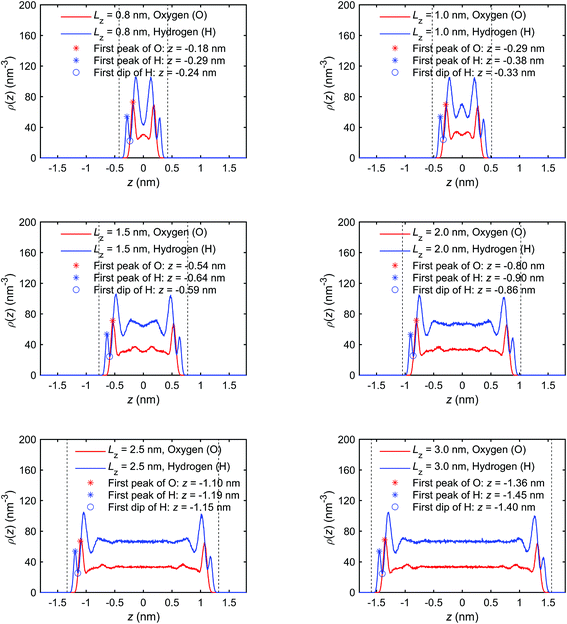 | ||
| Fig. 24 Number density distribution profiles of the interfacial water obtained for the quartz slit nanochannels with different sizes (MD simulations with the mechano-caloric system). | ||
 | ||
| Fig. 25 Pressure distribution profiles of the interfacial water obtained for the quartz slit nanochannels with different sizes (MD simulations with the mechano-caloric system). | ||
The peaks and troughs in number density profiles show good agreements with other distribution profiles. It can be seen that: (1) the position of the first peak in the number density profile of O-atoms is the same as the position of the first peak in the mass density profile, the position of the first trough in the charge profile, and the position of the first peak in the pressure profile; (2) the position of the first peak in the number density profile of H-atoms is the same as the position of the first peak in the charge profile, and the position of the first trough in the pressure profile; (3) the position of the first peak in the excess enthalpy profile is between the first peak position of the H-atom number density profile and the first peak position of the O-atom number density profile, approximately coinciding with the first peak in O number density distributions. Other peaks/troughs on these profiles coincide with each other in the same way.
Acknowledgements
Jivkov acknowledges gratefully the financial support from the Engineering and Physical Sciences Research Council (EPSRC), UK, via Grant EP/N026136/1. Chen acknowledges the President Doctoral Scholarship Award (PDS Award 2019) by The University of Manchester, UK. The authors acknowledge the assistance provided by the Research IT team for the use of Computational Shared Facility at The University of Manchester.References
- R. Galbreath, J. Exp. Biol., 1975, 62, 115–120 CAS
.
- S. Kim and M. M. Mench, J. Membr. Sci., 2009, 328, 113–120 CrossRef CAS
.
- W. A. Phillip, Nat. Energy, 2016, 1, 1–2 Search PubMed
.
- M. Rahimi, A. P. Straub, F. Zhang, X. Zhu, M. Elimelech, C. A. Gorski and B. E. Logan, Energy Environ. Sci., 2018, 11, 276–285 RSC
.
- A. F. Al-Alawy and R. M. Al-Alawy, Iraqi J. Chem. Pet. Eng., 2016, 17, 53–68 Search PubMed
.
- R. Zagorscak, M. Sedighi and H. R. Thomas, Int. J. Geomech., 2017, 17, 04016068 CrossRef
.
- J. Goncalves, G. de Marsily and J. Tremosa, Earth Planet. Sci. Lett., 2012, 339, 1–10 CrossRef
.
- G. Lippmann, C. R. Acad. Sci., 1907, 145, 104–105 CAS
.
- M. Sedighi, H. R. Thomas and P. J. Vardon, J. Geotech. Geoenviron., 2018, 144, 04018075 CrossRef
.
- H. Yan, M. Sedighi and H. Xie, Int. J. Heat Mass Transfer, 2020, 153, 119664 CrossRef CAS
.
- V. Yasnou, A. Mialdun, D. Melnikov and V. Shevtsova, Int. J. Heat Mass Transfer, 2019, 143, 118480 CrossRef CAS
.
- Y. Yang and M. Wang, J. Colloid Interface Sci., 2018, 514, 443–451 CrossRef CAS
.
- A. L. Sehnem, D. Niether, S. Wiegand and A. M. F. Neto, J. Phys. Chem. B, 2018, 122, 4093–4100 CrossRef CAS
.
- X. Chen, W. Pao and X. Li, Int. J. Eng. Sci., 2013, 64, 1–13 CrossRef
.
- X. Chen, M. Wang, M. A. Hicks and H. R. Thomas, Int. J. Numer. Anal. Methods Geomech., 2018, 42, 1144–1153 CrossRef
.
- K. G. Denbigh and G. Raumann, Proc. R. Soc. London, Ser. A, 1952, 210, 377–387 CAS
.
- K. G. Denbigh and G. Raumann, Proc. R. Soc. London, Ser. A, 1952, 210, 518–533 CAS
.
- S. Marbach and L. Bocquet, Chem. Soc. Rev., 2019, 48, 3102–3144 RSC
.
- A. P. Bregulla, A. Wurger, K. Gunther, M. Mertig and F. Cichos, Phys. Rev. Lett., 2016, 116, 188303 CrossRef
.
- L. Fu, S. Merabia and L. Joly, Phys. Rev. Lett., 2017, 119, 214501 CrossRef
.
- R. Ganti, Y. Liu and D. Frenkel, Phys. Rev. Lett., 2017, 119, 038002 CrossRef
.
- O. Farago, Eur. Phys. J. E, 2019, 42, 136 CrossRef CAS
.
- K. Proesmans and D. Frenkel, J. Chem. Phys., 2019, 151, 124109 CrossRef
.
- V. M. Barragan and S. Kjelstrup, J. Non-Equilib. Thermodyn., 2017, 42, 217–236 CAS
.
- S. A. Putnam and D. G. Cahill, Langmuir, 2005, 21, 5317–5323 CrossRef CAS
.
- J. L. Anderson, Annu. Rev. Fluid Mech., 1989, 21, 61–99 CrossRef
.
- A. A. Skelton, P. Fenter, J. D. Kubicki, D. J. Wesolowski and P. T. Cummings, J. Phys. Chem. C, 2011, 115, 2076–2088 CrossRef CAS
.
- X. Shi, S. Mao, J. Hu, J. Zhang and J. Zheng, Chem. Geol., 2019, 513, 73–87 CrossRef CAS
.
- J. Lee, H. A. Lee, M. Shin, L. J. Juang, C. J. Kastrup, G. M. Go and H. Lee, ACS Nano, 2020, 14, 4755–4766 CrossRef CAS
.
- S. J. Chen, W. Q. Chen, Y. B. Ouyang, T. Matthai and L. H. Zhang, Nanoscale, 2019, 11, 22954–22963 RSC
.
- M. Collin, S. Gin, B. Dazas, T. Mahadevan, J. C. Du and I. C. Bourg, J. Phys. Chem. C, 2018, 122, 17764–17776 CrossRef CAS
.
- A. M. Schrader, J. I. Monroe, R. Sheil, H. A. Dobbs, T. J. Keller, Y. X. Li, S. Jain, M. S. Shell, J. N. Israelachvili and S. G. Han, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 2890–2895 CrossRef CAS
.
- Z. Brkljaca, D. Namjesnik, J. Lutzenkirchen, M. Predota and T. Preocanin, J. Phys. Chem. C, 2018, 122, 24025–24036 CrossRef CAS
.
- C. Perrino, S. Canepari and M. Catrambone, Aerosol Air Qual. Res., 2012, 13, 137–147 CrossRef
.
- H. R. Lee, T. Shibata, M. Kanezashi, T. Mizumo, J. Ohshita and T. Tsuru, J. Membr. Sci., 2011, 383, 152–158 CrossRef CAS
.
- Y. Deng, L. Xu, H. Lu, H. Wang and Y. Shi, Chem. Eng. Sci., 2018, 177, 445–454 CrossRef CAS
.
-
B. V. Derjaguin, N. V. Churaev and V. M. Muller, Surface forces, Plenum, New York, 1987 Search PubMed
.
-
S. Kjelstrup and D. Bedeaux, Non-equilibrium thermodynamics of heterogeneous systems, World Scientific, Hackensack, 2008 Search PubMed
.
- E. Brunet and A. Ajdari, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 016306 CrossRef
.
-
S. R. de Groot and P. Mazur, Non-equilibrium thermodynamics, Dover, New York, 1984 Search PubMed
.
- M. Han, J. Colloid Interface Sci., 2005, 284, 339–348 CrossRef CAS
.
- L. Fu, S. Merabia and L. Joly, J. Phys. Chem. Lett., 2018, 9, 2086–2092 CrossRef CAS
.
- K. L. Wu, Z. X. Chen, J. Li, X. F. Li, J. Z. Xu and X. H. Dong, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 3358–3363 CrossRef CAS
.
- L. Bocquet and J. L. Barrat, Soft Matter, 2007, 3, 685–693 RSC
.
- L. Onsager, Phys. Rev., 1931, 37, 405–426 CrossRef CAS
.
- L. Onsager, Phys. Rev., 1931, 38, 2265–2279 CrossRef CAS
.
- B. Corry, J. Phys. Chem. B, 2008, 112, 1427–1434 CrossRef CAS
.
- J. Azamat, A. Khataee and S. W. Joo, Chem. Eng. Sci., 2015, 127, 285–292 CrossRef CAS
.
- Y. H. Wang, Z. J. He, K. M. Gupta, Q. Shi and R. F. Lu, Carbon, 2017, 116, 120–127 CrossRef CAS
.
- R. Richard, S. Anthony and A. Ghoufi, Mol. Phys., 2016, 114, 2655–2663 CrossRef CAS
.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS
.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics Modell., 1996, 14, 33–38 CrossRef CAS
.
- M. R. Du, S. J. Chen, W. H. Duan, W. Q. Chen and H. W. Jing, ACS Appl. Nano Mater., 2018, 1, 1731–1740 CrossRef CAS
.
- N. H. de Leeuw, F. M. Higgins and S. C. Parker, J. Phys. Chem. B, 1999, 103, 1270–1277 CrossRef CAS
.
- T. P. M. Goumans, A. Wander, W. A. Brown and C. R. A. Catlow, Phys. Chem. Chem. Phys., 2007, 9, 2146–2152 RSC
.
- I. C. Bourg and C. I. Steefel, J. Phys. Chem. C, 2012, 116, 11556–11564 CrossRef CAS
.
- Y. Ouyang, S. Chen, W. Chen, L. Zhang, S. Matthai and W. Duan, J. Phys. Chem. C, 2020, 124, 19166–19173 CrossRef CAS
.
-
R. W. Hockney and J. W. Eastwood, Computer simulation using particles, IOP, Bristol, 2nd edn, 1988 Search PubMed
.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef
.
- R. T. Cygan, J. J. Liang and A. G. Kalinichev, J. Phys. Chem. B, 2004, 108, 1255–1266 CrossRef CAS
.
- H. J. C. Berendsen, J. R. Grigera and T. P. Straatsma, J. Phys. Chem., 1987, 91, 6269–6271 CrossRef CAS
.
-
H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren and J. Hermans, in Intermolecular forces, ed. B. Pullman, Springer, Dordrecht, 1981, vol. 14, pp. 331–342 Search PubMed
.
- I. C. Bourg and G. Sposito, J. Colloid Interface Sci., 2011, 360, 701–715 CrossRef CAS
.
- L. Y. Wang, R. S. Dumont and J. M. Dickson, J. Chem. Phys., 2013, 138, 124701 CrossRef
.
-
J. P. Hansen and I. R. McDonald, Theory of simple liquids, Elsevier, New York, 1990 Search PubMed
.
- J. L. Barrat and L. Bocquet, Phys. Rev. Lett., 1999, 82, 4671–4674 CrossRef CAS
.
- K. Falk, F. Sedlmeier, L. Joly, R. R. Netz and L. Bocquet, Nano Lett., 2010, 10, 4067–4073 CrossRef CAS
.
- A. P. Markesteijn, R. Hartkamp, S. Luding and J. Westerweel, J. Chem. Phys., 2012, 136, 134104 CrossRef CAS
.
- T. Q. Vo and B. Kim, Int. J. Precise Eng Manuf., 2015, 16, 1341–1346 CrossRef
.
- C. Lee, C. Cottin-Bizonne, R. Fulcrand, L. Joly and C. Ybert, J. Phys. Chem. Lett., 2017, 8, 478–483 CrossRef CAS
.
- D. Bergman and A. Laaksonen, Mol. Simul., 1998, 20, 245–264 CrossRef CAS
.
- W. H. Robertson, E. G. Diken, E. A. Price, J. W. Shin and M. A. Johnson, Science, 2003, 299, 1367–1372 CrossRef CAS
.
- Y. M. Song and L. L. Dai, Mol. Simul., 2010, 36, 560–567 CrossRef CAS
.
- R. Ganti, Y. W. Liu and D. Frenkel, Phys. Rev. Lett., 2018, 121, 068002 CrossRef CAS
.
- O. A. Karim, P. A. Kay and A. D. J. Haymet, J. Chem. Phys., 1990, 92, 4634–4635 CrossRef CAS
.
- C. Vega, J. L. F. Abascal, E. Sanz, L. G. MacDowell and C. McBride, J. Phys.: Condens. Matter, 2005, 17, S3283–S3288 CrossRef CAS
.
| This journal is © The Royal Society of Chemistry 2021 |