Open Access Article
Open Access ArticlePredicted structure and selectivity of 3d transition metal complexes with glutamic N,N-bis(carboxymethyl) acid†
Fatima
Mechachti
a,
Salima
Lakehal
 *ab,
Aicha
Lakehal
*ab,
Aicha
Lakehal
 c,
Christophe
Morell
c,
Christophe
Morell
 d,
Lynda
Merzoud
d,
Lynda
Merzoud
 d and
Henry
Chermette
d and
Henry
Chermette
 *d
*d
aLaboratoire de Chimie des Matériaux et des Vivants, Activité & Réactivité, Université Batna1, Batna, Algerie. E-mail: lakehal.salima@yahoo.fr
bInstitut des Sciences de La Terre et de L'univers, Université de Batna2, Batna, Algerie
cFaculté des Sciences Techniques, Université de Batna2, Batna, Algerie
dUniversité de Lyon, Université Claude Bernard Lyon 1, Institut des Sciences Analytiques, UMR CNRS 5280, 69622 Villeurbanne Cedex, France. E-mail: henry.chermette@univ-lyon1.fr
First published on 15th September 2021
Abstract
The complexation of transition metals with a rather new aminopolycarboxilic ligand, the glutamic N,N-bis(carboxymethyl) acid (GLDA) is investigated using the density functional at the PBE/TPZ level of theory. In order to predict the selectivity of metals and to gain insight into factors influencing the calculated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values, the GLDA ligand is studied in the gas phase and in solvent with the electrostatic COSMO model. In the absence of crystallographic data, most complexes prefer a pentacoordinated structure in gas phase. On the contrary, in presence of solvent the two structures can coexist, copper excepted, which does not adopt the octahedral form. Good correlations are found between the experimental thermodynamic values and several calculated parameters such as charge transfer, bond descriptors, or bonding free energy energies. The obtained calculations show that, copper excepted, the complexes are octahedral and for a selective separation of cations, the copper cation will be the first to be efficiently complexed.
K values, the GLDA ligand is studied in the gas phase and in solvent with the electrostatic COSMO model. In the absence of crystallographic data, most complexes prefer a pentacoordinated structure in gas phase. On the contrary, in presence of solvent the two structures can coexist, copper excepted, which does not adopt the octahedral form. Good correlations are found between the experimental thermodynamic values and several calculated parameters such as charge transfer, bond descriptors, or bonding free energy energies. The obtained calculations show that, copper excepted, the complexes are octahedral and for a selective separation of cations, the copper cation will be the first to be efficiently complexed.
Introduction
Industrial wastes contain significant amounts of heavy metals that can harm human health and threaten the ecosystem. The development of innovative technologies that respect the environment has become essential to protect them. To this end, new approaches minimizing the risks of hazardous chemicals, and in particular green chemical engineering for the extraction of heavy metals from industrial wastes must be widely developed.Chelation technology,1–4 one of the innovative research trends, has shown for a long time its potential to develop a sustainable technology for metal extraction from various metal-contaminated sites.5–15 However, the interaction mechanism of ligands with metals and the ecotoxicological risk related to the increased bioavailability of heavy metals due to the formation of metal chelate complexes (see, e.g. ref. 16–19) are yet to be satisfactory explained. Accordingly, researchers are pushed to rely on theoretical studies to interpret and strengthen experimental studies in this field.
Density Functional Theory (DFT) methods have been used for the calculation of various chelating agents to study the coordination properties of chelating agents with metal ions.20–24 Chen et al.25 showed that metal complexation process occurs as a substitution reaction of coordinated water molecules by chelating agents. Garima et al.26 studied the stability of some transition metal complexes with different chelating aminopolycarboxylic ligands: ethylenediaminetetraacetic acid (EDTA), ethylenediamine-N,N′-disuccinic acid (EDDS), Nitrilotriacetic acid (NTA) and examined the processes of desolvation and complexation to rationalize the dynamics of ligand substitution reactions. In this context, this paper focuses the L-glutamic acid N,N diacetic acid (GLDA).
GLDA, a pentadentate ligand of new generation, is one of the most important biodegradable aminopolycarboxylates (APCs) agents; this ligand has one nitrogen atom which makes it more easily biodegraded in comparison to the conventional APCs (Scheme 1).27 This ligand has no toxic effect on human health, and is known as a chelate controlling the reactivity and property of metal ions applications in different fields such as industry, domestic, and agriculture. It is utilized for the complexation of different bi- and trivalent metal ions.28,29
To the best of our knowledge, very little research has been undertaken on the complexation of any metals with the GLDA chelator30–36 and it had not yet been characterized for any ion chelation. At the same time, there is at present a need for a rational approach toward ligand design for selective complexation of metal ions in solution and for understanding the features controlling that selectivity. In light of this, the aim of the present research is to perform electronic structure calculations and chelation thermodynamics conceptualized initially by Martell37 to provide insight into the factors controlling the chelating ability of GLDA with the first row transition metal bivalent ions.
This investigation will explore how GLDA interacts with late transition metal ions, Mn2+, Fe2+, Co2+, Ni2+, Cu2+ and Zn2+. The paper is organized as follows: After a necessary description of the retained computational method, the next part will be devoted to the study of hydrated cation [M(H2O)6]2+, the third section will describe the structure and energetics of the complexed metal cations. The paper ends with some concluding remarks.
Computational method
In the present work, DFT calculations were carried out using the Amsterdam Density Functional (ADF) program developed by Baerends et al.38–40 Electron correlation was treated within a generalized gradient approximation (GGA) using the Perdew, Burke, and Ernzerhof (PBE) functional.41 Computation was performed using a triple-ζ Slater-type orbital (STO) basis set for all elements, augmented by two single-ζ polarization functions. Small frozen cores were retained for inner orbitals. Relativistic corrections were taken into account using the relativistic scalar zero-order regular approximation method (ZORA).42 Topological analysis was performed with ADF and DGrid43 using ADF's tape21 file.Two different GLDA–ion complex configurations were optimized. The first configuration is hexa-coordinated (four oxygen, one nitrogen atoms of GLDA and one water molecule) in close proximity to the cations, while the second configuration is penta-coordinated (no water molecule) (Fig. 3). Interaction energies (Eint) between GLDA and the different metal ions are calculated using the following equation:44
| Eint-complex = Ecomplex − EGLDA − EM | (1) |
It should be noted that in aqueous solution, the reaction of GLDA with the ion is considered to be a substitution reaction of water molecules of the hydrated ion by the GLDA. The chelation reaction in solution can therefore be defined as eqn (2) and (3):
| [M(H2O)6]2+ + GLDA4− → [M(GLDA)]2− + 6H2O | (2) |
| [M(H2O)6]2+ + GLDA4− → [M(GLDA)(H2O)]2− + 5H2O | (3) |
| Eint-H2O = Ewater–M − EM − 6EH2O | (4) |
Due to the competitive interactions in the GLDA-ion and H2O–ion complexes, the chelation interaction energy can be defined as:
| Ecomplex–water = Eint-complex − Eint-H2O | (5) |
Formation of the [M(H2O)6]2+ complexes
Because the complexation of the cation is obtained in solution, it is necessary to consider the hydrated cation as the reactant, and to calculate in a first step the energy of the solvation. The hydration of metal ions has been extensively studied experimentally and theoretically, as for instance in ref. 25 and 45. The nature of the coordinating sphere is usually determined by the chemical and physical properties of the central metal ion (e.g. size, charge, and electronics).For sake of simplicity, in a first step, only the first coordination sphere, with a fixed coordination number of six, has been adopted for our calculations. Despite the fact that the inclusion of a second shell of solvent is relevant to increase the precision of the hydration energies.46,47 It is surmised that neglecting the contribution of the second shell should just induce a limited underestimation of the complexation energy. The point will be discussed below (vide infra). For bivalent ions, the calculated hydration enthalpies between the single first coordination sphere only and the first and second ones together should not differ much.48,49 Optimization calculations show that these complexes are almost in octahedral symmetry. Besides, the solvation around the hydrated cluster has been implicitly described using the COSMO model.50–52 Geometric parameters are included in ESI† (Table S6).
The results gathered in Table 1 show that neglecting the second solvent shell is indeed rather crude. The hydration energy of the different cations are shifted by ca. 5 kcal mol−1 going from 6H2O to a cluster of 6 water molecules. This underlines the importance of hydrogen bonds between the water molecules of the first shell of H2O. Moreover this is slightly enhanced by a negligible shift (0.03 kcal mol−1) when going from the largest cation to the smallest (the ionic radii vary from 0.83 to 0.73 Å for Mn2+ to Ni2+, respectively,53 in agreement with the distances in Table S6 (ESI†). (The smaller the cation, the closer the water molecules, the greater the hydrogen bonds between the water molecules).
| Ionic radius53 | ΔGgasr1 | ΔGgasr2 | ΔGsolv1(M2+) | ΔGsolv2(M2+) | ΔGexp55 | Other ΔGtheor | ΔΔGsol(M2+)* | |
|---|---|---|---|---|---|---|---|---|
| *ΔΔGsolv(M2+) = ΔGsolv1(M2+) − ΔGsolv2(M2+). Ref. 25 B3LYP functional, PCM solvent model. Ref. 45 B3LYP functional, SMD solvent model. Ref. 54 B3LYP functional, COSMO solvent model. Ref.56 COSMO-B3LYP/LACV3P+/6-311G++(d,p) level. | ||||||||
| Mn | 0.830 | −257.05 | −263.61 | −441.35 | −446.19 | −427.09 | 4.84 | |
| Fe | 0.780 | −280.89 | −287.46 | −468.44 | −473.29 | −445.50 | 4.85 | |
| Co | 0.745 | −298.11 | −304.69 | −484.97 | −489.83 | −462.70 | −460.1620 | 4.86 |
| Ni | 0.690 | −326.05 | −332.64 | −508.79 | −513.66 | −481.35 | −496.9440 | 4.87 |
| −480.8120 | ||||||||
| Cu | 0.730 | −327.38 | −333.98 | −503.02 | −507.9 | −484.69 | −480.0620 | 4.88 |
| −505.4440 | ||||||||
| −509.049 | ||||||||
| −481.9051 | ||||||||
| Zn | 0.740 | −304.85 | −311.46 | −482.67 | −487.56 | −472.02 | −458.2020 | 4.89 |
| −492.5340 | ||||||||
To determine the M2+ hydration free energies, we use the thermodynamic cycles used by Bryantsev et al. for the hydration of copper(II)54 shown in Fig. 1.
 | ||
| Fig. 1 The two thermodynamic cycles used for the hydration and complexation of the metal ion. Cycle 1 with 6H2O and cycle 2 with cluster of 6 water molecules. | ||
From Fig. 1, ΔGsolv(M2+) can be expressed as two way:
 | (6) |
 | (7) |
 is the standard free energy of solvation for [M(H2O)6]2+, and ΔGsolv(H2O) is the standard free energy of solvation for (H2O). ΔG0→* = RT
is the standard free energy of solvation for [M(H2O)6]2+, and ΔGsolv(H2O) is the standard free energy of solvation for (H2O). ΔG0→* = RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ln(24.46) = 1.89 kcal mol−1 (T = 298.15 K) is the free energy change of 1 mol of gas from 1 atm (24.46 l mol−1) to its concentration in one liter liquid state. The concentrations of H2O and (H2O)6 in liquid water are 55.34 mol l−1 and 55.34/6 mol l−1, respectively. To combine the two hydration reactions presented in cycles 1 and 2 with standard free energies of solvation defined by a standard state of 1 mol l−1, a correction term must be added. In cycle 1, the correction term is the free-energy change of 6 moles of H2O gas from 55.34 mol l−1 liquid state to 1 mol l−1: −6RT
ln(24.46) = 1.89 kcal mol−1 (T = 298.15 K) is the free energy change of 1 mol of gas from 1 atm (24.46 l mol−1) to its concentration in one liter liquid state. The concentrations of H2O and (H2O)6 in liquid water are 55.34 mol l−1 and 55.34/6 mol l−1, respectively. To combine the two hydration reactions presented in cycles 1 and 2 with standard free energies of solvation defined by a standard state of 1 mol l−1, a correction term must be added. In cycle 1, the correction term is the free-energy change of 6 moles of H2O gas from 55.34 mol l−1 liquid state to 1 mol l−1: −6RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(55.34) = −2.38 × 6 = −14.3 kcal mol−1. For cycle 2, the correction term is the free-energy change of 1 mol of (H2O)6 gas from 55.34/6 mol l−1 liquid state to 1 mol l−1: −RT
ln(55.34) = −2.38 × 6 = −14.3 kcal mol−1. For cycle 2, the correction term is the free-energy change of 1 mol of (H2O)6 gas from 55.34/6 mol l−1 liquid state to 1 mol l−1: −RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(55.34/6) = −1.31 kcal mol−1 at T= 298.15 K.
ln(55.34/6) = −1.31 kcal mol−1 at T= 298.15 K.
The correction related to the free energy of 1 mol l−1 of water, as suggested by Bryantsev et al.54 leads to a significant shift in the energies (14.3 kcal mol−1) if one considers free water molecules (eqn (6)), whereas it becomes small (1.31 kcal mol−1) if one considers clusters of 6 molecules, in fact smaller than the expected accuracy of the calculation. Indeed, if one has considered an even larger cluster of water molecules (e.g. 18 molecules), the correction would have become negligible. On the other hand, the correction for the free energy change of 1 mol of gas from 1 atm to its concentration in one liter liquid state is also reduced when a cluster of 6 molecules is considered. In their calculations, Bryantsev et al.54 recommended the corrections taking into account clusters of water molecules rather free water molecules. In our case, slightly better results with eqn (6) are also obtained. Finally, the corrections of the free energy change of 1 mol of gas from 1 atm to its concentration in one liter liquid state and the hydration energy of water are rather smaller than the errors with respect to the experimental values. Looking at results from ref. 25 and 45, the better results are obtained by ref. 25, who did not take into account the correction. The relative deviation of the hydration free energy varies from 2% to 6%. This variation can be attributed to two factors, on the one hand the neglect of the second sphere of coordination and on the other hand the quality of the method used in our calculations. This precision would be acceptable as far as relative energies are concerned, but insufficient for the estimation of reliable stability constants. The importance of the hydrogen bonds between the water molecules around the [M(H2O)6]2+ cluster or within bulk water, i.e. (H2O)(H2O)6 contributes significantly to the discrepancy in the solvation energies or the underestimation of the binding energies of water clusters. Among the factors leading to the discrepancies, one can mention the nature of the exchange–correlation functional (e.g. B3LYP in ref. 54, PBE in the present work), and the poorness of dielectric continuum solvation methods to provide accurate solvation energies, in particular of water clusters. One could also argue that dispersion has not been explicitly taken into account, but it is known that hydrogen bonds in hydrogen-bond-dominated or mixed (i.e. hydrogen bond + dispersion) molecular systems are rather well taken into account by GGA functionals like PBE.57,58
Fig. 2 shows an excellent correlation (with R2 = 0.99) between the solvation energy and the ionic radius of the cation. This indicates: (a) the discrepancy in the calculated solvation energy is systematic and is related to description of the water part, as discussed later (vide infra), (b) the contribution of the cation to the solvation energy is mainly electrostatic, and therefore directly linked to the distance of the first shell water molecules to the cation, and consequently to the ionic radius of the cation: the smaller the cation, the larger solvation energy. In the case of the [Zn(H2O)6]2+ complex, the fit could be found as excellent if the ionic radius of the Zn2+ cation was fixed to 0.75 Å instead of 0.74 Å. This is reasonable because Clavaguéra et al.59 have shown that the octahedral water shell around this cation exists only under pressure (e.g. the liquid medium), so that a slightly looser Zn–O bond is reasonable. The case of Cu2+ is totally different because its H2O shell is not octahedral, as already pointed out by Bryantsev et al.;56 this will be reminded a little further (vide infra). This point will be more acute for the GLDA complexes discussed below.
 | ||
| Fig. 2 Correlations of ion solvation energy with Shannon's ionic radius48 in aqueous solution. The correlation line does not take into account Cu and Zn. The blue Zn2+ cation radius is increased by 0.01 Å with respect to the value from ref. 53. Black points for cycle 1 and red for cycle 2. | ||
Structure and energetics of the metal–ion complex geometries
To our knowledge, no crystallographic structure of GLDA complexes is available, so two geometries can be proposed: the first one depicts the coordination sphere by the nitrogen and four oxygen from the carboxylic functions, forming a square pyramid complex (A), the second one completes its coordination sphere with a water molecule leading to an octahedral structure (B). (see Fig. 3)The two structures were optimized under vacuum and in the solvent state without any constraint; the calculation did not lead to coordination 6 in gas phase. The main results are gathered in Table 2 for the two structures A and B at High spin (HS).
| M–O17 | M–O12 | M–O14 | M–O16 | M–O29 | M–N | ||
|---|---|---|---|---|---|---|---|
| Italic values indicate the values in aqueous medium (continuum COSMO model). | |||||||
| A Structure | Mn | 2.28/2.22 | 2.06/2.07 | 2.18/2.20 | 2.01/2.03 | — | 2.23/2.22 |
| Fe | 2.18/2.12 | 2.08/2.08 | 2.08/1.98 | 1.98/2.12 | — | 2.19/2.17 | |
| Co | 2.17/2.13 | 2.01/2.01 | 2.09/2.09 | 1.97/1.95 | — | 2.10/2.07 | |
| Ni | 2.15/2.08 | 2.01/2.00 | 2.08/2.08 | 1.95/1.96 | — | 2.03/2.00 | |
| Cu | 2.07/2.02 | 2.01/1.99 | 2.03/2.03 | 1.95/1.95 | — | 2.23/2.17 | |
| Zn | 2.34/2.21 | 2.00/2.00 | 2.15/2.17 | 1.93/1.95 | — | 2.11/2.09 | |
| B Structure | Mn | 2.21 | 2.14 | 2.21 | 2.08 | 2.30 | 2.27 |
| Fe | 2.11 | 2.13 | 2.09 | 2.12 | 2.24 | 2.21 | |
| Co | 2.12 | 2.08 | 2.13 | 2.02 | 2.22 | 1.94/2.11 | |
| Ni | 2.08 | 2.04 | 2.09 | 2.06 | 2.17 | 2.03 | |
| Cu | — | — | — | — | — | — | |
| Zn | 2.15 | 2.10 | 2.17 | 2.05 | 2.19 | 2.14 | |
In complex A all M–O bonds are equatorial, M–O17 presents the largest bond length in the range from 2.07 Å for Cu2+ to 2.34 Å for Zn2+ and follows the trend: Zn2+ > Mn2+ > Fe2+ > Co2+ > Ni2+ > Cu2+. The same tendency is noted for the B complexes structure, with an elongation of the M–O axial bond Table 2. (For additional information, see Tables S1, S2 and Fig. S1, ESI†). The variation of the dihedral angle O12O14O16O17 is illustrated in Fig. 4. Noted that the lowest value is observed for the nickel complexes.
As expected, the calculations performed on the complexes A presenting High Spin (HS) and Low Spin (LS) configurations show that the HS complexes A are more stable than LS by 33.9 kcal mol−1 for Mn2+, 16.84 kcal mol−1 for Fe and 1.66 kcal mol−1 for Co. This stability has a considerable influence on the distortion of the dihedral angle varying between 10 and 20 degrees. The reason stems from the electronic occupation of the HS HOMO and, to a lesser extent, the HOMO−1, with a (anti-bonding Sigma) dx2−y2 character, whereas these orbitals are empty in the LS configuration.
QTAIM analysis
In order to explore the different interactions in the studied systems, the QTAIM theory is used. These interactions are identified between atoms by bond critical points (BCP, in red in the Fig. 5 and 6) and the formation of cycles characterized by ring critical points RCP (indicated in green).60–63 As expected, the presence of BCPs visible in the Fig. 5 and 6 indicates the coordination bonded interactions and some additional intermolecular interactions in the two complexes A and B. In addition to the four rings formed by the metal and the donor atoms in the ligand and which are characterized by RCPs, we note the existence of other RCPs due to the formation of additional intermolecular interactions. The results of the topological analysis of complexes namely the values of the electron density, ρ(r), and its Laplacian, ∇2ρ(r), are collected in Tables S3 and S4, respectively, in ESI.† | ||
| Fig. 5 GLDA-ions structure B with Bond critical points (BCPs, red) and ring critical points (RCPs, green). | ||
 | ||
| Fig. 6 Bond critical points (BCPs, red) and ring critical points (RCPs, green) of GLDA-ions structure A. | ||
Analyzing the results of the tables shows that all the values of the M-ligand BCP density are less than 0.1. These values, accompanied by relatively small and positive Laplacian values ∇2ρ indicate a closed shell interaction (mainly noncovalent).64,65
The largest values of ρBCP at M–N and M–O interactions are found for complexes A and follow the trend: Mn2+ < Fe2+ < Co2+ < Ni2+ < Cu2+ > Zn2+. A good linear correlation can be noticed between the ρBCP and the bond lengths M–O and M–N (Fig. 7).
 | ||
| Fig. 7 Dependence of electron density bond critical point on the Metal ion–oxygen bond length (a and b) and Metal ion–nitrogen bond length (c and d) for structure A and B, respectively. | ||
However, the ρRCP values of the 7-member cycles (ring1) are very low, suggesting that the M–O16 interaction is unfavorable for both structures A and B. On the other hand the three ρRCP of the 5-membered cycles are stronger in the complexes A in agreement with the ρBCP of the interactions M–O and M–N. This suggests that the M–O, M–N interactions are stronger in the complexes A (Fig. 8).
Excluding the Cu and Zn complexes, a good correlation between the three ρRCP and the experimental complex formation constants20 is found. As shown in Fig. 6, the strength of the pentadentate complex formation, as measured by the formation constants, is nicely estimated by the ρRCP values. The case of Cu and Zn complexes differs just because these cations accept only tetradentate ligands, in agreement with the 17 and 18 electrons rule,66 respectively, as expected.
All complexes have additional H–H interactions, Fe2+ complexes exhibit another interatomic O15–H interaction, apparently absent in the other complexes. These H–H close contacts in the complexes are related to a kind of wrapping of the ligand around the cation, the ligand curvature enabling the interaction of the neighboring H–H atom pairs.
The ligand-to-metal charge transfer (ΔQ) upon complex formation is calculated from the difference between the formal +2 charge on the metal and its calculated charge in the complex. For the latter, the Bader charges are given in Table 3 whereas energies are given in Table 4. It is interesting to observe a high correlation between the Bader charges and the preorganization energy (defined and calculated in the next section, vide infra) (Fig. 9)
| Q A | Q B | ΔQA | ΔQB | |
|---|---|---|---|---|
| Mn2+ | 1.478 | 1.490 | 0.522 | 0.510 |
| Fe2+ | 1.377 | 1.400 | 0.623 | 0.600 |
| Co2+ | 1.261 | 1.296 | 0.739 | 0.704 |
| Ni2+ | 1.167 | 1.196 | 0.833 | 0.804 |
| Cu2+ | 1.134 | — | 0.866 | — |
| Zn2+ | 1.278 | 1.300 | 0.722 | 0.700 |
| Eqn | E stabilization | E pre-org | E int-complex | E int-H2O | E complex–water |
|---|---|---|---|---|---|
| (9) | (1) | (4) | (5) | ||
| Mn2+ | −822.80 | 89.35 | −912.15 | −306.69 | −605.46 |
| Fe2+ | −851.36 | 92.90 | −944.26 | −330.90 | −613.36 |
| Co2+ | −868.01 | 97.88 | −965.89 | −349.21 | −616.68 |
| Ni2+ | −899.21 | 99.32 | −998.53 | −380.33 | −618.20 |
| Cu2+ | −897.16 | 102.81 | −999.97 | −378.48 | −621.49 |
| Zn2+ | −872.65 | 95.51 | −968.16 | −354.78 | −613.38 |
 | ||
| Fig. 9 Correlation between ΔQ values of A structures calculated by DFT for the complexation of metal GLDA4− and the preorganization energy of ligand. | ||
Metal–ligand energies and stability
The stabilization energy of a metal–GLDA ligand complex in gas phase is calculated following eqn (1). It can be divided into a preorganization energy and the contribution arising from electronic effects. The first involves the geometrical changes of the ligand related to the preorganization and complementarity principles Epre-org,67 whereas the second is the total interaction energy between the ligand in its geometry in the complex, and the metal ion, and it corresponds to all electrostatic, polarization, and charge-transfer contributions Eint.44,68 The stabilization energy can be written as:| Estabilization = Epre-org + Eint | (8) |
According to Hay et al.,69,70 the preorganization energy is determined by the following expression:
| Epre-org = Eligand–complex − Eligand | (9) |
To understand the factors influencing the chelation energy (Ecomplex–water), i.e. the formation energy of the complex in water, the different energy terms calculated and gathered in Table 4, must be analyzed. These values give an overview of the binding of GLDA with the different ions. Note that the values for Eint-complex in the absence of water molecules (eqn (1)) are more negative than the chelation energy Ecomplex–water values. The latter are even more negative than Eint-H2O, which makes the attraction of water by the cations weaker than the attraction of GLDA4− by the ions. This evident condition is required to have a complexation by the ligand onto a hydrated cation. Overall, the trend observed in all the energy values gathered in Table 4 follows the Irving–Williams series: Mn2+ < Fe2+ < Co2+ < Ni2+ < Cu2+ > Zn2+.71,72 The charge transfer (ΔQ) is strongly related to the preorganization energy and the interaction energies of different complexes (A structure), as it can be seen in Fig. 9 and 10 respectively.
Formation of [M-GLDA]2−, metal–ligand energies, and stability
To determine the free energy for the reaction, the methodology suggested in similar studies by Chen et al.25 and Franklin et al.45 is followed. As already stated, we used six times the energy of one water molecule instead of the energy of a cluster of six water molecules. Indeed, this is just to neglect the weak interactions between the water molecules of the first shell, which are a little more distant than in water medium, because of their fixed location constrained by the octahedral shape. Indeed Chen et al.25 showed, in their study of the complexation of transition metals by EDTA, that the difference between a cluster of 6 and of 18 water molecules (inside the electrostatic continuum) is rather small (0.2–3.2%.), so that one can reasonably consider it as constant for all our studied complexes which possess a size within the same range (all belonging to the first 3d row of the periodic classification).The substitution reaction according to reactions (1) and (2) in gas phase and in solution is studied in this section. The free energies in gas phase for structure A and complexation free energies in solution for the two structures A and B are summarized in Table 5. The changes in complexation free energies of eqn (1) are calculated in analogy to the analysis of hydration reaction with the thermodynamic cycle given in Fig. S4 (ESI†). The free energies of eqn (2) are calculated directly without going through the thermodynamic cycle. As can be seen in Table 5, the complex formation process is thermodynamically favorable since the free energy changes are negative for all complexes in both solution and gas phases. This free energy decreases from left to right in a row of the periodic table. On the other hand, a good linear correlation, copper ion excepted, between free energy and ionic radius is observed (see Fig. 11). The smaller the ionic radius the greater free energy of the corresponding complex.
| ΔGgasr | ΔGsolutionr(A) | ΔGsolutionr(B) | ΔGexpa | log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K18 K18 |
|
|---|---|---|---|---|---|
a ΔGexp is derived from log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K values using equation ΔG = −2.302RT K values using equation ΔG = −2.302RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K. K.
|
|||||
| Mn | −649.93 | −78.25(−72.13) | −72.46(−66.36) | −10.33 | 7.6 |
| Fe | −657.87 | −82.50(−76.38) | −76.96(−70.86) | −11.83 | 8.7 |
| Co | −661.75 | −87.37(−81.25) | −81.37(−75.27) | −13.60 | 10.0 |
| Ni | −665.70 | −96.37(−90.25) | −93.34(−87.24) | −14.82 | 10.9 |
| Cu | −666.70 | −103.16(−97.04) | — | −17.81 | 13.1 |
| Zn | −657.80 | −92.54(−86.42) | −86.32(−80.22) | −13.60 | 10.0 |
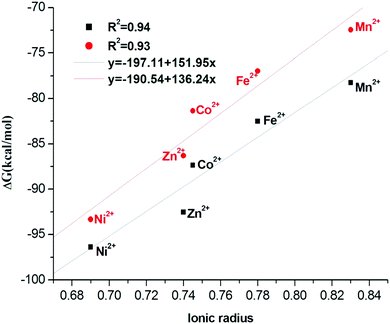 | ||
| Fig. 11 Correlations of the complexation free energy in aqueous solution with Shannon's ionic radius.53 Red points for B structure and black one for A structure. | ||
The correlation between free energy and charge transfer of complexation reaction is well established, as can be observed in Fig. 12. The greater the charge transfer between GLDA4− and the metal ions, the most negative value of ΔG of the complexation reaction. This indicates that the formation of [Cu-GLDA ]2− and [Ni-GLDA]2− in aqueous solutions is more favorable than the others.
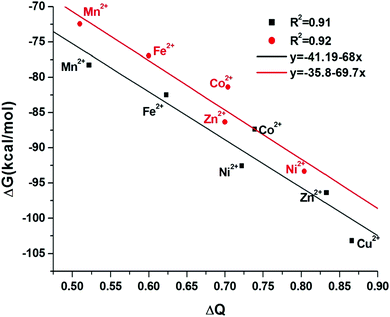 | ||
| Fig. 12 Correlations of ΔG with ΔQ in aqueous solution. Red points for B structure and black one for A structure. | ||
The values between brackets correspond to complexation free energies calculated from eqn (10) and (11).
As can be seen in Table 5, the estimation of the stability constant is overshooted by several order of magnitudes. (dozens of log units). The failure has been already underlined by Bryantsev et al. in a study of the complexation of uranyl cation by several ligands.73 The reason of this failure can be undoubtedly attributed to the poor description of the solvation of ions, particularly anions, by electrostatic continuum models. For example, the correlation of the residual error in the energy of water clusters with respect to the number of involved hydrogen bonds54 could be as large as 30 kcal/mol with the COSMO model,50 and 60 kcal mol−1 with the SM6 model74 (for 30 bonds). The feature is made smaller if error compensations may occur. In that case, good correlations may be obtained if different ligands are compared for the complexation of a given cation-the case of the complexation of uranyl cation by Bryantsev et al.,73 or the complexation of several cations by a given anion-our case of cations complexation by GLDA4−. In the first case Bryantsev et al. obtained a 0.3 factor between their calculated constants and the experimental ones.73 In our case, the correlation for the complexation of cations by [GLDA]4−, as depicted in Fig. 13, shows a similar factor amounting 2.7 leading to a range of nearly 7 log units.
 | ||
Fig. 13 Plots of calculated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K versus experimental log K versus experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K, K,  red dots for B structure and square ■ black points for A structure. Correlation for Ni, Zn and Cu red dots for B structure and square ■ black points for A structure. Correlation for Ni, Zn and Cu  , ,  green points have been obtained independently from the ones for Mn, Fe, Co. log green points have been obtained independently from the ones for Mn, Fe, Co. log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K calculated from ΔG of eqn (2) and (3). K calculated from ΔG of eqn (2) and (3). | ||
As can be seen in Fig. 13, and already underlined, the correlation of the calculated complexation constant with the experimental complexation constants is rather good. However, a huge systematic error appeared and it is too large to be related only to either the choice of the exchange–correlation functional, or/and the basis set. Indeed the solvation model used, but this is true for other models, fails to deliver correct interaction energies of molecular ions and water medium. This has been already underlined by Bryantsev et al.73 More specifically, one obtains a correlation R2= 0.99 if one considers only the Mn–Co transition elements, and Ni2+, Cu2+ and Zn2+ are a little off of the correlation line (same slope indeed, but different shift). This is not to surprise, because of the electronic configuration of these elements within the complexes (and in their solvated structure): For them, the so-called 18 electrons rule is exceeded in case of octahedral environment, due to the occupation of anti-bonding MOs involving metal 4s and 4p orbitals. The position of these cations above the correlation line corresponds to a weaker interaction energy of axial water in the solvated [M(H2O)6]2+. Nevertheless, a sixth coordination of water can be obtained, but either the involved axial water molecules may be at larger distances than the equatorial ones, or all M–O bonds should be longer. The effect is, however, off set by the smaller size of the cation when one goes from Mn to Zn (see Table S6, ESI†).
In case of the copper complex, one has a (well-known) strong Jahn–Teller effect which is responsible of the spatial structure far from a regular octahedron,75 and pushes one H2O molecule on the z axis far away from Cu with respect to the other water molecules in [Cu(H2O)6]2+, or [CuGLDA]2− (no B structure).
In case of the zinc complex, a simple VSEPR76 model already lets expect a preference to tetracoordinated species. Indeed, as it has been shown in several works, zinc can easily accept pentadentate coordination77,78 and hexadentate environment in liquid water,55 because of a low LUMO consisting of Zn 4s orbital.
Complexation by HGLDA3−
Up to now, the cation complexation by GLDA as occurring with the [GLDA]4− anion is considered. Indeed, the complexation is generally realized at a pH close to neutrality. In these conditions, the major species is the monohydrated [HGLDA]3− and one should consider the complexation reaction| [M(H2O)6]2+ + HGLDA3− → [M(GLDA)]2− + 6H2O + H+ | (10) |
| [M(H2O6)]2+ + HGLDA3− → [M(GLDA)(H2O)]2− + 5H2O + H+ | (11) |
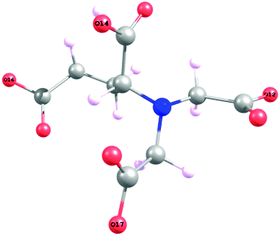
If the hydrogen in HGDLA3− is supposed to be fixed to any carboxylic function, the formation energy of the 4 isomers is calculated. The hydrogen atoms are fixed in oxygen atoms labeled O12, O14, O16, O17, see Fig. 14. As expected the hydrogen is preferentially fixed to O14 (see Table S7 in ESI:† relative energies of isomers: the O14–H bond is 1 kcal mol−1 more stable than the three other O–H bonds). However, it is known36 that the hydrogen in HGDLA3− is first fixed to the Nitrogen, and the calculated corresponding formation energy is found to be roughly larger by ca. 20 kcal mol−1 with respect to the formation energy of the hydrogenated carboxylate groups.
In a first step, one has to estimate the first acidity constant Ka4 of GLDA4−, i.e. the free energy of the reaction:
| HGLDA3− → GLDA4− + H+ | (12) |
As previously underlined, the small hydrogenated systems are poorly described by DFT, in particular within LDA or GGA approximations.80,81 The reason is the self-interaction error energy which dramatically over stabilize the systems because of an over delocalization of the electronic density. The archetype is the H2+ system, discussed twenty years ago,82 and the three centers-two electron systems.83 For instance, the calculated energies of proton solvation have been found, at the same level of calculation, equal to: −121.6 kcal mol−1 for H2O + H+ → H3O+, and −129.8 kcal mol−1 for 2 H2O + H+ →H5O2+. Similar values were obtained at higher levels of calculation.84
This is a strong effect which involves energies which, at more sophisticated level of calculations, in gas phase, are amounting 165 kcal mol−1 for H3O+,85 193 kcal mol−1 for H5O2+,86 270 kcal mol−1 for bulk water.87 Values in the same range have been obtained at DFT level.88,89 In their study of the pKa calculations of amines, Bryantsev et al.90 treated the proton solvation energy as a parameter with its value adjusted to give the best match between theory and experiment, and retained a value in the −268 kcal mol−1 and −267 kcal mol−1 range. Therefore, in the present work, an approximate hydration energy of the proton used.
The complexation energies from (Nprotonated)[HGDLA]3− are reported in Table 5 (values between brackets). Indeed, looking at the values reported in that table, and in Fig. 15 (which does not contain different physics than Fig. 13), it is important to indicate that a rather good correlation between the calculated constants and the experimental ones is obtained. The regression line provides a constant shift which is related to the solvation energy of the proton, and a slope, significantly different from unity, which is related to the solvation of the complex.
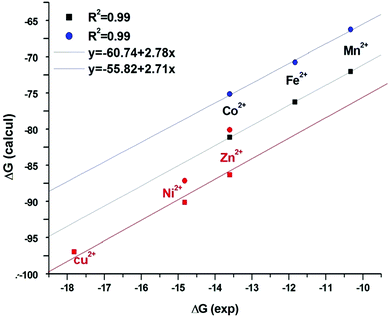 | ||
Fig. 15 Plots of calculated ΔG according to eqn (10) and (11)versus experimental ΔG, ■ black points for A structure and  blue one for B structure. Correlation for Ni, Zn and Cu points ( blue one for B structure. Correlation for Ni, Zn and Cu points ( red, A structure) have been obtained independently from the one for Mn, Fe, Co. red, A structure) have been obtained independently from the one for Mn, Fe, Co. | ||
These correlations support the use of the calculated values to predict the relative complexation energies of transition metal by GLDA, and therefore, analytical applications to selectively extract these cations from solutions.
Concluding remarks
In this paper, a series of complexes between the late transition metals of the first row in their +2 oxidation state, the GLDA4− ligand and one H2O molecule, both in gas phase and in solvent are studied. More specifically, we have been able to predict the structure and the relative stabilities of formed complexes. A correlation with available experimental thermodynamic data20 in absence of crystallographic data is found.In gas phase, most complexes prefer a pentacoordinated structure. On the contrary, in presence of solvent the two structures can coexist, copper excepted, which does not adopt the octahedral form, as expected. The charge transfer from ligands to metal ions as measured by Bader charges is controlled by the preorganization energy of the ligand, and decreases in the order of Mn2+ < Fe2+ < Co2+ < Ni2+ < Cu2+ > Zn2+ in reasonable agreement with the Irving–Williams series. A good linear correlation is found between these two quantities.
The calculated free energies are in a good agreement with the Irving–Williams series and correlate well with experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) K of complex formations. Copper complex has the most negative ΔG both in gas phase and in solvent, which indicates that its formation is much more favorable than that of other metals. The same complex has the largest binding amongst the series. This indicates that for analytic selective separations of cations, the copper cation will be the first to be efficiently complexed.
K of complex formations. Copper complex has the most negative ΔG both in gas phase and in solvent, which indicates that its formation is much more favorable than that of other metals. The same complex has the largest binding amongst the series. This indicates that for analytic selective separations of cations, the copper cation will be the first to be efficiently complexed.
This investigation has explored how GLDA interacts with late 3d transition metal ions, Mn2+, Fe2+, Co2+, Ni2+, Cu2+ and Zn2+. In a further work, such approach will be extended to predict the chelating power of GLDA of other cations.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. L. acknowledges the financial support of the Algerian Ministry of Higher Education and Scientific Research and the DGRSDT. The GENCI/CINES (Project cpt2130) and the PSMN of the ENS-Lyon are acknowledged for HPC resources/computer time.References
- L. Wang, L. Yang, Y. Li, Y. Zhang, Z. Ma and X. Ye, Chem. Eng. J., 2010, 163, 364–372 CrossRef CAS.
- E. Repo, J. K. Warchoł, A. Bhatnagar and M. Sillanpää, J. Colloid Interface Sci., 2011, 358, 261–267 CrossRef CAS PubMed.
- D. C. W. Tsang and N. R. Hartley, Environ. Sci. Pollut. Res., 2014, 21, 3987–3995 CrossRef CAS PubMed.
- D. Voglar and D. Lestan, Environ. Technol., 2014, 35, 1389–1400 CrossRef CAS PubMed.
- D. D. Sun, J. H. Tay, H. K. Cheong, D. L. K. Leung and G. R. Qian, J. Hazard. Mater., 2001, 87, 213–223 CrossRef CAS PubMed.
- D. J. Kim, D. Mishra, J. G. Ahn, G. R. Chaudhury and D. E. Ralph, J. Environ. Sci. Health, Part A: Toxic/Hazard. Subst. Environ. Eng., 2009, 44, 1585–1591 CrossRef CAS PubMed.
- D. Mishra, G. R. Chaudhury, D. J. Kim and J. G. Ahn, Hydrometallurgy, 2010, 101, 35–40 CrossRef CAS.
- A. Stark, Energy Environ. Sci., 2011, 4, 19–32 RSC.
- G. Z. Kyzas and M. Kostoglou, Materials, 2014, 7, 333–364 CrossRef PubMed.
- P. d’Abzac, F. Bordas, E. Joussein, E. D. van Hullebusch, P. N. L. Lens and G. Guibaud, Environ. Sci. Pollut. Res., 2013, 20, 4509–4519 CrossRef PubMed.
- Y. Shen, W. Li, J. Wu, S. Li, H. Luo, S. Dai and W. Wu, Dalton Trans., 2014, 43, 10023–10032 RSC.
- A. Dubey, A. Mishra and S. Singhal, Int. J. Environ. Sci. Technol., 2014, 11, 1043–1050 CrossRef CAS.
- J. M. Lee, Fluid Phase Equilib., 2012, 319, 30–36 CrossRef CAS.
- B. B. Kar, B. V. R. Murthy and V. N. Misra, Int. J. Miner. Process., 2005, 76, 143–147 CrossRef CAS.
- L. Luo, B. Wang, J. Jiang, M. Fitzgerald, Q. Huang, Z. Yu, H. Li, J. Zhang, J. Wei, C. Yang, H. Zhang, L. Dong and S. Chen, Front. Pharmacol., 2021, 11, 1–14 Search PubMed.
- H. S. S. Gazwi, E. E. Yassien and H. M. Hassan, Ecotoxicol. Environ. Saf., 2020, 192, 110297 CrossRef CAS PubMed.
- M. Costa, Toxicol. Appl. Pharmacol., 2019, 375, 1–4 CrossRef CAS PubMed.
- P. B. Tchounwou, C. G. Yedjou, A. K. Patlolla and D. J. Sutton, Molecular, clinical and environmental toxicicology Volume 3: Environmental Toxicology, 2012, vol. 101 Search PubMed.
- M. Vahter, A. Åkesson, C. Lidén, S. Ceccatelli and M. Berglund, Environ. Res., 2007, 104, 85–95 CrossRef CAS PubMed.
- D. Kołodyńska and Z. Hubicki, Ann. UMCS, Chem., 2009, 16, 227–245, DOI:10.2478/v10063-008-0017-4.
- M. Bühl, Inorg. Chem., 2005, 44, 6277–6283 CrossRef PubMed.
- H. Pesonen, R. Aksela and K. Laasonen, THEOCHEM, 2007, 804, 101–110 CrossRef CAS.
- I. Georgieva and N. Trendafilova, J. Phys. Chem. A, 2007, 111, 13075–13087 CrossRef CAS PubMed.
- H. F. T. I. Mn, T. Marino, M. Toscano and N. Russo, J. Phys. Chem. B, 2006, 24666–24673 Search PubMed.
- L. Chen, T. Liu and C. Ma, J. Phys. Chem. A, 2010, 114, 443–454 CrossRef CAS PubMed.
- G. Chauhan, M. Stein, A. Seidel-Morgenstern, K. K. Pant and K. D. P. Nigam, Chem. Eng. Sci., 2015, 137, 768–785 CrossRef CAS.
- I. S. S. Pinto, I. F. F. Neto and H. M. V. M. Soares, Environ. Sci. Pollut. Res., 2014, 21, 11893–11906 CrossRef CAS PubMed.
- Z. A. Begum, I. M. M. Rahman and H. Hasegawa, J. Mol. Liq., 2017, 242, 1123–1130 CrossRef CAS.
- Z. A. Begum, I. M. M. Rahman, Y. Tate, Y. Egawa, T. Maki and H. Hasegawa, J. Solution Chem., 2012, 41, 1713–1728 CrossRef CAS.
- Z. A. Begum, I. M. M. Rahman, T. Takase and H. Hasegawa, J. Inorg. Biochem., 2019, 195, 141–148 CrossRef CAS PubMed.
- K. Majlesi, C. Bretti, C. De Stefano, K. Majlesi, S. Sammartano and S. Zeighaminezhad, J. Solution Chem., 2018, 47, 1965–1979 CrossRef CAS.
- S. Miah, I. M. M. Rahman, M. Takemura, S. Fukiage, A. S. Mashio, T. Maki and H. Hasegawa, Talanta, 2019, 194, 980–990 CrossRef CAS PubMed.
- J. Tang, J. He, T. Liu, X. Xin and H. Hu, Chemosphere, 2017, 189, 599–608 CrossRef CAS PubMed.
- Q. Wu, Y. Cui, Q. Li and J. Sun, J. Hazard. Mater., 2015, 283, 748–754 CrossRef CAS PubMed.
- C. Bretti, K. Majlesi, C. De Stefano and S. Sammartano, J. Chem. Eng. Data, 2016, 61, 1895–1903 CAS.
- Z. A. Begum, I. M. M. Rahman, H. Sawai, Y. Tate, T. Maki and H. Hasegawa, J. Chem. Eng. Data, 2012, 57, 2723–2732 CrossRef CAS.
- R. D. Hancock and A. E. Martell, Chem. Rev., 1989, 89, 1875–1914 CrossRef CAS.
- C. Fonseca Guerra, J. G. Snijders, G. Te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391–403 Search PubMed.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- E. J. Baerends, T. Ziegler, A. J. Atkins, J. Autschbach, D. Bashford, A. Bérces, F. M. Bickelhaupt, C. Bo, P. M. Boerrigter, L. Cavallo, D. P. Chong, D. V. Chulhai, L. Deng, R. M. Dickson, J. M. Dieterich, D. E. Ellis, M. van Faassen, L. Fan, T. H. Fischer, C. Fonseca Guerra, M. Franchini, A. Ghysels, A. Giammona, S. J. A. van Gisbergen, A. W. Götz, J. A. Groeneveld, O. V. Gritsenko, M. Grüning, S. Gusarov, F. E. Harris, P. van den Hoek, C. R. Jacob, H. Jacobsen, L. Jensen, J. W. Kaminski, G. van Kessel, F. Kootstra, A. Kovalenko, M. V. Krykunov, E. van Lenthe, D. A. McCormack, A. Michalak, M. Mitoraj, S. M. Morton, J. Neugebauer, V. P. Nicu, L. Noodleman, V. P. Osinga, S. Patchkovskii, M. Pavanello, C. A. Peeples, P. H. T. Philipsen, D. Post, C. C. Pye, W. Ravenek, J. I. Rodríguez, P. Ros, R. Rüger, P. R. T. Schipper, H. van Schoot, G. Schreckenbach, J. S. Seldenthuis, M. Seth, J. G. Snijders, M. Solá, M. Swart, D. Swerhone, G. te Velde, P. Vernooijs, L. Versluis, L. Visscher, O. Visser, F. Wang, T. A. Wesolowski, E. M. van Wezenbeek, G. Wiesenekker, S. K. Wolff, T. K. Woo and A. L. Yakovlev, ADF2016.01, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, 2016, http://www.scm.com Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- E. Van Lenthe, J. Chem. Phys., 1999, 110, 8943–8953 CrossRef CAS.
- M. Kohout, DGrid, version 4.3, Radebeul Search PubMed.
- J. Z. Ramírez-Ramírez, R. Vargas, J. Garza and J. L. Gázquez, J. Phys. Chem. A, 2010, 114, 7945–7951 CrossRef PubMed.
- L. M. Franklin, S. M. Walker and G. Hill, J. Mol. Model., 2020, 26, 116, DOI:10.1007/s00894-020-04389-2.
- W. W. Rudolph, R. Mason and C. C. Pye, Phys. Chem. Chem. Phys., 2000, 2, 5030–5040 RSC.
- T. Remsungnen and B. M. Rode, J. Phys. Chem. A, 2003, 107, 2324–2328 CrossRef CAS.
- E. Makkos, A. Kerridge and N. Kaltsoyannis, Dalton Trans., 2015, 44, 11572–11581 RSC.
- M. Uudsemaa and T. Tamm, Chem. Phys. Lett., 2004, 400, 54–58 CrossRef CAS.
- A. Klamt and G. Schüürmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235 CrossRef CAS.
- A. Klamt and V. Jonas, J. Chem. Phys., 1996, 105, 9972–9981 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, A32, 751–767 CrossRef CAS.
- V. S. Bryantsev, M. S. Diallo and W. A. Goddard, J. Phys. Chem. B, 2008, 112, 9709–9719 CrossRef CAS PubMed.
- Y. Marcus, Ions in solution and their solvation, Wiley, 2015, p. 1377 Search PubMed.
- V. S. Bryantsev, M. S. Diallo, A. C. T. Van Duin and W. A. Goddard, J. Phys. Chem. A, 2008, 112, 9104–9112 CrossRef CAS PubMed.
- I. A. W. Filot, A. R. A. Palmans, P. A. J. Hilbers, R. A. Van Santen, E. A. Pidko and T. F. A. De Greef, J. Phys. Chem. B, 2010, 114, 13667–13674 CrossRef CAS PubMed.
- T. van der Wijst, C. F. Guerra, M. Swart and F. M. Bickelhaupt, Chem. Phys. Lett., 2006, 426, 415–421 CrossRef CAS.
- C. Jana, G. Ohanessian and C. Clavaguéra, Theor. Chem. Acc., 2016, 135, 141, DOI:10.1007/s00214-016-1887-8.
- C. F. Matta, J. Hernández-Trujillo, T. H. Tang and R. F. W. Bader, Chem. – Eur. J., 2003, 9, 1940–1951 CrossRef CAS PubMed.
- C. F. Matta, N. Castillo and R. J. Boyd, J. Phys. Chem. A, 2005, 109, 3669–3681 CrossRef CAS PubMed.
- S. J. Grabowski, A. Pfitzner, M. Zabel and A. T. Dubis, J. Phys. Chem. B, 2004, 108, 1831–1837 CrossRef CAS.
- A. Martín Pendás, E. Francisco, M. A. Blanco and C. Gatti, Chem. – Eur. J., 2007, 13, 9362–9371 CrossRef PubMed.
- R. F. W. Bader and H. Essén, J. Chem. Phys., 1983, 80, 1943–1960 CrossRef.
- R. G. A. Bone and R. F. W. Bader, J. Phys. Chem., 1996, 100, 10892–10911 CrossRef CAS.
- W. B. Jensen, J. Chem. Educ., 2005, 82, 28 CrossRef CAS.
- D. J. Cram, T. Kaneda, R. C. Helgeson, S. B. Brown, C. B. Knobler, E. Maverick and K. N. Trueblood, J. Chem. Inf. Model., 2013, 53, 1689–1699 CrossRef PubMed.
- Q. Wu, P. W. Ayers and Y. Zhang, J. Chem. Phys., 2009, 131, 164112 CrossRef PubMed.
- B. P. Hay and J. R. Rustad, J. Am. Chem. Soc., 1994, 116, 6316–6326 CrossRef CAS.
- B. P. Hay, D. Zhang and J. R. Rustad, Inorg. Chem., 1996, 35, 2650–2658 CrossRef CAS PubMed.
- H. Irving and R. J. P. Williams, J. Chem. Soc., 1953, 637, 3192–3210 RSC.
- H. Irving and R. J. P. Williams, Nature, 1948, 162, 746–747 CrossRef CAS.
- S. Vukovic, B. P. Hay and V. S. Bryantsev, Inorg. Chem., 2015, 54, 3995–4001 CrossRef CAS PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef CAS PubMed.
- R. Åkesson, L. G. M. Pettersson, M. Sandström and U. Wahlgren, J. Am. Chem. Soc., 1994, 116, 8691–8704 CrossRef.
- G. Keifer and F. Effenberger, Angew. Chem., Int. Ed. Engl., 1967, 6, 951–952 CrossRef.
- W. Lamine, S. Boughdiri, L. Christ, C. Morell and H. Chermette, J. Comput. Chem., 2019, 40, 717–725 CAS.
- W. Lamine, S. Boughdiri, E. Jeanneau, C. Sanglar, C. Morell, L. Christ and H. Chermette, ChemPhysChem, 2018, 19, 2938–2946 CrossRef CAS PubMed.
- AkzoNobel. Dissolvine GL Technical Brochure. 2015.
- F. Berthias, L. Feketeová, H. Chermette, V. Forquet, C. Morell, H. Abdoul-Carime, B. Farizon, M. Farizon and T. D. Märk, Chem. Phys. Chem., 2015, 16, 3151–3155 CrossRef CAS PubMed.
- H. Abdoul-Carime, F. Berthias, L. Feketeová, M. Marciante, F. Calvo, V. Forquet, H. Chermette, B. Farizon, M. Farizon and T. D. Märk, Angew. Chem., Int. Ed., 2015, 54, 14685–14689 CrossRef CAS PubMed.
- H. Chermette, I. Ciofini, F. Mariotti and C. Daul, J. Chem. Phys., 2001, 114, 1447–1453 CrossRef CAS.
- H. Chermette, I. Ciofini, F. Mariotti and C. Daul, J. Chem. Phys., 2001, 115, 11068–11079 CrossRef CAS.
- V. S. Bryantsev, M. S. Diallo, A. C. T. Van Duin and W. A. Goddard, J. Chem. Theory Comput., 2009, 5, 1016–1026 CrossRef CAS PubMed.
- S. G. Lias, J. F. Liebman and R. D. Levin, J. Phys. Chem. Ref. Data, 1984, 13, 695–808 CrossRef CAS.
- D. J. Goebbert and P. G. Wenthold, Eur. J. Mass Spectrom., 2004, 10, 837–845 CrossRef CAS PubMed.
- T. Wròblewski, L. Ziemczonek and G. P. Karwasz, Czech. J. Phys., 2004, 54, 747–752 CrossRef.
- Y. Kawai, S. Yamaguchi, Y. Okada, K. Takeuchi, Y. Yamauchi, S. Ozawa and H. Nakai, Chem. Phys. Lett., 2003, 377, 69–73 CrossRef CAS.
- H. P. Cheng, J. Phys. Chem. A, 1998, 102(31), 6201–6204 CrossRef CAS.
- V. S. Bryantsev, M. S. Diallo and W. A. Goddard, J. Phys. Chem. A, 2007, 111, 4422–4430 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Geometrical parameters topological data energies and free energy of the 5 HGLDA3− isomers, the thermodynamic cycle used for the complexation of the metal ion, dependence of DFT calculated free energy, complexation energy, preorganization energy, stabilization, energy and GLDA–metal charge transfer ΔQ on the atomic number of the late first-row transition series some properties of GLDA4−: MEPs, Dual descriptors, NPA numerical charges, Bader charges). See DOI: 10.1039/d1nj03298d |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2021 |